扩展功能
文章信息
- 高亚聪, 周晨静, 荣建
- GAO Ya-cong, ZHOU Chen-jing, RONG Jian
- 基于行程时间累积分布曲线的微观交通仿真模型参数标定
- Parameter Calibration of Microscopic Traffic Simulation Model Based on Cumulative Distribution Curve of Travel Time
- 公路交通科技, 2021, 38(4): 121-130
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 121-130
- 10.3969/j.issn.1002-0268.2021.04.015
-
文章历史
- 收稿日期: 2020-08-18
2. 北京建筑大学 土木与交通工程学院, 北京 102616
2. School of Civil and Traffic Engineering, Beijing University of Civil Engineering and Architecture, Beijing 102616, China
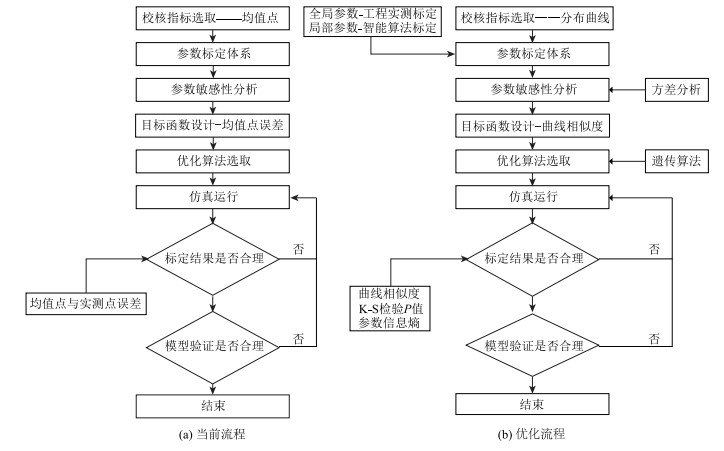
仿真模型参数标定是科学应用微观仿真技术的前提。微观交通仿真模型通常由多个子模型构成[1],包括跟驰、换道、横向运动等模型,而子模型中包含着多个参数控制着单个车辆操控行为,仿真参数标定实质即通过调整各个模型参数,使得模型输出参数与现实交通运行参数相吻合,由此来刻画出本地交通流运行特征。目前微观仿真模型参数标定已经形成相对稳定的工作流程,如图 1(a)所示[2]。在既有研究中选取一定时间段内延误、速度、排队长度等[3]指标的均值作为校核指标来对比模拟试验结果与现实场景运行结果的误差,并以此判定参数标定值是否可取是常见做法[4]。但均值点表征一段时间内交通流运行特性的集计值,难以有效核查车辆运行过程特征,致使参数标定结果存在多种组合形式[5],也降低了仿真标定模型结果的可移植性。本次研究提出以行程时间累积分布曲线作为校核事项,将校核对象由一个集计点拓展为一条分布曲线开展模型参数标定研究,刻画设施内部车流整体运行过程,以提升微观交通仿真模型参数标定工作的有效性。研究重新设计校核目标函数,吸纳最近研究成果,优化模型参数标定流程,选取信号交叉口作为仿真试验场景开展均值点标定方法的对照试验,以期验证改善方法的有效性,提高仿真模型参数标定的精度和物理解释力。
|
| 图 1 微观交通仿真模型参数标定框架 Fig. 1 Parameter calibration framework of microscopic traffic simulation model |
| |
1 仿真模型参数标定优化设计
优化校核指标取值[6]、提出全局参数工程实测获取、局部模型参数智能寻优标定[7]、明确智能算法寻优标定结果取值方法[8],在既有模型参数标定流程的基础上,我国学者也做出了一定的推进性研究[9]。本次研究融合这些成果,进一步对参数校核指标选取进行拓展,提出基于曲线标定的优化思路。具体优化流程见图 1(b),详细内容如下所述。
第一,通常校核指标选取要遵循以下规则[10]:(1)能够反映实际场景交通运行特征(2)易于实测获得。常用校核指标有行程时间、延误、排队长度、速度等,其中延误被认为是综合影响指标而得到更多应用[4]。本次研究选取实际行程时间累积分布曲线为校核对象开展仿真模型参数标定工作。
第二,在微观交通仿真模型中,模型参数可大致分为两类[11]:(1)不可控参数,即实际场景中的物理参数,分别为几何、流量和信号配时参数,用于搭建仿真场景;(2)可控参数:可调节的驾驶行为参数。本次研究将标定参数分为两类,第1类为全局参数,控制车辆运动性能,有最大加减速度、期望速度与速度关系等,通过工程实测获取[12];第2类为局部参数,控制车辆跟驰和换道行为,种类繁多,如表 1所示,在参数敏感性分析的基础上[13],通过智能算法寻优获得。由此对既有标定流程中全部参数通过智能算法寻优获得的做法进行改善。
| 序号 | 参数 | 取值范围 |
| 1 | OB_d | (150,350) |
| 2 | N_pr | (1, 5) |
| 3 | AX_average | (1, 4) |
| 4 | BX_add | (1, 5) |
| 5 | BX_mult | (1, 6) |
| 6 | ACC_max | (-6,-2) |
| 7 | ACC_ac | (-2,-0.5) |
| 8 | D | (50, 250) |
| 9 | T_dis | (20, 60) |
| 10 | GAP_min | (0.5, 5) |
| 11 | ABX | (0.1, 1) |
| 12 | CO_ac | (-5,-1) |
第三,重新设计校核目标函数。动态时间规整算法[14] (DTW)作用于时间序列长度不等两条曲线相似度的计算。研究选取行程时间累积分布曲线作为校核事项,需要对比仿真输出曲线与真实场景交通运行曲线,由此采用DTW算法计算两条分布曲线相似度来表征标定结果的效果。DTW算法详细过程如下:
假设仿真模拟行程时间和实测行程时间概率累计分布曲线的时间序列分别为A和B,他们的长度分别为n和m:
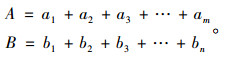
|
(1) |
DTW算法整体实现过程即按照式(1)构建A、B之间距离矩阵d(m,n),并在d(m,n)中寻找两个点之间的局部最优路径,沿着局部最优路径逐步得到两条曲线的DTW距离。以点(am,bn)为例,点(am,bn)前一个点存在3种可能,分别为:(am-1,bn),(am,bn-1),(am-1,bn-1),此时需选择距离最小点作为前面的一个点,按照上述原则依次递推,根据公式(2)和(3)最终计算出累积距离D(m,n),即两条曲线的相似度大小。
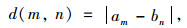
|
(2) |
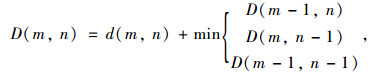
|
(3) |
式中,d为两点间距离;D为累积距离。
第四,在智能算法选取上,常用的有遗传算法、粒子群算法、模拟退火算法、天牛须算法等,不同算法运行机理不同,虽均能较好解决仿真标定问题,但在运行效率和求解精度上存在差异。文献[15]对比了智能算法解决组合优化问题的性能,综合考虑效率和精度两方面,认为遗传算法更优,因此本文选取遗传算法对仿真模型参数进行标定求解。遗传算法主要包括:编码初始化、适应度函数选择、交叉变异、迭代终止条件,详细步骤见下:
(1) 编码初始化。编码建立模型参数与校核指标之间的关系,即各模型参数(基因)在取值范围内均匀分布,各参数随机组合成参数组合方案(染色体),初始化种群规模为50。
(2) 适应度函数。仿真模型参数标定问题的适应度函数即第3步设计的校核目标函数。同时选择每代适应度最小的前10条染色体进行交叉、变异。
(3) 交叉变异。变异规则,在每代选择遗留下来的染色体基础上,各参数按照5%幅度波动,生成20条变异染色体;交叉规则,在每代选择遗留下来的染色体基础上,各参数随机组合生成30条交叉染色体。重新运行新生成的50种模型并进行适应度函数评价,若评价结果满足迭代终止条件,则停止迭代,否则继续进行交叉、变异等操作直至满足终止条件。
(4) 迭代终止条件。适应度函数评价结果逐渐趋于稳定值。
第五,经遗传算法迭代优化可确定一定误差范围内的参数集,依据优化后参数集描述仿真输出行程时间累积分布曲线,接下来需检验仿真输出行程时间分布曲线与实测值的拟合程度。Kolmogorov-Smirnov检验(K-S检验)[16]是一种非参数两样本检验方法,事先无需对曲线分布做任何假设,可用于检验仿真模拟结果与实际调查结果是否服从同一分布。除此之外,由于均值点标定方法其标定参数集存在多种取值方案[5],数据离散程度较大,与实际驾驶行为特性并不相符,因此,研究应用信息熵[17]方法对比分析两种标定方法的标定参数分布情况。K-S检验与信息熵详细介绍如下所示:
(1) K-S检验
假设X1,X2 ,X3 , …, Xm是现场实测行程时间,其累积分布曲线为F1;Y1,Y2,Y3, …, Yn是仿真模型输出行程时间,其累积分布曲线为F2。则其零假设:
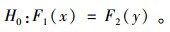
|
(4) |
其检验统计量定义如下:
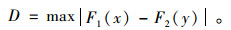
|
(5) |
若D大于在5%误差水平的测试统计量D※,则拒绝零假设,两条曲线存在显著性差异,否则认为两条曲线服从相同分布。
(2) 信息熵
信息熵可用来表征参数标定结果分布的聚集程度。假设集合D中第k类样本所占的比例为pk (k=1, 2, …|y|), 则D的信息熵为:

|
(6) |
Ent(D)值越小,参数标定结果数据集中程度越高,越符合实际交通流特性。
2 仿真模型参数标定试验按照上述优化的仿真模型参数标定流程,实测调查北京市信号交叉口相关数据,借助VISSIM搭建仿真场景,分别开展基于行程时间累计概率分布曲线标定方法和基于行程时间均值标定方法的对比试验。
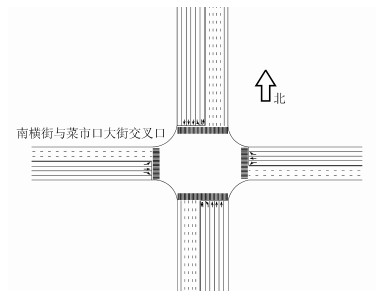
2.1 数据采集与仿真模型构建选取北京市南横街与菜市口大街交叉口作为研究对象,见图 2,南北双向10车道,东西双向6车道,车道宽度均为3.5 m。通过测距仪实测调查交叉口几何特征,同时在工作日早高峰时段(6:50—8:50)使用摄像机拍摄交叉口,并以5 min为统计间隔,分流向、车辆类型提取交通量数据,信号控制条件为周期159 s的3相位配时方案,每个相位绿灯结束后均有3 s黄灯和3 s全红时间,具体情况见图 3。
|
| 图 2 南横街与菜市口大街交叉口示意图 Fig. 2 Schematic diagram of the intersection of Street and Caishikou Road |
| |

|
| 图 3 信号交叉口配时方案 Fig. 3 Timing scheme of signalized intersection |
| |
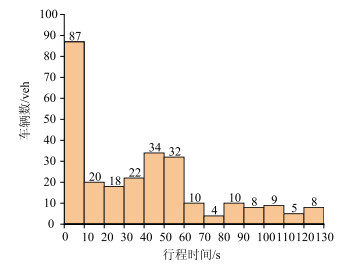
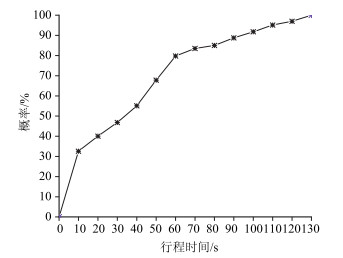
行程时间数据采集过程如图 4所示,为了排除行人、非机动车对交通流的干扰,研究选取直行车道进口道停止线向后50 m范围作为调查区域,实测车辆通过图 4蓝色区域的行程时间,具体调查方法:从车辆进入调查区域开始计时,跟踪进入调查区域的车辆,每间隔10 s统计车辆通过调查区域的时间和车辆数,统计结果如图 5所示,统计形成实测行程时间累积分布曲线如图 6所示。

|
| 图 4 行程时间采集数据区域 Fig. 4 Travel time collection data area |
| |
|
| 图 5 车辆数频数分布直方图 Fig. 5 Histogram of vehicle frequency distribution |
| |
|
| 图 6 实测行程时间累积分布曲线 Fig. 6 Probability cumulative curve of measured travel time |
| |
依据上述实际调查数据,应用VISSIM仿真软件搭建交叉口仿真场景,如图 7所示,为了更好地刻画车辆通过交叉口的运行特征,本研究设置仿真场景中的行程时间检测器区域与实际采集行程时间数据区域相匹配,仿真模型输出数据间隔为10 s。
|
| 图 7 信号交叉口仿真场景 Fig. 7 Simulation scene of signalized intersection |
| |
2.2 仿真参数标定
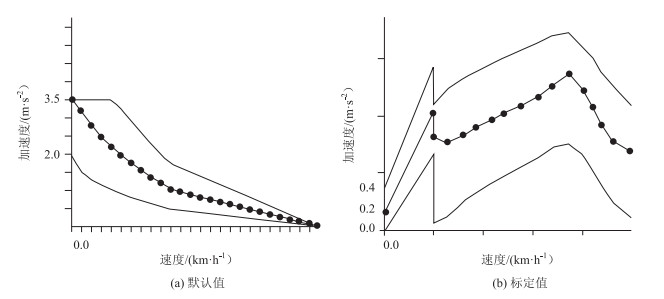
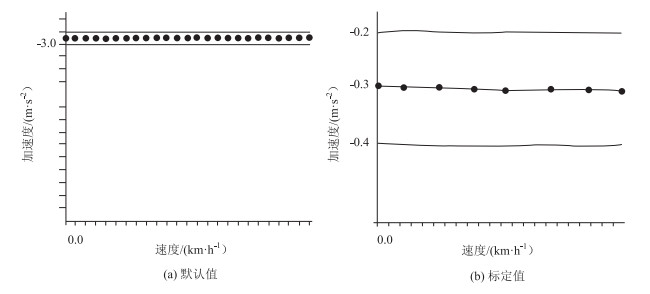
全局参数应用团队既有研究[12, 18]的工程测量结果进行设置,模型参数默认值与实测结果对比如表 2、图 8和图 9所示。
| 默认值 | 标定值 | |
| 最大加速度 | 0-3.28 | 0-2.17 |
| 最大减速度 | -3.48-0 | -2.25-0 |
|
| 图 8 期望加速度默认值与标定值对比 Fig. 8 Default desired acceleration vs calibrated value |
| |
|
| 图 9 期望减速度默认值与标定值对比 Fig. 9 Default desired deceleration vs calibrated value |
| |
对局部参数进行敏感性分析,确定标定参数为ABX、BX_add、AX_average、和BX_mult。应用VBA调用VISSIM仿真的COM接口,实现仿真参数标定自动化处理,同时结合遗传算法开展仿真参数标定试验。为排除遗传算法本身对两个对比试验的影响,研究在应用遗传算法时均设置相同条件,同时设置仿真随机种子为5种水平(40,60,80,100,120),最终曲线标定和均值标定方法参数标定结果如表 3所示。
| 方法 | 参数 | |||
| ABX | BX_add | AX_average | BX_mult | |
| 曲线标定 | 0.26 | 3.71 | 1.12 | 4.97 |
| 均值标定 | 0.98 | 4.82 | 2.97 | 4.04 |
| 默认值 | 0.60 | 3.00 | 2.00 | 2.00 |
2.3 标定结果分析
将不同方案的参数标定结果代入VISSIM仿真模型,对输出行程时间进行统计,形成的行程时间累积分布曲线如图 10所示。
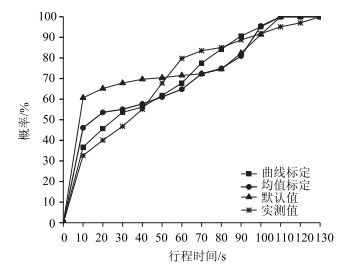
|
| 图 10 行程时间累积分布曲线 Fig. 10 Probability cumulative curve of travel time |
| |
从图 10中可以看出,仿真模拟行程时间概率累积分布的3条曲线与实测行程时间分布情况有一定差异。应用DTW算法和K-S检验方法对不同方法仿真模拟的行程时间累计分布曲线进行定量化分析,结果如表 4所示,其中曲线标定方法的相似度和P值优于均值标定和参数默认值的输出结果,表明曲线标定方法输出的行程时间累积分布曲线与实测曲线拟合程度更好,标定结果精度更高。
| 不同方法 | 相似度 | P值 |
| 曲线标定 | 0.258 | 0.999 |
| 均值标定 | 0.618 | 0.905 |
| 默认值 | 1.022 | 0.617 |
同时为进一步分析单一集计点均值标定方法的局限性,计算了不同方法行程时间分布曲线的均值,如图 11所示。
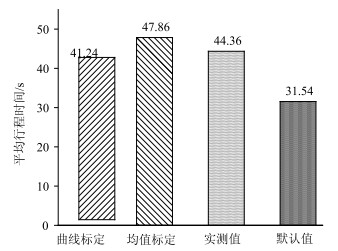
|
| 图 11 不同方法平均行程时间 Fig. 11 Average travel time of different methods |
| |
从图 10、图 11和表 4均可以看出,无论是曲线标定结果还是均值标定结果均比默认值输出行程时间均值更接近实测值,说明两种方法均能较好地解决微观交通仿真模型参数标定问题,但计算出曲线标定和均值标定与实测值的误差分别为7.03%,7.89%,两种方法与实测值误差相差并不大,说明仅用均值点去标定模型参数行程时间会存在多种分布情况,并不能刻画车辆通过交叉口的运行特征,均值标定方法多为一种组合优化问题,只考虑了模拟仿真结果与实测值的误差,并没有考虑实际车辆运行特性,因此并不能说明标定结果的有效性。
进一步对曲线标定和均值标定方法的标定参数集分布情况进行研究,对各参数归一化得到散点图如图 12~图 15所示。
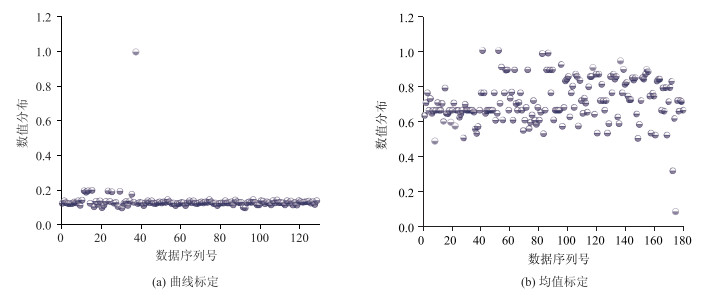
|
| 图 12 参数ABX数值分布情况 Fig. 12 Calibration result distribution diagram of ABX |
| |
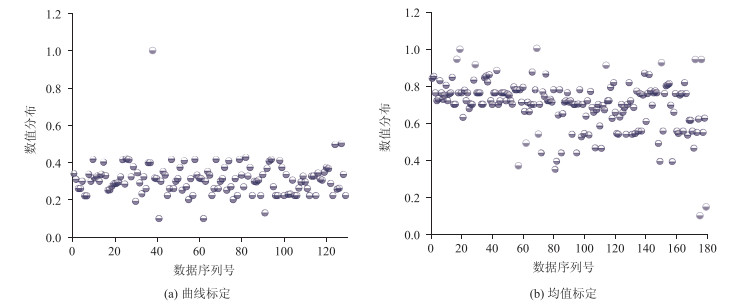
|
| 图 13 参数BX_add数值分布情况 Fig. 13 Calibration result distribution diagram of BX_add |
| |
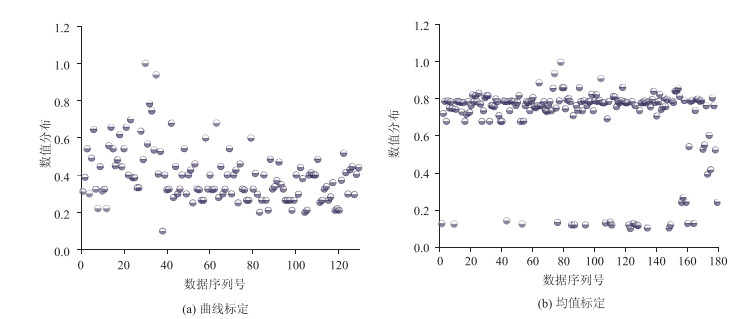
|
| 图 14 参数AX_average数值分布情况 Fig. 14 Calibration result distribution diagram of AX_average |
| |
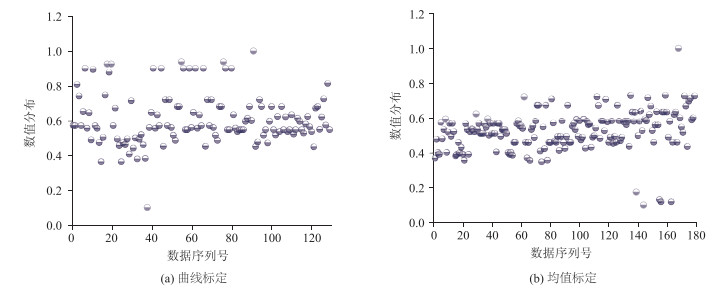
|
| 图 15 参数BX_mult数值分布情况 Fig. 15 Calibration result distribution diagram of BX_mult |
| |
从参数标定集分布情况看,曲线标定方法中各参数分布情况相对集中,数据波动程度很小,最为典型的是参数ABX和参数BX_add,两个参数归一化值基本向同一水平聚集,而均值标定方法中的各参数均向多种水平靠拢。按照公式(6),计算出各参数分布情况的信息熵结果如表 5所示。
| 不同方法 | 信息熵 | |||
| ABX | BX_add | AX_average | BX_mult | |
| 曲线标定 | 0.07 | 0.07 | 0.96 | 0.87 |
| 均值标定 | 0.95 | 1.33 | 1.24 | 0.99 |
从两种方法各参数信息熵可以看出,曲线标定方法的所有标定参数信息熵均低于均值标定方法,说明曲线标定方法的各标定参数数据分布更集中,更符合实际交通流特性,证明了曲线标定方法的有效性。
2.4 标定模型验证研究选取北京市石榴庄路与榴乡路交叉口来验证上述标定模型的有效性,即验证标定模型在此场景下的适用性。该路口是一个主-主干路相交路口,与模型参数标定过程中采集数据方法、行程时间测量区域均保持一致,搭建VISSIM仿真场景并运行仿真模型,最终行程时间模拟输出结果与实测CDF如图 16所示,DTW算法、K-S检验的计算结果如表 6所示。

|
| 图 16 行程时间累积分布曲线 Fig. 16 Probability cumulative curve of the travel time |
| |
| 不同方法 | 相似度 | P值 |
| 曲线标定 | 0.214 | 0.976 |
| 均值标定 | 0.849 | 0.873 |
| 默认值 | 1.124 | 0.568 |
从图 14和表 6中可看出,曲线标定方法与实际行程时间统计结果的相似度更小。K-S检验的P值更大,说明了曲线标定方法与实际行程时间累计分布曲线拟合程度更好,参数标定结果的可移植性更好,因此验证了曲线标定方法的合理性。
3 结论研究考虑到车辆通过交通设施的运行特征并非一个统计值可完全刻画,以易于实测获得的行程时间为基础,分别设计行程时间累积分布曲线标定和均值标定的对比试验,经遗传算法的迭代优化,提出以DTW相似度、K-S检验P值、信息熵等指标对参数标定结果进行分析,并对标定模型进行验证。主要结论如下:
(1) 曲线标定方法优于均值标定方法,标定结果更接近实际场景。对仿真模型参数标定结果进行分析发现,曲线标定方法与实测行程时间的相似度、K-S检验结果均优于均值标定和参数默认值输出结果,说明曲线标定方法不仅可以提高微观交通仿真模型参数标定工作的精度,还可有效刻画车辆通过交叉口的运行特征。
(2) 均值点标定模型参数方法并不能说明模型参数标定结果的有效性。研究分别计算曲线标定和均值标定方法的行程时间均值发现:两种方法仿真输出行程时间与实测值的误差相差并不大,但两条行程时间累积分布曲线存在差异,说明仅用均值点标定模型参数时输出的行程时间会呈现多种分布曲线,与实际交通流特性并不符合。
(3) 曲线标定方法比均值标定方法的标定参数集分布情况更集中,更符合实际驾驶行为特性。对遗传算法的标定结果进行统计发现:曲线标定方法的标定参数集分布更集中,尤为体现在参数BX_ADD和参数ABX,两个参数几乎向同一水平取值,同时定量化计算各参数的信息熵显示,曲线标定方法所有参数的信息熵均小于均值标定方法,说明了曲线标定方法的有效性。
(4) 曲线标定方法的模型验证结果更合理。分别将曲线标定和均值标定方法的参数标定结果代入新的交叉口仿真模型发现,曲线标定方法的模拟输出结果仍优于均值标定方法,因此验证了曲线标定方法的合理性。
研究过程中排除了行人、非机动车对车辆运行过程的干扰,而我国实际情况为行人、非机动车、机动车混合交通流现状,下一步将考虑行人、非机动车的干扰,继续展开曲线标定方法的适用性。
| [1] |
于泉, 王萌, 邓小惠. 基于正交试验法的单个信号交叉口仿真参数标定[J]. 公路交通科技, 2012, 29(增1): 57-63. YU Quan, WANG Meng, DENG Xiao-hui. Simulation Parameter Calibration of Single Signalized Intersection Based on Orthogonal Experiment Method[J]. Journal of Highway and Transportation Research and Development, 2012, 29(S1): 57-63. |
| [2] |
BHATTACHARYYA K, MAITRA B, MANFRED B, et al. Calibration of Micro-Simulation Model Parameters for Heterogeneous Traffic Using Mode-Specific Performance Measure[J]. Transportation Research Record: Journal of the Transportation Research Board, 2020, 2674: 135-147. |
| [3] |
杨艳芳, 秦勇. 基于SOGA的VISSIM仿真模型参数标定方法[J]. 交通运输系统工程与信息, 2017(3): 91-97. YANG Yan-fang, QIN Yong. VISSIM Model Calibration Based on SOGA[J]. Journal of Transportation Systems Engineering and Information Technology, 2017(3): 91-97. |
| [4] |
周晨静, 荣建, 郭琳科. 微观交通仿真模型参数标定结果取值方法研究[J]. 系统仿真学报, 2019, 31(12): 2802-2809. ZHOU Chen-jing, RONG Jian, GUO Lin-ke. Research on the Value Accessing Method for Calibrating Micro Traffic Simulation Model Parameters[J]. Journal of System Simulation, 2019, 31(12): 2802-2809. |
| [5] |
周晨静, 荣建, 陈春安. 面向微观交通仿真实验的模型参数敏感性分析方法[J]. 北京工业大学学报, 2016, 42(11): 1728-1733. ZHOU Chen-jing, RONG Jian, CHEN Chun-an. Parameter Sensitivity Analysis Method for Microscopic Traffic Simulation Experiment[J]. Journal of Beijing University of Technology, 2016, 42(11): 1728-1733. |
| [6] |
周晨静. 基于微观仿真的城市快速路交织区运行速度模型研究[D]. 北京: 北京工业大学, 2015. ZHOU Chen-jing. Research on the speed analysis method of urban expressway weaving area depended on microscopic simulation model[D].Beijing: Beijing University of Technology, 2015. |
| [7] |
周晨静, 高亚聪, 荣建. 微观交通仿真模型参数标定方法改善研究[J/OL]. 系统仿真学报: 1-9[2020-08-12]. http://kns.cnki.net/kcms/detail/11.3092.V.20200731.1600.004.html. ZHOU Chen-jing, GAO Ya-cong, RONG Jian. Research on the Improvement of Parameters Calibration Method of Microscopic Traffic Simulation Model[J/OL]. Journal of system simulation: 1-9[2020-08-12].http://kns.cnki.net/kcms/detail/11.3092.V.20200731.1600.004.html. |
| [8] |
姚佼, 戴亚轩, 倪屹聆, 等. 基于车辆行驶轨迹的信号交叉口排队长度估计[J]. 公路交通科技, 2020, 37(5): 123-130. YAO Jiao, DAI Ya-xuan, NI Qian-ling, et al. Estimation of Queue Length at Signalized Intersection Based on Vehicle Trajectory[J]. Journal of Highway and Transportation Research and Development, 2020, 37(5): 123-130. |
| [9] |
尹俊淞. 基于道路速度-排队长度的VISSIM参数标定建模与算法[J]. 交通运输工程与信息学报, 2019, 17(3): 144-151. YIN Jun-song. Modeling and Algorithm for Parameter Calibration in VISSIM Simulation Based on Link Speed and Queue Length[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 17(3): 144-151. |
| [10] |
孙剑, 杨晓光. 微观交通仿真模型系统参数校正研究-以VISSIM的应用为例[J]. 交通信息与安全, 2004(3): 3-6. SUN Jian, YANG Xiao-guang. Study on Parameter Calibration of Microscopic Traffic Simulation Model System-Taking the Application of Vissim as An Example[J]. Journal of Transport Information and Safety, 2004(3): 3-6. |
| [11] |
孙剑, 杨晓光, 刘好德, 等. 微观交通仿真系统参数校正研究[J]. 系统仿真学报, 2007, 19(1): 48-50, 159. SUN Jian, YANG Xiao-guang, LIU Hao-de, et al. Study on Microscopic Traffic Simulation Model Systematic Parameter Calibration[J]. Journal of System Simulation, 2007, 19(1): 48-50, 159. |
| [12] |
林子赫, 周晨静, 荣建, 等. 基于工程实测的加速度-速度参数阈值分析[J]. 交通信息与安全, 2019, 37(2): 107-113. LIN Zi-he, ZHOU Chen-jing, RONG Jian, et al. An Analysis of Acceleration-speed Parameter Threshold Based on Actual Engineering Measurement[J]. Journal of Transport Information and Safety, 2019, 37(2): 107-113. |
| [13] |
李美影. 基于改进遗传算法的微观交通仿真模型参数标定方法研究[D]. 济南: 山东大学, 2019. LI Mei-ying. Research on Parameter Calibration of Microscopic Traffic Simulation Model Based on Improved Genetic Algorithm[D].Jinan: Shandong University, 2019. |
| [14] |
YE Tian, WANG Zi-li. Self-adaptive Bearing Fault Diagnosis based on Permutation Entropy and Manifold-Based Dynamic Time Warping[J]. Mechanical Systems and Signal Processing, 2019, 114: 658-673. |
| [15] |
马敬敬, 阎朝坤, 郑金格. 九种智能算法在科学工作流调度中的应用比较[J]. 周口师范学院学报, 2018, 35(5): 90-95. MA Jing-jing, YAN Chao-kun, ZHENG Jin-ge. Analysis of Nine Intelligent Algorithms Applied to Sientific Workflow Scheduling[J]. Journal of Zhoukou Normal University, 2018, 35(5): 90-95. |
| [16] |
SRIKANTH S, MEHAR A, PARIHAR A, et al. Calibration of Vissim Model for Multilane Highways Using Speed Flow Curves[J]. The Civil Engineering Journal, 2017(3): 303-314. |
| [17] |
马静, 戴维佳. 基于AHP-信息熵决策的城市轨道建设期交通组织方案评价[J]. 长安大学学报: 自然科学版, 2020, 40(4): 101-108. MA Jing, DAI Wei-jia. Evaluating on Traffic Management During Traffic Construction of Urban Rail Based on AHO-information Entropy[J]. Journal of Chang'an University: Natural Science Edition, 2020, 40(4): 101-108. |
| [18] |
常鑫, 荣建, 周晨静, 等. 基于驾驶感受的车辆运行特性研究[J]. 交通信息与安全, 2016, 34(1): 51-56. CHANG Xin, RONG Jian, ZHOU Chen-jing, et al. Research on Vehicle Running Characteristics Based on Driver's Perception[J]. Journal of Transport Information and Safety, 2016, 34(1): 51-56. |
 2021, Vol. 38
2021, Vol. 38
