扩展功能
文章信息
- 戴学臻, 龙怡昕, 周亚男, 刘青云
- DAI Xue-zhen, LONG Yi-xin, ZHOU Ya-nan, LIU Qing-yun
- 基于综合权重和物元可拓模型的城市道路运行状态评价
- Evaluation of Urban Road Operational Status Based on Comprehensive Weight and Matter Element Extension Model
- 公路交通科技, 2021, 38(4): 112-120
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 112-120
- 10.3969/j.issn.1002-0268.2021.04.014
-
文章历史
- 收稿日期: 2020-06-03
2. 南京市城市与交通规划设计研究院 股份有限公司, 江苏 南京 210008
2. Nanjing Institute of City and Transport Planning Co., Ltd., Nanjing Jiangsu 210008, China
随着社会经济的发展,小汽车保有量逐年在增加[1],城市道路拥挤的现象也越来越明显,从而导致城市道路服务水平的下降,严重影响人们的出行。因此,科学、合理的对城市道路运行状况进行评价,可为城市道路提供规划的相关依据。
国内外学者对城市道路运行状况评价模型的研究和应用很广泛,如模糊综合评价法[2-4]、聚类分析法[5]、神经网络模型[6-7]、统计分析法[8-9]、指标评价法[10-11]等,这些方法可以取得一定的成效,但存在一定的缺陷。如统计分析法只能反映数据本身的规律,不能表现出数据的内在联系;指标评价法利用多个指标判断道路运行状态,然而忽略了指标之间的内在关联;模糊综合评价法偏向于最高和最低两极状态的研究,仅考虑了两级状态的隶属程度;聚类分析法在构建数学函数过程中,容易受到主观因素影响,导致评价结果不准确。
与其他城市道路运行状况评价方法相比,物元可拓评价方法通过物元理论确定经典域物元、节域物元、待评物元以及关联数,利用物元的可拓性进行定性分析,同时借助关联函数进行定量计算,定量化的表示评价结果[12]。其次可以将评价交通状态指标的不相容问题通过系统物元变换和结构变换方式,转换成相容问题[13-16],从而实现多目标与单目标的转换,为城市道路交通状态评价提供新思路。
1 建立指标体系根据《城市交通运行状况评价规范》[17]道路交通运行状态评价指标可以划分为基础性指标和特征性指标,其中基础性指标是以交通流3要素为基础,主要包括平均交通流量、自由流速度、平均行程速度。交通特征性指标是通过基础性指标扩展出来的,通过道路交通流数据和道路路段特征(如路段通行能力、路段长度)相结合,按照一定的准则所能表现出来的道路特征。交通特征性指标主要包括路段的饱和度、平均行程时间比、延误时间比、拥堵里程比等。
其中饱和度(V/C)可以反映道路交通流相对于道路通行能力的供需状况;延误时间比与路段的交通密度有关,可以从时间上反映道路的延误状态和车辆的相对行驶效率;平均行程速度可以表现路段所有车辆的运行速度。因此研究以饱和度、延误时间比(DTP)、平均行程车速作为评价指标。具体指标如下式所示:
(1) 饱和度(V/C)等于某一路段的实际流率与道路通行能力之比,可以反映道路交通供需状态:
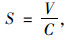
|
(1) |
式中,S为道路饱和度;V为实际交通量;C为道路通行能力。
(2) 延误时间比(DTP):

|
(2) |
式中,DTPkj为k时间段内路段j的延误时间比;tkj为k时间段内路段j内所有车辆的平均行程时间;tjf为j路段车辆在自由流状态下的行程时间;当路段内的平均行程时间小于车辆在自由流状态下的行程时间时,说明道路交通处于畅行状态,此时DTP=0;当DTP=1时,说明当路段内的平均行程时间远大于自由流状态下的行程时间时,道路处于严重拥堵状态。
(3) 平均行程车速:
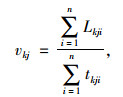
|
(3) |
式中,vkj为时间间隔k内路段j的平均行程速度;Lkji为时间间隔k内第i辆车在路段j上行驶的距离;tkji为在时间间隔k内第i辆车在路段j的行程时间;n为观测行程时间的车次数。
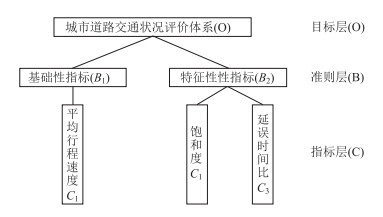
本研究从基础性指标和特征性指标2个方面选取有代表性的3个指标,构建城市道路交通运行状况评价指标体系,如图 1所示。
|
| 图 1 城市道路交通运行状况评价体系模型 Fig. 1 Urban road traffic operation status evaluation model |
| |
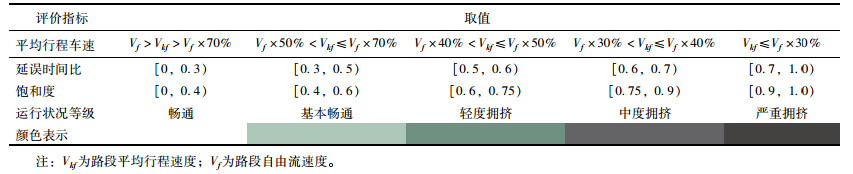
参照《城市交通运行状况评价规范》[17],将车辆平均行程车速、延误时间比和饱和度作为交通运行状况的3个评价指标,各评价指标标准如表 1所示。
2 建立物元可拓模型
设Qj是城市交通运行状况第j个评价等级,Ci是第i个评价指标,Vi是第i个评价指标的值,则构成物元R=[Q, C, V]。
2.1 构建物元可拓评价模型的经典域物元物元可拓评价模型的经典域物元矩阵Rj,可以表示为:
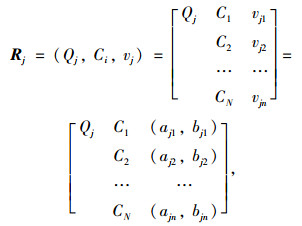
|
(4) |
式中,Qj(j=1, 2, 3, 4, 5)为评价等级;Ci(i=1, 2, 3, …, n)为评价指标;vji(aji, bji)为评价指标Ci在评价等级Qj所对应的阈值范围,即构成物元可拓评价模型的经典域。
2.2 构建物元可拓评价模型的节域物元节域物元矩阵Rp,可以表示为:

|
(5) |
式中,Rp为评价等级的全体;vpi为Ci所取的量值范围,即指城市交通的节域。
2.3 确定待评物元待评物元Ml(l=1, 2, 3, …, m)的物元矩阵RMl可以表示为:
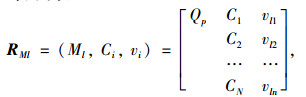
|
(6) |
式中,vli表示第l时间内Ml关于评价指标Ci的实际值,即待评时间间隔内评价指标的具体数值。
2.4 计算指标等级关联度物元可拓评价过程的关键是确定关联度,关联度反映了各评价指标与各评价等级之间的联系程度。根据可拓理论中的中距定义,选取初等关联函数计算关联度Kj(vi),计算公式为:
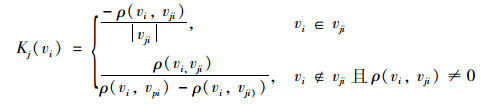
|
(7) |
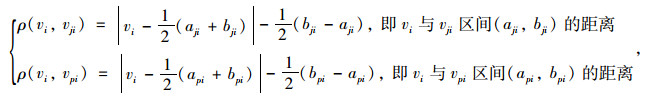
|
式中,Kj(vi)为vi的联系函数;vi为待评物元在各评价指标Ci下对应的实际量值;vji为经典域中各评价指标Ci下对应的阈值范围(aji, bji),|vji|=|aji-bji|。
为了使关联度能进行分析和比较,将计算得到的关联度Kj(vi)根据公式(8)进行规范化处理,得到关联度Kji:
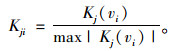
|
(8) |
在城市道路运行状态评价过程中指标权重的确定方法可按照计算方式的不同分为主观权重法和客观权重法。主观权重法通过专家主观经验及判断对影响道路的指标进行权重赋值,这类方法存在的缺点是绝对主观,缺乏对客观数据的分析,如层次分析法、三角模糊数法等;客观权重法通过采集到的数据对道路指标进行客观分析并赋予权重,这类方法的缺点是绝对客观,缺少主观经验值,如熵权法、相关系数法等。因此,研究将主观经验和基于客观数据的权重计算方法相结合,从而使指标权重与实际程度相符合,提高评价的准确性。本研究将三角模糊数法和熵权法与物元可拓评价模型结合,利用三角模糊数法经专家给出各评价指标分数进而确定主观权重,利用熵权法经各评价指标对应的数据进行计算进而确定客观权重,由二者确定评价指标的综合权重,进而采用物元可拓评价模型对城市交通运行状况进行定量评价,从而科学合理的确定城市道路的运行状况。
(1) 基于三角模糊数确定权重
① 专家评分。设第i个专家对第j个评价指标给出的评价分数为rij=[aij, bij, cij] (i=1, 2, …, n; j=1, 2, …, m)。aij为第i个专家对评价指标j影响程度给出的最保守分数;bij为第i个专家对指标j影响程度给出的最可能分数;cij为第i个专家对指标j影响程度给出的最乐观分数。
② 确定专家评价的权重集E=[e1, e2, e3, …, en],en为第n个专家给出的分数值在综合分数中所站的比例。
③ 设模糊合成矩阵T=[a1, b1, c1], [a2, b2, c2], …, [am, bm, cm];tj为合成矩阵T的第j项。
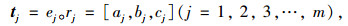
|
(9) |
式中,aj为评价指标j最保守的分数值;bj为评价指标j最可能的分数值;cj为评价指标j最乐观的分数值。“。”为模糊合成算子,研究采用加权平均型算子M(⊗, 
④ 确定三角模糊数权重。第j个评价指标的模糊得分为:
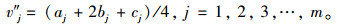
|
(10) |
设评价指标三角模糊集a=[a1, a2, a3, …, am]T,通过归一化处理得到第j个指标模糊数权重:
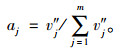
|
(11) |
(2) 基于熵权法确定权重
① 对原始评价矩阵X=(vli)m×n进行标准化处理,设yli为对各评价值vli标准化后的结果,计算公式为:
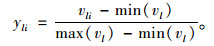
|
(12) |
② 计算评价指标Ci的熵值ei,计算公式为:
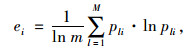
|
(13) |
式中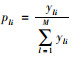
③ 计算评价指标Ci的熵权bi,且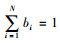
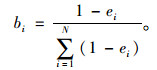
|
(14) |
即b1, b2, b3, …, bn分别为C1, C2, C3, …, CN的权重。
(3) 确定综合权重
设综合权重为w,为使综合权重wi与ai和bi尽可能接近,依据最小鉴别信息原理[19],建立目标函数:
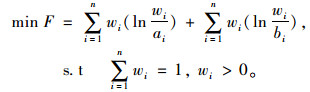
|
(15) |
采用Lagrange乘子法求解上述问题,可得
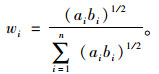
|
(16) |
根据式(16)计算评价对象各指标的综合权重。
2.6 判断评价等级根据三角模糊数法和熵权法确定的各评价指标Ci的综合权重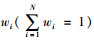
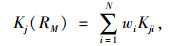
|
(17) |
式中,Kj(RM)为待评路段RM符合评价等级Nj的隶属程度。取Kj(RM)=max{Kj(RM)},则待评物元属于等级j。
3 实例分析选择陕西省西安市南二环路东段长安中路与雁塔北路之间路段为评价对象,设有3个调查站点,其中雁塔北路立交为路段起点设为调查站点1,长安路立交路段终点设为调查站点3,两个调查点之间利用摄影法记录来往车辆的牌照及通过时刻,调查点1与调查点3之间的距离为1.3 km;在长安大学彩虹桥上设置调查站点2,调查站点设置如图 2所示。

|
| 图 2 调查站点示意图 Fig. 2 Schematic diagram of survey site |
| |
在2019年1月21日(周一)16:30—17:30对该路段交通状况进行调查,通过记录调查站点1和调查站点3的车辆牌照,以5 min为一个时间间隔,从16:30—19:30划分为36个时间段,计算该路段在每个5 min内的平均行程车速,每个时间段的平均行程车速(V)如表 2所示。
| 时间段 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| V/(km·h-1) | 31.00 | 35.00 | 32.00 | 28.00 | 30.00 | 30.00 | 31.00 | 29.00 | 31.00 | 29.00 | 31.00 | 31.60 |
| 时间段 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| V/(km·h-1) | 30.40 | 28.60 | 28.90 | 30.30 | 29.10 | 30.50 | 28.78 | 27.65 | 31.37 | 26.27 | 23.32 | 9.98 |
| 时间段 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| V/(km·h-1) | 9.76 | 6.46 | 8.70 | 17.52 | 23.75 | 28.14 | 37.16 | 38.44 | 38.86 | 40.40 | 41.00 | 43.00 |
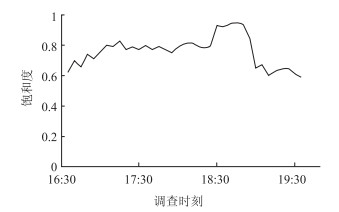
以经过调查点2的每个5 min的饱和流量计算该时刻路段饱和度,饱和度如图 3所示。
|
| 图 3 路段内饱和度变化 Fig. 3 Variation of saturation in road section |
| |
由于该路段长为1.3 km,畅行速度为70 km/h,故tjf取1.14 min,通过对比车辆通过两个调查站点的时间,可以得到该路段车辆延误时间比如表 3所示。
| 时间段 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| DTPk | 0.55 | 0.49 | 0.53 | 0.59 | 0.56 | 0.56 | 0.55 | 0.58 | 0.55 | 0.58 | 0.55 | 0.54 |
| 时间段 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| DTPk | 0.56 | 0.58 | 0.58 | 0.56 | 0.57 | 0.55 | 0.58 | 0.60 | 0.54 | 0.62 | 0.66 | 0.85 |
| 时间段 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 |
| DTPk | 0.86 | 0.91 | 0.87 | 0.74 | 0.65 | 0.59 | 0.46 | 0.44 | 0.43 | 0.41 | 0.40 | 0.37 |
3.1 构建模型
城市交通运行状况评价等级Q,评价指标C和其具体值v共同构成城市交通运行状况物元。根据表 2、表 3和图 3中数据构造1, 2, 3, 4, 5级分级标准的经典域矩阵RQ和节域矩阵RP:

|
以第一个时间间隔为例,构造待评物元矩阵R1,共36个待评物元矩阵。

|
根据式(7),利用matlab计算关联度Kj(vi),并根据式(8)规范化关联度Kj(vi),得到规范化关联度Kji,所得结果如表 4所示。
| 评价指标 | C1 | C2 | C3 | ||||||||||||||
| 编号 | k1 | k2 | k3 | k4 | k5 | k1 | k2 | k3 | k4 | k5 | k1 | k2 | k3 | k4 | k5 | ||
| 1 | -0.42 | -0.14 | 0.14 | -0.2 | -0.45 | -0.41 | -0.1 | 0.161 | -0.22 | -0.5 | -0.4 | -0.06 | 0.1 | -0.98 | -0.93 | ||
| 2 | -0.33 | 0 | 0 | -0.47 | -0.64 | -0.31 | 0.02 | -0.03 | -0.48 | -0.6 | -0.55 | -0.29 | 0.25 | -0.9 | -0.67 | ||
| 3 | -0.4 | -0.11 | 0.14 | -0.27 | -0.5 | -0.38 | -0.1 | 0.097 | -0.3 | -0.5 | -0.47 | -0.17 | 0.3 | -0.94 | -0.8 | ||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| 18 | -0.43 | -0.16 | 0.12 | -0.17 | -0.43 | -0.41 | -0.1 | 0.161 | -0.22 | -0.5 | -0.71 | -0.54 | -0.2 | -0.81 | -0.37 | ||
| 19 | -0.48 | -0.22 | 0.04 | -0.05 | -0.35 | -0.46 | -0.2 | 0.065 | -0.09 | -0.4 | -0.75 | -0.6 | -0.3 | -0.78 | -0.3 | ||
| ⋮ | … | … | … | … | … | … | … | … | … | … | … | … | … | … | … | ||
| 36 | -0.14 | 0.21 | -0.4 | -1 | -1 | -0.11 | 0.17 | -0.42 | -1 | -1 | -0.38 | -0.03 | 0.05 | -0.99 | -0.97 | ||
3.3 确定综合权重
(1) 三角模糊数法计算权重
基于城市交通运行状况评价指标,首先,选择3位专家参加本研究的评分,由专家给出各评价指标的最保守分数值、最可能分数值和最乐观分数值;3位专家给出C1分数值分别为[61,72,90],[73,80,95]和[69,85,93];C2分数值分别为[63,70,88],[65,76,90]和[68,80,95];C3分数值分别为[70,82,92],[68,79,89]和[70,85,95]。其次,根据各专家给出的分数值在综合分数中所站的比例确定权重集E=[0.29,0.37,0.34]。最后将各专家对各评价指标的分数值和权重集代入式(9)~式(11)得到各指标的三角模糊数权重为:aj=[0.332 036,0.32 1678,0.346 287]。
(2) 熵权法计算权重
根据熵权法式(12)~式(14)计算得到权重:bj=[0.326 018, 0.336 334, 0.337 648]。
(3) 确定综合权重
将aj,bj代入式(16),计算得到综合权重wj=[0.329 054, 0.328 964, 0.341 982]。
3.4 判断评价等级将计算得到的综合权重代入式(17),计算出待评路段关于平均行程速度、延误时间比和饱和度的加权关联度,取各等级中最大的关联度数值,最终得到各时间段对于等级j的关联度数值Kj(RM),如表 5所示。
| 编号 | 1级 | 2级 | 3级 | 4级 | 5级 |
| 1 | -0.415 | -0.106 | 0.133 | -0.472 | -0.618 |
| 2 | -0.403 | -0.090 | 0.075 | -0.618 | -0.647 |
| 3 | -0.425 | -0.117 | 0.180 | -0.509 | -0.608 |
| ⋮ | … | … | … | … | … |
| 17 | -0.525 | -0.271 | 0.049 | -0.356 | -0.422 |
| 18 | -0.529 | -0.278 | 0.023 | -0.402 | -0.417 |
| 19 | -0.568 | -0.341 | -0.069 | -0.314 | -0.339 |
| ⋮ | … | … | … | … | … |
| 34 | -0.282 | 0.095 | -0.110 | -0.872 | -0.876 |
| 35 | -0.279 | 0.101 | -0.112 | -0.896 | -0.883 |
| 36 | -0.223 | 0.116 | -0.243 | -0.996 | -0.989 |
表中编号表示评价各时间段,1级表示交通状态与一级服务水平的关联程度;2级表示交通状态与二级服务水平的联系程…,表中数字表示各时间编号对各等级的关联度数值。
根据表 6,基于物元可拓评价方法计算出的联系度值能够更直观地反映出与评价区间的贴近程度,如在时间段1时,各等级的联系度值中,3级的联系度值最高,说明此时车辆的运行状态最贴近3级,路段的运行状况较好。其次,物元可拓方法通过系统物元变换和结构变换,将平均行程运行速度、饱和度和延误时间比3个指标的不相容问题转换成相容问题,不再依赖单一指标确定道路状态等级,该方法最终以联系度值反映出道路状态等级,从而使得评价过程更加准确。
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 联系度值 | 0.133 | 0.075 | 0.180 | 0.278 | 0.141 | 0.056 | 0.013 | -0.032 | -0.038 | 0.002 |
| 评价等级 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 模糊等级 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 编号 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 联系度值 | 0.030 | 0.060 | -0.006 | -0.004 | -0.033 | 0.043 | 0.049 | 0.023 | -0.068 | -0.125 |
| 评价等级 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 |
| 模糊等级 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
| 编号 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 联系度值 | 0.025 | -0.099 | -0.167 | 0.258 | 0.233 | 0.157 | 0.241 | 0.137 | -0.122 | 0.098 |
| 评价等级 | 3 | 3 | 4 | 5 | 5 | 5 | 5 | 5 | 4 | 3 |
| 模糊等级 | 3 | 4 | 4 | 5 | 5 | 5 | 5 | 5 | 4 | 3 |
| 编号 | 31 | 32 | 33 | 34 | 35 | 36 | ||||
| 联系度值 | 0.044 | 0.088 | 0.071 | 0.095 | 0.100 | 0.115 | ||||
| 评价等级 | 3 | 2 | 2 | 2 | 2 | 2 | ||||
| 模糊等级 | 3 | 2 | 2 | 2 | 2 | 2 | ||||
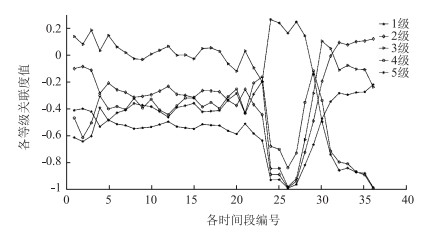
各时间段内交通状态对各等级关联度值变化状况图如图 4所示:
|
| 图 4 各时间段内交通状态对各等级关联度的变化 Fig. 4 Change of correlation of traffic state to each level in each time period |
| |
根据图 4,基于组合权重的城市交通运行状况物元可拓评价模型可以分析得到:首先在0—23时间段内,该路段3级服务水平为主,路段的运行状况较好,此时间段内路段比较畅通,但此时车辆有一定的延误;23—29时间段内,路段服务水平由3级骤降为5级,该路段在这个时间段内运行状况差,此时路段出现严重拥堵;30—32时间段内,路段服务水平由5级逐渐上升为3级,拥挤路段逐渐消散,车辆运行状况也逐渐趋于稳定;32—36时间段内,路段服务水平恢复为2级,路段交通状况趋于畅通。
根据表 4,取1—36时间段中关联度数值最大的值,得到各个时间段与各等级的联系程度,判断出各时间段的拥挤等级。为了进一步对该方法的评价结果进行对比分析,研究采用模糊综合评价法对道路交通运行状态进行评价,采用最大隶属度原则计算得到各时间段的评价等级,如表 6所示。
根据表 6可以看出,模糊综合评价法和物元可拓评价法结果的趋势基本相同。在时间20和时间22出现模糊等级大于评价等级的情况,这是因为模糊综合评价法根据最大隶属度原则只能判断出该指标值属于某个评价区间,而不能判断出指标值对评价区间临界值的贴近程度;基于物元可拓方法能反映出与评价区间临界值的贴近程度。因此,基于双重权重的物元可拓评价模型能够准确、有效地反映道路各时间段内的运行状况。
4 结论(1) 针对城市道路运行状态判别,本研究从基础性指标和特征性指标两个方面构建了城市道路运行状况评价指标体系,并根据三角模糊数法和熵权法计算了各评价指标的综合权重,提出了基于综合权重和物元可拓模型的城市道路运行状态评价。
(2) 基于综合权重和物元可拓模型的城市道路运行状况评价克服了指标权重绝对主观性和绝对客观性的缺陷,从而使指标权重与实际程度相符合,提高评价的准确性。
(3) 物元可拓模型考虑了各指标与各等级之间的联系程度、指标之间的不相容问题以及各关联度值与干扰评价区间临界值的贴近度。
(4) 以西安市南二环路东段长安中路与雁塔北路之间路段的实测数据为例,通过与模糊综合评价法对道路交通运行状态进行评价,验证了基于双重权重的物元可拓评价模型能够准确、有效地反映道路各时间段内的运行状况。
| [1] |
戴学臻, 王妍, 彭志鹏, 等. 基于双重Logistic曲线模型汽车保有量预测方法[J]. 重庆交通大学学报: 自然科学版, 2019, 38(11): 21-26. DAI Xue-zhen, WANG Yan, PENG Zhi-peng, et al. Prediction Method of Car Ownership Based on Double Logistic Curve Model[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2019, 38(11): 21-26. |
| [2] |
WANG W X, GUO R J, YU J. Research on Road Traffic Congestion Index Based on Comprehensive Parameters: Taking Dalian City as an Example[J]. Advances in Mechanical Engineering, 2018, 10(6): 16878140187848. |
| [3] |
高朝晖, 张晓春, 王遥, 等. 高速公路路段交通运行状态的模糊综合评价方法[J]. 中国矿业大学学报, 2014, 43(2): 339-344. GAO Chao-hui, ZHANG Xiao-chun, WANG Yao, et al. Evaluation of Running State for Freeway Section Based on FCE[J]. Journal of China University of Mining and Technology, 2014, 43(2): 339-344. |
| [4] |
李梅红, 孙棣华, 涂平. 基于GPS浮动车的城市主干道交通服务水平实时评估模型[J]. 交通运输工程与信息学报, 2008, 6(1): 73-78. LI Mei-hong, SUN Li-hua, TU Ping. Real-time Road Traffic Service Level Model (SLM) for Urban Arteries Based on GPS Equipped Floating Vehicles[J]. Journal of Transportation Engineering and Information, 2008, 6(1): 73-78. |
| [5] |
韦伟, 毛保华, 陈绍宽, 等. 基于时空自相关的道路交通状态聚类方法[J]. 交通运输系统工程与信息, 2016, 16(2): 57-63. WEI Wei, MAO Bao-ping, CHEN Shao-kuan, et al. Urban Traffic Status Clustering Method Based on Spatio-temporal Autocorrelation[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(2): 57-63. |
| [6] |
JAIN S, JAIN S S, JAIN G. Traffic Congestion Modelling Based on Origin and Destination[J]. Procedia Engineering, 2017, 187: 442-450. |
| [7] |
诸云, 王建宇, 杨莹, 等. 城市道路交通拥堵的模糊神经网络评析[J]. 北京理工大学学报, 2018, 38(5): 487-492. ZHU Yun, WANG Jian-yu, YANG Ying, et al. Fuzzy Evaluation of Urban Traffic Congestion Based on Neural Network[J]. Transactions of Beijing Institute of Technology, 2018, 38(5): 487-492. |
| [8] |
马亚锋, 刘澜, 骆晨. 基于累积流量比里程分布的区域交通状态评价[J]. 公路交通科技, 2019, 36(3): 152-158. MA Ya-feng, LIU Lan, LUO Chen. Evaluation of Regional Traffic Status Based on VKT Distribution of Accumulative Volume Ratio[J]. Journal of Highway and Transportation Research and Development, 2019, 36(3): 152-158. |
| [9] |
TERROSO-SAENZ F. A Cooperative Approach to Traffic Congestion Detection with Complex Event Processing and VANET[J]. IEEE Transactions on Intelligent Transportation Systems, 2012, 13(2): 914-929. |
| [10] |
LOGI F, RITCHIE S G. Development and Evaluation of a Knowledge-based System for Traffic Congestion Manangement and Contral[J]. Transportation Research Part C: Emerging Technologies, 2001, 9(6): 433-459. |
| [11] |
黄艳国, 宋二猛, 钟建新. 城市区域路网交通状态分析与评价方法[J]. 重庆交通大学学报: 自然科学版, 2017, 36(12): 91-96, 109. HUANG Yan-guo, SONG Er-meng, ZHONG Jian-xin. Analysis and Evaluation Method for Traffic State of Urban Regional Road Network[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2017, 36(12): 91-96, 109. |
| [12] |
李晓峰, 徐玖平. 基于物元与可拓集合理论的企业技术创新综合风险测度模型[J]. 中国管理科学, 2011, 19(3): 103-110. LI Xiao-feng, XU Jiu-ping. The Comprehensive Risk Measure Model of Enterprise Technological Innovation Based on Matter-element and Extension Set Theories[J]. Chinese Journal of Management Science, 2011, 19(3): 103-110. |
| [13] |
蔡文, 杨春燕, 林伟初. 可拓工程方法[M]. 北京: 科学出版社, 2000. CAI Wen, YANG Chun-yan, LIN Wei-chu. Extension Engineering Method[M]. Beijing: Science Press, 2000. |
| [14] |
崔春生, 王梦冉, 王国成. 一种基于可拓学的电子商务内容推荐算法研究[J]. 运筹与管理, 2018, 27(6): 75-81. CUI Chun-sheng, WANG Meng-ran, WANG Guo-cheng. Research on E-commerce Content-based Recommendation Based on Extension Theory[J]. Operations Research and Management Science, 2018, 27(6): 75-81. |
| [15] |
袁瑞萍, 师鸣若. 基于可拓学理论的高维大数据相似性研究[J]. 运筹与管理, 2015, 24(5): 184-188. YUAN Rui-ping, SHI Ming-ruo. Research on the Similarity of High Dimensional Big Data Based on Extenics[J]. Operations Research and Management Science, 2015, 24(5): 184-188. |
| [16] |
韩亚坤, 陈汉利. 基于层次分析-可拓学的绿色建筑节能技术经济评价[J]. 工程管理学报, 2018, 32(5): 18-23. HAN Ya-kun, CHEN Han-li. Research on the Economic Evaluation Regarding the Energy-saving Technologies of Green Buildings Based on AHP-extenics[J]. Journal of Engineering Management, 2018, 32(5): 18-23. |
| [17] |
GB/T33171-2016, 城市交通运行状况评价规范[S]. GB/T33171-2016, Specification for Urban Traffic Performance Evaluation[S]. |
| [18] |
DETILLEUX J, THERON L, BENDUIN J M. A Structural Equation Model to Evaluate Direct and Indirect Factors Associated with a Latent Measure of Mastitis in Belgian Dairy Herds[J]. Preventve Veterinary Medicine, 2012, 107(3/4): 107-179. |
| [19] |
薛希龙, 王新民, 张钦礼. 充填管道磨损风险评估的组合权重与可变模糊耦合模型[J]. 中南大学学报: 自然科学版, 2016, 47(11): 3752-3758. XUE Xi-long, WANG Xin-ming, ZHANG Qin-li. An Integrated Model of Combination Weights and Variable Fuzzy on Evaluating Backfill Pipeline Wear Risk[J]. Journal of Central South University: Science and Technology Edition, 2016, 47(11): 3752-3758. |
 2021, Vol. 38
2021, Vol. 38