扩展功能
文章信息
- 李晓娟, 刘晶鑫, 霍月英, 朱建文, 陈冰淼
- LI Xiao-juan, LIU Jing-xin, HUO Yue-ying, ZHU Jian-wen, CHEN Bing-miao
- 基于电力损耗预测的共享纯电动汽车路径优化方法
- A Route Optimization Method for Shared Pure Electric Vehicle Based on Power Loss Prediction
- 公路交通科技, 2021, 38(4): 103-111
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 103-111
- 10.3969/j.issn.1002-0268.2021.04.013
-
文章历史
- 收稿日期: 2020-11-19
2. 华东交通大学 先进材料研究院, 江西 南昌 330052
2. Institute of Advanced Materials, East China Jiaotong University, Nanchang Jiangxi 330052, China
在全世界面临能源紧张和环境污染的双重背景条件下,共享纯电动汽车以其能源结构多元化和车辆结构简单等优点以及运行理念深化可持续发展战略,已成为国内外汽车产业重点发展方向,但同时也带来了新的挑战。用户无法掌握纯电动汽车的电池消耗状况,无法更好地规划出行路径,如果车辆半路抛锚,将为用户带来一定损失。朱柏睿[1]对纯电动汽车应用现状进行宏观分析及发展纯电动汽车的策略进行深入探讨,分析纯电动汽车现状存在问题,如电力的损耗和不完善的充电桩空间覆盖水平成为当前纯电动汽车最主要的发展瓶颈。因此精确地预测车辆剩余电量,降低共享纯电动汽车用户的里程焦虑有重要的意义。国内外学者对相关问题的研究逐渐丰富。本研究以此为背景,考虑影响电量损耗的几个关键因素(外界温度、空调及暖风的使用、拥堵情况等),提前进行电量预测,为用户出行规划合理路径。
随着纯电动汽车技术的发展不断深入,对纯电动汽车剩余电量的预测估计的理论研究及方法科学性不断提高。Liu等[2]探索环境温度和车辆辅助负载对电动汽车电量的交互影响,明确不同温度和开启空调和热风对车辆电力损耗的影响。Xing等[3]结合了温度系数及模型复杂性提出了基于温度模型的SOC估算方法,考虑电池在不同环境温度下,分析了较小均方根误差的准确SOC估计。Jaguemont等[4]综述了低温对锂离子电池技术容量/功率衰减的影响。Wu等[5]通过对测试车辆的评估结果进行分析,利用所提出的模型可以成功地估计EV的瞬时功率和跳闸能量消耗,为纯电动汽车的瞬时电量的损耗分析提供分析思路。Liu等[6]使用多级混合效应线性回归模型估计电动汽车的实际能源效率, 对日本爱知县的68个使用中的电动汽车进行数据分析,揭示了每公里电量损耗的潜在相关性和非恒定性变化规律。Qiu等[7]提出一种基于模糊逻辑的再生制动策略(RBS)与系列再生制动相结合的方法,分析纯电动汽车再生制动的能量回收效率。
随着车联网+互联网模式的不断发展,不仅可以科学合理地为电动汽车规划充电路径,而且需要通过对电动汽车共享站点位置的定位,为用户规划更加合理的行进路线,并为用户提供最佳的节能模式驾驶信息。而现阶段车联网+互联网的发展模式可以为用户规划更加合理的行进路线,优化用户的驾驶出行方案,为动态路径诱导系统提供一定的理论基础与技术支持。而既有研究中大多数针对物流车辆的路径优化。庞燕等[8]对国内外车辆径路的研究现状(包括半开放式VRP、多级VRP、多目标VRP、绿色VRP等)进行了总结分析。刘长石等[9]通过分析车辆离散行驶速度和连续行驶时间的关系,研究了以所有车辆的碳排放量最小为目标,同时考虑交通拥堵因素的车辆路径问题。范厚明等[10]研究了针对客户需求且有时间窗约束的时间依赖性车辆路径问题。郭放等[11]研究了基于物流专员、配送车辆、服务对象与匹配策略共同优化的多车型电动汽车配送路径问题。针对路径优化的算法也有诸多研究,安健等[12]通过分析快速公交网络的乘客出行行为,构建了以网络平衡配流和路径优化的双层规划模型,并提出基于遗传算法和粒子群算法的混合启发式算法。叶勇等[13]针对车辆路径优化问题,设计了狼群算法,并通过与其他智能算法的对比证明其有效性及收敛速度快等优势。徐里等[14]针对带动态障碍区的自由区域路径实时优化问题,提出了一种遗传算法和滑动地平线控制的混合算法。姜彦宁等[15]针对资源共享模式下的整车物流路径优化问题,构建了以运输成本最小为目标的优化模型,并设计了遗传算法进行求解。
本研究主要解决共享纯电动汽车路径优化的问题,从用户角度出发,为用户提供相应的路径选择支持。此外,针对电动无人驾驶汽车,在车载导航设备中的径路优化方面提供一定理论基础。本研究基于电力损耗及充电桩位置等因素对共享纯电动汽车路径进行优化,在充分考虑纯电动汽车的不同温度空调使用情况下分析其电力损耗,预测车辆电量剩余,构建共享纯电动汽车的动态路径优化模型及求解算法。最后通过实际案例设计及分析,并借助VS开发平台开发了共享电动汽车多路径选择的动态路径诱导系统。
1 电力损耗分析电池的放电温度、电池参数与性能、辅助装置的能量消耗等问题都会影响共享纯电动汽车预计行驶路程。因此如何通过预测电池剩余电量,实现不同行驶环境下电量损耗情况的研究至关重要。
在所有的环境因素中,温度对电池的充放电性能影响最大,如果温度下降,电极的反应速率也下降。外界温度对电池内部进行的化学反应、电动汽车润滑油的黏度以及能量消耗率等均有影响。图 1[16]所示共享电动汽车在不同温度下放电对电池容量的影响,锂电池在0,-10,-20 ℃温度下的可用容量分别是常温环境(25 ℃)下的75%~85%、60%~70%、40%~55%,如北方车辆在低温情况下电量损耗较大,可用容量也会明显降低,可见低温对共享电动汽车电池容量的损耗明显。图 2[2]表示在行驶过程中不同环境温度对共享纯电动汽车电池性能以及开启空调和开启暖风的影响。在低温条件下,车辆开启暖风的耗电量对车辆的损耗最大;高温空调对车辆电力损耗更明显,其中与人的开车行为特性相关。在15 ℃时,总体消耗电量最低。暖风和空调冬天使用空调比夏天消耗的电量更多。

|
| 图 1 三元锂电池在不同温度下的放电曲线 Fig. 1 Discharge curves of ternary lithium battery at different temperatures |
| |

|
| 图 2 环境温度对空调、暖风、电池损耗的影响 Fig. 2 Influence of ambient temperature on air conditioning, heating and battery loss |
| |
文中的各参数设定如表 1所示:
| 参数 | 参数含义 |
| Tdrive, Tch | 车辆从起点行驶至终点的总行驶时间和快速充电时间 |
| Cdrive, Chc | 车辆从起点行驶至终点的驾驶费用和换车费用 |
| Ecost | 车辆在某一路段的行驶总电量损耗 |
| YvePC | 车辆在某一路段的平均电量损耗 |
| Srest | 车辆在通过某一路段后的剩余续驶里程 |
| pk | 充电桩的快速充电功率 |
| μfast | 共享电动汽车的充电效率 |
| Qj | 在充电站节点vj的快充电量 |
| Ldrive | 车辆在起点到终点之间的总行驶距离 |
| lij | 节点vi到vj的行驶距离 |
| tij | 节点vi到vj的路段行驶时间 |
| Cang | 为用户换乘车辆的服务费用为(7元/次) |
| xij | 0-1变量,当路段wij被占用时,标记为1,否则为0 |
| yi | 0-1变量,当节点vi被占用时,标记为1,否则为0 |
| Evj | 车辆在节点vj时的剩余电量 |
| Evjtotal | 车辆在节点vj时的总电量 |
| Eijcos t | 车辆在节点vi和vj之间的行驶损耗电量 |
| Eijtep | 车辆在节点vi和vj之间由于外界温度导致的损耗电量 |
| Eijkong | 车辆在节点vi和vj之间由于开启空调或暖风的损耗电量 |
| Eε | 最小剩余电量 |
| Etotalcar | 汽车最大充电量 |
基于出行的复杂性以及随机性,考虑到充电容量、充电方式、起始电量状态以及起始出行时间等因素,采用平均能耗方法,选取一定的行驶里程累积为例来计算剩余续驶里程[17]。
假设每行驶1 km共享电动汽车诱导系统更新一次剩余里程,其平均电量损耗按照每循环迭代5 km计算一次。每行驶1 km更新一次剩余续驶里程是为了提高显示剩余续驶里程的精度;每循环迭代5 km计算一次平均电量损耗采用5 km增强迭代灵敏度。在循环迭代过程中,根据已经行驶的里程未满5 km和已经超过5 km。采用不同的计算方法,其具体方法如下:
(1) 行驶里程未满5 km
当车辆实际行驶里程低于5 km时弥补里程(5-Sa)km。此时5 km的总电量损耗为:

|
(1) |
式中,U, I分别为电池端电压和总电流,因此该路段内平均电量损耗和剩余续驶里程由式(2)和(3)计算。
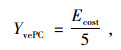
|
(2) |
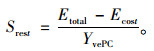
|
(3) |
(2) 行驶里程超过5 km
当实际行驶里程超过5 km时,每行驶1 km就舍弃最后1 km数据,新增最近一次1 km数据,始终保持一个最新的5 km片段数据。则已经消耗的总电量损耗和该片段消耗的电量由式(4)和(5)计算。

|
(4) |
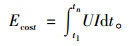
|
(5) |
因此,该时刻的平均电量和剩余续驶里程由上式(2)和(3)重复计算可得。
2 模型建立首先建立车辆行驶网络G(V, W),其中V={va, vs, vh|0≤a≤Na; 0≤s≤Ns; 0≤h≤Nh }表示路网中所有节点的集合,其中va表示路段交叉口节点,vs表示充电桩节点,vh表示换车节点。Na,Ns和Nh分别为3种节点的数量。W为路网所有弧的集合W={wij|i, j∈V}。
模型目标由式(6)所示,综合考虑距离、时间、费用等因素来选择用户出行综合费用最小的行车路径。设η为权系数1.1(元/分钟),表示用户对于时间延迟所折算的成本系数。不同用户的权系数不同,对于出行时间要求越高的用户,其权系数越大。

|
(6) |
基于以上电力损耗和电量剩余预测方法对目标函数中各参数的量化方法进行分析。
(1) 车辆行驶时间
在路径优化中,基于车辆在行驶中时间和空间的变化性,考虑实时交通路况,采用目前使用较广泛美国公路局提出的BPR路阻函数,则共享电动汽车从起点节点O行驶至终点节点D的路径行驶时间:

|
(7) |
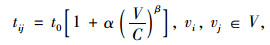
|
(8) |
式中, t0为零流量俩节点行驶时间;V为此路段交通流量;C为此路段可用通行能力。
(2) 快速充电时间
对于共享电动汽车访问充电桩节点vj,在充电站的快充电量为Qj则共享电动汽车在充电桩的快速充电时间为:
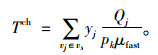
|
(9) |
(3) 车辆行驶费用
共享电动汽车的行驶费用受用车时间、行驶距离以及用车起步费用影响,其中用车时间为车辆行驶时间Tdrive,χ为共享电动汽车服务时间收费标准,δ为共享电动汽车行驶里程收费标准,则车辆的行驶费用为:

|
(10) |
式中车辆的总行驶距离为

|
(11) |
(4) 换车费用
换乘费用主要为重新使用其他车辆的起步费用,则共享电动汽车在换乘节点换乘车辆的费用为:

|
(12) |
模型的约束条件为:
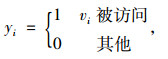
|
(13) |

|
(14) |

|
(15) |
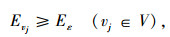
|
(16) |
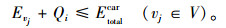
|
(17) |
约束(13)表示网络中节点是否被访问的0-1变量,若节点被访问则为1,否则为0;约束(14)表示网络中弧是否被占用,若弧两段节点均被访问,则该弧被标定为被占用,值为1,否则为0;约束(15)为不同情况下,车辆电池剩余电量的计算条件;约束(17)表示在充电桩节点快速充电过程中,电池容量不应该超出额定电池容量限制;约束(18)表示车辆在行驶中剩余电量一直不能小于该车辆可剩余的最小电量值Eε,其中Eε值可由共享电动汽车企业规定。
3 求解算法本研究在纯电动汽车行驶过程中,每途径一个节点更新一次路径信息。如果有更优的路径时或者电量不满足行驶里程时,可提醒用户切换到更优路径。每次路径更新时,采用基于动态权重值的Dijkstra算法的最短路径问题找到行最优路径。为车辆提供包括行驶路线、行车时间、充电计划等多种方案的多条最优路径。具体算法步骤如下:
Step1:确定源节点vi=1,更新车辆在该节点的当前电量Etotalvi;
Step2:更新当前路网中的路况信息、车辆行驶状态信息(是否开启空调或暖风)、充电桩及可换乘车辆信息,建立当前车辆行驶网络Gvi;
Step3:采用动态权重值的Dijkstra算法求解当前最优路径;
| 1.初始化总权重值Dis=正无穷,各节点的权重值dis[N]; 2.For i=1 to N %N=Na+Ns+Nh 3. If节点vi被标记then 4. For j=1 to N 5. If wij=1 then 6. 基于公式(15)更新当前电量; 7. If公式(16)和(17)满足then 8. 基于公式(6)计算弧wij当前权重值dij 9. If dis[i]+dij < Dis then 10. Dis= dis[i]+dij; 11. yj=1;xij=1;节点vj被标记; 12. End If 13. End If 14. End If 15. End For 16. End If 17.End For |
Step 4: 判断是否到达终点,若到达则算法结束,否则返回Step1。
4 案例分析采用C#作为开发语言,基于Microsoft Visual Studio 2017平台引入地图,在WPF(Windows Presentation Foundation)交互用户图形界面设计共享纯电动汽车路径诱导系统。以呼市绕城路1号加油站至内蒙古科技职业学院为案例进行分析,并基于文中第1节内容电量损耗关系进行电量损耗分析。表 2为某品牌共享纯电动汽车参数。规定共享电动汽车行驶完成剩余里程不低于20 km。χ为共享电动汽车服务时间收费标准,0.11元/min,δ为共享电动汽车行驶里程收费标准,0.89元/km。以呼和浩特市主干道为例,对BPR函数进行了参数α=1.002,β=2.001的重新标定[18]。
| 上市时间 | 车身型式 | 电池类型 | 耗电量[kW·h·(100 km)-1] | 电动机总功率/kW | 最大续航里程/km | 电池充电时间/min | 电池容量/(kW·h) |
| 2018/3/20 | 两厢 | 三元锂电池 | 14.6 | 30 | 150 | 快充45 | 16.5 |
利用路径诱导系统分别规划不同路径方案如图 3所示。图 3(a)为初始规划出的3种不同最短路方案及预计行驶里程和行驶时间,路径形式如图例所示。图 3(b)、(c)分别为行驶某一时刻,重新规划3种不同最短路方案。图 3(d),(e),(f)为用户在选择换车路线时的更新路径。图 3(g),(h),(i)为用户选择充电路线时的更新路径。

|
| 图 3 更新最短路径及最短备选路径图 Fig. 3 Maps of updating shortest path and shortest alternate path |
| |
为满足共享电动汽车在本案例的可实施性(1)假定共享电动汽车初始剩余里程为80 km。(2)所有案例在相同交通流量水平下计算。(3)本案例设定不同外界温度的条件。表中预测剩余里程为车辆至终点后剩余里程。不同方案得到的结果分析如表 4所示。通过对不同温度下相同初始电量行驶中损耗电量对比分析,外界温度对放置车辆电力损耗严重,尤其在北方冬季,损耗达到40%。其次车辆在行驶中的延误会增加空调或暖风的耗电。通过表 3分析,冬季对车辆的电力损耗严重,导致车辆半路抛锚概率增大,用户需寻找充电或换车节点,势必增加里程和行程时间,导致成本增加。外界温度变化和开启空调状态对成本影响主要体现在剩余里程约束下的路径改变,当电量满足约束,用户综合最小成本变动微弱,当温度下降,剩余里程不满足电量约束,路径方案改变与充电时间增加使得用户最小成本增加。表 3为不同温度的条件下共享纯电动汽车的相关行驶数据及成本分析。基于表中数据对不同温度影响下,开启空调或暖风对用户成本影响分析见图 4,对共享纯电动汽车最终电量损耗影响分析如图 5。

|
| 图 4 温度对用户最小成本的影响 Fig. 4 Influence of temperature on user's minimum cost |
| |

|
| 图 5 温度对损耗里程的影响 Fig. 5 Influence of temperature on wasted mileage |
| |
| 室外温度/℃ | 更新次数 | 初始剩余里程/km | 放电损耗里程/km | 开启空调/暖风/kW | 外界温度/(kW·h·km-1) | 路径方案选择 | 充电时间/min | 已消耗里程/km | 预测剩余里程/km | 综合最小成本/元 |
| 30 | 1 | 80 | 0 | 3.1 | 0.17 | 最短 | 0 | 0 | 32.4 | 114.8 |
| 2 | 68.9 | 最短 | 0 | 11.1 | 32.4 | |||||
| 3 | 57 | 最短 | 0 | 11.9 | 32.4 | |||||
| 15 | 1 | 80 | 1.1 | 2 | 0.13 | 最短 | 0 | 1.1 | 44.6 | 115 |
| 2 | 68.9 | 最短 | 0 | 10 | 44.6 | |||||
| 3 | 59.2 | 最短 | 0 | 10.7 | 44.6 | |||||
| 0 | 0 | 80 | 2.4 | 3 influenceof.1 | 0.20 | 最短 | 0 | 2.4 | 27.4 | 113.8 |
| 1 | 60.3 | 最短 | 0 | 17.3 | 27.4 | |||||
| 2 | 40.9 | 最短 | 0 | 19.4 | 27.4 | |||||
| -10 | 0 | 80 | 12 | 3.2 | 0.27 | 最短 | 0 | 12 | 2.7 | 131.7 |
| 1 | 65 | 充电 | 6 | 15 | 20.5 | |||||
| 2 | 44 | 最短 | 0 | 21 | 20.3 | |||||
| -25 | 0 | 80 | 25 | 3.4 | 0.35 | 最短 | 0 | 25 | -24.8 | 141 |
| 1 | 75 | 充电 | 13 | 17 | 20.5 | |||||
| 2 | 55 | 最短 | 0 | 20 | 20.5 |
| 室外温度 | 拥堵程度 | 最优路径 | 预测路径行驶时间/min | 整体消耗里程/km | 总成本/元 |
| 15 | 不拥堵 | 最短 | 55 | 35.4 | 115 |
| 15 | 拥堵 | 最短 | 65 | 37.6 | 128 |
| 15 | 非常拥堵 | 最短 | 75 | 39.8 | 141 |
| 0 | 不拥堵 | 最短 | 55 | 52.6 | 113.8 |
| 0 | 拥堵 | 最短 | 65 | 56.1 | 126.8 |
| 0 | 非常拥堵 | 充电(充电桩1) | 89 | 71.3 | 157 |
| -10 | 不拥堵 | 充电(充电桩1) | 76 | 59.3 | 135.7 |
| -10 | 拥堵 | 充电(充电桩1) | 85 | 69.8 | 154.4 |
| -10 | 非常拥堵 | 充电(充电桩1) | 97 | 81.9 | 175 |
由图 4中可得以下结论:(1)在0~30 ℃外界温度和空调开启状态满足电量约束,路径不发生改变,成本无明显变化。(2)-10 ℃开启热风导致剩余电量小于20 km,用户需改变行驶路径寻找充电或换车节点,势必增加里程和行程时间,导致成本增加。(3)关闭暖风与开启暖风都会改变路径,成本差值主要为充电时间所致。
由图 5中可得以下结论:(1)15 ℃电量损耗最小,高温与低温都会使电量损耗增加。(2)温度越低,暖风对电量损耗的影响越大。
此外,本研究对道路拥堵对车辆行驶过程的影响如表 4所示。
对于道路拥堵影响,不同的拥堵情况影响道路行驶时间,时间影响路径上的空调或者热风对于电量的损耗,所以空调或热风在不同温度下都为开启状态。在拥堵一定时间之内,不改变路径的选择。路径行驶时间和成本随着拥堵情况不断增加。拥堵导致车辆耗电量增加,当预测剩余电量不能满足电量约束,则路径诱导系统提前规划路径选择方案(充电)。所以,纯电动汽车在路径行驶中,应该考虑拥堵对于动态路径诱导的影响。
高峰时段会造成区域拥堵现象,道路特殊事件会导致路径堵塞增加路径行驶时间。拥堵对电动汽车启动耗电量与制动能量回收所造成的耗电量几乎相等,所以当路程不改变时,时间的增加只改变空调和热风对与电力的损耗。
如图 6可得: (1)相同的道路通行能力,在温度影响下电量满足剩余里程时,用户综合最小成本几乎不发生变化,当温度影响下电量不满足剩余里程约束时,用户最小成本会随着路径改变或充电时间增加而变大。(2)相同温度下,拥堵情况会增加用户出行时间和辅助设备(如空调,热风)的电量损耗,导致出行时间成本增加,从而导致用户综合最小成本增加。

|
| 图 6 不同温度及拥堵条件下的用户成本 Fig. 6 User cost under different temperatures and congestion conditions |
| |
如图 7可得:(1)相同温度下,拥堵对纯电动汽车的损耗主要为辅助设备(空调,热风)的开启时间对电量的损耗,当电量不满足剩余里程时,路径方案发生改变也会增加耗电量的增加。(2)相同道路通行能力下,温度越低,对纯电动汽车的电量损耗越明显。

|
| 图 7 不同温度及拥堵条件下的汽车电量损耗 Fig. 7 Vehicle power consumption under different temperatures and congestion conditions |
| |
5 结论
本研究通过分析共享纯电动汽车的电力损耗对出行路径的影响等,建立运行网络模型和动态最短路径优化模型及算法,使共享纯电动车系统能更好的适用于复杂交通状态。提出充电和换车最短路经的备选路径,具有更强的动态性和自适应性。得出不同外界温度、空调(暖风)的开启、路面的拥堵情况都会对车辆的电量损耗造成一定影响,甚至会改变用户的出行路径。未来可以应用于适合共享纯电动汽车的导航系统,为提高共享纯电动车出行服务质量提供了一个崭新的视角。
| [1] |
朱柏睿. 纯电动汽车应用现状分析及策略探讨[J]. 交通节能与环保, 2017, 13(6): 35-38. ZHU Bai-rui. Application Status Analysis and Strategy Discussion of Pure Electric Vehicle[J]. Energy Conservation & Environmental Protection in Transportation, 2017, 13(6): 35-38. |
| [2] |
LIU K, WANG J B, YAMAMOTO T, et al. Exploring the Interactive Effects of Ambient Temperature and Vehicle Auxiliary Loads on Electric Vehicle Energy Consumption[J]. Applied Energy, 2018, 227: 324-331. |
| [3] |
XING Y, HE W, PECHT M, et al. State of Charge Estimation of Lithium-ion Batteries Using the Open-circuit Voltage at Various Ambient Temperatures[J]. Applied Energy, 2014, 113: 106-115. |
| [4] |
JAGUEMOUT J, BOULON L, DUBÉ Y. A Comprehensive Review of Lithium-ion Batteries Used in Hybrid and Electric Vehicles at Cold Temperatures[J]. Applied Energy, 2016, 164: 99-114. |
| [5] |
WU X K, FREESE D, CABRERA A, et al. Electric Vehicles' Energy Consumption Measurement and Estimation[J]. Transportation Research Part D: Transport and Environment, 2015, 34: 52-67. |
| [6] |
LIU K, WANG J B, YAMAMOTO T, et al. Modeling the Multilevel Structure and Mixed Effects of the Factors Influencing the Energy Consumption of Electric Vehicles[J]. Applied Energy, 2016, 183: 1351-1360. |
| [7] |
QIU C, WANG G. New Evaluation Methodology of Regenerative Braking Contribution to Energy Efficiency Improvement of Electric Vehicles[J]. Energy Conversion and Management, 2016, 119: 389-398. |
| [8] |
庞燕, 罗华丽, 邢立宁, 等. 车辆路径优化问题及求解方法研究综述[J]. 控制理论与应用, 2019, 36(10): 1573-1584. PANG Yan, LUO Hua-li, XING Li-ning, et al. A Survey of Vehicle Routing Optimization Problems and Solution Methods[J]. Control Theory & Applications, 2019, 36(10): 1573-1584. |
| [9] |
刘长石, 申立智, 盛虎宜, 等. 考虑交通拥堵规避的低碳时变车辆路径问题研究[J]. 控制与决策, 2020, 35(10): 2486-2496. LIU Chang-shi, SHEN Li-zhi, SHENG Hu-yi, et al. Research on Low-carbon Time-dependent Vehicle Routing Problem with Traffic Congestion Avoidance Approaches[J]. Control and Decision, 2020, 35(10): 2486-2496. |
| [10] |
范厚明, 李荡, 孔靓, 等. 模糊需求下时间依赖型车辆路径优化[J]. 控制理论与应用, 2020, 37(5): 950-960. FAN Hou-ming, LI Dang, KONG Liang, et al. Optimization for Time Dependent Vehicle Routing Problem with Fuzzy Demand[J]. Control Theory & Applications, 2020, 37(5): 950-960. |
| [11] |
郭放, 杨珺, 杨超. 考虑差异化服务时间的多车型电动汽车路径优化与充电策略研究[J]. 中国管理科学, 2019, 27(8): 118-128. GUO Fang, YANG Jun, YANG Chao. Study on Heterogeneous Electric Vehicle Routing and Batterycharging Problem with the Consideration of Differentiated Service Cost[J]. Chinese Journal of Management Science, 2019, 27(8): 118-128. |
| [12] |
安健, 刘好德, 藤靖, 等. 快速公交路径优化设计模型及算法研究[J]. 公路交通科技, 2010, 27(3): 147-153. AN Jian, LIU Hao-de, TENG Jing, et al. Research on Model and Algorithm of BRT Route Optimal Design[J]. Journal of Highway and Transportation Research and Development, 2010, 27(3): 147-153. |
| [13] |
叶勇, 张惠珍. 求解带时间窗车辆路径问题的狼群算法[J]. 公路交通科技, 2017, 34(10): 100-107. YE Yong, ZHANG Hui-zhen. Wolf Pack Algorithm for Solving Vehicle Routing Problem with Time Windows[J]. Journal of Highway and Transportation Research and Development, 2017, 34(10): 100-107. |
| [14] |
徐里, 丁炜, 施进, 等. 带动态障碍区的自由区域路径实时优化问题的混合算法[J]. 公路交通科技, 2017, 34(11): 116-125. XU Li, DING Wei, SHI Jin, et al. A Hybrid Algorithm for Real-time Optimization of Path in Free Area with Dynamic Obstacle Area[J]. Journal of Highway and Transportation Research and Development, 2017, 34(11): 116-125. |
| [15] |
姜彦宁, 徐奇, 任晗, 等. 资源共享模式下的整车物流路径优化[J]. 公路交通科技, 2017, 34(6): 114-121. JIANG Yan-ning, XU Qi, REN Han, et al. Automobile Logistics Routing Problem Optimization under Resource Sharing Mode[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 114-121. |
| [16] |
陈德兵, 叶磊, 杨杰. 低温对纯电动汽车续驶里程的影响分析[J]. 客车技术与研究, 2012(2): 49-51. CHEN De-bing, YE Lei, YANG Jie. Analysis of Endurance Mileages of Electric Vehicle at Low Temperature[J]. Bus & Coach Technology and Research, 2012(2): 49-51. |
| [17] |
谢明维. 纯电动汽车剩余续驶里程估算研究[D]. 镇江: 江苏大学, 2016. XEI Ming-wei. Research on Estimation of Remaining Driving Range of Battery Electric Vehicle[D].Zhenjiang: Jiangsu University, 2016. |
| [18] |
刘芳, 田莉莉, 唐进君, 等. 呼和浩特市城市道路交通阻抗函数分析研究[J]. 农业装备与车辆工程, 2014, 52(5): 6-9. LIU Fang, TIAN Li-li, TANG Jin-jun, et al. Analysis on Urban Traffic Impedance Function of Hohhot City[J]. Agricultural Equipment & Vehicle Engineering,, 2014, 52(5): 6-9. |
 2021, Vol. 38
2021, Vol. 38
