扩展功能
文章信息
- 王鹏, 唐清华, 闫海青, 周涛
- WANG Peng, TANG Qing-hua, YAN Hai-qing, ZHOU Tao
- 空间缆索悬索桥吊索断裂时的强健性分析
- Analysis on Robustness of Spatial Cable Suspension Bridge with Fracture of Slings
- 公路交通科技, 2021, 38(4): 71-75, 91
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 71-75, 91
- 10.3969/j.issn.1002-0268.2021.04.009
-
文章历史
- 收稿日期: 2020-01-15
由于环境锈蚀、疲劳荷载以及人为等因素的影响,悬索桥的吊索在服役期间存在着断裂的风险。一旦某根吊索发生断裂,剩余吊索内力将会发生重分布,与原来设计值发生偏差,影响结构安全;再者吊索断裂的瞬间,考虑动力冲击效应,附件吊索内力还会瞬间放大,超过平衡状态内力,进一步增加连续断索的风险。由于吊索发生疲劳断裂,建成于1998年的新疆库尔勒孔雀河大桥,2011年4月,由于两根吊索断裂,桥面坠落,最后进行了拆除重建,造成了严重的经济损失。建成于2002年的印尼MahakamⅡ悬索桥在2011年发生倒塌,从吊索断裂到整桥倒塌全过程只有30 s,造成了巨大的损失。2019年10月,台湾省宜兰大桥第6根吊杆在靠近拱肋处首先发生断裂,其他吊杆由于内力突然增大,超出其承载能力,故由跨中向两侧依次发生破坏,最终导致大桥垮塌。
结构强健性[1]是指结构系统抵抗未曾遇见或超乎正常的环境作用的能力,当桥梁的某一构件发生破坏时,是否会影响整个结构的安全性以及结构能否继续工作是值得关注的。Ruiz-Teran[2]等通过对板式索桥拉索突然断裂的研究,发现断索响应的分析必须采用动力分析方法。孙宗光[3]通过对悬索桥加劲梁、主缆、吊索等基本构建的损伤状态模型,研究了各构件破坏对结构安全性的影响。沈锐利[4]以某在建自锚式悬索桥为例,研究了单根吊索破坏是否会引起其余吊索的连续性破坏。邱文亮[5]以某200 m的自锚式悬索桥为例,进行吊索断索后的分析,结果表明双吊索可以降低断索后的结构响应。杨世聪[6]通过研究发现,复杂空间应力下,吊索更易发生脆断。胡柏学[7]以矮寨大桥为工程背景,研究了吊索在桥梁运营期间的疲劳稳定性。袁腾文[8]以某城市中承式钢桁架拱桥为例,运用Midas/Civil软件建立桥梁仿真模型,研究了不同吊杆断裂情形下的静力响应结果。朱劲松[9]研究结果表明,越靠近跨中的吊索失效对悬索桥的冗余度影响越大。曾勇[10]以江阴大桥的吊杆为研究对象,建立了疲劳评估和疲劳损伤评定方法,得出跨中短吊杆的疲劳退化快于桥塔附近的长吊杆。徐宏[11]通过仿真计算,对钢丝锈蚀全寿命周期、各阶段经历时间所占比重进行了分析,进而对拉索的锈蚀寿命进行了近似评估。夏欢[12]模拟吊杆突然破断, 以吊杆损伤程度为参数, 研究吊杆破断对结构动力放大系数和结构需求能力比值的影响,评估吊杆发生连锁破断的风险。
1 工程背景本工程研究背景为宝塔坪特大桥,该桥跨度为800 m,主桥横桥向设2%横坡,桥面系宽21.5 m,加劲梁全宽25 m。全桥采用两根空间主缆,加劲梁上吊点横向中心距均为23.5 m,两主缆右岸散索点处横向中心距为23.5 m,左岸散索点处横向中心距为32 m,两塔顶处横向中心距为10 m。吊索纵向标准间距12 m,塔侧吊索距离主塔中心线16 m,全桥采用65对吊索。主跨梁高3.0 m,加劲梁在桥塔处设竖向支座和横向抗风支座。
主缆采用预制平行钢丝索股,每股由127根直径为5.3 mm的镀锌铝合金高强平行钢丝组成,钢丝标准抗拉强度为1 960 MPa。1#和65#端吊索由109根钢丝组成,2#~64#普通吊索由91根钢丝组成,吊索钢丝采用直径为5.0 mm的镀锌高强钢丝,钢丝标准抗拉强度为1 770 MPa。
2 有限元模拟悬索桥吊索断裂后的行为为瞬态动力响应,邻近吊索内力会在瞬间放大,甚至存在破坏的风险,因此本研究基于ANSYS有限元分析软件对宝塔坪空间缆索悬索桥吊索断裂时的强健性进行分析。ANSYS中建立结构三维有限元模型如图 1所示,其中吊杆和主缆采用link10单元模拟,使用beam4单元模拟主塔和主梁,考虑车辆荷载影响,在ANSYS中进行瞬态非线性时程分析。

|
| 图 1 有限元模型 Fig. 1 Finite element model |
| |
模拟过程中采用间接法中的构件拆除法进行计算分析,并利用瞬态动力学分析有损模型[13]。模拟“瞬时断裂”时,根据文献[14]提供的准则,确定合理的时间步长Δt=1/20f=1s,f为结构响应的最高阶频率。考虑结构阻尼的影响,悬索桥的阻尼比依据《公路悬索桥设计规范》(JTG-T D65-05—2015)[15]取0.02,参考文献[16-17],本研究取前200个振型,得出该桥的质量阻尼系数为0.016、刚度阻尼系数为0.001 7。分析过程中计入汽车活载、汽车偏载、冲击力主要荷载。
3 吊索断裂时的强健性分析 3.1 单根吊索断裂时的强健性分析为了研究不同位置单根吊索断裂后剩余吊索的受力情况,本研究在ANSYS中进行非线性瞬态动力分析时,采用杀死单元的方式依次将上游端吊索、1/4跨、1/2跨以及3/4跨的1#,17#,33#,49#,65#单根吊索杀死,分析其相邻多根吊索的内力情况。图 2为单根吊索断裂后相邻吊索的内力情况,其中无损内力为吊索断裂前的平衡静力;损伤静力为吊索断裂之后,重新完成内力重分布的平衡静力;损伤动力为吊索断裂瞬间,考虑动力效应,吊索的瞬间最大内力。
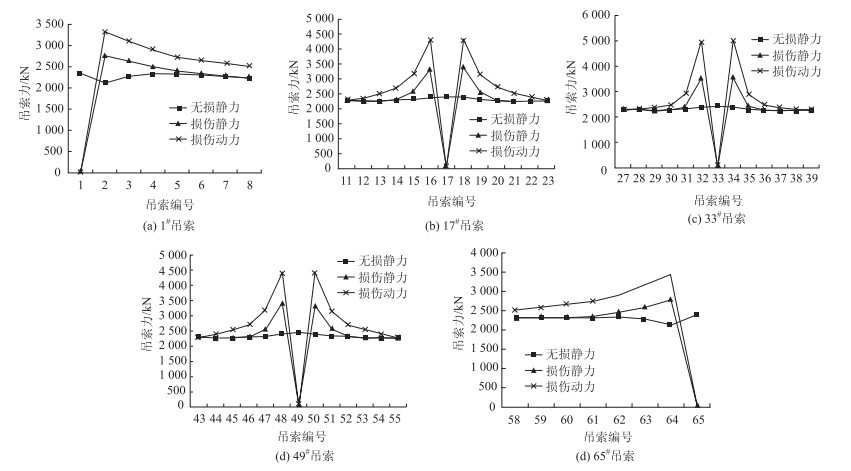
|
| 图 2 吊索断裂后相邻吊索内力 Fig. 2 Internal forces of adjacent slings after breaking |
| |
从图 2可以发现,单根吊索断裂之后,对相邻3根吊索的内力扰动较大,更远处的吊索在内力重分布平衡之后,其损伤静力变化值很小。另外,端吊索断裂时,相邻吊索内力的增幅要小于其他位置,吊索断裂位置越往跨中靠拢,其相邻的吊索损伤动力响应越大。这主要是因为在靠近桥塔位置的吊索断裂后,由于支座的竖向刚度大于主缆的竖向刚度,该片主梁荷载主要传递到桥塔横梁的支座上;而跨中吊索断裂后,该片主梁的荷载只能由相邻吊索来分担。
本研究采用文献[18]提出的评价准则,在无损伤静力及有损伤静力分析时均仅考虑恒载及汽车荷载作用,在动力损伤分析时还需要考虑动力冲击效应。对评价参数说明如下:(1)静力响应增量=损伤静力-无损伤静力;(2)动力响应增量=损伤动力-无损伤静力;(3)动力放大系数=动力响应增量/静力响应增量。从表 1中的数据可以看出,吊索断裂时,其相邻吊索的动力放大系数在2.1左右,且吊索断裂位置越往跨中靠拢,其相邻的吊索损伤动力响应越大,对结构安全影响越大。再者跨中短吊杆的疲劳退化快于桥塔附近的长吊杆,也就导致跨中吊索段断裂的概率更大,因此有必要在跨中短吊杆处设置中央扣或者采用刚性短吊杆,达到提高其强健性的目的,同时有必要加强跨中短吊索的疲劳检测频率。
| 工况 | 吊索编号 | 无损静力/kN | 损伤静力/kN | 损伤动力/kN | 动力放大系数 |
| 1#吊索断裂 | 2# | 2 116.14 | 2 773.71 | 3 314.02 | 1.82 |
| 17#吊索断裂 | 16# | 2 387.79 | 3 333.09 | 4 306.74 | 2.03 |
| 18# | 2 389.74 | 3 397.13 | 4 351.85 | 1.95 | |
| 33#吊索断裂 | 32# | 2 390.82 | 3 556.59 | 5 039.47 | 2.27 |
| 34# | 2 392.40 | 3 566.73 | 5 041.10 | 2.26 | |
| 49#吊索断裂 | 48# | 2 390.94 | 3 406.38 | 4 432.73 | 2.01 |
| 50# | 2 389.16 | 3 338.04 | 4 424.78 | 2.15 | |
| 65#吊索断裂 | 64# | 2 128.54 | 2 779.58 | 3 437.20 | 2.01 |
销接式吊索强度分项系数取2.2[15],该桥吊索设计强度标准值1 770 MPa,双肢91根直径为5.0 mm镀锌高强钢丝吊杆内力设计值为2 875.1 kN,破断力为6 326.0 kN。从表 1数据可以看出,各位置无损静力<2 875.1 kN。如果采用瞬时损伤动力作为评价标准,可以发现跨中吊索断裂时,相邻吊索的损伤动力达到5 041.1 kN,虽然还没有超过吊索的破断力,但是已经远远超过其设计强度。
3.2 多根吊索断裂时结构的强健性分析由3.1节分析可以发现,越往跨中靠拢,吊索断裂时相邻吊索的损伤动力越大。为了考虑极端情况,该节分别使跨中上下游的两根吊索或上游跨中相邻两根吊索同时断裂,分析相邻吊索的响应情况。表 2、表 3为两根吊索断裂后附近吊索的内力响应情况。从表中数据分析可以发现,跨中33#吊索处上下游两根吊索同时断裂后,附近吊索内力的响应情况与上游33#单根吊索断裂后的响应情况没有太大差别,表明上下游两幅主缆以及吊索基本是独立工作,虽然有主梁作为联系,但是相互之间影响极小。跨中上游33#,34#两根吊索断裂后,相邻32#和35#吊索的损伤静力分别达到4 831 kN和4 759 kN,远大于其设计强度2 875.1 kN;32#和35#吊索的瞬时损伤动力也分别达到7 174 kN和7 112 kN,超过吊索的破断力6 326.0 kN,断索瞬间可能导致相邻吊索发生断裂,进一步可能引起吊索依次连续断裂,最终导致整个桥破坏。
| 吊索编号 | 29 | 30 | 31 | 32 | 34 | 35 | 36 | 37 |
| 无损静力 | 2 263 | 2 283 | 2 321 | 2 391 | 2 392 | 2 320 | 2 282 | 2 264 |
| 损伤静力 | 2 234 | 2 253 | 2 427 | 3 578 | 3 588 | 2 423 | 2 250 | 2 235 |
| 损伤动力 | 2 384 | 2 471 | 2 887 | 5 007 | 5 008 | 2 876 | 2 460 | 2 377 |
| 吊索编号 | 29 | 30 | 31 | 32 | 35 | 36 | 37 | 38 |
| 无损静力 | 2 263 | 2 283 | 2 321 | 2 391 | 2 320 | 2 282 | 2 264 | 2 430 |
| 损伤静力 | 2 201 | 2 196 | 2 478 | 4 831 | 4 759 | 2 431 | 2 172 | 2 491 |
| 损伤动力 | 2 364 | 2 408 | 2 855 | 7 174 | 7 112 | 2 798 | 2 380 | 2 594 |
图 3展示了跨中32#吊索在33#单根吊索断裂以及33#,34#相邻两根吊索断裂时的内力响应时程曲线。从中可以发现,吊索断裂后,相邻的32#吊索内力迅速增加,并且在稳定后的损伤静力值附近按照特定频率简谐振动,内力振动持续的时间不长,在结构阻尼的影响下,大约在3~5 s后逐渐趋于损伤静力值。也就意味着吊索断裂后,相邻吊索在3~5 s内按照新的平衡状态完成内力重分布。
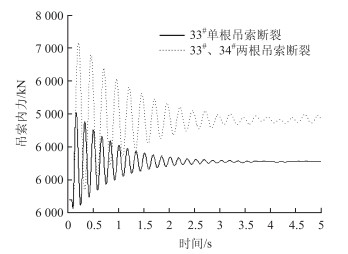
|
| 图 3 32#吊索内力响应时程曲线 Fig. 3 Time history curves of internal force response of sling No.32 |
| |
4 结论
本研究依托宝塔坪大桥,分别考虑单根或者多根吊索断裂,在ANSYS中进行瞬态非线性动力时程分析,研究空间缆索悬索桥吊索断裂时的强健性。本研究主要结论如下:
(1) 单根吊索断裂时,对相邻3根吊索的内力扰动较大,更远处的吊索在内力重分布平衡之后,其损伤静力变化值很小。
(2) 吊索断裂位置越往跨中靠拢,相邻的吊索损伤动力响应越大,结构安全风险也就越大,强健性越低。
(3) 跨中同侧连续两根吊索同时断裂时,相邻的吊索损伤动力超过吊索的破断力,可能导致吊索断裂,进一步可能引起吊索依次连续断裂,最终导致整个桥垮塌,严重影响结构强健性,有必要在跨中短吊杆处设置中央扣或者采用刚性短吊杆,达到提高其强健性的目的,同时有必要加强跨中短吊索的疲劳检测频率。
| [1] |
葛耀君, 夏青, 赵林. 大跨度桥梁的抗风强健性及颤振评价[J]. 土木工程学报, 2019, 52(11): 66-70, 119. GE Yao-jun, XIA Qing, ZHAO Lin. Evaluation on Wind Resistance Robustness and Flutter Stability of Long-span Bridges[J]. China Civil Engineering Journal, 2019, 52(11): 66-70, 119. |
| [2] |
RUIZ-TERAN A M, APARICIO A C. Response of Under-deck Cable-stayed Bridges to the Accidental Breakage of Stay Cables[J]. Engineering Structures, 2009, 31(7): 1425-1434. |
| [3] |
孙宗光, 栗燕娜, 石健, 等. 损伤状态下悬索桥静动态响应的模型试验研究[J]. 公路交通科技, 2009, 26(4): 59-63. SUN Zong-guang, LI Yan-na, SHI Jian, et al. Model Test of Static and Dynamic Responses of Suspension Bridge under Damage Condition[J]. Journal of Highway and Transportation Research and Development, 2009, 26(4): 59-63. |
| [4] |
沈锐利, 房凯, 官快. 单根吊索断裂时自锚式悬索桥强健性分析[J]. 桥梁建设, 2014, 44(6): 35-39. SHEN Rui-li, FANG Kai, GUAN Kuai. Robustness Analysis of Self-anchored Suspension Bridge with Loss of a Single Sling[J]. Bridge Construction, 2014, 44(6): 35-39. |
| [5] |
邱文亮, 吴广润, 张哲, 等. 突然断索后双吊索形式自锚式悬索桥安全分析[J]. 大连理工大学学报, 2016, 56(6): 600-607. QIU Wen-liang, WU Guang-run, ZHANG Zhe, et al. Safety Analysis of Self-anchored Suspension Bridge with Dual-shaped Hanger after Sudden Breakage of Hanger[J]. Journal of Dalian University of Technology, 2016, 56(6): 600-607. |
| [6] |
杨世聪, 张劲泉, 姚国文. 在役桥梁拉吊索腐蚀-疲劳损伤与破断机理分析[J]. 公路交通科技, 2019, 36(3): 80-86. YANG Shi-cong, ZHANG Jin-quan, YAO Guo-wen. Analysis on Corrosion-fatigue Damage and Fracture Mechanism of Cables/Hangers in Service Bridges[J]. Journal of Highway and Transportation Research and Development, 2019, 36(3): 80-86. |
| [7] |
胡柏学, 黄浩, 曾威. 基于健康监测的悬索桥吊索疲劳可靠性评估[J]. 公路交通科技, 2015, 32(6): 76-80. HU Bo-xue, HUANG Hao, ZENG Wei. Assessment of Fatigue Reliability for Hanger Cables of Suspension Bridge Based on Health Monitoring[J]. Journal of Highway and Transportation Research and Development, 2015, 32(6): 76-80. |
| [8] |
袁腾文. 吊杆断裂对钢桁架拱桥结构静力影响分析[J]. 湖南交通科技, 2018, 44(3): 145-148. YU Teng-wen. The Effect of Hangers Failure on Structural Static Force of Steel Trussed Frame Arch Bridge[J]. Hunan Communication Science and Technology, 2018, 44(3): 145-148. |
| [9] |
朱劲松, 王洋. 基于吊索重要性的大跨度悬索桥冗余度分析[J]. 重庆交通大学学报: 自然科学版, 2017, 36(7): 1-6. ZHU Jin-song, WANG Yang. Redundancy Analysis on Long-span Suspension Bridge Based on Sling Importance[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2017, 36(7): 1-6. |
| [10] |
曾勇, 陈艾荣, 谭红梅. 基于实测车流的悬索桥吊杆钢丝寿命期内的疲劳评定[J]. 防灾减灾工程学报, 2014, 34(2): 185-191. ZENG Yong, CHEN Ai-rong, TAN Hong-mei. Fatigue Assessment of Hanger Wires of Suspension Bridges in Its Operation Life Based on In-situ Traffic Flow[J]. Journal of Disaster Prevention and Mitigation Engineering, 2014, 34(2): 185-191. |
| [11] |
徐宏. 桥梁拉(吊)索损伤后力学分析及安全评价[D]. 西安: 长安大学, 2008. XU Hong. Mechanical Analysis and Safety Evaluation of Damaged Bridge Cable[D]. Xi'an: Chang'an University, 2008. |
| [12] |
夏欢, 金晓勤, 晏班夫. 拱桥在役损伤吊杆破断安全性研究[J]. 中外公路, 2017, 37(1): 89-93. XIA Huan, JIN Xiao-qin, YAN Ban-fu. Research on Safety of Suspender Breaking in Service of Arch Bridge[J]. Journal of China & Foreign Highway, 2017, 37(1): 89-93. |
| [13] |
HURTY W C, RUBINSTEIN M F. Dynamics of Structures[M]. London: Prentice Hall, 2005.
|
| [14] |
王新敏. ANSYS工程结构数值分析[M]. 北京: 人民交通出版社, 2007. WANG Xin-min. Numerical Analysis of ANSYS Engineering Structure[M]. Beijing: China Communications Press, 2007. |
| [15] |
JTG-T D65-05-2015, 公路悬索桥设计规范[S]. JTG-T D65-05-2015, Specifications for Design of Highway Suspension Bridge[S]. |
| [16] |
王鹏. 公轨人三线合一空间缆索悬索桥动力响应与行人走行舒适度研究[D]. 成都: 西南交通大学, 2018. WANG Peng. Study on Dynamic Response and Pedestrian Comfort of a Three-line Space Cable Suspension Bridge[D]. Chengdu: Southwest Jiaotong University, 2018. |
| [17] |
唐茂林, 王鹏, 李翠娟. 考虑行人舒适度的空间缆索悬索桥车致振动控制[J]. 公路交通科技, 2020, 37(1): 58-65. TANG Mao-lin, WANG Peng, LI Cui-juan. Control of Vehicle-induced Vibration of Suspension Bridge with Spatial Cable Considering Pedestrian Comfort[J]. Journal of Highway and Transportation Research and Development, 2020, 37(1): 58-65. |
| [18] |
ZOLI T, WOODWARD R. Design of Long Span Bridges for Cable Loss[J]. IABSE Symposium Report, 2011, 90(9): 17-25. |
 2021, Vol. 38
2021, Vol. 38
