扩展功能
文章信息
- 毛德均, 余文正, 许鹏, 黄云, 徐佰顺
- MAO De-jun, YU Wen-zheng, XU Peng, HUANG Yun, XU Bai-shun
- 钢板-混凝土组合加固RC梁抗弯承载力计算方法
- A Method for Calculating Flexural Capacity of RC Beam Strengthened by Steel Plate-concrete Composite
- 公路交通科技, 2021, 38(4): 63-70
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 63-70
- 10.3969/j.issn.1002-0268.2021.04.008
-
文章历史
- 收稿日期: 2020-04-12
2. 云南通衢工程检测有限公司, 云南 昆明 650041;
3. 华东交通大学 土木建筑学院, 江西 南昌 330013;
4. 内蒙古大学 交通学院, 内蒙古 呼和浩特 010070
2. Yunnan Tongqu Engineering Testing Co., Ltd., Kunming Yunnan 650041, China;
3. School of Civil Engineering and Architecture, East China Jiaotong University, Nanchang Jianqgxi 330013, China;
4. School of Transportation, Inner Mongolia University, Hohhot Inner Mongolia 010070, China
钢筋混凝土(RC)梁是各类RC桥梁结构的重要组成部分,其安全性能与桥梁正常使用密切相关。在实际工程中,常常由于各种原因,导致RC桥梁结构的部分RC梁构件承载力不足、安全可靠性降低,需要对其进行加固,以保障桥梁的正常使用功能。目前常用的加固方法有增大截面加固法、粘贴钢板加固法、粘贴纤维复合材料加固法、体外预应力加固法和改变结构体系加固法等[1]。钢板-混凝土组合加固法一般指通过在旧混凝土的受拉侧表面植筋、在加固钢板上焊接栓钉,并在旧混凝土与加固钢板之间浇注新混凝土,以提高构件承载能力和刚度的方法[2],这种加固方法是增大截面和粘贴钢板加固法的组合,具有加固效果好、施工简便、造价较低、加固后结构外观效果好等技术特点,作为一种相对比较新颖的加固方法,在桥梁加固工程中已有不少应用,且多用于RC梁的抗弯加固和抗剪加固[2-5]。
国内外学者采用试验研究、理论分析和有限元数值模拟对钢板-混凝土组合加固RC梁的承载性能、破坏模式、计算理论、疲劳性能等开展了研究。文献[6]通过模型试验研究了加固梁的受弯性能。文献[5, 7-11]也开展了文献[6]类似的试验,并对加固梁的承载力计算分析方法进行了研究。文献[12]采用有限元方法研究了不同加载情况下加固梁受力全过程和不同破坏形态下加固梁的受力性能。文献[13]对加固梁进行了弹性理论分析,得到了沿梁纵向钢板与混凝土间滑移分布曲线的表达式。文献[14]采用等幅疲劳试验,研究了加固梁在疲劳荷载作用下的疲劳寿命及应变变化规律。文献[15]采用有限元方法研究了界面黏结失效对加固梁的受力性能影响。诚然,既有研究取得了大量成果,但文献[16]对既有研究成果进行综述分析后指出现阶段该加固技术相关的设计计算理论尚不完善。因此,有必要在既有成果基础上继续深入开展相关研究。
对于加固梁的抗弯承载力计算分析,目前我国没有专门的规范方法供相关人员严格参照执行,在具体操作时,有采用GB50367—2013《混凝土结构加固设计规范》粘贴钢板加固相关规定的[17],有建议采用JTG/T J22—2008《公路桥梁加固设计规范》粘贴钢板加固相关规定的[16],也有相关文献给出了可供参考的不同方法[7-8]。GB50367—2013,JTG/T J22—2008和不同文献给出的典型方法在具体计算公式上存在差异,详细比较分析不同方法的异同点和计算效果是必要的,但目前未见相关研究成果的文献报道。本研究对GB50367—2013,JTG/T J22—2008和文献[7-8]给出的方法进行了详细比较分析,指出了其异同性;基于平截面等假定,根据加固梁的受力破坏特性,明确了3种界限破坏状态,基于3种界限状态下的截面应变分布分析,提出了抗弯承载力计算方法并建立了公式;利用既有试验给出的20个试件资料,将试件抗弯承载力理论值与试验值进行对比分析,探讨了所比较分析的4种既有方法和本研究提出方法的计算效果。
1 既有抗弯承载力计算方法比较分析本研究主要比较4种典型方法的异同性,为便于分析,先给出4种方法的主要公式。
方法1:由文献[7]给出,主要公式如下:
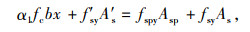
|
(1) |
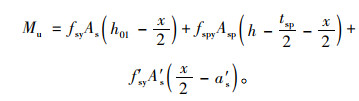
|
(2) |
方法2:由GB50367—2013[18]给出,主要公式:
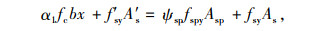
|
(3) |
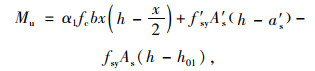
|
(4) |

|
(5) |
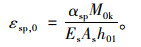
|
(6) |
方法3:由JTG/T J22—2008[1]给出,主要公式:
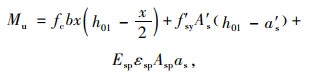
|
(7) |
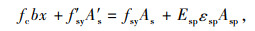
|
(8) |
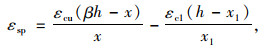
|
(9) |
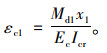
|
(10) |
方法4:由文献[8]给出,主要公式:
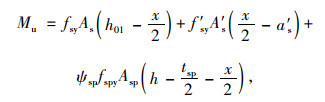
|
(11) |
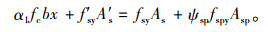
|
(12) |
公式(1)~(12)的符号意义详见文献[7-8]、GB50367—2013和JTG/T J22—2008。
方法3受压区混凝土的合力计算没有系数α1,而方法1,2,4都有α1且其取值方法均为:当混凝土强度等级不超过C50时,α1=1.0;当混凝土强度等级为C80时,α1=0.94,其间按线性内插法确定。在实际工程中,RC桥梁所用混凝土强度等级一般在C60以内,因此,是否采用系数α1对公式实际应用效果影响有限。4种方法的弯矩平衡方程形式存在差异,主要是取矩位置不同和确定钢板合力点作用位置是否考虑钢板厚度tsp影响所致。方法1和4都是对受压区混凝土的压应力合力点取矩且钢板合力作用点考虑了tsp影响;方法2是对加固梁底部边缘取矩且忽略了tsp影响;方法3是对受拉钢筋合力点取矩且忽略tsp影响。取矩位置不同对结果不产生影响,但是否考虑钢板厚度tsp对结果会有一定影响。
方法1~4都是在平截面等假定基础上,根据界限破坏状态建立承载力计算公式,这是目前RC受弯构件和偏压构件承载能力计算分析的常用思路和方法。采用这种方法时,由于加固构件的钢板、钢筋在屈服后均有较强的塑性变形性能,对于加固构件存在的钢板、钢筋先后屈服的情况,在建立承载力计算公式时,先屈服者采用屈服强度,后屈服者不采用屈服强度,而是采用根据先屈服者和压区混凝土边缘达到极限压应变εcu建立的界限破坏状态,基于平截面假定求出的应变所对应的应力值。文献[10]的试验结果显示,对于钢板、钢筋先后屈服的情况,二者均屈服后承载力相对其一先屈服时会有一定提高。可见,采用这种计算分析方法在理论上是安全的。
不难看出,4种方法对应了加固构件的两种界限破坏状态,其中,方法1对应受压区混凝土边缘极限压应变εcu和受拉钢板屈服应变εspy、受拉钢筋屈服应变εy同时达到的界限破坏状态,方法2~4对应εcu和εy同时达到的界限破坏状态。为保证发生适筋破坏,混凝土受压区高度x需小于等于对应界限破坏状态的界限受压区高度xb。在这两种界限破坏状态下,方法1与方法2~4的差异就主要体现在建立公式时钢板拉应力的取值上。方法1的取值为屈服强度fspy,方法2~4的取值均为界限破坏状态时的实际应力值fsp。fsp与加固前构件受到的一阶段荷载M1直接相关,M1越大,fsp越小;M1越小,fsp越大。对于fsp的计算,方法2和方法4采用的方式相同,均采用系数Ψsp且Ψsp的计算方法相同,方法3与方法2~4原理相通,但εsp的确定公式不同。
试验结果表明[6, 8, 10],界面剥离破坏是加固梁的常见破坏形式,发生时钢板一般都不能屈服,试件承载力偏低具有脆性破坏特点。界面剥离破坏与界面黏结处理效果、界面连接构造措施和端部锚固措施等的设计施工有关,应予以避免但往往又难以完全避免。加固梁的界面包括钢板与新混凝土黏结界面和新旧混凝土黏结界面,但剥离破坏主要发生于新旧混凝土界面,原因是加载过程中钢板与新混凝土界面纵向相对滑移量远小于新旧混凝土界面。文献[7]指出,M1小到一定程度时,可忽略其影响,根据M1是否可忽略,加固梁发生界面剥离破坏时钢板不屈服将对应两种状况,具体见表 1。由于加固梁发生界面剥离破坏时的承载力一般要低于实际承载力,而4种方法计算公式的建立是基于上述两种不同界限破坏状态,故对表 1中状况2,4种方法计算效果差别不大,但对状况1,方法2~4理论上比方法1更安全。
| 现象 | 状况1 | 状况2 |
| 界面剥离钢板不屈服 | M1不能忽略+界面剥离 | M1可忽略+界面剥离 |
由此可知,4种计算方法存在一定差异,实际应用时计算效果如何在本研究第4节作进一步分析。
2 加固梁的抗弯承载力理论分析 2.1 基本前提参照GB50010—2010《混凝土结构设计规范》[19]及有关试验研究[6-11],进行理论分析时遵循下列基本前提:
(1) 构件截面在变形前后均保持平面。
(2) 新混凝土与旧混凝土、钢板与新混凝土之间均黏结良好,无相对滑移。
(3) 钢筋本构关系为理想弹塑性。
(4) 不考虑混凝土的抗拉强度。
(5) 在界限破坏状态分析和承载力计算公式的力矩平衡方程建立时,均不考虑钢板厚度tsp影响。GB50367—2013和JTG/T J22—2008均是如此操作,从实际工程应用看,tsp通常为8~12 mm,相对于被加固构件高度和新浇注混凝土厚度而言均较小,忽略tsp影响对计算结果影响有限。
2.2 界限破坏状态确定钢筋、钢板的应力状态是计算加固构件抗弯承载力的关键。加固设计应保证构件加固后仍发生适筋破坏,避免发生超筋破坏,因此,本研究只考虑适筋情况。界限破坏状态的截面分析模型见图 1所示,图 1(a)为加固截面示意图,其中,上部阴影部分为截面等效矩形受压区;h为构件加固后截面高度;hc为混凝土加固层厚度;b为构件宽度;a′s为加固前构件受压钢筋合力点至受压区边缘的距离;h01为加固前构件截面有限高度;as为加固前构件受拉钢筋合力点至受拉边缘的距离;tsp为加固钢板厚度。图 1(b)为加固前构件的截面应变分布,其中,x1c为压区边缘至中性轴的距离;x1s为受拉钢筋合力点至中性轴的距离;x1sp为加固钢板合力点至中性轴的距离;ϕ1为加固前构件控制截面的曲率;εc1为加固前在压区混凝土边缘位置产生的应变;εs1为加固前在受拉钢筋合力点位置产生的应变;ε′sp为加固前在钢板位置产生的虚拟应变。图 1(c)为加固后构件的截面应变分布,其中,xb为构件加固后按平截面假定确定的界限受压区高度;ϕj为构件加固后控制截面的界限曲率;εc2为加固后在压区混凝土边缘位置产生的应变;εs2为加固后在受拉钢筋合力点位置产生的应变;εsp为加固后在钢板位置产生的应变。图 1(b)~(c)中的虚线表示在相应阶段非实际发生的状态。
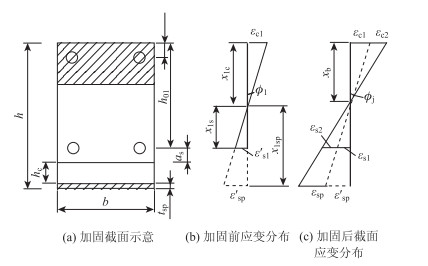
|
| 图 1 截面分析模型 Fig. 1 Section analysis model |
| |
加固前控制截面的曲率ϕ1可采用式(13)计算[1]:
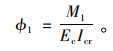
|
(13) |
式中,M1为加固前原构件承受的弯矩组合设计值;Ec为加固前原构件混凝土的弹性模量;Icr为加固前原构件开裂截面换算截面的惯性矩。
由图 1可知:
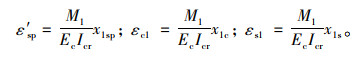
|
(14) |
在混凝土极限压应变εcu和受拉钢筋屈服应变εy、受拉钢板屈服应变εspy一定时,对于适筋加固构件理论上存在3种界限破坏状态,下面对分析3种界限状态的钢板和钢筋的应力确定方法。
(1) 界限状态1
受压区混凝土边缘极限压应变εcu和εspy同时达到。此时,钢板应力等于其屈服强度fspy,受拉钢筋应力fs由应变增量εs2决定。根据图 1可知以下公式成立:
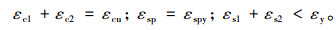
|
(15) |
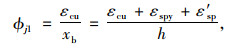
|
(16) |
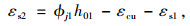
|
(17) |
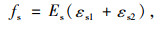
|
(18) |
式中ϕj1为界限状态1的界限曲率。
按等效矩形应力分布得到的受压区高度x须满足x≥2a′s和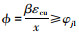
(2) 界限状态2
受压区混凝土边缘极限压应变εcu和εy同时达到。此时,受拉钢筋应力等于其屈服强度fsy,钢板应力fsp由εsp决定。由图 1可知以下公式成立:
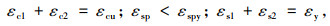
|
(19) |
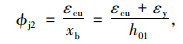
|
(20) |
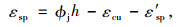
|
(21) |
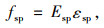
|
(22) |
式中ϕj2为界限状态2的界限曲率。
按等效矩形应力分布得到的受压区高度x需满足x≥2a′s和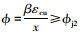
(3) 界限状态3
受压区混凝土边缘极限压应变εcu和εspy,εy均同时达到,即有:
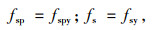
|
(23) |
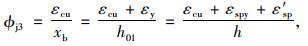
|
(24) |
式中ϕj3为界限状态3的界限曲率。
界限状态3必须满足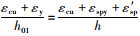
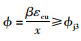
理论上,不论何种界限破坏状态,均有受压区混凝土边缘达到εcu,此时必有:
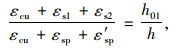
|
(25) |
则有:
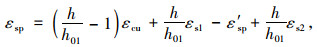
|
(26) |
式中,h,h01,εcu,εs1,ε′sp都是已知,令:
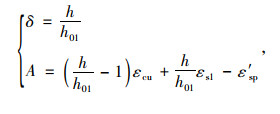
|
(27) |
可得:
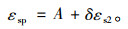
|
(28) |
假定钢筋屈服有εs2=εy-εs1,可得此时的εsp:
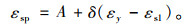
|
(29) |
可知,故可根据εsp与εspy的关系判断构件发生何种界限破坏状态。
当εsp>εspy时,说明钢筋屈服时钢板应变已经超过了其屈服应变,故钢板先于钢筋屈服,此时,对应的界限破坏状态为状态1;当εsp < εspy时,说明钢筋屈服时钢板应变尚未达到其屈服应变,即钢筋先于钢板屈服,此时,对应的界限破坏状态为状态2;当εsp=εspy时,说明钢筋屈服时钢板应变也刚好达到其屈服应变,即钢筋和钢板同时屈服,此时,对应的界限破坏状态为状态3。
2.3 承载力计算公式根据界限破坏状态分析,针对钢板-混凝土组合加固的RC梁抗弯承载力计算,本研究提出如下公式:
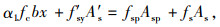
|
(30) |
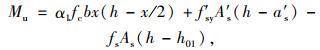
|
(31) |
式中,α1为系数,按文献[18]第5.2.3条规定取值;fc为原构件混凝土轴心抗压强度设计值;f′sy为受压钢筋抗压强度设计值;A′s为受压钢筋截面面积;fsp为钢板应力值;Asp为钢板截面面积;fs为受拉钢筋应力值;As为受拉钢筋截面面积。
将3种破坏状态对应的fsp,fs的实际值代入以上两公式,可得出极限承载力。
3 计算结果对比分析结合现有试验资料对4种既有方法和本研究提出方法的计算效果进行计算分析,文献试件主要参数见表 2。采用有限元软件ANSYS18.0对表 2中的试件进行计算分析,得到承载力有限元计算值MuF。在有限元模型中:混凝土采用SOLID65单元,钢筋采用LINK180单元,钢板采用SHELL143单元,加载和支承垫板均采用SOLID185单元;钢筋和混凝土的本构关系采用文献[19]中提供的模型,材料特性参数采用各文献的给出值;不考虑钢筋与混凝土、钢板与新混凝土、新旧混凝土之间的黏结滑移;对于加固前承受荷载的试件,采用软件提供的单元生死(Birth and Death)命令来模拟其二次受力状态;采用牛顿-拉普森迭代法求解,收敛容差釆用ANSYS默认值,取荷载-位移曲线的峰值点作为极限承载力。表 2试件的承载力相关结果见表 3、表 4。
| 试件编号 | 数据来源 | l0/cm | h1/mm | fcu1/MPa | bs/mm | ts/mm | fcu2/MPa | fspy/MPa | fsy/MPa | h/mm | a/mm | F1/kN |
| SCCSB1 | [6] | 500 | 500 | 47.3 | 250 | 8 | 39.1 | 327 | 384 | 580 | 1 500 | 0 |
| SCCSB2 | [6] | 500 | 500 | 49.8 | 250 | 8 | 45.7 | 327 | 384 | 580 | 1 500 | 0 |
| SCCSB3 | [6] | 500 | 500 | 48.7 | 250 | 8 | 56.6 | 327 | 384 | 580 | 2 500 | 100 |
| SCCSB4 | [6] | 500 | 500 | 46.7 | 250 | 8 | 55.2 | 327 | 384 | 580 | 2 500 | 191 |
| SCCSB5 | [6] | 500 | 500 | 48.8 | 250 | 8 | 52.0 | 327 | 384 | 580 | 2 500 | 257 |
| SCCSB6 | [6] | 500 | 500 | 54.5 | 250 | 8 | 55.8 | 327 | 384 | 580 | 1 500 | 0 |
| SCCSB7 | [6] | 500 | 500 | 53.8 | 250 | 8 | 53.0 | 327 | 384 | 580 | 2 500 | 0 |
| SCCSB8 | [6] | 500 | 500 | 52.4 | 250 | 8 | 50.1 | 327 | 384 | 580 | 2 500 | 66 |
| SCCSB9 | [6] | 500 | 500 | 49.6 | 250 | 8 | 46.5 | 327 | 384 | 580 | 2 500 | 119 |
| SCCSB10 | [6] | 500 | 500 | 48.0 | 250 | 8 | 42.6 | 327 | 384 | 580 | 2 500 | 143 |
| spccsb1 | [8] | 345 | 320 | 61.5 | 200 | 6 | 54.2 | 304 | 412 | 406 | 1 325 | 0 |
| spccsb2 | [8] | 345 | 320 | 61.5 | 200 | 6 | 54.2 | 304 | 412 | 406 | 1 325 | 0 |
| spccsb3 | [8] | 345 | 320 | 61.5 | 200 | 6 | 54.2 | 304 | 412 | 406 | 1 725 | 91 |
| spccsb4 | [8] | 345 | 320 | 61.5 | 200 | 6 | 54.2 | 304 | 412 | 406 | 1 725 | 50 |
| SPCCSB1 | [10] | 280 | 250 | 37.7 | 150 | 2.75 | 42.9 | 207 | 379 | 250 | 933.3 | 0 |
| SPCCSB2 | [10] | 280 | 250 | 37.7 | 150 | 2.75 | 42.9 | 207 | 379 | 250 | 933.3 | 12 |
| SPCCSB3 | [10] | 280 | 250 | 37.7 | 150 | 2.75 | 42.9 | 207 | 379 | 250 | 933.3 | 18 |
| SPCCSB4 | [10] | 280 | 250 | 37.7 | 150 | 2.75 | 42.9 | 207 | 379 | 250 | 933.3 | 0 |
| SPCCSB5 | [10] | 280 | 250 | 37.7 | 150 | 2.75 | 42.9 | 207 | 379 | 250 | 933.3 | 0 |
| SPCCSB6 | [10] | 280 | 250 | 37.7 | 150 | 2.75 | 42.9 | 207 | 379 | 250 | 933.3 | 0 |
| 注:l0为梁计算跨径;h1,h分别为原梁高和加固后梁高;fcu1,fcu2分别为老混凝土和新混凝土的立方体抗压强度;bs,ts分别为加固钢板的宽度和厚度;fspy,fsy分别为钢板和受拉钢筋的屈服强度;a为剪跨长度;F1为加固前施加的荷载值。 | ||||||||||||
| 试件编号 | Mut | MuF | Mu1 | Mu2 | Mu3 | Mu4 | Mu5 |
| SCCSB1 | 441.8 | 478.7 | 565.9 | 568.5 | 568.5 | 565.9 | 410.3 |
| SCCSB2 | 396.5 | 490.2 | 569.7 | 572.3 | 572.3 | 569.7 | 411.7 |
| SCCSB3 | 593.9 | 622.0 | 568.1 | 570.7 | 570.7 | 568.1 | 520.4 |
| SCCSB4 | 601.6 | 626.8 | 564.9 | 567.5 | 567.5 | 564.9 | 606.7 |
| SCCSB5 | 616.7 | 620.0 | 568.2 | 570.8 | 570.8 | 568.2 | 671.0 |
| SCCSB6 | 428.9 | 482.4 | 575.9 | 578.6 | 578.6 | 575.9 | 413.9 |
| SCCSB7 | 609.9 | 620.8 | 575.1 | 577.7 | 577.7 | 575.1 | 413.6 |
| SCCSB8 | 594.6 | 614.7 | 573.3 | 575.9 | 575.9 | 573.3 | 487.6 |
| SCCSB9 | 578.6 | 622.4 | 569.4 | 572.0 | 572.0 | 569.4 | 541.1 |
| SCCSB10 | 599.7 | 628.2 | 567.0 | 569.6 | 569.6 | 567.0 | 563.1 |
| spccsb1 | 149.7 | 182.8 | 203.1 | 202.4 | 202.4 | 203.1 | 145.1 |
| spccsb2 | 136.5 | 182.8 | 203.1 | 202.4 | 202.4 | 203.1 | 145.1 |
| spccsb3 | 198.6 | 210.2 | 203.1 | 202.4 | 202.4 | 203.1 | 219.4 |
| spccsb4 | 204.4 | 217.2 | 203.1 | 202.4 | 202.4 | 203.1 | 187.2 |
| SPCCSB1 | 41.0 | 44.2 | 41.2 | 41.4 | 41.4 | 41.2 | 30.2 |
| SPCCSB2 | 29.8 | 46.8 | 41.2 | 41.4 | 41.4 | 41.2 | 31.9 |
| SPCCSB3 | 32.6 | 47.4 | 41.2 | 41.4 | 41.4 | 41.2 | 34.2 |
| SPCCSB4 | 42.9 | 44.2 | 41.2 | 41.4 | 41.4 | 41.2 | 30.2 |
| SPCCSB5 | 57.8 | 44.2 | 41.2 | 41.4 | 41.4 | 41.2 | 30.2 |
| SPCCSB6 | 48.5 | 44.2 | 41.2 | 41.4 | 41.4 | 41.2 | 30.2 |
| 注:Mut,MuF为试件承载力实测值和有限元计算值;Mu1,Mu2,Mu3和Mu4分别为方法1~4的承载力计算值;Mu5为本研究方法的承载力计算值。 | |||||||
| m | D | CV | r | ||
| 方法1 | 1.087 44 | 0.047 12 | 0.199 61 | 0.966 65 | |
| 方法2 | 1.090 56 | 0.046 92 | 0.198 63 | 0.966 74 | |
| 方法3 | 1.090 56 | 0.046 92 | 0.198 63 | 0.966 74 | |
| 方法4 | 1.087 44 | 0.047 12 | 0.199 61 | 0.966 65 | |
| 本研究方法 | 0.901 77 | 0.061 45 | 0.274 91 | 0.977 13 | |
| 注:m,D,CV分别为计算值和实测值比值的平均值、方差和变异系数;r为计算值和试验值的相关系数。 | |||||
从表 3可知,有限元计算结果和试验结果总体吻合较好,说明本研究采用的有限元建模方法能够模拟试验梁的受力破坏状况,同时表明各试验研究结果正常可靠,有限元结果偏大,原因是有限元模型的材料、尺寸、边界条件都为理想状态,试验状况与理想状况之间难免存在偏差。结合表 3和表 4可知,对于5种理论计算方法,方法1,4的计算结果表现完全一致,方法2,3结果表现也是如此,方法1,4与方法2,3的结果表现有细微差异,而本研究方法的结果表现则与方法1~4有明显差异;总体上看,方法1~4结果均偏大,而本研究方法结果表现安全,5种方法与试验结果都有一定的吻合度,方法1~4的结果离散性相对于本研究方法表现较好,但与试验结果的相关性相对本研究方法表现较差。
对于以系数Ψsp考虑加固钢板受力特性的方法2,4,将Ψsp表达式代入力的平衡方程求解一个关于受压区高度x的一元二次方程,可得出x值,将x值代入Ψsp的表达式可得出Ψsp值。但对表 2中的试件,所有Ψsp计算值均大于1而不能采用,Ψsp最后取值均为1,相当于计算试件承载力Mu时钢板应力值最终还是采用了屈服强度fspy。此时,通过解一元二次方程求出的x也不可用,需要重新用力的平衡方程通过解一元一次方程得出可用的x,再将x代入力矩平衡方程得出Mu。对于表 2中的试件,方法2,4中Ψsp的计算没有体现出应有效能。
对于方法3,计算过程和方法2,4基本一致,也是先要将εsp的表达式代入力的平衡方程求解一个关于受压区高度x的一元二次方程,可得出x值,将x值代入εsp的表达式可得出εsp值。但对表 2中的试件,所有εsp计算值均大于钢板屈服应变εspy,求出的εsp同样不可用,计算Mu时钢板应力值最终也还是采用了fspy。此时,通过解一元二次方程求出的x也不可用,需要重新用力的平衡方程通过解一元一次方程得出最终可用的x,再将x代入力矩平衡方程得出Mu。对表 2中的试件,方法3中εsp的计算没有体现出应有效能。方法3与方法2,4考虑加固钢板受力特性的具体方法看似不同,但“殊途同归”效果完全相同。
对于表 2中的试件,Ψsp和εsp失去应有效能导致方法1,4结果表现完全一致,方法2,3结果表现也完全一致。而方法1,4与方法2,3的结果表现有细微差异的原因是方法1,4考虑了钢板厚度tsp,而方法2,3没考虑tsp,除此外无其他原因,从结果表现不难看出,是否考虑tsp影响极小。本研究方法考虑了加固钢板的受力特性,但不需要通过解一元二次方程来求受压区高度x,这是本研究方法与方法2~4的区别所在,本研究方法和方法1一样,都是直接通过力的平衡方程解一元一次方程得到x,不同的是方法1的钢板、钢筋直接采用了屈服强度,而本研究方法的钢板、钢筋应力是发生界限破坏时的实际应力值,需要经过一系列计算方可得出。总体上看,在计算Mu时,5种方法的基本过程一致,均需通过力的平衡方程求解受压区高度x,然后再将x代入力矩平衡方程得到Mu,具体操作时,方法1最简单,方法2~4繁琐程度相当且比方法1复杂,本研究方法又要比方法2~4略显繁琐。
4 结论(1) GB50367—2013《混凝土结构加固设计规范》、JTG/T J22—2008《公路桥梁加固设计规范》及另外2种公开文献报道中的计算方法公式建立思路相通,但实现途径存在差异。
(2) 根据加固梁的受力破坏特性,明确了3种界限破坏状态,基于3种界限状态下的截面应变分布分析,推导了每种状态下钢板和受拉钢筋的应力确定方法,建立了加固梁的抗弯承载力计算公式。
(3) 对于钢板-混凝土组合加固RC梁的抗弯承载力计算,4种既有方法均表现为结果总体偏大,本研究提出的方法虽然计算过程略显繁琐,但结果总体安全,可为加固计算提供参考。
(4) 对本研究用于计算分析的试件,《混凝土结构加固设计规范》(GB50367—2013)中的系数Ψsp和《公路桥梁加固设计规范》(JTG/T J22—2008)中的加固钢板的拉应变εsp计算均没有体现出应有效能。
| [1] |
JTG/TJ22-2008, 公路桥梁加固设计规范[S]. JTG/TJ22-2008, Specifications for Strengthening Design of Highway Bridges[S]. |
| [2] |
聂建国, 赵洁, 唐亮. 钢板-混凝土组合在钢筋混凝土梁加固中的应用[J]. 桥梁建设, 2007(3): 76-79. NIE Jian-guo, ZHAO Jie, TANG Liang. Application of Steel Plate and Concrete Composite to Strengthening of Reinforced Concrete Girder[J]. Bridge Construction, 2007(3): 76-79. |
| [3] |
聂建国, 陶慕轩, 樊键生, 等. 钢-混凝土组合结构在桥梁加固改造中的应用研究[J]. 防灾减灾工程学报, 2010, 30(增1): 335-344. NIE Jian-guo, TAO Mu-xuan, FAN Jian-sheng, et al. Application Research on Steel-concrete Composite Structure in Bridge Reinforcement and Reconstruction[J]. Journal of Disaster Prevention and Mitigation Engineering, 2010, 30(S1): 335-344. |
| [4] |
石雄伟. 钢板-混凝土组合加固方法试验研究及实桥应用[D]. 西安: 长安大学, 2012. SHI Xiong-wei. Experiment of Methodology of Steel Plate-concrete Composite Strengthening and Its Application in Bridges[D]. Xi'an: Chang'an University, 2012. |
| [5] |
冯林军. 钢板-混凝土组合加固试验与实桥应用研究[D]. 西安: 长安大学, 2011. FENG Lin-jun. Study on Experiment of Steel Plate-concrete Composite Strengthening and Its Application in Bridges[D]. Xi'an: Chang'an University, 2011. |
| [6] |
聂建国, 赵洁. 钢板-混凝土组合加固钢筋混凝土简支梁试验研究[J]. 建筑结构学报, 2008(5): 50-56. NIE Jian-guo, ZHAO Jie. Experimental Study on Simply Supported RC Beams Strengthened by Steel Plate-concrete Composite Technique[J]. Journal of Building Structures, 2008(5): 50-56. |
| [7] |
王春生, 袁卓亚, 高珊, 等. 钢板-混凝土组合加固矩形梁的抗弯性能试验[J]. 中国公路学报, 2011, 24(5): 65-73. WANG Chun-sheng, YUAN Zhuo-ya, GAO Shan, et al. Flexural Behavior Test of Rectangular Reinforced Concrete Beams of Steel Plate-concrete Composite Strengthening[J]. China Journal of Highway and Transport, 2011, 24(5): 65-73. |
| [8] |
郭晓宇. 钢板-混凝土组合加固混凝土梁抗弯性能试验研究[D]. 西安: 长安大学, 2010. GUO Xiao-yu. Study on Flexural Behavior of Reinforced Concrete Beams Using Steel Plate and Concrete Composite Strengthening Technique[D]. Xi'an: Chang'an University, 2010. |
| [9] |
王世超, 王春生, 段兰, 等. 组合加固足尺预应力混凝土箱梁抗弯性能试验[J]. 交通运输工程学报, 2018, 18(5): 56-65. WANG Shi-chao, WANG Chun-sheng, DUAN Lan, et al. Flexural Behavior Experiment of Full-scale PC Box Girder Strengthened by Composite Technique[J]. Journal of Traffic and Transportation Engineering, 2018, 18(5): 56-65. |
| [10] |
张凯. 钢板-混凝土组合加固矩形梁抗弯承载能力试验研究[D]. 重庆: 重庆交通大学, 2015. ZHANG Kai. Experimental Study on Rectangular Beams Strengthened by Steel Plate-concrete Composite Technique[D]. Chongqing: Chongqing Jiaotong University, 2015. |
| [11] |
高珊. 钢板-混凝土组合加固钢筋混凝土T梁抗弯性能试验研究[D]. 西安: 长安大学, 2009. GAO Shan. Experimental Investigation of Bending Behavior of RC T-shape Beams Strengthened by Steel Plate and Concrete Composite[D]. Xi'an: Chang'an University, 2009. |
| [12] |
赵洁, 聂建国. 钢板-混凝土组合加固钢筋混凝土梁的非线性有限元分析[J]. 计算力学学报, 2009, 26(6): 906-912. ZHAO Jie, NIE Jian-guo. Nonlinear Finite Element Analysis of RC Beams Strengthened Using Steel Plate-concrete Composite Technique[J]. Chinese Journal of Computational Mechanics, 2009, 26(6): 906-912. |
| [13] |
聂建国, 赵洁. 钢板-混凝土组合抗弯加固中滑移分布分析[J]. 清华大学学报: 自然科学版, 2007(12): 2085-2088, 2094. NIE Jian-guo, ZHAO Jie. Slip Distribution Analysis of Steel Plate-concrete Composite Flexural Members[J]. Journal of Tsinghua University: Science and Technology Edition, 2007(12): 2085-2088, 2094. |
| [14] |
聂建国, 王宇航. 钢板-混凝土组合受弯加固梁疲劳性能试验研究[J]. 建筑结构学报, 2011, 32(2): 1-9. NIE Jian-guo, WANG Yu-hang. Experimental Research on Fatigue Behavior of RC Beams Strengthened by Steel Plate-concrete Composite Technique[J]. Journal of Building Structures, 2011, 32(2): 1-9. |
| [15] |
GRECO F, LONETTI P, BLASI P N. An Analytical Investigation of Debonding Problems in Beams Strengthened Using Composite Plates[J]. Engineering Fracture Mechanics, 2007, 74(3): 346-372. |
| [16] |
刘亚明, 曹娟丽. 钢板-混凝土组合加固技术研究综述[J]. 中外公路, 2011, 31(4): 146-148. LIU Ya-ming, CAO Juan-li. Summary of Research on Steel Plate-concrete Composite Strengthening Technique[J]. Journal of China & Foreign Highway, 2011, 31(4): 146-148. |
| [17] |
鲁林. 钢板-混凝土组合结构在简支梁桥加固中的应用研究[D]. 武汉: 华中科技大学, 2019. LU Lin. Research on Application of Steel-concrete Composite Structure in Reinforcement of Simply Supported Girder Bridge D]. Wuhan: Huazhong University of Science and Technology, 2019. |
| [18] |
GB 50367-2013, 混凝土结构加固设计规范[S]. GB 50367-2013, Code for Design of Strengthening Concrete Structure[S]. |
| [19] |
GB 50010-2010, 混凝土结构设计规范[S]. GB 50367-2010, Code for Design of Concrete Structures[S]. |
 2021, Vol. 38
2021, Vol. 38
