扩展功能
文章信息
- 李茜, 左新黛, 文坡
- LI Qian, ZUO Xin-dai, WEN Po
- 斜拉桥索塔分组集聚锚固体系设计探讨
- Discussion on Design of Cable Pylon Grouping-anchorage-system of Cable-stayed Bridge
- 公路交通科技, 2021, 38(4): 55-62
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 55-62
- 10.3969/j.issn.1002-0268.2021.04.007
-
文章历史
- 收稿日期: 2020-07-06
2. 中铁大桥勘测设计院集团有限公司, 湖北 武汉 430056
2. China Railway Major Bridge Reconnaissance & Design Institute Co., Ltd., Wuhan Hubei 430056, China
斜拉桥索塔锚固体系是将斜拉索的局部集中力分散到索塔全截面,并安全、均匀地传递到锚固区以下的重要受力体系,其受力状态复杂,是斜拉桥设计施工中的重点和难点。分组集聚式索塔锚固体系是近年来出现的一种较为新型的锚固形式,与其他传统的锚固形式不同的是,它将斜拉索分组锚固于塔柱间钢横梁横隔板之间的锚固构造内,形成索塔体外锚固体系。目前国内仅应用于安徽池州长江公路大桥(主跨828 m),在国外仅有韩国巨加桥采用了塔外锚固方式[1]。
本研究以池州大桥为工程背景,围绕斜拉桥分组集聚式锚固体系的分组、作用等问题,探讨分组集聚锚固体系的设计思路,研究斜拉索布索形式、塔-横梁刚度匹配对斜拉桥受力的影响,旨在明确索塔联合作用行为,探索最优设计方法,以利于今后在全国推广应用。
1 分组集聚锚固体系 1.1 体系特点传统的斜拉桥混凝土索塔锚固方式主要有环形预应力锚固,如润杨长江大桥[2]、芜湖长江大桥[3];钢锚梁锚固,如加拿大安娜西斯桥、金塘大桥[4]。内置型钢锚箱,如香港昂船洲大桥、苏通长江大桥[5];外露型钢锚箱,如法国诺曼底大桥、杭州湾跨海大桥[6]这4种类型。内置型和外露型钢锚箱如图 1所示。

|
| 图 1 索塔内置型和外露型钢锚箱示意图 Fig. 1 Schematic diagram of cable pylon built-in and exposed steel anchor boxes |
| |
4种锚固方式各有利弊,主要弊端在于环形预应力不能有效解决混凝土横梁受拉开裂的难题。钢锚梁锚固区需设置较多牛腿结构,施工装模拆模繁琐;外露型钢锚箱需施加预应力,施工难度和工程造价都会随之提高;内置型钢锚箱端塔壁外侧的混凝土抗裂性不易控制等[7-10]。
分组集聚式锚固体系是塔柱外钢箱梁索塔锚固体系,与钢锚梁和钢锚箱相比,它的特点体现在以下4点:
(1) 可有效降低塔柱混凝土开裂风险。文献[7]对该体系进行了详细的空间有限元分析,结果表明,由于预应力锚杆作用,混凝土与钢横梁承压板连接位置始终处于受压状态,与传统体系相比,减少了混凝土塔柱开裂的风险。
(2) 1道钢横梁可同时挂设多对斜拉索,可实现塔梁同步施工,具有施工便捷性与经济性优势。
(3) 可在钢横梁内对斜拉索进行后期检修维护及更换斜拉索。
(4) 斜拉桥更具观赏性,视觉冲击效果更强。
1.2 设计思路 1.2.1 斜拉索分组斜拉桥索面布置通常有辐射形、竖琴形和扇形几种[11],分组集聚式索塔锚固体系是将索分为若干组,每组分开锚固,兼有幅射形和扇形索的优点。斜拉索分组时需综合考虑拉索倾角、结构受力、拉索张拉空间、景观造型和施工等方面的因素。由于主塔上方的斜拉索在梁端倾角较小,斜拉索效率相对较低,单组拉索数量可适当增加,宜布置5~6对拉索。主塔下方的斜拉索在梁端倾角较大,斜拉索效率相对较高,单组拉索数量可适当减少,宜布置3~4对拉索。池州大桥斜拉索采用分组集聚方式锚固于6道钢横梁结构内部,由上而下分别锚固10,10,10,10,8,6对斜拉索,如图 2所示。
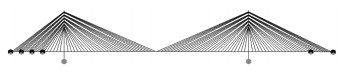
|
| 图 2 池州大桥斜拉索分组布置 Fig. 2 Layout of cable grouping of Chizhou Bridge |
| |
1.2.2 钢横梁设计
通常情况下,靠近上面的斜拉索顺桥向和横桥向的竖倾角较为匀顺,斜拉索锚固钢锚箱布置较为均匀。而靠近下面的斜拉索竖向倾角变化较大,由于斜拉索锚固张拉空间的需要,钢锚箱布置需要有一定的间距,钢横梁的数量和尺寸还应与上塔柱的高度和宽度协调,体现结构韵律的工程之美。由于钢横梁一般在工厂预制,整体吊装,对施工设备的吊装能力和安装精度要求较高,尺寸不宜过大。所以在确定钢横梁的间距、数量时,需同时考虑拉索倾角、结构受力、桥塔造型、拉索张拉空间和施工等因素,建议大跨度斜拉桥单个主塔间宜设置4~6根钢横梁。在池州大桥钢横梁设计时,综合考虑以上因素,在上塔柱等间距设置了6道钢横梁,间距为13.5 m,如图 3所示。
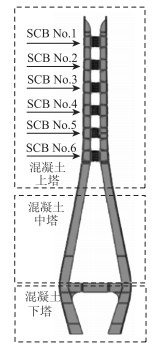
|
| 图 3 池州大桥主塔钢横梁布置 Fig. 3 Layout of Steel beam of main pylon of Chizhou Bridge |
| |
在进行池州大桥设计时,在全桥总体计算基础上,建立了主塔空间有限元模型并进行了精细化计算,提取6根钢横梁最大内力,如表 1所示。从中可看出,控制钢横梁设计的要素主要是顺桥向弯矩及竖向剪力,但是2者不同时出现在同一道钢横梁上,靠近上面的钢横梁竖向剪力较大,而下面的钢横梁顺桥向弯矩较大。
| 位置(自上而下编号) | 扭矩/(kN·m) | 顺桥向弯矩/(kN·m) | 竖向弯矩/(kN·m) |
| 钢横梁1 | 3 353 | 101 868 | -6 427 |
| 钢横梁2 | 3 068 | 87 540 | -5 941 |
| 钢横梁3 | 3 196 | -92 298 | 5 022 |
| 钢横梁4 | 3 069 | -95 727 | 10 539 |
| 钢横梁5 | 8 037 | -98 847 | 15 725 |
| 钢横梁6 | 2 056 | -139 777 | 15 696 |
| 位置(自上而下编号) | 轴力/kN | 顺桥向剪力/kN | 竖向剪力/kN |
| 钢横梁1 | -4 872 | -1 778 | 36 122 |
| 钢横梁2 | 3 709 | 1 856 | 36 057 |
| 钢横梁3 | 3 392 | 1 287 | 37 590 |
| 钢横梁4 | 3 828 | 2 550 | 34 788 |
| 钢横梁5 | -1 911 | -2 926 | 28 941 |
| 钢横梁6 | -39 902 | 834 | 22 861 |
考虑到各个钢横梁内部索塔锚固结构行为复杂,因此重点针对各个钢横梁的顶、底板的板厚按结构内力来选配。对钢横梁进行了等结构设计和等强度设计的用钢量比较,6道钢横梁采用相同结构尺寸的等结构设计,相比按结构内力的等强度设计增加用钢量43.8 t(见表 2)。综合考虑结构设计的经济性及加工制造的便捷性,最终确定钢横梁设计采用等结构设计,即6道钢横梁采用相同的截面尺寸。
| 设计方式 | 等结构设计/t | 等强度设计/t |
| 材料用量(Q370qE) | 4 229.5 | 4 185.7 |
为抵抗弯矩、剪力、轴力及扭矩等结构内力,并考虑6~10对斜拉索的锚固空间需要,池州大桥的钢横梁最终采用箱形结构形式。钢横梁截面高7.0 m,顺桥向宽5.5 m,内部沿横桥向设置有3道横隔板,斜拉索对称锚固于横隔板中间,在钢横梁壁板外缘横向和顺桥向分别设置有加劲肋,如图 4所示。
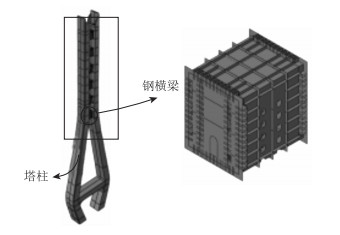
|
| 图 4 池州大桥钢横梁截面示意图 Fig. 4 Schematic diagram of steel beam section of Chizhou Bridge |
| |
1.2.3 塔梁构造连接
由于塔柱为钢筋混凝土结构,横梁为钢结构,为确保两个结构的有效连接,将斜拉索索力顺利传递到塔柱是钢横梁锚固的一个关键问题。国内外常用的钢混连接方式有承压板、剪力钉、PBL剪力键和锚筋等[12-13]。考虑到池州大桥钢混结合面受力的特性,采用高强度锚杆、剪力钉及PBL剪力键结合的方式确保结合面的受力。塔梁构造连接示意图见图 5。
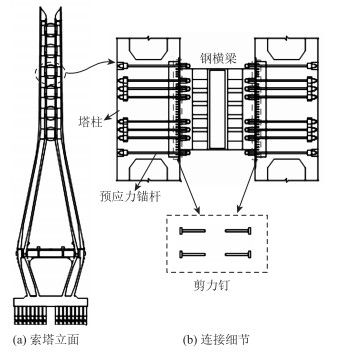
|
| 图 5 塔梁构造连接示意图 Fig. 5 Schematic diagram of structures and connection of pylon and beams |
| |
斜拉索锚固于钢横梁隔板间,斜拉索竖向分力传力路径为[14]:锚固支承板→钢横梁竖腹板→预埋板→剪力钉、PBL剪力键→塔柱。斜拉索不平衡水平分力由预埋钢板上的剪力钉传给塔柱,为抵抗钢横梁与塔柱之间的顺桥向和竖向弯矩,在钢横梁、预埋板及塔柱间设置有ϕ110 mm高强度预应力锚杆。钢横梁端部与塔柱之间的竖向和水平剪力由通过50 mm厚预埋钢板与塔柱内ϕ32 mm竖向钢筋的焊缝、预埋钢板与塔柱混凝土的摩擦力及剪力钉进行传递。钢横梁所承受的轴力和扭矩不控制设计,可由上述结构共同来承受。
2 斜拉索布索形式影响分析 2.1 有限元模型采用有限元软件Midas/civil建立池州大桥全桥模型,全桥共计216个桁架单元模拟斜拉索,476个梁单元模拟主梁、塔柱及钢横梁,两侧边跨共计4个辅助墩,用拉压支座模拟,边跨端部约束为双向支座,全桥模型如图 6所示。由于仅进行参数对比分析,荷载仅考虑材料自重、斜拉索成桥索力和车辆荷载,车辆荷载按主跨跨中主梁横向弯矩My影响线进行纵向最不利布载,横向布置分满载和偏载2种工况,最终提取结果是在恒活载最不利组合下内力和位移包络图的最值。

|
| 图 6 池州大桥全桥计算模型 Fig. 6 Full bridge calculation model of Chizhou Bridge |
| |
2.2 工况设置
为了分析斜拉索布索形式对体系受力的影响,设计了3种工况,分别为分组集聚钢横梁中央锚固(原设计)、分组集聚两侧分开锚固、等间距两侧分开锚固, 如表 3所示。
| 工况 | 设计参数 |
| 工况1:横梁中央集聚锚固(原设计) | 6根钢横梁,竖向中心间距均为13.5 m,分别锚固10,10,10,10,8,6对斜拉索 |
| 工况2:两侧分开集聚锚固 | 斜拉索的竖向位置不变,由钢横梁中央集中锚固变为两侧分开,分别锚固于上塔柱两侧 |
| 工况3:等间距锚固(扇形索面) | 在工况2基础上,将27对索在塔间、梁间等间距布置,塔间间距3 m |
2.3 有限元分析
对3种工况下的塔柱、钢横梁、主梁内力、位移及索力进行对比分析,总体分析结果见表 4,提取了典型工况内力、位移对比图,如图 7~图 9所示。
| 位置 | 内力 | 工况1相比工况2 | 工况2相比工况3 |
| 主塔横梁 | 横梁轴力 | 增大80% | 增大5% |
| 横梁扭矩 | 减小25%~50% | 几乎无变化 | |
| 横、竖向弯矩 | 增大100% | 几乎无变化 | |
| 上塔柱底 | 扭矩 | 减小40% | 几乎无变化 |
| 塔顶 | 纵向位移 | 增大4 cm | 几乎无变化 |
| 主梁跨中 | 竖向弯矩 | 减小23% | 几乎无变化 |
| 竖向位移 | 增大7 cm | 减小2 cm | |
| 横向位移 | 减小4 cm | 增大1 cm | |
| 扭矩 | 减小0.88% | 几乎无变化 | |
| 轴力 | 几乎无变化 | 减小10% | |
| 斜拉索 | 索力 | 增大1% | 减小2% |
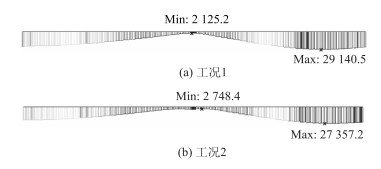
|
| 图 7 主梁跨中竖向弯矩对比(单位: kN·m) Fig. 7 Comparison of mid-span vertical bending moments of main beam (unit: kN·m) |
| |
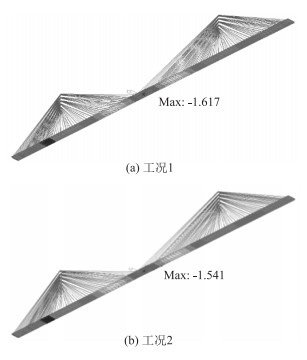
|
| 图 8 主梁竖向位移对比(单位: m) Fig. 8 Comparison of vertical displacements of main beam (unit: m) |
| |
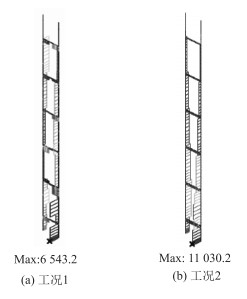
|
| 图 9 上塔柱扭矩对比(单位: kN·m) Fig. 9 Comparison of torques of upper pylon column (unit: kN·m) |
| |
通过分析可得出:
(1) 中央集聚锚固(工况1)与两侧分开集聚锚固(工况2)相比,前者上塔柱底扭矩减小40%,横梁扭矩减小25%~50%,表明工况1对上塔柱抗扭转更有利;前者主梁跨中横向位移减小4 cm、竖向弯矩减小23%,说明工况1的主梁横向稳定性、竖向抗弯性更好,而钢横梁受力更加复杂。这是由于中央集聚锚固体系的横桥向由斜拉索、主梁形成了封闭的三角形结构,与工况2两侧分开形成上部开口的三角形相比,斜拉桥整体横向刚度更大、稳定性更好;而由于中央集聚锚的锚固点集中在钢横梁中部,造成钢横梁的受力更加复杂。
(2) 工况2与工况3对比结果表明,同样是分开锚固在塔柱两侧,分组集聚索面与等间距索面两种工况下, 塔、梁的内力、位移及索力几乎变化不大,说明索面的改变对体系受力影响不大。
3 塔-横梁刚度匹配影响分析 3.1 工况设置应用上述有限元模型,设置工况4~6,通过与原设计工况1的对比分析,以求得到改变钢横梁长度和间距对塔-横梁的刚度匹配性和体系受力的影响。3种工况设置如下。
工况4:上塔柱横向间距拉开2 m,由原设计的7 m变为9 m,其他不变。
工况5:钢横梁竖向间距由原设计的13.5 m调整为11.5 m,塔锚固端拉索竖向间距也随横梁变化。
工况6:钢横梁竖向间距由原设计的13.5 m调整为15.3 m,索竖向间距也随之变化。
3.2 塔梁线刚度比为了分析斜拉桥塔-横梁的适宜刚度比,引入建筑结构的塔梁刚度比的概念[15-16]。梁柱刚度比是决定框架结构整体性能的一个重要因素,它决定了结构的侧向刚度分布、内力分布、延性、耗能能力等抗震性能。梁柱刚度比不宜过小,过小则整体刚度弱,抗震能力差;也不宜过大,过大则违背强柱弱梁的原则,柱端也容易出现塑性铰。虽然在我国结构设计规范中对梁柱线刚度比限值没有明确规定,但有一些文献[17-18]对其合理线刚度比做出了研究。
斜拉桥中塔梁刚度比定义为上塔柱和钢横梁的线刚度之比,将塔柱与钢横梁的线刚度均用
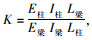
在材料和截面保持不变的情况下,钢横梁间距由7 m变为9 m(工况4),塔梁线刚度比增大约28%;钢横梁间距由13.5 m缩小到11.5 m(工况5),塔梁线刚度比增大17%;钢横梁间距由13.5 m增大到15.3 m(工况6),塔梁线刚度比减小12%。无论按Iyy计算还是Izz计算,得到的线刚度比的变化率基本保持一致。
3.3 钢横梁长度、间距对体系的影响分析对4种工况下的塔柱、钢横梁、主梁的内力、位移及索力进行对比分析,结果见表 5。提取了典型工况的内力位移对比图,如图 10~图 13所示。
| 构件部位 | 工况4与工况1相比 | 工况5与工况1相比 | 工况6与工况1相比 |
| 主塔横梁 | 轴力最大增大30%;竖向剪力最大增大84%(GH6);横、竖向弯矩分别增大30%和33% | 轴力有增有减,变化在30%以内;横、竖向弯矩分别最大减少18%、增大20% | 轴力减小20%;横、竖向弯矩有增有减,分别变化在18%和20%以内 |
| 上塔柱 | 扭矩、剪力、弯矩减小在17%以内 | 竖向剪力增大23%;扭矩、横向弯矩均增大在26%以内 | 竖向剪力减小16%、扭矩减小25%、横向弯矩减小24% |
| 主梁跨中 | 横向弯矩有增有减,最大变化13%、扭矩和轴力接近 | 5#主梁跨中轴力增加23%、横向弯矩增大11%、扭矩增大0.88% | 5#主梁跨中轴力减少16%、横向弯矩减小14%、扭矩减小0.84% |
| 5#跨中竖向位移减小6.2 cm | 5#跨中竖向位移增加4 cm | 5#跨中竖向位移减小4.4 cm | |
| 主跨索力 | 有增有减,变化不到1% | 增大3.5%~4.6% | 减小3.5~3.9% |
| 注:1.表中各内力的规定与表 2中相同。2.未提及的参数表示变化很小,可以忽略。 | |||
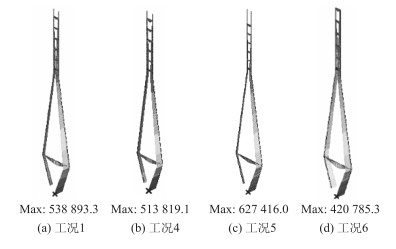
|
| 图 10 主塔横向弯矩(单位: kN·m) Fig. 10 Transverse bending moments of main pylon (unit: kN·m) |
| |

|
| 图 11 主梁横向弯矩弯矩(单位: kN·m) Fig. 11 Transverse bending moment of main beam (unit: kN·m) |
| |
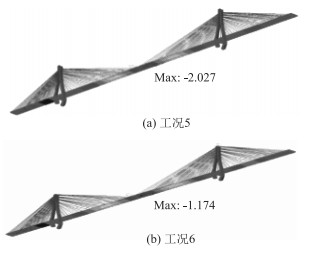
|
| 图 12 主梁竖向位移(单位: m) Fig. 12 Vertical displacement of main beam (unit: m) |
| |

|
| 图 13 主塔钢横梁竖向弯矩(单位: kN·m) Fig. 13 Vertical bending moment of steel beam of main pylon(unit: kN·m) |
| |
通过分析可得出:
(1) 钢横梁长度增大2 m,塔梁线刚度比增大28%,上塔柱部分内力减小,钢横梁部分内力增大,规律性不明显。从表 5可以看出,改变横梁长度,带来的仅是主塔-横梁局部受力的变化,对主梁影响不大。
(2) 钢横梁间距缩小2 m,塔梁线性刚度比增大17%,由于最下缘的斜拉索位置保持不变,斜拉索与主梁倾角减小,斜拉索效率降低,跨中索力增大约4%左右,塔柱和横梁内力均增大,主梁横向弯矩增大18%,扭矩增大0.88%,跨中竖向位移增大26%。反之,横梁间距增大1.8 m,塔梁线刚度比减小12%,索力减小,体系内力、位移均减小。可以得出,改变横梁间距,带来的是斜拉桥整体受力的变化。
通过以上分析,可得到两点设计建议:
(1) 在满足施工空间和构造要求的前提下,尽可能减小钢横梁长度,以减小塔梁线刚度比,对钢横梁受力和经济性均有利。
(2) 在考虑上塔柱布设空间的前提下,尽可能增大横梁间距,以减小塔梁线刚度比,提高斜拉索效率,对全桥受力更有利。
4 结论本研究围绕斜拉桥索塔分组集聚锚固体系的行为特性和设计方法,以池州大桥为例,分析了中央集聚锚固体系的设计特点,通过主塔、钢横梁的设计参数敏感性分析,得到积极的设计建议。在中央集聚锚固体系的设计特点方面和设计参数敏感性分析方面,得到以下结论:
(1) 中央集聚锚固体系(原设计)与两侧分开集聚锚固体系的对比分析表明,前者形成横桥向由斜拉索、主梁组成的封闭三角形,而后者形成上部开口的半封闭三角形。2者相比,原设计对上塔柱和钢横梁的抗扭转性及主梁的横向稳定性更有利,但由于集聚锚的锚固点集中在钢横梁中部,钢横梁受力更加复杂,是该体系的设计重点。
(2) 同样是斜拉索在塔柱两侧分开锚固,等间距扇形索面与集聚索面对比分析表明,两种布索形式对全桥体系的受力影响不大。
(3) 分组集聚锚固体系(原设计)的塔柱混凝土与钢横梁承压板连接位置始终处于受压状态,可有效降低塔柱开裂风险,并能实现塔梁同步施工,后期维护更换更加方便,具有施工便捷性与经济性优势。
(4) 引入了建筑结构中塔梁刚度比的概念,提出了主塔与塔间钢横梁的塔梁线刚度比,研究主塔和钢横梁的刚度匹配,得到钢横梁设计参数与刚度比的敏感性关系,通过内力分析最终给出了设计建议:在满足施工空间和构造要求的前提下,建议尽可能减小钢横梁长度、增大钢横梁间距,以减小塔梁线刚度比,对提高斜拉索效率、全桥受力和经济性均有利。
(5) 改变横梁长度,带来的是主塔-横梁局部受力的变化,对主梁影响不大;改变横梁间距,带来的却是斜拉桥全桥的塔、横梁、主梁受力的变化。
| [1] |
游新鹏. 韩国巨加大桥的设计与施工[J]. 世界桥梁, 2014, 42(1): 1-4. YOU Xin-peng. Design and Construction of Juga Bridge in Korea[J]. World Bridges, 2014, 42(1): 1-4. |
| [2] |
欧庆保, 王强. 润扬长江公路大桥北汊斜拉桥索塔锚固区足尺模型试验[C]//中国公路学会桥梁和结构工程学会2003年全国桥梁学术会议论文集. 北京: 人民交通出版社, 2003: 739-747. OU Qing-bao, WANG Qiang. Full Scale Model Test of Cable Pylon Anchorage Zone in North Branch of Runyang Changjiang Highway Bridge[C]//2003 National Bridge Academic Conference of Bridge and Structural Engineering Society of China Highway Society. Beijing: China Communications Press, 2003: 739-747. |
| [3] |
王念. 商合杭铁路芜湖长江公铁大桥桥塔环向预应力技术[J]. 桥梁建设, 2019, 49(4): 7-12. WANG Nian. Hoop Prestressing Technique on Pylons of Wuhu Changjiang River Rail-cum-road Bridge on Shangqiu-Hefei-Hangzhou Railway[J]. Bridge Construction, 2019, 49(4): 7-12. |
| [4] |
陈向阳, 王昌将, 白雨东, 等. 金塘大桥钢牛腿钢锚梁组合结构足尺模型试验研究[J]. 公路, 2011(8): 1-4. CHEN Xiang-yang, WANG Chang-jiang, BAI Yu-dong, et al. Full-scale Model Segmental Test and Study on Composite Structure of Steel Corbel and Steel Anchor Beam of Jintang Bridge[J]. Highway, 2011(8): 1-4. |
| [5] |
张清华, 李乔. 超大跨度钢箱梁斜拉桥索梁锚固结构试验研究[J]. 土木工程学报, 2011, 44(9): 71-80. ZHANG Qing-hua, LI Qiao. Experiment Study on Cable-girder Anchorage for Super Long-span Cable-stayed Bridges with Steel Box Girders[J]. Journal of Civil Engineering, 2011, 44(9): 71-80. |
| [6] |
张奇志, 李明俊. 斜拉桥钢-混组合索塔锚固区节段模型试验研究[J]. 桥梁建设, 2006, 36(3): 16-19. ZHANG Qi-zhi, LI Ming-jun. Segmental Model Test Study of Steel and Concrete Composite Anchor Zone on Pylon of Cable-stayed Bridge[J]. Bridge Construction, 2006, 36(3): 16-19. |
| [7] |
刘玉擎, 陈聪, 郑双杰. 钢锚箱嵌固型索塔锚固结构受力机理分析[J]. 桥梁建设, 2015, 45(1): 33-38. LIU Yu-qing, CHEN Cong, ZHENG Shuang-jie. Analysis of Force Mechanism of Pylon Anchorage Structure of Fixed-end Steel Anchor Box Type[J]. Bridge Construction, 2015, 45(1): 33-38. |
| [8] |
徐海军, 刘玉擎. 外露型钢锚箱索塔锚固结构受力机理试验[J]. 同济大学学报: 自然科学版, 2014, 42(5): 672-676. XU Hai-jun, LIU Yu-qing. Experimental Study on Stress Mechanism of Exposed Steel Anchor Box Cable-tower Achorage[J]. Journal of Tongji University; Natural Science Edition, 2014, 42(5): 672-676. |
| [9] |
杨涛. 斜拉桥钢-混凝土组合结构索塔锚固区受力研究[D]. 长沙: 湖南大学, 2008. YANG Tao. Study on Stress of Cable Pylon Anchorage Zone of Steel-concrete Composite Structure of Cable-stayed Bridge[D]. Changsha: Hunan University, 2008. |
| [10] |
魏奇芬. 钢锚箱在斜拉桥索塔锚固区中的应用[J]. 世界桥梁, 2008(2): 27-30. WEI QI-fen. Application of Steel Anchor Boxes to Anchorage Zones in Pylons of Cable-stayed Bridges[J]. World Bridges, 2008(2): 27-30. |
| [11] |
周孟波. 斜拉桥手册[M]. 北京: 人民交通出版社, 2004. ZHOU Meng-bo. Manual of Cable-stayed Bridge[M]. Beijing: China Communications Press, 2004. |
| [12] |
逯文茹. 钢锚箱式钢-混组合索塔锚固体系受力性能与设计方法研究[D]. 西安: 长安大学, 2016. LU Wen-ru. Study on Mechanical Behavior and Design Method of Steel-concrete Composite Cable Pylon Anchorage System with Steel Anchor Box[D]. Xi'an: Chang'an University, 2016. |
| [13] |
俞先林, 张奇志. 斜拉桥索塔钢混组合锚固结构力学性能分析和试验研究[J]. 铁道科学与工程学报, 2009, 6(5): 16-20. YU Xian-lin, ZHANG Qi-zhi. Analysis and Test Research on Mechanical Performance for Steel-concrete Composite Anchor Structure of Cable-stayed Bridge Pylon[J]. Journal of Railway Science and Engineering, 2009, 6(5): 16-20. |
| [14] |
王萌, 孙新阳, 李茜, 等. 分组集聚式斜拉桥索塔锚固区传力机制[J]. 哈尔滨工业大学学报, 2017, 49(12): 176-183. WANG Meng, SUN Xin-yang, LI Qian, et al. Mechanical Behavior for Anchorage Zone of Cable-stayed Bridge with Group Aggregation Anchor System[J]. Journal of Harbin Institute of Technology, 2017, 49(12): 176-183. |
| [15] |
杨锴. 基于梁柱刚度比、柱梁强度比对框架结构破坏模式的影响研究[D]. 重庆: 重庆大学, 2015. YANG Kai. Study on Effects of Failure Modes of Frame Structures from Beam-column's Flexural Stiffness Ratio and Column-beam's Flexural Strength Ratio[D]. Chongqing: Chongqing University, 2015. |
| [16] |
白国良, 孙海水, 李晓文, 等. 基于梁柱线刚度比的型钢混凝土柱-钢梁混合框架静力弹塑性分析[J]. 建筑结构, 2009, 39(4): 7-9. BAI Guo-liang, SUN Hai-shui, LI Xiao-wen, et al. Pushover Analysis for Hybrid Frame of SRC Column-steel Beam Based on Linear Stiffness Ratio of Beam to Column[J]. Building Structure, 2009, 39(4): 7-9. |
| [17] |
刘钦. 基于优化原理的框架梁柱合理线刚度比研究[J]. 河南城建学院学报, 2009, 18(5): 21-23. LIU Qin. Research on Study on Reasonable Line Stiffness Ratio of Framework Beam and Column Based on Optimization Theory[J]. Journal of Henan University of Urban Construction, 2009, 18(5): 21-23. |
| [18] |
张少钦, 程华虎. 梁柱线刚度比对框架内力和侧移影响的分析[J]. 南昌航空大学学报: 自然科学版, 2011, 25(3): 84-88. ZHANG Shao-qin, CHENG Hua-hu. The Analysis of the Influence of Beam-column Line Stiffness Ratio on the Internal Force and Lateral Displacement of the Frame[J]. Journal of Nanchang Hangkong University: Natural Science Edition, 2011, 25(3): 84-88. |
 2021, Vol. 38
2021, Vol. 38
