扩展功能
文章信息
- 彭旺虎, 李院军, 刘嘉欣
- PENG Wang-hu, LI Yuan-jun, LIU Jia-xin
- 基于静力模型修正的装配式T梁桥荷载横向分布计算
- Calculation of Transverse Load Distribution of Prefabricated T-beam Bridge Based on Static Model Updating
- 公路交通科技, 2021, 38(4): 45-54
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(4): 45-54
- 10.3969/j.issn.1002-0268.2021.04.006
-
文章历史
- 收稿日期: 2020-04-20
2. 广东省交通规划设计研究院股份有限公司, 广东 广州 510507;
3. 长安大学 公路学院, 陕西 西安 710064
2. Guangdong Transport Planning and Design Institute Co., Ltd., Guangzhou Guangdong 510507, China;
3. School of Highway, Chang'an University, Xi'an, Shaanxi 710064, China
装配式桥梁随着其服役年限的增加,在重载交通和特殊环境腐蚀下,主梁和横向连接病害问题日益突出,严重影响桥梁横向受力性能,甚至可能出现单板受力的情况[1-2]。桥梁的横向传力能力通常用荷载横向分布系数来衡量。对于装配式桥梁荷载横向分布系数的计算,传统的理论计算仅仅适用于未发生损伤的装配式桥梁,对于桥梁损伤后的荷载横向分布系数的计算方法存在空白,故亟须解决桥梁发生损伤后的荷载横向分布系数计算问题。
国内外学者在荷载横向分布系数计算方法上做了许多有益的工作。Kim[3]分析了横隔板对横向荷载分配系数的影响,发现增大横隔板可以减小横向荷载分配系数,但增加横隔梁数量对荷载横向分布系数的影响不大。Eom[4]通过对3座连续钢梁桥梁的现场试验,分析发现现场试验测得的应变小于分析结果预期的应变,AASHTO规范计算结果会低估实际的荷载横向分布系数。Zhang[5]为了解决现有AASHTO LRFD桥梁设计规范中方程式对桥梁参数适用范围的限制,对假设桥梁进行了严格的分析,在评价和比较现有方程和程序的基础上,发展了一套新的简化分布系数方程。Fausett[6]对一座预应力梁桥进行长期监测和定期测试,并测量挠度和应变,将这些测试中收集的数据用于创建和校准桥梁的有限元模型,然后使用该校准模型获得实际的荷载横向分布系数。刘华等[7]为了得到一种新的计算桥梁荷载横向分布的方法,以动力参数与主梁挠度的关系为出发点,选取模态质量、频率和振型作为参数进行了理论推导。聂瑞锋等[8]以关键参数为自变量,以弯矩比为因变量,采用多元非线性回归分析法拟合得到弯矩横向分布系数简化计算公式。魏志刚等[9]考虑混凝土桥面铺装与主梁间存在的剪切滑移效应,采用结构力学中的基本方法提出了一种考虑桥面铺装的简支梁桥荷载横向分布系数计算方法。项贻强等[10]考虑多梁式钢-混凝土组合小箱梁桥界面滑移问题,对计算荷载横向分布系数经典理论进行了修正。然而上述研究主要是对没有发生损伤的桥梁进行荷载横向分布系数的研究,且使用模型修正理论对损伤参数进行修正的情况更少。使用模型修正理论对损伤参数进行修正使计算模型更加接近真实的受力情况,可以得出反映实际情况的荷载横向分布系数。
目前,一般采用基于原有经典理论对具有代表性的相关参数进行修正的方法。模型修正理论以实测数据为依据对模型的参数进行修正,具有一定的认可度[11]。魏锦辉等[12]以各阶模态柔度矩阵中各元素相对变化作为指标,提出了基于模态柔度灵敏度解析表达式的有限元模型修正方法。张征文等[13]通过桥梁荷载试验的静、动载试验数据,建立了变形、频率及振型等静动联合目标函数,得到了能够模拟桥梁真实状态的模型。宗周红等[14]根据一个简支梁有限元模型,提出了基于联合静动力的模型修正法,并通过实例进行了验证,取得了较好的效果。彭涛等[15]在静动联合目标函数的优化方面,引入快速非支配排序遗传算法(NSGA-Ⅱ),对模型修正多目标函数算法进行了优化。然而上述学者都是对有限元模型进行了修正,并没有对其他理论计算模型进行修正。
有限元模型修正法虽然可以针对特定断面的损伤进行识别,并建立损伤后的有限元模型,但是损伤识别过程是一个反复迭代的过程,每次迭代都需要调用一次有限元模型,在复杂的模型和损伤识别参数较多时,有限元模型修正的计算工作量是极大的。对于基于计算荷载横向分布系数的原有理论模型进行修正,能够利用理论模型进行运算,不需要调用有限元模型,且修正后的理论模型可直接计算出实际荷载横向分布系数,给修正过程和计算工作带来极大方便。
笔者针对在役装配式桥梁发生主梁和铰缝损伤后的荷载横向分布的计算方法进行研究,以铰接板(梁)法为基础,建立一种考虑桥梁损伤的简化模型。基于静力的模型修正法对简化模型进行修正,首先确定待识别参数,并选择静力参数构造目标函数,再对目标函数进行优化算法,最终得到修正后的参数,代入简化模型,便得到一种考虑桥梁损伤的荷载横向分布的计算方法。
1 损伤评估指标早期装配式梁桥的主梁横向连接大多以铰接为主,而且对于发生损伤的在役装配式梁桥,采用铰接板(梁)法计算其荷载横向分布更为真实和安全。因此本研究以铰接板(梁)法为基础,同时考虑主梁损伤和主梁间铰缝损伤,建立损伤修正模型。
(1) 主梁刚度损伤折减系数
由文献[16]可知,主梁刚度的损伤可由主梁刚度损伤折减系数来体现。假定主梁损伤后,弯曲挠度的增加只与其抗弯刚度的折减相关,因此可以定义主梁刚度损伤折减系数ηk为[1, 17]:
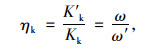
|
(1) |
式中,Kk和K′k分别为梁体未损伤和出现损伤状况下的抗弯刚度;ω和ω′分别为梁体未损伤和出现损伤状况下,在荷载作用下某区段所产生的挠度值。
(2) 铰缝刚度损伤折减系数
在桥梁使用年限、交通量增长及外界环境变化的多重压力下,主梁间的铰缝出现了开裂甚至失效情况,使相邻主梁在铰缝处发生相对位移,出现一个位移差Δωi(见图 1)。

|
| 图 1 铰缝计算图示 Fig. 1 Calculation diagram of hinge joint |
| |
在荷载作用下,铰缝损伤将会使相邻两梁中受荷载的主梁增加1个附加挠度,而没有荷载作用的主梁将会少1个附加挠度[1]。
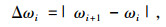
|
(2) |
式中ωi和ωi+1分别为第i条铰缝两侧的挠度。
可定义参数ϕi来反映铰缝损伤程度,称为铰缝协同工作系数[1]:
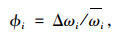
|
(3) |
式中ωi为铰缝两侧相邻主梁的挠度均值。
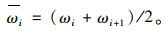
|
(4) |
ϕi数值越小,则该铰缝两侧主梁协同工作性能越好。ϕi最大值为2,表示铰缝完全开裂,失去传递剪力的能力,两侧主梁独立工作。
由文献[1]知,考虑铰缝设计材料、施工技术和服役阶段的实际情况,通过回归分析铰缝协同工作系数ϕ可表示为:
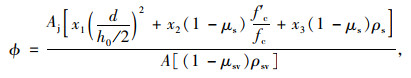
|
(5) |
式中, Aj为铰缝截面积;A为计算单元截面积;d为主梁与铰缝之间的形心间距;h0为计算截面的有效高度;μs和μsv分别为铰缝纵向和横向钢筋的腐蚀率;f′c和fc分别为铰缝、主梁的混凝土强度;ρs和ρsv分别为铰缝纵向和横向钢筋配筋情况;x1,x2,x3分别为回归系数。
为了便于在后面计算模型中计算铰缝损伤对其传递剪力性能的影响,定义铰缝刚度折减系数ηq为:

|
(6) |
式中Kq和K′q分别为铰缝未损伤和出现损伤后的刚度。
铰缝刚度折减系数ηq与铰缝协同工作系数ϕ之间的关系可近似地表达为:

|
(7) |
利用式(5)、式(7)可将模型修正后确定的铰缝刚度折减系数与铰缝结构参数联系起来,评定具体损伤要素的状况。
2 基于铰接板梁法的损伤模型对于横桥向采用铰缝连接的装配式板梁桥和T梁桥,主梁和铰缝都对其荷载横向分布有较大影响,因此,计算损伤桥梁的荷载横向分布时,必须计入主梁和铰缝的破损情况。主梁和铰缝的损伤分别通过对主梁抗弯刚度和铰缝抗剪刚度的折减来考虑。通过第1节的主梁和铰缝刚度损伤折减系数,便可建立损伤后的计算模型。
2.1 基本假设与正则方程研究对象为装配式板梁或T梁桥,考虑其主梁和铰缝发生损伤,提出以下基本假设:
(1) 在竖向荷载作用下,铰缝处仅传递竖向剪力,不传递横向弯矩。
(2) 在桥梁纵向,各主梁和铰缝的位移、内力和外载荷都是半波正弦分布。
(3) 铰缝两侧的相对位移与铰缝传递的剪力成正比,与铰缝的抗剪刚度成反比[2]。
图 2为铰接装配式T梁桥计算图示,以5片梁为例。T梁从左到右编号依次为1~5,铰缝从左到右编号依次为1~4。切开每条铰缝构成基本体系,在每片梁上作用荷载pk,通过接缝处的位移变形协调条件,便可求出全部铰接力峰值gj和g′j,在接缝处利用位移的变形协调条件,便可求出全部铰接力峰值,但是当铰缝出现破损时,铰缝处会发生相对位移。

|
| 图 2 铰接装配式T梁桥计算模型 Fig. 2 Calculation model of hinge-connected fabricated T-beam bridge |
| |
在建立正则方程时,需要考虑主梁的损伤和铰缝损伤所带来的相对位移。现根据假设(3)有:
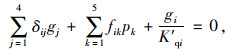
|
(8) |
式中,δij为作用在第j条铰缝处的单位铰缝剪力在第i条铰缝处产生的相对位移;fik为作用在k号梁上的单位荷载在第i条铰缝处产生的相对位移;gj和gi分别为第j条铰缝处和第i条铰缝处的剪力;pk为作用在k号主梁中心处的荷载;K′qi为i号铰缝抗剪刚度实际值。
2.2 参数计算与模型简化单片T梁的受力和位移状况如图 3所示,T梁宽度为b。作用在铰缝处的单位竖向荷载,可以等效为单位中心荷载和1个附加扭矩T=b/2。中心荷载带来的挠度为ω,扭矩带来的截面扭转角为φ,此外主梁翼缘板悬臂端的弹性挠度为fF。需注意,考虑主梁抗弯刚度损伤条件,则各主梁在单位荷载作用下的挠度并不会相同,将i号梁的挠度记作ω′i,以下标i加以区分。不计主梁的横向变位,则相对位移δij可表示为:

|
| 图 3 T梁受力图示 Fig. 3 Force diagram of T-beam |
| |
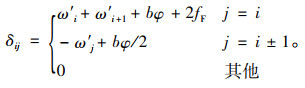
|
(9) |
同理,可写出k号主梁上作用单位竖向荷载时,第i条铰缝处引起的竖向相对位移fik为:

|
(10) |
由材料力学可知,简支板梁的跨中竖向挠度ω′、扭转角φ和悬臂端弹性挠度fF分别为:
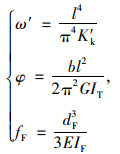
|
(11) |
式中,l为主梁计算跨径;K′k为T梁损伤后的抗弯刚度;GIT为T梁抗扭刚度;EIF为T梁翼缘板抗弯刚度;dF为翼缘板悬臂长度。对于装配式铰接板桥,fF项取为0。
将式(9)~(11)代入式(8),再在等式两边同时除以未发生损伤的主梁在单位荷载作用下的挠度ω,并令刚度参数γ=(φb/2)/ω,β=fF/ω,δg=γ+β,ζi=1/ηki=ω′i/ω,αi=1/(ηqiKqω),可得到包含损伤折减系数的正则方程,其展开形式为:

|
(12) |
结构静力模型修正是利用结构静力测试响应信息,通过各种方法使结构静力响应的理论计算值与实测值尽可能一致,从而得到修正后的结构模型参数。静载试验测得的响应比动载试验测得的结构响应更精确,在比较测量误差对损伤检测结果的影响时,利用静载试验数据的方法比动力方法更能得到可靠的结果,基于静力模型修正技术的优点越来越凸显[14]。
3.1 识别参数上述的损伤模型是通过定义主梁刚度损伤折减系数ηk和铰缝刚度损伤折减系数ηq来考虑损伤。本研究选择5片T梁桥进行理论推导,因此有5个不同的主梁刚度损伤折减系数和4个铰缝刚度损伤折减系数,分别对应5片T梁的主梁抗弯刚度Kk和4条铰缝抗剪刚度Kqi。由式(13)可知,装配式梁桥发生损伤后,其计算模型的每片主梁抗弯刚度Kk和铰缝抗剪刚度Kqi均需要修正,以达到模拟真实桥梁的受力和使用状态。但如果待修正参数的数值及其数量级均相差较大,这将会造成较大的数值计算截断误差[18]。为了减小这误差的影响,一般对修正参数的系数进行修正,因此接下来的修正皆采用主梁刚度损伤折减系数ηk和铰缝刚度损伤折减系数ηq。
3.2 目标函数根据结构类型、试验工况及测量响应的不同,选择静力位移,即每片梁的挠度值来构造目标函数。
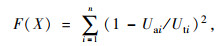
|
(13) |
式中, F(X)为基于静力响应的目标函数;Uti是现场试验的实测挠度值;Uai结构理论模型计算的挠度值;n为荷载试验中挠度测试点数量。
为了使结构理论模型的计算挠度值与荷载试验测试挠度值的差异值越小,即求解最小值问题。
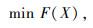
|
(14) |
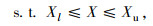
|
(15) |
式中, X为待修正的结构模型参数集;Xl和XU为结构模型参数集X的上限和下限,是优化问题的约束条件。
3.3 模型修正过程目标函数求解是一个不断寻优的过程,本研究采用L-M法与G-N法相结合对目标函数进行优化。综合法结合了两者的优点,能准确可靠地完成迭代计算过程[19]。整个优化计算通过MATLAB自编程序实现。具体的修正过程见图 4。

|
| 图 4 模型修正流程图 Fig. 4 Flowchart of model updating |
| |
(1) 建立损伤理论模型。基于铰接板(梁)法,考虑主梁和铰缝损伤,会带来各主梁刚度差异和铰缝处的相对位移。建立正则方程,再通过主梁刚度损伤折减系数和铰缝刚度损伤折减系数,来体现主梁和铰缝的损伤程度,最终建立损伤理论模型,见式(12),并根据桥梁的荷载试验加载工况,通过式(12)计算各片梁跨中挠度值。
(2) 选择待修正的参数。应该选择影响模型较为敏感的参数,并对参数的修正范围做一定的约束,防止修正时出现不在参数范围内的数值。这里主要是选择主梁的抗弯刚度和铰缝的抗剪刚度作为修正参数。
(3) 构造目标函数是为了修正时有一个判断函数值,最终目标是在相应的约束条件下,目标函数取得最小值,即最优化过程。这里基于静力相应来构造目标函数,见式(13)。判断目标函数值是否小于设定误差值,如果小于则输出模型修正结果,并计算修正后的主梁抗弯刚度和铰缝抗剪刚度,反之,则进入下一步,采用算法优化修正。
(4) 对目标函数进行优化,这一步是采用数学工具对待修正参数的求解过程。这里采用L-M法和G-N法相结合进行优化,加快运算过程。首先通过G-N法对目标函数式(14)进行线性化,在点Xk对F(X)进行一阶泰勒展开,并在G-N迭代格式中增加1个阻尼项μkI,变为L-M法迭代格式,不断迭代,输出修正结果,代入第1步损伤理论模型,如此反复循环,直到满足F(X) < 设定值。
4 实例验证 4.1 工程概况与试验内容该桥于2004年建成,共3跨,标准跨径20 m,梁高1.5 m,桥宽15 m,横桥向6片T梁,每个T梁宽度为2.5 m,桥面布置为0.5 m(护栏)+14 m(车行道)+0.5 m(护栏)。横向连接方式为桥面(翼缘)铰接和横隔梁连接,每跨横隔梁仅3片,包括2片端横隔梁和1片中横隔梁。
在荷载试验前,对桥梁进行外观检查,发现桥梁南边跨出现破损情况。损伤位置如图 5所示,其中第1条与第2条铰缝出现连续裂缝和钢筋锈蚀病害,此外1#~3#主梁出现不同程度的损伤,表现为主梁部分地方显现腹板侧面竖向裂缝及底面横向和纵向裂缝,其他主梁和铰缝外观较为完好。

|
| 图 5 桥梁病害位置示意图 Fig. 5 Schematic diagram of bridge disease positions |
| |
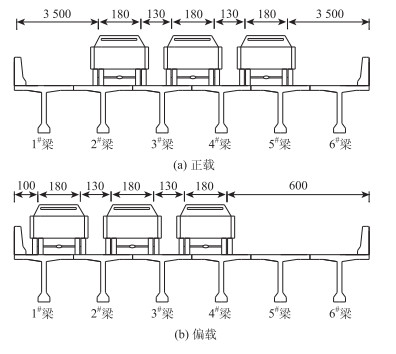
静力荷载试验主要为了得到在车辆静载作用下每片主梁的挠度值,以静力挠度值作为模型修正的响应值。静载试验分为中载(正载)与偏载2个工况,车辆布载按照通用桥规加载,如图 6所示。选取南边跨和中跨作为试验跨,以2跨跨中作为测试截面,在梁底布置6个位移传感器(见图 7)。中跨整体受力性能优于南边跨,因此下面的分析及数据对比均针对南边跨跨中截面。由静载试验的挠度数据即可进行模型修正。
|
| 图 6 静载试验车辆横向布置(单位:cm) Fig. 6 Lateral arrangement of vehicles in static load test (unit: cm) |
| |

|
| 图 7 单辆车加载和位移传感器布置(单位:cm) Fig. 7 Arrangement of vehicle loadings and displacement sensors(unit: cm) |
| |
为了比对和验证模型修正结果,还选择南边跨跨中截面进行了单辆车荷载加载试验,获得实测的荷载横向分布影响线。单梁车荷载加载位置见表 1和图 7,其中车辆横向布载位置x系指车辆荷载中线到左栏杆边缘的距离。
| 测点编号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 布载位置x/cm | 190 | 375 | 625 | 875 | 1 125 | 1 310 |
4.2 确定修正参数和目标函数
由前期的桥梁外观检测和荷载试验数据可知,损伤主要发生在1#~3#梁和第1~2条铰缝。为了减少迭代运算量,本算例选择上述3片主梁的抗弯刚度和2条铰缝的抗剪刚度作为修正参数,再分别通过两类损伤折减系数ηk和ηq来代表修正。迭代运算中实质采用的是上述参数的损伤折减系数,即ηk1,ηk2,ηk3,ηq1和ηq2。铰缝的损伤情况会比主梁严重,确定修正参数范围时,铰缝抗剪刚度折减系数的变化范围要大于主梁抗弯刚度折减系数,具体变化范围列于表 2。
| 参数 | 最小值 | 中间值 | 最大值 |
| 主梁刚度损伤折减系数ηki | 0.7 | 0.875 | 1.05 |
| 铰缝刚度损伤折减系数ηqi | 0.5 | 0.775 | 1.05 |
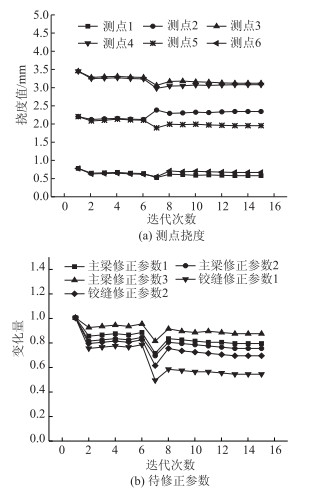
本算例中,采用了实测挠度与计算的残差作为目标函数。采用L-M法和G-N法相结合对损伤模型进行迭代计算。5个修正参数初始值均为1.0,即假定全部主梁和铰缝均为无损伤状态。图 8为模型迭代过程中各测点挠度和待修正参数的变化过程,可以看出当迭代到步数15时,各修正参数值就已经趋于稳定,迭代过程快捷。
|
| 图 8 模型迭代过程中参数变化曲线 Fig. 8 Curves of parameter variation during model iteration |
| |
4.3 模型修正结果
表 3列出挠度实测值和模型修正前后的挠度计算值,图 9则直观示出相应挠度。由表 3、图 9可知,当结构发生损伤后如果不对结构参数进行修正,则挠度计算值与实测值相比误差较大,最大误差达41.5%,远超由《公路桥梁承载能力检测评定规程》(JTG/T J21—2011)规定的20%的误差,而模型修正后的挠度计算值与实测值吻合度较高,误差范围在2.7%~5.9%之间,满足规程要求。
| 测试工况 | 测试位置 | 实测值/mm | 计算值/mm | 相对误差/% | |||
| 修正前 | 修正后 | 修正前 | 修正后 | ||||
| Ⅰ | 1 | 0.53 | 0.75 | 0.55 | 41.5 | 4 | |
| 2 | 2.2 | 2.18 | 2.32 | -0.9 | 5.5 | ||
| 3 | 2.99 | 3.43 | 3.10 | 14.7 | 3.7 | ||
| 4 | 2.9 | 3.43 | 3.06 | 18.3 | 5.4 | ||
| 5 | 1.84 | 2.18 | 1.93 | 18.5 | 5 | ||
| 6 | 0.62 | 0.75 | 0.64 | 21.0 | 2.7 | ||
| Ⅱ | 1 | 3.87 | 3.8 | 4.05 | -1.8 | 4.7 | |
| 2 | 2.71 | 2.76 | 2.85 | 1.8 | 5.1 | ||
| 3 | 1.28 | 1.39 | 1.34 | 8.6 | 4.7 | ||
| 4 | 0.37 | 0.44 | 0.38 | 18.9 | 3.4 | ||
| 5 | 0.05 | 0.06 | 0.05 | 20.0 | 5.9 | ||
| 6 | -0.14 | -0.17 | -0.15 | 21.4 | 3.8 | ||

|
| 图 9 挠度在模型修正前后的变化 Fig. 9 Variation of deflections before and after model updating |
| |
表 4和图 10为模型修正前后识别参数的数值比较。可以看出,选定的5个刚度折减系数的终值均比它们的初始值有所减少。对于主梁,2#主梁的抗弯刚度折减系数ηk2下降最大;对于铰缝,第1条铰缝的抗剪刚度折减系数ηq2下降最大。1#主梁的抗弯刚度折减系数终值大于2#主梁,但是考虑事实上1#主梁处的防撞护杆对其抗弯能力有一定的协助作用,故1#梁自身的损伤程度是大于2#主梁的。该桥梁的损伤情况是,从1#主梁到3#主梁逐渐减弱,铰缝也是类同。折减系数参数识别结果也表明,该桥1#、2#主梁和铰缝损伤已造成其实际刚度比初始刚度(设计刚度)降低很多,其自身性能及协同工作性能较差,需要及时进行维修加固。
| 参数 | 修正前后对比 | |||
| 修正前 | 修正后 | 参数变化/% | ||
| 主梁刚度损伤折减系数 | ηk1 | 1 | 0.79 | -21.0 |
| ηk2 | 1 | 0.75 | -25.0 | |
| ηk3 | 1 | 0.92 | -8.0 | |
| 铰缝刚度损伤折减系数 | ηq1 | 1 | 0.54 | -46.0 |
| ηq2 | 1 | 0.69 | -31.0 | |

|
| 图 10 待修正参数变化 Fig. 10 Variation of parameters to be updated |
| |
4.4 荷载横向分布系数计算结果
根据前面模型修正的结果,得到了主梁刚度损伤折减系数ηk1,ηk2,ηk3和铰缝刚度损伤折减系数ηq1,ηq2修正后的数值,代入式(13),便可计算得到每条铰缝的剪力值,再根据剪力与影响线竖标值关系,得到修正后的各主梁荷载横向分布影响线的竖标值。
图 11示出了各梁荷载横向分布的实测影响线及模型修正前后的计算影响线。在影响线上,按照规范加载,得到各主梁的荷载横向分布系数(已计入横向车道布载系数),列于表 5。

|
| 图 11 横向分布影响线对比 Fig. 11 Comparison of influence lines of horizontal distribution |
| |
| 梁号 | 实测值 | 模型修正法 | 相对误差/% | |||
| 修正前 | 修正后 | 修正前 | 修正后 | |||
| 1# | 0.636 | 0.676 | 0.633 | 6.3 | -0.5 | |
| 2# | 0.576 | 0.606 | 0.569 | 5.2 | -1.2 | |
| 3# | 0.493 | 0.504 | 0.494 | 2.2 | -0.2 | |
| 4# | 0.483 | 0.496 | 0.488 | 2.7 | 1.0 | |
| 5# | 0.594 | 0.606 | 0.597 | 2.0 | 0.5 | |
| 6# | 0.661 | 0.676 | 0.665 | 2.3 | 0.6 | |
由图 11和表 5可知,荷载横向分布影响线竖标值和分布系数在模型得到修正后均与实测值吻合度良好。对于荷载横向分布系数,在模型修正前,计算值与实测值偏差较大,最大误差值为6.3%,而在模型修正后计算值与实测值很吻合,最大误差仅为1.2%。算例结果验证了本研究方法对于求解发生损伤的装配式T梁桥的荷载横向分布系数的可靠性。
5 结论针对铰缝连接的装配式T梁桥或板桥,基于铰接板(梁)法及模型修正理论,提出了改进方法,用来识别桥梁损伤程度,以及计算荷载横向分布。
(1) 先建立一个同时计入主梁和铰缝刚度劣化影响的简化计算模型,确定以主梁抗弯刚度和铰缝抗剪刚度作为待修正参数,并引入相应的损伤折减系数ηk和ηq,即结构损伤刚度与未损伤刚度(设计刚度)的比值。
(2) 以静力响应实测值与计算值的残差作为目标函数,通过L-M法和G-N法相结合对目标函数进行优化,最终得到修正后的刚度参数。刚度参数修正终值可反映主梁和铰缝的损伤程度,同时由它们计算现状荷载横向分布影响线及横向分布系数。
(3) 以一座在役T梁桥为实例验证,选取损伤主梁和铰缝刚度的折减系数进行修正,以静载试验工况下各梁跨中挠度为目标,优化计算过程快捷稳定。结果显示,修正模型的挠度与荷载横向分布的计算值与实测值吻合良好,而模型修正前两者误差较大,不可接受。因此对于损伤桥梁,需对其计算计算模型修正,本研究计算方法可行,结果可靠。
| [1] |
卫军, 李沛, 徐岳, 等. 空心板铰缝协同工作性能影响因素分析[J]. 中国公路学报, 2011, 24(2): 29-33. WEI Jun, LI Pei, XU Yue, et al. Influencing Factor Analysis on Coordinated Working Performance of Hinge Joint in Hollow Slab[J]. China Journal of Highway and Transport, 2011, 24(2): 29-33. |
| [2] |
周正茂, 袁桂芳, 田清勇. 基于铰缝刚度的板梁桥铰缝损伤评价方法[J]. 中国公路学报, 2013, 26(5): 121-130. ZHOU Zheng-mao, YUAN Gui-fang, TIAN Qing-yong. Evaluation Method for Hinge Joint Damage in Multi-slab Girder Bridge Based on Stiffness of Hinge Joint[J]. China Journal of Highway and Transport, 2013, 26(5): 121-130. |
| [3] |
KIM Y J, TANOVIC R, WIGHT R G. Recent Advances in Performance Evaluation and Flexural Response of Existing Bridges[J]. Journal of Performance of Constructed Facilities, 2009, 23(3): 190-200. |
| [4] |
EOM J. Verification of Lateral Live Load Distribution Factors for Continuous Steel Girder Bridges Based on Diagnostic Testing Results[J]. Journal of the Korea Institute for Structural Maintenance & Inspection, 2009, 13(4): 180-187. |
| [5] |
ZHANG S K. Simplified Live Load Distribution Factor Equations for Tennessee Highway Bridge Design[D]. Cookeville: Tennessee Technological University, 2012.
|
| [6] |
FAUSETT R W. Live-load Test and Finite-element Model Analysis of an Integral Abutment Concrete Girder Bridge[D]. Logan: Utah State University, 2013.
|
| [7] |
刘华, 叶见曙, 俞博, 等. 桥梁荷载横向分布系数计算方法[J]. 交通运输工程学报, 2009, 9(1): 62-66. LIU Hua, YE Jian-shu, YU Bo, et al. Calculation Method of Transversal Distribution Factor for Bridge Load[J]. Journal of Traffic and Transportation Engineering, 2009, 9(1): 62-66. |
| [8] |
聂瑞锋, 石雪飞, 阮欣, 等. 在役多车道空心板梁桥弯矩横向分布系数计算方法研究[J]. 桥梁建设, 2014, 44(2): 56-60. NIE Rui-feng, SHI Xue-fei, RUAN Xin, et al. Research of Calculation Method for Moment Lateral Distribution Factors of Multi-lane Hollow Slab Beam Bridges in Service[J]. Bridge Construction, 2014, 44(2): 56-60. |
| [9] |
魏志刚, 刘寒冰, 时成林, 等. 考虑桥面铺装作用的简支梁桥横向分布系数计算[J]. 吉林大学学报: 工学版, 2018, 48(1): 105-112. WEI Zhi-gang, LIU Han-bing, SHI Cheng-lin, et al. Calculation of Transverse Distribution Coefficient of Simply Supported Beam Bridge with Effect of Bridge Deck Pavement[J]. Journal of Jilin University: Engineering and Technology Edition, 2018, 48(1): 105-112. |
| [10] |
项贻强, 何余良, 刘丽思, 等. 考虑滑移的多梁式组合小箱梁桥荷载横向分布[J]. 哈尔滨工业大学学报, 2012, 44(8): 113-118. XIANG Yi-qiang, HE Yu-liang, LIU Li-si, et al. Lateral Load Distribution of Multi-box Steel-concrete Composite Girder Bridges for Considering Slipping Effect[J]. Journal of Harbin Institute of Technology, 2012, 44(8): 113-118. |
| [11] |
梁鹏, 李斌, 王秀兰, 等. 基于桥梁健康监测的有限元模型修正研究现状与发展趋势[J]. 长安大学学报: 自然科学版, 2014, 34(4): 52-61. LIANG Peng, LI Bin, WANG Xiu-lan, et al. Present Research Status and Development Trend of Finite Element Model Updating Based on Bridge Health Monitoring[J]. Journal of Chang'an University: Natural Science Edition, 2014, 34(4): 52-61. |
| [12] |
魏锦辉, 任伟新, 万华平. 基于模态柔度的有限元模型修正方法[J]. 振动与冲击, 2013, 32(13): 106-111. WEI Jin-hui, REN Wei-xin, WAN Hua-ping. Finite Element Model Updating Method Based on Modal Flexibility[J]. Vibration and Impact, 2013, 32(13): 106-111. |
| [13] |
张征文, 李永庆. 基于荷载试验数据修正桥梁结构有限元计算模型的研究[J]. 西安建筑科技大学学报: 自然科学版, 2014, 46(2): 233-240. ZHANG Zheng-wen, LI Yong-qing. Study of Bridge Structure FEM Updating Based on Load Test Experimental Data[J]. Journal of Xi'an University of Architectural Science and Technology: Natural Science Edition, 2014, 46(2): 233-240. |
| [14] |
宗周红, 夏樟华. 联合模态柔度和静力位移的桥梁有限元模型修正方法[J]. 中国公路学报, 2008, 21(6): 43-49. ZONG Zhou-hong, XIA Zhang-hua. Finite Element Model Updating Method of Bridge Combined Modal Flexibility and Static Displacement[J]. China Journal of Highway and Transport, 2008, 21(6): 43-49. |
| [15] |
彭涛, 田仲初, 张建仁, 等. 基于多目标优化的混凝土斜拉桥静动力有限元模型修正[J]. 振动与冲击, 2018, 37(21): 108-116. PENG Tao, TIAN Zhong-chu, ZHANG Jian-ren, et al. Static and Dynamic Finite Element Model Updating for a Concrete Cable-stayed Bridge Based on Multi-objective Optimization[J]. Vibration and Impact, 2018, 37(21): 108-116. |
| [16] |
李院军, 邬晓光, 黄成, 等. 考虑主梁损伤的装配式梁桥荷载横向分布系数计算[J]. 铁道科学与工程学报, 2019, 16(6): 1459-1465. LI Yuan-jun, WU Xiao-guang, HUANG Cheng, et al. Calculation of Transverse Load Distribution Coefficient of Assembled Girder Bridge Considering Main Girder Damage[J]. Journal of Railway Science and Engineering, 2019, 16(6): 1459-1465. |
| [17] |
成琛, 沈成武, 许亮. 用铰接板(梁)法计算有损伤桥梁的横向分布系数[J]. 武汉理工大学学报: 交通科学与工程版, 2004, 28(2): 229-231, 251. CHENG Chen, SHEN Cheng-wu, XU Liang. The Hinged-jointed Plate Method for Calculating Transverse Load Distribution on a Damaged Bridge[J]. Journal of Wuhan University of Technology: Transportation Science & Engineering, 2004, 28(2): 229-231, 251. |
| [18] |
宗周红, 任伟新. 桥梁有限元模型修正和模型确认[M]. 北京: 人民交通出版社, 2012. ZONG Zhou-hong, REN Wei-xin. Finite Element Model Updating and Model Validation of Bridge Structures[M]. Beijing: China Communications Press, 2012. |
| [19] |
谭冬莲, 肖汝诚. Levenberg-Marquardt法与Gauss-Newton法相结合在桥梁结构静力参数识别中的应用[J]. 公路交通科技, 2007, 24(4): 95-98. TAN Dong-lian, XIAO Ru-cheng. Application of the Combination of Levenberg-Marquart with Gauss-Newton in Static Parameter Identification of Bridge Structure[J]. Journal of Highway and Transportation Research and Development, 2007, 24(4): 95-98. |
 2021, Vol. 38
2021, Vol. 38
