扩展功能
文章信息
- 丛华锋, 苗瑞
- CONG Hua-feng, MIAO Rui
- 基于动态时空特征关联规则的多种服务类型网约车补贴策略研究
- Study on Subsidy Strategy of Multi-service Online Car-hailing Based on Dynamic Spatio-temporal Characteristic Association Rule
- 公路交通科技, 2021, 38(3): 144-150
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 144-150
- 10.3969/j.issn.1002-0268.2021.03.018
-
文章历史
- 收稿日期: 2020-11-26
2. 上海交通大学 船舶海洋与建筑工程学院,上海 200240;
3. 上海交通大学 中国城市治理研究院,上海 200030;
4. 上海交通大学 海洋工程国家重点实验室,上海 200240
2. School of Naval Architecture, Ocean & Civil Engineering, Shanghai Jiaotong University, Shanghai 200240, China;
3. China Institute for Urban Governance, Shanghai Jiaotong University, Shanghai 200030, China;
4. State Key Laboratory of Ocean Engineering, Shanghai Jiaotong University, Shanghai 200240, China
随着共享经济的蓬勃发展, 网约车行业市场需求逐年增长, 市场交易规模快速扩张。网约车的服务类型从早期的单一类型, 转变为普通车型、高端车型等多种服务类型[1]。不同服务类型在不同时空状态下, 存在人车不匹配的问题[2], 例如, 在用车高峰时段, 以快车为代表的普通车型需求较大, 常常出现需要等待的情况[3], 以专车、豪华车为代表的具有高利润高附加值的高端车型却仍有运力, 因此, 基于时空特征判断各种服务类型在不同时空特征下的用车需求, 协调普通车型与高端车型人车匹配, 实现精细化运营, 是下一阶段网约车企业实现收益增长的关键[4], 也是中国城市治理的有效手段。
研究乘客在不同时空特征下对于服务类型选择的关联规则及替代关系是网约车平台进行补贴决策的重要参考依据[5]。目前, 基于时空特征的关联规则研究在网约车领域应用较少, 主要应用于事故分析[6]、位置匹配[7]等方面, 基于时空特征的数据挖掘研究主要集中在收益优化方面[8-9]。在网约车的运营策略方面, 面对某种服务类型人车不匹配的情况, 网约车企业会通过发放补贴的运营策略进行调节, 尤其是针对高端车型的补贴策略, 一方面直接影响空载率, 另一方面, 影响平台整体收益。金振广通过优化网约车整体补贴策略提升平台整体收益[10]。Zhang采用动态定价方法增加网约车企业收益[11]。JIANG利用支持向量机对短期网约车需求进行预测, 帮助网约车企业制定相应策略[12]。Bellos通过设计多样化网约车产品实现收益增长[13]。左文明研究网约车服务质量对乘客使用意向的影响, 改进产品设计[14]。此外, 部分研究考虑到网约车进入传统出租车市场的垄断性影响[15]、基于地域比较的运营策略[16]和不同出行方式的乘客选择[17]。
大多数研究把网约车当成一个整体作为研究对象, 没有考虑到不同服务类型间的区别和双边市场效应[18]。此外, 现有的网约车运营策略缺乏基于关联规则的研究, 没有考虑时空特征的动态影响。因此, 本研究基于双边市场效应, 采用Apriori算法对不同网约车服务类型的时空特征关联规则进行研究。根据关联规则结果设定动态参数, 作为演化博弈的初始条件, 使初始条件随时空特征动态变化, 最终, 在不同时空特征下, 依据演化博弈结果制定相应的补贴策略, 提高整体收益, 实现精细化经营。
1 基于时空特征的服务类型关联规则 1.1 数据收集本研究使用的数据来自合作企业内部订单数据及外部POI(point of information信息点)、天气等数据, 涵盖普通车型、高端车型多种网约车类型的订单情况。
1.2 数据预处理将收集的原始数据进行数据预处理, 调整为算法输入的结构。
(1) 数据清洗: 针对订单关键数据、GPS经纬度数据等不能直接填写或计算缺失值的数据, 利用删除元组等方法进行数据清洗。
(2) 数据集成: 将内部数据与外部天气数据、POI数据进行投影坐标系转换及区域匹配, 将订单数据表、外部POI信息表、外部天气表归并为一个表。
(3) 将原始的时间戳转化为时间片。对时间进行有监督的切片离散化, 考虑到1 h的颗粒度基本可以满足本研究场景时间上的分层要求, 因此, 本研究选择以1 h为时间片, 一天分为24个时间片。
相关的参数及符号如表 1所示。设定是否工作日WD有2种情况, WD_1表示是工作日, WD_0表示不是工作日, 同理, 出发时间DT共24种表达, POI类型PT共6种表达(商务PT_1、餐饮PT_2、商区PT_3、学区PT_4、景区PT_5、住宅PT_6), 是否雨天RA有2种表达(晴天RA_0、雨天RA_1), 服务类型FA有2种表达(普通车型FA_0、高端车型FA_1), 归并后的样例数据见表 1。预处理后的数据可以直接应用于Apriori算法。
| 字段 | 符号 | 类型 | 实例 | 表达 |
| 是否工作日 | WD | Bool | 1 | WD_1 |
| 出发时间 | DT | String | 13∶09∶46 | DT_13 |
| POI类型 | PT | String | 餐饮 | PT_2 |
| 是否雨天 | RA | Bool | 0 | RA_0 |
| 服务类型 | FA | String | 普通车型 | FA_1 |
1.3 基于Apriori的网约车服务类型关联规则分析
由于Apriori算法的支持度有最小阈值限制, 针对原始数据各服务类型订单数量差距较大的情况, 从预处理后的数据中随机挑选相同数量各10 000条普通车型订单和高端车型订单, 形成集合D。对数据进行多次测试处理, 设定最小支持度阈值为5%, 最小置信度阈值为40%, 利用Apriori算法进行关联规则分析。结果如图 1所示, 普通车型FA_0、高端车型FA_1共有12条关联规则。

|
| 图 1 车辆服务类型关联规则 Fig. 1 Association rules of vehicle service types |
| |
在图 1中, 利用Apriori算法挖掘的关联规则较多, 难以进行有效分析, 仅仅设定支持度和置信度无法筛除较弱的关联规则, 利用χ2检验进一步遴选, 得到强关联规则。以任意两个参数DT和PT为例, 若DT有c个可能值, PT有r个可能值, 令(DTi, PTj)表示DT=dti、PT=ptj的联合事件, 其计算方式为
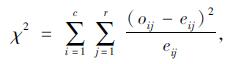
|
(1) |
式中, oij为联合事件(DTi, PTj)的观测频度; eij为联合事件(DTi, PTj)的期望频度。通过χ2检验后, 得到部分关联规则如表 2所示。
| 服务类型 | 强关联规则 | 支持度/% | 置信度/% |
| 普通车型 | PT_2, RA_1 | 7.7 | 42.6 |
| 普通车型 | DT_18, PT_2 | 6.4 | 45.5 |
| 高端车型 | PT_3, RA_1 | 10.4 | 57.4 |
| 高端车型 | DT_18, PT_2 | 7.6 | 54.5 |
在表 2中, 两种服务类型强关联规则的支持度都超过7%, 表明强关联规则对应的时空特征的用车需求极大, 极有可能出现人车不匹配的情况。此外, 普通车型和高端车型出现的强关联规则存在差异, 相比而言, 高端车型的支持度和置信度都高于普通车型, 这说明高端车型的需求比普通车型的需求更加集中。
普通车型与高端车型有相同的强关联规则DT_18, PT_2, 即17点至18点的餐饮区域, 说明原本一部分普通车型乘客, 在这样的场景下转而选择使用价格更高、舒适度更好的高端车型, 在特定时空特征下, 普通车型与高端车型存在替代品关系。这是因为在高峰时期或在天气条件恶劣的状态下, 普通车型往往等车时间过久, 体验更好的高端车型却仍有运力, 出现人车不匹配的情况。一部分普通车型乘客为了提升消费体验, 会显著减低价格敏感度, 选择花更多钱乘坐高端车型。因此, 网约车企业可以利用普通车型和高端车型的替代关系, 在用车高峰期对高端车型实施补贴, 让一部分原来选择普通车型的乘客转而选择高端车型。一方面实现人车匹配, 另一方面增加整体收益。
为了实施最优补贴策略, 实现精细化运营, 本研究基于时空特征得到的关联规则, 利用演化博弈制定补贴策略。因此, 需要设计一个随时空特征动态变化的参数, 用其衡量特定时空特征下网约车服务需求, 将时空特征的关联规则结果与后文针对补贴策略的演化博弈连接起来, 使演化博弈的条件受时空特征的影响动态变化, 最终得到特定时空特征下的最优补贴策略。
本研究设定参数α, 表示网约车服务需求大小。考虑到乘客对于天气、消费场景以及等车时间等需求因素可利用前文关联规则中的支持度和置信度客观表示, 将α值的计算方法设置为某一特定时空特征对应的参数集合A与普通车型关联规则的支持度及置信度之和乘以调整系数1.2。同时, α值也反映双边市场中普通车型乘客选择高端车型作为替代方案的可能性。

|
(2) |
时空特征的动态变化使α值不断变化, 导致网约车企业在不同时空特征下, 需要采取不同的补贴策略应对市场需求的变化。本研究使用演化博弈方法, 将时空特征的关联规则结果与演化博弈结果联系起来, α的值对应一个特定的时空特征, 演化博弈的初始条件在α的影响下动态变化, 最终获得特定时空特征下的最优补贴策略。为了直观地表达, 假设高端车型不会出现运力不足的情况; 补贴策略仅针对高端车型服务; 乘客在做出决策时, 只能选择“普通车型”和“高端车型”两种服务类型, 并且拥有完全信息; 研究的乘客群体为理性消费人, 在相同客观条件下, 优先选择高性价比的普通车型服务; 在网约车企业进行价格补贴时, 基于理性的收益效果, 仍会产生正收益。
演化博弈的参与者是网约车和乘客, 二者都有两种行动策略。网约车企业可以选择“补贴”策略或“无补贴”策略。乘客可以选择“普通车型”策略或“高端车型”策略。二者的目标是最大程度地提升自身收益, 相关符号如表 3所示, 其中, α值基于时空特征动态变化。
| 符号 | 名称 | 含义 |
| S | 补贴收益 | 指网约车企业提供高端车型补贴而付出的成本,也是乘客享受的补贴收益。 |
| C | 价格收益 | 指乘客因为选择普通车型,获得的低价格收益。 |
| T | 时间收益 | 指乘客选择高级车型时,节约时间产生的效用收益。 |
| E | 服务收益 | 指乘客选择高级车型时,提升舒适度而产生的效用收益。 |
| αI | 机会增加收益 | 指网约车企业因为实施补贴策略而增加各类车型的增值收益。 |
| αP | 非补贴等待损失 | 指网约车企业因为无补贴而使得普通车型承载力不够时损失的机会收益且P < I。 |
当网约车企业选择补贴策略而乘客选择高端车型时, 网约车企业的收益为αI-S, 网约车企业获得机会增加收益。需求α越大, 机会增加收益αI越大。乘客的收益为S+T+E, 包括补贴收益、时间收益和服务收益。
当网约车企业选择补贴策略而乘客选择普通车型时, 网约车企业的收益为-S。乘客的收益为C。
当网约车企业选择无补贴策略而乘客选择高端车型时, 网约车企业的收益为0。乘客的收益为T+E。
当网约车企业选择无补贴策略而乘客选择普通车型时, 网约车企业的收益为αP, 在这种情况下, 需求α越大, 非补贴等待损失αP就越大, 乘客的收益为C。
基于以上分析, 建立了演化博弈模型, 如表 4所示。
| 网约车企业 | 乘客 | |
| 高端车型 | 普通车型 | |
| 补贴 | αI-S,S+T+E | -S,C |
| 无补贴 | 0,T+E | αP,C |
2.2 复制动态分析
设网约车企业选择“补贴”的策略比例是x, 则“无补贴”的策略比例是1-x; 乘客选择“高端车型”的策略比例是y, 则乘客选择“普通车型”的策略比例是1-y。
设网约车企业选择“补贴”策略、“无补贴”策略的期望收益和平均期望收益分别为Ex1, Ex2和Ex:
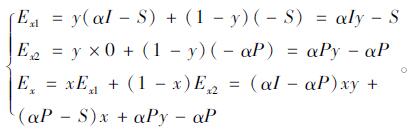
|
(3) |
网约车企业决策的复制动态方程为:
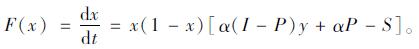
|
(4) |

|
(5) |
依据复制动态方程稳定性定理,
当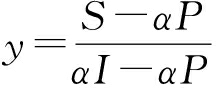 时, F(x)≡0, 此时, 对于任何策略比例的x值, 网约车企业的策略都是稳定策略, 且策略比例不会随时间产生变化。
时, F(x)≡0, 此时, 对于任何策略比例的x值, 网约车企业的策略都是稳定策略, 且策略比例不会随时间产生变化。
当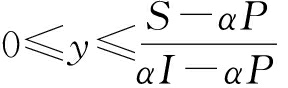 时, F′(x)|x=0 < 0, F′(x)|x=1 > 0, 此时, x=0为稳定演化点, 即当乘客选择高端车型的策略比例低于
时, F′(x)|x=0 < 0, F′(x)|x=1 > 0, 此时, x=0为稳定演化点, 即当乘客选择高端车型的策略比例低于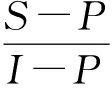 时, 网约车企业选择无补贴策略是稳定策略。
时, 网约车企业选择无补贴策略是稳定策略。
当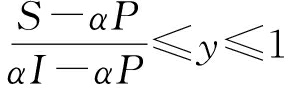 时, F′(x)|x=0 > 0, F′(x)|x=1 < 0, 此时, x=1为稳定演化点, 即当乘客选择高端车型的策略比例高于
时, F′(x)|x=0 > 0, F′(x)|x=1 < 0, 此时, x=1为稳定演化点, 即当乘客选择高端车型的策略比例高于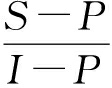 时, 网约车企业择补贴策略是稳定策略。
时, 网约车企业择补贴策略是稳定策略。
同理, 乘客选择“高端车型”策略的期望收益为Ey1, “普通车型”策略的期望收益为Ey2, 平均期望为Ey。
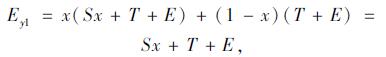
|
(6) |
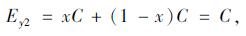
|
(7) |
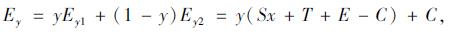
|
(8) |
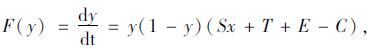
|
(9) |
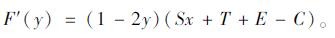
|
(10) |
当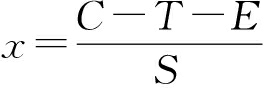 时, F(y)≡0, 对于乘客而言, 无论什么决策都达到稳定策略。
时, F(y)≡0, 对于乘客而言, 无论什么决策都达到稳定策略。
依据上文网约车企业和乘客的复制动态方程分析, 共得到5个局部均衡点(0, 0), (0, 1), (1, 0), (1, 1), 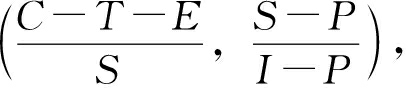 对局部均衡点进行渐近稳定性分析。雅克比矩阵为:
对局部均衡点进行渐近稳定性分析。雅克比矩阵为:
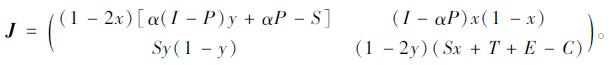
|
(11) |
雅克比矩阵的迹为:
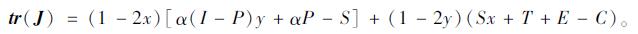
|
(12) |
雅克比矩阵的行列式为:
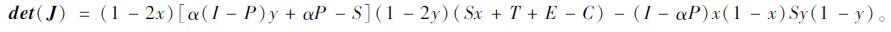
|
(13) |
依据李雅普诺夫第一法则, 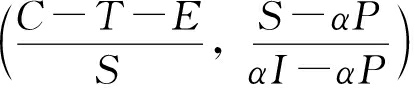 在雅可比矩阵的迹恒等于0, 因此
在雅可比矩阵的迹恒等于0, 因此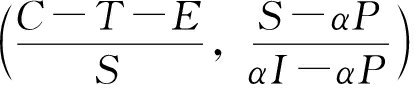 为鞍点, (0, 1)和(0, 1)无渐进稳定点(EES)。局部均衡点(0, 0), (1, 1)的渐进稳定性分析如表 5所示。当满足条件αP-S < 0且T+E-C < 0时, (0, 0)状态为策略稳定点; 当满足条件S-αI < 0且C-S-T-E < 0时, (1, 1)为该策略稳定点。
为鞍点, (0, 1)和(0, 1)无渐进稳定点(EES)。局部均衡点(0, 0), (1, 1)的渐进稳定性分析如表 5所示。当满足条件αP-S < 0且T+E-C < 0时, (0, 0)状态为策略稳定点; 当满足条件S-αI < 0且C-S-T-E < 0时, (1, 1)为该策略稳定点。
| 稳定点 | 条件 | 矩阵判断 | 状态 |
| (0, 0) | αP-S>0且T+E-C>0 | tr(J)>0,det(J)>0 | 不稳定 |
| αP-S>0且T+E-C < 0 | tr(J)未知,det(J) < 0 | 不稳定 | |
| αP-S < 0且T+E-C>0 | tr(J)未知,det(J) < 0 | 不稳定 | |
| αP-S < 0且T+E-C < 0 | tr(J) < 0,det(J)>0 | 渐进稳定点 | |
| (1, 1) | S-αI>0且C-S-T-E>0 | tr(J)>0,det(J)>0 | 不稳定 |
| S-αI>0且C-S-T-E < 0 | tr(J)未知,det(J) < 0 | 不稳定 | |
| S-αI < 0且C-S-T-E>0 | tr(J)未知,det(J) < 0 | 不稳定 | |
| S-αI < 0且C-S-T-E < 0 | tr(J) < 0,det(J)>0 | 渐进稳定点 |
2.4 数值算例分析
设定x, y分别以0.1至0.9为初始策略比例, 步长为0.1, 在α=0.2及α=0.8的情况下分别进行算例仿真。设定其他参数的数值为I=10, S=6, P=8, C=12, E=2, T=2。
情况1:当α=0.2时, 满足条件αP-S < 0且T+E-C < 0, 无论x, y初值如何, 都收敛于(0, 0), 即ç。仿真结果如图 2所示, 横坐标为时间, 纵坐标为初始策略比例, (0, 0)为ESS。

|
| 图 2 α=0.2时仿真结果 Fig. 2 α=0.2 Simulation result when α=0.2 |
| |
在这种时空特征下, α=0.2, 网约车整体需求相对较小。因此, 大多数乘客对价格仍然敏感, 不同服务类型之间的替代关系较弱, 选择乘坐普通车型不需要等待。低价收益C大于时间收益T和服务收益E的和, 即T+E-C < 0, 大多数乘客会选择“普通车型”策略。从网约车企业的角度来看, 如果企业选择“补贴”策略, 只有少数乘客会选择价格较高的高端车型。补贴产生的成本大于非补贴等待损失产生的盈利机会, 即αP-S < 0, 因此, 网约车企业会选择“无补贴”策略, 以实现整体收入最大化。
情况2:当α=0.8时, 满足条件S-αI < 0且C-S-T-E < 0, 无论x, y初值如何, 最终都收敛于(1, 1), 仿真结果如图 3所示, 横坐标为时间, 纵坐标为初始策略比例, (1, 1)为ESS。

|
| 图 3 α=0.8时仿真结果 Fig. 3 Simulation result when α=0.8 |
| |
此时α=0.8, 部分普通车型乘客可能会选择价格更高的高端车型。根据关联规则研究, 这种时空特征可能对应较长的等待时间或恶劣天气, 此时, 乘客对价格的敏感度大幅下降, 高端车型更容易被接受。部分原本选择普通车型的乘客转而选择“高端车型”。由于该时空特征的需求量很大, 通过规模效应, 机会增加收益αI可以补偿补贴所付出的成本S, 即S-αI < 0。因此, 网约车企业会选择“补贴”策略。一方面可以缓解普通车型的过剩需求, 另一方面可以通过高端车型的高附加值来增加网约车企业整体收益。
仿真的参数α代表某种特定的时空特征, α值随关联规则对应的时空特征变化, 因此, 本模型适用于无监督学习, 在拥有一定历史数据基础上, 本模型可以为网约车企业直接提供运营策略。
3 结论本研究旨在找出不同时空特征下多种网约车服务类型的关联规则, 为网约车企业提供精细化补贴策略建议。以历史数据为基础, 利用Apriori算法寻找多种网约车服务类型的关联规则, 将关联规则结果作为演化博弈的初始条件, 以收益最大化为目的, 对网约车企业补贴策略与乘客选择进行演化博弈分析。本研究结论如下:
(1) 在不同时空特征下, 普通车型与高端车型的需求存在差异, 不同服务类型在不同时空特征下存在人车不匹配的情况。
(2) 高端车型的需求集中度更高, 且高端车型与普通车型互为替代品。针对高端车型的补贴会同时影响两种服务类型的需求。
(3) 当代表网约车需求的参数α较小时, 即整体需求较小的时空特征下, 企业选择“无补贴”策略是最优策略; 当α较大时, 乘客对不同服务类型网约车价格的敏感程度会显著降低, 进而影响演化博弈的结果, 此时企业选择“补贴”策略是最优策略。
以上研究结果是以本研究建立的模型和部分历史数据为前提。但是, 由于数据的限制, 还有一些细节有提升的空间。例如, 本研究以1 h为时间片间隔, 将一天分成24个时间片, 忽略了其他时间属性的影响, 如节假日和特殊事件等。此外, 在演化博弈中, 也没有考虑安全风险和社会影响等其他因素。因此, 未来的研究需要关注更具体的问题。
| [1] |
张爱萍, 林晓言, 陈小君. 网约车颠覆性创新的理论与实证: 以滴滴出行为例[J]. 广东财经大学学报, 2017, 32(2): 31-40. ZHANG Ai-ping, LIN Xiao-yan, CHEN Xiao-jun. Analysis of the Disruptive Innovation and Impact of IPHV with the Case of DiDi[J]. Journal of Guangdong University of Finance and Economics, 2017, 32(2): 31-40. |
| [2] |
KE J T, ZHENG H Y, YANG H Y, et al. Short-term Forecasting of Passenger Demand under On-demand Ride Services: A Spatio-temporal Deep Learning Approach[J]. Transportation Research Part C: Emerging Technologies, 2017, 85: 591-608. |
| [3] |
赵道致, 杨洁, 李志保. 考虑等待时间的网约车与出租车均衡定价研究[J]. 系统工程理论与实践, 2020, 40(5): 1229-1241. ZHAO Dao-zhi, YANG Jie, LI Zhi-bao. Research on the Equilibrium Pricing of Online Car-hailing and Taxi Services Considering the Waiting Time[J]. System Engineering-Theory and Practice, 2020, 40(5): 1229-1241. |
| [4] |
CRAMER J, KRUEGER A B. Disruptive Change in the Taxi Business: The Case of Uber[J]. American Economic Review, 2016, 106(5): 177-182. |
| [5] |
ZHANG Jun-bo, ZHENG Yu, QI De-kang, et al. Predicting Citywide Crowd Flows Using Deep Spatiotemporal Residual, Networks[J]. Artificial Intelligence, 2018, 259: 147-166. |
| [6] |
DILLS A K, MULHOLLAND S E. Ride-sharing, Fatal Crashes, and Crime[J]. Southern Economic Journal, 2016, 84(4): 965-991. |
| [7] |
HARISH G, SUBRAMANIAN U. Your Uber Is Arriving: Managing On-demand Workers Through Surge Pricing, Forecast Communication, and Worker Incentives[J]. Management Science, 2019, 65(5): 1995-2014. |
| [8] |
LI Y X, LU J, ZHANG L. Taxi Booking Mobile App Order Demand Prediction Based on Short-term Traffic Forecasting[J]. Transportation Research Record, 2017, 2634: 57-68. |
| [9] |
CHAUDHARI H A, BYERS J W, TERZI E. Putting Data in the Driver's Seat: Optimizing Earnings for On-demand Ride-hailing[C]//The Eleventh ACM International Conference. [S. l. ]: ACM, 2018: 90-98.
|
| [10] |
金振广, 胡大伟, 吴雪. 网约车排队等候条件下乘客服务类型选择演化博弈分析[J]. 交通工程, 2019, 19(6): 66-71, 78. JIN Zhen-guang, HU Da-wei, WU Xue. Evolutionary Game Analysis of Passengers' Service Type Selection under Queuing and Waiting Conditions of Online Car-hailing[J]. Journal of Transportation Engineering, 2019, 19(6): 66-71, 78. |
| [11] |
ZHANG W B, UKKUSURI S V. Optimal Fleet Size and Fare Setting in Emerging Taxi Markets with Stochastic Demand[J]. Computer-Aided Civil and Infrastructure Engineering, 2016, 31(9): 647-660. |
| [12] |
JIANG S, CHEN W T, LI Z H, et al. Short-term Demand Prediction Method for Online Car-hailing Services Based on a Least Squares Support Vector Machine[J]. IEEE Access, 2019, 99(7): 11882-11891. |
| [13] |
BELLOS I, FERGUSON M, TOKTAY L B. The Car Sharing Economy: Interaction of Business Model Choice and Product Line Design[J]. |
| [14] |
左文明, 朱文锋. 分享经济下基于SERVQUAL的网约车服务质量管理研究: 以滴滴出行和优步为例[J]. 管理案例研究与评论, 2018, 11(4): 349-367. ZUO Wen-ming, ZHU Wen-feng. Research on Service Quality Management of Online Car-hailing Based on SERVQUAL in Sharing Economy: Case Study of Didichuxing and Uber[J]. Journal of Management Case Studies, 2018, 11(4): 349-367. |
| [15] |
HARDING S, KANDLIKAR M, GULATI S. Taxi Apps, Regulation, and the Market for Taxi Journeys[J]. Transportation Research Part A: Policy and Practice, 2016, 88: 15-25. |
| [16] |
RAYLE L, DANIELLE D, CHAN N, et al. Just a Better Taxi? A Survey-based Comparison of Taxis, Transit, and Ridesourcing Services in San Francisco[J]. Transport Policy, 2016, 45: 168-178. |
| [17] |
董小楠, 闫章存, 赵怀明, 等. 基于时空约束的出行方式选择行为分析[J]. 公路交通科技, 2020, 37(9): 104-112. DONG Xiao-nan, YAN Zhang-cun, ZHAO huai-ming, et al. Analysis on Travel Mode Choice Behavior Based on Spatial-temporal Constraint[J]. Journal of Highway and Transportation Research and Development, 2020, 37(9): 104-112. |
| [18] |
程贵孙, 陈宏民, 孙武军. 双边市场视角下的平台企业行为研究[J]. 经济理论与经济管理, 2006(9): 55-60. CHENG Gui-sun, CHEN Hong-min, SUN Wu-jun. Behaviors of Platform Firms from the Perspective of Bilateral Market[J]. Economic Theory and Business Management, 2006(9): 55-60. |
 2021, Vol. 38
2021, Vol. 38
