扩展功能
文章信息
- 姚昌宇, 柳祖鹏, 何雅琴, 张涛
- YAO Chang-yu, LIU Zu-peng, HE Ya-qin, ZHANG Tao
- 基于NEMA双环相位与合流相位的感应控制策略
- Actuated Control Strategy Based on NEMA Dual-ring and Merging Phases
- 公路交通科技, 2021, 38(3): 105-112
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 105-112
- 10.3969/j.issn.1002-0268.2021.03.014
-
文章历史
- 收稿日期: 2020-04-09
信号交叉口的通行能力影响城市交通网络服务水平, 优化交叉口的信号控制方案, 可以提高信号交叉口的通行效率, 从而改善交通网络的性能。
国内研究者对于信号交叉口的放行策略研究大多数是将感应控制和算法进行结合, 罗霞等学者[1]将交叉口分为变速控制区和匀速行驶区, 对即将进入交叉口的车辆通过遍历树算法搜索出所有无冲突通行次序, 再利用人工蚁群算法求得最优解以确定最终方案。魏欣[2]提出的批处理策略中, 将车辆的到达形成车队形式, 并赋予每车队通行优先级, 利用贪心冲突矩阵决策算法和K平移优化算法求放行车队的最优次序。He[3]提出了一种启发式算法, 用于单交叉口内优先交通车辆(例如紧急车辆和公交车)在基础设施通信情况良好的情况下, 解决了同时具有多个优先权请求车辆的通行次序问题。
国内的交叉口相位设计方案中[4-5], 大多基于单环结构, 单环相位结构要求一股或多股交通流同时获得通行权, 但如果单环结构下某一相位的两股交通流不对称, 就会降低交叉口的通行效率。美国电气制造商协会(National Electrical Manufacturers Association, NEMA)制定的TS-2标准中对相位的规定有效解决了这种交通流不对称的情况。Koonce[6]和蔡云[7]介绍了NEMA相位方案中任意调整位于同环、同段的2个相位的顺序或时长完全不会对交叉口中其他相位的正常运行产生任何不良影响。研究者[8-11]发现相对于传统相位的配时方案, NEMA相位在处理相序和相位时长方面有着更高的灵活性, 它能够根据相邻信号交叉口自身的特点, 通过合理调整相序结构以及滤波带宽来保证交通流的连续。朱和等[12]提出了基于NEMA相位的绿波最大化模型。王逸[13]在双环相位方案的基础上建立了以交叉口平均延误为目标函数的双环信号配时优化模型, 并采用自适应遗传算法对模型进行求解。修伟杰[14]通过运用Visvap调节NEMA双环相位使之更适合交通流不平衡的交叉口。MA等[15]提出了一种基于双环方案的回旋处信号优化模型, 并采用两条左转弯控制线来消除回旋处的冲突点和编织段。国内外学者大都将NEMA相位和算法相结合做研究, 对于NEMA结构中主干路与次干路之间的屏障对相位方案的灵活性的影响研究课题较少。
针对已有不足, 本研究提出一种将NEMA双环相位与合流相位结合的控制策略, 以提高感应控制的灵活性。
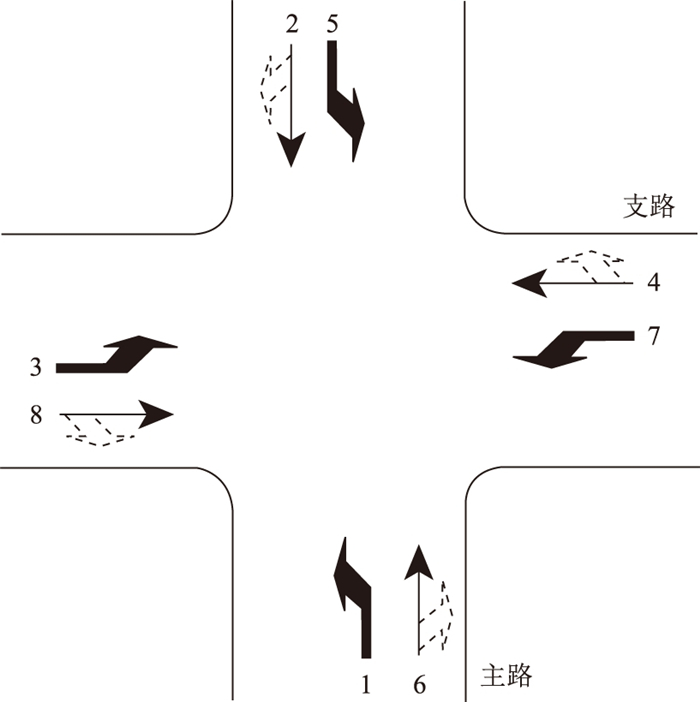
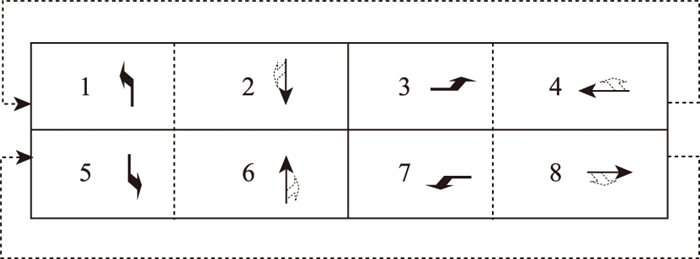
1 相位结构 1.1 NEMA双环相位NEMA相位方案主要采用双环相位结构, 由8股车流组成, 每一个方向就代表一个相位, 如图 1所示。NEMA相位结构中的上下2个环可以相对独立运行, 任意调整同环同一方向里的相位顺序和时间都不会与其他相位产生相位冲突。在双环相位方案中, 只有遇到“屏障”时, 分别处于2个环内的两股车流才必须同时开始或结束, 如车流2和5必须同时结束。NEMA双环结构如图 2所示。
|
| 图 1 NEMA相位结构的车流编号 Fig. 1 Traffic numbers of NEMA phase structure |
| |
|
| 图 2 NEMA双环相位结构 Fig. 2 NEMA dual-ring phase structure |
| |
1.2 合流相位
合流相位指在同一出口道汇合的左转和直行车流同时放行的绿灯相位。相对于现阶段国内交叉口单口放行或对向放行方式, 合流相位更适合拥有复杂的不平衡交通流的交叉口。郭英明等[16-19]利用VISSIM验证了合流相位在理论上的可行性: 当出口车道数等于或大于同时放行的左转与直行车道数之和时, 合流放行相位在理论上具备可行性。
本研究假设交叉口的道路条件符合车道均衡原则, 车辆在交叉口内左转或直行时严格按照规定车道行驶。在未来面向智能网联汽车的交通流中, 在车道均衡条件下, 假设智能车辆能自动按照车道行驶。
|
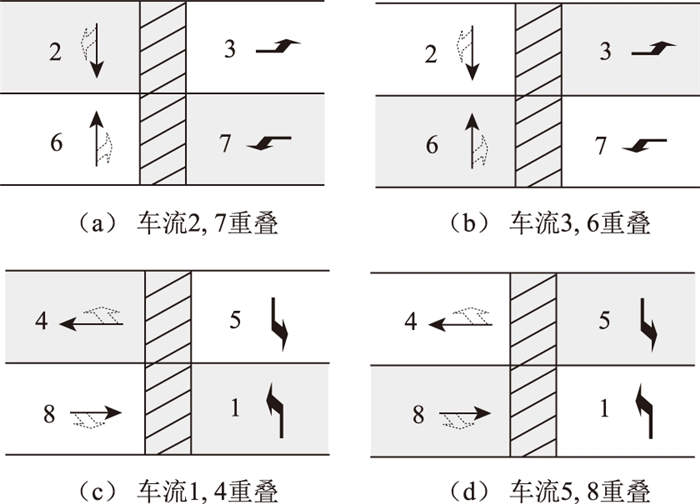
| 图 3 NEMA双环相位结构中的合流相位组合 Fig. 3 Merging phase combinations of NEMA dual-ring phase structure |
| |
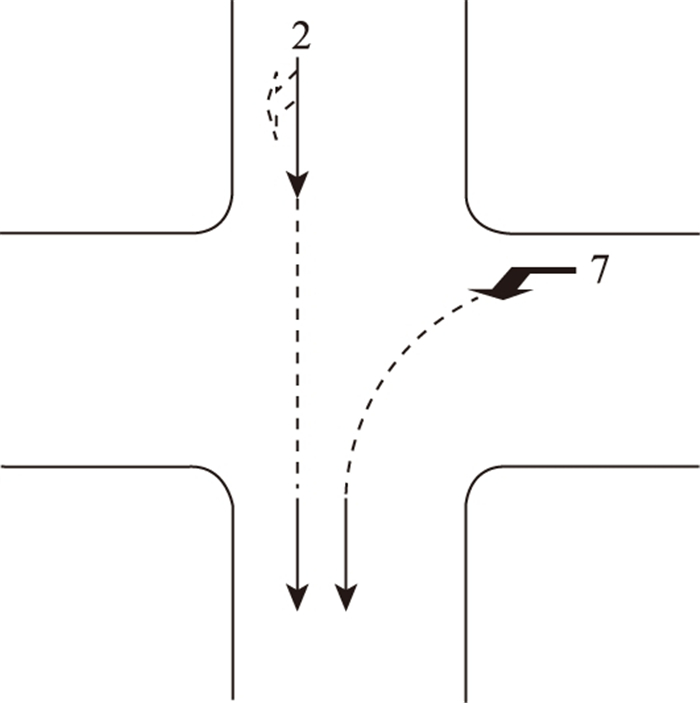
以图 3(a)为例, 车流2和车流7可同时放行, 如图中的斜线重叠部分, 这2股车流在南出口形成合流, 如图 4所示, 即北进口的直行车流和东进口的左转车流同时放行。
|
| 图 4 车流2, 7合流相位示意图 Fig. 4 Schematic diagram of merging phase of traffic flow 2 and traffic flow 7 |
| |
1.3 改进的相位结构
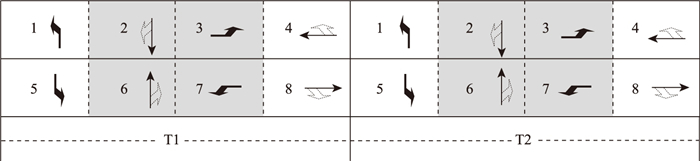
为了获得更加灵活和合理的相位切换结构, 在图 2所示的相序基础上, 考虑到合流相位(2, 7)、(3, 6)合流的可行性, 如图 5中的阴影部分, 将单个周期内主干路与次干路之间的屏障取消, 使主干道的相位和次干道的相位形成搭接结构。
|
| 图 5 在周期内融合(2, 7)、(3, 6)合流相位 Fig. 5 Merging (2, 7) and (3, 6) merging phases in a cycle |
| |
相位结构如图 5所示, 在保证车流无冲突的前提下, 图中车流之间的虚线表示各相位可自由结束, 实线表示两末尾相位须同时结束。
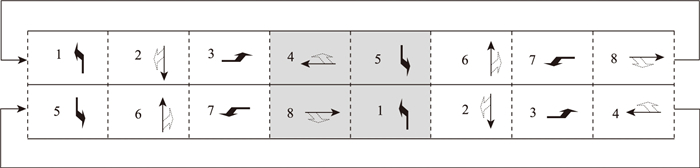
图 5所示的相位结构虽然在同一相位周期内无屏障, 但是周期末尾仍然要求相位同时结束。为了突破周期之间的屏障, 将图 5中第2周期的上下两环的位置互换, 即T2中的车流1, 2, 3, 4移至下环, 车流5, 6, 7, 8移至上环, 形成上下两环依次从车流1到车流8的顺序循环放行结构, 如图 6所示。
|
| 图 6 周期之间融合(1, 4)、(5, 8)合流相位 Fig. 6 Merging (1, 4) and (5, 8) merging phases between cycles |
| |
在该相位结构中, 通过车流(1, 4)、(5, 8)合流相位可以对原来两周期的相位形成搭接, 如图 6中的阴影部分, 使NEMA相位中的屏障完全消失, 形成8相位的大双环结构。
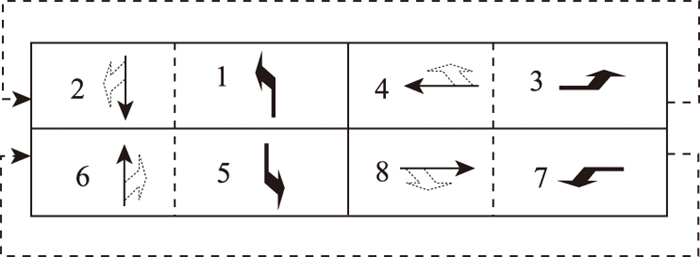
在原NEMA双环相位结构中, 车流1和2之间可以互换, 在4组车流都进行互换的情况下, 相位结构如图 7所示。
|
| 图 7 调序后的NEMA相位结构 Fig. 7 NEMA phase structure after sequence adjustment |
| |
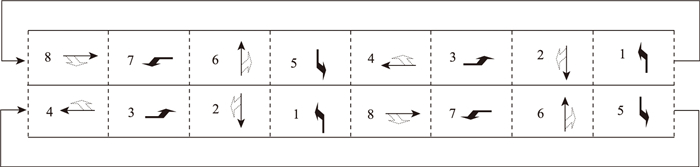
在图 7所示的相位结构中, 同时考虑2个周期前后衔接的情况, 通过车流1, 2, 3, 4和车流5, 6, 7, 8上下互换, 在周期内融合(1, 4)、(5, 8)合流相位, 在周期之间融合(2, 7)、(3, 6)合流相位, 也可以形成8相位大双环结构, 如图 8所示。
|
| 图 8 逆序的8相位大双环结构 Fig. 8 Eight-phase large dual-ring structure in reverse sequence |
| |
2 感应控制策略
交叉口的8股车流独立运行感应控制策略, 即当车流间存在较大的空档时, 结束当前相位的绿灯, 下一相位的选择是以图 6或图 8的标准相位结构为基础。感应控制策略各控制参数取值参照文献[20]: 最小绿灯时间必须确保检测器前的所有车辆在一个信号周期内全部驶离停止线。单位绿灯延长时间必须确保被检测车辆从感应检测器位置驶离停车线, 一般取3~5 s。最大绿灯时间是为了保证各相位绿灯时间延长的限度, 当达到最大绿灯时间时, 为避免其他相位排队长度过长, 则强制切换下一相位。
2.1 基本策略在感应控制策略中, 每股车流都有各自独立的控制参数, 如最小绿灯时间、最大绿灯时间、单位绿灯延长时间等。
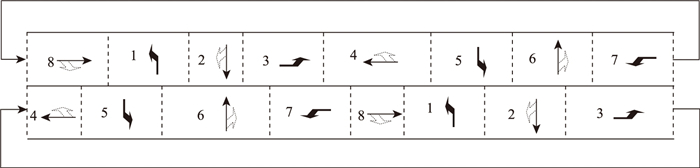
在相位结构中, 上下两环独立按次序循环放行, 可形成灵活多样的相位组合。以图 6的正序标准相位结构为基础, 8股车流放行不同的绿灯时间, 某一时段的控制状态如图 9所示。
|
| 图 9 某时段各相位绿灯时间示意图 Fig. 9 Schematic diagram of green light time for each phase in a certain period |
| |
2.2 跨越相位的冲突
基于NEMA双环相位与合流相位的感应控制策略虽然在相位结构中消除了屏障对于灵活性的影响, 但没有屏障的约束作用会发生跨越合流相位的冲突情况。为了避免切换后的下一绿灯相位和此时放行的另一绿灯相位发生冲突, 必须采取保证合流相位同时结束的措施。
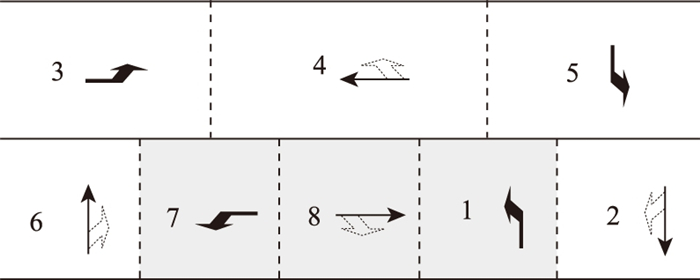
以图 6中上环的车流4为分析对象, 车流4可以与下环中的车流7, 8, 1同时放行, 如图中阴影部分。将这3股车流称为车流4的相容车流, 如图 10所示。
|
| 图 10 车流7, 8, 1是车流4的相容车流 Fig. 10 Traffic flows 7, 8, 1 are compatible flows for traffic flow 4 |
| |
在图 10中, 车流4比车流1先结束绿灯, 则下环的车流1切换到车流2时, 车流2与上环的车流5是相容的, 不会产生冲突。
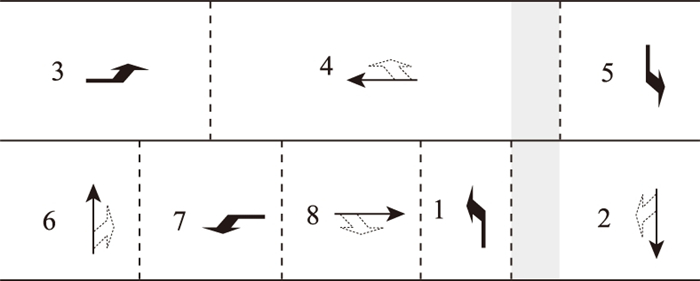
当车流1比车流4先结束绿灯, 此时下环的车流2将与上环的车流4产生冲突, 需同时结束车流1和车流4的绿灯时间, 如图 11所示。
|
| 图 11 车流4与车流1必须同时结束 Fig. 11 Traffic flow 4 and traffic flow 1 must be ended simultaneously |
| |
由图 11可见, 车流4与相容车流中的末尾车流必须同时结束绿灯, 否则会产生跨越相位的冲突。此处存在一个隐形的屏障: 当前车流的绿灯时间不能超过最后一个相容车流的绿灯时间, 如车流4的绿灯结束时间不能超过车流1绿灯结束时间。因此, 在车流1切换到车流2时, 必须同时将车流4切换到车流5。相对而言, 车流1→2的切换是主动, 车流4→5的切换是被动的。
以此类推, 车流2切换到车流3的时候, 必须同时将车流5切换到车流6。完整的8种主动和被动相位切换如表 1所示。
| 主动的相位切换 | 被动的相位切换 |
| 1→2 | 4→5 |
| 2→3 | 5→6 |
| 3→4 | 6→7 |
| 4→5 | 7→8 |
| 5→6 | 8→1 |
| 6→7 | 1→2 |
| 7→8 | 2→3 |
| 8→1 | 3→4 |
2.3 构建隐形屏障
为了保证不发生跨越相位的冲突, 在感应控制逻辑中必须为每个主动相位切换构建一道隐形屏障。在感应控制中, 如果发生如图 11所示的情况, 则控制逻辑将启动该隐形屏障, 同步进行被动相位切换。
以图 11所示的情况为例, 当车流1和4都为绿灯且必须结束车流1时, 分两种情况进行分析:
(1) 当车流1的绿灯时间达到最大绿灯时间, 为了避免下一放行车流和车流4产生冲突, 会强制结束车流1和4, 放行车流2和5。
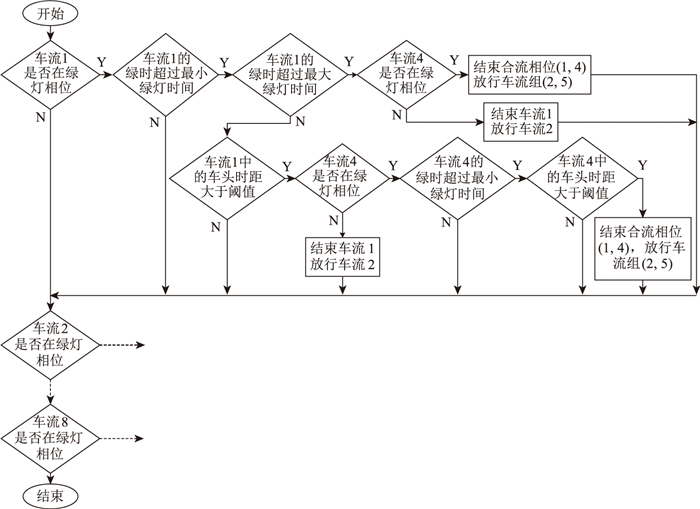
(2) 当车流1的绿灯时间大于最小绿灯时间, 小于最大绿灯时间且车头时距大于规定值时, 首先判断车流4的绿灯时间是否满足最小绿灯条件, 然后判断车头时距条件, 这两个判断有一个结果为假时, 车流1和4继续延长绿灯时间, 直到车流4满足结束条件或者车流1达到最大绿灯时间, 才同时结束车流1和4, 放行车流2和5。控制逻辑如图 12所示。
|
| 图 12 构建隐形屏障的控制逻辑 Fig. 12 Control logic for building invisible barrier |
| |
3 仿真试验
在VISSIM仿真软件中构建交叉口模型, 在VAP模块中构建感应控制逻辑, 对提出的感应控制策略进行仿真验证。
3.1 交叉口仿真模型以武汉市团结大道-园林路交叉口为仿真背景构建模型, 该交叉口4个进口道均设有3车道, 其中直行与右转共用2车道、左转专用1车道。交叉口各个出口车道数等于左转与直行车道数之和, 符合合流相位放行的要求。交叉口一共布置12个检测器, 主干路、次干路检测器的位置距离停车线50, 30 m。
3.2 仿真场景根据流量差异设置“流量均衡”、“流量不均衡”和“特殊流量”3种场景。
(1) 流量均衡场景下, 主、次干路流量比约为3∶2, 左、直、右流量之比为3∶6∶1。
(2) 流量不均衡场景下, 车流1+2≈车流5+6;车流3+ 4≈车流7+8。
(3) 特殊流量场景下, 上下两环的流量之和相等, 车流1+2 > 车流5+6;车流7+8 > 车流3+4。
以上3种场景下, 再分别设置低、中、高3种不同的饱和度, 交叉口的流量分别约为每小时2 000, 4 000辆和5 600辆。
设置两种感应控制方案: (1)基于常规NEMA双环结构的感应控制方案, 用“NEMA”表示; (2)基于NEMA和合流相位的改进感应控制方案, 用“NEMA+M”表示。
4 仿真结果及分析汇总多次仿真试验的评价数据, 得到不同条件下的交叉口平均延误对比分析图, 如图 13、图 14所示。
|
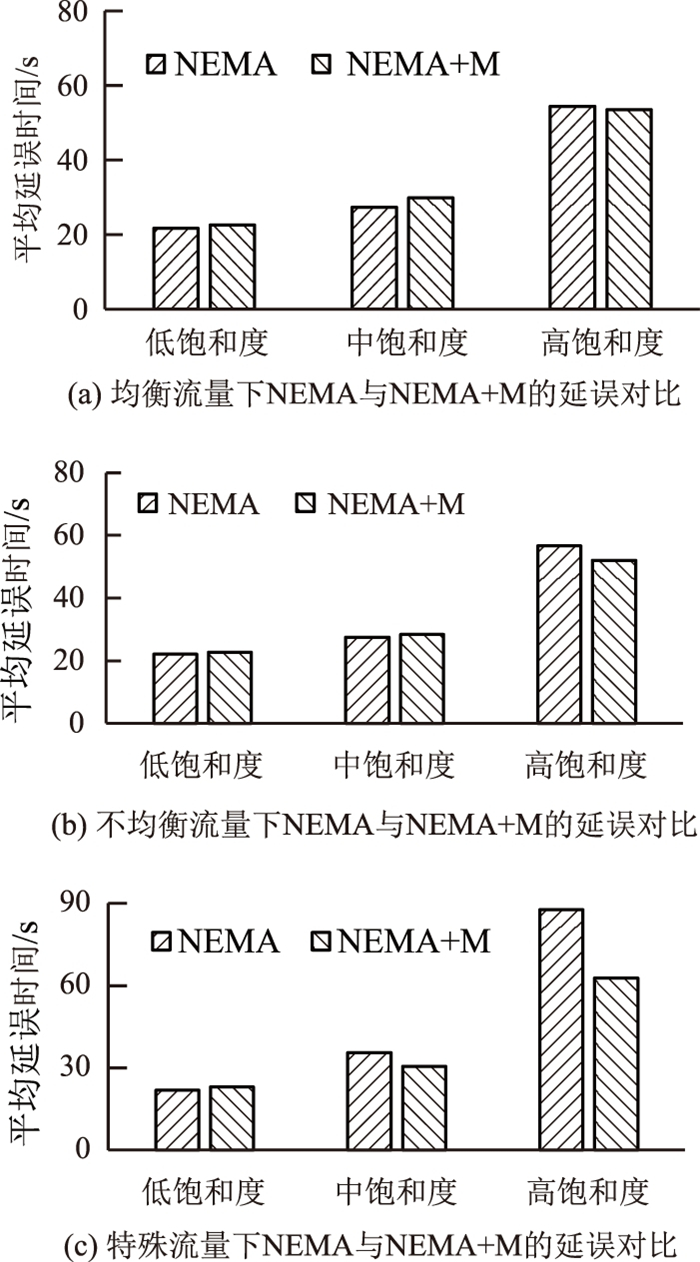
| 图 13 不同场景下,不同饱和度的延误对比 Fig. 13 Comparison of delays with different saturations in different scenarios |
| |
|
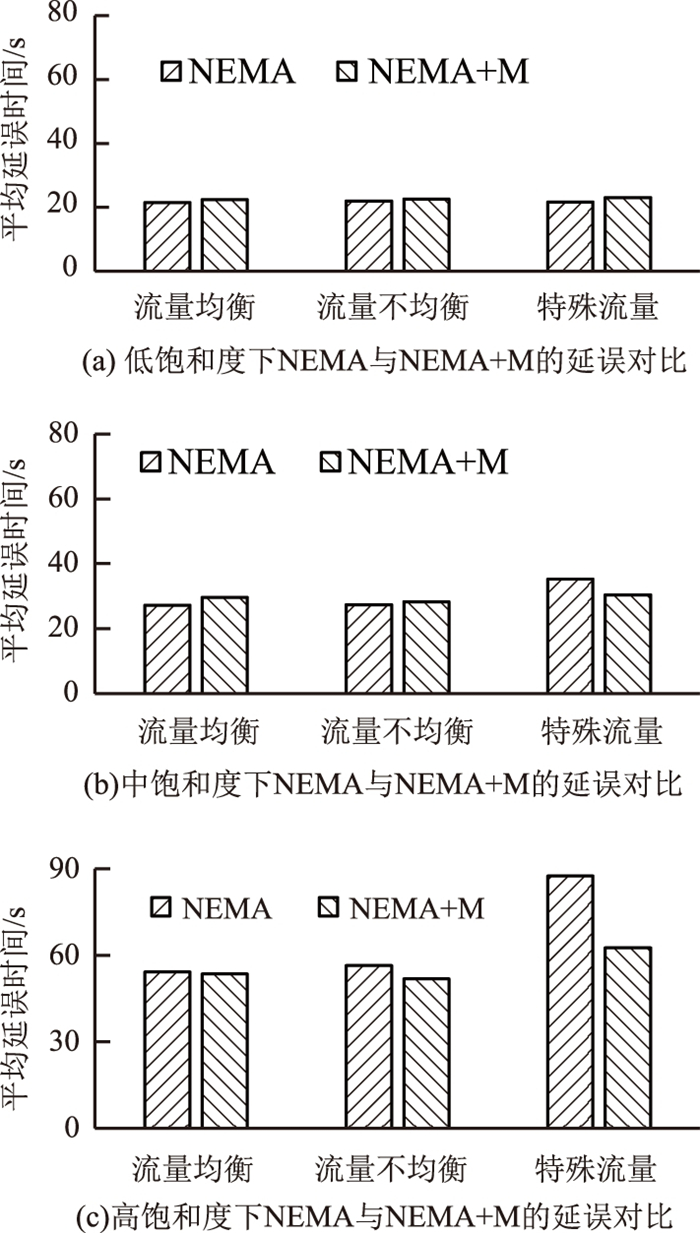
| 图 14 不同饱和度条件下,不同场景的延误对比 Fig. 14 Comparison of delays in different scenarios under different saturation conditions |
| |
如图 13所示, 流量均衡场景下, 两种控制策略的效果相差不大。流量不均衡场景下, 在高饱和度情况下, NEMA+M控制策略下的延误减少了4.6 s。在特殊流量场景下, 中饱和度的NEMA+M控制策略的延误减少了4.9 s, 降低了13.8%;高饱和度的NEMA+M控制策略的延误减少了25.0 s, 降低了28.5%。
如图 14所示, 在低饱和度条件下, 3种场景的两种控制策略的延误水平相近, 原因是交通流量过小, 各车流在最小绿灯时间内均完全驶入交叉口, 无法凸显控制策略调节效果。在中饱和度和高饱和度条件下, 特殊流量场景中NEMA+M控制策略的延误水平都明显低于NEMA控制策略, 原因是当主干道或次干道上下两环的交通量之和相差较多, NEMA相位不能实现主干道和次干道车流的共同放行, 使排队车辆数量增加, 严重时还会发生二次排队现象, 致使延误增大。
汇总不同的流量场景和不同的饱和度条件, NEMA和NEMA+M控制策略的延误对比, 如图 15所示。
|
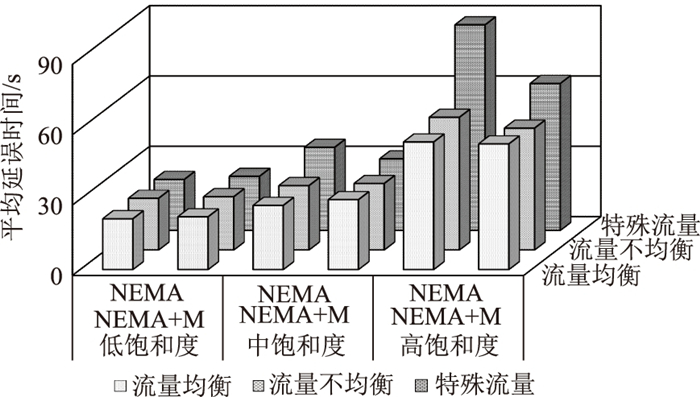
| 图 15 各种组成场景下的延误对比 Fig. 15 Comparison of delays in different composition scenarios |
| |
从该图可以看出, 在特殊流量场景的高饱和度条件下, 最小绿灯时间内排队车辆无法全部驶出交叉口, 由于流量的不对称性, 各相位对于绿灯时间的需求度不一, 而NEMA相位中的硬性屏障使得主干路、次干路的上下环绿灯时间同时结束, 必然造成二次排队或者绿灯空放的现象发生, 导致平均延误增大。相较于NEMA相位, NEMA+M相位在保证车流无冲突的情况下, 允许主干路相位与次干路相位产生搭接效果, 极大程度地满足了各相位根据自身车流量调节绿灯时间, 平均延误时间降低了约29.0%, 说明在这种特殊的情况下, NEMA+M控制策略有很明显的优势。
5 结论为消除NEMA方案中屏障对于相位放行灵活性的影响, 在NEMA相位方案的基础上融入合流相位, 提出了一种改进的交叉口感应控制方案, 通过仿真试验验证了此感应控制策略的有效性, 在特殊流量条件下该控制策略有较明显的优势。后续拟在车队行驶条件下, 进一步对该控制策略进行验证和改进。
| [1] |
罗霞, 何彪, 刘硕智, 等. 车联网环境下交叉口车辆路径优化控制研究[J]. 计算机仿真, 2017, 34(4): 166-171. LUO Xia, HE Biao, LIU Shuo-zhi, et al. Research of Vehicle Routing Optimization of Intersection Control in Connected-vehicle Network Environment[J]. Computer Simulation, 2017, 34(4): 166-171. |
| [2] |
魏欣. 基于V21的自治交叉口控制策略设计与仿真研究[D]. 大连: 大连理工大学, 2014. WEI Xin. Design of V2I-based Autonomous Intersection Control Policy and Simulation Research[D]. Dalian: Dalian University of Technology, 2014. |
| [3] |
HE Q, HEAD K, DING J. Heuristic Algorithm for Priority Traffic Signal Control[J]. Transportation Research Record, 2015, 2259: 1-7. |
| [4] |
曹政, 李华明, 卓为, 等. 基于优先度规则的交叉口反溢流动态控制方法[J]. 交通信息与安全, 2019, 37(2): 62-69. CAO Zheng, LI Hua-ming, ZHUO Wei, et al. A Dynamic Control Method of Restraining Spillover at Intersections Based on Priority Rules[J]. Journal of Transport Information and Safety, 2019, 37(2): 62-69. |
| [5] |
景泰. 随机条件下交叉口感应信号控制优化研究[D]. 兰州: 兰州交通大学, 2014. JING Tai. Research on Optimization of Single Intersection Actuated Signal Control under Stochastic Conditions[D]. Lanzhou: Lanzhou Jiaotong University, 2014. |
| [6] |
KOONCE P, RODEGERDTS L, LEE K, et al. Traffic Signal Timing Manual, FHWA-Hop-08-024[R]. Washington, D. C. : Federal Highway Administration, 2008.
|
| [7] |
蔡云, 杨晓光, 王浩. 一种灵活的在线交通信号相位切换结构[J]. 城市交通, 2009, 7(3): 80-85. CAI Yun, YANG Xiao-guang, WANG Hao. A Flexible On-line Transition Structure of Traffic Signal Phases[J]. Urban Transport of China, 2009, 7(3): 80-85. |
| [8] |
杨斐. 现代城市交叉口信号控制系统研究及工程应用[D]. 南京: 东南大学, 2018. YANG Fei. Research and Engineering Application of Traffic Signal Control System for Modern Urban Intersections[D]. Nanjing: Southeast University, 2018. |
| [9] |
李鸿粮, 刘圳岚, 王霞, 等. 基于NEMA相位方案的平面交叉口相位优化研究[J]. 科技资讯, 2019, 17(10): 253-254, 256. LI Hong-liang, LIU Zhen-lan, WANG Xia, et al. Phase Optimization of Plane Intersection Based on NEMA Phase Scheme[J]. Science & Technology Information, 2019, 17(10): 253-254, 256. |
| [10] |
赵文涛. 交通干线协调控制方法及仿真研究[D]. 南昌: 华东交通大学, 2012. ZHAO Wen-tao. Research on Arterial Coordination and Simulation[D]. Nanchang: East China Jiaotong University, 2012. |
| [11] |
杨斐. 中美交通信号控制机标准化研究[J]. 交通世界, 2018, 25(31): 10-11. YANG Fei. Research on the Standardization of Traffic Signal Controllers in China and America[J]. TranspoWorld, 2018, 25(31): 10-11. |
| [12] |
朱和, 常玉林. 基于灵活相位的双向绿波协调控制[J]. 公路交通科技, 2013, 30(7): 140-143, 158. ZHU He, CHANG Yu-lin. Bidirectional Green Wave Coordinative Control Based on Flexible Phase[J]. Journal of Highway and Transportation Research and Development, 2013, 30(7): 140-143, 158. |
| [13] |
王逸, 姚志洪, 蒋阳升, 等. 基于自适应遗传算法的双环信号配时优化模型[J]. 工业工程, 2018, 21(5): 72-80. WANG Yi, YAO Zhi-hong, JIANG Yang-sheng, et al. The Dual-phase Signal Timing Optimization Model Based on Adaptive Genetic Algorithm[J]. Industrial Engineering Journal, 2018, 21(5): 72-80. |
| [14] |
修伟杰, 张立立, 王力, 等. 基于VisVAP的改进双环相位感应控制[J]. 交通标准化, 2014, 42(15): 115-117, 121. XIU Wei-jie, ZHANG Li-li, WANG Li, et al. Improved Vehicle Actuated Control with Bicyclic Phase Based on VisVAP[J]. Transportation Standardization, 2014, 42(15): 115-117, 121. |
| [15] |
MA W J, XIE H Z, BAI Y, et al. Signal Timing Optimization Model Based on Dual-ring Phase Scheme for Roundabout[J]. Journal of Central South University: English Edition, 2013, 20(2): 563-571. |
| [16] |
彭国雄, 张扬. 叠加相位设计方法研究[J]. 中国公路学报, 2001, 14(增1): 59-62. PENG Guo-xiong, ZHANG Yang. Study of the Way of Setting Ripple Changes[J]. China Journal of Highway and Transport, 2001, 14(S1): 59-62. |
| [17] |
郭英明, 史清华. 基于VISSIM仿真的交叉口合流放行相位可行性分析[J]. 道路交通与安全, 2010, 10(2): 18-22. GUO Yin-ming, SHI Qing-hua. Feasibility Analysis of Intersection Confluence Phase Base on VISSIM Simulation[J]. Road Traffic & Safety, 2010, 10(2): 18-22. |
| [18] |
朱顺应, 肖文彬, 卢华, 等. 一种考虑合流流线相容的交叉口信号控制方案生成方法: 中国, CN201710254450.7[P]. 2017-08-15. ZHU Shun-ying, XIAO Wen-bin, LU Hua, et al. A Method for Generating Intersection Signal Control Scheme Considering Confluence Streamline Compatibility: China, CN201710254450.7[P]. 2017-08-15. |
| [19] |
张奕源, 李进龙, 李祥尘, 等. 基于叠加相位的干线绿波协调控制方法研究[J]. 交通运输工程与信息学报, 2019, 17(3): 52-61. ZHANG Yi-yuan, LI Jin-long, LI Xiang-chen, et al. Study on Green Wave Coordination Control Method Based on Ripple Changes[J]. Journal of Transportation Engineering and Information, 2019, 17(3): 52-61. |
| [20] |
罗小芹, 王殿海, 金盛. 面向混合交通的感应式交通信号控制方法[J]. 吉林大学学报: 工学版, 2019, 17(3): 695-704. LUO Xiao-qin, WANG Dian-hai, JIN Sheng. Traffic Signal Actuated Control at Isolated Intersections for Heterogeneous Traffic[J]. Journal of Jilin University: Engineering and Technology Edition, 2019, 17(3): 695-704. |
 2021, Vol. 38
2021, Vol. 38
