扩展功能
文章信息
- 童蔚苹, 袁诗琳, 刘菲菲, 徐志红, 王健
- TONG Wei-ping, YUAN Shi-lin, LIU Fei-fei, XU Zhi-hong, WANG Jian
- 基于通行能力的借对向车道左转交叉口信号控制模型优化
- Optimization of Signal Control Model for Contraflow Left-turn Intersection Based on Capacity
- 公路交通科技, 2021, 38(3): 87-95
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 87-95
- 10.3969/j.issn.1002-0268.2021.03.012
-
文章历史
- 收稿日期: 2020-06-10
2. 宁波市公安局交通警察局,浙江 宁波 315000;
3. 哈尔滨理工大学,黑龙江 哈尔滨 150080;
4. 悉地(苏州)勘察设计顾问有限公司,江苏 苏州 215000
2. Traffic Police Division of Ningbo Municipal Public Security Bureau, Ningbo Zhejiang 315000, China;
3. Harbin University of Science and Technology, Harbin Heilongjiang 150080, China;
4. CCDI (Suzhou) Exploration & Design Consultant Co., Ltd., Suzhou Jiangsu 215000, China
近10年来, 我国机动车出行需求的持续快速增长对城市的交通环境提出了愈来愈高的要求。作为城市道路的关键节点和瓶颈, 交叉口的通行能力决定和制约了城市路网的通行效率。在有限的交叉口设施空间内, 对交通流进行引导疏散, 合理分配时空资源, 提高交叉口的供给能力, 是城市交通运输管理的当务之急。
在交叉口内, 左转车流与对向直行车流、邻向直行车流的冲突是影响整个交叉口运行效率的重要因素, 特别是在左转车流量较大的交叉口, 车流冲突、车辆滞留引起的排队拥塞严重约束了交叉口的通行能力。对此, 管理部门和研究学者提出了一些非常规性对策来减少左转车流与直行车流的冲突或重新组织各方向车流通行权, 从而提升交叉口通行能力和服务水平。Esawey等[1]总结了传统U形车道(Conventional Median U-turn, MUT)、特殊U形车道、超级中间车道(Superstreet Median, SSM)、环形车道、壶形车道等10余种非常规主线交叉口渠化方式的优缺点、适用性、研究现状和评价方法, 指出延误分析和安全性分析是交叉口优化研究中最常用的评价方式。成卫[2]、Bie等[3]提出了存在有轨电车交叉口处的钩型弯设计和基于延误分析的优化, 通过左转车借右侧进口车道完成转弯的交通组织方法, 实现左转机动车与直行机动车、电车的时空分离, 避免了这几类车流间的冲突, 但该方法只适用于左转车流量较低的交叉口。
借道左转是一种在交叉口现有车道设置基本不变的情况下, 为了保证更多的左转车辆可以快速通过交叉口, 借用对向出口车道进行左转的交通组织方式, 近年来在邯郸市[4]、呼和浩特市[5]、昆明市等地区得到了实际应用。该方法适用于有专用左转信号相位且左转车流量较大的交叉口, 通过设置预信号灯和进出口道之间的可变车道开口[6], 来提高交叉口内左转车流可用的时空资源。
国内对于借道左转的研究目前主要聚焦于借道左转的适用性和方案设计。罗丹丹等[7]基于车流波动理论和仿真试验, 确定了设置借道左转车道的左转车流量临界条件, 验证了借道左转的设置能够提高交叉口通行能力。刘洋等[8]提出了设置借道左转的交叉口软硬件条件, 并总结了与借道左转方案相配套的渠化设计和安全设施的设计方法。杜倩等[9]结合借用对向左转车道设计方法、串联信号组织优化设计方法、公交优先策略的预信号等非传统交通组织方法, 提出了基于自适应控制的主预信号相协调控制的综合待行区交通组织优化方法。刘扬等[10]通过仿真试验, 研究了借道左转在流量较大的非平衡转向交叉口的适用性, 结果显示适用性良好。此外, 部分学者将研究重点放在借道左转信号控制方案的优化上。陈松等[11]考虑了借道左转组织方案下排队车辆到达和消散的8种情况, 以车均延误最小为目标分别建立延误模型, 对借道左转信号控制方案中的周期、相位绿灯时间、借道左转车道长度参数进行优化。Wu等[6]基于邯郸市借道左转交叉口的运行数据, 研究了借道左转组织方式对交叉口通行能力、车均延误的影响, 建立了通行能力模型和延误模型, 提出了基于通行能力最大目标的信号控制优化方案, 但研究中开放借道的车道并没有得到时间最大化的利用。
总体来说, 目前国内对借道左转的研究大多停留在适用性、实用性的层面, 信号控制方案设计则多是基于传统交叉口信控方案, 对预信号进行数值上的调整, 缺少科学依据。因此, 本研究结合苏州市人民路-十梓街交叉口的实际运行现状, 对该交叉口进行借道左转组织方案下的信号控制方案设计, 并以交叉口通行能力最大为目标优化信号配时方案, 最后通过VISSIM仿真试验进行结果验证, 评价信号控制方案的优化效果。
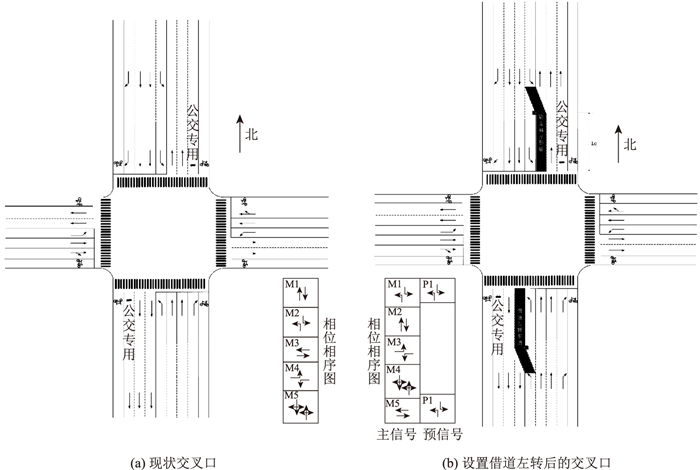
1 借道左转方案设计 1.1 案例介绍人民路-十梓街交叉口是位于苏州市姑苏区的一个信号控制交叉口, 附近商业、住宅、景点较密集, 南北方向车流量较大, 高峰期车辆排队严重。该交叉口南北方向人民路为主干路, 双向七车道, 最外侧为公交专用道, 在交叉口处与右转社会车辆共用; 东西方向为次干路, 双向五车道, 4个方向均设有机非分隔带。交叉口现状布置如图 1(a)所示。
|
| 图 1 交叉口布置与相位相序 Fig. 1 Intersection layout and phase sequence |
| |
现状车流量(见表 1)调查显示, 该交叉口高峰时段南北进口道车流量超过1 000 pcu/h, 南进口道左转车流量高达351 pcu/h。在现状信号方案(见图 1(a)、表 2)控制下, 南北方向左转车道饱和度较高, 经常出现排队情况, 交叉口服务水平较低, 车辆延误较大。此外, 南北方向的公交车有专用信号相位M5, 由于与右转车流共用车道, 理论上直行和左转的公交车会对右转社会车辆产生影响, 右转社会车辆也会占用M5的相位资源。但在实际的交叉口运行中, M5相位时间基本满足一个信号周期内到达交叉口的公交车通行需求, 公交车能够在相位结束前清空。
| 进口道方向 | 流向 | 流量/(pcu·h-1) |
| 东 | 左转 | 114 |
| 直行 | 483 | |
| 右转 | 203 | |
| 西 | 左转 | 197 |
| 直行 | 288 | |
| 右转 | 200 | |
| 南 | 左转 | 351 |
| 直行 | 512 | |
| 右转 | 267 | |
| 北 | 左转 | 292 |
| 直行 | 411 | |
| 右转 | 311 |
| 相位 | M1 | M2 | M3 | M4 | M5 | 周期 |
| 时长/s | 65 | 30 | 45 | 30 | 10 | 180 |
另一方面, 人民路路段中为双向七车道, 包括双向的两条公交专用道, 在交叉口处已经通过最大化压缩中央分隔带(物理隔离栏)增加了进口道的车道数。因而, 已无法在不降低其他流向车道通行能力的前提下, 通过对现有的交叉口空间内进行更多的渠化设计来提高左转车道的通行能力。因此, 本研究提出通过设置借道左转车道来调节交叉口的时空资源、缓解左转车辆通行压力的对策, 探讨该方案在案例交叉口实施的可行性。
1.2 借道左转控制方案设计基于运行现状, 重点解决该交叉口南北进口道左转车流过饱和的问题, 对该交叉口进行借道左转的渠化设计和信号控制方案设计。如图 1(b)所示, 将南北方向出口道内侧车道设置为可变借道左转车道, 在进口道上游设置预信号灯, 控制左转车辆进入对向车道, 车道开口距离停车线Lc。相序相位如图 1(b)所示, M1相位为南北方向左转, M2相位为南北方向直行, M3相位为东西方向左转, M4为公交专用相位, M5为东西方向直行相位。为充分利用信号相位资源, 在公交车专用相位M4后期剩余γ秒时开启预信号P1, 允许左转车辆驶入并使用对向车道, 借道左转车道和原进口道左转车道的左转车辆共同在主信号左转相位M1内实现左转。此外, 为避免滞留在车道内的左转车流对对向直行车流的影响, 预信号相位P1应比主信号相位M1早断χ秒。由于除南北进口道左转车流外其他流向车流运行情况尚可, 主信号相位配时沿用现有的配时方案, 仅对相序做调整(见表 3)。由于公交车在南北方向出口道最外侧有专用车道, 借道左转车道不会影响到公交车的正常运行, γ可以利用M4相位的全红时间, 取为2 s。
| 相位 | M1 | M2 | M3 | M4 | M5 | P1 | 周期 |
| 时长/s | 30 | 65 | 30 | 10 | 45 | 77-χ | 180 |
在此渠化设计和信号方案的基础上, 借对向车道左转的车道长度Lc和预信号相位P1的信号时长选择对进口道的通行能力和交叉口的运行效率起决定性作用。既有文献[12-16]对交叉口单个车道的饱和流率和通行能力的研究中, 基于模型的数值化研究方法适用性较高。因此, 本研究以借道左转车道长度Lc和P1相位的信号时长为自变量, 基于通行能力公式, 建立以通行能力最大为目标的优化模型, 求解使该方案下交叉口通行能力最大的借道左转车道长度和预信号相位时长, 并结合仿真实例验证模型有效性。
2 基于通行能力最大目标的优化模型 2.1 通行能力模型根据美国道路通行能力手册(HCM 2010)[17], 交叉口进口道单车道组通行能力可以通过下列公式计算得到:
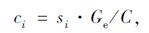
|
(1) |
式中, si为车道组i的饱和流率; Ge为车道组转向所在信号相位的有效绿灯时间; C为交叉口的信号总周期。
在交叉口中, 直行车道组和公交专用道车道组不受到借道左转车道设置的影响, 可以由上述公式直接计算得到; 左转车道组的通行能力则由原左转车道和借道左转车道两部分组成, 通行能力计算表达式如下:
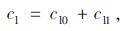
|
(2) |
式中, cl0为原左转车道通行能力; cl1为借道左转车道通行能力。
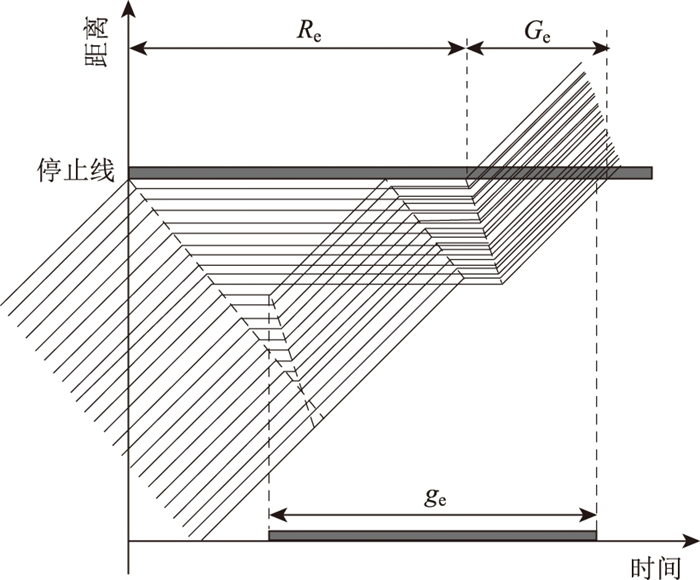
左转车辆到达-离开时空图如图 2所示(受图幅空间限制, 仅展示排队情况), 每条折线代表一辆车的轨迹。图中Ge为主信号相位绿灯时间; Re为主信号相位红灯时间, ge为预信号相位绿灯时间。对于原左转车道, 车辆到达停止线后停车等待, 并向后传播形成队列; 借道左转车道预信号灯开启前, 车辆在原左转车道内排队, 预信号灯开启后, 借道左转车道开口之后的车辆启动, 队列消散, 进入借道左转车道到达停止线后停车等待, 并形成排队队列; 左转主信号灯开启后, 所有左转车辆启动离开, 队列消散。因此, 原左转车道通行能力受到借道左转车道影响较小, 可近似用HCM公式求出:
|
| 图 2 左转车辆到达-离开时空图 Fig. 2 Arrival-departure space-time diagram of left-turn vehicles |
| |
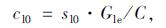
|
(3) |
式中, sl0为原左转车道的饱和流率; Gle为左转信号相位的有效绿灯时间。
借道左转车道利用了部分公交专用相位和东西直行相位使车辆进入原对向进口道, 在主信号左转相位绿灯期间消散, 消散率可近似等价于原左转车道饱和流率[18]。但是, 为了保证借道左转车辆及时消散, 防止车辆滞留对南北方向的直行车辆产生影响, 借道左转车道的预信号应提前结束, 并通过限制借道左转车道进口道的长度Lc, 保证所有进入该车道的车辆都能在南北直行相位开启前清空。因此, 借道左转车道的通行能力由两部分组成: 提前进入车道排队并在主信号左转相位内消散的最大车辆数N1, 主信号左转相位内进入车道并以消散速度离开的最大车辆数N2。
由于进入借道左转车道需要进行一次变道, 所以默认在原左转车道排队未满的情况下, 左转车辆会优先选择原左转车道进行排队; 自由消散阶段则均匀选择原左转车道和借道左转车道。提前进入车道排队并在主信号左转相位内消散的最大车辆数为:
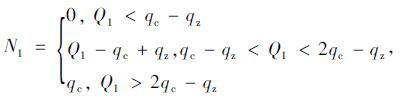
|
(4) |
式中, qc为借道左转车道进口道最多可容纳的车辆数(即原左转车道内从停车线到借道左转开口处可容纳的车辆数, 由Lc决定, 工程经验中, 平均每辆车占据车道的长度为6~12 m[19], 本研究案例交叉口中左转小汽车较多, 车均长度取8 m, 因此, 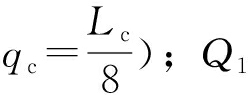 为左转主信号灯开启前到达交叉口的左转车辆数; q2为上个周期滞留在原左转车道中的左转车辆数。
为左转主信号灯开启前到达交叉口的左转车辆数; q2为上个周期滞留在原左转车道中的左转车辆数。
令左转主信号灯开启后到达交叉口的左转车辆数为Q2, 主信号左转相位内进入借道左转车道并以消散速度离开的最大车辆数为:
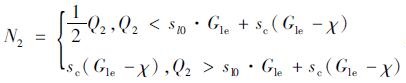
|
(5) |
式中, χ为借道左转车道预信号相位比主相位早断的时间; sc为借道左转车道的饱和流率。
交叉口处车辆到达属于离散型分布, 经验上通常采用泊松分布拟合[20]。因此, 基于式(2), 左转车道的总通行能力可通过下述表达式计算:
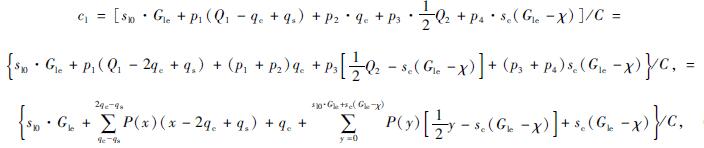
|
(6) |
式中, p1为qc-qz < Q1 < 2qc-qs的概率; p2为Q1 > 2qc-qz的概率; p3为Q2 < sl0·Gle+sc(Gle-χ)的概率; p4为Q2 > sl0·Gle+sc(Gle-χ)的概率。p1, p2和p3, p4可通过泊松分布概率密度函数计算。通常情况下, 该交叉口左转车流量较大, 因此, Q1 < qc-qs的概率可忽略不计, p1+p2近似等于1;p3+p4等于1。式(6)可以进一步简化为:
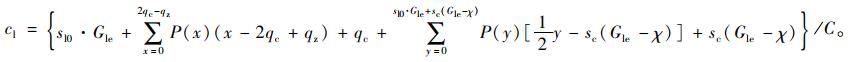
|
(7) |
通过对左转通行能力的构成分析, 可以看出在主信号控制方案确定的前提下, 决定通行能力的主要参数是借道左转车道进口道最多可容纳的车辆数qc和借道左转车道预信号相位比主相位早断的时间χ, 而借道左转车道的车辆清空规则又对qc和χ这两个参数有所限制。为了保证所有进入借道左转车道的车辆都能在主信号左转相位结束前清空, 不影响其他相位的运行, 需满足下列约束条件:
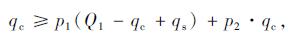
|
(8) |
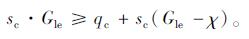
|
(9) |
其中式(8)保证了进入借道左转车道排队的车辆不会溢出, 式(9)保证了进入借道左转车道的车辆能够及时全部清空。
令式(7)中一个信号周期内左转车道能通过的左转车辆数为Z, 则Z满足:
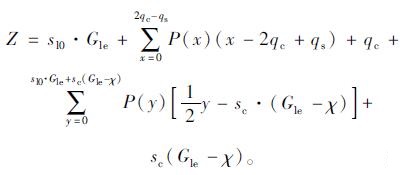
|
(10) |
前文已假定交叉口左转车辆的到达服从泊松分布, 则P(x), P(y)可以通过泊松分布概率密度函数公式计算得到:
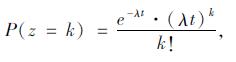
|
(11) |
式中λ为左转车辆到达率的期望值。
将概率密度函数代入到式(10)中, 得:
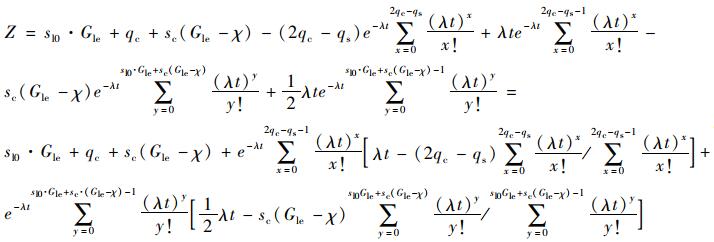
|
(12) |
通行能力最大化问题可以转化为以式(12)为目标函数、求满足式(8)、式(9)约束情况下Z最大值的求解问题。在借道左转方案下, 预设上个周期滞留在原左转车道中的左转车辆都能清空, 即qs=0, 则Z满足下述关系:
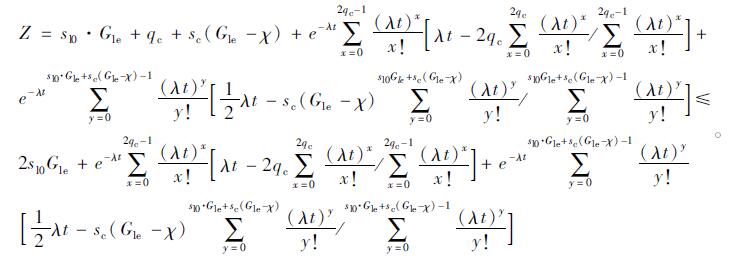
|
(13) |
式(8)整理可得:
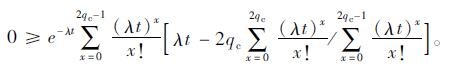
|
(14) |
式(9)整理可得:
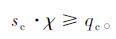
|
(15) |
因此, Z还须满足下述关系:
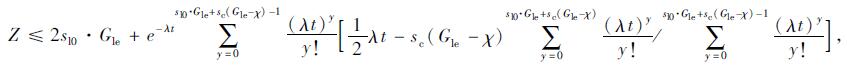
|
(16) |
令Zmax=2sl0·Gle+
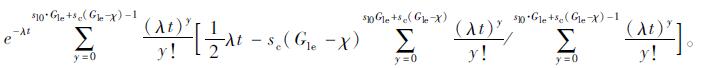
|
(17) |
基于上述讨论, Z的最大值可以通过以sc(Gle-χ)为变量、使式(17)取得最大值的算法解出。本研究采用迭代算法进行求解, 具体迭代步骤如下:
Step 1:初始化, 将左转车辆到达率、左转车道的饱和流率、信号控制方案等参数代入式(17)中, 令迭代次数n=1;
Step 2:调用梯度下降法极值函数, 求解使公式(17)达到最大值sc(Gle-χ)和Zmax, 令Zmax=Zn;
Step 3:根据式(17), 获得Zmax取得最大值情况下的qc最大值;
Step 4:验证是否满足式(8)~式(9)中的约束, 若满足, 则为平衡解; 若不满足, 令n=n+1, 返回Step 2。
3 实例验证 3.1 模型求解在本研究的交叉口实例中, sl0=0.4 veh/s, C=180 s, Gle=25 s, sc=0.4 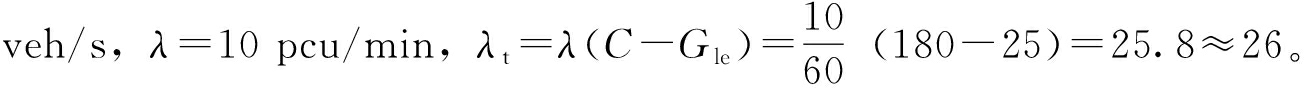 将参数代入式(17)中, 通过算法求解, 可以得到如图 3所示的sc(Gle-χ)-Zmax关系图, Zmax随sc(Gle-χ)的取值增大先增大后减小, 在sc(Gle-χ)=6时取得极值, 此时χ=10 s, qc≤sc·χ=0.4×10=4, 满足约束条件, 即为模型的最终解。
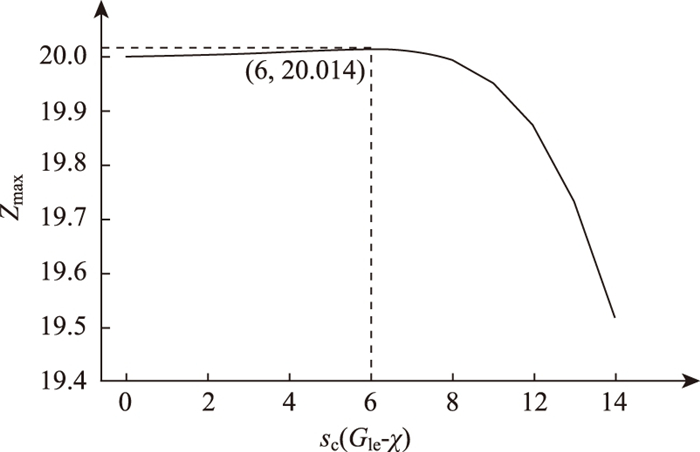
将参数代入式(17)中, 通过算法求解, 可以得到如图 3所示的sc(Gle-χ)-Zmax关系图, Zmax随sc(Gle-χ)的取值增大先增大后减小, 在sc(Gle-χ)=6时取得极值, 此时χ=10 s, qc≤sc·χ=0.4×10=4, 满足约束条件, 即为模型的最终解。
|
| 图 3 sc(Gle-χ)-Zmax关系 Fig. 3 sc(Gle-χ)-Zmax curve |
| |
此外, 从曲线图可以看出, 极值点左侧目标函数的变化率较小, 右侧变化率较大, 说明当预信号相位早断的时间χ取值较大, 甚至接近主信号左转绿灯时间时, 左转通行能力受其影响不大, 能保持在较稳定的水平内; 而当预信号相位早断较迟时, 左转通行能力会受到明显的负面影响。这与借道左转车道的实际运行规律一致, 借道左转车道的作用主要是分担在原左转车道的左转车辆排队压力, 并提供使车队消散的时空资源, 在自由流阶段提供通行服务还是应该以原左转车道为主。
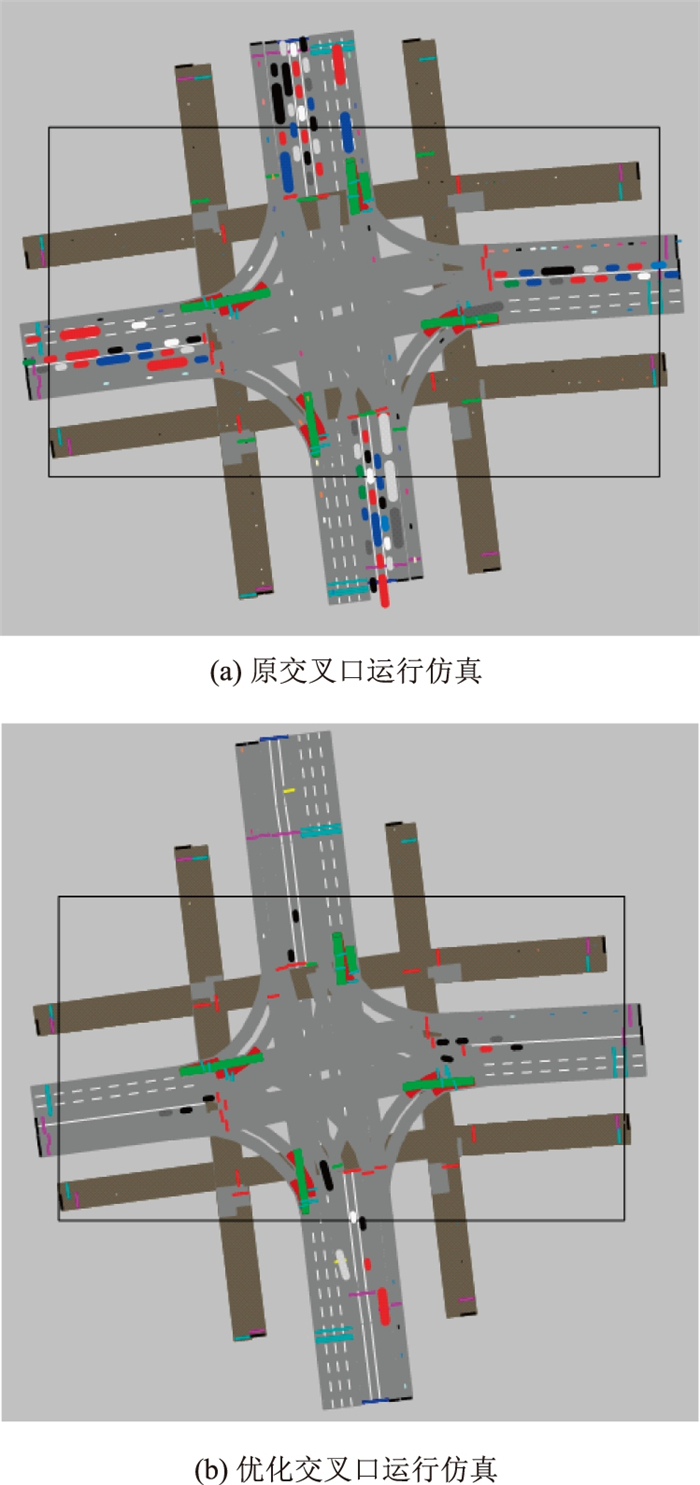
3.2 VISSIM仿真为了验证借道左转方案对交叉口运行状况的提升效果, 将交叉口设置借道左转前后的信号控制方案、交通流数据、交叉口设施数据输入到仿真试验中, 输出仿真运行参数, 仿真环境为VISSIM 11.0, 仿真时间为10 min, 进行了3次仿真试验以规避偶然性, 取3组试验的平均值为试验最终结果, 如图 4所示。
|
| 图 4 仿真试验过程 Fig. 4 Simulation experiment process |
| |
仿真输出结果如表 4所示, 主要评价指标为车辆平均延误和排队长度。由于左转车流量较大, 原交叉口的南进口道比北进口道延误大, 排队严重。由表 4可知, 对于设置了借道左转车道的南北进口道, 左转车道的平均延误分别降低了35%和33%, 平均排队长度也有显著下降。这说明借道左转车道的设置对缓解左转车流量大而带来的拥堵效果较好, 符合预期。
| 情况 | 南进口道左转车道 | 北进口道左转车道 | |||
| 平均延误 时间/s |
平均排队 长度/m |
平均延误 时间/s |
平均排队 长度/m |
||
| 原交叉口 | 208.3 | 57.24 | 193.2 | 53.45 | |
| 借道左转交叉口 | 135.7 | 36.81 | 129.5 | 32.37 | |
对于交叉口整体运行情况来说, 如表 5所示, 南北进口道的总车均延误和排队长度均有了明显的降低, 运行情况得到了显著改善。此外, 仿真结果表明, 东西进口道的车辆平均延误和排队长度没有发生明显的变化, 说明南北进口道的借道左转方案对没有设置借道左转的东西进口道影响较小。
| 情况 | 南北进口道 | 东西进口道 | |||
| 车辆平均 延误时间/s |
平均排队 长度/m |
车辆平均 延误时间/s |
平均排队 长度/m |
||
| 原交叉口 | 184.1 | 43.84 | 61.7 | 17.74 | |
| 借道左转交叉口 | 124.4 | 24.56 | 60.9 | 17.08 | |
4 结论
本研究基于苏州市城区一个交叉口的实际运行困境, 针对性地提出了借道左转改善方案和对应的信号控制方案。通过剖析设置借道左转的交叉口处左转车辆的到达规律, 将左转通行能力拆解, 建立了普适性的借道左转交叉口单进口道左转车道通行能力公式。随后, 为了保证借道左转车道通行能力最大化且不对其他车道产生影响, 建立了基于借道左转车道长度和借道左转相位时长的左转车道通行能力最大化模型。最后结合实例, 通过求解模型、开展仿真试验对公式和模型进行了验证。结果表明, 借道左转方案在左转流量较大的交叉口适用性较好, 对通行能力有明显的提高效果, 且对其他车道、进口道影响较小, 是一项易于实施的交叉口交通管理手段。
尽管如此, 借道左转方案在设置过程中对驾驶员车道选择的影响、预信号灯的设置位置与驾驶员的反应时间等因素尚未在研究中考虑, 通行能力公式和通行能力最大化模型可以在此基础上进行拓展。而左转先于直行的相位方案对驾驶员的考验和对交叉口运行情况的影响, 也是可以进一步研究的方向。此外, 借道左转在我国的应用还不是很广泛, 缺少实际运行数据, 实用价值亟待在实践中进一步验证。
| [1] |
El ESAWEY M, SAYED T. Analysis of Unconventional Arterial Intersection Designs(UAIDs): State-of-the-art Methodologies and Future Research Directions[J]. Transportmetrica A: Transport Science, 2013, 9(9/10): 860-895. |
| [2] |
成卫, 别一鸣, 刘志远. 基于机动车延误的Hook-turn交叉口信号控制方案优化方法[J]. 中国公路学报, 2015, 28(3): 94-101. CHENG Wei, BIE Yi-ming, LIU Zhi-yuan. Signal Control Scheme Optimization Method for Intersection with Hook-turn Based on Motor Vehicle Delay[J]. China Journal of Highway and Transport, 2015, 28(3): 94-101. |
| [3] |
BIE Y, LIU Z. Evaluation of a Signalized Intersection with Hook Turns under Traffic Actuated Control Circumstance[J]. Journal of Transportation Engineering, 2015, 141(5): 04014093. |
| [4] |
李佳芯, 张贵民. 邯郸: 借道左转"金点子", 推动精细化管理[J]. 道路交通管理, 2015(8): 38-39. LI Jia-xin, ZHANG Gui-min. Handan: Using "Golden Idea" of Contraflow Left-turn to PromoteFine Management[J]. Road Traffic Management, 2015(8): 38-39. |
| [5] |
贾家妹, 宋莹, 蒋蕾. 借道左转待行法: "借"?"行"![J]. 江西建材, 2017(14): 141-142. JIA Jia-mei, SONG Ying, JIANG Lei. Contraflow Left-turn: "Excuse Me"? "Yes"![J]. Jiangxi Building Materials, 2017(14): 141-142. |
| [6] |
WU J, LIU P, TIAN Z Z, et al. Operational Analysis of the Contraflow Left-turn Lane Design at Signalized Intersections in China[J]. Transportation Research Part C: Emerging Technologies, 2016, 69: 228-241. |
| [7] |
罗丹丹, 陈群. 借道左转交叉口的适用条件与特性分析[J]. 计算机工程, 2019(6): 21-25, 31. LUO Dan-dan, CHEN Qun. Applicable Conditions and Characteristics Analysis of Contraflow Left-turn Intersection[J]. Computer Engineering, 2019(6): 21-25, 31. |
| [8] |
刘洋, 顾金刚, 卢健, 等. 借道左转交通组织适用条件及管理设施设计研究[J]. 中国公共安全: 学术版, 2018(4): 18. LIU Yang, GU Jin-gang, LU Jian, et al. Research on Conditions of Application and Traffic Management Facilities Design of Reversible Left Turn Traffic Organization[J]. China Public Security: Academy Edition, 2018(4): 18. |
| [9] |
杜倩. 平面交叉口综合待行区的交通组织优化设计研究[D]. 成都: 西南交通大学, 2017. DU Qian. Traffic Organization Optimization Design of Intersection Comprehensive Waiting Area[D]. Chengdu: Southwest Jiaotong University, 2017. |
| [10] |
刘扬. 借道左转在非平衡转向交叉口中的适应性分析[J]. 数字化用户, 2019(2): 265-267. LIU Yang. Analysis on Adaptability of Contraflow Left-turn at Non-equilibrium Turning Intersection[J]. Digitization User, 2019(2): 265-267. |
| [11] |
陈松, 李显生, 王运豪, 等. 借对向出口车道左转交叉口交通控制方案优化[J]. 哈尔滨工业大学学报, 2018, 50(3): 75-82. CHEN Song, LI Xian-sheng, WANG Yun-hao, et al. Traffic Control Plan Optimization for the Intersection with Contraflow Left-turn Lane[J]. Journal of Harbin Institute of Technology, 2018, 50(3): 75-82. |
| [12] |
栗波, 别一鸣, 成卫. 基于车均延误的预信号交叉口信号配时优化[J]. 华南理工大学学报: 自然科学版, 2018, 46(4): 35-43. LI Bo, BIE Yi-ming, CHENG Wei. Signal Timing Optimization for the Intersection with Pre-signals Based on Average Vehicle Delay[J]. Journal of South China University of Technology: Natural Science Edition, 2018, 46(4): 35-43. |
| [13] |
CHEN P, QI H, SUN J. Investigation of Saturation Flow on Shared Right-turn Lane at Signalized Intersections[J]. Transportation Research Record, 2014, 2461: 66-75. |
| [14] |
CHEN P, NAKAMURA H, ASANO M. Saturation Flow Rate Analysis for Shared Left-turn Lane at Ignalized Intersections in Japan[J]. Procedia-Social and Behavioral Sciences, 2011, 16: 548-559. |
| [15] |
CHEN P, NAKAMURA H, ASANO M. Lane Utilization Analysis of Shared Left-turn Lane Based on Saturation Flow Rate Modeling[J]. Procedia-Social and Behavioral Sciences, 2012, 43: 178-191. |
| [16] |
XU J, YANG X, LAO Y. Study on the Capacity of Left-through Shared Lane with Permitted Left-turn Phasing[C]//2008 International Conference on Intelligent Computation Technology and Automation(ICICTA). Hunan: IEEE, 2008: 498-503.
|
| [17] |
MANUAL H C. HCM2010[M]. Washington, D.C.: Transportation Research Board, 2010: 1207.
|
| [18] |
张萌萌, 贾磊, 邹难, 等. 单点交叉口鲁棒优化信号配时研究[J]. 公路交通科技, 2011, 28(1): 107-111. ZHANG Meng-meng, JIA Lei, ZOU Nan, et al. Robust Optimal Traffic Signal Timing of Urban Single-point Intersection[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 107-111. |
| [19] |
吴潜蛟, 罗向龙, 武奇生, 等. 车辆排队间距对交叉口通行能力的影响[J]. 公路交通科技, 2009, 26(12): 112-115. WU Qian-jiao, LUO Xiang-long, WU Qi-sheng, et al. Impact of Vehicle Headway on Intersection Capacity[J]. Journal of Highway and Transportation Research and Development, 2009, 26(12): 112-115. |
| [20] |
王炜, 陈峻, 过秀成, 等. 交通工程学[M]. 3版. 南京: 东南大学出版社, 2019. WANG Wei, CHEN Jun, GUO Xiu-cheng, et al. Traffic Engineering[M]. 3rd ed. Nanjing: Southeast University Press, 2019. |
 2021, Vol. 38
2021, Vol. 38
