扩展功能
文章信息
- 卢毅, 付帅, 李论之
- LU Yi, FU Shuai, LI Lun-zhi
- 矩形大断面水下隧道射流风机布设位置优化仿真
- Simulation of Optimal Layout of Jet Fans in Large Rectangular Sectional Underwater Tunnel
- 公路交通科技, 2021, 38(3): 81-86, 121
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 81-86, 121
- 10.3969/j.issn.1002-0268.2021.03.011
-
文章历史
- 收稿日期: 2021-01-27
2. 长安大学 电子与控制工程学院,陕西 西安 710064
2. School of Electronic and Control Engineering, Chang'an University, Xi'an Shaanxi 710064, China
随着纵向通风方式在我国公路隧道中的广泛应用, 射流风机的作用也日益凸显[1-2]。射流风机在隧道中的升压效果不仅与风机本身的性能有关, 还与隧道截面空间布局、风机布设位置等条件相关[3-6]。此外, 随着我国交通建设的不断推进, 具有空间利用率高、运输载荷量大等优点的矩形大断面水下隧道数量不断增多, 如: 港珠澳大桥海底沉管隧道、上海长江隧道、上海沿江隧道及设计中的深中通道等, 其物理结构均具有“超宽扁平”化的特点。其纵向通风中射流风机布设方式、风速场及射流作用也和一般圆形隧道呈现差异[7]。因此, 研究矩形大断面水下隧道空间中射流风机的布局参数, 对于优化隧道纵向射流通风, 降低运营成本, 提高隧道防火灾能力[7], 实现隧道经济、安全的运行均具有重要意义, 并能为同类型隧道通风设计提供数值模拟经验和参考。
关于射流风机在隧道空间内的布局, 国内外学者展开了诸多研究。温玉辉等[8]利用CFD方法对双射流风机组升压效率的影响因素进行数值分析; 张林[6]分析了风机在不同布设位置参数(如风机高度, 每组风机内部间距等)对射流作用产生的影响, 并针对不同功率的风机组合也进行了研究; 杨秀军等[9]利用射流风机工作原理及射流作用对风机纵向最小间距进行分析, 并利用CFD软件进行数值模拟验证[9]; 胡纯良等[10]对隧道内不同射流风机气流均匀性及稳定状态进行了研究; 方勇等[11]研究了三车道公路隧道射流风机布设位置与通风效果的研究, 建模并进行模拟计算, 得出风机的最佳横向净距应为3~4倍风机直径, 可有效减小射流间的干扰及隧道壁面影响; 赵黎等[12]依托明堂山隧道工程, 使用CFD软件进行了建模计算, 结果表明风机应设在距建筑限界15~30 cm高度处, 风机横向净距应设为1.5~2倍风机直径, 风机纵向间距应设在150 m以上; Wang等[13]对小半径曲线隧道的通风进行了研究, 并对射流风机的布设位置参数进行了优化; Lee等[14]利用CFD软件分析并评价不同倾斜角对公路隧道射流风机的通风特性的影响, 并确定了风机最佳安装角度; Betta等[15]利用数值计算流体力学(CFD)分析方法, 模拟在无车辆和交通拥堵工况下, 射流风机不同安装角度对隧道出口及周围空气平均速度变化的影响进行了评价; YU等[16]基于计算流体力学理论, 以1120型风机为例, 综合分析了风机高度、风机轴线与隧道轴线夹角对风机垂直效果的影响, 得到最优安装高度和角度, 达到了对公路隧道风机射流效果的优化。
以上研究从射流风机距隧道顶壁高度、风机横向间距和纵向间距对射流风机升压力进行了数值模拟研究, 但研究对象均集中于两车道和三车道的普通高速公路隧道, 且隧道纵向风机横向并列一组为2台风机。对于纵向通风单组布置3台风机的扁平型矩形大断面水下公路隧道, 其射流风机的设计和布设则鲜有研究。
因此, 本研究结合太湖隧道具体工况, 利用CFD软件Fluent, 按隧道实际横截面尺寸建模, 研究单组3台射流风机纵向通风时, 改变风机布设高度、横向净间距及纵向间距, 其升压力将产生何种变化, 及如何影响整体隧道通风的效果。通过升压系数判断通风质量, 获得了矩形大断面公路隧道射流风机最优布设位置参数。
1 仿真模型建立 1.1 依托工程背景太湖隧道穿越太湖, 全长10.79 km, 其中暗埋段长度为10 km, 为“双向六车道+紧急停车带”的高速公路水下隧道, 设计车速100 km/h, 单洞隧道截面宽17.45 m, 高7.25 m, 面积为120 m[7]。隧道及风机布置平面图如图 1所示。
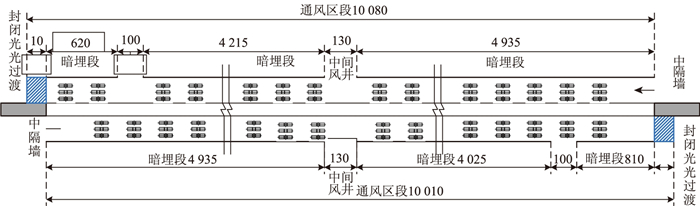
|
| 图 1 太湖隧道风机布置图(单位:m) Fig. 1 Layout of jet fans in Taihu Tunnel(unit: m) |
| |
图 2为隧道矩形大断面截面图(左洞), 拟每组布置3台1120型射流风机, 其轴向推力1 148 N, 风机横向净间距为d, 风机距隧道顶壁距离为h, 隧道模型总长取600 m。共布设2组风机, 每组3台, 其中风机距顶部高度h和风机净间距d如图 2所示。射流风机模型采用圆柱体模拟, 底面直径为1.12 m, 长1.5 m。建模完成后, 需进行三维网格划分以便于有限元模拟计算, 三维网格模型划分如图 3所示。
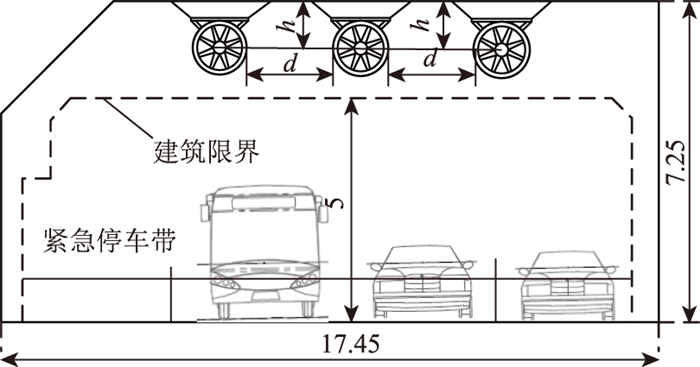
|
| 图 2 太湖隧道标准横断面(左洞)(单位:m) Fig. 2 Standard cross-section of Taihu Tunnel(left)(unit: m) |
| |

|
| 图 3 三维网格划分正视图 Fig. 3 Front view of 3D meshing |
| |
1.2 边界条件
为了保证数值模拟结果的可靠性, 需要在计算区域边界上给定边界条件[17-18]。本研究中外界大气与隧道进出口相连, 因此隧道进出口均为压力边界条件, 且设为大气压强值。风机进出口边界条件根据射流风机自身参数设定, 进口取流量为29 m3/s, 出口取速度边界为30 m/s。隧道底部和顶部采用无滑移边界条件, 壁面温度不变, 壁面粗糙高度取0.007, 粗糙常数取0.8。
1.3 通风质量评价方法为更加直观地对比风机不同布设位置产生的通风效果, 本研究采用风机升压综合影响系数来定量评价不同风机布设位置的通风质量。
本研究的模型中没有设定隧道入口风速, 由射流风机的升压作用完成隧道出入口与外界大气压的空气交换流动。为得到升压系数k, 首先完成整个模型的通风模拟计算, 计算得出隧道入口的风速, 以及2组风机前后截面的静压差Ps。隧道入口风速即为隧道断面的平均风速, 代入式(1), 计算出射流风机提供升压力的理论值Pm; Ps与Pm的比值即为风机升压综合影响系数k[6], 见式(2)。
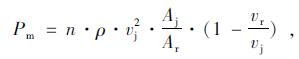
|
(1) |
式中, n为单组风机台数; ρ为空气密度; vj为射流风机出口风速; Ar为隧道截面积; Aj为风机截面积; vr为隧道断面平均风速(即计算得出的隧道入口风速)。
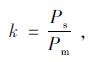
|
(2) |
式中, k值越大, 表明升压力值越大, 即模拟计算值与理论值越接近, 通风效果更好。
2 射流风机空间布设位置仿真研究 2.1 射流风机安装高度对通风效果的影响依照《公路隧道通风设计细则》(JTG/T D70/2-02—2014)中的规定, 射流风机在隧道横断面上的布置应不侵入建筑限界, 边沿与隧道建筑限界净距不宜小于15 cm[19]。本研究在建立CFD几何模型时考虑上述规范中的规定, 设置风机距隧道顶壁距离h为0.7D~1.5D(间隔为0.1D, D为射流风机直径, 为1.12 m)共9种工况, 对风机升压系数进行计算。共设置2组风机, 依照风机组常规间隔, 设置第1组射流风机位置为距隧道入口为50 m, 第2组位置为距隧道入口200 m。
风机距隧道顶壁0.8D和1.4D时, 沿风机轴线剖面速度变化云图如图 4所示。
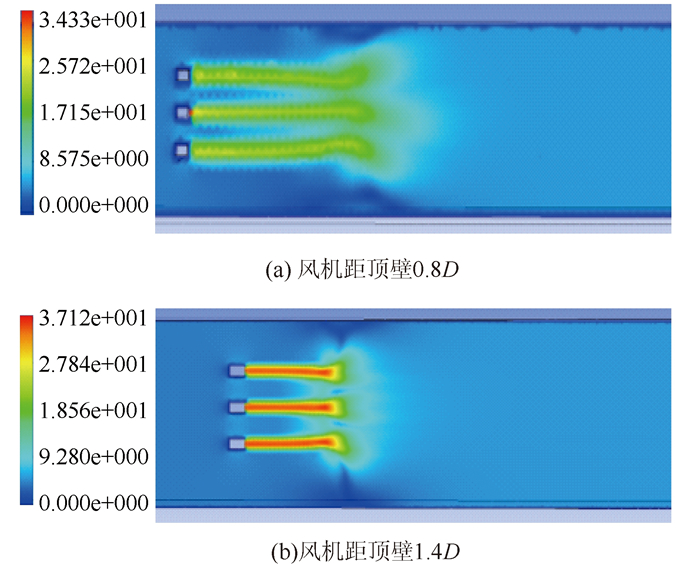
|
| 图 4 风机轴线剖面速度变化云图(单位:m·s-1) Fig. 4 Nephogram of velocity change in axial section of fans (unit: m·s-1) |
| |
将模拟计算得出的隧道入口风速代入式(1)得到不同风机高度下升压力的理论计算值, 并根据模拟计算得出的2组射流风机前后截面压力, 利用式(2)求出风机在不同高度时的升压综合影响系数。将不同风机高度的升压力模拟值和影响系数绘制如图 5所示。
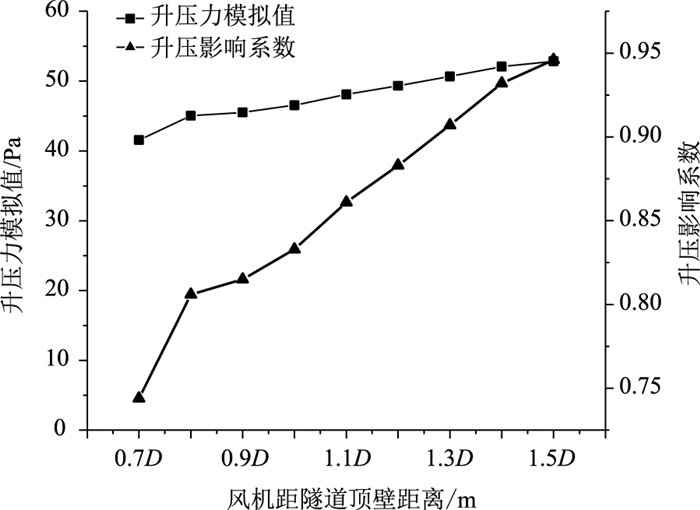
|
| 图 5 风机距隧道顶壁不同距离时升压力和影响系数变化 Fig. 5 Variations of pressure rises and influence coefficients with different distances from fan to tunnel top wall |
| |
由图 4和图 5分析可知, 随风机距隧道顶壁距离h的增加, 出口附近风速越来越大, 升压综合影响系数越来越高, 表明隧道内由风机带动的纵向通风能力更佳。这可能是因为当风机距离隧道顶壁距离较近时, 风机的竖向射流撞击道顶壁, 射流无法继续推进并回流干扰正常风机的射流; 同时, 风机纵向射流会受到隧道壁面摩阻力的影响。受上述因素影响, 风机射流损失了大量动能, 无法有效带动低速风流进行流动。
而当风机距隧道顶壁距离h越大, 即风机位置越靠近建筑限界, 风机升压影响系数越大。此时风机出口风流受隧道顶壁影响变小, 摩擦阻力也减小, 其气流动能损失较小, 因此其射流扩散更充分, 有助于提升隧道通风效果。因此, 建议此类矩形大断面隧道在进行射流风机布置时, 在满足不侵入建筑限界条件时, 风机距隧道顶壁距离h为1.2D~1.4D为宜, 此时风机综合升压系数能达到0.887~0.931以上, 具有良好的通风效果。
2.2 射流风机横向间距对通风效果的影响依据《公路隧道通风设计细则》(JTG/T D70/2-02—2014)规定, 同一断面布置2台及以上射流风机时, 相邻风机的横向净距不宜小于1倍风机直径[19]。本研究在建立CFD几何模型时考虑上述规范中的规定, 根据隧道具体工况, 设置风机净距1D~3D(间隔为0.2D, )共11组工况, 对风机升压力和影响系数进行模拟计算。风机不同间距下升压力模拟值及升压影响系数的计算结果如图 6所示。
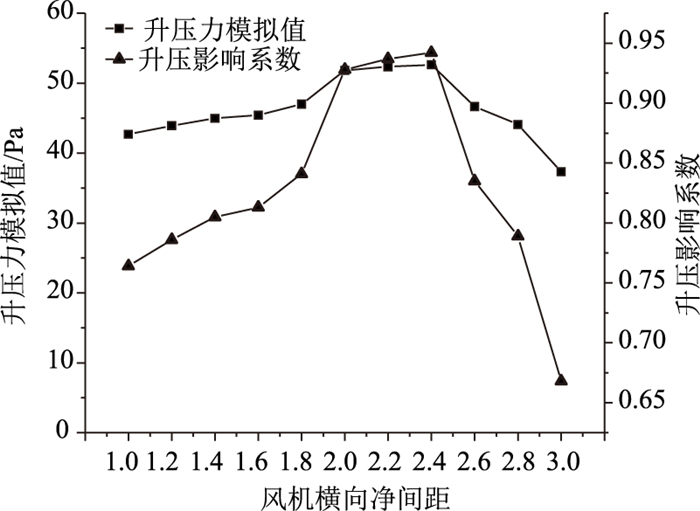
|
| 图 6 不同横向净间距风机升压力及影响系数变化 Fig. 6 Variations of pressure rise and influence coefficient with different transverse clear spacings |
| |
由图 6分析可知, 随着风机横向间距从1D开始增大, 其升压力模拟值及升压影响系数明显增大; 当风机横向间距增大到2D~2.4D时, 风机整体升压力模拟值和升压影响系数到达一个顶峰且基本维持不变; 当风机间距由2.4D继续增大至3D时, 升压力模拟值和升压影响系数急剧降低。
这是由于当3台风机间距过近时, 3台风机自身的吸气排气气流会互相影响互相干扰, 从而降低了3台风机的整体升压能力。随着间距增大, 这种风机之间的互相干扰会逐渐减弱, 因此其升压能力和升压影响系数不断增大。
而当风机间距达到一定距离时, 虽然风机间距的增大减小了3台风机之间气流的互相干扰, 但两端的风机距隧道侧壁的距离则越来越近, 隧道壁给风机射流带来的负面影响越来越大, 严重降低了射流的动能, 削弱了风机带动气流的效果。风机间距增加带来的升压能力增加与隧道侧壁影响带来的升压能力减小两者作用互相抵消时, 便出现了升压力模拟值与升压影响系数的峰值。
当风机间距继续增大, 此时两侧风机距隧道侧壁距离过近, 侧壁对射流的影响愈发显著, 此时风机升压力与影响系数便出现了急剧的减小。因此, 类似太湖隧道的大断面矩形模型隧道, 建议最佳风机横向间距应设置为2D~2.4D, 此时风机整体升压系数可以达到0.9以上。
2.3 射流风机纵向间距对通风效果的影响为了保证风机出口射流的充分发展, 每组风机之间应保持足够的纵向间距, 使经过风机加速的喷射气流到达下一组风机位置之前充分发展并减速, 否则将会影响到下一级风机的工作性能, 同时也能获取最大的经济效益。为研究射流风机纵向间距对通风效果的影响, 设置2组风机纵向间距50~200 m(间隔为30 m)共6组工况条件, 其中风机距隧道顶部距离为1.2D, 建模计算隧道断面的平均风速。
风机纵向间距为50, 200 m时, 沿风机轴线剖面速度变化云图如图 7所示。
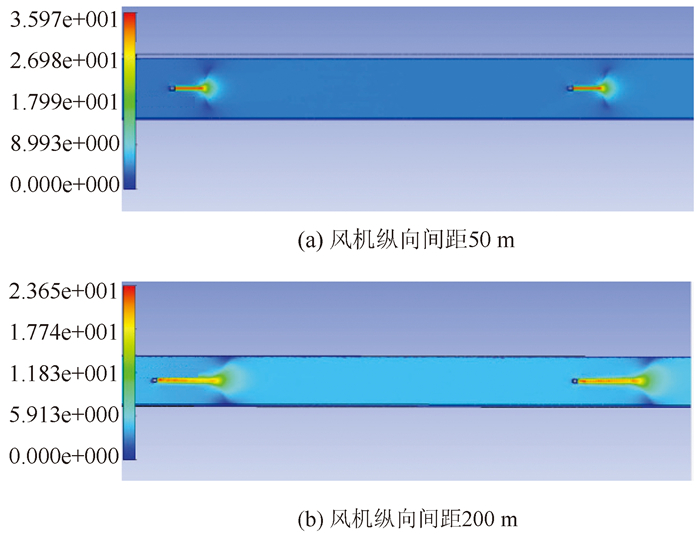
|
| 图 7 风机轴线剖面速度变化云图(单位: m·s-1) Fig. 7 Nephogram of velocity change in axial section of fans(unit: m·s-1) |
| |
为了详细地分析隧道断面风速变化细节, 我们在2组风机之间每间隔10 m的断面设置采样点(第1组风机后10 m设为采样点1, 第1组风机后20 m设为采样点2…依次类推), 并计算其断面平均风速作为采样点的风速。经过模拟计算并进行结果统计, 将风机在不同间距的6种工况下, 2组风机间隧道断面采样点的风速模拟值变化绘制如图 8所示。
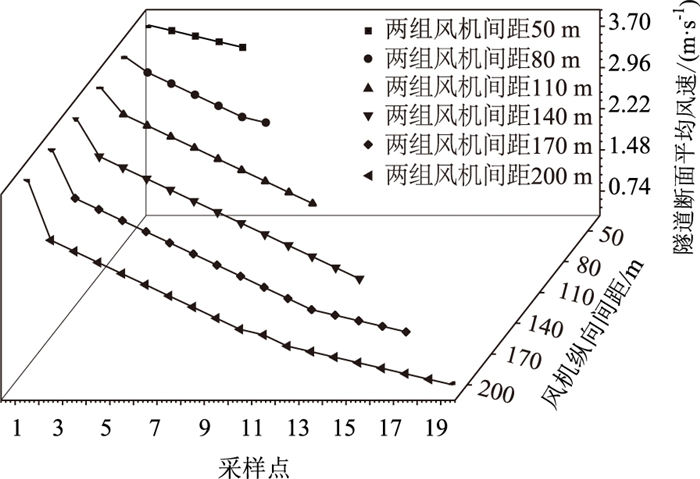
|
| 图 8 风机不同纵向间距隧道断面风速变化 Fig. 8 Variations of wind speed at tunnel section with different longitudinal spacings of fans |
| |
分析图 7和图 8可知, 第1组风机和第2组风机之间风速由大逐渐减小, 且在第1组风机后一定区间内隧道截面的风速并不均匀, 高速气流由中心向两边逐渐扩散, 最后整个隧道内风速达到较为均匀的水平。这是由于隧道内一部分空气由风机吸入后, 经叶轮做功后高速喷出, 高速气流的速度间断面不连续, 形成漩涡, 产生卷吸现象, 将周围低速空气卷吸进入射流。这个过程伴随着动量和动能在隧道空气中的交换传递, 射流范围不断扩展, 此时隧道截面的平均速度很大。当射流不断向前发展一段距离后, 伴随流动范围逐渐减少, 压力同步上升, 射流的诱导效应会使气流在隧道截面形成均匀速度分布。当隧道截面气流速度均匀分布后, 风机产生的射流在动能交换的过程中逐渐减弱, 风速逐渐减小。
从图 8可知, 当2组风机距离为50 m时, 第1组风机出口射流并未得到充分发展, 在第2组风机入口处风速很大, 且截面风速不均匀, 造成空气紊乱, 不利于第2组风机再次对空气升压, 降低了风机的升压工作效率; 当风机纵向间距达到110 m时, 第2组风机入口处射流紊乱明显得到改善, 隧道截面风速趋于均匀, 但并未下降到隧道断面的平均风速; 当风机纵向间距达到170 m时, 气流速度已基本下降到隧道断面平均速度大小, 此时第2组风机对空气的升压效率和效果达到最佳; 当纵向间距继续增大到200 m时, 由于风机纵向间距过长, 第1组风机的射流发展到一定距离时基本消失, 导致未被风机吸入的低速风流流动的效果变差。因此, 建议隧道在进行射流风机布置时, 将风机纵向间距设置在140~170 m为宜, 此时升压系数经计算为0.887~0.936。最佳纵向间距可取150 m, 此时2组风机的升压效率最高, 既保证了隧道内的通风效果, 又降低了经济成本。
3 结论本研究以矩形大断面水下隧道通风设计和布局为目的, 以太湖水下隧道为背景模型, 针对单组3台射流风机的布设位置问题, 建立了CFD隧道仿真模型, 并使用FLUENT有限元软件工具进行数值模拟计算和分析, 得到以下结论。
(1) 风机距隧道顶壁距离h越大, 即风机位置越靠近建筑限界, 风机升压系数越大, 表明风机出口射流扩散更充分, 受到隧道顶壁影响越小, 有助于提升隧道通风效果。因此, 建议太湖隧道在进行射流风机布置时, 在满足不侵入建筑限界条件时, 风机距隧道顶壁距离h以1.2D~1.4D为宜。
(2) 风机升压系数随风机横向净间距的增大呈现先增大后减小的趋势。风机横向间距为1D~2.4D时, 风机升压系数随横向间距的增大而增大; 但当风机横向净距为2.4D~3D时, 升压系数值急剧减小, 通风效果变差。因此, 建议太湖隧道的射流风机横向净间距应设置为2D~2.4D。
(3) 通过风机纵向间距与通风效果的模拟分析研究, 表明太湖隧道在进行风机布置时, 2组风机在纵向上的间距宜设为140~170 m, 最佳纵向间距为150 m, 使2组风机的升压效率和整个隧道的通风效果达到最佳匹配。建议类似太湖隧道的矩形大断面隧道在进行风机布置时, 2组风机在纵向上的间距应为140~170 m, 最佳纵向间距为150 m。
| [1] |
王永东. 长大公路隧道纵向通风数值模拟研究[D]. 西安: 长安大学, 2000. WANG Yong-dong. Research on Numerical Simulation of Longitudinal Ventilation of Long and Large Road Tunnel[D]. Xi'an: Chang'an University, 2000. |
| [2] |
石平. 公路隧道通风局部效应三维数值模拟分析与研究[D]. 西安: 长安大学, 2004. SHI Ping. Three-dimensional Numerical Simulation Analysis and Research on Local Effect of Road Tunnel Ventilation[D]. Xi'an: Chang'an University, 2004. |
| [3] |
赵录学. 长大隧道通风与防灾技术研究[J]. 隧道建设, 2007, 27(增2): 171-173. ZHAO Lu-xue. Research on Techniques of Ventilation and Disaster Prevention in Long Tunnels[J]. Tunnel Construction, 2007, 27(S2): 171-173. |
| [4] |
BRING A, MALMSTROM T G, BOMAN C A. Simulation and Measurement of Road Tunnel Ventilation[J]. Tunnelling and Underground Space Technology, 1997, 12(3): 417-424. |
| [5] |
BARI S, NASER J. Simulation of Airflow and Pollution Levels Caused by Severe Traffic Jam in a Road Tunnel[J]. Tunnelling and Underground Space Technology, 2010, 25(1): 70-77. |
| [6] |
张林. 公路隧道射流通风数值模拟与风机安装参数优化[D]. 重庆: 重庆交通大学, 2009. ZHANG Lin. Numerical Simulation of Jet Ventilation and Optimization of Installation Parameters of Fan of Road Tunnel[D]. Chongqing: Chongqing Jiaotong University, 2009. |
| [7] |
刘宇. 矩形断面水下隧道火灾排烟试验研究[D]. 重庆: 重庆交通大学, 2019. LIU Yu. Experimental Study on Exhausting Fire Smoke in Rectangular Section Underwater Tunnel[D]. Chongqing: Chongqing Jiaotong University, 2019. |
| [8] |
温玉辉. 特长公路隧道纵向通风系统CFD三维仿真分析[D]. 西安: 长安大学, 2004. WEN Yu-hui. Three-dimensional CFD Simulation Analysis for Longitudinal Ventilation System in Super Long Highway Tunnel[D]. Xi'an: Chang'an University, 2004. |
| [9] |
杨秀军, 王晓雯, 陈建忠. 公路隧道通风中射流风机纵向最小间距研究[J]. 重庆交通大学学报: 自然科学版, 2008, 27(1): 40-43, 164. YANG Xiu-jun, WANG Xiao-wen, CHEN Jian-zhong. Study on Minimum Longitudinal Distance of Jet Fan in Ventilation of Highway Tunnel[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2008, 27(1): 40-43, 164. |
| [10] |
胡纯良, 张海琳, 王敏, 等. 不同风机轴距下某隧道内气流分布研究[J]. 四川建筑科学研究, 2014, 40(1): 94-97. HU Chun-liang, ZHANG Hai-lin, WANG Min, et al. Study on Air Flow Distribution in Tunnel under Different Axial Distances among Fans[J]. Sichuan Building Science, 2014, 40(1): 94-97. |
| [11] |
方勇, 兰宇, 曾艳华, 等. 三车道公路隧道射流风机设置位置研究[J]. 现代隧道技术, 2009, 46(2): 90-93, 98. FANG Yong, LAN Yu, ZENG Yan-hua, et al. Study on the Installation of Jet Fans in a Three-lane Highway Tunnel[J]. Modern Tunnelling Technology, 2009, 46(2): 90-93, 98. |
| [12] |
赵黎, 闫治国. 2车道公路隧道射流风机空间布局优化的CFD分析[J]. 隧道建设, 2016, 36(4): 411-417. ZHAO Li, YAN Zhi-guo. Computational Fluid Dynamics(CFD)Analysis of Spatial Layout Optimization of Jet Ventilation Fan Used in Two-lane Road Tunnel[J]. Tunnel Construction, 2016, 36(4): 411-417. |
| [13] |
WANG F, WANG M N, WANG Q Y. Numerical Study of Effects of Deflected Angles of Jet Fans on the Normal Ventilation in a Curved Tunnel[J]. Tunnelling and Underground Space Technology, 2012, 31: 80-85. |
| [14] |
LEE S C, LEE S, LEE J. CFD Analysis on Ventilation Characteristics of Jet Fan with Different Pitch Angle[J]. KSCE Journal of Civil Engineering, 2014, 18(3): 812-818. |
| [15] |
BETTA V, CASCETTA F, MUSTO M, et al. Numerical Study of the Optimization of the Pitch Angle of an Alternative Jet Fan in a Longitudinal Tunnel Ventilation System[J]. Tunnelling & Underground Space Technology, 2009, 24(2): 164-172. |
| [16] |
YU F H, HE Y Y. Optimization on Ventilation Effect of Jet Fan in Highway Tunnel[J]. Computer Engineering & Applications, 2010, 46(11): 214-216. |
| [17] |
孙详海. 流体力学[M]. 上海: 上海交通大学出版社, 2000: 23-35. SUN Xiang-hai. Fluid Mechanics[M]. Shanghai: Shanghai Jiaotong University Press, 2000: 23-35. |
| [18] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004: 135-180. WANG Fu-jun. Computational Fluid Dynamics Analysis: Theory and Application of CFD Software[M]. Beijing: Tsinghua University Press, 2004: 135-180. |
| [19] |
JTG/TD70/2-02—2014, 公路隧道通风设计细则[S]. JTG/TD70/2-02—2014, Guidelines for Design of Ventilation of Highway Tunnels[S]. |
 2021, Vol. 38
2021, Vol. 38
