扩展功能
文章信息
- 张超, 白允, 安永林, 汪辉平, 曾兴
- ZHANG Chao, BAI Yun, AN Yong-lin, WANG Hui-ping, ZENG Xing
- 基于全应力应变曲线的岩石脆性特征评价新方法
- A New Method for Evaluating Rock Brittle Characteristics Based on Full Stress-strain Curve
- 公路交通科技, 2021, 38(3): 63-72
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 63-72
- 10.3969/j.issn.1002-0268.2021.03.009
-
文章历史
- 收稿日期: 2020-07-14
2. 中国市政工程中南设计研究总院有限公司,湖北 武汉 430010
2. Central and Southern China Municipal Engineering Design & Research institute Co., Ltd., Wuhan Hubei 430010, China
脆性指标是评价页岩可压裂性以及预测崩滑、岩爆和地震的重要因素[1-2], 同时, 脆性不仅对岩石可削性、可钻性和可掘性造成显著影响, 也与煤矿的持续开采及安全施工密切相关[3-4], 因此, 建立一种合理有效的岩石脆性评价新方法对岩石工程有着重要的理论意义与应用价值。
目前, 国内外学者对岩石脆性特征评价方法开展了大量研究, V.Hucka和B.Das[5]通过岩石的单轴抗压强度以及劈裂抗拉强度提出了几种基于压拉强度比、压拉强度乘积等的岩石脆性指标; 王宇等[6]归纳了已有的岩石脆性测试方法, 对岩石起裂应力进行了研究, 为基于起裂机制的脆性指标的建立提供了一种角度; 周辉等[7]以应力-应变曲线峰后应力降的相对大小和绝对速率为基础, 提出了考虑了岩石塑形屈服特性和应力状态影响的脆性指标; 在此基础上, 夏英杰等[8-9]提出了基于岩石峰后应力跌落速率及失稳破坏时所释放弹性能与峰前储存总能量比值共同表征的岩石脆性指标; 陈国庆等[10]在分析夏英杰等[8-9]的基础上, 提出了基于全应力-应变曲线及起裂应力的岩石脆性指标; 胡清波[11]等在分析岩石损伤演化特性的基础上, 提出了基于统计损伤本构关系的岩石脆性特征评价方法; R.Rickman[12]等分别提出了基于岩石矿物组分以及归一化弹性模量与泊松比的脆性指标; 廖东良等[13]提出基于矿物组分和断裂韧度的岩石脆性指标。上述分析充分说明了脆性指标研究的复杂性以及对实际工程的重要意义, 但目前绝大多数脆性指标存在着明显的局限性, 有些指标不适合定量分析岩石脆性程度, 有些指标并没有充分考虑岩石的力学状态, 有些则无法描述岩石在复杂应力条件下的脆性差异, 还有些指标因参数获取方法不够成熟, 其结果的可靠性有待商榷。
为此, 本研究对前人研究成果进行了优缺点分析, 结合具体的工程实际提出了基于全应力应变曲线的岩石脆性指标, 通过大理岩、砂岩等室内试验数据进行了验证, 以期获得一种能反映岩石在各种应力条件下脆性程度, 又具有可操作性的脆性评价方法。
1 岩石脆性指标研究现状分析国内外学者根据不同应用目的从不同角度对岩石脆性特征进行了研究, 提出了大量的脆性指标。本研究总结了目前常用的基于岩石强度特性、应力应变曲线、断裂韧度、破裂角等的脆性指标, 见表 1, 现对其进行归纳分析。
| 分类依据 | 计算公式 | 公式说明 |
| 基于压拉强度 | B1=σc/σt B2=(σc-σt)/(σc+σt) B3=σcσt/2 |
σc为单轴抗压强度; σt为单轴抗拉强度 |
| 基于应力应变曲线 | B4=εr/εp B5=(σp-σr)/σp B6=(εr-εp)/εp B7=[(σp-σr)/σp]·[lg|kac|/10] B8=εR/εp B9=(σp-σr)/(εr-εp)+(σp-σr)(εr-εp)/σpεp B10=[(σp-σi)/σp]/[(εp-εi)/εp]+[(σp-σr)/σp]/[(εp-εr)/εp] B11=(εBRIT-εn)/(εm-εn)+αCSBRIT+βCSBRIT+η, CSBRIT=[εp(σp-σr)]/[σp(εr-εp)] |
εr为残余应变; εp为峰值应变; εR为峰前可恢复应变; σp为峰值强度; σr为残余强度; kac为峰后应力降的斜率; εBRIT为岩体的峰值应变; εm和εn分别为最大、最小峰值应变参考值,α,β,η为标准化系数 |
| 基于莫尔圆 | B12=sin α B13=π/2+α |
α为内摩擦角 |
| 基于矿物组分 | B14=(Wqtz+Wcarb)/Wtotal B15=(Hμ-H)/K |
(Wqtz+Wcarb)为岩体中脆性矿物的含量; Wtotal为矿物总含量; Hμ为宏观硬度; H为微观硬度; K为系数 |
| 基于弹性模量及 泊松比 |
B16=E+v | E为岩体弹性模量的平均值; v为泊松比的平均值 |
| 基于断裂韧度 | B17=∑kiHi/KICi B18=(KCmax-KC)/(KCmax-KCmin) |
ki为某脆性矿物的组分; Hi为脆性矿物的硬度;KICi为断裂韧度;KC为页岩底层综合断裂韧度;KCmax和KCmin分别为断裂韧度的最大值和最小值 |
| 基于破裂角 | B19=sin α | α为岩体破裂角 |
| 基于碎屑含量 | B20=qσc | q为粒径小于0.6 mm的碎屑百分比;σc为单轴抗压强度 |
| 基于贯入试验 | B21=Fmax/P | Fmax为最大冲击荷载;P为贯入深度 |
1.1 基于强度特性的脆性指标分析
目前, 基于岩体强度特征的脆性指标B1~B3被广泛使用, 这是由于岩石的抗压、抗拉强度可以通过单轴压缩试验和劈裂试验直接获取, 且B1~B3公式简单, 参数较少, 计算方法易于掌握。但该方法是否可以作为岩石脆性的判断依据仍存在争议, 众多学者也对其进行了验证。周辉[7]认为, 岩石的压拉强度比值虽然可以表示岩石的某种性质, 但更多反映的是岩石的强度特征, 对岩石脆性的表征不明显, 以此作为岩石的脆性指标并不准确。此外, 根据夏英杰[8]的分析可知, 岩石抗压-抗拉强度之间呈较好的线性关系, 抗拉强度较大的岩石同时具有较高的抗压强度, 因此, 即使压拉强度差距较大的岩石仍有可能出现比值相同的情况, 这也导致B1~B2计算结果相对集中, 不利于岩石脆性的定量分析。不仅如此, 具有高压拉强度的岩石相较于低压拉强度的岩石其压拉强度乘积自然较大, 但压拉强度比值不一定符合此规律, 因此, B1~B3在计算上可能存在互相矛盾的情况。
由此可知, 脆性指标B1~B3不仅准确性上存在争议, 对岩石力学参数及应力条件的考虑也过于单一, 在使用上存在明显的局限性。
1.2 基于应力应变曲线的岩石脆性指标分析应力-应变曲线作为岩石内部性质的体现, 一方面直观有效地反映了岩石的力学状态, 另一方面对岩石的脆性有直接的影响, 因此众多学者提出了大量基于应力应变曲线的脆性指标。
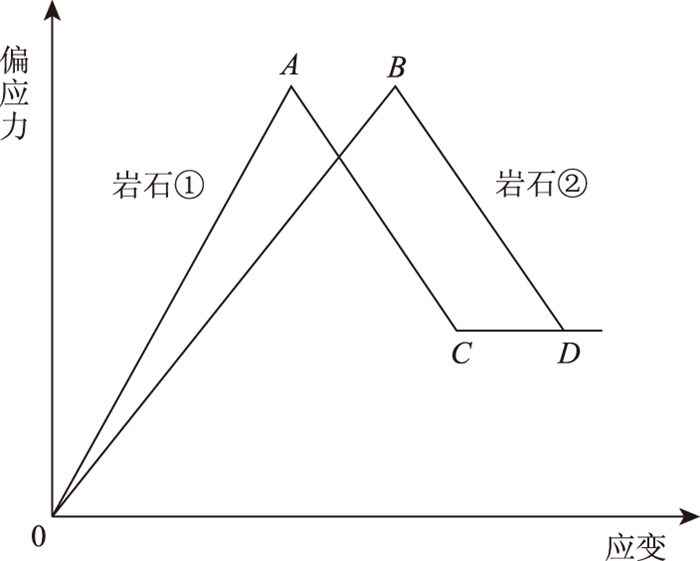
以脆性指标B6为例, 如图 1所示, 若两种岩石的峰后应力降速率相同, 因此由B6计算得到的脆性指标也相同, 但是通过图 1可以看出, 岩石①到达峰值应力所经过的应变更小, 显然岩石①的脆性更高, 但是B6并不能够衡量这一特性。此外, 脆性指标B5中所使用的起裂应力目前获取难度较大, 方法不成熟, 误差不易控制, 因此计算结果的可靠度不高。与此相近的脆性指标B8只是考虑了峰前可恢复应变与峰值应变, 忽略了峰后应力状态的影响, 因此也无法准确表征岩石的脆性程度。
|
| 图 1 脆性指标B6未能反映的情况 Fig. 1 Situations that brittleness indicator B6 fails to reflect |
| |
B7是在总结前人的基础上提出的通过峰后应力降的绝对大小和相对速率表征脆性指标。但是, 该方法的合理性有待商榷。其中, 该脆性指标将峰后应力降的绝对速率取对数并除以10, 目的是将其转换成0~1变化范围的取值, 但lg|kac(AC)|的实际取值范围为-∞~∞, 因此, 该指标的理论取值与实际不符。同时, 脆性指标B7同样没有考虑到峰前力学行为对岩石脆性特征的影响, 因此, 同样无法反映图 1所示的脆性差异。
B9是在分析B7的基础上提出的基于岩石应力-应变曲线峰后应力跌落速率及失稳时所释放弹性能与峰前储存总能量比值共同表征的脆性指标, 但其在应用中同样具有局限性。如图 2所示, 该方法用应力-应变曲线围成的面积表示对应能量, 若两种岩石峰前总量相同, 即SOAG等于SOBH, 失稳时释放的能量相同, 即SAEC等于SBFD, 且峰后应力降的速率也相同, 则由脆性指标B9计算得到两种岩石的脆性指标相同。但是岩石①的峰值应力更高且峰值应变更小, 显然岩石①的脆性更高, B9并不能够反映这一情况。此外, 即使两种岩体失稳时所释放弹性能与峰前储存总能量差别很大, 其比值仍有可能出现相等的结果。

|
| 图 2 脆性指标B9未能反映的情况 Fig. 2 Situations that brittleness indicator B9 fails to reflect |
| |
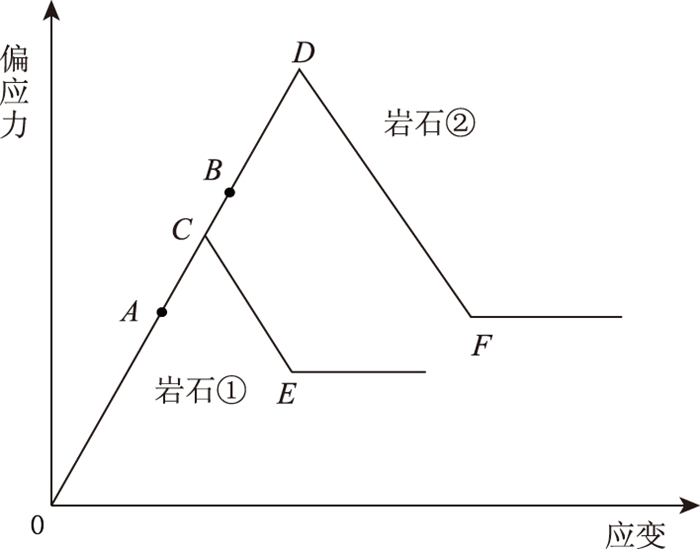
B10是在分析B9的基础上提出的基于全应力-应变曲线及起裂应力的岩石脆性指标。该指标利用起裂应力至峰值应力的增长幅度与起裂应变增长幅度的比值表征峰前的岩石脆性特征。如图 3所示, 若岩石①于A点起裂, 岩石②于B点起裂, 岩石①、②起裂应力至峰值应力的增长幅度相同, 且峰后应力跌落幅度也相同, 则由B5计算得到的脆性指标相同。但是岩石②到达峰值应力经过的应变更小, 显然岩石②的脆性高于岩石①, 而脆性指标B10不能反映这一情况。
|
| 图 3 脆性指标B10未能反映的情况 Fig. 3 Situations that brittleness indicator B10 fails to reflect |
| |
1.3 其他脆性指标分析
R.Rickman等[12]基于岩石的矿物成分提出了脆性指标B15, 基于归一化弹性模量和泊松比提出了脆性指标B16, 该方法适用于北美FORT-WORTH盆地页岩储层的岩石, 具有明显的地域局限性, 同时也未考虑到复杂应力条件及其他力学参数对岩石脆性的影响。廖东良等[13]认为材料断裂是由裂纹失稳造成的, 断裂韧度和矿物组分影响了材料抵抗断裂的性能, 于是提出了基于矿物组分及断裂韧度的岩石脆性指标B18。该指标只考虑了脆性矿物对岩石脆性的影响, 应用时存在较大的局限性。此外还有基于破裂角的脆性指标B19[14], 但在实际使用时还需要其他手段的辅助。另外, 基于冲击试验碎屑含量的脆性指标B20[15], 基于贯入试验的脆性指标B21[16], 这些方法由于试验设备昂贵、过程复杂繁琐、参数不易获取等原因不常使用。
2 基于全应力应变曲线新脆性指标建立大量的三轴压缩试验表明, 岩石在达到峰值强度后不是立刻丧失承载能力, 而是逐渐降低至残余强度, 岩石脆性破坏与其内部微裂纹产生, 扩展, 贯通以及峰后岩石破坏模式的全过程密切相关[17], 因此, 岩石应力-应变曲线作为岩石力学性质的体现, 其整个过程都反映了岩石非均质性和结构上的差异, 在建立脆性指标时应当予以综合考虑。
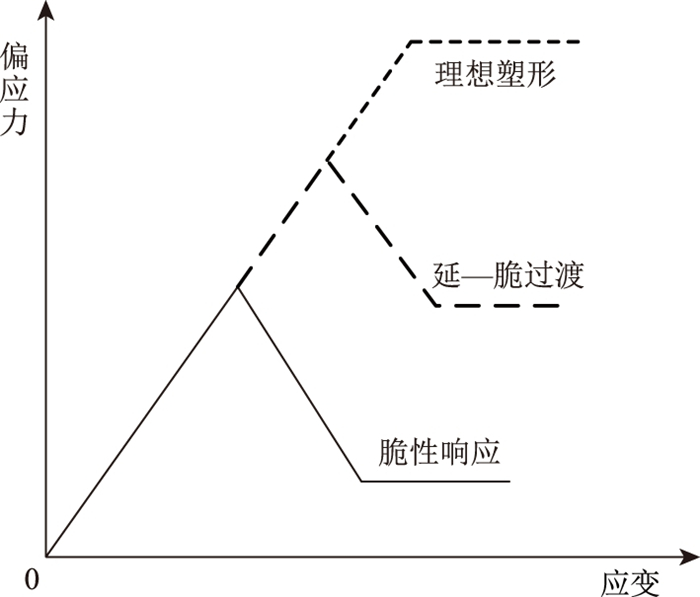
同时, 由于岩石大都处于三向受压状态, 受压应力状态下岩石的力学响应并非是单一模式, 而是表现出明显的围压相关性[18], 如图 4所示, 岩体在低围压条件下表现出明显的脆性特征; 随着围压的增大, 岩石峰值强度与残余强度均逐渐增大, 岩石强度衰减量(峰值强度与残余强度的差值)逐渐减小, 此时呈脆—延或延—塑过渡模式, 在力学响应上表现出脆性减小的趋势; 当围压继续升高, 岩石呈现明显的塑形特征, 其脆性特征在定量描述上很小[18-19], 因此同样要考虑应力状态对岩石脆性特征的影响。
|
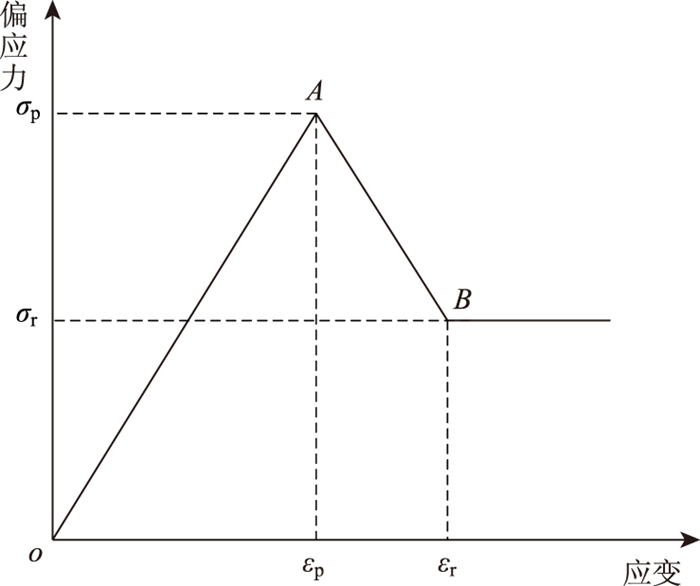
| 图 4 应力-应变曲线简图 Fig. 4 Simplified stress-strain curve |
| |
基于上述分析, 综合考虑不同围压对岩石内部性质的影响, 并通过其力学响应(全应力-应变曲线)确定岩石脆性程度。在脆性指标的建立过程中, 将岩石脆性分为峰前峰后两个部分, 如图 4所示, 点A(εp, σp)为峰值点, 点B(εr, σr)为残余点。对于峰前部分, 岩石越快到达峰值强度, 说明脆性越高, 在几何关系上, 通过线OA的斜率及峰值应变εp确定。
|
| 图 5 不同围压作用下岩石应力应变简图 Fig. 5 Simplified stress-strain curve of rocks under different confining pressures |
| |
首先, 对岩石峰前脆性程度评价方法进行定义, 即:

|
(1) |
其中,

|
(2) |
式中, σp为峰值强度; εp为峰值应变; Ba为峰前应力增长的绝对速率。σp/εp的几何意义为O点至A点连线的斜率(若在加载过程中出现屈服平台, 则以刚进入屈服平台时的点为A点), 进一步将其转化为0~1范围内变化的数值, 用以表征峰前应力增长速率对脆性的影响。但是, 峰前应力增长速率相同但增长幅度不同的岩石, 其脆性也不相同, 岩石到达峰值应力所经过的应变越小说明脆性越高, 将峰前的应力增长速率除以εp可以避免上述情况造成的计算误差。
对于峰后部分, 岩石脆性与应力降的幅度及速率有关, 应力降幅度越大, 速率越快, 说明岩石脆性越高, 因此可通过峰后应力降的幅度与应变增长幅度的比值表征峰后岩石脆性程度。
进一步, 对岩石峰后脆性程度评价方法进行定义, 即:

|
(3) |
式中, σr为残余强度; εr为残余应变。
于是, 综合考虑曲线峰前峰后对岩石脆性程度的共同影响, 提出本研究岩石的新脆性指标, 即:

|
(4) |
显然, BL取值越大, 表示岩石脆性程度越高。
3 脆性指标BL的适用性验证通常, 在岩石脆性指标应用中需考虑岩性和应力条件两方面, 因此, 本研究将通过不同种类岩石相同应力状态和同种岩石不同应力状态对BL的适用性进行验证。
3.1 不同种类岩石相同应力状态下脆性指标BL的验证根据已有研究表明, 岩石脆性越高, 其破坏程度越高, 碎块越明显, 破裂角度越大, 因此宏观上可根据岩石破环现象对岩石脆性程度进行判断。本研究选用了大理岩、砂岩、灰岩、花岗岩4种岩石单轴压缩试验结果[20], 如图 6所示。图中, 花岗岩破坏最为严重, 破裂面贯穿试样整体且出现大量碎块, 其破裂角度接近90°, 因此其脆性最大; 灰岩破坏角度略小于花岗岩, 虽然破裂面贯穿整体但并没有出现明显的碎块, 其脆性略低于花岗岩; 砂岩只是局部出现裂缝且裂缝未贯穿整个岩体, 其脆性略低于砂岩; 大理岩整体出现鼓胀, 并未出现明显的碎裂, 因此其脆性最小。由此可知, 这4种岩石的脆性程度由高到低依次为花岗岩、灰岩、砂岩、大理岩。
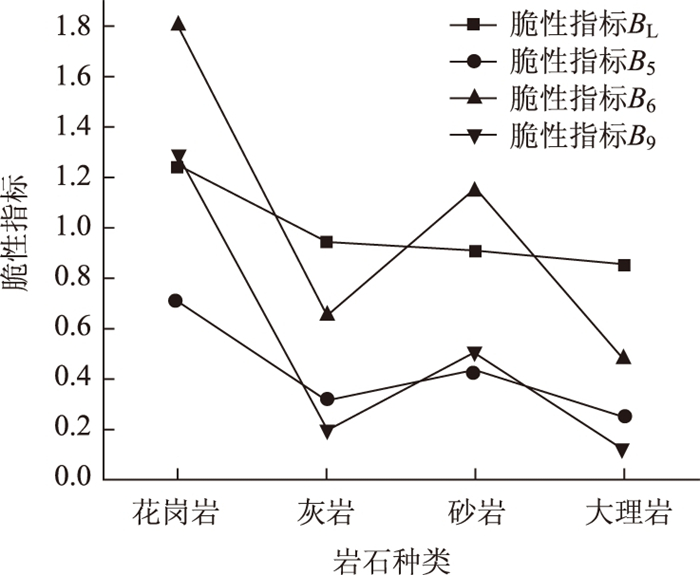
表 2是单轴压缩下4种岩石的单轴压缩试验数据, 利用4种不同脆性指标对结果进行计算并绘制了指标的变化趋势, 如图 7所示。从图中可以看到, 由脆性指标BL计算所得4种岩体的脆性程度由高到低依次为花岗岩、灰岩、砂岩、大理岩, 这一结果与上文分析的结论一致。对于B5, B6, B9的变化趋势, 均出现砂岩脆性判断与前文分析不符的现象, 通过2.2节分析可知, 这是由于对岩石应力-应变曲线考虑不够全面造成的。由此表明, BL相较于其他脆性指标能够更好地衡量不同岩石的脆性程度。
| 岩性 | σp/MPa | εp/(×10-3) | σr/MPa | εr/(×10-3) |
| 大理岩 | 176.03 | 12.10 | 132.17 | 43.86 |
| 砂岩 | 274.68 | 10.98 | 154.38 | 120.30 |
| 灰岩 | 301.27 | 7.22 | 205.58 | 95.69 |
| 花岗岩 | 420.37 | 7.25 | 120.47 | 299.90 |
|
| 图 7 单轴压缩应力状态下不同种类岩石脆性指标 Fig. 7 Brittleness indicators of different rocks under uniaxial compression |
| |
3.2 同种岩石不同应力状态下脆性指标BL的验证
为验证脆性指标BL是否适用于同种岩石不同应力状态下的脆性评价, 本研究选取了2组大理岩以及2组节理砂岩试验数据[19, 21], 并通过BL与其他脆性指标的分析对比进行验证。
3.2.1 大理岩脆性指标BL的验证表 3为两组大理岩三轴压缩试验数据。为了更清晰直观地对比各个脆性指标随围压变化趋势的差别, 根据表 3中的试验数据利用4种不同脆性指标进行了计算, 并绘制了各个脆性指标随围压的变化规律曲线, 如图 8所示。
| 组别 | 围压/MPa | σp/MPa | εp/(×10-3) | σr/MPa | εr/(×10-3) |
| 第1组 | 0 | 60.668 | 27.77 | 8.393 | 41.80 |
| 10 | 92.267 | 46.44 | 56.928 | 101.66 | |
| 20 | 118.055 | 55.04 | 89.253 | 150.48 | |
| 40 | 149.426 | 94.05 | 123.834 | 272.29 | |
| 60 | 164.675 | 131.97 | 156.235 | 303.55 | |
| 70 | 177.349 | 171.23 | 175.349 | 305.01 | |
| 第2组 | 0 | 50.265 | 0.53 | 12.887 | 0.94 |
| 5 | 88.125 | 0.60 | 39.501 | 1.30 | |
| 10 | 106.51 | 0.80 | 55.661 | 2.00 | |
| 20 | 149.53 | 1.10 | 107.577 | 3.20 | |
| 30 | 168.89 | 1.40 | 142.250 | 3.90 | |
| 54 | 240.40 | 2.30 | 238.709 | 4.54 |
|
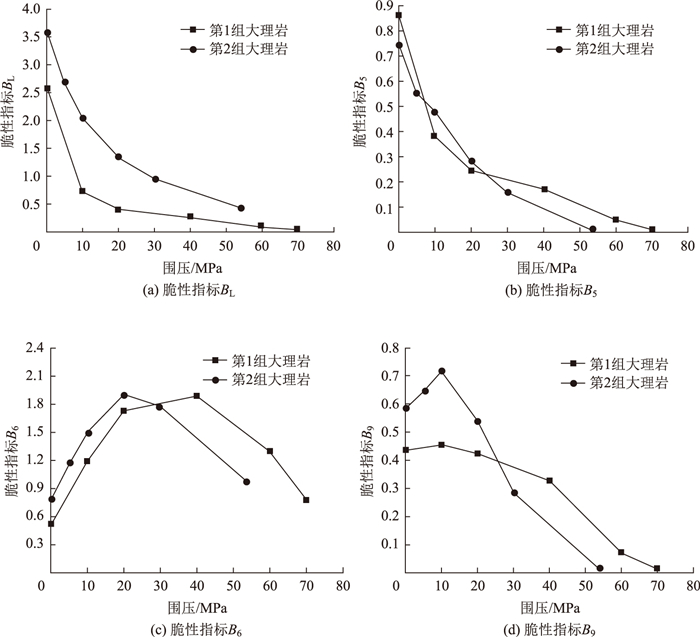
| 图 8 不同应力状态下大理岩脆性指标变化规律 Fig. 8 Variations of brittle indicator of marble under different stresses |
| |
根据表 3可知, 随着围压的升高, 大理岩的峰值强度与残余强度均有提升, 这说明在围压作用下, 大理岩表现出一定的延性特点, 并且随着围压的增大, 该特点越发明显, 同时, 岩石脆性也会随围压的升高逐渐降低, 这一结果与图 8(a)中脆性指标BL描述结果相一致。
图 8(b)为脆性指标B5随围压的变化趋势, 从图中可以看到, B5随围压的升高逐渐降低, 较好地描述了岩石围压作用下的脆性变化趋势, 这是由于大理岩在围压作用下峰后应力-应变曲线呈现出较好的规律性。
图 8(c)为脆性指标B6随围压的变化趋势, 从图中可以发现, B6随着围压的升高出现了先升后降的现象, 这是由于B6仅以峰后应变增长幅度表征岩石脆性, 不仅忽略了峰前部分, 同时也忽略了应力变化规律对脆性的影响。
图 8(d)为脆性指标B9随围压的变化趋势, B9出现了在低围压下计算不准确的现象, 这是因为B9的计算公式中的能量比部分, 只考虑了能量的相对大小, 在计算中, 即使两种岩体失稳时所释放弹性能与峰前储存总能量差别很大, 其比值仍有可能出现相等的结果。
3.2.2 节理砂岩脆性指标BB的验证为进一步验证脆性指标BL在复杂应力条件下的适用性, 本研究在大理岩的基础上增加2组节理砂岩试验数据[21]进行分析。
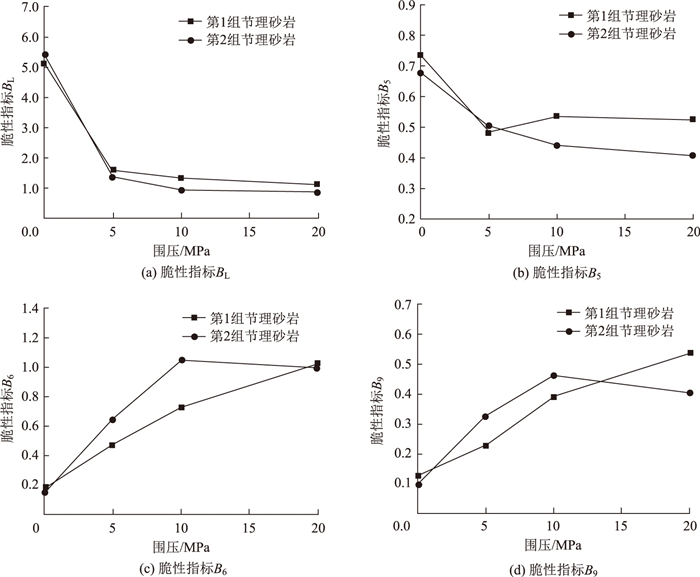
通过表 4可知, 与大理岩相似, 节理砂岩随着围压的升高, 峰值强度与残余强度均有提升, 故其脆性也会随围压的增大而降低。同时, 由于节理结构的存在, 砂岩受到结构面的交切作用, 使得岩石内部应力状态更加复杂。通过图 9(a)可知, 在这种复杂应力条件下, 脆性指标BL的变化趋势依然与上述分析一致, 通过图 9(b)、(c)、(d)可知, 脆性指标B5, B6, B9都出现了不同程度的误差, 说明BL相较于其他脆性指标可以更好地反映岩石复杂条件下的脆性程度。
| 组别 | 围压/MPa | σp/MPa | εp/(×10-3) | σr/MPa | εr/(×10-3) |
| 第1组 | 0 | 77.232 | 10.476 | 24.967 | 12.000 |
| 5 | 113.792 | 12.381 | 56.753 | 20.381 | |
| 10 | 117.744 | 12.571 | 65.766 | 25.714 | |
| 20 | 142.495 | 15.809 | 84.661 | 31.619 | |
| 第2组 | 0 | 78.431 | 10.095 | 20.915 | 11.809 |
| 5 | 116.340 | 11.238 | 60.130 | 16.571 | |
| 10 | 132.026 | 13.333 | 61.438 | 23.048 | |
| 20 | 162.092 | 15.809 | 77.124 | 32.000 |
|
| 图 9 不同应力状态下节理砂岩脆性指标变化规律 Fig. 9 Variation of brittle indicator of jointed sandstone under different stresses |
| |
此外, 节理结构使得砂岩强度和变形都表现出明显的各项异性, 单轴压缩条件下其残余强度值非常小, 随着围压的增大残余强度出现明显提高, 屈服阶段也逐渐明显[22], 因此节理砂岩在单轴压缩条件下的脆性值较高, 与围压条件下的脆性值相比有明显差值, BL同样反映了这一特点, 说明BL在对岩石脆性的定量分析上比较敏感, 且符合岩石的力学规律。
综上所述, 本研究提出的新脆性指标BL具有以下优点:
(1) 能够满足不同种类岩石及不同围压下的脆性评价。
(2) 对复杂应力条件下的岩石脆性评价有较好的可行性, 同时对岩石内部缺陷有一定的预测作用。
(3) 对岩石脆性的定量分析上较为敏感, 能够更好地体现岩石间的脆性差异。
(4) 由于应力应变试验常用于各类岩体工程中, 其试验方法和条件已经非常成熟, 因此该评价方法所涉及的参数方便获取, 数据的可靠度高。
4 结论(1) 提出了基于全应力-应变曲线的岩石脆性特征评价方法, 将岩石脆性分为峰前和峰后两部分, 综合考量了峰前应力增长速率、幅度及峰后应力应变关系。
(2) 通过试验数据的验证, 本研究提出的脆性特征评价方法不仅能够对不同岩石的脆性做出较为准确的评价, 而且对于复杂应力条件下的岩石也能较好地反映其脆性特征, 同时, 该方法在定量分析上较为敏感, 对实际的工程具有指导作用。
(3) 本研究提出的评价方法覆盖整个应力-应变全过程, 对于岩石不同应力状态下其内部性质的外部反映进行了全面考虑, 且该方法中所使用的参数均为常规三轴压缩试验容易获取的参数, 因此其具有适用范围广和可操作性强的特点。
| [1] |
王洪建, 刘大安, 黄志全, 等. 层状页岩岩石力学特性及其脆性评价[J]. 工程地质学报, 2017, 25(6): 1414-1423. WANG Hong-jian, LIU Da-an, HUANG Zhi-quan, et al. Mechanical Properties and Brittleness Evaluation of Layered Shale Rock[J]. Journal of Engineering Geology, 2017, 25(6): 1414-1423. |
| [2] |
陈竑然, 秦四清, 薛雷, 等. 岩石脆性破坏表征与Weibull分布适用范围[J]. 地球物理学进展, 2017, 32(5): 2200-2206. CHEN Hong-ran, QIN Si-qing, XUE Lei, et al. Characterization of Brittle Failure of Rock and Limitation of Weibull Distribution[J]. Progress in Geophysics, 2017, 32(5): 2200-2206. |
| [3] |
刘泉声, 刘建平, 时凯, 等. 评价岩石脆性指标对滚刀破岩效率的影响[J]. 岩石力学与工程学报, 2016, 35(3): 498-510. LIU Quan-sheng, LIU Jian-ping, SHI Kai, et al. Evaluation of Rock Brittleness Indexes on Rock Fragmentation Efficiency by Disc Cutter[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 498-510. |
| [4] |
刘晓辉, 余洁, 康家辉, 等. 不同围压下煤岩强度及变形特征研究[J]. 地下空间与工程学报, 2019, 15(5): 1341-1352. LIU Xiao-hui, YU Jie, KANG Jia-hui, et al. Study on Strength and Deformation Characteristics of Coal-rock under Different Confining Pressures[J]. Chinese Journal of Underground Space and Engineering, 2019, 15(5): 1341-1352. |
| [5] |
HUCKA V, DAS B. Brittleness Determination of Rocks by Different Methods[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1974, 11(10): 389-392. |
| [6] |
王宇, 李晓, 武艳芳, 等. 脆性岩石起裂应力水平与脆性指标关系探讨[J]. 岩石力学与工程学报, 2014, 33(2): 264-275. WANG Yu, LI Xiao, WU Yan-fang, et al. Research on Relationship between Crack Initiation Stress Level and Brittleness Indices for Brittle Rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(2): 264-275. |
| [7] |
周辉, 孟凡震, 张传庆, 等. 基于应力-应变曲线的岩石脆性特征定量评价方法[J]. 岩石力学与工程学报, 2014, 33(6): 1114-1122. ZHOU Hui, MENG Fan-zhen, ZHANG Chuan-qing, et al. Quantitative Evaluation of Rock Brittleness Based on Stress-strain Curve[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1114-1122. |
| [8] |
夏英杰, 李连崇, 唐春安, 等. 基于峰后应力跌落速率及能量比的岩体脆性特征评价方法[J]. 岩石力学与工程学报, 2016, 35(6): 1141-1154. XIA Ying-jie, LI Lian-chong, TANG Chun-an, et al. Rock Brittleness Evaluation Based on Stress Dropping Rate after Peak Stress and Energy Ratio[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(6): 1141-1154. |
| [9] |
夏英杰, 李连崇, 唐春安, 等. 储层砂岩破坏特征与脆性指数相关性影响的试验及数值研究[J]. 岩石力学与工程学报, 2017, 36(1): 10-28. XIA Ying-jie, LI Lian-chong, TANG Chun-an, et al. Experiment and Numerical Research on Failure Characteristic and Brittleness Index for Reservoir Sandstone[J]. Chinese Journal of Rock Mechanics and Engineering, 2017, 36(1): 10-28. |
| [10] |
陈国庆, 赵聪, 魏涛, 等. 基于全应力-应变曲线及起裂应力的岩石脆性特征评价方法[J]. 岩石力学与工程学报, 2018, 37(1): 51-59. CHEN Guo-qing, ZHAO Cong, WEI Tao, et al. Evaluation Method of Brittle Characteristics of Rock Based on Full Stress-strain Curve and Crack Initiation Stress[J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(1): 51-59. |
| [11] |
胡清波, 梁海安, 杨婷, 等. 一种基于统计损伤本构关系的岩石脆性评价新方法[J]. 哈尔滨工业大学学报, 2020, 52(11): 147-156. HU Qing-bo, LIANG Hai-an, YANG Ting, et al. A New Method for Rock Brittleness Evaluation Based on Statistical Damage Constitutive Relation[J]. Journal of Harbin Institute of Technology, 2020, 52(11): 147-156. |
| [12] |
RICKMAN R, MULLEN M, PETRE E, et al. A Practical Use of Shale Petrophysics for Stimulation Design Optimization: All Shale Plays Are Not Clones of the Barnett Shale[R]. Colorado, US: Society of Petroleum Engineer, 2008.
|
| [13] |
廖东良, 肖立志, 张元春. 基于矿物组分与断裂韧度的页岩地层脆性指数评价模型[J]. 石油钻探技术, 2014, 42(4): 37-41. LIAO Dong-liang, XIAO Li-zhi, ZHANG Yuan-chun. Evaluation Model for Shale Brittleness Index Based on Mineral Content and Fracture Toughness[J]. Petroleum Drilling Techniques, 2014, 42(4): 37-41. |
| [14] |
TARASOV B, POTVIN Y. Universal Criteria for Rock Brittleness Estimation under Triaxial Compression[J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 59: 57-69. |
| [15] |
PROTODYAKONOV M M. Mechanical Properties and Drill-ability of Rocks[C]// Proceedings of the 5th Symposium on Rock Mechanics. Twin Cities: University of Minnesota Press, 1963: 103-118.
|
| [16] |
YAGIZ S. Assessment of Brittleness Using Rock Strength and Density with Punch Penetration Test[J]. Tunnelling and Underground Space Technology, 2009, 24(1): 66-74. |
| [17] |
陈国庆, 吴家尘, 蒋万增, 等. 基于弹性能演化全过程的岩石脆性评价方法[J]. 岩石力学与工程学报, 2020, 39(5): 901-911. CHEN Guo-qing, WU Jia-chen, JIANG Wan-zeng, et al. An Evaluation Method of Rock Brittleness Based on the Whole Process of Elastic Energy Evolution[J]. Chinese Journal of Rock Mechanics and Engineering, 2020, 39(5): 901-911. |
| [18] |
余华中, 阮怀宁, 褚卫江. 大理岩脆-延-塑转换特性的细观模拟研究[J]. 岩石力学与工程学报, 2013, 32(1): 55-64. YU Hua-zhong, RUAN Huai-ning, CHU Wei-jiang. Mesoscopic Simulation Study of Brittle-ductile-plastic Transition Character of Marble[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(1): 55-64. |
| [19] |
徐松林, 吴文, 王广印, 等. 大理岩等围压三轴压缩全过程研究Ⅰ: 三轴压缩全过程和峰前、峰后卸围压全过程实验[J]. 岩石力学与工程学报, 2001, 20(6): 763-767. XU Song-lin, WU Wen, WANG Guang-yin, et al. Study on Complete Procedures of Marble Undertriaxial Compression Ⅰ: Testing Study on Complete Procedure of Triaxial Compression and the Processes of Unloading Confining at the Pre-peak and Post-peak[J]. Chinese Journal of Rock Mechanics and Engineering, 2001, 20(6): 763-767. |
| [20] |
刘晨阳. 一种基于应力-应变曲线的岩石脆性评价方法研究[D]. 长春: 吉林大学, 2019. LIU Chen-yang. Research on a Method of Rock Brittleness Evaluation Based on Stress-strain Curve[D]. Changchun: Jilin University, 2019. |
| [21] |
邓华锋, 潘登, 许晓亮, 等. 三轴压缩作用下断续节理砂岩力学特性研究[J]. 岩土工程学报, 2019, 41(11): 2133-2141. DENG Hua-feng, PAN Deng, XU Xiao-liang, et al. Mechanical Characteristics of Intermittent Jointed Sandstone under Triaxial Compression[J]. Chinese Journal of Geotechnical Engineering, 2019, 41(11): 2133-2141. |
| [22] |
肖维民, 邓荣贵, 付小敏, 等. 单轴压缩条件下柱状节理岩体变形和强度各向异性模型试验研究[J]. 岩石力学与工程学报, 2014, 33(5): 957-963. XIAO Wei-min, DENG Rong-gui, FU Xiao-min, et al. Model Experiments on Deformation and Strength Anisotropy of Columnar Jointed Rock Masses under Uniaxial Compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(5): 957-963. |
 2021, Vol. 38
2021, Vol. 38

