扩展功能
文章信息
- 吴兵, 梁瑶, 唐晓波, 赵晓彦, 蒋楚生
- WU Bing, LIANG Yao, TANG Xiao-bo, ZHAO Xiao-yan, JIANG Chu-sheng
- 锚索与抗滑桩组合加固折线型滑面高边坡受力计算及优化设计
- Force Calculation and Optimal Design for High Slope with Broken-line Sliding Surface Reinforced by Combination of Anchor Cable and Anti-slide Pile
- 公路交通科技, 2021, 38(3): 40-48
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 40-48
- 10.3969/j.issn.1002-0268.2021.03.006
-
文章历史
- 收稿日期: 2020-07-06
2. 西南交通大学 地球科学与环境工程学院,四川 成都 611756;
3. 中铁二院工程集团有限责任公司,四川 成都 610031
2. School of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu Sichuan 611756, China;
3. China Railway Eryuan Engineering Group Co., Ltd., Chengdu Sichuan 610031, China
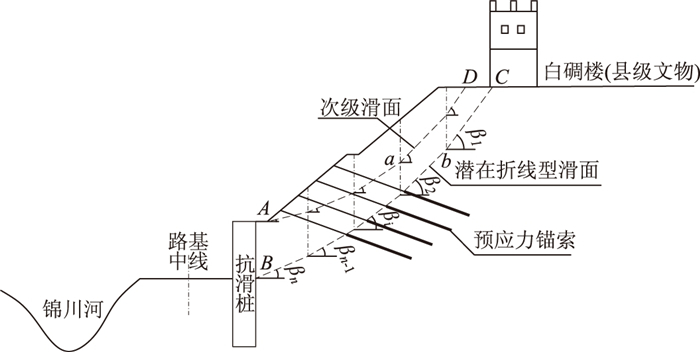
山区道路设计中高陡堑坡多采用“分级开挖、逐层加固”原则及“固脚强腰”理念, 单一加固措施难以同时保证上部坡面及整个坡体稳定。设计中一般上部采用框架锚索, 下部设置抗滑桩或锚拉桩组合加固[1-3]。该措施可争取有效空间、减少边坡开挖, 对坡顶有重要构筑物, 边坡变形及移位控制要求高时, 具有较大优越性, 在工程实践中广泛应用, 取得了良好的效果[2-4]。如图 1所示, 拟建公路堑坡受左侧河流及右侧坡顶县级文物保护建筑(碉楼)限制, 放坡空间有限, 边坡陡峭。为防止上级边坡因次级滑动或变形过大, 造成碉楼基础失稳, 采用框架锚索加固; 下部为满足高等级公路平纵要求, 在道路右侧采用抗滑桩加固, 以保证线路顺利通过该地段、减少挖方量。
|
| 图 1 锚索与桩组合加固折线型滑面边坡示意图 Fig. 1 Schematic diagram of slope with broken-line sliding surface reinforced by combination of anchor cable and slide-resistant pile |
| |
然而规范[5-6]仅对直线型(顺层)滑面给出了锚固受力计算方法, 而对工程中多为折线型(圆弧)滑面的土质及类土质边坡, 则无直接计算公式, 导致设计者难以采用较为合理的方法对锚索与抗滑桩的联合受力进行分析。由于折线滑动条块倾角无固定值, 目前工程中多采用试算法。通过对锚固范围内的锚体布设位置不断进行调整, 用与多数单体相交的某一滑面代替整个潜在滑面, 计算其稳定性直至满足规范中安全系数要求。该方法具有随意性, 将造成计算工作量大大增加。此外, 当单体大部分落于某段滑面时, 用该段倾角代替整个潜在滑面倾角是合适的。然而, 当采用多级框架锚索时, 由于锚索多排分散布置, 该方法适用性将大大降低。
学者们多对单一锚索或抗滑桩受力计算进行了研究[7-8], 对于锚索锚固力作用, 赵晓彦等[9]、赵洪岭等[10]认为单一锚索锚固力均匀分散在其所穿过条块的滑面上; 任红卓等[11]基于锚固力利用率提出了锚固角优化设计方法。对于折线滑动边坡, 徐鸿彪等[12]基于概率理论从最大概然入射线、期望角等方面研究了折线型滑动边坡的锚固设计方法; 蒋楚生等[13]提出通过采用力的水平投影来计算边坡稳定性系数。对于优化设计方面, 李起龙等[14]、谈华宇等[15]分别对抗滑桩及锚索布设进行了研究; 罗丽娟等[16]基于投资-效益准则构建了抗滑桩结构优化设计模型。而目前对组合结构研究则多集中在较复杂的锚拉桩上[17-18], 对本研究所述折线型滑面边坡采用锚索+桩分离式组合结构研究则较少, 其设计方法并不成熟, 以致难以准确获得折线滑动边坡各结构受力的实际情况, 边坡下滑力分配前后出现误差, 不能实现二者受力协调, 各结构优势难以发挥, 造成工程浪费或设计失败。
基于此, 本研究依托德会高速某实际边坡, 对锚索+桩组合加固折线滑动边坡设计方法进行研究, 为类似工程设计提供参考。
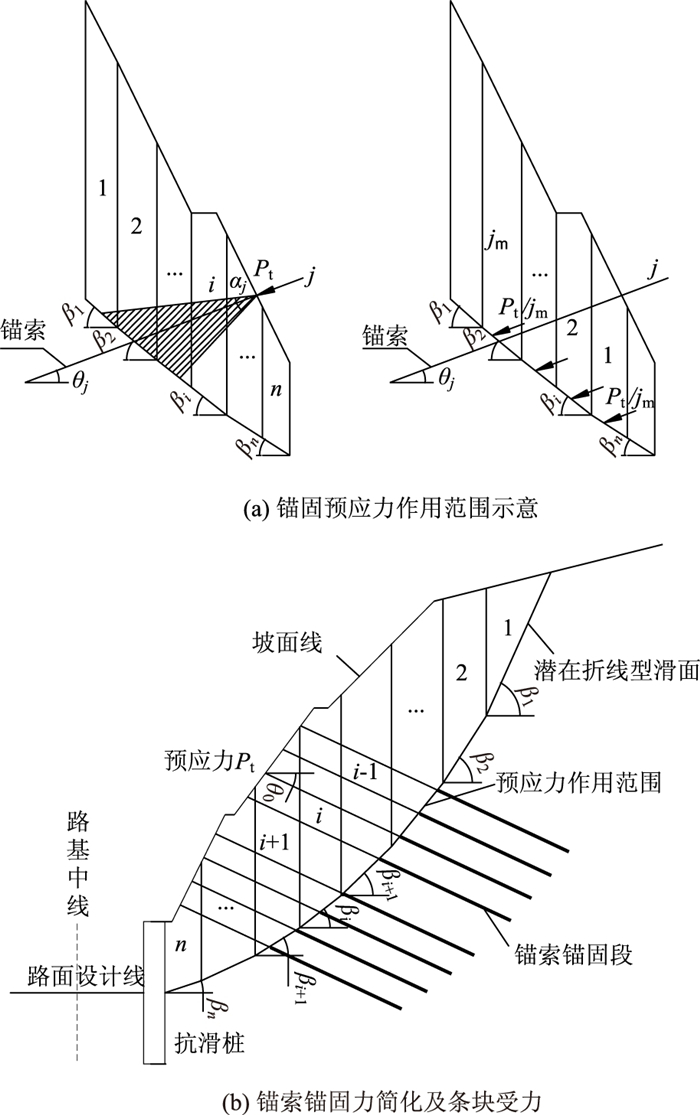
1 折线滑动边坡加固设计计算 1.1 锚索锚固预应力设计计算锚索为主动加固措施, 通过施加预应力, 限制边坡变形。工程实践中, 同一级边坡上的框架锚索具有相同的布置间距和锚固力。如图 2(a)所示, 设每束锚索的锚固力为Pt, 第j排锚索的锚固角为θj, 其所穿越第i个条块处的滑面倾角为βi。锚索锚固力从坡面锚墩处按一定的扩散角αj向滑动条块内传播, 传至潜在滑动面时, 应为一分布力, 而非集中力。本研究不考虑锚索预应力传递损失量, 则滑面处分布的作用力合力等于锚端预应力。
|
| 图 2 锚索与桩组合加固折线型滑面边坡受力计算图 Fig. 2 Calculation diagram of force of slope with broken-line sliding surface reinforced by combination of anchor cable and slide-resistant pile |
| |
如图 2(b)所示, 对挖方边坡进行条块划分, 采用折线滑动法(传递系数法)[5-6]计算潜在滑体的总剩余下滑力E。根据研究结果[9-10], 如图 2(a)所示, 本研究认为锚索锚固预应力Pt的作用范围覆盖锚体所穿越的全部条块, 即每个条块在计算剩余下滑力时, 均应考虑穿越该条块的锚索锚固作用力。为简化计算, 认为每束锚索锚固力Pt均分在所穿越的每个条块上, 其方向与锚索总预应力Pt方向一致。如图 2(a)所示, 设第i个条块共有ni束锚索穿越, 其中第j束锚索共穿越mj个条块, (第k-1块至第k+mj-1块), 则第i个条块的剩余下滑力可按式(1)~(5)进行计算。
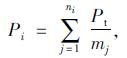
|
(1) |
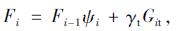
|
(2) |
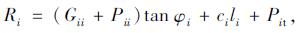
|
(3) |
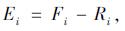
|
(4) |
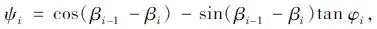
|
(5) |
式中, Git=Gisin βi, Gii=Gicos βi, Pii=Pisin(βi+θj), Pit=Picos(βi+θj); ci, φi, βi, ψi分别为第i个条块底部滑面的黏聚力、内摩擦角、倾角及传递系数; Gi, Pi, Fi, Ri, Ei分别第i条块的重力、锚索锚固力、下滑力、抗滑力及剩余下滑力; θj为锚索锚固角。
1.2 抗滑桩受力设计计算抗滑桩为被动加固措施, 桩前土体开挖后, 桩顶锚索锚固坡体后的剩余下滑力传递至桩上, 因此抗滑桩受力设计计算的关键为锚固预应力的计入[9-10]。如图 2(b)所示, 设桩处第n条块的剩余下滑力En即为抗滑桩上的作用荷载, 可根据1.1节中方法计算得出。由此可见组合加固中抗滑桩受力与锚索锚固预应力存在受力协调关系。
2 组合加固优化设计 2.1 组合结构合理设计抗滑桩设计既要满足规范要求, 又要考虑上部锚索加固及工程特点提高安全性、降低总造价。当边坡开挖线确定后, 桩身悬臂段已知, 勘察后桩位地质条件明确, 抗滑桩设计可由桩后滑坡推力大小结合规范确定桩长、间距、截面、配筋等。此时, 若滑坡推力分配不合理, 可能造成桩身受力偏大, 导致桩间距过小, 截面参数过大, 桩身过长。同时地质条件偏差时会影响人工挖桩安全, 此时应调整锚索布设间距、钢绞线数量, 增大坡面单宽锚固力设计值, 以降低抗滑桩受力, 使桩身设计趋于合理。
同理, 若受力分配不合理导致抗滑桩受力过小(设计截面1.0 m×1.5 m), 而锚索锚固力偏大(设计吨位1 000 kN)。则应在满足次级滑动加固的基础上, 减小锚索预应力设计值, 降低因设计吨位过大, 由锚索超张拉带来的后期预应力损失量偏大的安全风险[19-20]。
工程设计中锚索设计通常采用4~8根钢绞线, 抗滑桩设计通常采用几种常用截面尺寸。在二者组合时, 可根据锚索规格(锚固体系、钢绞线数量、钻孔大小、注浆量等)及框架结构调整的造价变化量与抗滑桩截面(桩体、锁口、护壁及配筋量等)调整的造价变化量进行工程经济比较。同时应结合施工条件、材料供应等进行技术经济综合比选, 以获得安全经济合理的锚索与抗滑桩组合设计。
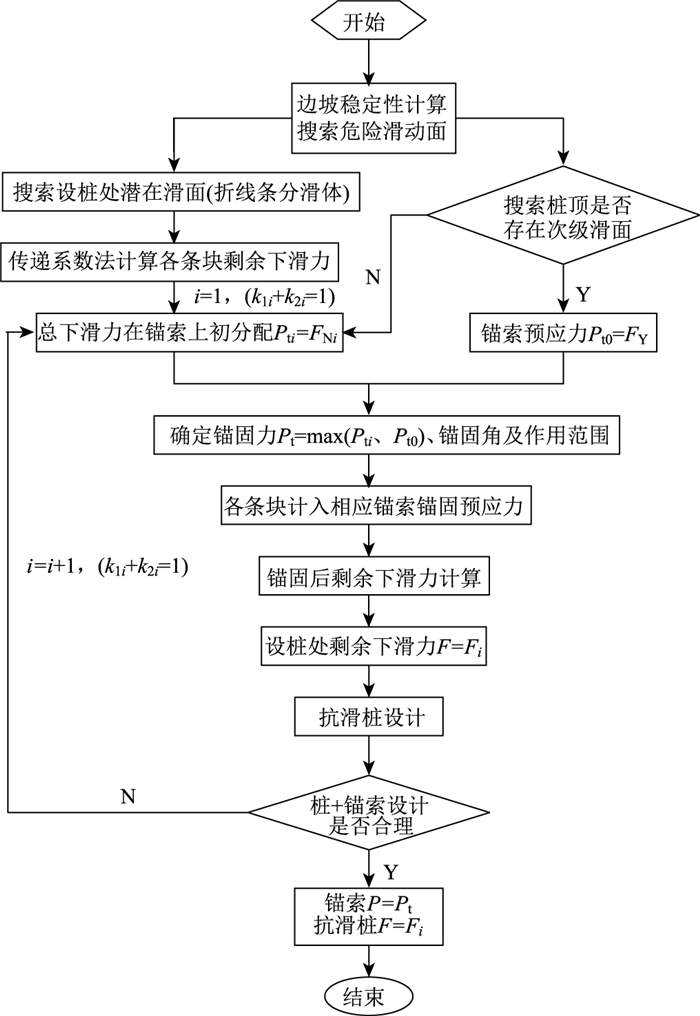
2.2 具体设计步骤为使预应力锚索+抗滑桩在组合加固边坡中实现相互协调, 提出以下设计计算步骤, 其流程图如图 3所示。
|
| 图 3 锚索与桩组合加固折线型滑面边坡设计流程图 Fig. 3 Flowchart of designing slope with broken-line sliding surface reinforced by combination of anchor cable and slide-resistant pile |
| |
(1) 加固前边坡稳定性计算
通过对开挖至设计线后的加固前边坡进行稳定性计算, 获得以下结果:
① 桩顶有无次级滑面
如图 1所示, 通过GeoSlope软件固定剪出口搜索范围计算边坡稳定性系数, 确定桩顶坡体AD是否可能在坡脚A沿滑面a滑动或在坡面产生剪出滑动。
② 设桩处总剩余下滑力E
通过边坡稳定性计算, 确定坡体加固前设桩处整体边坡的总剩余下滑力。
(2) 计算锚索预应力
① 若桩顶上部坡体存在次级滑面, 则按其滑动剩余下滑力E′, 依据规范及1.1节计算锚索锚固力设计值Pt0=FY。
② 若桩顶坡体不存在次级滑面, 则以设桩处总剩余下滑力水平分力Eh为基数, 乘以系数k1i作为锚索预应力设计初始值Pti=FNi=k1iEh/cos θ0, k1i+k2i=1, k1i, k2i分别为总剩余下滑力在锚索和抗滑桩上的分配系数, 其取值应综合考虑坡面上锚索布设、坡脚抗滑桩设置、各自工程建设及造价费用后, 综合确定。
③ 在第①、②条中取二者中的最大值作为预应力锚索设计值Ptmax。
(3) 计入预应力Pt=Ptmax, 在有锚索穿过的条块上计入相应锚固预应力Pi, 采用折线滑动法, 重新计算锚索锚固后的剩余下滑力Ei, 取设桩处的剩余下滑力Fi=Ei。
(4) 按Fi进行抗滑桩受力评估和设计。假如抗滑桩尺寸、锚索受力及布设合理, 则结束设计。否则, 返回第(2)步, 调整锚索预应力Pt=Pti(应保证Pti≥Pt0), 重新进行第(3)步和第(4)步, 重复该过程, 直至桩+锚索结构设计合理。
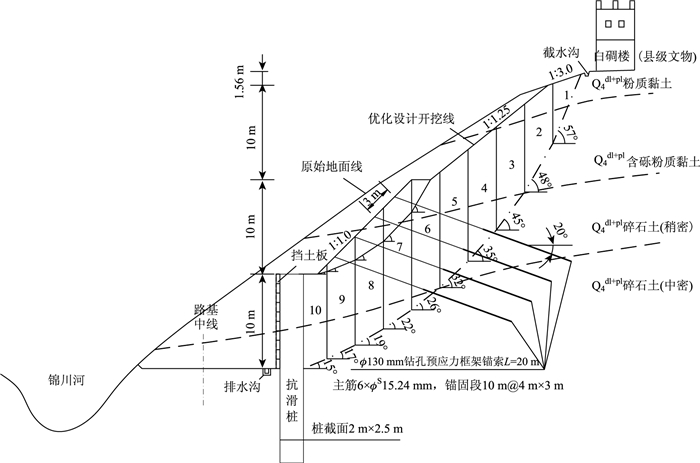
3 工程设计实例 3.1 边坡概况实例边坡位于会理县老碾乡纸房村内, 德会高速K12+560—K12+660段右侧, 长100 m, 在锦川河右岸阶地上。由于该段堑坡左侧临锦川河, 右侧坡顶有县级文物(白碉楼)。受线位及重要构筑物限制, 放坡空间小, 边坡较陡, 拟采用锚索+桩组合加固。如图 4所示, 在二级边坡施作框架锚索, 在坡脚设置抗滑桩, 采用桩间挂板进行加固。
|
| 图 4 实例折线型滑面边坡锚索与桩组合加固代表断面 Fig. 4 An example of typical section of slope with broken-line sliding surface reinforced by combination of anchor cable and slide-resistant pile |
| |
边坡属中山区河谷剥蚀、堆积地貌。由第四系全新统坡洪积(Q4dl+pl)粉质黏土、上更新统坡洪积(Q3dl+pl)含砾粉质黏土及碎石土构成。土层厚达28.1m(钻孔未揭穿), 各层岩土体物理力学参数如表 1所示。工区地震烈度为7度, 加速度为0.10g, 分组为第3组。
| 土层名称 | 状态 | 天然 | 暴雨 | |||||
| 容重r/(kN·m-3) | 黏聚力c/kPa | 内摩擦角φ/(°) | 容重r/(kN·m-3) | 黏聚力c/kPa | 内摩擦角φ/(°) | |||
| 粉质黏土 | 软塑-可塑 | 19 | 16 | 12 | 20 | 14 | 10 | |
| 含砾粉质黏土 | 硬塑 | 19.5 | 25 | 20 | 20.5 | 22 | 18 | |
| 碎石土 | 稍密 | 20.5 | 6 | 29 | 21.5 | 4.5 | 28 | |
| 中密 | 20.5 | 6 | 34 | 21.5 | 4.5 | 33 | ||
根据规范[5]中3.7.7条, 考虑坡顶文物建筑安全, 分别对天然工况(K0=1.3)、暴雨工况(KⅠ=1.2)及地震工况(KⅡ=1.15)按圆弧滑动进行潜在滑动面搜索。计算得出暴雨工况滑坡推力最大, 为最不利工况, 最终搜索的主滑面及次级滑面如图 4所示。
3.2 组合结构加固设计计算(1) 加固前边坡稳定性计算
根据《公路路基设计规范》[5]要求和边坡实际情况, 取安全系数K=1.2(暴雨工况)。按图 4所示的条块划分, 采用折线滑动法进行设桩处剩余下滑力计算, 计算结果如表 2所示, 剩余下滑力E=1 800.81 kN/m, 水平夹角为15°。
| 条块 编号 |
重力 W/kN |
滑面倾角 α/(°) |
传递系数 Ψ |
下滑力 T/kN |
抗滑力 R/kN |
剩余下滑力 E/kN |
| 1 | 219 | 57 | 0.000 0 | 238.77 | 157.95 | 80.82 |
| 2 | 742 | 48 | 0.954 4 | 716.74 | 250.02 | 543.86 |
| 3 | 621 | 45 | 0.987 5 | 570.94 | 176.14 | 931.86 |
| 4 | 727 | 35 | 0.947 9 | 542.39 | 209.95 | 1 215.74 |
| 5 | 772 | 32 | 0.987 5 | 532.10 | 217.94 | 1 514.71 |
| 6 | 787 | 26 | 0.972 3 | 448.33 | 225.60 | 1 695.48 |
| 7 | 701 | 22 | 0.982 7 | 341.48 | 210.95 | 1 796.74 |
| 8 | 574 | 19 | 0.987 5 | 242.73 | 186.66 | 1 830.36 |
| 9 | 279 | 17 | 0.992 0 | 105.88 | 98.78 | 1 822.76 |
| 10 | 437 | 15 | 0.992 0 | 146.97 | 154.28 | 1 800.81 |
同理, 对桩顶坡体进行稳定性计算, 桩顶坡脚处存在次级滑面, 计算剩余下滑力E2=165.9 kN/m(E2 < 0.2E1)。
(2) 框架锚索设计计算
设计拟采用4 m×3 m的锚索框架梁, 锚索锚固力水平分力按设桩处剩余下滑力水平分力Eh乘以分配系数k1确定。通过分别对k1=0.2, 0.3, 0.4, 0.5进行估算, 获得锚索+桩组合结构设计如表 3所示。
| 序号 | 锚索分配系数k1 | 锚索钢绞线/根 | 桩截面/(m×m) |
| ① | 0.2 | 3~4 | 2.5×3.0 |
| ② | 0.3 | 4~5 | 2.0×3.0 |
| ③ | 0.4 | 6 | 1.8×2.5 |
| ④ | 0.5 | 8 | 1.5×2.0 |
结果表明: k1=0.2, 0.3时, 桩截面为2.5 m×3 m(过大)、2.0 m×3 m(较大), 而锚索钢绞线为3~4、4~5根, 设计不合理; k1=0.5时, 桩截面为1.5 m×2.0 m, 锚索钢绞线为8根(过多), 设计不合理; k1=0.4时, 桩截面为1.8 m×2.5 m, 锚索钢绞线为6根, 二者受力协调, 结构设计合理。
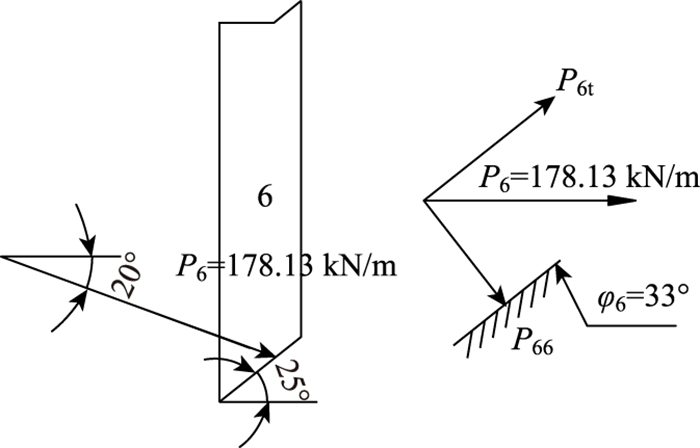
在初步确定锚索应承担40%剩余下滑力后, 即Pth=Ecos15°×40%=695.78 kN, 按式(6)计算图 5中每束锚索锚固预应力设计值:
|
| 图 5 锚索加固条块6作用力分解示意图 Fig. 5 Schematic diagram of force decomposition of anchor cable reinforced strip 6 |
| |
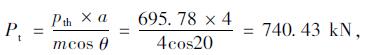
|
(6) |
式中, a为锚索水平间距; m为断面中锚索根数; θ为锚索水平向夹角, 本算例中a=4 m, m=4, θ=20°。
按现行规范[5]设计, 单根φS15.24低松弛钢绞线(1 860 MPa级)可提供125 kN的锚固力, 为便于锚索张拉施工控制, 计算取整值, 每束锚索预应力设计值Pt=125×6=750 kN, 即锚固段设计长度为10 m, 钢绞线为6根。反算后实际承担40.52%的总剩余下滑力。
(3) 抗滑桩设计计算
在采用锚索对桩顶坡体进行加固后, 坡体应力重新分布, 且稳定性发生改变。应重新计算边坡设桩处剩余下滑力, 由式(1)可计算作用于每个条块上的锚固预应力。
假定锚索锚固后最危险滑面仍为图 4所示, 同理计算设桩处的剩余下滑力, 如表 4所示。
| 条块 编号 |
穿越锚 索根数 |
锚固力 Pt/kN |
传递系数 Ψ |
下滑力 T/kN |
抗滑力 R/kN |
剩余下滑力 E/kN |
| 1 | 0 | 0 | 0.000 0 | 238.77 | 157.95 | 80.82 |
| 2 | 0 | 0 | 0.954 4 | 716.74 | 250.02 | 543.86 |
| 3 | 0 | 0 | 0.987 5 | 570.94 | 176.14 | 931.86 |
| 4 | 2 | 84.38 | 0.947 9 | 542.39 | 273.04 | 1 152.65 |
| 5 | 3 | 131.25 | 0.987 5 | 532.10 | 320.73 | 1 349.62 |
| 6 | 4 | 178.13 | 0.972 3 | 448.33 | 376.58 | 1 383.99 |
| 7 | 4 | 178.13 | 0.982 7 | 341.48 | 368.66 | 1 332.92 |
| 8 | 3 | 131.25 | 0.987 5 | 242.73 | 306.22 | 1 252.78 |
| 9 | 1 | 46.88 | 0.992 0 | 105.88 | 142.21 | 1 206.38 |
| 10 | 0 | 0 | 0.992 0 | 146.97 | 154.28 | 1 189.38 |
按桩上实际受力1 189.38 kN/m, 依据规范[5]进行抗滑桩设计, 结果为: 桩截面应为2 m×2.5 m; 桩长为20 m(悬臂段10 m, 锚固段10 m, 其中嵌入中密~密实碎石土10 m); 桩间距为5 m; 桩身配筋率和位移、变形等均满足规范要求, 抗滑桩设计合理。
(4) 受力分配差异分析
由表 2、表 4可知, 采用锚索锚固后, 设桩处剩余下滑力为1 189.38 kN/m, 与锚固前总剩余下滑力的59.48%, 即1 800.81×0.594 8=1 071.18 kN/m, 相比二者差值较大(118.26 kN/m), 经分析是由以下两个原因造成的:
① 式(5)中折线滑动传递系数对4#~9#条块锚固力均进行了折减, 如表 3所, 经计算共折减了约16.06 kN/m。
② 锚索所穿越4#~9#条块滑面倾角为变量且角度均大于最后(10#)条块, 如图 5所示, 以图 4中的条块6进行示例, 由式(3)可知锚索提供的法向锚固力Pii、切向锚固力Pit在锚固角θ0=20°与滑块倾角βi=26°换算后均进行了折减, 同时式(3)中Pii值乘以基底摩擦系数tan φi=0.577 4再次进行了折减。算例中4#~9#条块综合折减幅度约102.20 kN/m。
以上说明: 采用锚索加固折线滑动边坡不同于直线滑动边坡, 因折线滑面倾角大多上陡下缓, 呈递减趋势(如图 4及表 2所示), 这些因素通常会导致锚索实际提供的锚固力偏小, 而桩身应提供的抗滑力增大, 本算例变化结果如表 5所示。
| 措施 | 分配受力/kN | 实际受力/kN | 变化百分比/% |
| 锚索 | 750.00 | 611.73 | -15.27 |
| 桩 | 1 050.81 | 1 189.38 | 10.16 |
这表明粗略地将总剩余下滑力在锚索和桩上进行分配是不合理的, 会造成抗滑桩受力偏小(约10.16%), 将降低桩身设计安全度, 导致工程设计失败。抗滑桩实际受力应取锚固后剩余下滑力的准确值, 以保证工程安全。
3.3 组合结构优化设计根据3.2节计算结果, 将实例中锚索分配系数k1提高到0.45后, 进行进一步迭代计算, 当采用7根钢绞线时锚索实际受力为713.69 kN, 抗滑桩实际受力为1 087.13 kN/m。抗滑桩设计结果: 桩截面为1.8 m×2.5 m, 桩长为20 m, 桩间距为5 m, 抗滑桩设计同样合理。对单跨间距5 m内的方案2(1根2.0 m×2.5 m的抗滑桩+5束6根钢绞线φ130 mm钻孔的锚索)与方案2(1根1.8 m×2.5 m的抗滑桩+5束7根钢绞线φ150 mm钻孔的锚索)进行工程经济比较, 方案1造价约为方案2的98.7%(锚索孔径影响较大)。
综上分析, 由于锚索实际提供的锚固力偏小, 当锚索分配受力与实际受力的差值接近单根钢绞线锚固力值(125 kN)的倍数时, 应考虑将增加钢绞线数量的锚索设计与调整抗滑桩设计进行安全经济比选。当钢绞线数量超过4~8根范围时, 应考虑减小锚索布置间距增加锚索数量。同时, 在进行初步受力分配时, 可根据滑面陡缓情况, 锚索锚固位置等, 适当提高锚索承担总剩余下滑力的百分比(如增大3%~5%), 以提前优化组合结构受力分配。
以上设计中, 方案1的锚索现场锚固拉拔试验满足设计规范要求, 锚索与桩组合结构设计合理, 实现了二者受力协调, 安全性、经济性均较高。相比引言中的设计方法, 该方法准确地计算了折线型滑面中的锚索锚固力及锚固后剩余下滑力在桩身上的分配, 避免了桩上荷载因不符实际所造成的设计失败及锚索预应力设计吨位过大给工程带来的安全隐患。
4 结论(1) 本研究提出锚索与抗滑桩组合加固折线型滑面边坡受力计算方法。认为锚索锚固力作用范围覆盖其所穿越的全部滑动条块, 并给出了锚固力在条块上的计入公式。指出锚索锚固力因条块折线滑动将产生折减, 抗滑桩实际受力应取边坡锚固后设桩处剩余下滑力的准确值, 而非分配取值。
(2) 本研究给出了锚索与抗滑桩分离式组合结构优化设计方法。通过计算锚索锚固力折减差值结合单根钢绞线锚固力大小, 调整总剩余下滑力水平分力分配系数, 将锚索设计与抗滑桩设计进行安全性与经济性综合比选, 直至二者受力协调, 组合结构设计合理。
(3) 本研究通过对德会高速实例边坡进行优化设计, 证明了该设计方法的合理性。实例计算表明锚索实际提供锚固力比分配受力小15.27%, 而抗滑桩实际承担滑坡推力比分配受力大10.16%。这说明人为粗略分配剩余下滑力不合理, 会造成工程浪费或设计失败。
| [1] |
刘建, 彭府华, 王春毅, 等. 多级框架锚索与微型抗滑桩群组合加固边坡技术[J]. 中国地质灾害防治学报, 2020, 31(2): 87-93. LIU Jian, PENG Fu-hua, WANG Chun-yi, et al. Application of Slope Reinforcement Technology of Combination of Multi-level Lattice Beams with Pre-stressed Anchor Cable and Anti-slide Micropiles[J]. The Chinese Journal of Geological Hazard and Control, 2020, 31(2): 87-93. |
| [2] |
阿比尔的, 郑颖人, 赖杰, 等. 牌坊坝滑坡双排桩+锚索支护性能研究[J]. 地下空间与工程报, 2016, 12(4): 1033-1038. ABI Erdi, ZHENG Ying-ren, LAI Jie, et al. Study on Supporting Properties of Double-row Piles with Anchor in Slide of Paifang Dam[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(4): 1033-1038. |
| [3] |
付晓, 张建经, 周立荣. 多级框架锚索和抗滑桩联合作用下边坡抗震性能的振动台试验研究[J]. 岩土力学, 2017, 38(2): 462-470. FU Xiao, ZHANG Jian-jing, ZHOU Li-rong. Shaking Table Test of Seismic Response of Slope Reinforced by Combination of Anti-slide Piles and Multi-frame Foundation Beam with Anchor Cable[J]. Rock and Soil Mechanics, 2017, 38(2): 462-470. |
| [4] |
姜华. 微型桩-锚索联合支护顺层岩质边坡的稳定性分析[J]. 铁道科学与工程学报, 2019, 16(9): 2184-2191. JIANG Hua. Stability Analysis of Bedding Rock Slope Reinforced by Micro-piles and Prestressed Anchor[J]. Journal of Railway Science and Engineering, 2019, 16(9): 2184-2191. |
| [5] |
JTG D30—2015, 公路路基设计规范[S]. JTG D30—2015, Specifications for Design of Highway Subgrades[S]. |
| [6] |
GB50330—2013, 建筑边坡工程技术规范[S]. GB50330—2013, Technical Code for Building Slope Engineering[S]. |
| [7] |
李会章, 冯君, 宋响军. 滑坡推力在多排抗滑桩上的分配情况研究[J]. 公路交通科技, 2014, 31(10): 26-31. LI Hui-zhang, FENG Jun, SONG Xiang-jun. Research of Thrust-sharing in Multi-row Anti-slide Piles[J]. Journal of Highway and Transportation Research and Development, 2014, 31(10): 26-31. |
| [8] |
刘瑞懿, 肖碧, 李洪斌, 等. 某岩质高边坡稳定性分析及预应力锚索加固设计[J]. 人民长江, 2016, 47(21): 77-80, 102. LIU Rui-yi, XIAO Bi, LI Hong-bin, et al. Stability Analysis of a High Rocky Slope and Its Pre-stress Anchorage Cable Design[J]. Yangtze River, 2016, 47(21): 77-80, 102. |
| [9] |
赵晓彦, 张京伍, 梁瑶, 等. 花岗岩类土质边坡主被动组合锚固设计方法[J]. 岩石力学与工程学报, 2013, 32(3): 633-639. ZHAO Xiao-yan, ZHANG Jing-wu, LIANG Yao, et al. Design Method for Combined Active/Passive Anchoring for Granitoid Soil Slope[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(3): 633-639. |
| [10] |
赵洪岭, 台佳佳, 朱大勇. 边坡稳定性计算中锚固力计入方式的讨论[J]. 中国水利水电科学研究院报, 2006, 4(4): 271-276. ZHAO Hong-ling, TAI Jia-jia, ZHU Da-yong. Discussion on the Method of Computing Anchoring Force in Slope Stability Analysis[J]. Journal of China Institute of Water Resources and Hydropower Research, 2006, 4(4): 271-276. |
| [11] |
任红卓, 郭文静. 边坡地梁锚索加固中的锚固角设计[J]. 水利与建筑工程学报, 2010, 8(2): 159-161. REN Hong-zhuo, GUO Wen-jing. Design of Anchorage Angle in Prestressed Anchor Rope Frame[J]. Journal of Water Resources and Architectural Engineering, 2010, 8(2): 159-161. |
| [12] |
徐鸿彪, 叶尚其, 刘汉香. 基于概率理论的折线形滑坡锚固结构受力[J]. 地质灾害与环境保护, 2014, 25(4): 93-98. XU Hong-biao, YE Shang-qi, LIU Han-xiang. A Method Based on Probability Theory for Calculating the Anchoring Force of Mansard Landslides[J]. Journal of Geological Hazards and Environment Preservation, 2014, 25(4): 93-98. |
| [13] |
蒋楚生, 邹川, 黄献璋, 等. 锚索与桩共同加固边(滑)坡的设计方法探讨[J]. 铁道工程学报, 2017, 34(12): 6-8, 23. JIANG Chu-sheng, ZOU Chuan, HUANG Xian-zhang, et al. Discussion of the Design Method for Slope(Landslide)Reinforced by Cable Anchors and Piles[J]. Journal of Railway Engineering Society, 2017, 34(12): 6-8, 23. |
| [14] |
李起龙, 魏红卫. 基于多目标综合评价法的边坡抗滑桩桩位优化设计[J]. 铁道科学与工程学报, 2018, 15(6): 1445-1452. LI Qi-long, WEI Hong-wei. Optimization Design of Pile Location on Slope Based on Multi-objective Comprehensive Evaluation Method[J]. Journal of Railway Science and Engineering, 2018, 15(6): 1445-1452. |
| [15] |
谈华宇, 夏元友. 土质边坡锚索加固位置布置优化的探讨[J]. 武汉理工大学学报, 2017, 39(9): 33-38. TAN Hua-yu, XIA Yuan-you. Discussion on Optimization of Anchor Reinforcement Location of Soil Slope[J]. Journal of Wuhan University of Technology, 2017, 39(9): 33-38. |
| [16] |
罗丽娟, 夏香波, 陈悦, 等. 基于投资—效益准则的滑坡抗滑桩结构目标性能[J]. 水土保持研究, 2016, 23(1): 319-324. LUO Li-juan, XIA Xiang-bo, CHEN Yue, et al. Target Performance of Anti-slide Pile Structure in Landslide Based on Investment-Benefit Criteria[J]. Research of Soil and Water Conservation, 2016, 23(1): 319-324. |
| [17] |
李世贵, 任仁, 朱大权, 等. 预应力锚索抗滑桩设计方法优化研究[J]. 公路工程, 2013, 38(2): 51-54. LI Shi-gui, REN Ren, ZHU Da-quan, et al. Study on Optimal Design Method of Anti-sliding Pile with Prestressed Anchoring Cable[J]. Highway Engineering, 2013, 38(2): 51-54. |
| [18] |
简文星, 邓先华. 优化的变形协调条件在桩-锚结构锚索拉力计算中的应用[J]. 岩土力学, 2014, 35(8): 2171-2178. JIAN Wen-xing, DENG Xian-hua. Application of Optimized Deformation Consistence Condition to Anchor Cable Tensile Force Calculation of Pile-anchor Cable Structure[J]. Rock and Soil Mechanics, 2014, 35(8): 2171-2178. |
| [19] |
王建松, 俞强山, 刘庆元, 等. 预应力锚索张拉方式对预应力损失影响探究[J]. 公路交通科技, 2019, 36(9): 37-42. WANG Jian-song, YU Qiang-shan, LIU Qing-yuan, et al. Study on Influence of Prestressed Anchor Cable Tensioning Mode on Prestress Loss[J]. Journal of Highway and Transportation Research and Development, 2019, 36(9): 37-42. |
| [20] |
邓建, 肖明, 谢冰冰. 预应力锚索受力特性与初始张拉吨位优化分析[J]. 岩土力学, 2016, 37(8): 2359-2365. DENG Jian, XIAO Ming, XIE Bing-bing. Analysis of Mechanical Characteristic and Optimization of Initial Tensile Tonnage of Prestressed Anchor Cable[J]. Rock and Soil Mechanics, 2016, 37(8): 2359-2365. |
 2021, Vol. 38
2021, Vol. 38
