扩展功能
文章信息
- 赵兰若, 赵鸿铎, 蔡爵威, 吴世涛
- ZHAO Lan-ruo, ZHAO Hong-duo, CAI Jue-wei, WU Shi-tao
- 考虑邻板高程差的装配式水泥路面行驶舒适性研究
- Study on Driving Comfort of Precast Concrete Pavement Considering Joint Faulting
- 公路交通科技, 2021, 38(3): 14-22, 48
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(3): 14-22, 48
- 10.3969/j.issn.1002-0268.2021.03.003
-
文章历史
- 收稿日期: 2020-03-24
2. 中国民航机场建设集团公司西南分公司,四川 成都 610202
2. Southwest Branch of CAAC Airport Construction Group Co., Ltd., Chengdu Sichuan 610202, China
装配式水泥路面是一种面向大面积新建、扩建、加铺、修复的铺装形式, 也是实现路面智能化、功能化的平台[1]。与普通现浇水泥路面不同, 装配式水泥路面采用工厂预制、现场安装的方式进行铺筑。由于板块安装相互独立, 受多种施工因素影响, 相邻板块间会不可避免地存在高程差, 从而造成路面在板块接缝处存在间断式突变, 使路面出现不平整。装配式水泥路面邻板高程差引起的路面不平整是以板长为波长的路面构造, 通常装配式路面板板长在1~15 m范围内, 按照PIARC对路面构造的分类[2], 此类不平整属于路面的不平度, 会影响行驶的舒适性。
装配式水泥路面邻板高程差对车辆产生的不平整激励与路桥过渡段相类似, 因此在研究邻板高程差对于行驶舒适性的影响时, 可以参考在路桥过渡段的相关研究中所采用的分析方法。张洪亮[3]等通过建立车辆模型, 考虑车辆上桥和下桥两个方向以及车路耦合的影响, 从振动舒适性的角度提出了不同影响因素下路桥过渡段的容许高程差。与路桥过渡段以及路面随机振动不同的是, 在装配式水泥路面中, 板块内部相对平整, 板块之间可能存在连续性的高程差, 因此会产生连续的阶跃瞬变不平整激励, 且随着板长与车速的不同, 相邻两个邻板高程差对于车辆行驶舒适性的影响会存在叠加效应。然而现阶段, 在装配式水泥路面的设计和施工中并未考虑邻板高程差对行驶舒适性的影响。在现有研究中, 评价乘客行驶舒适性的方法有很多[4-5], 如乘坐舒适性系数法、吸收功率法、单一不舒适性指数法、汽车振动舒适度法等。在本研究中, 参考1997年由国际标准化组织颁布的《机械振动与冲击——人体承受全身振动的评价》[6], 选取座椅的竖向加权加速度均方根值作为行驶舒适性的评价指标, 探究邻板高程差对于装配式路面行驶舒适性的影响。
要计算车辆行驶过程中座椅的竖向加权加速度均方根值, 关键在于获取车辆在路面不平整激励下的振动响应, 对此, 学者们常利用弹簧、质量和阻尼将汽车模型抽象成有限个自由度的力学模型进行理论计算, 常用的模型有二自由度1/4车模型、四自由度1/2车模型、七自由度、十一自由度、十七自由度的整车模型[7-13]。其中1/4车模型仅能反映竖向振动, 不能反映车辆的转动和平动; 1/2车模型利用车辆左右的对称性对模型进行简化, 忽略了车辆横向的倾覆和转动; 整车模型能够较为真实地模拟车辆实际的振动规律, 但自由度数和参数的增多, 会使计算变得非常复杂, 计算误差也会相应增大。
在本研究中, 主要考虑由邻板高程差引起的路面纵向不平整, 因此假定路面横向是平整的, 选用1/2车模型进行研究。在四自由度1/2车模型的基础上, 增加座椅质心竖向位移作为一个自由度, 考虑座椅在行驶过程中的振动。通过计算车辆驶过不同邻板高程差时振动方程的解, 获取座椅处的加权加速度均方根值, 来分析邻板高程差对装配式水泥路面行驶舒适性的影响, 进而为装配式路面板的尺寸设计和施工控制提供参考。
1 模型建立 1.1 五自由度1/2车模型根据钟阳[14]等的研究结果, 轮胎阻尼系数对车辆振动的影响很小, 在计算中忽略轮胎的阻尼作用。同时由于波在路面的传播速度远大于车辆的行驶速度, 并且路面在荷载作用下产生的变形与路面的不平整相比要小得多, 因此忽略车辆和路面的耦合作用。由此形成如图 1所示的五自由度1/2理想车模型。
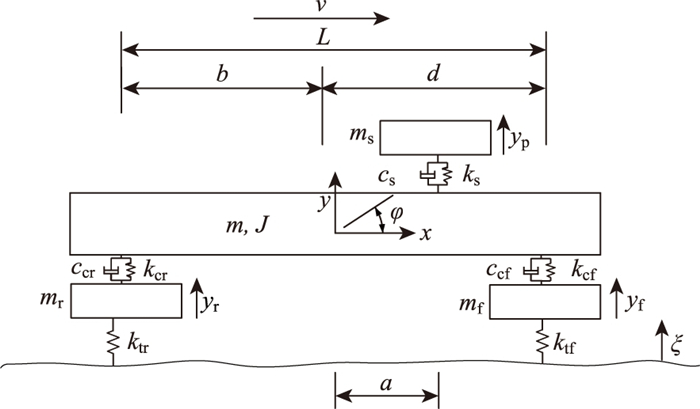
|
| 图 1 五自由度1/2车计算模型 Fig. 1 Five-degree-of-freedom half vehicle model |
| |
图中a, d, b分别为座椅中心、前轮中心、后轮中心到车辆质心的距离; L为前轮中心到后轮中心的距离。
5个自由度分别是: 座椅质心处垂直位移ys、前轮胎中心处垂直位移yf、后轮胎中心处垂直位移yr、车架质心处垂直位移y、车架绕质心转角φ。
ms, mf, mr, m, J分别为座椅和人的质量、前轮非簧载质量、后轮非簧载质量、车架质量、车架绕质心的转动惯量。cs, ccf, ccr分别为座椅阻尼系数、前悬架系统阻尼系数、后悬架系统阻尼系数。ks, kcf, kcr, ktf, ktr分别为座椅刚度系数、前悬架系统刚度系数、后悬架系统刚度系数、前轮刚度系数、后轮刚度系数。
ζ为路面位移; ζ1, ζ2分别为前轮和后轮的路面位移; v为车速。
依据文献[15]中采用的模型, 在求解过程中选择典型的小车福特福克斯CAF7810M作为典型的小车车型, 具体车辆模型参数见表 1。
| 符号 | 数值 | 符号 | 数值 | |
| ms/kg | 65 | ks/(kg·m-1) | 20 | |
| mf/kg | 40.5 | kcf/(kg·m-1) | 17 | |
| mr kg | 45.4 | kcr/(kN·m-1) | 22 | |
| m/kg | 663 | ktf/(kN·m-1) | 192 | |
| J/(kg·m2) | 1 222 | ktr/(kN·m-1) | 192 | |
| cs/(N·s·m-1) | 1 000 | d/m | 1.18 | |
| ccf/(N·s·m-1) | 1 400 | b/m | 1.46 | |
| ccr/(N·s·m-1) | 1 400 | a/m | 0.48 | |
| L/m | 2.64 |
1.2 汽车振动方程
令u=[ys, yr, yf, y, φ]′, 根据达朗贝尔原理, 该理想汽车车模型的振动方程如下:
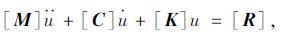
|
(1) |
式中, M为质量矩阵; C为阻尼矩阵; K为刚度矩阵; R为激励向量。参数含义如下所示。
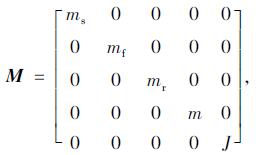
|
(2) |

|
(3) |

|
(4) |
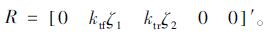
|
(5) |
要对方程(1)进行求解, 需要给定车轮与路面接触点的位移或荷载, 其数值与车辆所受到的不平整激励有关。因此, 需要对车轮经过邻板高程差时的运动轨迹进行计算和分析。
1.3 不平整激励对于装配式水泥路面, 单块装配式路面板的表面可看作是完全平整的, 即板块内部的不平整激励不予考虑。因此装配式混凝土路面的不平整激励表现为由邻板高程差引起的单个或多个等间距出现的间断性高差。基于此, 可通过计算车辆经过接缝时的车轮轨迹, 从而获得车辆在行驶过程中受到的不平整激励。
将车轮假设为圆盘模型, 描述其运动过程。圆盘模型中不考虑车轮与路面的接触长度, 对于普通问题的分析具有一定可行性, 但在邻板高程差分析中, 行驶轨迹与轮胎的状况密切相关, 忽略轮胎和路面的接触长度会引起显著的差异。本研究参考丁勇[16]等人提出的计算方法, 对车轮经过邻板高程差时的运动轨迹进行计算。计算中假设轮胎与地面接触为一定接触长度的圆盘。轮胎向上与向下驶过接缝过程如图 2所示。

|
| 图 2 轮胎驶过接缝时轨迹示意图 Fig. 2 Schematic diagram of track of tire passing through joint |
| |
驶过接缝时轮胎未与路面接触部分保持圆形、半径不变, 接触部分为直线, 设接触部分长度为Lt。上接缝过程从轮胎接触板边开始, 直至轮胎运动到完全在上板位置。设轨迹线AA′为圆弧, 在A′处轨迹线与水平相切。轮胎中心轨迹线为O1O2, 同样为圆弧, 设O1O2的半径为R′。通过几何关系可以推导得到式(6)。
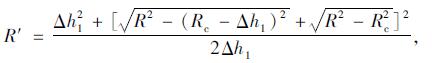
|
(6) |
式中, R′为轮胎中心上接缝行驶轨迹半径; R为轮胎半径; Rc为轮胎接地半径; Δh1为上接缝时的邻板高程差。
由此可知轮胎接地中心点A的高程函数h(x1)的表达式如下:
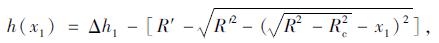
|
(7) |
式中, x1为轨迹点到A点的水平距离, 其他参数同上。
类似的, 下接缝轮底轨迹线为DD′, 轮心轨迹线为O3O4。下接缝从轮胎离开上板开始, 至完全运动到下板为止。由几何关系推导轮胎中心轨迹半径的方法同向上接缝, 得到下接缝时轮心轨迹半径如式(8):
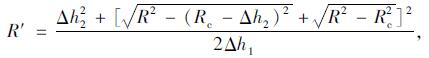
|
(8) |
式中, Δh2为下邻板高程差。由此即可得到下接缝中轮胎接地中心D点的高程函数h(x2)。

|
(9) |
式中, x2为轨迹点到D点的水平距离, 其他参数同上。
根据式(7)和式(9)即可得到轮胎的运动轨迹, 从而获取路面对车辆的不平整激励。
2 模型计算与求解式(1)~(5)描述了五自由度1/2小车模型在不平整激励下的动力学响应, 本研究采用Newmark-β法[17]求解振动微分方程(1)。Newmark-β是一种逐步积分法, 求解振动方程较为简便, 并且对非线性问题也具有较好的适应性。
2.1 Newmark-β法求解方法Newmark-β法的基本思想是对时间步长内加速度变化的分布做出适当的假定, 然后通过积分获得速度变化和位移变化的表达式, 进而求得步距末点的值[18]。
Newmark-β法假定t+Δt时刻的速度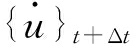 和位移{u}t+Δt可按式(10)进行计算。
和位移{u}t+Δt可按式(10)进行计算。
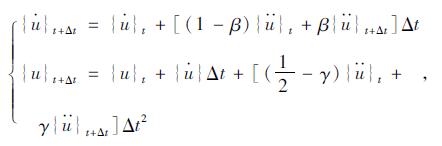
|
(10) |
式中, {u}t为t时刻的广义位移,
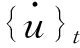 为t时刻的速度,
为t时刻的速度,
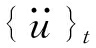 为t时刻的加速度; β和γ是按积分的精度和稳定性要求进行调整的参数。本研究采用常平均加速度法进行计算, 即假定从t到t+Δt时刻的加速度不变, 取β=0.5, γ=0.25, 则此Δt时间内加速度为
为t时刻的加速度; β和γ是按积分的精度和稳定性要求进行调整的参数。本研究采用常平均加速度法进行计算, 即假定从t到t+Δt时刻的加速度不变, 取β=0.5, γ=0.25, 则此Δt时间内加速度为
由式(10)可以得到用 表示的
表示的 和
和

|
(11) |
由此可得t+Δt时刻的振动微分方程如式(12)所示:
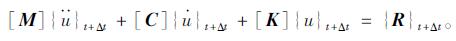
|
(12) |
将式(11)代入式(12), 得到关于ut+Δtt的方程如式(13)所示:

|
(13) |
其中有效刚度矩阵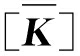 和有效荷载矩阵
和有效荷载矩阵 按照式(14)计算。
按照式(14)计算。

|
(14) |
式中,

求解式(14)可得{u}t+Δt, 然后由式(11)可解出 和
和 由此即可计算获得车模型中各个自由度上任意时刻的位移、速度、加速度值, 整个求解过程在Matlab程序中进行。
由此即可计算获得车模型中各个自由度上任意时刻的位移、速度、加速度值, 整个求解过程在Matlab程序中进行。
因采用逐步积分法求解, 初始条件对前期求解结果有较大的影响, 但是随着时间的增加, 求解结果会逐渐稳定下来。为使求解结果可靠, 初始条件应与求解初始状态相对应。以车辆匀速沿直线行驶为起始状况, 不考虑轮胎和车身悬架在自重下的变形, 以此状态为各自由度竖向位移的起始点。前轮、后轮的初始值为初始条件下的竖向位移值。通过几何关系来确定车身质心和座椅的初始位移, 按下式计算:

|
(15) |

|
(16) |
座椅、前轮、后轮和车身的速度初始值取经过第10个点和第1个点两点间的平均速度, 以相应位移除以时间即可求得。车身绕车身质心旋转值的初始值按照 来取。各个自由度的加速度的初始值都为0。
来取。各个自由度的加速度的初始值都为0。
根据求解得到的车辆节点位移、速度和加速度等指标, 可按照式(17)计算座椅加权加速度均方根值。
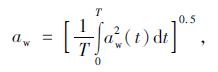
|
(17) |
式中, aw(t)为瞬时频率加权加速度值; T为分析的时间长度; t为时间。
加权加速度指对人体最敏感频率范围以外的其他频段的振动加速度进行频率加权, 等效折算为最敏感频率范围的振动加速度[6], 用awi表示, 与原竖向加速度afi的关系是:

|
(18) |
式中, wfi为频率加权函数, 可按式(19)进行计算[19]:

|
(19) |
采用加权加速度均方根值对车辆的行驶舒适性进行评价, 加权加速度均方根值与行驶舒适性的关系见表 2[6]。
| aw/(m·s-2) | 人体的舒适程度 |
| < 0.315 | 保持舒适 |
| 0.315~0.63 | 稍不舒适 |
| 0.5~0.1 | 有些不舒适 |
| 0.8~1.6 | 不舒适 |
| 1.25~2.5 | 非常不舒适 |
| >2.0 | 特别不舒适 |
3 结果与分析 3.1 单个接缝的影响
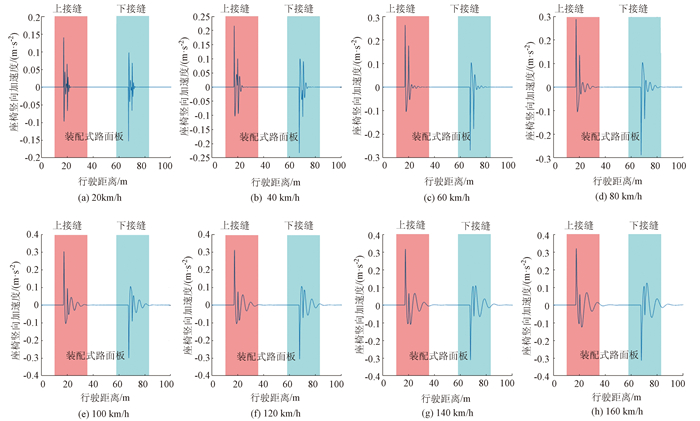
为探究单个接缝下, 邻板高程差对于行驶舒适性的影响, 计算了不同车速下座椅处竖向加速度随行驶距离的变化情况, 部分计算结果如图 3所示, 计算中邻板高程差高度为5 mm。
|
| 图 3 座椅竖向加速度随行驶距离的变化情况 Fig. 3 Vertical acceleration of seat varying with driving distance |
| |
从图中可以看出, 在车辆的行进过程中, 车辆的前后轮会先后通过接缝, 从而产生两次振动响应, 前轮通过接缝时产生的座椅处竖向加速度要明显高于后轮。车辆在上接缝和下接缝时座椅处竖向加速度的大小相近, 方向相反。当车速较低(如10 km/h)时, 前轮产生的振动在后轮通过接缝时已经基本消散, 两次振动响应几乎互不影响; 而当车速较高时(如80, 160 km/h), 前后轮产生的振动响应会相互叠加, 从而产生振动响应的增强或减弱。
3.1.1 车速和邻板高程差的影响计算不同车速和不同邻板高程差下座椅竖向加速度的最大值, 如图 4所示。结合图 3的结果可知, 车速的增大会增加车辆的振动, 座椅竖向加速度最大值会随着车速的增加逐渐增加, 但其增长速度会逐渐趋于平缓。座椅竖向加速度最大值与邻板高程差接近线性关系, 邻板高程差的增大会使座椅竖向的振动更加剧烈, 且这种促进作用在车速较高时更加明显。在上接缝时座椅竖向加速度最大值略高于下接缝, 但二者相差不大, 最大的相对差值仅为7.4%。

|
| 图 4 不同邻板高程差下座椅竖向加速度最大值 Fig. 4 Maximum vertical acceleration of seat with different joint faultings |
| |
3.1.2 接缝影响距离
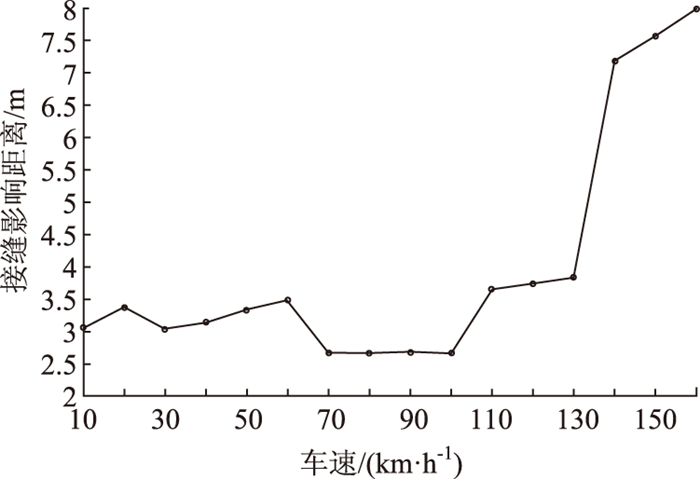
将从竖向加速度出现第一个峰值到波动峰值衰减到最大值的10%以下时, 车辆驶过的距离定义为接缝影响距离, 可以计算得到不同邻板高程差和不同车速下接缝影响距离的大小。计算结果表明, 高程差大小及其方向对接缝影响距离影响很小(小于0.01 m), 因此仅给出接缝影响距离随车速的变化情况, 如图 5所示。可以看出, 随着车速的增加, 车辆的振动更加剧烈, 从而使得接缝影响距离整体呈现上升的趋势。但是当车速在70~100 km/h之间时, 接缝影响距离稳定在2.64 m左右, 与前后轮距相等。这是由于前后轮仅在车轮恰好经过接缝时产生较大的座椅竖向加速度, 而在车轮通过之后其产生的振动相互抵消, 从而导致后续产生的竖向加速度被大大减弱(如图 3(b)、(e)所示), 从而使得接缝影响距离被缩短, 其值与前后轮距相等。当车速大于130 km/h后, 接缝影响距离则大大增加, 这是由于一方面较高的车速下产生的车辆振动响应会更加剧烈, 另一方面由于车速较快, 前后轮近乎同时通过接缝, 后续产生的振动响应相互叠加(如图 3(c)、(f)所示), 从而使得接缝影响距离大幅增大。因此在板长的设计过程中, 可根据设计车型和车速计算接缝影响距离, 尽可能使板长大于接缝影响距离, 避免连续接缝对于座椅竖向加速度产生叠加效应, 从而增加行驶舒适性。
|
| 图 5 不同车速下的接缝影响距离 Fig. 5 Joint influence distances at different drying velocities |
| |
3.2 多个接缝的影响 3.2.1 多个接缝邻板高程差的模拟
在装配式水泥路面设计中, 设计邻板高程差为0, 但装配式路面板预制以及现场施工中存在的误差会导致邻板间高程差的出现, 受多种因素的影响, 邻板高程差通常具有一定的随机性。
为对多个接缝邻板高程差进行模拟, 假定邻板高程差呈均值为0的正态分布。在本研究中, 实测了某装配式修复工程中的22块装配式路面轮迹带上邻板高程差, 将行驶方向前板高记为正值、前板低记为负值, 得到78个邻板高程差数据。统计邻板高程差的分布, 计算频率和频数, 并计算该均值和方差下的正态分布函数值, 制成频数分布直方图如下。
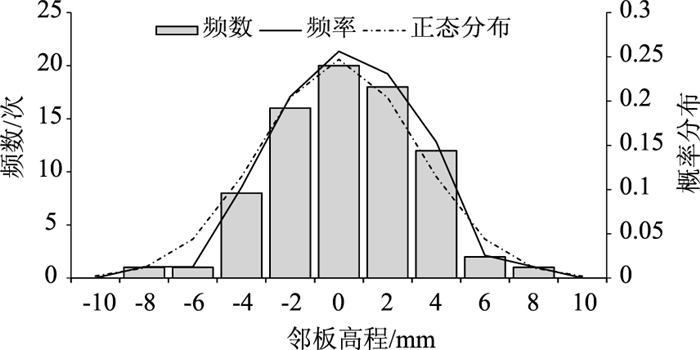
|
| 图 6 邻板高程差分布统计值 Fig. 6 Statistics of distribution of joint faultings |
| |
采用均值为0的正态分布函数进行拟合, 通过拟合优度检验来判断是否符合正态分布, 计算检验统计量 因此在95%的置信水平下, 不能拒绝原假设, 可认为邻板高程差的分布服从正态分布。假设装配式路面施工中在95%的保证率下, 其邻板高程差控制在2σ以内, 由此即可得到邻板高程差的分布函数, 如式(12)所示。式中σ为邻板高程差的方差, 其大小反映了施工质量, σ越小, 说明邻板高程差的波动越小, 其值越接近0, 即施工质量越高; 反之, 施工质量越低, 出现较大邻板高程差的可能性越高。
因此在95%的置信水平下, 不能拒绝原假设, 可认为邻板高程差的分布服从正态分布。假设装配式路面施工中在95%的保证率下, 其邻板高程差控制在2σ以内, 由此即可得到邻板高程差的分布函数, 如式(12)所示。式中σ为邻板高程差的方差, 其大小反映了施工质量, σ越小, 说明邻板高程差的波动越小, 其值越接近0, 即施工质量越高; 反之, 施工质量越低, 出现较大邻板高程差的可能性越高。

|
(12) |
在以下的分析计算中, 计算长度取3 000 m, 相邻两采样点的水平距离取0.25 m[20]。假定每个接缝处邻板高程差服从相同的分布, 并且相互独立, 按照式(12)给出的分布函数随机生成路面工况100个, 并统计95%分位的座椅竖向加权加速度均方根值作为行驶舒适性的评价指标。得到某一工况下的路面纵断面形式如图 7所示。
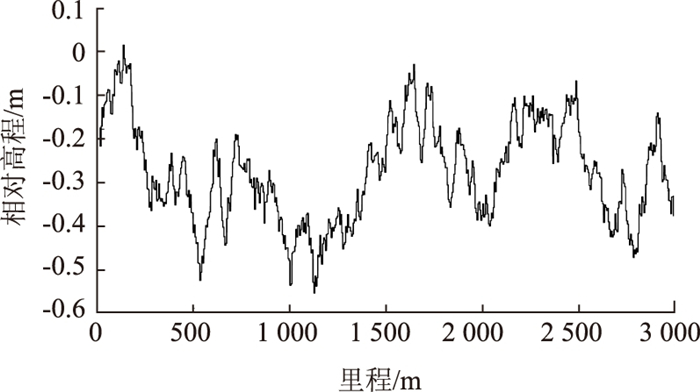
|
| 图 7 某一工况下的路面纵断面 Fig. 7 Pavement profile in a certain case |
| |
3.2.2 施工质量的的影响
为探究施工质量对行驶舒适性的影响, 计算不同邻板高程差控制值2σ下座椅竖向加权加速度均方根值, 计算中取板长为5 m, 计算结果如图 8所示。从中可以看出, 加权加速度均方根值与高程差控制值之间表现出明显的线性正相关性, 且车速越大时, 高程差控制值对加权加速度均方根值的影响越强。根据表 2中加权加速度均方根值与行车舒适性的关系, 当加权加速度均方根值小于0.315时, 人体会保持舒适, 处于0.315~0.63之间时, 人体会感到稍不舒适。本研究取0.315 m/s2作为加权加速度均方根值的控制值, 由此可以得到设计车速分别为60, 80, 100, 120 km/h下邻板高程差控制值的最大值, 如表 3所示。在装配式路面的施工中可通过提高板块的预制精度、控制基层整平效果、调节调平螺杆高度等方法, 保证邻板高程差小于表 3中的给出的最大值, 从而保障车辆行驶过程中具有足够的舒适性。
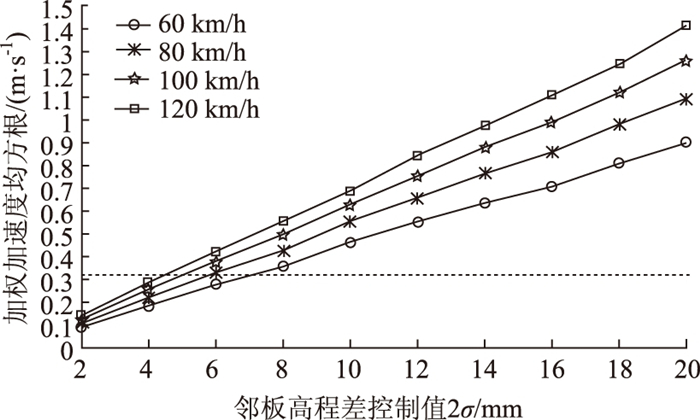
|
| 图 8 不同邻板高程差控制值下加权加速度均方根值 Fig. 8 WRMSAs controlled by of different joint faultings |
| |
| 设计速度/(km·h-1) | 60 | 80 | 100 | 120 |
| 邻板高程差控制值/mm | 6.9 | 5.7 | 4.9 | 4.3 |
3.2.3 板长的影响
根据3.1.2的分析可知, 车辆在装配式路面板间的行驶舒适性还与板长有关, 过短的板长会使车辆通过多块装配式路面板时产生更加剧烈的振动, 从而使行驶舒适性降低, 图 9为不同板长下加权加速度均方根值的变化情况, 计算中取邻板高程差控制值为5 mm。计算结果表明, 板长的增加会降低加权加速度均方根值, 但这种降低作用会随着板长的增加而削弱。与之前的分析类似, 取0.315 m/s2作为加权加速度均方根值的控制值, 由此得到表 4所示的不同设计车速下的最小板长, 在装配式水泥路面设计中, 在满足结构受力、板块运输、吊装安全等要求的前提下, 可参考表 4进行装配式路面板的平面尺寸设计, 当施工质量较高时(邻板高程差控制值小于5 mm时), 该最小板长可将根据实际设计需求适当放低。
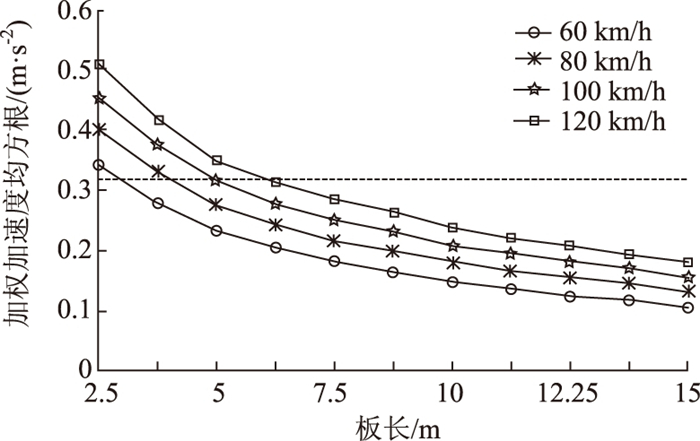
|
| 图 9 不同板长下加权加速度均方根值 Fig. 9 WRMSAs with different panel lengths |
| |
| 设计速度/(km·h-1) | 60 | 80 | 100 | 120 |
| 最小板长/m | 3.0 | 4.0 | 4.9 | 6.0 |
4 结论
本研究通过建立五自由度1/2车模型, 对小客车驶过装配式水泥路面的振动响应进行分析求解, 分析了邻板高程差对行驶舒适性的影响, 并得到以下结论:
(1) 邻板高程差引起的装配式水泥路面不平整对行驶舒适性影响显著, 且受车型、行驶速度、邻板高程差大小、板长等因素的影响。
(2) 在驶过单个接缝时, 座椅竖向加速度最大值会随着车速和邻板高程差的增加而增加, 且它与邻板高程差呈近线性关系, 而车速对它的影响会随车速的增加而逐渐减弱。
(3) 接缝影响距离随车速呈现整体上升趋势, 对于计算中所用的小客车而言, 但当车速在70~100 km/h之间时, 会由于前后轮产生振动的相互抵消使接缝的影响距离减小至与前后轮距相等; 而当车速大于130 km/h时, 会由于前后轮产生振动的相互叠加使接缝影响距离大幅增加。
(4) 在驶过多个接缝时, 加权加速度均方根值会随邻板高程差的增加而增加, 随板长的增加而减少。在板块设计和施工中, 可以通过控制最小板长、提高施工水平、降低邻板高程差, 来保证路面的行驶舒适性满足设计的要求。
(5) 下一步工作将采用加速度传感器, 通过现场测试对提出的评价方法进行验证, 并探究其他因素如车型、板块数量等对行驶舒适性的影响。
| [1] |
TAYABJI S, YE D, BUCH N. Precast Concrete Pavement Technology[R]. Sheffield: University of Sheffield, 2013.
|
| [2] |
姚祖康. 公路设计手册: 路面[M]. 2版. 北京: 人民交通出版社, 1999. YAO Zu-kang. Manual of Highway Design: Pavement[M]. 2nd ed. Beijing: China Communications Press, 1999. |
| [3] |
张洪亮, 胡长顺, 高江平. 路桥过渡段容许台阶高度确定的参数影响[J]. 公路交通科技, 2005, 22(3): 42-46, 50. ZHANG Hong-liang, HU Chang-shun, GAO Jiang-ping. Parameters' Influence on Determination of Allowable Differential Settlement between Bridge and Approach Embankment[J]. Journal of Highway and Transportation Research and Development, 2005, 22(3): 42-46, 50. |
| [4] |
贾瑞雨. 基于行车舒适性的高速公路沉降评价和扩建纵面设计研究[D]. 杭州: 浙江大学, 2016. JIA Rui-yu. Study on Expressway Settlement Evaluation and Profile Design of Extension Project Based on Driving Comfort[D]. Hangzhou: Zhejiang University, 2016. |
| [5] |
PAPAGIANNAKIS A T, RAVEENDRAN B. International Standards Organization-compatible Index for Pavement Roughness[J]. Transportation Research Record, 1998, 1643: 110-115. |
| [6] |
ISO 2631-1, Mechanical Vibration and Shock: Evaluation of Human Exposure to Whole-body Vibration-Part 1-General Requirements[S].
|
| [7] |
袁明, 余钱华, 颜东煌. 基于车-桥系统耦合振动理论的大跨PC连续刚构桥冲击系数研究[J]. 中国公路学报, 2008, 21(1): 72-76. YUAN Ming, YU Qian-hua, YAN Dong-huang. Research on Impact Coefficient for PC Continuous Rigid Frame Bridges with Long-span under Theory of Vehicle-bridge System Coupling Vibration[J]. China Journal of Highway & Transport, 2008, 21(1): 72-76. |
| [8] |
KIM C W, KAWATANI M, KWON Y R. Impact Coefficient of Reinforced Concrete Slab on a Steel Girder Bridge[J]. Engineering Structures, 2007, 29(4): 576-590. |
| [9] |
CANTISANI G, LOPRENCIPE G. Road Roughness and Whole Body Vibration: Evaluation Tools and Comfort Limits[J]. Journal of Transportation Engineering, 2010, 9(9): 818-826. |
| [10] |
SUN LU, LUO F. Nonstationary Dynamic Pavement Loads Generated by Vehicles Traveling at Varying Speed[J]. Journal of Transportation Engineering, 2007, 133(4): 252-263. |
| [11] |
SAYERS M W. Two Quarter-car Models for Defining Road Roughness: IRI and HRI[J]. Transportation Research Record, 1989, 1215: 165-172. |
| [12] |
DU Y, LIU C, ZHANG X, et al. Rapid Accelerometer Measurements of Vehicle Bumps at Bridge Approaches[J]. Transportation Research Record, 2015, 2528: 1-8. |
| [13] |
张洪亮, 王秉纲, 杨万桥. 基于人-车-路三自由度振动模型的路面平整度评价方法[J]. 重庆交通大学学报: 自然科学版, 2009, 28(6): 1041-1045. ZHANG Hong-liang, WANG Bing-gang, YANG Wan-qiao. Pavement Roughness Evaluation Method Based on Three-degree-freedom Models Including Human, Vehicle and Road[J]. Journal of Chongqing Jiaotong University: Nature Science Edition, 2009, 28(6): 1041-1045. |
| [14] |
钟阳, 刘季. 路面车辆随机动荷载理论分析[J]. 工程力学, 1993, 10(4): 26-31. ZHONG Yang, LIU Ji. Theoretical Analysis of Random Dynamaic Load between Road and Vehicle[J]. Engineering Mechanics, 1993, 10(4): 26-31. |
| [15] |
刘淳. 基于二分之一车的主动悬架设计[D]. 长春: 吉林大学, 2003. LIU Chun. Active Suspension Control Based on a Half-car Model[D]. Changchun: Jilin University, 2003. |
| [16] |
丁勇, 诸葛萍, 谢旭, 等. 考虑车轮-路面接触长度的桥头跳车动力荷载分析[J]. 振动与冲击, 2013, 32(9): 28-34. DING Yong, ZHUGE Ping, XIE Xu, et al. Numerical Analysis of Dynamic Load in Bridge-head Bumping Considering the Contact Length between Tire and Road[J]. Journal of Vibration and Shock, 2013, 32(9): 28-34. |
| [17] |
NEWMARK N M. A Method of Computation for Structural Dynamics[J]. Journal of the Engineering Mechanics Division, 1959, 85(3): 67-94. |
| [18] |
LIU C, HERMAN R. Road Profiles, Vehicle Dynamics, and Human Judgment of Serviceability of Roads: Spectral Frequency Domain Analysis[J]. Journal of Transportation Engineering, 1998, 124(2): 106-111. |
| [19] |
余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009. YU Zhi-sheng. Automobile Theory[M]. 5th ed. Beijing: China Machine Press, 2009. |
| [20] |
凌建明, 刘诗福, 袁捷, 等. 不平整激励下机场道面和公路路面平整度评价综合分析[J]. 同济大学学报: 自然科学版, 2017, 45(4): 519-526. LING Jian-ming, LIU Shi-fu, YUAN Jie, et al. Comprehensive Analysis of Pavement Roughness Evaluation for Airport and Road with Different Roughness Excitation[J]. Journal of Tongji University: Nature Science Edition, 2017, 45(4): 519-526. |
 2021, Vol. 38
2021, Vol. 38
