扩展功能
文章信息
- 李茹雪, 刘澜
- LI Ru-xue, LIU Lan
- 基于MFD与距离的边界收费策略
- Cordon Tolling Strategy Based on MFD and Distance
- 公路交通科技, 2021, 38(2): 139-145
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 139-145
- 10.3969/j.issn.1002-0268.2021.02.018
-
文章历史
- 收稿日期: 2020-03-24
2. 西南交通大学 综合交通运输智能化国家地方联合工程实验室, 四川 成都 610031
2. National United Engineering Laboratory of Integrated and Intelligent Transportation, Chengdu Sichuan 610031, China
随着城镇化进程的发展和人们生活水平的提高,私人小汽车的拥有量快速增长,交通拥挤成为制约大城市经济发展的一个重要问题。同时,人们也逐渐从世界各地解决交通拥堵的实践中认识到:从交通供给层面新建或扩展道路,在缓解拥堵的同时也产生了新的需求,结果便是导致交通出行环境的进一步恶化。因此,拥挤收费作为一有效的交通需求管理手段被提出,通过在特定的时段或路段对车辆实行收费的方法,限制车辆的使用频率,降低用户出行需求的增长速度,从而维持系统合理的运行和服务水平。
在过去的几十年里,拥挤收费在伦敦[1]、新加坡[2]、斯德哥尔摩[3]等多个国家或地区得到了实践。这些拥挤收费策略大都采用了边界收费的方法,即对划定边界区域实行收费从而达到目标函数最优。大多数边界收费研究采用收费相同的单一费率方法,如Verhoef建立了仿真模型来研究边界收费,并通过启发式算法求解得到费率和收费点的最佳位置[4]。但随着研究的深入,单一费率的收费模式逐渐显现出不公平、造成资源浪费等弊端。2000年,May和Milne首先提出了分别基于时间、拥挤度和距离的3种多费率边界收费策略[5]。其中前两种收费策略通常与其他收费方法结合使用,而基于距离的边界收费策略因其公平高效的特点得到了众多学者的关注。在May的基础之上,早期的学者们对英国[6]和德国[7]进行了基于距离的收费策略研究,但将费用定义为行驶距离的线性函数的做法与现实不符。随后,Lawphongpanich和Yin提出了一种非线性的收费策略,即利用分段线性函数表达非线性距离函数进而求得费用,但该分段线性方法只能将分段数量限制在两段及以下[8]。为了满足交通网络对更多分段形式的要求,Meng研究了将非线性距离函数等分成n段线性函数来获取最优距离收费的方法,并提出最优距离收费函数是关于距离的非递减正函数[9]。国内的孙鑫[10]和程启秀[11]分别研究了基于距离的静态与动态收费策略,前者对求解非线性距离函数中基于路段的算法进行了改进,后者则考虑交通流的时变性,研究随机逐日动态拥挤收费下的最优费率。Zheng首先将宏观基本图(Macroscopic Fundamental Diagram)作为判断最优收费的工具来实施边界收费策略[12],证明了MFD相比其他方法更为直观有效,但单一费率的边界收费忽略了车辆在边界区域中行驶的距离。因此为了提高拥挤收费的公平性与有效性,本研究提出将MFD与多费率边界收费策略相结合的方法,即考虑车辆在边界区域中行驶的距离对费率产生的影响,将MFD的相关特性应用于收费模型,得到使边界收费区域的通行能力维持在最优水平的收费策略。
智能交通技术的迅猛发展为该收费策略在数据的获取上提供了技术保障。以电子警察系统、治安卡口系统和各类城市交通监控系统为代表的智能交通系统建设,基本上实现了在我国大中城市主要路段和交叉口信息采集点位的完整覆盖[13];结合GPS和北斗卫星导航定位系统、电子地图和ETC等技术的应用,能够实现车辆的精确定位,从而获取车辆在边界区域内的行驶距离,再根据收费函数即可计算出出行者应支付的费用。现代信息技术提供的大数据环境,加之数据采集、存储、传输和计算等方面软硬件技术的飞速进步,为在实际交通管控业务中完备、精细地处理各种复杂因素提供了可能。
为此,本研究首先在第1部分介绍了MFD的基本概念和相关特性,在此基础上第2部分定义了收费函数的非线性形式,并结合MFD特性建立了固定需求下的双层规划收费模型,第3部分则提出了一种基于非线性收费函数的改进FW算法,以求解该收费模型。为了验证模型和算法的可行性,论文在第4部分中进行了算例分析,并在第5部分总结了研究工作的结论,提出了面向实际应用,进一步深化研究的方向。
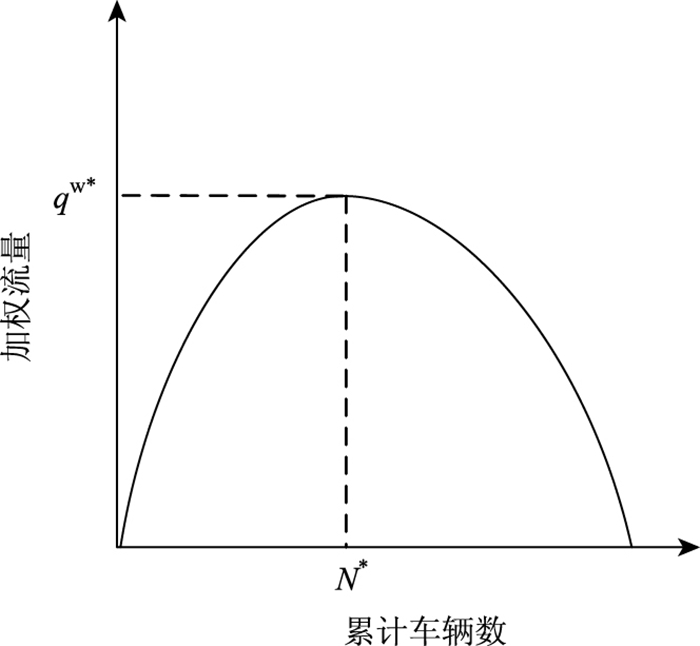
1 基于MFD的边界收费策略的提出MFD作为路网的固有属性,不会随交通需求的变化而改变,是一个可以从宏观层面监测路网交通拥挤状态的工具[14]。对于某一区域来说,该区域内出行车辆所完成的加权流量
|
| 图 1 区域路网宏观基本图 Fig. 1 Macroscopic fundamental diagram of regional road network |
| |
定义加权流量

|
(1) |
式中,a和da分别为路段a和该路段的长度;qa为路段a上的流量。
从图中可看出,当路网内的车辆数累积到一定数值时,加权流量到达临界值,路网整体运行效益最优[16];若车辆数继续增长,则加权流量会随之降低,此时路网处于过拥挤状态。基于此性质,许多学者将MFD应用于构建控制模型[17]或经济学模型[9]中。
因此,借鉴相关策略中通过MFD调节进入边界的车辆数这一思想,在实施收费策略时,将MFD的相关参数与收费模型相结合,让区域内的累计车辆数N尽量保持在临界车辆数N*附近,从而使收费区域的运行效益最大,保证区域内交通运行畅通。
2 基于距离的边界收费方案设计 2.1 距离收费函数假设用G=(N, A)来表示一个实施收费策略的强连接交通网络,其中N和A分别表示网络中的节点集合和有向路段集合,进一步将其划分为不收费的外部网络





在以往将距离收费函数设置为线性形式的收费策略中,曲线斜率多是人为主观设定,导致无法准确获得系统最优目标值。因此,本研究将基于距离的收费函数定义为非线性函数:
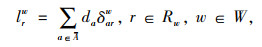
|
(2) |
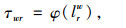
|
(3) |
式中,Rw为OD对w∈W间的路径集合;lrw为OD对w∈W间的路径r∈Rw属于边界区域部分的长度;da为收费区域内路段a的长度;δarw为路段与路径的关系变量,当路段a在路径r上时,δarw=1,否则为0;τwr为基于距离的收费费率。
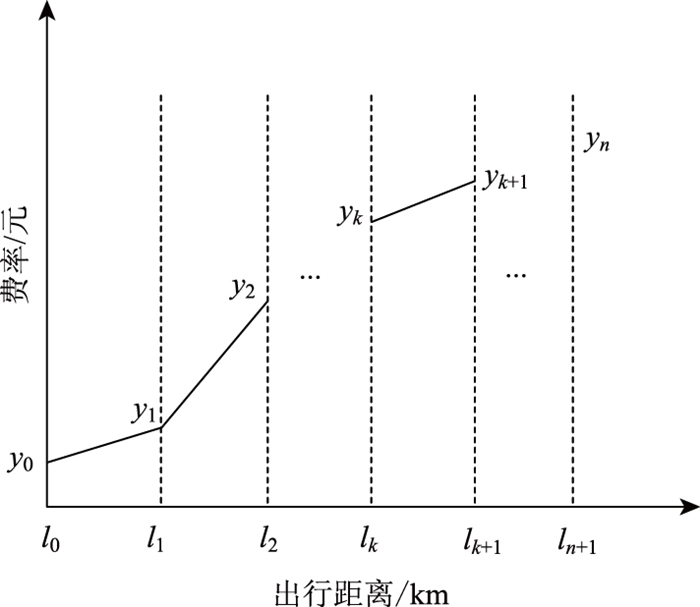
由于该收费函数是非线性的,造成广义路径出行时间不等于该路径上各条路段出行时间之和,这被称为路径成本的不可加性[16]。在此采用分段线性逼近的方法来解决此非线性收费问题。首先用lmax和lmin分别为边界区域中最大和最小的路径长度,对应于收费费率ymin和ymax。将该范围等分为n个相同的间隔,并假设收费费率是车辆在收费区域中行驶距离的非递减函数,则非线性函数近似由n个线性函数组成,且每个线性函数由间隔的两个边界值唯一确定。如图 2所示,当车辆在边界区域中的行驶距离值属于某个间隔范围内时,就使用该间隔的线性函数计算费率。
|
| 图 2 分段线性收费原理 Fig. 2 Piecewise-linear tolling principle |
| |
因此得到计算基于距离的收费费率公式为:
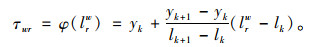
|
(4) |
用MFD判断上层目标函数是否达到最优的方法,既简化了求解双层规划模型过程中的计算,又能根据收费区域的MFD图像,较为直观清晰地观测出系统处于最优运行状态下的临界值,从而找到使收费区域输出流量最大的费率组合y=[y0, y1, …,yk, yk+1, …,yn]Τ。因此,以收费区域输出流量最大为目标建立上层模型,目标函数如下:
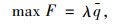
|
(5) |
式中,λ为车辆离去率。从MFD图中可得到使输出流量值最大的加权流量



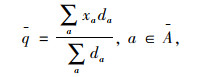
|
(6) |
式中,a和da分别为收费区域内路段a和该路段的长度; xa为收费区域内路段a上的流量。
假定交通网络中用户的路径选择行为服从Wardrop第一定理,即用户知道每条可选择路径的交通时间,并能选择其中的最短路,此时就达到了用户平衡状态(UE)。在实行收费方案后,用户在交通网络内进行路径选择时不仅要考虑路径的出行时间,还要考虑收费所造成的出行成本的增加。利用出行时间价值这一参数,将收费所造成的出行成本换算为时间费用,得到广义出行成本如下:
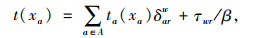
|
(7) |
式中,β为用户的出行时间价值,路段出行时间ta(xa)采用BPR函数计算,如下公式所示:

|
(8) |
式中,Ca为路段a的通行能力。在给定的距离收费函数下,得到的下层用户均衡模型如下:
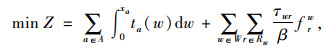
|
(9) |
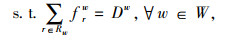
|
(10) |
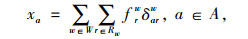
|
(11) |
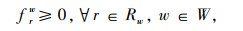
|
(12) |
式中,τwr为费率;frw为OD对w之间路径r上的流量;Dw为OD对w之间的交通需求总量;δarw为路段与路径的关系变量,当路段a在路径r上时,δarw=1,否则为0。式(9)代表收费区域的均衡状态。式(10)为流量守恒约束,即OD对w之间路径r上的流量之和等于OD对交通需求总量。式(11)表示路段流量与路径流量之间的关系,式(12)为路径流量的非负约束。
3 基于路段的FW算法Frank-Wolfe(FW)算法作为一种可行方向法,广泛运用于求解含线性约束的非线性规划问题。该算法主要可分为确定可行下降方向和确定步长两个步骤,其中确定可行下降方向等价于求解线性规划问题,进一步等价于求解最短路问题[9]。但由于非线性距离收费函数导致了路径成本的不可加性,使用传统的最短路算法不再可行。因此Meng等人提出了一种网络转换法(Network Reformation Technique)以解决路径成本的不可加性问题[18]。该方法通过用虚拟路段(Dummy Link)替代收费区域中的路径,从而将路径不可加成本转换为基于路段的可加成本。
对收费区域中的每一个OD对(m, n)∈ψ,至少有1条非循环路径连接起点m和终点n,即内部路径,收费区域中所有的内部路径构成集合E。用虚拟路段替代OD对(m, n)间所有的内部路径e∈E后,包含虚拟路段的新收费区域与外部网络就组成了新的交通网络G′=(N′, A′)。
如图 3所示,原始收费区域由节点1,2,3和路段1,2,3构成,OD对1-3之间的两条内部路径分别1→2→3和1→3。经过网络变换后,内部路径由1-3-1和1-3-2两条虚拟路段代替。这就将原本基于距离的路径不可加收费转化为只存在于虚拟路段上的可加收费,每条路径上的广义出行成本就等于其上各路段的成本之和[10]。解决了路径成本的不可加性问题后,基于虚拟路段的FW算法步骤如下:

|
| 图 3 网络变换法示例 Fig. 3 Illustrative example of network transformation method |
| |
Step 0:初始化。令原始网络G=(N, A)中的tao=ta(0),再在新的交通网络G′=(N′, A′)中进行全有或全无分配,得到路段流量{x′a0}。
Step 1:重新分配流量。将新的交通网络G′=(N′, A′)中的路段流量{x′a0}分配到原网络对应的路段上,得到原网络的路段流量{xa0},此时n=1。
Step 2:更新路段出行时间。令tan=ta(xan),∀a∈A。并根据式(8)计算新网络中虚拟路段的广义出行成本。
Step 3:确定搜索方向。根据Step 2中得到的广义出行成本,在新的交通网络上进行基于{tan}的全有或全无分配,得到辅助路段流量集合{y′an},重复Step 1得到原网络中上的辅助路段流量集合{yan}。
Step 4:线性搜索。求满足

Step 5:移动。令

Step 6:收敛性验证。若满足收敛准则
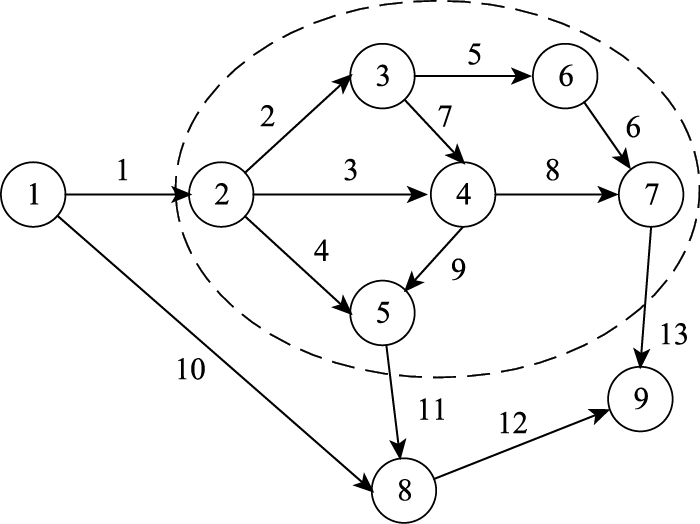
此部分采用一个小型网络进行算例分析,以验证本研究提出的模型及算法的可行性。如图 4所示,该网络包含2个OD对(1→8和1→9)、9个节点和12条路段。路段的相关参数如表 1所示,OD需求分别为D=1 000。虚线围成的区域即为收费区域

|
| 图 4 路网拓扑结构 Fig. 4 Road network topology |
| |
| 路段 | 自由流时间/s | 通行能力/(veh·h-1) | 长度/m |
| 1 | 20 | 2 400 | 200 |
| 2 | 30 | 1 200 | 300 |
| 3 | 40 | 600 | 400 |
| 4 | 30 | 600 | 300 |
| 5 | 20 | 600 | 200 |
| 6 | 30 | 600 | 300 |
| 7 | 30 | 700 | 300 |
| 8 | 20 | 1 500 | 200 |
| 9 | 30 | 700 | 300 |
| 10 | 70 | 600 | 500 |
| 11 | 10 | 1 200 | 100 |
| 12 | 20 | 600 | 200 |
| 13 | 30 | 1 200 | 300 |
| 内部路径 | 组成路段 | 长度/m |
| 1 | 2, 7, 9 | 900 |
| 2 | 3, 9 | 700 |
| 3 | 4 | 300 |
| 4 | 2, 5, 6 | 600 |
| 5 | 2, 7, 8 | 600 |
| 6 | 3, 8 | 600 |
由表 1中的数据可知,收费区域中的最短和最长距离分别为300 m和900 m。假设分段线性函数有3个间隔,每个间隔长度为200 m,得到4个边界值l0=3,l1=5,l2=7,l3=9。参考新加坡的收费制度,将最小收费和最大收费分别定为y0=ymin=5,ymax=20。
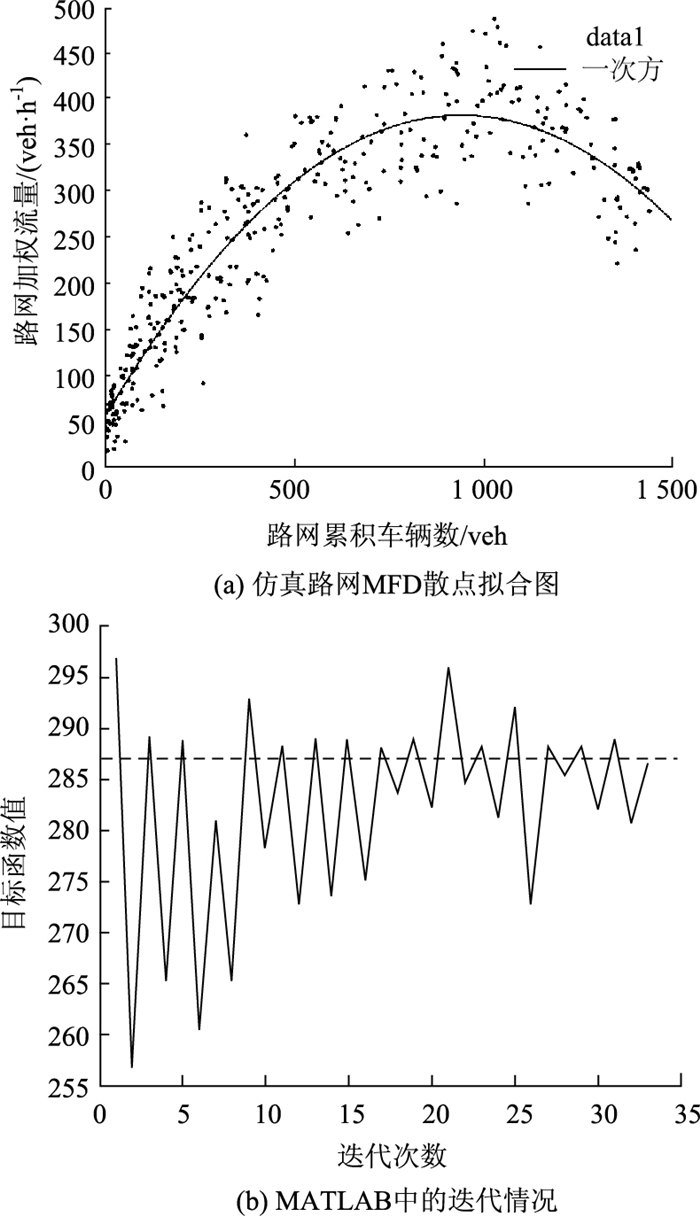
在Vissim中构建上述简单网络的仿真路网,将该仿真路网的仿真周期设置为3 600 s,每隔90 s采集1次数据,对出入路网的车辆数、路网内各路段流量、路网平均行程时间、路网平均延误时间进行统计。由于拥挤收费策略的对象不包括行人、自行车和公交车,因此仅针对小汽车进行仿真。通过在路网进出路段布设数据采集点,得到仿真时间间隔路网内的累积车辆数,再对各路段流量进行距离加权,最后得到表示路网加权流量与累积车辆数的关系如图 5(a)所示。
|
| 图 5 模拟迭代过程 Fig. 5 Simulation and interative process |
| |
利用MATLAB对MFD散点图进行拟合后,发现得到的拟合函数符合二次曲线形式:

|
(13) |
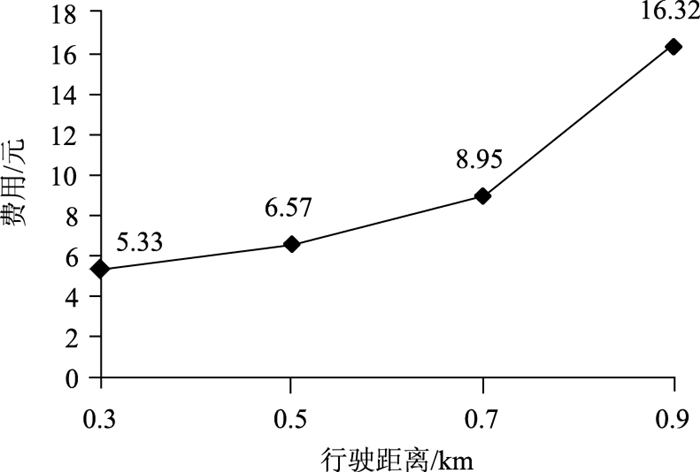
从MFD散点拟合图和拟合函数中可以看出,当路网内累积车辆数处于870辆附近时,路网的加权流量达到其峰值359 veh/h,此时的流出量最大。而在本研究提出的收费模型中,上层目标函数正是要使路网的输出流量最大,从而使系统的整体运行效益最优。因此,这就确定了收费模型中上层模型的目标函数值,将离去率λ取为0.8,则路网最大输出流量为287 veh/h。通过MATLAB求解文中提出的双层规划收费模型,在收费条件下得到目标函数值的迭代情况如图 5(b)所示。在算法迭代到33次时,输出流量最接近于目标函数值,为286.79 veh/h。这一结果表明,此时在模型中应用的收费函数使路网整体运行效益最优,即为最优收费策略。由此得到的非线性最优收费函数如图 6所示。
|
| 图 6 基于距离的最优收费函数 Fig. 6 Distance-based optimal tolling function |
| |
从图 6中可以看出,该路网最低收费为5元,最高收费为16元。对在边界内行驶距离较短的车辆,费用曲线增长平缓,收费力度较小,因此行驶中小距离的车辆可能还是倾向于选择汽车出行。而对于边界内的长距离行驶车辆,费用增长幅度较大,出行费用的明显增加能在一定程度上鼓励用户缩短在边界区域中的出行距离,同时也促进用户的出行方式向公共交通转变。
5 结论本研究建立了一种将MFD与距离收费理论相结合的最优定价模型,该模型中考虑固定需求下的用户平衡,采用非线性距离收费函数影响用户的出行选择行为,从而使网络的输出流量最大。在求解过程中通过网络变换的方式构建虚拟网络,以解决非线性距离函数所引起的路径成本不可加性问题,并基于虚拟网络设计了基于路段的FW算法。通过算例验证得到了使路网内车辆数维持在最优水平附近的分段线性收费函数,证明了该收费模型和算法的可行性。值得指出的是,由于现实应用场景的多样性,受制于基础数据获取的困难,各种影响收费的复杂因素往往难以完整考虑,需要根据不同的现场实际,选取适用因素并简化模型应用。特别是实施收费后可能引发的各路段交通量变化和数据叠加效应,为制定收费方案增加了新的难度;同时,考虑到更好的公平性和接受度,后续的研究可在基于距离收费的基础上加入时间或拥挤度等因素,结合MFD进一步探讨多费率下的最优定价及动态优化问题,提出一种不仅精确并且具有广泛实用性的改进模型及方法。
| [1] |
PRUD'HOMME R, BOCAREJO J P. The London Congestion Charge: A Tentative Economic Appraisal[J]. Transport Policy, 2005, 12(3): 279-287. |
| [2] |
TAN W H L, SUBRAMANIAM R. Congestion Control of Heavy Vehicles Using Electronic Road Pricing: The Singapore Experience[J]. International Journal of Heavy Vehicle Systems, 2006, 13(1/2): 37-55. |
| [3] |
ELIASSON J, MATTSSON L G. Equity Effects of Congestion Pricing: Quantitative Methodology and a Case Study for Stockholm[J]. Transportation Research Part A: Policy & Practice, 2006, 40(7): 602-620. |
| [4] |
VERHOEF E T. Second-best Congestion Pricing in General Networks. Heuristic Algorithms for Finding Second-best Optimal Toll Levels and Toll Points[J]. Transportation Research Part B: Methodological, 2002, 707-729. |
| [5] |
MAY A D, MILNE D S. Effects of Alternative Road Pricing Systems on Network Performance[J]. Transportation Research Part A: Policy and Practice, 2000, 34(6): 407-436. |
| [6] |
MITCHELL G, NAMDEO A, MILNE D S, et al. The Air Quality Impact of Cordon and Distance Based Road User Charging: An Empirical Study of Leeds[J]. Atmospheric Environment, 2005, 39(33): 6231-6242. |
| [7] |
HENSHER D A, PUCKETT S M. Assessing the Influence of Distance-based Charges on Freight Transporters[J]. Transport Reviews, 2008, 28(1): 1-19. |
| [8] |
LAWPHONGPANICH S, YIN Y. Nonlinear Pricing on Transportation Networks[J]. Transportation Research Part C: Emerging Technologies, 2012, 20(1): 218-235. |
| [9] |
MENG Q, LIU Z, WANG S. Optimal Distance Tolls Under Congestion Pricing and Continuously Distributed Value of Time[J]. Transportation Research Part E: Logistics & Transportation Review, 2012, 48(5): 937-957. |
| [10] |
孙鑫. 基于距离的交通拥挤收费模型与算法研究[D]. 南京: 东南大学, 2015. SUN Xin. Research on Distance-based Congestion Pricing Model and Algorithm[D]. Nanjing: Southeast University, 2015. |
| [11] |
程启秀. 基于距离的城市道路动态拥堵收费最优费率研究[D]. 南京: 东南大学, 2016. CHENG Qi-xiu. Research on Optimal Toll Rate of Distance-based Urban Road Dynamic Congestion Pricing[D]. Nanjing: Southeast University, 2016. |
| [12] |
NAN Z, WARAICH R A, AXHAUSEN K W, et al. A Dynamic Cordon Pricing Scheme Combining the Macroscopic Fundamental Diagram and an Agent-based Traffic Model[J]. Transportation Research Part A: Policy & Practice, 2012, 46(8): 1291-1303. |
| [13] |
孙玉砚, 孙利民, 朱红松, 等. 基于车牌识别系统车辆轨迹的行为异常检测[J]. 计算机研究与发展, 2015, 52(8): 1921-1929. SUN Yu-yan, SUN Li-min, ZHU Hong-song, et al. Activity Anomaly Detection Based on Vehicle Trajectory of Automatic Number Plate Recognition System[J]. Journal of Computer Research and Development, 2015, 52(8): 1921-1929. |
| [14] |
廖大彬, 马万经. 网络交通流宏观基本图研究综述[C]//第七届中国智能交通年会优秀论文集: 智能交通技术. 北京: 电子工业出版社, 2012. LIAO Da-bin, MA Wan-jing. Review of Macroscopic Fundamental Diagram of Network Traffic Flow[C]//Proceedings of the 7th China ITS Conference: Intelligent Transportation Technology. Beijing: Electronic Industry Press, 2012. |
| [15] |
李新. 基于MFD的区域路网边界控制研究[D]. 成都: 西南交通大学, 2018. LIN Xin. Study on Regional Road Network Perimeter Control Based on MFD[D]. Chengdu: Southwest Jiaotong University, 2018. |
| [16] |
DAGANZO C F, GONZALES E J, GAYAH V. Traffic Congestion in Networks, and Alleviating It with Public Transportation and Pricing[R]. Berkeley: University of California, 2011.
|
| [17] |
DAGANZO C F. Urban Gridlock: Macroscopic Modeling and Mitigation Approaches[J]. Transportation Research B: Methodological, 2007, 41(1): 49-62. |
| [18] |
YANG H, ZHANG X, MENG Q. Modeling Private Highways in Networks with Entry-exit Based Toll Charges[J]. Transportation Research Part B: Methodological, 2004, 38(3): 191-213. |
 2021, Vol. 38
2021, Vol. 38
