扩展功能
文章信息
- 徐婷, 崔世超, 刘明, 贺玉龙, 石锋
- XU Ting, CUI Shi-chao, LIU Ming, HE Yu-long, SHI Feng
- 高原山区乘用车行驶工况构建方法研究
- Study on Construction Method of Driving Cycle of Passenger Vehicle in Plateau Mountainous Area
- 公路交通科技, 2021, 38(2): 117-124
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 117-124
- 10.3969/j.issn.1002-0268.2021.02.015
-
文章历史
- 收稿日期: 2020-03-02
2. 长安大学 汽车学院, 陕西 西安 710064;
3. 北京工业大学 城市交通学院, 北京 100124;
4. 中国汽车工程研究院股份有限公司, 重庆 401122
2. School of Automobile, Chang'an University, Xi'an Shaanxi 710064, China;
3. School of Metropolitan Transportation, Beijing University of Technology, Beijing 100124, China;
4. China Automotive Engineering Research Institute Co., Ltd. Chongqing 401122, China
汽车行驶工况是描述特定交通环境下车辆行驶特征的速度-时间曲线[1],它能够代表被测区域内车速变化规律[2],对汽车节能减排有重大意义。中国国家标准化管理委员会于2019年10月下旬发布了中国标准行驶循环工况(CATC),包括乘用车、轻型商用车、重型商用车的8条整车测试工况曲线及发动机工况曲线。此外,很多学者致力于汽车行驶工况研究: 王楠楠[3]通过短行程法,采用模糊C均值聚类方法构建了合肥市的行驶工况。张宏等[4]通过短行程法,对不同车速区间赋予权重构建了呼和浩特市典型汽车行驶工况。姜平等[5]通过马尔可夫链方法,利用最大似然估计分类方法构建了合肥市的行驶工况。刘应吉等[6]提出用组合主成分分析进行汽车行驶工况的构建。李耀华等[7]通过马尔可夫蒙特卡洛方法构建了西安市城市公交行驶工况。国外[8-11]主要针对城市道路进行工况构建。查阅文献发现,目前的工况曲线无法涵盖高海拔地区。
高海拔地区生态薄弱,且随着海拔升高,汽车动力性能下降,汽车排放引起的环境问题尤为严重,多山的地形条件让汽车行驶工况与城市工况有很大差异。
本文以高原山区车辆的车况为研究对象,基于青藏高原川藏线(得达乡—海子山段)试验道路采集数据,根据汽车运行特点,提出了改进的短行程法,进行高原山区汽车行驶工况的构建。
1 数据采集及预处理 1.1 数据采集通过对我国高原地区道路线形复杂程度、地理环境特点对比,选取青藏高原G318川藏公路南段(得达乡—海子山段)道路为试验道路。试验路段最低海拔3 610.4 m,最高海拔4 591.6 m。
本次试验选用多次参加道路试验的3名驾驶员,试验车辆为乘用车,车辆外廓尺寸等参数均在典型乘用车设计范围内,具有代表性,车辆状况良好。通过自主行驶法驾驶试验车辆在试验道路上行驶。车辆信息如表 1所示:
| 名称 | 参数 |
| 车辆品牌 | 长安逸动 |
| 变速器类型 | 6挡手自一体 |
| 挡位 | 6 |
| 发动机排量 | 1.4 T |
| 排放标准 | 国V |
试验车辆上装有OBD(On Board Diagnostics)车载终端,通过OBD对车辆行驶过程中行驶车速、行驶里程、时间、发动机输出扭矩、地理位置等信息以1 Hz的频率进行采集记录。
1.2 数据预处理在数据采集过程中可能会出现外界引号干扰、车辆颠簸导致数据采集出现噪声或者传输错误。因此,将采集到的数据进行预处理,再对过滤后的数据进行工况构建。通过调查,高原地区道路车流量不大,服务水平高。结合高原地区汽车行驶特点,设定以下车速数据筛选条件:
(1) 车速长时间(超过200 s)为0 km/h认为数据采集装置与试验车辆脱离,采集数据无效(试验路段为公路,拥堵情况较少发生)。
(2) 加速度超过5 m/s2认为加速度异常(平原地区汽车百公里加速时间为7 s左右,高原地区车辆动力性能会降低)。
(3) 速度超过90 km/h为超速值(试验道路设计速度80 km/h。但根据相关研究,路段限速80 km/h,道路服务水平较高时,驾驶员平均倾向速度为90 km/h左右[12]),进行剔除。
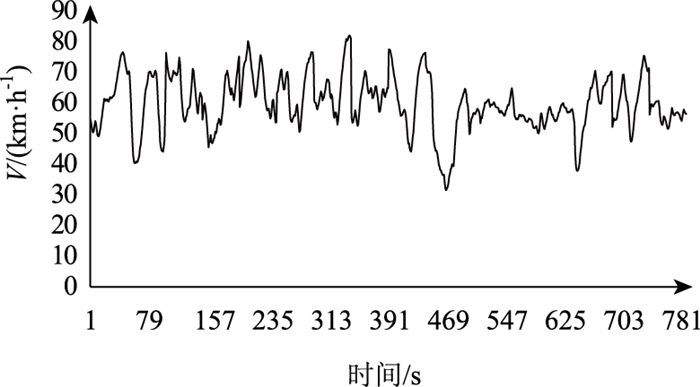
过滤后的部分速度与时间工况数据片段如图 1所示。

|
| 图 1 采集数据片段 Fig. 1 Collected data fragments |
| |
2 车速-时间工况构建
常用的汽车行驶工况构建方法有马尔可夫链法、短行程法。
马尔可夫链法:将采集数据按照统计学特征划分为若干状态,计算出各状态的转移概率矩阵,通过随机数和转移矩阵进行行驶工况构建[13-15]。
短行程法:将采集数据以怠速点划分成若干运动学片段,然后再选取特征值,通过主成分分析,聚类方法进行典型行驶工况的构建[15-17]。
高原地区有高海拔、多山的地形特点,且交通量较少,交通处于自由流。汽车行驶过程中为了适应道路线形,需要不断变化车速,导致怠速工况少,采用常规的短行程法不能构建出理想的行驶工况。
首先采用马尔可夫链法进行高原山区行驶工况提取,并基于实际行驶工况特点,提出改进的短行程法:将采集数据按照固定时长划分为若干片段,计算各个片段特征值,再进行主成分分析,通过聚类方法进行工况构建。
2.1 马尔可夫链法 2.1.1 马尔可夫特性的证明“无后效应”是马尔可夫链的典型特征。下一状态的条件概率分布仅依赖于当前状态,而与历史状态无关。假设汽车行驶过程中车速变化具有马尔可夫特性,根据试验数据分别构建不同时间间隔的子序列,理论上时间间隔越短,相关性越强[18]。分别采取1 s, 5 s和10 s间隔进行车速马尔可夫特性分析。
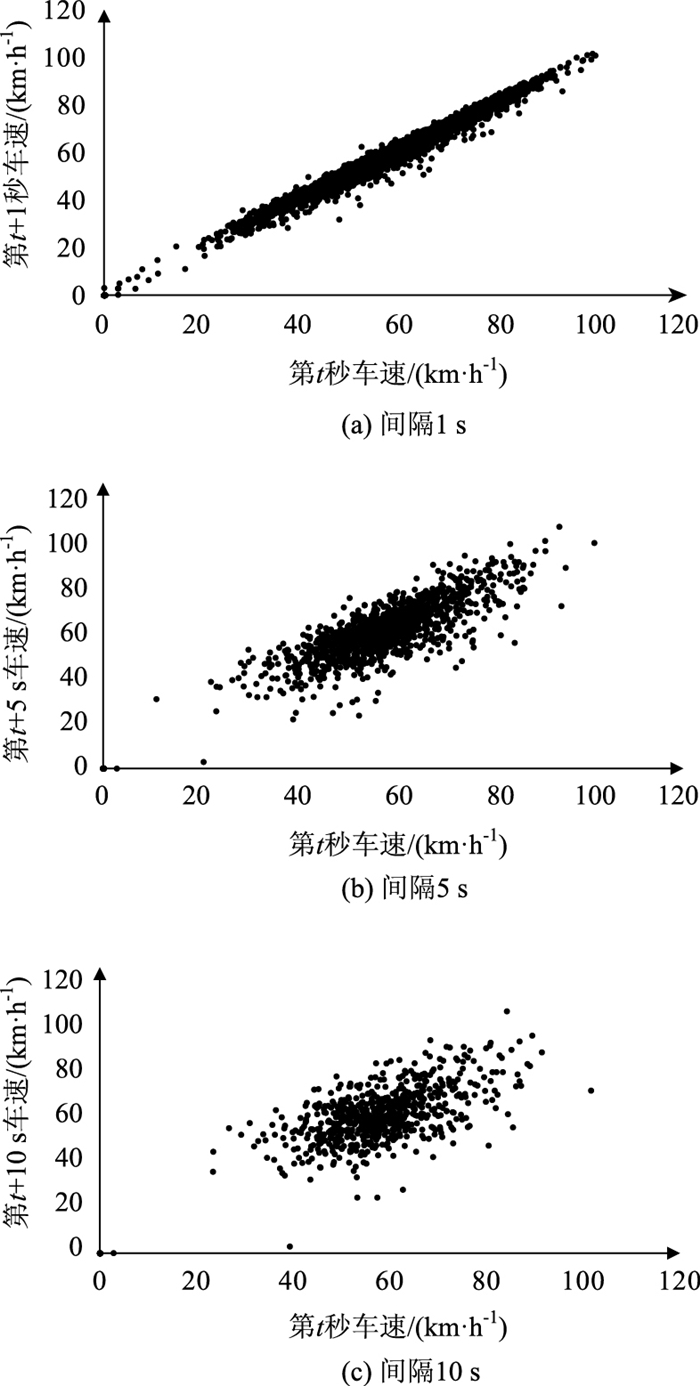
相关性图可以直观反映两个变量相互影响的强弱。由图 2可知,当时间间隔为1 s时,采集数据呈现出强相关性,各点分布接近于一条直线;随着时间间隔的增加,采样点松散分布,变量之间的相关性逐渐减弱。为了量化第t秒车速与第t+s秒车速两变量相关性,使用公式(1)皮尔逊相关系数进行计算, 结果如表 2所示。
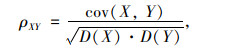
|
(1) |
|
| 图 2 不同时间间隔下的车速相关性图 Fig. 2 Correlation diagram of vehicle speed at different time intervals |
| |
| 时间间隔/s | 1 | 5 | 10 |
| 相关性系数 | 0.990 3 | 0.854 3 | 0.702 8 |
式中,X为第t秒的车速;Y为第t+s秒的车速;s为时间间隔。
由图 2和表 2可知,车速的时间间隔越小,第t秒与第t+s秒的相关性越强。其中,时间间隔为1 s时第t秒的车速与第t+1秒的车速相关性系数达到0.990 3,且随着时间间隔增加,逐渐失去相关性。综上两点,汽车行驶速度具有明显的马尔可夫特性,在研究中能够采用马尔可夫链法构建高原山区汽车行驶工况。
2.1.2 状态转移矩阵的计算车速从某一时刻某一状态变化到下一时刻某一状态,叫做状态转移,所有的状态转移组合在一起组成状态转移矩阵P,如公式(2)所示。

|
(2) |
且状态转移矩阵具有如下特征:
(1) 矩阵中每个元素均非负;
(2) 矩阵中每行和为1。
先将采集数据进行状态划分,然后再根据相邻两点之间关系进行状态模型事件频率的统计,用频率代替概率,如公式(3)所示。
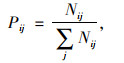
|
(3) |
式中,Nij为状态i转移到状态j发生的频数;pij为从状态i转移到状态j的概率。
对预处理后的数据进行统计分析,得出汽车行驶车速主要分布在40~80 km/h区间内。将片段划分为10个状态(状态1: v≤40 km/h, 状态2: 40 km/h <v≤45 km/h, …, 状态9: 75 km/h <v≤80 km/h, 状态10: v>80 km/h)。根据状态转移矩阵公式及状态模型事件频率得到状态转移矩阵P:

|
将采集片段以50 s间隔划分[7, 16],得到138个片段,选取并求出每个片段的加速工况(加速度a≥0.15 m/s2)的比例Pa,匀速工况(|a| < 0.15 m/s2)比例Pc,减速工况(a≤-0.15 m/s2)比例Pd[19],以及平均加速度
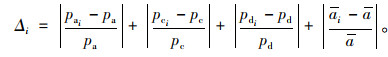
|
(4) |
图 3为Δ最小的片段,选择其最后1 s的车速作为马尔可夫初始状态,v初始=53.254 km/h。
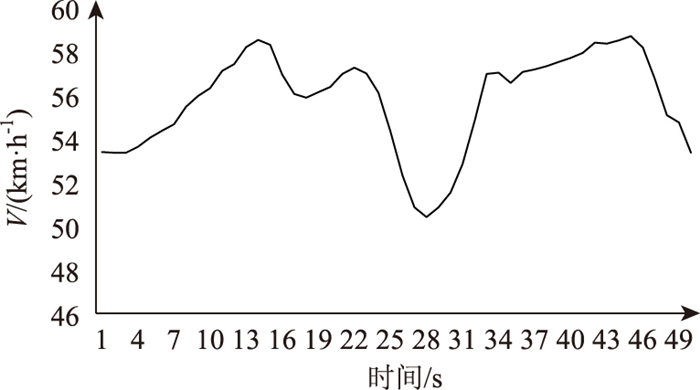
|
| 图 3 Δ值最小的片段 Fig. 3 Segment with smallest Δ value |
| |
将确定好的马尔可夫初始状态按照蒙特卡洛模拟法,通过状态转移矩阵进行工况构建。因为马尔可夫链蒙特卡洛算法采用随机数进行工况构建,即使初始状态相同,也会构建出完全不同的行驶工况。本研究构建了10条行驶工况曲线,通过计算加速比例(Pa)、匀速比例(Pc)、减速比例(Pd)、平均速度(vm)、平均加速度(am)、速度标准偏差(vsd)、加速度标准偏差(asd),选出与实际工况所有指标相对误差之和最小的一条,如图 4所示。
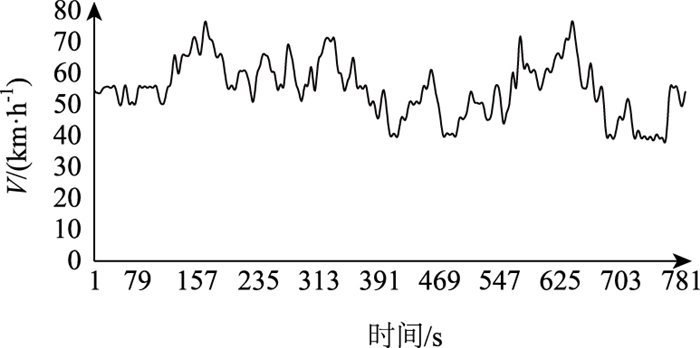
|
| 图 4 马尔可夫链法构建工况 Fig. 4 Driving cycle constructed by Markov chain method |
| |
2.2 改进的短行程法 2.2.1 特征值选取
根据高海拔地区道路线形设计规范和汽车行驶特点,将预处理后的数据按照50 s的时长划分为若干运动学片段。选取加速比例(Pa)、匀速比例(Pc)、减速比例(Pd)、平均速度(vm)、平均加速度(am)、速度标准偏差(vsd)、加速度标准偏差(asd)为特征值。这些片段的特征值能够详细地描述汽车在高原地区的行驶特性,是构建典型工况的依据[17-19]。
2.2.2 主成分分析每个特征值都能够提供一定的车辆道路行驶状态信息,这些变量有的会包含部分重叠信息,即变量之间具有一定的相关性,相互之间不独立。因此,可以通过主成分分析法简化变量个数,以便于后续处理。
主成分分析法的基本思想是尝试组合更多的原始变量,相互独立地构建一些新的变量,并从实际的研究需求中选择一些综合变量[20]。通常,选择80%或更多原始变量信息的线性组合可以简化问题而不会忽略太多实际信息。
通过主成分分析法对特征值进行处理,得到各主成分贡献率和累积贡献率,如表 3所示。
| 序号 | 特征值 | 贡献率/% | 累计贡献率/% |
| M1 | 2.939 2 | 41.99 | 41.99 |
| M2 | 1.972 8 | 28.18 | 70.17 |
| M3 | 1.048 0 | 14.97 | 85.14 |
| M4 | 0.660 2 | 9.43 | 94.57 |
| M5 | 0.264 5 | 3.78 | 98.35 |
| M6 | 0.115 3 | 1.65 | 100.00 |
| M7 | 0 | 0.00 | 100.00 |
表 3中Mi为各个主成分序号,特征值的大小反映主成分方差贡献大小。前3个主成分累计贡献率达到85.14%,且M1, M2, M3特征值均大于1,可以全面反映片段信息,达到了主成分分析的目的。
通过主成分分析结果绘制双标图如图 5所示。以提取出的前3个主成分为坐标轴,以中心为原点,将各变量在前3个主成分上的载荷用矢量线段表示,各矢量夹角的余弦值是它们的相关系数,余弦值越大,相关性越强。各片段在前3个主成分的得分情况可在双标图上显示。
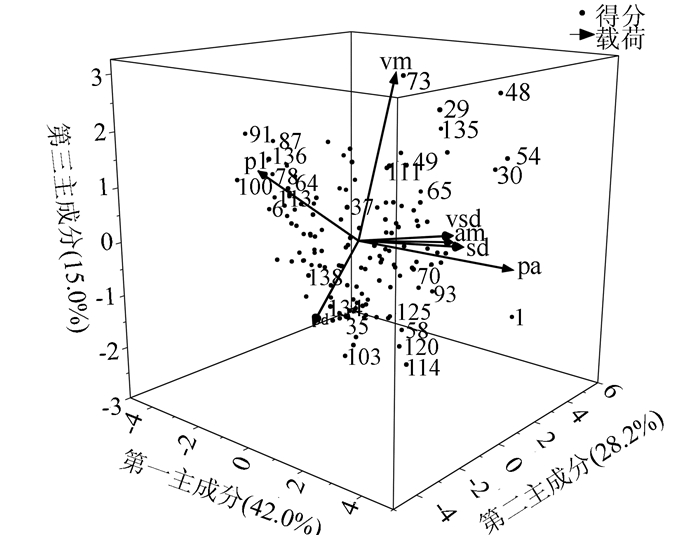
|
| 图 5 双标图 Fig. 5 Biplot |
| |
由图 5可知,第1主成分主要反映加速比例、匀速比例、速度标准差、加速度标准差等信息;第2主成分主要反映减速比例、平均加速度等信息;第3主成分主要反映平均速度等信息。
2.2.3 k-means聚类k-means聚类是一种简洁高效的聚类算法,通过计算不同样本间的距离判断它们之间的相近关系,将具有相同特性的数据对象划到同一类别中,与相关度较小的数据做以区分。基于各片段距各聚类中心的距离进行聚类[21-22]。
k-means聚类算法具体步骤如下:
(1) 在主成分分析后的得分矩阵中选择k个样本点,将k个样本点值分别作为k个初始聚类中心。
(2) 依次计算各个样本数据集中的所有数据点到各个初始聚类中心点的欧式距离,如公式(5)所示。

|
(5) |
式中, xi为第i个样本; μj为质心向量,μj= 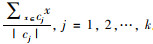
(3) 迭代收敛
计算每个聚类的平均值,并作为新的中心点,重复上述过程,直到这k个中线点收敛了,输出划分结果。
图 6是聚类后的结果,将138个样本聚为3簇。
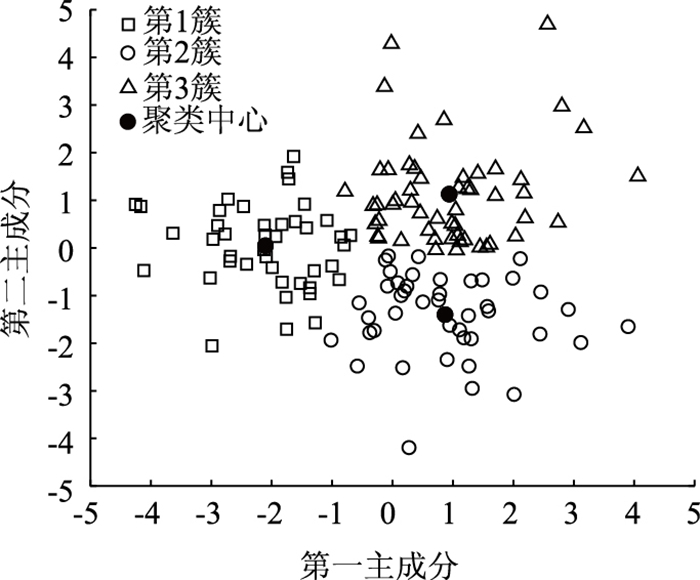
|
| 图 6 聚类结果 Fig. 6 Clustering result |
| |
第1簇有53个片段,第2簇有42个片段,第3簇有43个片段。将各运动学片段按照类别重新编号,并根据典型特征值进行分析,如图 7所示。第1簇加速工况占比最大,为加速路段;第2簇匀速工况占比最大,为匀速路段;第3簇的3种工况占比差别不大,分析为试验车辆行驶路段线形复杂,驾驶员需要不断变化车速以适应道路变化。
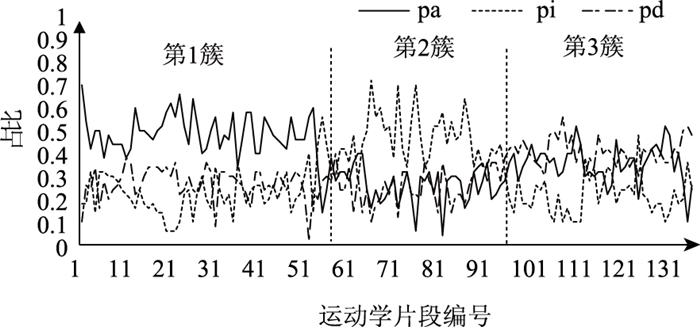
|
| 图 7 聚类结果分析 Fig. 7 Cluster result analysis |
| |
根据各片段到聚类中心的距离大小,按照运动学片段原始序号,第1簇选择片段63,36,50,68,127,23;第2簇选择片段129,77,102,108,97;第3簇选择片段74,31,76,25,41。将所选片段按照时间顺序进行工况构建。
在工况构建过程中,可能会出现车速较大的点与车速较小的点相连接,导致加减速强度过大或加速度数值异常。对这些点采取中位值平均滤波法进行滤波:以加速度异常值处为中心,选择14个前后相邻点,去掉这些点中的速度最大值和速度最小值,用剩余点的平均速度代替加速度数值异常处的点,并控制连续加速时间。构建工况如图 8所示。
|
| 图 8 改进的短行程法构建工况 Fig. 8 Driving cycle constructed by improved short stroke method |
| |
3 对比分析
将马尔可夫链法构建高原山区典型行驶工况1和改进的短行程法构建的高原山区典型行驶工况2与实际工况进行对比,如表 4、表 5所示:
| 特征值 | Pa/% | Pi/% | Pd/% | vm/(m·s-2) | am/(m·s-2) | vad | asd |
| 实际工况 | 38.60 | 29.80 | 31.59 | 58.266 0 | -0.000 1 | 11.107 8 | 0.508 5 |
| 构建工况1 | 26.50 | 47.82 | 25.68 | 54.590 4 | 0.000 1 | 8.555 0 | 0.293 5 |
| 误差1 | -12.10 | 18.02 | -5.91 | -3.675 6 | 0.000 2 | -2.552 8 | -0.215 0 |
| 特征值 | Pa/% | Pi/% | Pd/% | vm/(km·h-1) | am/(m·s-2) | vad | asd |
| 实际工况 | 38.60 | 29.80 | 31.59 | 58.266 0 | -0.000 1 | 11.107 8 | 0.508 5 |
| 构建工况2 | 39.42 | 26.54 | 34.04 | 60.951 3 | 0.000 7 | 8.800 3 | 0.609 8 |
| 误差2 | 0.82 | -3.26 | 2.45 | 2.685 3 | 0.000 8 | -2.307 5 | 0.101 3 |
由表 4、表 5可知,马尔可夫链法构建工况的特征值与实际工况偏差较大,其中,匀速工况误差最大。分析原因为状态转移矩阵主对角线数值最大,即通过马尔可夫链法构建的行驶工况偏向于车辆稳定行驶工况,这一特点与城市工况较为符合;改进的短行程法构建工况车速变化复杂,特征值与实际工况特征值误差较小,能够较好地拟合高原山区汽车行驶工况。
将马尔可夫链法与改进的短行程法构建的工况进行对比,如图 9所示。马尔可夫链方法构建的高原地区行驶工况较为平稳,车速变化幅度及频率较小;改进的短行程法构建的行驶工况车速变化频繁,与高海拔地区多山的道路环境特征相符。
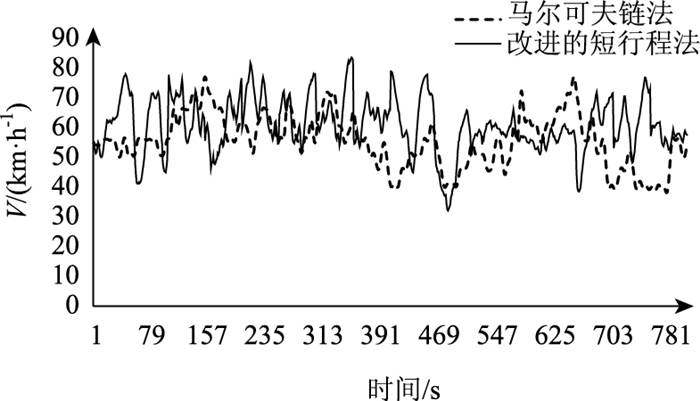
|
| 图 9 构建工况对比 Fig. 9 Comparison of constructed driving cycles |
| |
4 结论
本研究以川藏线道路采集工况数据为研究对象提出了构建高原山区乘用车行驶工况的方法。
(1) 通过不同时间间隔证明汽车行驶工况具有马尔可夫特性。根据马尔可夫蒙特卡洛法构建的高原山区行驶工况较为平稳,以匀速工况为主,车速变化幅度及频率较小。
(2) 用改进的短行程法按照50 s的固定时长将汽车行驶工况划分为138个运动学片段,通过主成分分析,k-means聚类构建行驶工况,并通过中位值平均滤波法进行异常点的滤波。改进的短行程法构建的行驶工况加速,减速的波动变化较为频繁,
(3) 通过比较指标(加速比例、匀速比例、减速比例、平均速度、平均加速度、速度标准偏差、加速度标准偏差),将两种方法构建的行驶工况与实际工况对比,发现用改进的短行程法构建的行驶工况误差较小,可以反映高原山区车辆行驶特点,这为研究行驶工况提供了新思路。
| [1] |
李耀华, 苟琦智, 任田园, 等. 城市公交线路模态行驶工况构建研究: 以西安市公交线路为例[J]. 交通信息与安全, 2018, 36(3): 92-98. LI Yao-hua, GOU Qi-zhi, REN Tian-yuan, et al. Conditions of Modal Driving of City Bus Lines: A Case Study in Xi'an[J]. Journal of Transport Information and Safety, 2018, 36(3): 92-98. |
| [2] |
刘炳姣, 石琴, 仇多洋, 等. 基于改进蚁群算法的行驶工况构建及精度分析[J]. 合肥工业大学学报: 自然科学版, 2017, 40(10): 1297-1302. LIU Bing-jiao, SHI Qin, QIU Duo-yang, et al. Driving Cycle Construction Based on Improved Ant Colony Optimization Algorithm and Precision Analysis[J]. Journal of Hefei University of Technology, 2017, 40(10): 1297-1302. |
| [3] |
王楠楠. 城市道路行驶工况构建及油耗研究[D]. 合肥: 合肥工业大学, 2012. WANG Nan-nan. Research of Construction of Urban Road Driving Cycle and Fuel Consumption[D]. Hefei: Hefei University of Technology, 2012. |
| [4] |
张宏, 姚延钢, 张露. 呼和浩特市轻型汽车运行工况构建研究[J]. 公路交通科技, 2019, 36(11): 104-110. ZHANG Hong, YAO Yan-gang, ZHANG Lu. Study on Construction of Light-duty Vehicle Driving Cycle in Hohhot City[J]. Journal of Highway and Transportation Research and Development, 2019, 36(11): 104-110. |
| [5] |
姜平, 石琴, 陈无畏. 基于马尔科夫的城市道路行驶工况构建方法[J]. 农业机械学报, 2009(11): 26-30. JIANG Ping, SHI Qin, CHEN Wu-wei. Driving Cycle Construction Methodology of City Road Based on Markov Process[J]. Transactions of the Chinese Society for Agricultural Machinery, 2009(11): 26-30. |
| [6] |
刘应吉, 夏鸿文, 姚羽, 等. 组合主成分分析和模糊C均值聚类的车辆行驶工况制定方法[J]. 公路交通科技, 2018, 35(3): 79-85. LIU Ying-ji, XIA Hong-wen, YAO Yu, et al. A Method of Vehicle Driving Cycle Development Based on Combined Principal Component Analysis and Fuzzy C Means Clustering[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 79-85. |
| [7] |
李耀华, 任田园, 邵攀登, 等. 基于马尔可夫链的西安市城市公交工况构建[J]. 中国科技论文, 2019, 14(2): 4-11. LI Yao-hua, REN Tian-yuan, SHAO Pan-deng, et al. Development of Driving Cycle of Bus in Xi'an City based on Markov Chain[J]. China Sciencepaper, 2019, 14(2): 4-11. |
| [8] |
MA M, BENEDIKT W, FERIT K, et al. A Statistical Method for Driving Cycle Construction Based on Path Geometry[C]//International Conference on Remote Sensing, Environment and Transportation Engineering. Nanjing: Atlantis Press, 2013: 890-893.
|
| [9] |
GAO X, ZHANG B, XIONG X, et al. Construction and Analysis of the Dalian Driving Cycle[J]. International Journal of Control & Automation, 2015, 8(6): 363-368. |
| [10] |
NYBERG P, FRISK E, NIELSEN L. Driving Cycle Equivalence and Transformation[J]. IEEE Transactions on Vehicular Technology, 2016, 66(3): 1-1. |
| [11] |
ZHAO X, MA J, WANG S, et al. Developing an Electric Vehicle Urban Driving Cycle to Study Differences in Energy Consumption[J]. Environmental Science and Pollution Research, 2019, 26(14): 13839-13853. |
| [12] |
徐瑶琳. 高速公路限速标准及实施对策研究[D]. 广州: 华南理工大学, 2013. XU Yao-lin. Study on Expressway Speed Limit Standard and Measures of Implementation[D]. Guangzhou: South China University of Technology, 2013. |
| [13] |
任田园. 基于马尔可夫链的西安市线路公交典型工况开发与应用研究[D]. 西安: 长安大学, 2019. REN Tian-yuan. Research on Development and Application of Typical Driving Cycle of Xi'an Public Transport Based on Markov Chain[D]. Xi'an: Chang'an University, 2019. |
| [14] |
苗强, 孙强, 白书战, 等. 基于聚类和马尔可夫链的公交车典型行驶工况构建[J]. 中国公路学报, 2016, 29(11): 161-169. MIAO Qiang, SUN Qiang, BAI Shu-zhan, et al. Construction of Typical Driving Cycle of Bus Based on Clustering and Markov Chain[J]. China Journal of Highway and Transport, 2016, 29(11): 161-169. |
| [15] |
姜平. 城市混合道路行驶工况的构建研究[D]. 合肥: 合肥工业大学, 2011. JIANG Ping. Investigation of Driving Cycle Construction of Mixed Road in City[D]. Hefei: Hefei University of Technology, 2011. |
| [16] |
曹冬旭. 城市车辆道路行驶工况在线构建方法的研究[D]. 北京: 北京理工大学, 2016. CAO Dong-xu. Research on Online Construction Method of Urban Vehicle Road Driving Cycle[D]. Beijing: Beijing Institute of Technology, 2016. |
| [17] |
石琴, 郑与波, 姜平. 基于运动学片段的城市道路行驶工况的研究[J]. 汽车工程, 2011, 33(3): 256-261. SHI Qin, ZHEN Yu-bo, JIANG Ping. A Research on Driving Cycle of City Roads Based on Microtrips[J]. Automotive Engineering, 2011, 33(3): 256-261. |
| [18] |
胡研研. 基于粒子滤波的目标跟踪算法研究[D]. 长春: 吉林大学, 2012. HU Yan-yan. Research on Target Tracking Algorithm Based on Particle Filter[D]. Changchun: Jilin University, 2012. |
| [19] |
潘登. 混合动力汽车城市循环工况构建及运行工况多尺度预测[D]. 北京: 北京理工大学, 2015. PAN Deng. Construction of Urban Cycle Condition and Multi-scale Prediction of Operation Condition of Hybrid Electric Vehicle[D]. Beijing: Beijing Institute of Technology, 2015. |
| [20] |
岳柄剑. 含道路坡度的汽车运行工况马尔可夫链设计方法[D]. 长春: 吉林大学, 2015. YUE Bing-jian. Design Method of Automobile Driving Cycle with Road Gradient Based on Markov Chain[D]. Changchun: Jilin University, 2015. |
| [21] |
李宁. 城市道路车辆行驶工况的构建与研究[D]. 保定: 河北农业大学, 2013. LI Ning. Construction and Study of Driving Cycle of Urban Road Vehicle[D]. Baoding: Hebei Agricultural University, 2013. |
| [22] |
刘子谭, 朱平, 刘旭鹏, 等. K均值聚类改进与行驶工况构建研究[J]. 汽车技术, 2019(11): 57-62. LIU Zi-tan, ZHU Ping, LIU Xu-peng, et al. Research on Improved K-means and Driving Cycle Construction[J]. Automobile Technology, 2019(11): 57-62. |
 2021, Vol. 38
2021, Vol. 38
