扩展功能
文章信息
- 郝艳广, 袁龙文, 韩劲龙, 梁济川, 欧阳彪
- HAO Yan-guang, YUAN Long-wen, HAN Jin-long, LIANG Ji-chuan, OUYANG Biao
- 基于车-桥耦合动力作用的车辆与桥梁力学行为
- Mechanical Behavior of Vehicle and Bridge Based on Vehicle-bridge Coupling Dynamic Action
- 公路交通科技, 2021, 38(2): 80-89
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 80-89
- 10.3969/j.issn.1002-0268.2021.02.011
-
文章历史
- 收稿日期: 2020-03-02
2. 海工结构新材料及维护加固技术湖北省重点实验室, 湖北 武汉 430040;
3. 广东省北江航道开发投资有限公司, 广东 清远 511500
2. Hubei Provincial Key Laboratory of New Materials and Maintenance and Reinforcement Technology for Offshore Structures, Wuhan Hubei 430040, China;
3. Guangdong Provincial Beijiang Channel Development Investment Co., Ltd., Qingyuan Guangdong 511500, China
车-桥耦合动力作用包括大量非线性因素,如橡胶轮胎大变形、沥青混合料黏弹性、路面不平度等[1-2]。桥面铺装层分层铺筑,各层材料在环境变化和车-桥耦合动力作用下出现大量病害,如沥青混合料推移、脱落、车辙等, 水泥混凝土裂缝、破损等, 钢板、钢梁焊接处锈蚀等。这些病害严重影响桥梁工作状态以及服役寿命,相关问题亟待解决[3-4]。
车辆与桥梁相关参数、路面不平度激励以及车桥工作状态对车-桥力学行为有巨大影响[5]。国内外学者针对车-桥耦合动力作用已进行大量研究:张彦玲等[6]研究桥梁在谐波荷载作用下力学行为,结果表明桥梁跨中动挠度受静载影响较大。魏志刚等[7]推导车辆动载作用下桥梁刚度分布函数,根据变形协调方程及荷载平衡条件,得到桥梁动力响应。张玥等[8]基于Midas/FEA软件,建立桥梁模型,研究不同工况下桥梁应力变化规律。李慧乐等[9]建立三维车辆模型与桥梁有限元模型,根据车辆与桥梁接触行为,求解桥梁动态响应。杨永清等[10]建立某公路桥正交异性桥面板有限元模型,研究其在移动荷载下不同桥梁部位应力特征,并基于应力等效原则建立足尺模型验证不同桥梁部位疲劳特性。综上可知,大量车-桥耦合动力研究采用移动荷载、移动质量块或者簧上质量模拟车辆荷载;桥面铺装层材料未能考虑沥青混合料黏弹性;轮胎简化为质量、刚度、阻尼模型,相关研究结果与工程实际存在较大差距。
建立四分之一车辆模型和简支桥模型,其中车辆模型考虑橡胶轮胎,简支桥模型考虑沥青混合料黏弹性。基于轮胎与桥面铺装层接触关系,建立车-桥耦合动力模型,采用中心差分法和有限元理论求解车-桥耦合动力方程以及车辆与桥梁时域响应, 将仿真值与测量值进行对比,验证该模型。计算分析桥面铺装层三向应力状态以及不同路面不平度激励下车辆和桥梁力学行为,以期为车辆和桥梁设计提供一定理论依据。
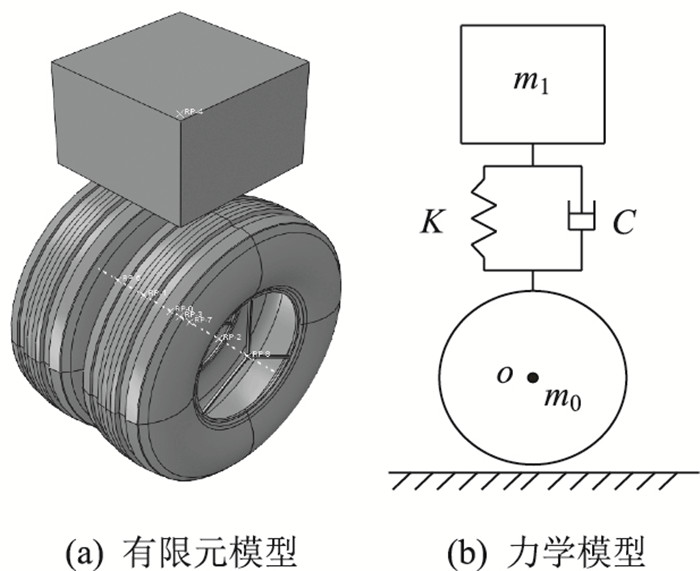
1 四分之一车辆模型车辆是复杂多自由度系统,一般由车体、悬架、轮胎构成。基于多体动力学理论,在ABAQUS中建立四分之一车辆有限元模型,其中车体假设为均质刚体,轮胎采用橡胶材料模拟。利用连接器将两轮胎分别耦合并采用连接器Hinge属性,模拟车轴;利用连接器将车体与车轴连接并采用连接器Cartesian属性,车辆有限元模型及力学模型如图 1所示,相关参数如表 1所示。
|
| 图 1 车辆有限元模型与力学模型 Fig. 1 FE model and mechanical model of vehicle |
| |
| 项目 | 参数 |
| 悬架刚度K/(N·mm-1) | 1 200 |
| 悬架阻尼C/(N·s·mm-1) | 20 |
| 车体质量m1/t | 5 |
| 轮胎质量m0/t | 0.8 |
2 橡胶轮胎模型
相关研究中,轮胎模型均采用如下假设:轮胎由质量、刚度和阻尼构成,根据D′alember原理列出微分方程,并进行求解。实际轮胎是由橡胶基体、帘布层、钢丝帘线等多种材料压制而成。为保证计算精度并提高计算效率,建立橡胶轮胎有限元模型并进行适当简化,保留胎侧与胎面、胎体等橡胶材料以及骨架材料。利用CAD绘制轮胎断面图,导入ABAQUS中生成轮胎有限元模型。轮胎断面图、各部分有限元模型以及相关网格划分如图 2所示。

|
| 图 2 轮胎模型 Fig. 2 Model of tire |
| |
ABAQUS包含Mooney-Rivlin模型、Yeoh模型、Neo-Hookean模型等本构模型,各模型均具有独特性质,针对不同问题,选择适当模型。Yeoh模型适用于描述橡胶材料大变形,本研究采用Yeoh模型。
橡胶具有体积不可压缩非线性力学特点,是三维正交各项异性复合结构物[11]。基于应力-应变关系以及唯象理论建立橡胶材料本构关系,采用体应变能表征其力学特性,其方程如下:
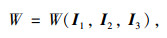
|
(1) |

|
(2) |
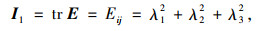
|
(3) |
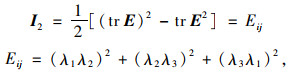
|
(4) |
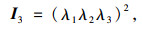
|
(5) |
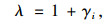
|
(6) |
式中,W为体应变能;I1,I2,I3分别为左Cauchy-green第一、第二、第三张量不变量,当I3=1时,橡胶材料不可压缩;γi为主应变;1,2,3下角标为相互垂直方向,橡胶材料只有单向拉伸,则λ1·λ2·λ3=1;对于橡胶材料,∂W/∂I2远小于∂W/∂I1,一般认为∂W/∂I2在应变能中贡献度很小,可以忽略,则应变能函数简化为[11-13]
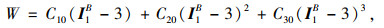
|
(7) |
式中Cij为橡胶轮胎材料参数。
| 橡胶部件 | 材料参数/MPa | ||
| C10 | C20 | C30 | |
| 胎面胶 | 0.603 5 | -0.369 1 | 0.092 0 |
| 基体胶 | 0.690 8 | -0.247 4 | 0.090 2 |
| 带束层胶 | 1.234 5 | -0.456 6 | 0.182 7 |
| 胎侧胶 | 0.479 1 | -0.179 5 | 0.051 2 |
| 胎体帘布胶 | 0.847 8 | -0.267 4 | 0.080 1 |
| 内衬层胶 | 0.584 7 | -0.208 9 | 0.078 1 |
| 加强层胶 | 1.677 6 | -0.345 5 | 0.150 7 |
| 胎圈胶 | 4.548 4 | -17.654 3 | 49.998 0 |
橡胶轮胎主要结构有带束层、胎体帘线、钢丝帘线、钢丝圈等。利用Rebar单元模拟钢丝帘线结构。橡胶材料是轮胎主要成分,采用CGAX4H单元和CGAX3H单元模拟二维橡胶材料,并经空间旋转成三维立体模型,相应单元类型改变为C3D8H单元和C3D6H单元[15]。
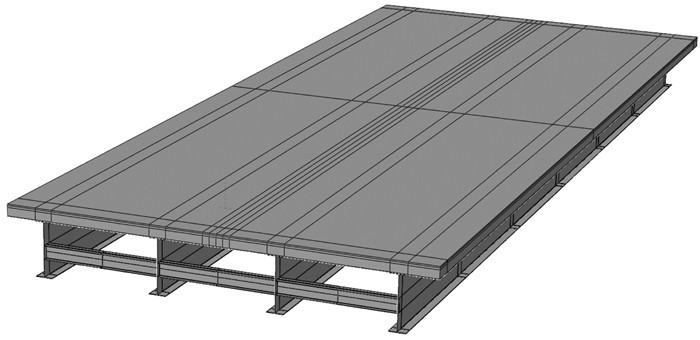
3 简支桥模型简支桥来自江西省某高速公路,全长24 m,采用4块纵向工字钢、21块横向工字钢以及桥面板焊接而成。纵梁高1.6 m,间距3 m,纵梁梁顶与桥面板底面焊接;横梁高0.4 m,间距4 m,横梁梁端与纵梁侧面焊接。纵梁、横梁、桥面板均采用Q345钢,桥面铺装层相关材料参数如表 3、表 4所示。
|
| 图 3 简支桥模型 Fig. 3 Model of simply supported bridge |
| |
| 结构 | 材料 | 厚度/ mm |
弹性模量/ MPa |
泊松比 | 密度/ (kg·m-3) |
| 上面层 | SMA-13 | 40 | 1 400 | 0.35 | 2 400 |
| 中面层 | AC-20 | 60 | 1 200 | 0.2 | 2 300 |
| 下面层 | 水泥混凝土 | 250 | 2.95×105 | 0.2 | 2 300 |
| 纵梁、横梁 及桥面板 |
钢 | — | 2.1×105 | 0.3 | 7 800 |
| 材料种类 | ti | gi |
| 上面层(SMA-13) | 0.85 | 0.673 |
| 10.34 | 0.285 | |
| 1 259.53 | 0.031 | |
| 17 500 | 0.01 | |
| 下面层(AC-20) | 0.000 002 | 0.093 33 |
| 0.000 02 | 0.150 75 | |
| 0.000 2 | 0.215 61 | |
| 0.002 | 0.236 01 | |
| 0.02 | 0.174 26 | |
| 0.2 | 0.083 28 | |
| 2 | 0.029 02 | |
| 20 | 0.009 29 | |
| 200 | 0.003 25 | |
| 2 000 | 0.001 28 | |
| 20 000 | 0.000 59 | |
| 200 000 | 0.000 17 | |
| 2 000 000 | 0.000 48 |
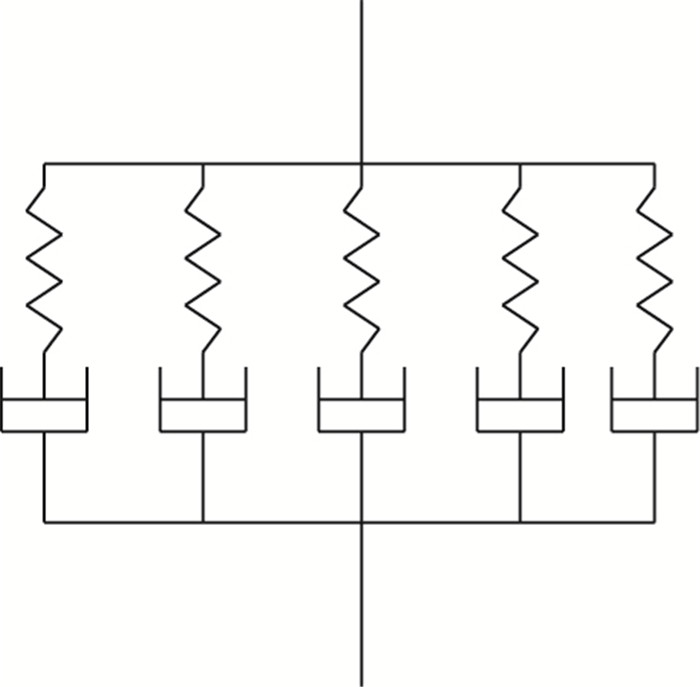
水泥混凝土采用线弹性本构模型;沥青混合料具有黏弹性,采用广义Maxwell模型模拟,广义Maxwell模型如图 4所示。
|
| 图 4 广义Maxwell模型 Fig. 4 Generalized Maxwell model |
| |
对广义Maxwell模型施加一定应变,每一个Maxwell元件均有同样应变,则:
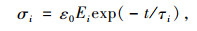
|
(8) |
总应力为:
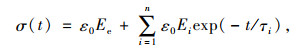
|
(9) |
则松弛模量函数为:
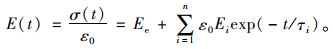
|
(10) |
当t=0时
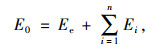
|
(11) |
式中,E0为初始松弛模量;Ee为松弛时间t无穷时刻平衡值;σ(t)为应力;ε0为初应变。
广义Maxwell高分子聚合物经典遗传积分形式可以写成:
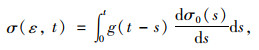
|
(12) |
式中,σ0(s)为弹性响应部分;g(t)为衰减函数,采用Prony级数表示:
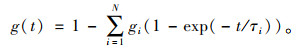
|
(13) |
沥青混合料黏弹性参数来自文献[16]。
4 车-桥耦合动力模型 4.1 路面不平度路面不平度是车-桥耦合振动主要原因,由《机械振动道路路面谱测量数据报告》(GB/T 7031—2005/ISO 8608: 1995)可得路面功率谱表达式为
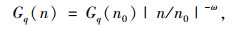
|
(14) |
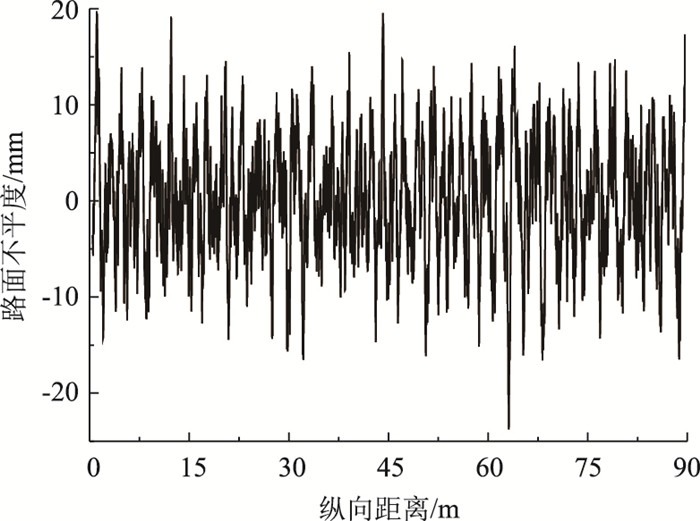
式中,n0=0.1 m-1,为空间参考频率;n为任意有效空间频率;Gq(n0)为参考空间频率对应的功率谱密度,B级路面取64×10-6 m2/m-1;ω为频率指数,用于确定路面不平度的频率结构,通常取2。B级路面不平度如图 5所示。
|
| 图 5 B级路面不平度 Fig. 5 Class B pavement roughness |
| |
4.2 接触关系
轮胎与桥面接触关系可分为法向接触行为和切向接触行为。法向接触行为采用“硬接触”表示,并通过罚函数计算法向力:
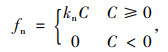
|
(15) |
式中,kn为法向接触刚度;C为间隙值。
切向接触行为采用库伦摩擦力表示,摩擦力数值取决于轮胎与路面接触状态

|
(16) |
式中,kt为切向刚度;ne为接触节点相对变形;μ为摩擦系数。
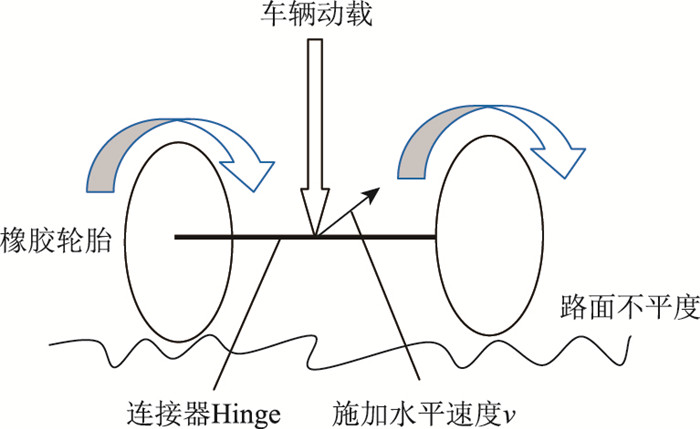
4.3 边界条件约束桥梁两端相关自由度,模拟简支桥边界条件。为保证橡胶轮胎自由滚动,对连接器施加沿z方向平动速度。桥面设置摩擦系数μ,轮胎与桥面之间摩擦力推动轮胎滚动,如图 6所示。
|
| 图 6 轮胎旋转示意图 Fig. 6 Schematic diagram of tire rotation |
| |
4.4 求解车-桥耦合动力方程
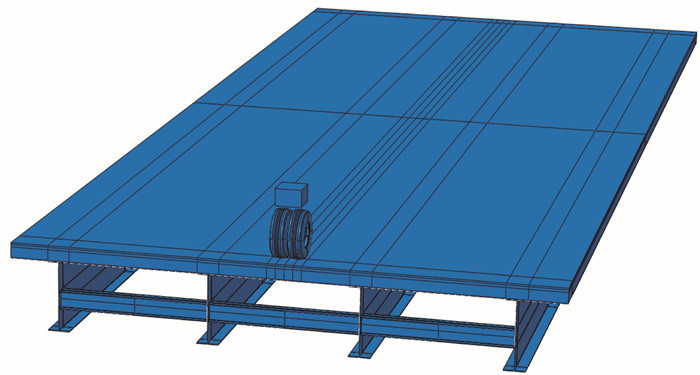
车-桥耦合动力模型分为车辆模型和桥梁模型,基于有限元理论将车辆、桥梁模型分别离散,如图 7所示。
|
| 图 7 车-桥耦合动力模型 Fig. 7 Vehicle-bride coupling dynamic model |
| |
通过轮胎-桥面接触关系实现两模型之间力学关系转换。路面不平度作为外部激励,形成车-桥耦合,其耦合效应随路面平整度降低而加剧[17-20]。接触理论将轮胎与桥面接触关系转换成时域上连续接触关系,则车-桥耦合动力方程为:
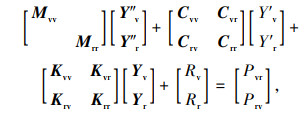
|
(17) |
式中,Y″,Y′,Y分别为加速度、速度、位移向量;M,C,K分别为质量、阻尼、刚度矩阵;下角标v,r分别表示车辆和桥梁;Rv,Rr分别为车辆与桥梁恢复力;Pvr,Prv分别为车辆与桥梁之间作用力。
所建模型考虑轮胎与桥面之间摩擦以及多种非线性材料,导致耦合动力方程中阻尼矩阵和刚度矩阵为非对称矩阵。针对这一问题,拟采用中心差分法求解。中心差分法每一时间步积分步长可由下式确定:
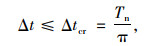
|
(18) |
式中,Tn为有限元模型最小固有频率。加速度和速度分别为:
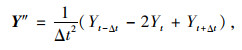
|
(19) |
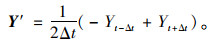
|
(20) |
将式(19)和式(20)代入式(17),可求得每个时间步位移。由有限元理论可知,位移与应变存在如下关系
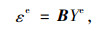
|
(21) |
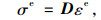
|
(22) |
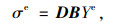
|
(23) |
式中,εe为单元应变;σe为单元应力;Y为单元节点位移;B为位移-应变关系矩阵;D为弹性矩阵。
综上所述,建立车-桥耦合动力方程,并基于中心差分法和有限元理论求解,可得车-桥耦合动力作用下时域响应,如位移、应力等。
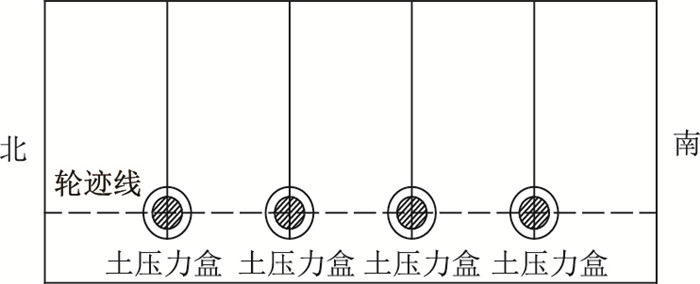
5 力学行为分析 5.1 模型验证为验证所建模型可行性,将上面层跨中竖向应力仿真值与测量值进行比较。待中面层沥青混合料铺设完成后,在桥梁跨中截面布设土压力盒以及连接导线,然后铺设上面层沥青混合料。相关施工工序完成后,进行车-桥耦合测量试验,测量车辆动载作用下桥面铺装层应力变化状态。土压力盒布设如图 8所示,对比结果如图 9所示,速度取30 m/s。
|
| 图 8 土压力盒布设示意图 Fig. 8 Schematic diagram of layout of earth pressure boxes |
| |
|
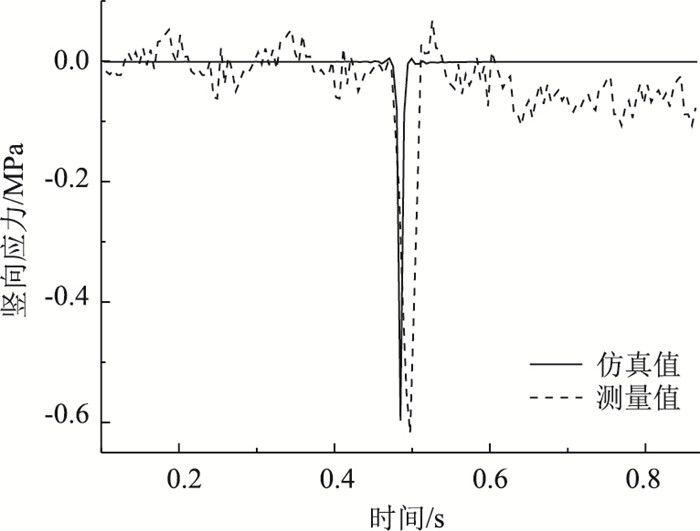
| 图 9 上面层竖向应力 Fig. 9 Vertical stress of upper surface layer |
| |
由图 9可知,车辆动载作用下,上面层跨中竖向应力仿真值为0.608 MPa,测量值为0.630 MPa,比仿真值大3.618%,表明基于相关理论构建车-桥耦合动力模型具有一定可行性,相关计算方法恰当。
5.2 铺装层三向应力以桥面铺装层跨中为观测点,提取该点三向应力时程曲线,分析车辆动载作用下桥面铺装层动力响应。
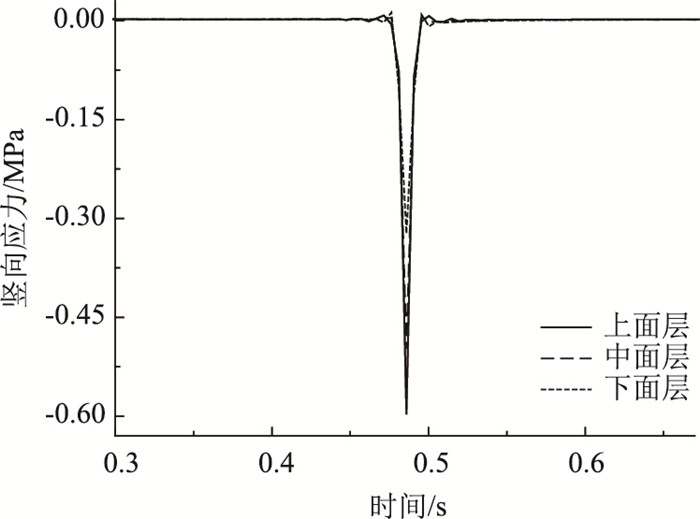
由图 10可知,车辆动载作用下,桥面铺装层竖向应力以受压为主,上、中、下面层最大竖向压应力分别为0.608,0.507,0.330 MPa,竖向压应力随桥面铺装层深度增加逐渐降低。
|
| 图 10 桥面铺装层竖向应力 Fig. 10 Vertical stress of bridge deck pavement |
| |
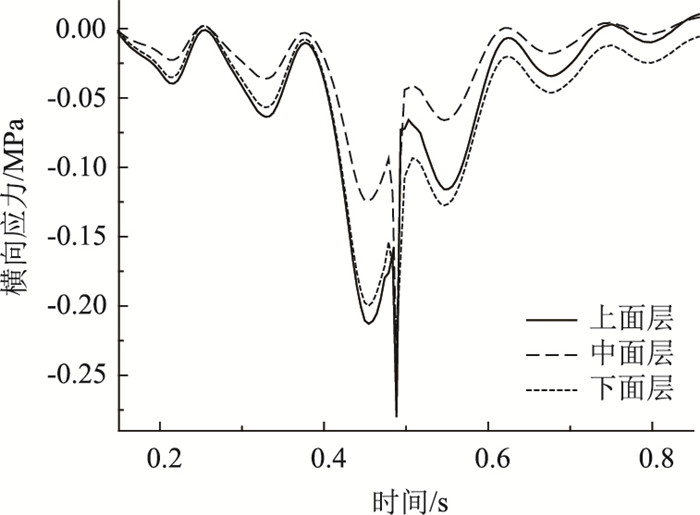
由图 11可知,车辆动载作用下,桥面铺装层横向应力以受压为主,并呈现出一定的振动形态。上、中、下面层最大横向压应力分别为0.283,0.245,0.227 MPa,横向压应力随桥面铺装层深度增加逐渐减小。
|
| 图 11 桥面铺装层横向应力 Fig. 11 Transverse stress of bridge deck pavement |
| |
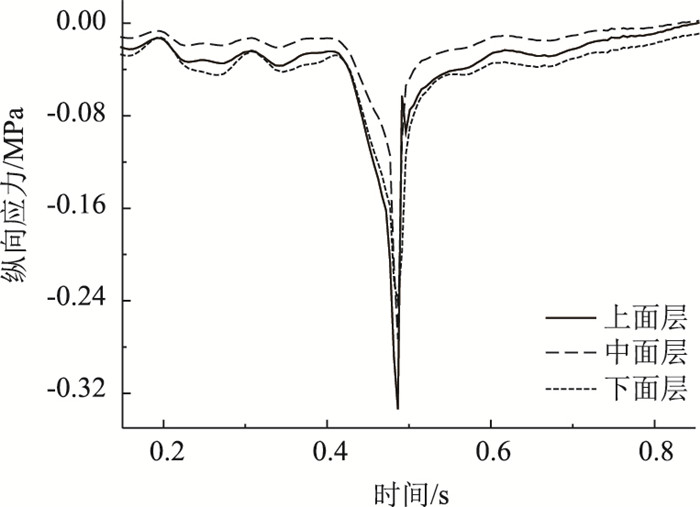
由图 12可知,车辆动载作用下,桥面铺装层纵向应力以受压为主,上、中、下面层最大纵向压应力分别为0.338,0.277,0.245 MPa,纵向压应力随桥面铺装层深度增加逐渐减小。
|
| 图 12 桥面铺装层纵向应力 Fig. 12 Longitudinal stress of bridge deck pavement |
| |
5.3 路面不平度对力学行为影响
本研究构建B级路面不平度,探究路面不平度激励对桥面铺装层、钢桥部件以及车辆动态响应影响规律。
5.3.1 上面层跨中由图 13可知,添加B级路面不平度,上面层跨中最大竖向压应力为1.327 MPa,比未添加不平度增大118.257%。

|
| 图 13 不同路面等级上面层竖向应力 Fig. 13 Vertical stress of upper surface layer in different road grades |
| |
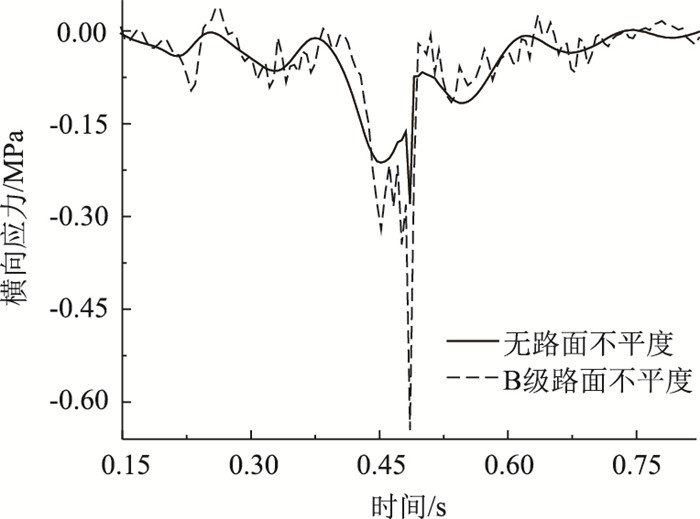
由图 14可知,添加B级路面不平度,上面层跨中最大横向压应力为0.652 MPa,比未添加不平度增大130.389%,且横向应力时程曲线振动形态加剧。
|
| 图 14 不同路面等级上面层横向应力 Fig. 14 Transverse stress of upper surface layer in different road grades |
| |
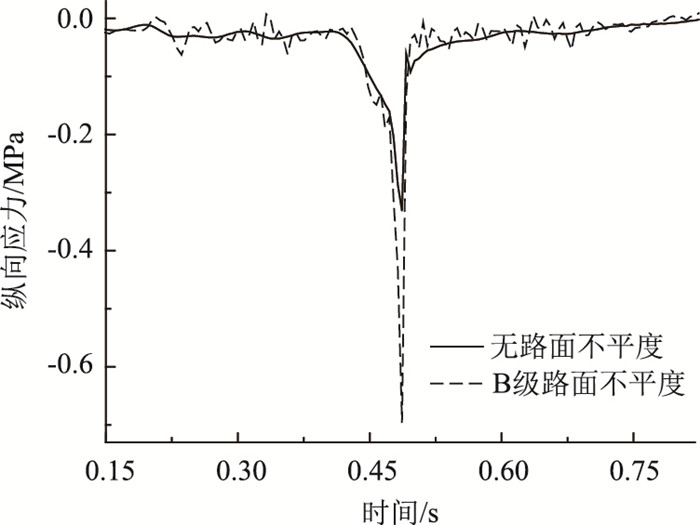
由图 15可知,添加B级路面不平度,上面层跨中最大纵向压应力为0.706 MPa,比未添加不平度增大108.876%,且纵向应力时程曲线呈现出波动状态。
|
| 图 15 不同路面等级上面层纵向应力 Fig. 15 Longitudinal stress of upper surface layer in different road grades |
| |
5.3.2 钢板顶面
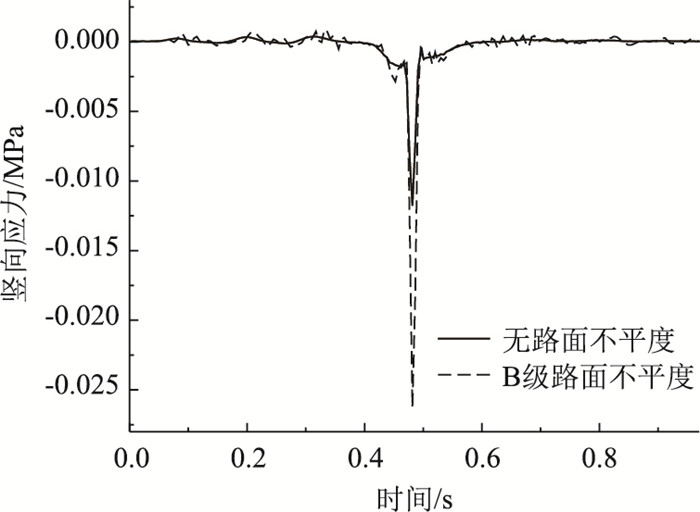
由图 16可知,未添加路面不平度,钢板顶面跨中最大竖向压应力为0.012 MPa;添加B级路面不平度为0.027 MPa,比未添加不平度增大125%。
|
| 图 16 不同路面等级钢板顶面竖向应力 Fig. 16 Vertical stress of top surface of steel plate in different road grades |
| |
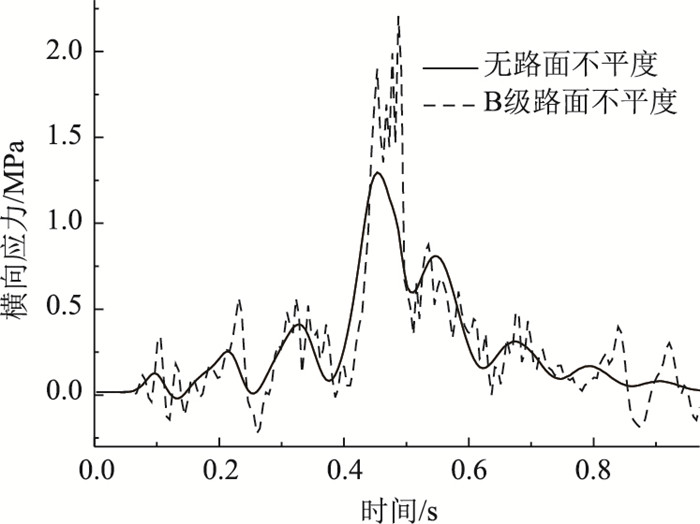
由图 17可知,未添加不平度,钢板顶面跨中最大横向拉应力为1.290 MPa;添加B级路面不平度为2.210 MPa,比未添加不平度增大71.318%,且横向应力时程曲线振动加剧。
|
| 图 17 不同路面等级钢板顶面横向应力 Fig. 17 Transverse stress of top surface of steel plate in different road grades |
| |
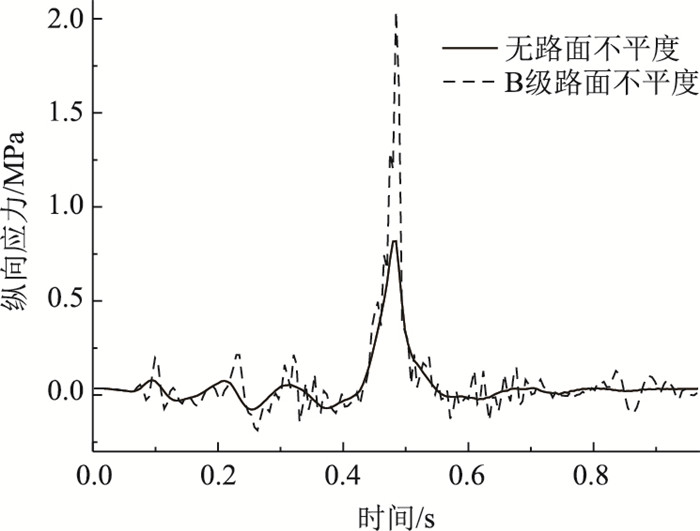
由图 18可知,未添加不平度;钢板顶面跨中最大纵向拉应力为0.793 MPa;添加B级路面不平度为2.030 MPa,比未添加不平度增大155.990%。
|
| 图 18 不同路面等级钢板顶面纵向应力 Fig. 18 Longitudinal stress of top surface of steel plate in different road grades |
| |
5.3.3 车辆悬架
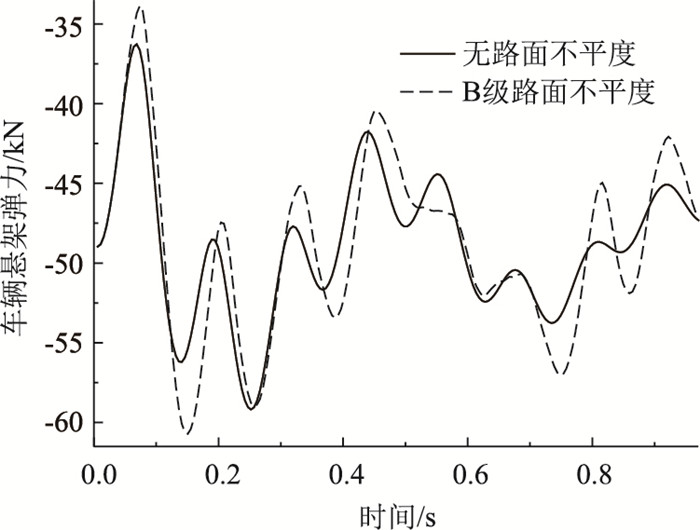
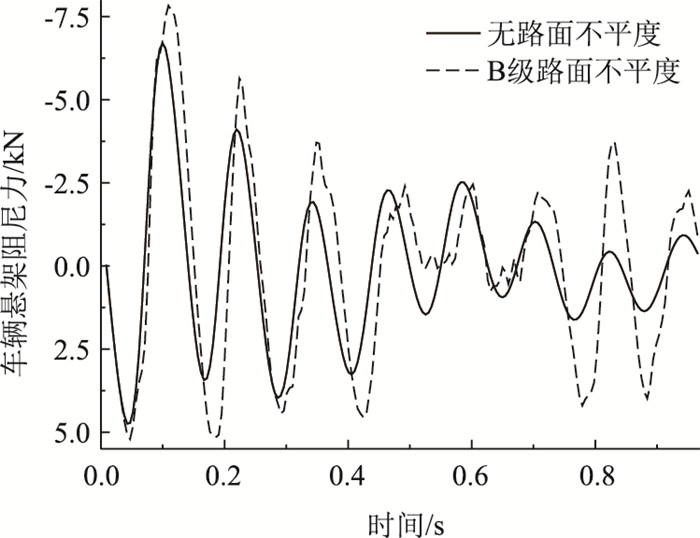
由图 19和图 20可知,添加B级路面不平度,车辆悬架弹力与阻尼力均增大,车辆振动明显,车-桥耦合动力效应增强。未添加不平度,最小和最大车辆悬架弹力分别为36.178,59.322 kN,变化幅度为63.973%;添加B级路面不平度,最小和最大悬架弹力分别为33.738,60.859 kN,变化幅度为80.387%。
|
| 图 19 不同路面等级车辆悬架弹力 Fig. 19 Elastic force of vehicle suspension in different road grades |
| |
|
| 图 20 不同路面等级悬架阻尼力 Fig. 20 Damping force of vehicle suspension in different road grades |
| |
5.3.4 纵梁跨中
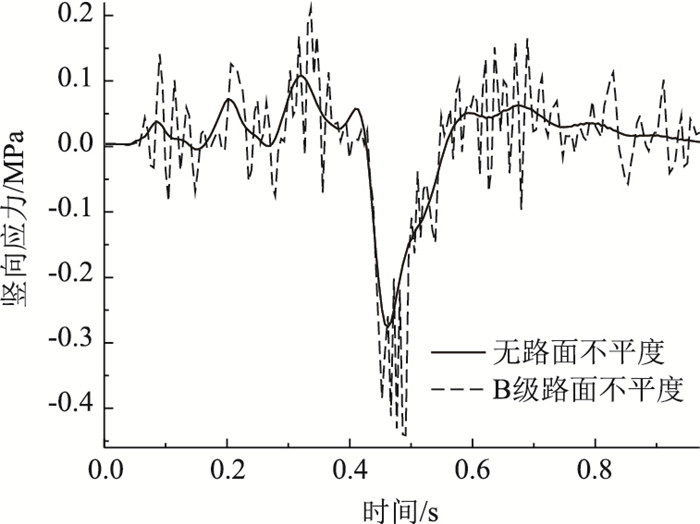
由图 21可知,未添加不平度,纵梁跨中最大竖向拉应力为0.105 MPa,最大竖向压应力为0.282 MPa;添加B级路面不平度,纵梁跨中最大竖向拉应力为0.209 MPa,最大竖向压应力为0.449 MPa,分别比未添加不平度增大99.048%、59.220%。
|
| 图 21 不同路面等级纵梁竖向应力 Fig. 21 Vertical stress of vertical beam in different road grades |
| |
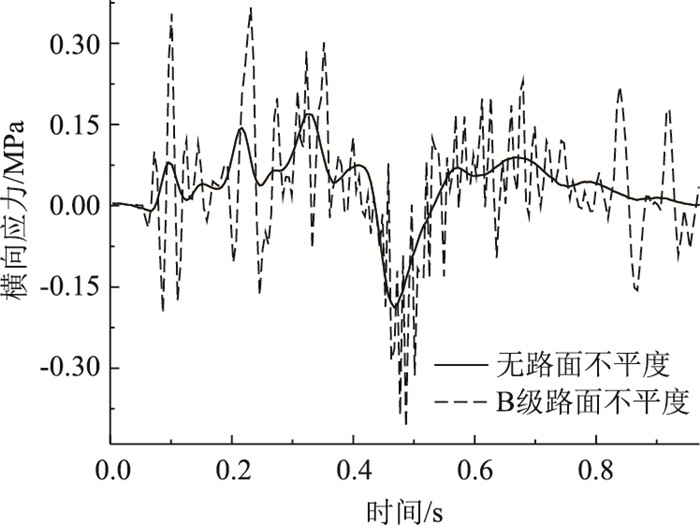
由图 22可知,未添加不平度,纵梁跨中最大横向拉应力为0.167 MPa,最大横向压应力为0.193 MPa;添加B级路面不平度,纵梁跨中最大横向拉应力为0.365 MPa,最大横向压应力为0.418 MPa,分别比未添加不平度增大118.563%, 116.580%。
|
| 图 22 不同路面等级纵梁横向应力 Fig. 22 Transverse stress of vertical beam in different road grades |
| |
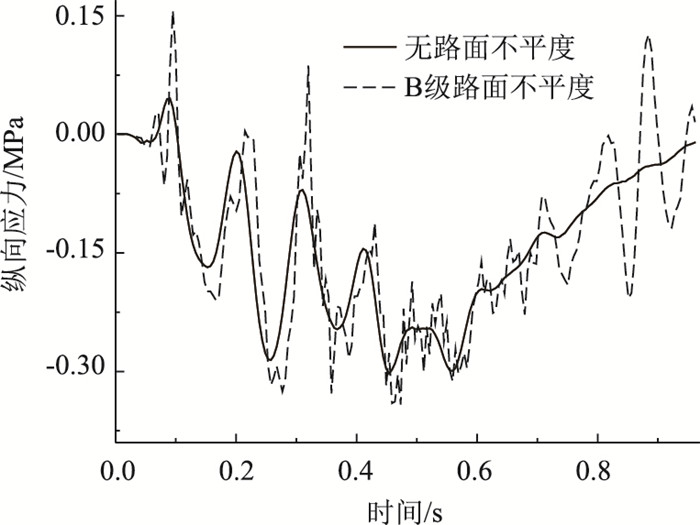
由图 23可知,未添加不平度,纵梁跨中最大纵向拉应力为0.046 MPa,最大纵向压应力为0.159 MPa;添加B级路面不平度,纵梁跨中最大纵向拉应力为0.309 MPa,最大纵向压应力为0.348 MPa,分别比未添加不平度增大245.652%, 118.868%。
|
| 图 23 不同路面等级纵梁纵向应力 Fig. 23 Longitudinal stress of vertical beam in different road grades |
| |
由以上分析可知,车辆动载作用下,纵梁跨中三向应力均以受压为主。受不平度以及车辆振动影响,当车辆接近或远离观测点时,纵梁跨中三向应力均表现出一定拉应力。桥面铺装层为B级路面不平度时,三向应力极值均增大,且应力时程曲线呈现出一定波动状态,应力状态复杂。
6 结论本研究建立两自由度四分之一车辆模型和简支桥模型,将桥面铺装层上面层跨中竖向应力仿真值与测量值对比,验证该模型, 进一步分析桥面铺装层三向应力状态以及不同路面等级下各项力学行为变化规律。结果表明:
(1) 车辆动载作用下,上面层跨中竖向应力测量值比仿真值大3.618%,表明所建车-路耦合动力模型具有一定可行性。
(2) 车辆动载作用下,三向压应力随桥面铺装层深度增加逐渐降低。
(3) 桥面铺装层为B级路面时,车-桥耦合效应增强,车辆与桥梁各项响应均增大。在桥梁运营期间应严格控制路面不平度,防止车辆以及桥梁耦合振动效应加剧。
(4) 因现场试验条件有限,无法保证改变车辆重量后相关测量数据的准确性,故只进行了车辆满载工况下,相关动力响应的测试与分析,并建立该工况有限元模型,验证其正确性。在后续研究中,将考虑多种工况,为理论分析提供更全面的参考。
| [1] |
侯忠明, 夏禾, 张彦玲, 等. 简谐荷载作用下组合梁动滑移响应分析[J]. 振动与冲击, 2016, 35(2): 18-23, 30. HOU Zhong-ming, XIA He, ZHANG Yan-ling, et al. Analytical Dynamic Slip Solution for Steel-concrete Composite Beams under Harmonic Load[J]. Journal of Vibration and Shock, 2016, 35(2): 18-23, 30. |
| [2] |
钱振东, 胡靖, 刘龑, 等. 浇注式沥青混凝土摊铺温度对钢箱梁力学响应及变形效应影响[J]. 土木工程学报, 2015, 48(2): 96-102. QIAN Zhen-dong, HU Jing, LIU Yan, et al. Influence of Gussasphalt Concrete Paving Temperature on Mechanical Responses and Deformation Effects of Steel Box Girder[J]. China Civil Engineering Journal, 2015, 48(2): 96-102. |
| [3] |
LIU Y, QIAN Z D, XIA K Q. Mechanical Response of Transmission Lines Based on Sliding Cable Element[J]. Journal of Central South University: English Edition, 2014, 21(8): 3370-3377. |
| [4] |
徐勋倩. 车-钢桥面铺装耦合振动系统动力效应分析[J]. 应用力学学报, 2009, 26(3): 501-506, 626. XU Xun-qian. Dynamic Analysis of Coupled Vibration System for Vehicle and Steel Bridge Deck Surfacing[J]. Chinese Journal of Applied Mechanics, 2009, 26(3): 501-506, 626. |
| [5] |
邓露, 段林利, 何维, 等. 中国公路车-桥耦合振动车辆模型研究[J]. 中国公路学报, 2018, 31(7): 92-100. DENG Lu, DUAN Lin-li, HE Wei, et al. Study on Vehicle Model for Vehicle-bridge Coupling Vibration of Highway Bridges in China[J]. China Journal of Highway and Transport, 2018, 31(7): 92-100. |
| [6] |
张彦玲, 冯康平, 刘欢, 等. 钢-混凝土组合梁动力特性试验研究[J]. 广西大学学报: 自然科学版, 2017, 42(1): 97-107. ZHANG Yan-ling, FENG Kang-ping, LIU Huan, et al. Experimental Research on Dynamic Responses of Steel-concrete Composite Beams[J]. Journal of Guangxi University: Natural Science Edition, 2017, 42(1): 97-107. |
| [7] |
魏志刚, 时成林, 刘寒冰, 等. 车辆作用下钢-混凝土组合简支梁动力特性[J]. 吉林大学学报: 工学版, 2017, 47(6): 1744-1752. WEI Zhi-gang, SHI Cheng-lin, LIU Han-bing, et al. Dynamic Characteristics of Steel-concrete Composite Simply Supported Beam under Vehicles[J]. Journal of Jilin University: Engineering and Technology Edition, 2017, 47(6): 1744-1752. |
| [8] |
张玥, 郭劲岑. 车辆荷载作用下钢板组合连续梁桥桥面板应力分析[J]. 应用力学学报, 2019, 36(3): 741-746. ZHANG Yue, GUO Jin-cen. Stress Analysis of Steel Plate Composite Continuous Girder Bridge Deck under Vehicle Load[J]. Chinese Journal of Applied Mechanics, 2019, 36(3): 741-746. |
| [9] |
李慧乐, 夏禾, 张楠, 等. 基于车桥耦合动力分析的桥梁动应力计算方法[J]. 中国铁道科学, 2015, 36(1): 68-74. LI Hui-le, XIA He, ZHANG Nan, et al. Calculation Method for Dynamic Stress of Bridge Based on Vehicle-Bridge Coupled Dynamic Analysis[J]. China Railway Science, 2015, 36(1): 68-74. |
| [10] |
杨永清, 程楚云, 张勇, 等. 车辆荷载对正交异性钢桥面疲劳细节应力影响研究[J]. 公路交通科技, 2019, 36(11): 50-58. YANG Yong-qing, CHENG Chu-yun, ZHANG Yong, et al. Study on Influence of Vehicle Loads on Fatigue Detail Stress of Orthotropic Steel Bridge Deck[J]. Journal of Highway and Transportation Research and Development, 2019, 36(11): 50-58. |
| [11] |
黄建龙, 解广娟, 刘正伟. 基于Mooney-Rivlin和Yeoh模型的超弹性橡胶材料有限元分析[J]. 橡塑技术与装备, 2008, 34(12): 22-26. HUANG Jian-long, XIE Guang-juan, LIU Zheng-wei. Finite Element Analysis of Super-elastic Rubber Materials Based on the Mooney-Rivlin and Yeoh Model[J]. China Rubber/Plastics Technology and Equipment, 2008, 34(12): 22-26. |
| [12] |
杨丰丰, 赵显新, 周兴林, 等. 轮胎-道路接触力动态加载装置的设计[J]. 机械设计与制造, 2018(8): 209-211. YANG Feng-feng, ZHAO Xian-xin, ZHOU Xing-lin, et al. Design of Tire Toad Contact Force Dynamic Loading Device[J]. Machinery Design & Manufacture, 2018(8): 209-211. |
| [13] |
王扬, 王丽娟, 路永婕, 等. 复杂移动轮胎力作用下沥青路面黏弹性力学行为模拟研究[J]. 振动与冲击, 2017, 36(15): 181-186. WANG Yang, WANG Li-juan, LU Yong-jie, et al. Simulation on Viscoelastic Behavior of Asphalt Pavement under Complex Moving Wheel Load[J]. Journal of Vibration and Shock, 2017, 36(15): 181-186. |
| [14] |
宿晓峰, 付平, 丁忠军, 等. 基于Abaqus软件的轮胎有限元模型建立及仿真分析[J]. 橡胶工业, 2019, 66(2): 121-127. SU Xiao-feng, FU Ping, DING Zhong-jun, et al. Establishment and Simulation Analysis of Tire Finite Element Model Based on Abaqus Software[J]. China Rubber Industry, 2019, 66(2): 121-127. |
| [15] |
哈斯巴根, 朱凌, 石琴, 等. 轮胎有限元建模过程优化及刚度特性仿真研究[J]. 合肥工业大学学报: 自然科学版, 2015, 38(7): 944-948. HA Si-ba-gen, ZHU Ling, SHI Qin, et al. Optimization of Finite Element Modeling of Tire and Simulation of Its Stiffness Characteristics[J]. Journal of Hefei University of Technology: Natural Science Edition, 2015, 38(7): 944-948. |
| [16] |
严明星, 王金昌. ABAQUS有限元软件在路面结构分析中的应用[M]. 杭州: 浙江大学出版社, 2016: 182-186. YAN Ming-xing, WANG Jin-chang. Application of ABAQUS Finite Element Software in Pavement Structure Analysis[M]. Hangzhou: Zhejiang University Press, 2016: 182-186. |
| [17] |
朱志辉, 王力东, 龚威, 等. 基于改进迭代模型的车-桥耦合系统竖向随机振动研究[J]. 湖南大学学报: 自然科学版, 2016, 43(11): 120-130. ZHU Zhi-hui, WANG Li-dong, GONG Wei, et al. Study on Vertical Random Vibration of Train-bridge Coupled System Based on Improved Iteration Model[J]. Journal of Hunan University: Natural Science Edition, 2016, 43(11): 120-130. |
| [18] |
钱振东, 刘云, 郑彬. 大跨度公铁两用斜拉桥公路桥面铺装层受力特点分析[J]. 土木工程学报, 2011, 44(6): 138-142. QIAN Zhen-dong, LIU Yun, ZHENG Bin. Mechanical Analysis of Steel Deck Pavement on Long Span Combined Road and Railway Cable-stayed Bridges[J]. China Civil Engineering Journal, 2011, 44(6): 138-142. |
| [19] |
侯忠明, 夏禾, 张彦玲, 等. 简谐荷载作用下组合梁动滑移响应分析[J]. 振动与冲击, 2016, 35(2): 18-23, 30. HOU Zhong-ming, XIA He, ZHANG Yan-ling, et al. Analytical Dynamic Slip Solution for Steel-concrete Composite Beams under Harmonic Load[J]. Journal of Vibration and Shock, 2016, 35(2): 18-23, 30. |
| [20] |
马如进, 崔传杰, 胡晓红, 等. 车辆激励下大跨径桥梁人非系统振动特性[J]. 振动与冲击, 2018, 37(12): 96-101. MA Ru-jin, CUI Chuan-jie, HU Xiao-hong, et al. Vibration Analysis of a Long-span Bridge with a Pedestrian and Non-motor System Caused by Vehicle Excitation[J]. Journal of Vibration and Shock, 2018, 37(12): 96-101. |
 2021, Vol. 38
2021, Vol. 38
