扩展功能
文章信息
- 王龙飞
- WANG Long-fei
- 桥梁混凝土收缩徐变效应时变过程综合仿真
- Comprehensive Simulation on Shrinkage and Creep Effects of Concrete in Bridges during Time-varying Process
- 公路交通科技, 2021, 38(2): 54-61
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 54-61
- 10.3969/j.issn.1002-0268.2021.02.008
-
文章历史
- 收稿日期: 2019-11-25
2. 长安大学 公路学院, 陕西 西安 710064
2. School of Highway, Chang'an University, Xi'an Shaanxi 710064, China
桥梁混凝土结构往往分阶段施工,为了缩短工期,混凝土加载龄期一般较早,所以结构收缩徐变效应较大。对于分阶段施工的超静定混凝土桥梁,收缩徐变会不断影响结构的内力和变形,对于钢混组合桥梁,还会导致截面应力不断重分布[1],所以规范要求必须考虑桥梁混凝结构收缩徐变效应[2]。由于徐变与结构混凝土应力有关,所以收缩徐变引起的应力不断变化会导致混凝土部分应力的加载龄期在不断改变,因此,要精确计算收缩徐变效应就应考虑其相互作用的整个时间变化过程。
收缩徐变是混凝土桥梁研究和设计的重要内容,所以,长期以来,许多学者对收缩徐变效应进行了多方面的研究。薛伟辰等[3]通过对6根预应力混凝土模型梁进行长期试验,系统研究了结构的徐变性能,并提出了徐变变形设计计算建议公式。Masovic等[4]设计了先简支后连续的钢筋混凝土试验梁,并对其收缩、徐变和裂缝发展等特性进行了4年以上的持续研究,获得了结构的长期性能和内力简化计算方法。刘沐宇等[5-6]研究了混凝土桥梁收缩徐变的时变性、不确定性以及有限元计算方法。项贻强等[7-9]对节段施工的连续刚构桥混凝土收缩徐变的时变特性进行了研究,并提出了相应的模拟计算方法。随着钢混组合结构的优势不断为人们所认识和接受,工程应用在不断增多,所以,对各种组合桥梁的受力性能和收缩徐变特性的研究也在快速发展。王春生等[10-12]对高强钢组合梁、管翼缘组合梁、波形钢腹板组合梁进行了试验研究,获得了相应的受力特性。樊健生等[13-14]对考虑收缩、徐变和裂缝影响的钢混组合梁长期性能进行了理论、试验和计算方法研究,提出了基于这些因素的计算模型,并得到试验验证。Al-deen等[15-16]通过研究钢混组合试验梁的长期性能,提出了考虑收缩徐变、材料特性和剪力键的结构计算方法、设计准则和长期变形评价方法。刘亚茹等[17-18]研究了钢混组合梁的长期变形、收缩徐变和剪力滑移等效应,获得结构相应特点并提出了有限元模拟计算方法。总体来看,对桥梁混凝土结构的收缩徐变效应等长期性能的研究一直在广泛开展,对其机理的认识不断加深,计算方法也在持续改进,获得了许多重要成果,指导了大批混凝土结构的设计和施工,保证了结构的安全和质量。但从结构设计工作的角度来看,目前很多收缩徐变效应分析方法比较复杂,不易为设计人员所掌握,常用的有限元分析软件,要么不能直接计算收缩徐变效应,要么不能考虑时变过程,要么不便与规范计算方法相衔接,因此,普通设计人员难以对结构进行精确的收缩徐变效应分析并严格按规范设计,影响了混凝土结构在这方面分析的有效性,需要有更广泛实用的计算方法。
本研究拟结合混凝土结构收缩徐变的特点和有限元法计算原理,利用APDL语言改进通用有限元软件ANSYS中一些计算功能,形成可以同时考虑混凝土收缩和徐变在整个时变过程中相互作用效应的仿真方法。由于ANSYS应用非常广泛,时变过程综合仿真分析方法使用简便,且可很好地与各种规范和试验研究相衔接,具有较强的实用性,便于推广应用。
1 增量法有限元计算原理徐变是混凝土在应力作用下应变不断变化的现象,当应力不大(不超过混凝土强度50%)时,具有对应力线性叠加的特点,根据试验研究及工程经验,已提出了多种基于老化理论和先天理论的徐变模型。收缩是混凝土随着时间的增长而出现不断增大的压缩应变,与结构应力无关,其变化规律可认为与徐变相似。混凝土规范中一般会给出收缩徐变的经验模型。
由于收缩徐变效应随时间不断变化,对钢混组合结构和超静定结构,会导致截面应力重分布和变化的次内力,非常复杂,其理论方程[19]如下:
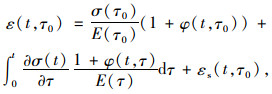
|
(1) |
式中,ε为含收缩徐变总应变;σ为应力;E为弹性模量;φ为徐变系数;εs为收缩应变;τ0为初始加载龄期;τ为加载龄期;t为计算龄期。
显然,该方程并不能直接积分求解,引入老化系数(即为狄辛格法),再通过微分方法或代数方法可求解。但是实际工程结构往往很复杂,有很多施工阶段和体系转换,采用狄辛格法计算非常困难,甚至不可能完成。随着计算机和有限元技术的发展,利用有限元法对结构进行分析越来越普遍,有限元法不仅可较好地解决复杂计算问题,也容易掌握,实际应用极为方便。参考相关的有限元法文献[20],易得到适合收缩徐变效应分析的增量法有限元计算原理。
假设结构处于线弹性状态,仅考虑弹性内力、徐变和收缩效应。在某一时段tn内,单元应变增量为:
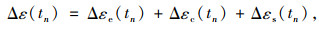
|
(2) |
式中,Δεe(tn)为单元内力变化引起的弹性应变增量;Δεc(tn)为单元徐变应变增量;Δεs(tn)为单元收缩应变增量,则应力增量为:
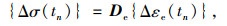
|
(3) |
式中,De为弹性矩阵,可得时段tn的切线矩阵:
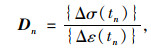
|
(4) |
于是单元外力、徐变和收缩效应节点荷载增量分别为:
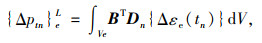
|
(5) |
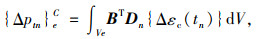
|
(6) |
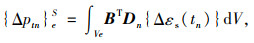
|
(7) |
式中,B为应变矩阵,单元切线刚度可表示为:
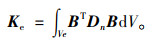
|
(8) |
将各单元节点荷载增量集合起来,形成结构总体平衡方程为:
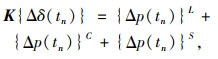
|
(9) |
式中,{Δδ(tn)}为节点位移增量。这样,可求出节点位移增量,再计算应变增量,再由式(2)、(3)得到应力增量,然后各时段累加,即可得到所有时段的整体应力:
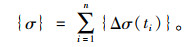
|
(10) |
从整个过程可以看出,有限元法思路简洁明了,容易理解,一个时段接一个时段地计算,符合结构整个受力时间演变过程,极便于对考虑施工阶段、体系转换和收缩徐变的结构进行时变过程仿真分析。
2 基于ANSYS的综合仿真方法ANSYS是国际著名的大型通用有限元软件,获得世界众多专业技术协会认可,广泛应用在各工程行业的科研、开发、设计、施工等领域,同时,该软件提供了APDL,UPFs等多种二次开发工具,可依需要高效扩充有限元计算功能。但是目前ANSYS有限元软件并没提供专门的混凝土收缩徐变效应计算模块,不能直接分析,但它提供了具有时变特性的金属蠕变计算准则和温度效应计算方法,通过二次开发后,可对混凝土收缩徐变效应进行分析。
2.1 徐变效应仿真计算可利用ANSYS中的金属蠕变计算准则来计算徐变效应,选取显式分析中C6=0时的计算准则:
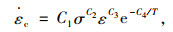
|
(11) |
式中,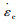
由上文的增量法有限元计算原理可知,只要确定了tn时段徐变应变增量就可以求出相应效应。假设该时段有效应力不变,根据徐变系数定义,可得:
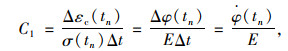
|
(12) |
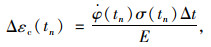
|
(13) |
式中,Δt为tn时段的时间长度; Δφ(tn)为tn时段徐变系数增量; 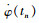
按照规范,通常混凝土初始加载龄期确定后,徐变系数对时间的变化模型是确定的,所以其任意时刻的变化率也是可知的,所以利用式(12)、式(13),有限元法就可以进行徐变效应计算。值得注意的是,徐变系数模型确定后,按初始加载龄期可准确计算后续加载的徐变系数变化率,不受后期加载大小影响,只需确定后续加载相对初始加载时间间隔,因此,本方法对具有施工阶段、体系转换、组合梁和超静定结构等有复杂时变过程的结构进行徐变效应分析,具有很大的优势。
2.2 收缩效应仿真计算收缩应变与应力无关,随着时间的增长而不断增大,这显然与结构持续降温相似,所以在ANSYS中可采用降温计算的方法来进行收缩效应分析。
首先通过混凝土材料、结构尺寸和使用环境确定混凝土结构的收缩时变模型,利用tn时段的起、终点时间求出该时段的收缩应变,计算出相应的降温值,再施加于混凝土结构上,就可以分析收缩效应。tn时段计算式如下:
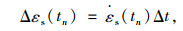
|
(14) |
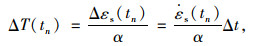
|
(15) |
式中,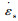
根据以上的收缩、徐变效应计算方法,可以看出,收缩徐变效应均是每个时段的函数,确定了时段,即可确定相应的效应。ANSYS具有荷载步计算功能,每一个荷载步相当于一个时段,利用其强大的二次开发功能,将每一时段的收缩徐变作用输入每一荷载步中,然后一步一步进行计算,就可以得到任一时间的含收缩、徐变的综合效应,综合仿真方法整个计算过程与结构实际受力时间演化过程极为相似。
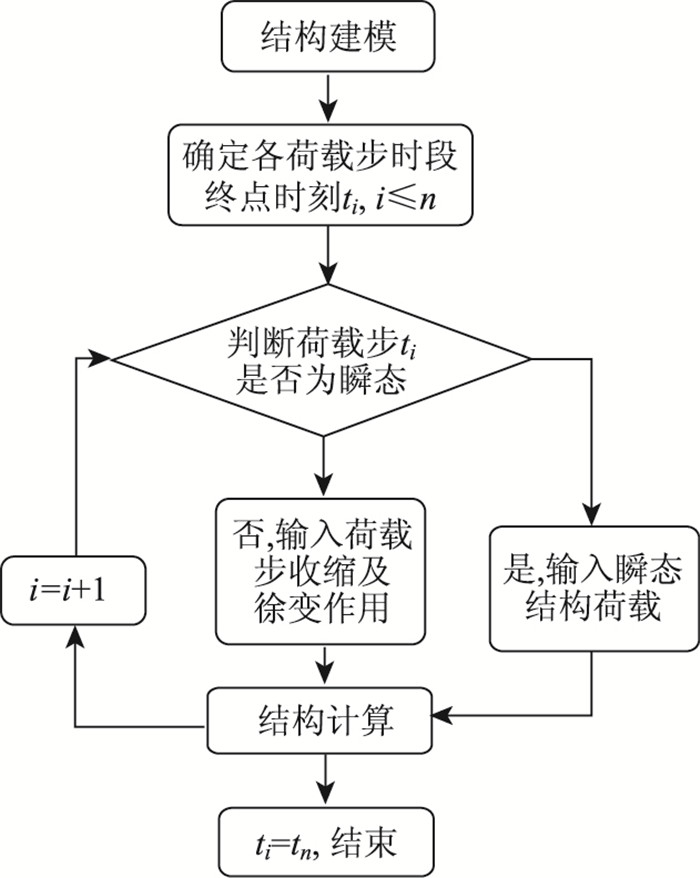
利用ANSYS中的APDL语言将整个计算过程编制成命令流,由计算机自动进行,非常方便,具体流程如图 1所示,关键步骤说明如下:
|
| 图 1 时变过程综合仿真流程 Fig. 1 Flowchart of comprehensive simulation during time-varying process |
| |
(1) 时段划分。由于收缩徐变均先期影响较大,所以时间分段时,前期较小,后期可较大。对于有施工阶段和体系转换的结构,应将其设置成瞬时时段,在ANSYS中建立数组输入所有时间节点,便于计算时调取。
(2) 收缩作用输入。利用收缩应变时变模型计算各时段的收缩应变增量,转化为各时段的降温量,编制成相应命令流。
(3) 徐变作用输入。按徐变系数时变模型计算各时段的徐变系数增量,形成各时段的C1值,编制成相应命令流。
(4) 对收缩徐变作用的输入,应尽量统一为时段的连续函数,充分利用ANSYS中的循环和判断命令,编制成系统的命令流,让程序自动计算。
3 与规范的衔接综合仿真方法可很方便地与各种设计规范相衔接,对结构的收缩徐变效应进行模拟计算,下面以公路桥梁规范[21]为例进行衔接应用。
3.1 徐变效应文献[21]提供的公式如下:
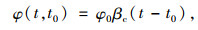
|
(16) |
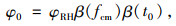
|
(17) |
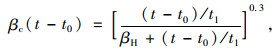
|
(18) |
式中,φ0为名义徐变系数,结构确定后,式(17)的计算参数均可以确定,是常数,同时βH也为常数;t0为加载时的混凝土龄期,t1=1 d。fcm为混凝土平均立方体抗压强度。
显然,规范公式是对时间的连续函数,并具有连续导数,也就是徐变系数变化率为:
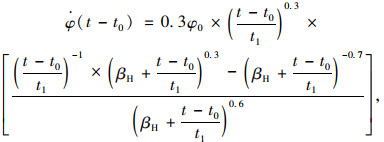
|
(19) |
将其代入式(12)即可直接计算徐变效应。
3.2 收缩效应文献[21]提供了如下公式:
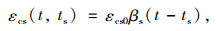
|
(20) |
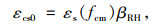
|
(21) |
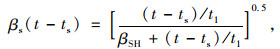
|
(22) |
式中,εcs0为名义收缩系数,结构确定后,式(21)的计算参数均可以确定,是常数,同时βSH也为常数; ts为收缩开始时的混凝土龄期,t1=1 d。
同样,规范公式具有对时间的连续导数,也就是收缩应变率为:
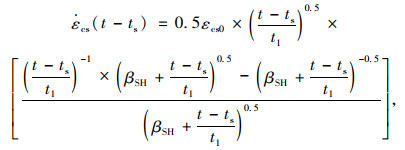
|
(23) |
将其代入式(15),即可求出各时段的降温值,从而计算结构收缩效应。混凝土收缩徐变效应综合计算时,将两种作用同时输入。当进行施工阶段、体系转换的结构计算时,应注意各阶段徐变、收缩龄期时间的协调。
4 算例验证 4.1 规范方法算例为了验证综合仿真方法的正确性,拟设计算例。由于要考虑整个时变过程,也为了便于理论计算,算例设计成方形受压柱,截面边长2 m,柱高10 m,采用C50混凝土,底部固结。分三阶段向柱端施加均布荷载,每阶段均增加5 MPa, 不计方柱重力荷载。初期加载龄期14 d,二期为44 d,三期为134 d,整个计算时间长度360 d。采用3个工况计算收缩徐变效应,分别为阶段荷载+收缩作用、阶段荷载+徐变作用、阶段荷载+徐变作用+收缩作用。
用理论方法和综合仿真方法计算各工况的收缩、徐变和荷载效应在计算时间长度的变化过程,并进行比较。理论和综合仿真计算均采用桥梁规范[21]提供的收缩徐变模型。环境年平均相对湿度取55%,收缩开始龄期3 d,徐变开始加载龄期为14 d。理论计算按天进行,分别形成3个工况整个时间过程的收缩徐变效应曲线。模拟计算利用ANSYS有限元软件进行,采用SOLID65单元模拟方柱实体(见图 2),施加阶段面荷载,整个计算时间分为71个荷载步,按上文方法计算各参数,利用APDL语言编制整个时变过程计算命令流。

|
| 图 2 混凝土柱ANSYS有限元模型 Fig. 2 Finite element model of concrete column in ANSYS |
| |
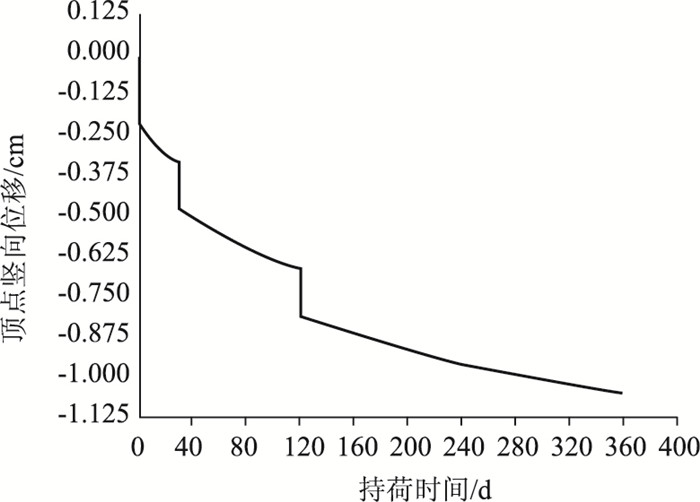
经计算,在ANSYS中可得到柱顶位移时间变化曲线,其中工况3的位移时变曲线见图 3,该图为软件计算结果截图,横坐标为持荷时间(d),纵坐标为顶点竖向位移(cm),可以看出模拟计算结果具有明显的阶段加载特点,同时整个变化过程中,初期收缩徐变效应变化较快,后期变化较慢,与混凝土收缩徐变效应特性相符。
|
| 图 3 工况3顶点位移时变曲线 Fig. 3 Curve of displacement vs. time in case 3 |
| |
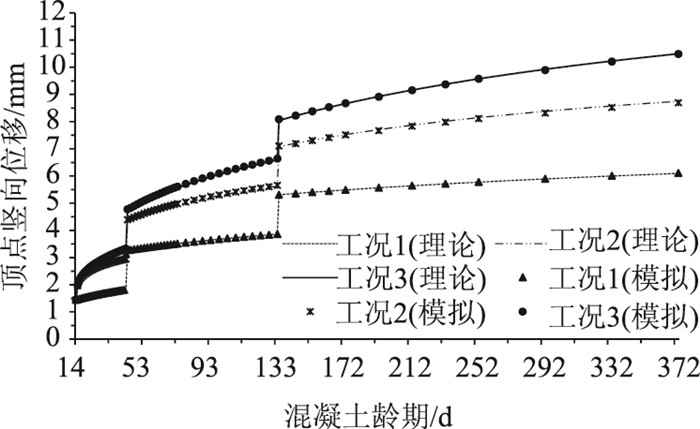
图 4为3个工况理论计算与模拟计算的柱顶位移时间变化曲线,可以看出,3个工况阶段加载效应和收缩徐变效应均很明显,模拟计算与理论计算偏差在整个时变过程中前期略大于后期。由表 1可以看出,前期最大偏差不超过3%,后期不大于0.6%,整个时变过程二者吻合很好。
|
| 图 4 各工况顶点位移时变过程对比(模拟/理论) Fig. 4 Comparison of displacement of top point during time-varying process in different cases (simulating/theory) |
| |
| 工况 | 名称 | 各龄期(d)顶点竖向位移/mm | |||||
| 19 | 48 | 99 | 144 | 234 | 374 | ||
| 1 | 理论 | 1.532 | 3.319 | 3.675 | 5.358 | 5.710 | 6.098 |
| 模拟 | 1.529 | 3.326 | 3.677 | 5.359 | 5.716 | 6.110 | |
| 偏差/% | -0.2 | 0.2 | 0.5 | 0.5 | 0.1 | 0.2 | |
| 2 | 理论 | 2.294 | 4.490 | 5.281 | 7.204 | 8.015 | 8.748 |
| 模拟 | 2.363 | 4.530 | 5.304 | 7.191 | 7.982 | 8.697 | |
| 偏差/% | 3 | 0.9 | 0.4 | -0.2 | -0.4 | -0.6 | |
| 3 | 理论 | 2.377 | 4.920 | 6.057 | 8.214 | 9.377 | 10.498 |
| 模拟 | 2.447 | 4.968 | 6.097 | 8.224 | 9.376 | 10.489 | |
| 偏差/% | 2.9 | 1.0 | 0.7 | 0.1 | 0.1 | -0.1 | |
从算例的各工况模拟计算时变过程结果对比可以看出,综合仿真方法计算过程及精度均较好,可以计算具有复杂施工阶段的收缩徐变时变过程综合效应,容易衔接规范,使用简便,很适合于设计分析。
4.2 试验研究算例文献[22]中对4片无黏结预应力缩尺模型梁进行了为期1年的徐变试验,其中1#梁为普通混凝土,其余均为不同参量的粉煤灰高性能混凝土。在此取1#梁与粉煤灰参量40%的4#梁进行模拟计算验证。
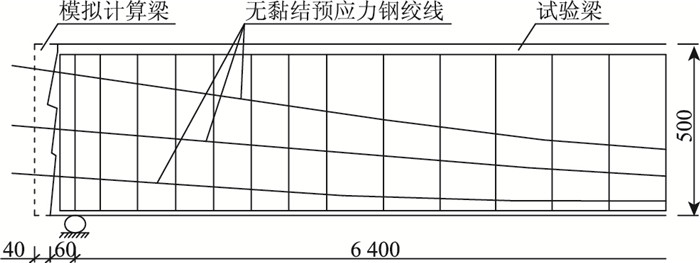
模型梁依据铁路标准图中的32 m跨简支梁制作,缩尺比例为1∶5,试验梁长6.52 m,模拟计算梁取6.6 m,无黏结预应力筋根据标准图布置采用3根ϕ15.2钢绞线,半跨模型梁立面如图 5所示,梁端及跨中截面如图 6所示。
|
| 图 5 模型梁立面示意图(单位:mm) Fig. 5 Schematic diagram of elevation of model beams (unit: mm) |
| |
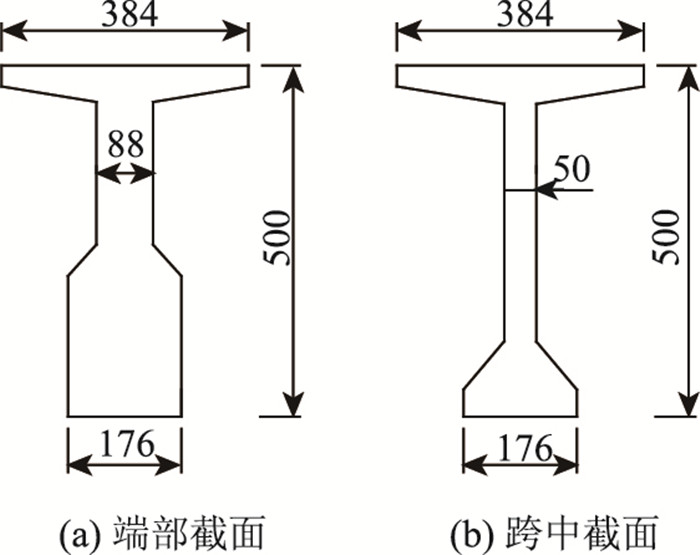
|
| 图 6 模型梁截面示意图(单位:mm) Fig. 6 Schematic diagram of cross-section of model beams (unit: mm) |
| |
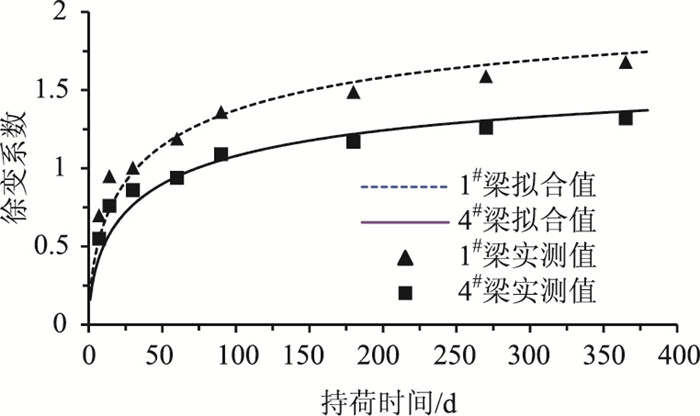
1#梁加载龄期为36 d,此时弹性模量为48.3 GPa;4#梁加载龄期为33 d,此时弹性模量为51.9 GPa。通过百分表测量的试验梁跨中挠度时间变化,计算徐变系数实测值见图 7。文献[22]中给出的徐变系数拟合公式如下:
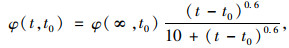
|
(24) |
式中,φ(∞, t0)为徐变系数终级值,1#梁为2.24,4#梁为1.76。两片模型梁的徐变系数拟合值时程曲线见图 7,前期拟合值与实测值相差较大,后期较为接近。
|
| 图 7 模型梁徐变系数时程图(拟合/实测) Fig. 7 Curves of creep coefficient of model beams vs. time (fitting/test) |
| |
由于文献[22]根据试验提出了1#梁和4#梁的徐变系数拟合公式,该公式为时间的连续函数,且具有连续导数,导数见式(25),所以适合采用综合仿真方法对结构在整个时变过程中的徐变效应进行分析。
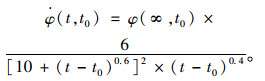
|
(25) |
计算时,混凝土均采用SOLID65单元模拟,材料特性采用试验值,由于试验徐变系数已考虑钢筋影响,所以模拟不计钢筋,无黏结预应力筋采用LINK10单元模拟,通过耦合设置来释放预应力钢绞线切向约束,利用初应力施加预应力,计算模型见图 8。自初始加载开始,试验持荷时间为365 d,分为64个荷载步,通过综合仿真方法编制整个时变过程计算命令流。

|
| 图 8 模型梁ANSYS有限元模型 Fig. 8 Finite element model of model beam in ANSYS |
| |
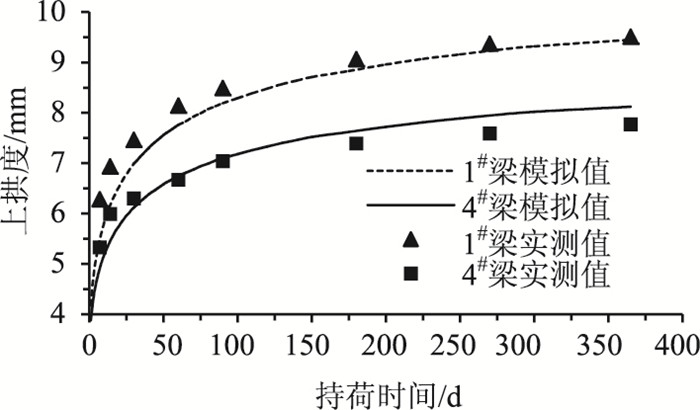
利用文献[22]提出的拟合徐变系数,在无黏结预应力作用下,利用本研究有限元综合仿真方法计算的1#梁和4#梁跨中上拱度在1年内的时变过程曲线如图 9所示,可以看出变化趋势与徐变系数时间变化相似,明确反映了徐变效应的规律。与两片试验模型梁跨中上拱度的实测值进行比较,可以看出,在初期模拟值与实测值相差较大,终期二者吻合较好,整个变化趋势相似。因为拟合徐变系数初期拟合值与实测值相差较大,所以前期效应也相差较大,如果根据实测值变化情况采用分段函数来拟合,徐变效应在整个时变过程的吻合情况将会更好。
|
| 图 9 模型梁跨中上拱度时程图(模拟/实测) Fig. 9 Curves of upward camber in middle span of model beams vs. time (simulating/test) |
| |
从以上两个算例可以看出,只要规范和试验研究所提出的结构混凝土收缩徐变模型具有对时间的函数关系,就可以利用综合仿真方法计算结构在整个时变过程的收缩徐变效应,因此,综合仿真方法与规范和试验研究均衔接方便,可广泛地应用在结构试验、设计和监测等领域,具有良好的实用性。
5 结论(1) 在混凝土结构的整个时变过程中,综合仿真方法计算的收缩、徐变效应与理论计算结果和试验徐变效应吻合较好,且结果精确度较高,说明方法完全可行。
(2) 综合仿真方法将复杂的收缩徐变和施工阶段过程分成一系列的时段,作用过程转化为时间函数,适合有限元法中的荷载步分析,并容易编制成命令流,让计算机自动计算,使用极简便。
(3) 只要收缩徐变模型是时间的函数或分段函数,均可采用综合仿真方法,尤其适合收缩徐变模型对时间有连续导数的情况,容易与规范及试验研究相衔接,所以方法具有较广泛的实用性。
| [1] |
聂建国, 陶慕轩, 吴丽丽, 等. 钢-混凝土组合结构桥梁研究新进展[J]. 土木工程学报, 2012, 45(6): 110-122. NIE Jian-guo, TAO Mu-xuan, WU Li-li, et al. Advances of Research on Steel-concrete Composite Bridges[J]. China Civil Engineering Journal, 2012, 45(6): 110-122. |
| [2] |
JTG/T D64-01-2015, 公路钢混组合桥梁设计与施工规范[S]. JTG/T D64-01-2015, Specifications for Design and Construction of Highway Steel-concrete Composite Bridge[S]. |
| [3] |
薛伟辰, 胡于明, 王巍. 预应力混凝土梁徐变性能试验[J]. 中国公路学报, 2008, 21(4): 61-66. XUE Wei-chen, HU Yu-ming, WANG Wei. Experiment on Creep Behaviors of Prestressed Concrete Beams[J]. China Journal of Highway and Transport, 2008, 21(4): 61-66. |
| [4] |
MASOVIC S R, STOVIC S R, PECIC N P. Research of Long-term Behaviour of Non-prestressed Precast Concrete Beams Made Continuous[J]. Engineering Structures, 2014, 70: 11-22. |
| [5] |
刘沐宇, 卢志芳. 混凝土桥梁时变性和不确定性下的收缩徐变分析[J]. 华中科技大学学报: 自然科学版, 2011, 39(10): 116-120. LIU Mu-yu, LU Zhi-fang. Shrinkage and Creep Analysis of Concrete Bridges with Time Variation and Uncertainty Considered[J]. Journal of Huanzhong University of Science and Technology: Natural Science Edition, 2011, 39(10): 116-120. |
| [6] |
黄海东, 向中富. 混凝土结构非线性徐变计算方法研究[J]. 工程力学, 2014, 31(2): 69-102. HUANG Hai-dong, XIANG Zhong-fu. Nonlinear Creep Analysis Method for Concrete Structures[J]. Engineering Mechanics, 2014, 31(2): 69-102. |
| [7] |
项贻强, 何晓阳. 考虑非均匀收缩徐变的PC箱梁桥时变性能[J]. 哈尔滨工业大学学报, 2015, 47(12): 117-122. XIANG Yi-qiang, HE Xiao-yang. Time-dependent Behavior of PC Box Girder Bridges Considering Non-uniform Shrinkage and Creep[J]. Journal of HARBIN Institute of Technology, 2015, 47(12): 117-122. |
| [8] |
陈太聪, 苏成, 韩大建. 桥梁节段施工过程中混凝土收缩徐变效应仿真计算[J]. 中国公路学报, 2003, 16(4): 55-58. CHEN Tai-cong, SU Cheng, HAN Da-jian. Simulation Calculation of Creep and Shrinkage Effects of Concrete during Segmental Construction of Bridges[J]. Journal of Highway and Transportation Research and Development, 2003, 16(4): 55-58. |
| [9] |
曾丁, 谢峻, 郑晓华, 等. 桥梁短期实测数据修正高强混凝土收缩徐变模型与长期挠度预测[J]. 公路交通科技, 2014, 31(11): 72-77. ZENG Ding, XIE Jun, ZHENG Xiao-hua, et al. Prediction of Long-term Deflection and Correction of Shrinkage and Creep Model of High-strength Concrete of Bridge Based on Measured Short-term Data[J]. China Journal of Highway and Transport, 2014, 31(11): 72-77. |
| [10] |
王春生, 朱经纬, 翟晓亮, 等. 双管翼缘钢-混凝土新型组合梁抗弯性能试验[J]. 中国公路学报, 2017, 30(3): 147-158. WANG Chun-shen, ZHU Jing-wei, ZHAI Xiao-liang, et al. Flexural Behavior Experiment of Steel and Concrete Composite Girder with Double Tubular Flanges[J]. China Journal of Highway and Transport, 2017, 30(3): 147-158. |
| [11] |
李立峰, 王芳, 刘志才. 体外预应力波形钢腹板组合箱梁徐变性能研究[J]. 湖南大学学报: 自然科学版, 2008, 35(5): 1-5. LI Li-feng, WANG Fang, LIU Zhi-cai. Study on the Creep Behavior of Externally Prestressed Composite Beam with Corrugated Steel Webs[J]. Journal of Hunan University: Natural Science Edition, 2008, 35(5): 1-5. |
| [12] |
刘晓刚, 樊健生, 聂建国. 预应力波形钢腹板组合梁承载力及变形研究[J]. 建筑结构学报, 2013, 34(增1): 28-32. LIU Xiao-gang, FAN Jian-sheng, NIE Jian-guo. Research on Flexual Capacity and Deflection of Prestressed Concrete Beams with Corrugated Steel Webs[J]. Journal of Building Structures, 2013, 34(S1): 28-32. |
| [13] |
樊健生, 聂建国, 王浩. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(I): 试验及计算[J]. 土木工程学报, 2009, 42(3): 8-15. FAN Jian-sheng, NIE Jian-guo, WANG Hao. Long-term Behavior of Composite Beams with Shrinkage, Creep and Cracking (I): Experiment and Calculation[J]. China Civil Engineering Journal, 2009, 42(3): 8-15. |
| [14] |
樊健生, 聂鑫, 李全旺. 考虑收缩、徐变及开裂影响的组合梁长期受力性能研究(II): 理论分析[J]. 土木工程学报, 2009, 42(3): 16-22. FAN Jian-sheng, NIE Xin, LI Quan-wang. Long-term Behavior of Composite Beams with Shrinkage, Creep and Cracking(Ⅱ): Theoretical Analysis[J]. China Civil Engineering Journal, 2009, 42(3): 16-22. |
| [15] |
AL-DEEN S, RANZI G, VRCELJ Z. Full-scale Long-term Experiments of Simply Supported Composite Beams with Solid Slabs[J]. Journal of Constructional Steel Research, 2011, 67(3): 308-321. |
| [16] |
AMADIO C, FRAGIACOMO M, MACORINI L. Evaluation of the Deflection of Steel-concrete Composite Beams at Serviceability Limit State[J]. Journal of Constructional Steel Research, 2012, 73: 95-104. |
| [17] |
刘亚茹, 刘小洁. 考虑徐变的钢-混凝土组合箱梁的变形计算[J]. 铁道科学与工程学报, 2015, 12(2): 317-322. LIU Ya-ru, LIU Xiao-jie. Long-term Deflection of Steel-concrete Composite Box-beam due to Creep[J]. Journal of Railway Science and Engineering, 2015, 12(2): 317-322. |
| [18] |
杨飞, 谭少华, 刘殿元, 等. 组合连续梁桥收缩徐变与滑移效应的影响分析[J]. 公路交通科技, 2017, 34(增1): 1-6, 14. YANG Fei, TAN Shao-hua, LIU Dian-yuan, et al. Analysis on Influence of Shrinkage Creep and Slip Effect on Composite Continuous Beam Bridge[J]. Journal of Highway and Transportation Research and Development, 2017, 34(S1): 1-6, 14. |
| [19] |
项海帆. 高等桥梁结构理论[M]. 北京: 人民交通出版社, 2001. XIANG HAI-fan. Advanced Theory of Bridge Structure[M]. Beijing: China Communications Press, 2001. |
| [20] |
王勖成. 有限单元法[M]. 北京: 清华大学出版社, 2003. WANG Xu-cheng. Finite Element Method[M]. Beijing: Tsinghua University Press, 2003. |
| [21] |
JTG 3362-2018, 公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. JTG 3362-2018, Code for Design of Highway Reinforced Concrete and Prestressed Concrete Bridges and Culverts[S]. |
| [22] |
罗许国, 钟新谷, 戴公连. 无粘结预应力粉煤灰高性能混凝土桥梁收缩与徐变变形试验研究[J]. 工程力学, 2006, 23(7): 136-141. LUO Xu-guo, ZHONG Xin-gu, DAI Gong-lian. Experimental Study on the Deformations for Shrinkage and Creep of Beams in Non-glued Prestressed High Performance Fly Ash Concrete Bridges[J]. Engineering Mechanics, 2006, 23(7): 136-141. |
 2021, Vol. 38
2021, Vol. 38
