扩展功能
文章信息
- 周德泉, 肖灿, 冯晨曦, 曹之烨, 周毅
- ZHOU De-quan, XIAO Can, FENG Chen-xi, CAO Zhi-ye, ZHOU Yi
- 侧向堆载下斜桩长度影响斜-直双排桩受力响应试验研究
- Experimental Study on Influence of Inclined Pile Length on Mechanical Response of Inclined-straight Double-row Piles under Lateral Surcharge
- 公路交通科技, 2021, 38(2): 24-32
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 24-32
- 10.3969/j.issn.1002-0268.2021.02.004
-
文章历史
- 收稿日期: 2020-02-10
2. 中交四航工程研究院有限公司, 广东 广州 510230;
3. 湖南中大检测技术集团有限公司, 湖南 长沙 410000;
4. 保利长大工程有限公司, 广东 广州 510620
2. CCCC Fourth Harbor Engineering Institute Co., Ltd., Guangzhou Guangdong 510230, China;
3. Hunan Zhongda Testing Technology Group Co., Ltd, Changsha Hunan 410000, China;
4. Poly Changda Engineering Co., Ltd., Guangzhou Guangdong 510620, China
国家大力加强基础设施建设,高速公路(铁路)的部分路段不得不修建在深厚软土地基上,路堤荷载传递至坡脚将产生水平荷载,路基可能产生滑移破坏。作者[1]提出在坡脚设置斜-直双排桩,发挥斜桩的“支撑”作用,以有效抵抗软土侧向移动,但其工作机制尚不清晰。
斜桩和双排桩工作机制方面,国内外开展了很多研究,例如,Zhang[2]利用离心机进行了砂土中倾斜单桩与倾斜群桩的水平荷载特性离心试验研究,试验结果表明其影响主要在于桩体布置、倾斜角度和土体密实度。Meyerhof等[3]通过室内模型试验研究了倾斜桩在倾斜荷载作用下的受力与变形特征,认为桩的承载力特性取决于荷载倾斜度、桩体倾斜角。Ghasemzadeh等[4]采用数值模拟软件对倾斜斜桩群在轴向和横向静载作用下相互作用系数的变化进行了研究,发现间距与桩径比值的增大会使倾斜桩的相互作用系数减小。龚健等[5]对软土地基中的微型桩进行了水平荷载试验,认为微型桩可以较好地抵抗水平荷载,尤其是斜桩基础能有效地减小水平荷载所产生的位移。双排桩结构因为其整体刚度大、侧向位移小、施工简捷等优点[6-8]成为新型水平承载桩体结构,目前广泛应用于基坑支护[9-11]、边坡抗滑[12-13]等工程中。何颐华[14]通过室内模型试验及工程分析, 研究了双排桩变形、内力分布特征,发现双排桩水平位移及内力比单排桩明显减少。杨德健[8]通过数值模拟软件对双排桩支护结构进行分析,认为双排桩支护结构具有较大的侧向刚度。郑刚[15]以考虑桩土相互作用的平面杆系有限元双排桩分析模型研究了双排桩与土的相互作用问题。申永江[16]基于Winker弹性地基梁模型和极限平衡条件,提出了柔性双排长短组合桩滑坡推力的计算方法。但是,斜桩和双排桩组合形成的斜-直双排桩工作机制少见报道。
本研究采用室内模型箱[17],测试在侧向加载下外侧斜桩(倾斜度为9°)4种长度时斜桩、直桩的水平土压力、桩身应变及直桩水平位移,分析其水平土压力、弯矩及直桩水平位移的变化规律及斜-直双排桩的破坏模式,推动路堤坡脚处斜-直双排桩工作机制的深入研究与推广应用。
1 模型试验概况 1.1 基本原理斜-直双排桩受力响应的影响因素很多,例如,桩和连梁的几何尺寸、外侧斜桩倾斜度、桩体刚度、地质条件、荷载大小等,仅依靠单次模型试验获得相应变化规律非常困难。本试验将4组斜-直双桩(其他均相同,仅有外侧斜桩长度不同)对称设置在承压板两侧,模拟实际工程中的斜-直双排桩单元,以砂土模拟均质地基,居中的承压板分级受载模拟路堤填筑。
承压板两侧对称布置的4组斜-直双桩必然承受对称荷载的作用,其受力响应的差异必然源自外侧斜桩长度的不同。
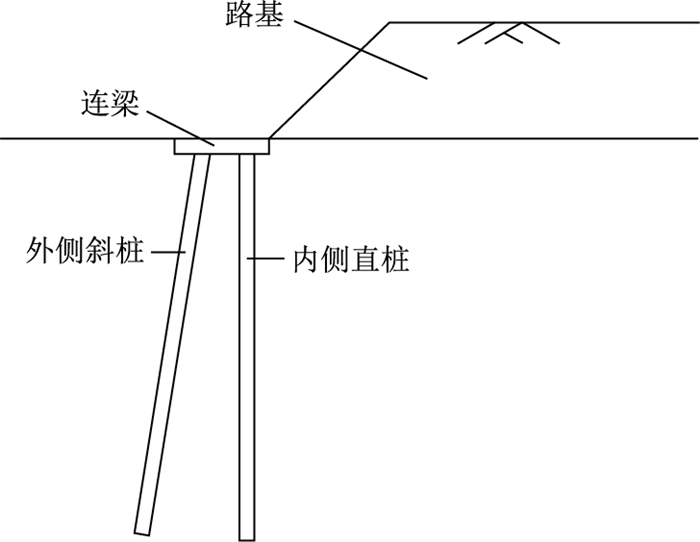
1.2 模型试验设计与安装在坡脚设置的斜-直双排桩[1]由内侧直桩、外侧斜桩和连梁3部分构成,见图 1。
|
| 图 1 斜-直双排桩 Fig. 1 Inclined-straight double-row piles |
| |
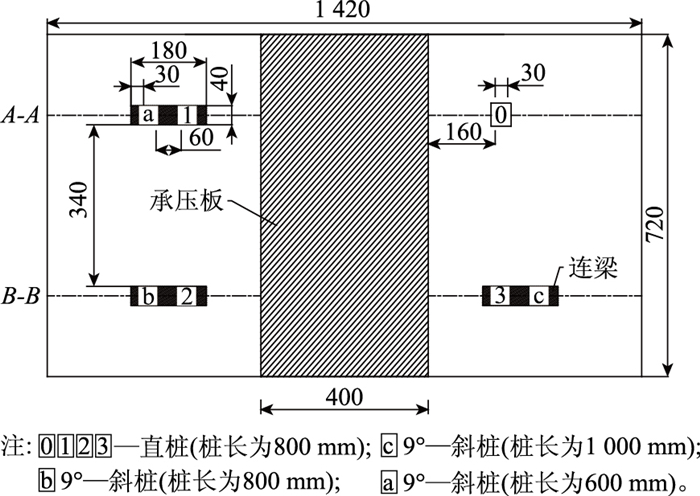
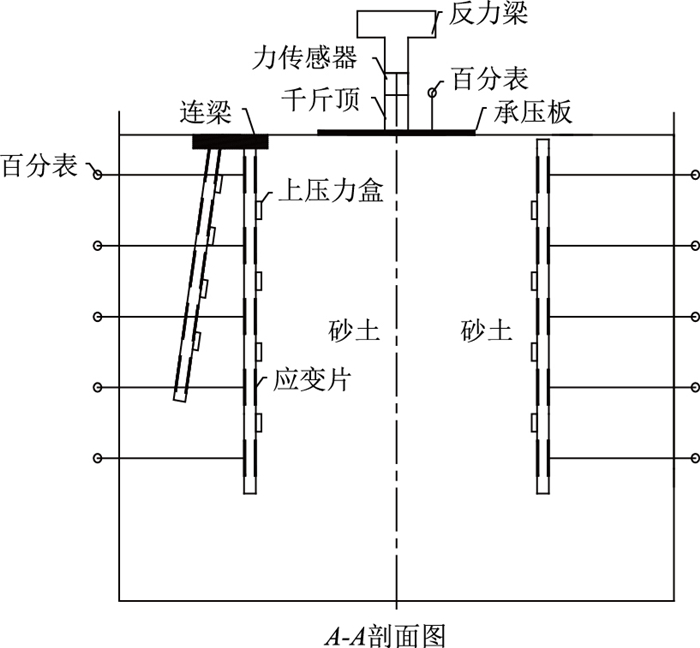
本次试验是在钢条焊接而成的框架及外加钢化玻璃与木板所组成的模型槽[16]中进行,尺寸为1 420 mm×720 mm×1 100 mm(长×宽×高)。槽内直桩与斜桩的平面、立面布置见图 2、图 3。
|
| 图 2 模型试验平面图(单位: mm) Fig. 2 Plan view of model test(unit: mm) |
| |
|
| 图 3 模型试验立面图 Fig. 3 Elevation view of model test |
| |
试验所用7根模型桩使用木板制成方形模具并充填水泥砂浆制作养护而成。模型桩边长均为30 mm,方形截面,斜桩和直桩分成4个组合(每个组合代表1种桩长比,即:斜桩与直桩桩身长度之比,4种桩长比分别为0,0.75,1,1.25),4根直桩(桩号为Z0,Z1,Z2,Z3)长度均为800 mm,3根斜桩(桩号为Xa,Xb,Xc)的倾斜角均为9°(桩轴线与垂线之间夹角),Xa,Xb,Xc对应桩长分别是600,800,1 000 mm。斜桩与直桩的顶部使用连梁连接,连梁采用硬质纸壳模具现浇水泥砂浆制作、养护成型。具体参数见表 1。
| 组合 | 桩号 | 直桩长度/mm | 斜桩长度/mm | 桩长比 | 边长/mm | 弹性模量/GPa |
| 组合0 | Z0 | 800 | — | 0 | 30 | 12.69 |
| 组合1 | Z1,Xa | 800 | 600 | 0.75 | 30 | 12.69 |
| 组合2 | Z2,Xb | 800 | 800 | 1 | 30 | 12.69 |
| 组合3 | Z3,Xc | 800 | 1 000 | 1.25 | 30 | 12.69 |
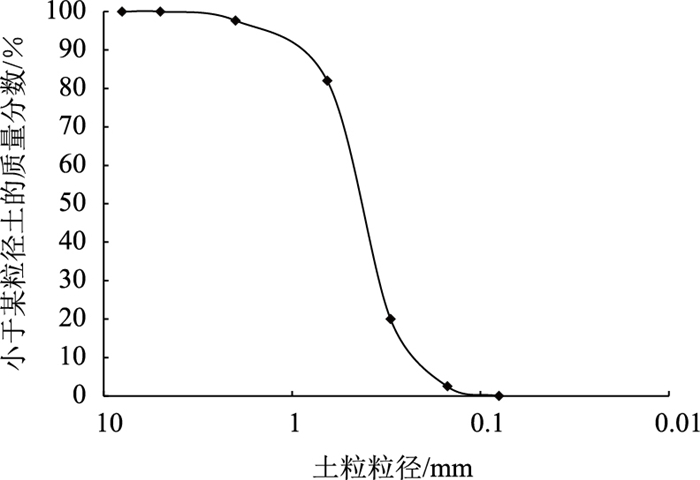
天然河砂经纱网过筛后晾干,形成模型土,其最大粒径5 mm,天然密度为1.84 g·cm-3,相对密度为2.68,含水率约为2%,不均匀系数Cu=5.5,曲率系数Cc=2.7,级配良好,级配曲线见图 4。在安装前,先填土250 mm厚度达到设计桩底,桩的位置按图 2、图 3固定,然后用塑料条和透明胶固定模型桩的中部与顶部。模型土采用砂雨法填筑,即:让砂土从一定高度下落,其势能转变为动能,砂土颗粒相互冲击碰撞、重新排列,这样,模型土填筑过程类似于砂土自然沉积。填土达到一定深度后再拆除固定用塑料条,确保填土时桩的位置、倾斜角稳定。完成填筑后,静置1个月,让模型土自重沉降。
|
| 图 4 模型土级配曲线 Fig. 4 Gradation curve of model soil |
| |
整个试验由千斤顶加载,通过固定式反力梁提供反力,压力传感器放置于千斤顶与反力梁之间,通过力传感器精准测得每级荷载大小。试验参照《建筑地基处理技术规范》(JGJ 79—2012)进行,此次试验分7级进行加载,测力计测得荷载大小依次为9.5,23.3,32.4,39.8,49.0,60.4,70.7 kN,在720 mm×400 mm×20 mm(长×宽×厚)的承压钢板上进行,模拟路基加载,并获得承压钢板侧面(相当于路堤坡脚处)不同桩长比的斜-直双桩土压力、弯矩及直桩侧移变化规律。
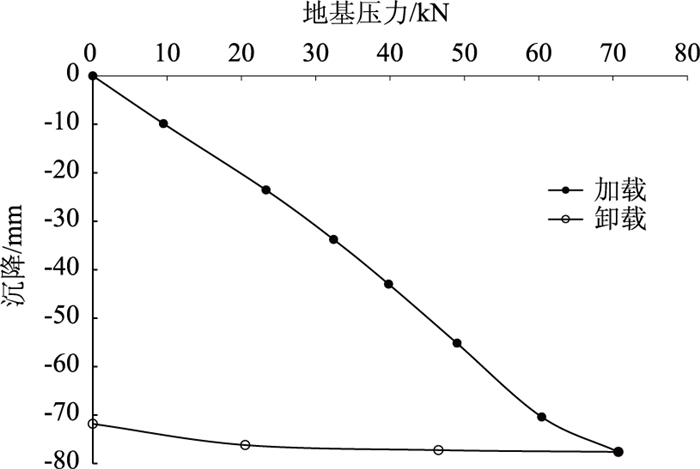
2 模型试验结果与分析 2.1 模型土加卸载沉降曲线特征图 5为模型土压力P-沉降s曲线。加载曲线整体呈上凸型。卸载前期体现不可恢复的塑性变形,模型土回弹很小,直至卸载至0才有明显的弹性变形,此规律与岩、土体的压缩-回弹曲线特征类似[18],说明本次试验的加载、位移测试系统可靠。
|
| 图 5 模型土的压力-沉降曲线 Fig. 5 Curve of pressure vs. settlement of model soil |
| |
2.2 斜-直双排桩水平土压力变化规律 2.2.1 内侧直桩水平土压力变化规律
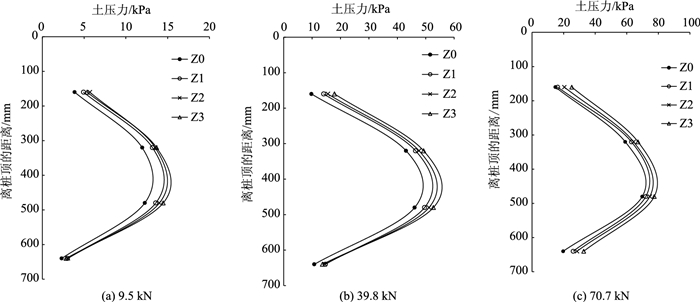
4根直桩的土压力盒布设位置相同,离桩顶分别为160,320,480,640 mm。通过TDS-530应变仪测读桩侧土压力应变,通过标定的压力-微应变关系曲线求得桩侧土压力。加载前期荷载(9.5 kN,相当于路基承受的垂直荷载,下同)、中期荷载(39.8 kN)、后期荷载(70.7 kN)时,4组斜-直双桩的直桩水平土压力p-离桩顶面距离z的变化曲线(简称p-z曲线,下同)变化规律如图 6所示。分析发现:
|
| 图 6 内侧直桩水平土压力变化规律 Fig. 6 Variation of horizontal soil pressure of inner straight piles |
| |
(1) 各直桩内侧土压力沿桩身自上而下均先增大后减少。加载过程中,土压力在距桩顶0.6H处出现峰值,桩身中部增长率较大,说明坡脚处各直桩中部对路基加载产生的侧向土压力较敏感。
(2) 相同荷载作用下,内侧直桩Z0,Z1,Z2,Z3水平土压力由小到大依次增大,说明内侧直桩水平土压力随外侧斜桩长度增大而增大,但增大幅度不大。
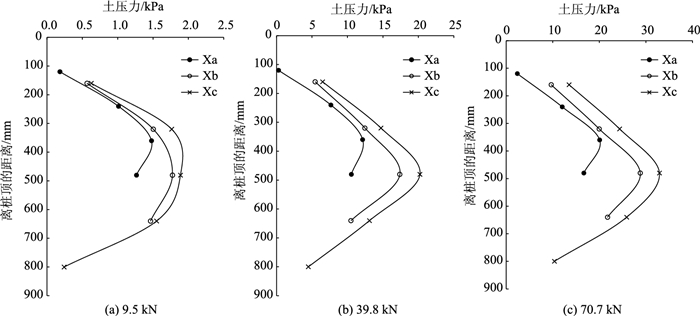
2.2.2 外侧斜桩水平土压力变化规律因斜桩的长度不一,土压力盒布设位置也不同。对于斜桩Xa,Xb,土压力盒离桩顶距离依次为0.2L,0.4L,0.6L,0.8L,对于斜桩Xc,则为0.17L,0.33L,0.50L,0.67L,0.83L。在加载9.5,39.8,70.7 kN时,3组斜-直双桩的斜桩p-z曲线变化规律如图 7所示。分析发现:
|
| 图 7 外侧斜桩水平土压力变化规律 Fig. 7 Variation of horizontal soil pressure of outer inclined piles |
| |
(1) 斜桩Xa,Xb,Xc内侧土压力沿桩身自上而下先增大后减少,Xa,Xb桩在0.6L处出现峰值、Xc在0.5L处出现峰值, 这与直桩内侧土压力沿桩身分布规律类似。
(2) 相同荷载作用下,斜桩相同位置处内侧土压力从大到小依次为:Xa,Xb,Xc,说明外侧斜桩的水平土压力随外侧斜桩长度增大而增大。
(3) 对比直桩土压力变化规律发现,内侧直桩与外侧斜桩的水平土压力峰值比均大于2。分析认为,内侧直桩对外侧斜桩的桩前土压力具有“遮帘效应”。
2.3 直桩水平位移变化规律准确测试各直桩水平位移的方法是:在直桩Z0,Z1,Z2,Z3外侧不同深度处(距离桩顶分别为80,240,400,560 mm)使用丙烯酸结构胶粘贴尺寸为60 mm×25 mm×3 mm(长×宽×厚)钢片,钢片在桩的横向外伸表面处,用于粘贴PVC管,PVC管端部粘贴磁铁片(用于加载时吸附百分表探针而不与之产生相对滑移),这样,PVC管端部与钢片牢固粘结。百分表伸长杆伸入PVC管并抵住磁铁片。在内侧直桩桩身外侧钢片处安装5个百分表,以测读桩身水平位移变化。
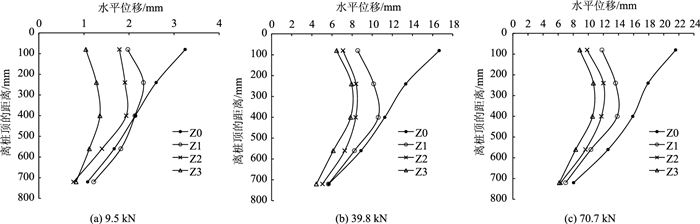
图 8为4组斜-直双排桩在模型土受压9.5,39.8,70.7 kN时,内侧直桩水平位移y与离桩顶距离z的变化曲线。分析发现:
|
| 图 8 内侧直桩水平位移变化规律 Fig. 8 Variation of horizontal displacement of inner straight piles |
| |
(1) 直桩桩身各点水平位移均随荷载的增大而逐渐增大,且桩底侧移最小,但不为0。其中,Z0桩与Z1,Z2,Z3桩侧移变化规律存在明显差异,表现在Z0桩侧移量从桩顶至桩底依次减小,即桩身上部侧移量明显大于下部,顶部侧移量最大,而Z1桩、Z2桩、Z3桩侧移最大值出现在桩身中部,侧移量由桩中向两端逐渐减小,且桩底的侧移递减速率稍大。相同荷载作用下,直桩桩身整体侧移由大到小排序为Z0,Z1,Z2,Z3,说明内侧直桩的水平位移随外侧斜桩长度增大而减小。
(2) 单直桩Z0整体侧移呈“平移+绕桩底转动”,而斜-直双桩中直桩Z1,Z2,Z3表现出“平移+中部向外弯曲”,其顶部水平位移远远小于Z0,说明外侧斜桩能有效减少内侧直桩的水平位移。
2.4 斜-直双排桩弯矩变化规律 2.4.1 内侧直桩弯矩变化规律4组斜-直双桩的直桩内外侧应变片位置相同,离桩顶距离分别为0.1H,0.3H,0.5H,0.7H,0.9H。通过TDS-530应变仪测读桩身距离桩顶相同位置正、反两侧应变量,则桩身截面弯曲应变为:
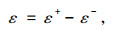
|
(1) |
式中,ε+为拉应变;ε-为压应变。
由材料力学弯矩计算公式可得到相应位置弯矩,弯矩计算公式为:
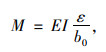
|
(2) |
式中,E为桩体弹性模量;I为截面对中性轴y的惯性矩;b0为测点的间距。
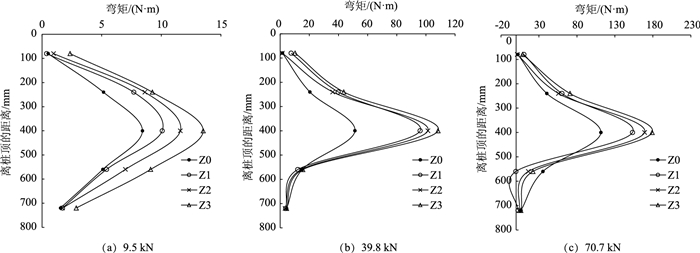
加载9.5,39.8,70.7 kN时,4组斜-直双桩的直桩弯矩M-离桩顶的距离z的变化曲线(简称M-z曲线,下同)变化规律如图 9所示,分析发现:
|
| 图 9 内侧直桩弯矩变化规律 Fig. 9 Variation of bending moment of inner straight piles |
| |
(1) 4根直桩桩身弯矩均沿桩身自上而下先增大后减小,且峰值均呈现在桩身中部,随着荷载的增加,桩身中部的弯矩增长率相较其他部位更大,说明在路基荷载作用下,坡脚处直桩中部弯矩对加载较为敏感,工程中应加大直桩中部抗弯刚度。
(2) 相同荷载作用下,直桩弯矩由小到大依次为:Z0,Z1,Z2,Z3,说明直桩桩身弯矩随外侧斜桩的长度增大而增大。
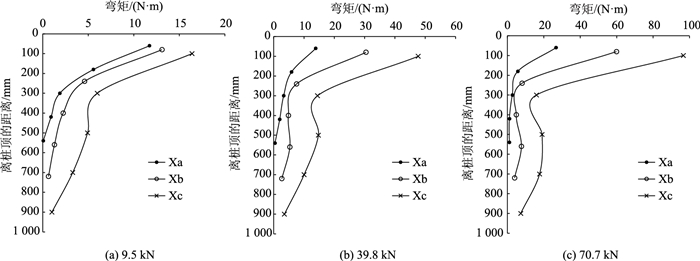
2.4.2 外侧斜桩弯矩变化规律3根斜桩应变片布设位置离桩顶距离分别为0.1L,0.3L,0.5L,0.7L,0.9L。在加载9.5,39.8,70.7 kN时,3根斜桩M-z曲线变化规律如图 10所示。分析发现:
|
| 图 10 外侧斜桩弯矩变化规律 Fig. 10 Bending moment variation of outer inclined piles |
| |
(1) 3根斜桩桩身弯矩变化规律相似,峰值均位于桩身顶部(距离桩顶0.1L处),弯矩沿桩身从上到小先快速减少,经拐点(距离桩顶0.3L处)呈缓慢减小趋势变化后,至桩身底部达到最小值。由此推断,在坡脚处斜-直双排桩水平支挡结构中,路基荷载先传递到直桩,再由连梁和土体传递到外侧斜桩,致使近连梁斜桩桩顶处作用效果较大,而对斜桩桩身下部作用效果不明显。推理认为,斜-直双排桩中斜桩桩顶处易发生弯曲破坏。
(2) 相同荷载作用下,外侧斜桩桩身弯矩由小到大依次为:Xa,Xb,Xc。随着荷载的增大,因桩长比增大而影响的桩顶处弯矩差值越来越明显,在后期荷载70.7 kN时,桩顶处Xc弯矩值超过了Xa弯矩值的4倍。这说明桩长比增大对其斜桩桩顶处弯矩值影响较大,更易使其在桩顶处发生弯曲破坏。
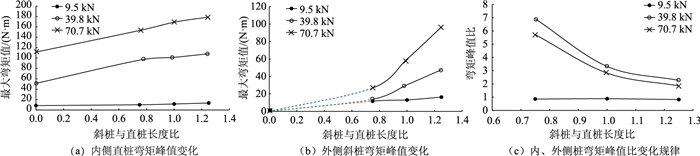
2.4.3 直桩、斜桩弯矩峰值变化规律内侧直桩弯矩峰值与外侧斜桩弯矩峰值之比简称弯矩峰值比。图 11为斜-直双排桩内侧直桩弯矩峰值与外侧斜桩弯矩峰值之比的变化曲线。分析认为:
|
| 图 11 斜-直双排桩桩身弯矩峰值变化规律 Fig. 11 Variation of peak bending moment of inclined-straight double-row piles |
| |
(1) 内侧直桩弯矩峰值、外侧斜桩弯矩峰值均随斜桩与直桩长度比(桩长比)的增大而增大,外侧斜桩弯矩峰值的增长率更大,说明桩长比增大将使内侧直桩、外侧斜桩弯曲程度越大、更容易发生弯曲破坏,这种效果随着荷载的增加而越明显。
(2) 在低荷载(9.5 kN)阶段,桩长比对斜-直双排桩内侧直桩弯矩峰值与外侧斜桩弯矩峰值比影响较小,比值较接近;高荷载(39.8,70.7 kN)阶段,弯矩峰值之比随桩长比增大而减小,且比值均大于2,推理认为,斜-直双排桩中,内侧直桩桩中先发生弯曲破坏,外侧斜桩桩顶处后破坏,且桩长比越大,外侧斜桩对内侧直桩的支撑作用越好。
3 斜-直双排桩破坏模式表 2为侧向加载下斜-直双桩受力响应,图 12、13所示为4个组合模型试验完成后破坏实物图。图 12~13表明:单直桩Z0未见破坏;组合1破坏裂缝出现在直桩桩身中上部(直桩出现两条裂缝,分别位于距桩顶302,335 mm处);组合2直桩与斜桩均出现破坏裂缝,分别位于直桩中部与斜桩桩顶(直桩与斜桩裂缝分别位于距桩顶355,32 mm处);组合3破坏模式与组合2一致,破坏裂缝分别位于直桩中部与斜桩桩顶(直桩与斜桩裂缝分别位于距桩顶351,48 mm处)。结合侧移、土压力、弯矩分析认为:
| 直桩水平位移 | 土压力 | 桩身弯矩 | 破坏位置 | |
| 0 | 桩顶处呈现峰值 | 0.6倍桩长处呈现峰值 | 0.5倍桩长处呈现峰值 | 未出现破坏 |
| 0.75 | 1.桩身中部呈现峰值; 2.桩身水平位移及峰值均随桩长比增大而减小,且均小于单桩。 |
直(斜)桩中下部呈现峰值 直(斜)桩水平土压力峰值随桩长比增大而增大。 |
1.直、斜桩弯矩峰值分别出现在桩中、桩顶处; 2.直、斜桩弯矩峰值比大于2; 3.直(斜)桩弯矩峰值随桩长比增大而增大; 4.直(斜)桩弯矩峰值比随桩长比增大而减小。 |
直桩0.4倍桩长处 |
| 1 | 同上 | 同上 | 同上 | 1.直桩0.4倍桩长处; 2.斜桩0.05倍桩长处。 |
| 1.75 | 同上 | 同上 | 同上 | 同上 |

|
| 图 12 斜-直双排桩破坏整体图 Fig. 12 Overall pictures of failure of inclined-straight double-row piles |
| |

|
| 图 13 斜-直双排桩破坏局部图 Fig. 13 Partial pictures of failure of inclined-straight double-row piles |
| |
(1) 单直桩未出现破坏,但是产生较大的水平位移,具有较低稳定性。斜-直双桩的水平位移较小,整体稳定性较高。
(2) 顶斜-直双桩中,所有直桩中部偏上、斜桩(Xb, Xc)部均出现裂缝,斜桩Xa未见破坏。这说明路堤荷载作用下,坡脚处内侧直桩对外侧斜桩具有“遮帘效应”,外侧斜桩对内侧直桩具有“斜撑作用”。砂土中斜-直双桩的破坏机制是,内侧直桩受到路堤荷载挤压而承受水平土压力和弯矩、产生水平移动和弯曲,并将荷载通过连梁和土体传递到外侧斜桩。荷载增大时,内侧直桩中部和外侧斜桩的顶部弯矩超过容许弯矩而开裂。内侧直桩先开裂破坏,外侧斜桩受到更大弯矩而随后破坏。外侧斜桩长度越长,内侧直桩顶部受到的约束作用越大、破坏荷载越小。
4 结论(1) 相同荷载作用下,单直桩内侧土压力较小,斜-直双桩内侧直桩水平土压力随外侧斜桩长度增大而增大,土压力峰值出现在直桩中下部;外侧斜桩水平土压力随其长度增大而增大,在桩身中下部出现峰值。内侧直桩水平土压力比外侧斜桩大、具有“遮帘效应”。
(2) 单直桩整体侧移呈“平移+绕桩底转动”,侧移峰值在桩顶处。斜-直双桩中直桩侧移表现出“平移+桩中朝外弯曲”,侧移峰值出现在桩身中部。外侧斜桩显著减少内侧直桩的侧移。内侧直桩侧移随着桩长比的增大而减小。实际工程中,可增大斜-直桩的桩长比来降低内侧直桩产生的侧移量。
(3) 内侧直桩桩身弯矩随外侧斜桩长度增大而增大,随着荷载增加,桩身中部对加载较为敏感。外侧斜桩桩身弯矩峰值位于桩身顶部。
(4) 路堤荷载作用下,砂土地基坡脚处斜-直双桩的内侧直桩中部、外侧斜桩顶部易发生弯曲破坏。直桩先破坏,斜桩后破坏。
(5) 增加外侧斜桩长度的工程效果是:内侧直桩的水平位移减小、内侧直桩弯矩峰值与外侧斜桩弯矩峰值之比(简称弯矩峰值比)减小。工程中,为了提高坡脚抗滑移能力,建议设置斜-直双排桩,并增加外侧斜桩的长度、使内侧直桩与外侧斜桩的抗弯刚度比大于2。
| [1] |
周德泉, 周果子. 一种加固倾斜软基的组合型复合地基: 中国, ZL 201621328014.7[P]. 2017-04-27. ZHOU De-quan, ZHOU Guo-zi. A Combined Composite Foundation for Strengthening Tilt Soft Foundation: China, ZL201621328014.7[P]. 2017-04-27. |
| [2] |
ZHANG L, MCVAY M C, LAI P W. Centrifuge Modelling of Laterally Loaded Single Battered Piles in Sands[J]. Canadian Geotechnical Journal, 1999, 36(6): 1074-1084. |
| [3] |
MEYERHOF G G YALCIN A S. Behaviour of Flexible Batter Piles under Inclined Loads in Layered Soil[J]. Canadian Geotechnical Journal, 1993, 30(2): 247-256. |
| [4] |
GHASEMZADEH H, TARZABAN M, HAJITAHERIHA M M. Numerical Analysis of Pile-soil-pile Interaction in Pile Groups with Batter Piles[J]. Geotechnical & Geological Engineering, 2018, 126(01): 1-27. |
| [5] |
龚健, 陈仁朋, 陈云敏, 等. 微型桩原型水平荷载试验研究[J]. 岩石力学与工程学报, 2004, 23(20): 3541-3546. GONG Jian, CHEN Ren-peng, CHEN Yun-min, et al. Prototype Testing Study on Micropiles under Lateral Loading[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(20): 3541-3546. |
| [6] |
万智, 王贻荪, 李刚. 双排桩支护结构的分析与计算[J]. 湖南大学学报: 自然科学版, 2001, 28(3): 116-120, 131. WAN Zhi, WANG Yi-sun, LI Gang. Analysis and Calculation of Retaining Structure with Double-row Piles[J]. Journal of Hunan University: Natural Sciences Edition, 2001, 28(3): 116-120, 131. |
| [7] |
王湛, 刘冰花. 双排桩计算方法探讨[J]. 东北地震研究, 2001, 17(2): 64-68. WANG Zhan, LIU Bing-hua. Research on Calculation Method for Double-piles[J]. Seismological Research of Northeast China, 2001, 17(2): 64-68. |
| [8] |
杨德健, 王铁成. 双排桩支护结构优化设计与工程应用研究[J]. 工程力学, 2010, 27(增2): 284-288. YANG De-jian, WANG Tie-cheng. Research on Optimum Design and Application of Double-row Pile Retaining Structure[J]. Engineering Mechanics, 2010, 27(S2): 284-288. |
| [9] |
邓小鹏, 陈征宙, 韦杰. 深基坑开挖中双排桩支护结构的数值分析与工程应用[J]. 西安工程学院学报, 2002, 24(4): 42-47. DENG Xiao-peng, CHEN Zheng-zhou, WEI Jie. Numerical Analysis and Application of Retaining Structure with Double-row Piles on Deep Excavation[J]. Journal of Xi'an Engineering University, 2002, 24(4): 42-47. |
| [10] |
林鹏, 王艳峰, 范志雄, 等. 双排桩支护结构在软土基坑工程中的应用分析[J]. 岩土工程学报, 2010, 32(增2): 331-334. LIN Peng, WANG Yan-feng, FAN Zhi-xiong, et al. Application and Analysis of Retaining Structure with Double-row Piles in Soft Ground Excavation Engineering[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S2): 331-334. |
| [11] |
陈师演, 何锦华. 双排桩支护结构在深基坑工程中的应用[J]. 建筑结构, 2019, 49(增1): 783-785. CHEN Shi-yan, HE Jing-hua. Application of Double-row Piles Retaining Structure in Deep Foundation Pit Project[J]. Building Structure, 2019, 49(S1): 783-785. |
| [12] |
刘鸣, 黄华, 韩冰, 等. 延安地区某边坡双排抗滑桩支护分析[J]. 长安大学学报: 自然科学版, 2011, 31(2): 63-67. LIU Ming, HUANG Hua, HAN Bing, et al. Analysis on Double-row Anti-slide Piles of Slope in Yanan[J]. Journal of Chang'an University: Natural Science Edition, 2011, 31(2): 63-67. |
| [13] |
邵广彪, 孙剑平, 崔冠科. 某永久边坡双排桩支护设计及应用[J]. 岩土工程学报, 2010, 32(增1): 215-218. SHAO Guang-biao, SUN Jian-ping, CUI Guan-ke. Design and Application of Double-row Pile Retaining Structures in a Permanent Slope[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(S1): 215-218. |
| [14] |
何颐华, 杨斌, 金宝森, 等. 双排护坡桩试验与计算的研究[J]. 建筑结构学报, 1996, 17(2): 58-66, 29. HE Yi-hua, YANG Bin, JIN Bao-sen, et al. A Study on the Test and Calculation of Double-row Fender Piles[J]. Journal of Building Structures, 1996, 17(2): 58-66, 29. |
| [15] |
郑刚, 李欣, 刘畅, 等. 考虑桩土相互作用的双排桩分析[J]. 建筑结构学报, 2004, 25(1): 99-106. ZHENG Gang, LI Xin, LIU Chang, et al. Analysis of Double-row Piles in Consideration of the Pile-soil Interaction[J]. Journal of Building Structures, 2004, 25(1): 99-106. |
| [16] |
申永江, 杨明, 项正良, 等. 柔性双排长短组合桩滑坡推力的计算方法[J]. 岩土力学, 2018, 39(10): 3597-3602. SHEN Yong-jiang, YANG Ming, XIANG Zheng-liang, et al. Calculation Method of Thrust Force on the Flexible Double Row Long-short Piles[J]. Rock and Soil Mechanics, 2018, 39(10): 3597-3602. |
| [17] |
周德泉, 罗坤, 冯晨曦, 等. 一种室内土工模型实验装置: 中国, ZL201520323607.3[P]. 2015-08-26. ZHOU De-quan, LUO Kun, FENG Chen-xi, et al. A Test Apparatus of Laboratory Geotechnical Model: China, ZL 201520323607.3[P].2015-08-26. |
| [18] |
周德泉, 谭焕杰, 徐一鸣, 等. 循环荷载作用下花岗岩残积土累积变形与湿化特性试验研究[J]. 中南大学学报: 自然科学版, 2013, 44(4): 1657-1665. ZHOU De-quan, TAN Huan-jie, XU Yi-ming, et al. Indoor Experimental Study for Accumulative and Wetting Deformation of Granite Residual Soil under Cyclic Loading[J]. Journal of Central South University: Science and Technology Edition, 2013, 44(4): 1657-1665. |
 2021, Vol. 38
2021, Vol. 38
