扩展功能
文章信息
- 李洛克, 刘海明, 张镇国, 曹鹏, 严圆
- LI Luo-ke, LIU Hai-ming, ZHANG Zhen-guo, CAO Peng, YAN Yuan
- 路用集料三维形貌的定量表征方法研究
- Study on Quantitative Characterization Method of 3D Morphology of Road Aggregate
- 公路交通科技, 2021, 38(2): 16-23
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 16-23
- 10.3969/j.issn.1002-0268.2021.02.003
-
文章历史
- 收稿日期: 2020-05-29
2. 中国航天科技集团公司第四研究院第四十一研究所 燃烧、流动和热结构国家重点实验室, 陕西 西安 710072;
3. 北京工业大学 建筑工程学院, 北京 100022;
4. 云南省公路科学技术研究院, 云南 昆明 650000
2. National Key Laboratory of Combustion, Flow and Thermo-structure, The 41st Institute of the 4th Academy of CASTC, Xi'an Shaanxi 710072, China;
3. School of Architecture and Civil Engineering, Beijing University of Technology, Beijing 100022, China;
4. Yunnan Provincial Highway Science and Technology Research Institute, Kunming Yunnan 650000, China
路用集料的三维轮廓形状、棱角特征和表面纹理粗糙程度,决定了沥青混凝土中集料骨架结构内颗粒间的接触与嵌锁能力,同时影响着沥青与集料在接触界面上的吸附作用。为表征岩石类集料的三维形貌特征,工程中常用游标卡尺法评价粗集料的形状特征,应用间隙率法和流动时间法评价细集料的棱角特征,根据加速磨光后的集料摩擦系数值评价集料表面粗糙纹理的耐磨耗抗滑性能[1]。然而,上述试验测试方法工作量大,存在人工操作误差的主观缺陷,同时无法定量分析集料颗粒的三维形貌特征。近年来,随着测量技术的不断发展,已有多种测量方法适用于获取岩石类材料表面的特征信息。其中,基于光学原理获取物体轮廓面特征信息的高精度非接触式测量技术,在岩石类材料表面形貌数据采集方面具有明显优势[2]。通过三维扫描设备能够快速地采集含有集料颗粒三维轮廓表面空间几何特征信息的扫描点云数据,为集料的实体重构与三维形态参数量化供了技术保障[3]。
基于上述原因,本研究通过集料三维轮廓面的扫描点云数据构建颗粒的数字化实体模型,采用6个相互独立的特征参数分别表征集料颗粒在不同层次的三维形貌特征。在此基础上,提出基于白光扫描点云数据的集料三维形貌特征参数分析与评价方法,探讨各类评价指标在定量分析过程中的适用性,研究试验样品集料三维形貌的评价标准。
1 集料的数字化三维重构基于白光干涉测量原理获取集料颗粒轮廓表面三维点云[4],使用配准与滤波后的三维坐标点阵重构集料的数字化实体模型,用于颗粒的三维形貌特征参数计算。
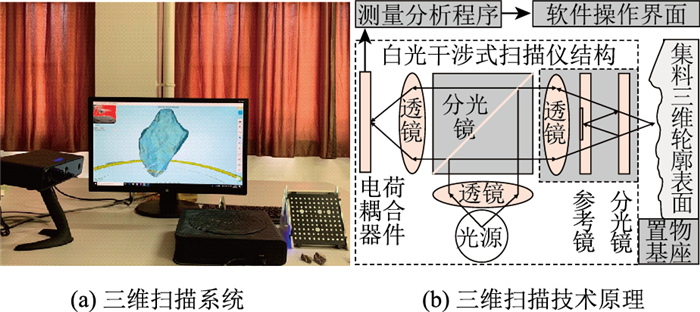
1.1 三维白光扫描使用EinScan-S型白光三维近景式高精度扫描仪,获取含有集料颗粒表面几何特征信息的点云数据(图 1(a))。在近景式三维扫描过程中,通过电荷耦合器件获取集料表面干涉条纹的多帧图像,用分析软件解算集料表面扫描点在扫描仪视觉坐标系中的三维坐标数据[5],技术原理如图 1(b)所示。
|
| 图 1 集料颗粒的三维扫描 Fig. 1 Three-dimensional scanning of aggregate particles |
| |
1.2 点云配准与去噪
以图 2(a)中的集料测试样品为例,为避免光源入射角度变化引起测试表面明暗差异所造成的点云数据偏差,对集料三维轮廓表面进行多角度采样后,在Imageware软件中应用ICP算法对多次扫描点云进行配准[6]。为剔除离群点和噪声,将配准合并数据导入PCL库,使用VoxelGrid滤波器进行降噪[7],在精简96%的点云数据量后,生成集料颗粒轮廓面的三维坐标点阵(图 2(b))。

|
| 图 2 集料颗粒的逆向三维重构 Fig. 2 Reverse 3D reconstruction of aggregate particle |
| |
1.3 曲面重构与实体构建
在Unigraphics NX软件中, 使用NURBS构面法将集料的三维坐标点阵拟合成NURBS曲面。在集料表面曲率变化较大的棱角处,采用分块生成法首先提取曲面边界线,然后使用边界线选取点集,最后利用边界线与点云拟合NURBS曲面(图 2(c))。曲面模型拟合完成后, 进行缝合与布尔运算,生成具有真实集料颗粒三维轮廓与表面形貌特征的数字化实体模型[8] (图 2(d))。
2 集料三维形貌的定量表征方法基于集料的三维点阵模型与数字化实体模型,采用相互独立的6个特征参数从不同角度评价集料颗粒的三维形貌特征。
2.1 集料颗粒形状表征方法(1) 整体形状特征
采用球度S评价集料的整体形状特征,反映颗粒轮廓是否紧凑[9]:
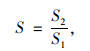
|
(1) |
式中,S1为集料颗粒的表面积;S2为集料同体积球体的表面积。
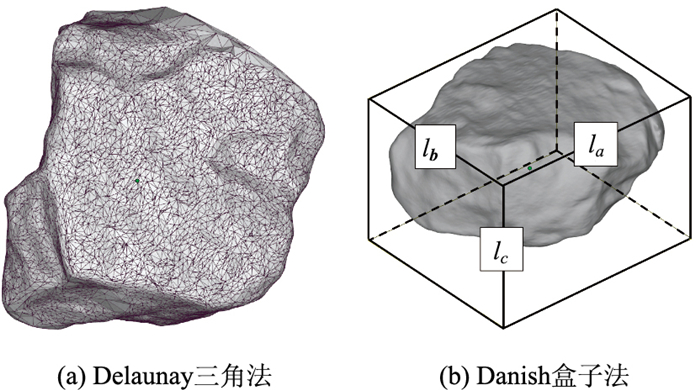
在UG软件中进行集料实体模型的Delaunay三角网格划分[10](图 3(a)),根据三角剖分算法获取颗粒的表面积S1和体积V1,对应的球体表面积为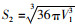
|
| 图 3 形状指标相关参数计算 Fig. 3 Calculation of relevant parameters of shape indicator |
| |
(2) 针片状特征
采用形状因子SF评价集料的针片状属性,反映颗粒趋近于针状、片状或是近矩形形态。
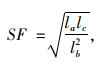
|
(2) |
式中,la为集料长轴尺寸;lb为集料的中轴尺寸;lc为集料的短轴尺寸。
通过Magics软件在集料三维点阵模型周围拟合矩形盒子,根据Danish法获得盒子体积最小时的3边参数为颗粒的三轴尺寸(图 3(b))[11]。
2.2 集料颗粒棱角性表征方法(1) 整体棱角特征
采用椭球度E描述集料颗粒的整体棱角特征[12]:
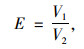
|
(3) |
式中,V1为集料颗粒体积;V2为集料最小外切三轴椭球的体积。
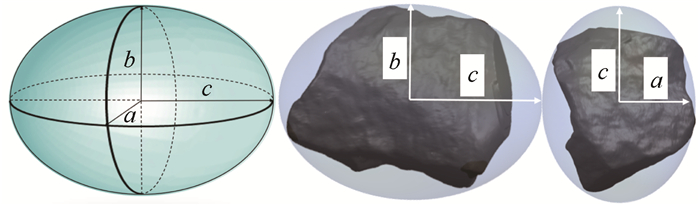
在UG中的集料三维实体模型周围拟合三轴不等椭球体,通过调整集料模型方位实时收缩椭球边界,获得椭球体积最小时的三轴半径a,b,c(图 4)。集料最小外切三轴椭球体积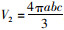
|
| 图 4 集料颗粒外切椭球 Fig. 4 Circumscribed ellipsoid of aggregate particle |
| |
(2) 局部棱角特征
采用主曲率矩阵H(x0, y0)表征集料表面任一点三维曲率,通过主曲率分布识别颗粒局部棱角特征。
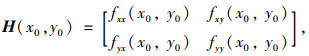
|
(4) |
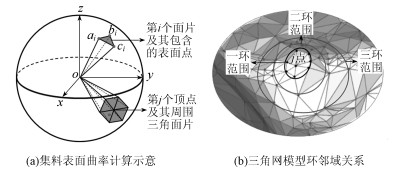
式中, H(x0, y0)为二阶海斯矩阵;fxx(x0, y0)=2e,fxy(x0, y0)=fyx(x0, y0)=d,fyy(x0, y0)=2g,均为图 5(a)中第j点周围由三角面片组成的7个顶点微型曲面的拟合函数z=f(x, y)的二阶导数。
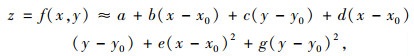
|
(5) |
|
| 图 5 集料颗粒的局部棱角识别 Fig. 5 Identifing local edges and corners of aggregate particles |
| |
式中,a,b,c分别为图 5(a)中第i个三角面片的顶点坐标;d,e,g分别为待定系数。
将含有集料颗粒表面空间坐标信息的三维点阵数据代入式(5),通过最小二乘法拟合得到含6个未知数的7个线性方程,解算后代入式(4)求得矩阵的特征值和特征向量,作为集料表面j点的主曲率及主曲率方向[13]。在UG中编写棱角区域识别命令,识别集料颗粒Delaunay三角网模型表面的顶点或脊点,根据环邻域关系将该点周围的三环范围定义为颗粒的棱角区域(图 5(b))。
2.3 集料颗粒纹理粗糙度表征方法采用国际岩石力学学会推荐的岩体表面粗糙度评价指标节理粗糙度系数(JRC2D)作为岩石类集料表面纹理粗糙程度的评价指标[14]。
(1) 二维轮廓线粗糙度特征
采用Tse和Cruden提出的轮廓曲线几何特征参数与粗糙度间的回归方程,计算集料表面轮廓线的二维粗糙度系数JRC2D值[15]。
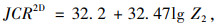
|
(6) |
式中Z2为轮廓线坡度特征参数, 用于计算集料表面的JRC2D,其近似计算公式为[16]:
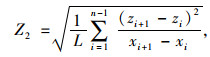
|
(7) |
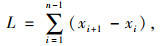
|
(8) |
式中,L为二维剖面轮廓线总长度;xi与zi为轮廓线上的点云坐标(图 6);n为采样点数量。

|
| 图 6 集料表面二维轮廓线 Fig. 6 Two-dimensional profile of aggregate surface |
| |
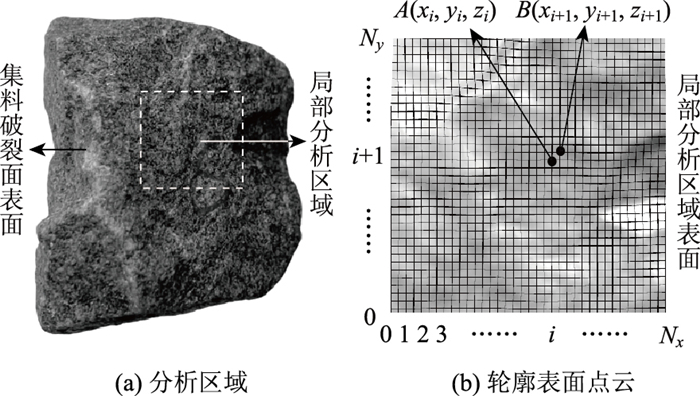
(3) 三维轮廓面粗糙度特征
考虑集料三维轮廓表面凹凸纹理的空间几何特征,可对颗粒破裂面表面局部区域的三维粗糙度系数JRC3D进行分析(图 7(a))。假定集料分析区域粗糙表面上的点云坐标连续可微[17],即相对起伏高度的三维特征参数均方根Z2s可表达为:
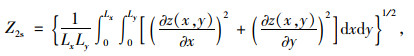
|
(9) |
|
| 图 7 集料三维轮廓面 Fig. 7 Three-dimensional profile of aggregate |
| |
式中Lx与Ly分别为集料表面分析区域在x轴和y轴方向上的取样长度。
利用集料的三维扫描点云数据计算颗粒表面三维粗糙度时,式(9)的近似计算公式为:
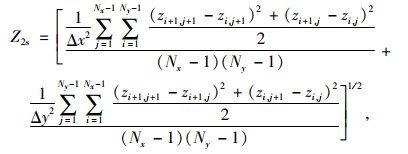
|
(10) |
式中,Nx为岩石轮廓面长度方向x轴上的点云数量;Ny为高度方向y轴上的点云数量;Δx为x轴上的点云采样间距;Δy为y轴上的点云采样间距;Zi,Zi+1分别为粗糙纹理高度z轴方向第i点和第i+1点的坐标。相关参数如图 7(b)所示。
3 集料的三维形貌评价 3.1 基于球度与形状引子的形状特征评价选取某路面材料测试中心的花岗岩、辉绿岩、玄武岩、石灰岩4种岩性粗集料作为研究对象,粒径在16~19 mm之间,生产工序均为鄂式加反击式。采用球度与形状因子评价集料样品的形状特征,结果如表 1所示。
| 岩性 | 技术性能 | 形状特征 | ||||||||||||||
| 压碎值/% | 磨耗值/% | 磨光值 | 吸水率/% | 表观相对密度/(g·cm-3) | 样本数量 | 球度 | 形状因子 | |||||||||
| 最大值 | 最小值 | 平均值 | 标准差 | 最大值 | 最小值 | 平均值 | 标准差 | |||||||||
| 花岗岩 | 18.1 | 21.5 | 46 | 0.37 | 2.65 | 20 | 0.86 | 0.68 | 0.81 | 0.040 6 | 1.35 | 0.69 | 0.96 | 0.205 9 | ||
| 辉绿岩 | 12.6 | 10.0 | 65 | 0.77 | 2.77 | 20 | 0.89 | 0.79 | 0.83 | 0.032 9 | 1.39 | 0.70 | 1.02 | 0.213 8 | ||
| 玄武岩 | 10.5 | 8.9 | 58 | 0.63 | 2.72 | 20 | 0.88 | 0.74 | 0.80 | 0.035 2 | 1.36 | 0.73 | 1.01 | 0.224 8 | ||
| 石灰岩 | 21.5 | 19.4 | 42 | 0.72 | 2.69 | 20 | 0.86 | 0.72 | 0.82 | 0.039 9 | 1.43 | 0.67 | 0.98 | 0.251 7 | ||
由评价结果可以看出,4种岩性集料样品的球度S评价结果在0.68~0.89之间变化,S值低的颗粒形状呈现狭长或薄片状特征,S值高的颗粒形状呈现近等轴矩形或椭球形特征。在本研究试验条件下,颗粒的球度S≥0.76时,粗集料的形状较为紧凑,抗压碎能力相对较强。颗粒的球度S<0.76时,粗集料呈现针状或片状特征。
集料样品的形状因子SF评价结果在0.67~1.43之间变化,不同形状颗粒对应的SF值由高到低的排序为:针状颗粒>正常颗粒(偏针状>偏扁平状)>扁平状颗粒。在本研究试验条件下,颗粒的形状因子SF<0.80时,粗集料为形状较差的扁平状颗粒;当0.80≤SF<1.00时,粗集料为形状良好的偏扁平状颗粒;当1.00≤SF≤1.20时,粗集料为形状良好的偏针状颗粒;当SF>1.20时,粗集料为形状较差的针状颗粒。
选取集料样品中形状差异明显的8颗粗集料进行对比,如表 2所示。
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 集料颗粒 | 
|

|

|

|

|

|

|

|
| 集料颗粒实体模型 | 
|

|

|

|

|

|

|

|
| 球度 | 0.68 | 0.73 | 0.82 | 0.89 | 0.88 | 0.79 | 0.76 | 0.72 |
| 形状因子 | 1.37 | 1.23 | 1.10 | 1.01 | 0.99 | 0.84 | 0.78 | 0.71 |
试验结果表明,使用球度指标S可以描述集料颗粒形状的紧凑程度,适用于计算粗集料中形状不良颗粒的含量,但不能区分颗粒的形状属性。相比而言,形状因子指标SF在表征粗集料的形状时,可以描述颗粒的针片状属性,适用于粗集料颗粒三维形状特征的定量评价。
3.2 基于椭球度与主曲率的棱角特征评价采用椭球度评价集料的整体棱角特征,同时依据Powers提出的碎石与砾石形貌评价标准评定颗粒的圆度级别[18],结果如表 3所示。
| 岩性 | 样本数量 | 集料颗粒的棱角特征 | ||||||||||
| 椭球度 | 圆度级别 | |||||||||||
| 最大值 | 最小值 | 平均值 | 标准差 | 尖棱角状 | 棱角状 | 次棱角状 | 次圆状 | 圆状 | 滚圆状 | |||
| 花岗岩 | 20 | 0.91 | 0.69 | 0.85 | 0.045 1 | 1 | 4 | 11 | 3 | 1 | 0 | |
| 辉绿岩 | 20 | 0.90 | 0.73 | 0.82 | 0.048 7 | 0 | 10 | 9 | 1 | 0 | 0 | |
| 玄武岩 | 20 | 0.88 | 0.67 | 0.83 | 0.046 7 | 1 | 12 | 6 | 1 | 0 | 0 | |
| 石灰岩 | 20 | 0.89 | 0.68 | 0.81 | 0.056 3 | 1 | 7 | 11 | 1 | 0 | 0 | |
由评价结果可以看出,4种岩性集料样品的椭球度E评价结果在0.68~0.91之间变化,E值低的颗粒的尖锐棱角相对较多,同时针片状特征明显;E值高的颗粒棱角相对较少且谷脊变幅平缓,多属于形状良好的近矩形形态。在本研究试验条件下,颗粒的椭球度E<0.71时,集料呈现尖棱角状,表面棱角易破裂折断;当0.71≤E<0.79和0.79≤E≤0.88时,集料分别呈现普通棱角状与次棱角状,棱角鲜明但不尖锐,在沥青混凝土中能够相互嵌挤形成传荷性能良好的力链型集料骨架结构;当E>0.88时,集料呈现次圆状,表面棱角呈磨圆状态[19],嵌挤能力较差。因此,路用集料中不应出现形状呈现尖棱角状、圆状及滚圆状集料颗粒。
对表 2中8颗集料的椭球度及圆度级别进行评价,同时利用二次开发程序在UG中对集料Delaunay三角网模型表面的顶点与脊点及其周围3环范围进行识别,结果如表 4所示。
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 椭球度 | 0.68 | 0.73 | 0.77 | 0.84 | 0.89 | 0.83 | 0.75 | 0.69 |
| 集料颗粒局部棱角区域识别 | 
|

|

|

|

|

|

|

|
| 圆度级别 | 尖棱角状 | 棱角状 | 棱角状 | 次棱角状 | 次圆状 | 次棱角状 | 棱角状 | 尖棱角状 |
试验结果表明,集料颗粒棱角区域的主曲率较大,破裂面的主曲率较小,利用主曲率分布二次开发程序识别的颗粒表面棱角区域与目测结果吻合。因此,使用椭球度指标E可以从整体角度评价集料的棱角性特征,以表面最大曲率为判定指标能够分析颗粒的局部棱角特征。
3.3 基于粗糙度的纹理特征评价(1) 二维粗糙度
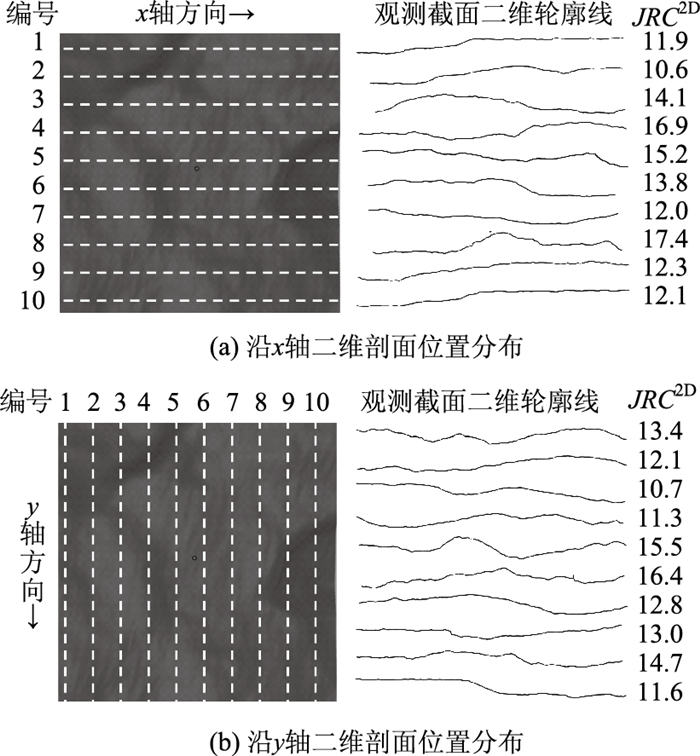
采用二维轮廓线粗糙度评价集料表面的纹理特征,将集料破裂面表面10 mm×10 mm范围作为局部分析区域(图 7(a))。分别沿x轴、y轴方向按1 mm等间距各设置10个观测截面,在集料的三维点阵模型中提取观测截面表面轮廓线的点云坐标数据,绘制二维轮廓曲线;依据式(6)与式(7)函数关系,在Matlab中编程计算每条曲线的二维轮廓线粗糙度JRC2D(图 8)。
|
| 图 8 集料表面的二维轮廓线粗糙度 Fig. 8 Two-dimensional profile roughness of aggregate surface |
| |
由计算结果可以看出,在曲率变幅较小的集料破裂面表面上各观测截面的轮廓线粗糙度各不相同,在二维层次上粗糙度的各向异性明显且随方向无明显变化规律[19],观测截面选取的随机性会造成粗糙度的评价结果出现较大差异。因此,二维粗糙度指标可用于分析集料表面轮廓线粗糙度的各向异性特征,但不能描述颗粒轮廓面的整体形貌,需要使用三维指标评价集料轮廓表面凹凸不平的形貌特征。
(2) 三维粗糙度
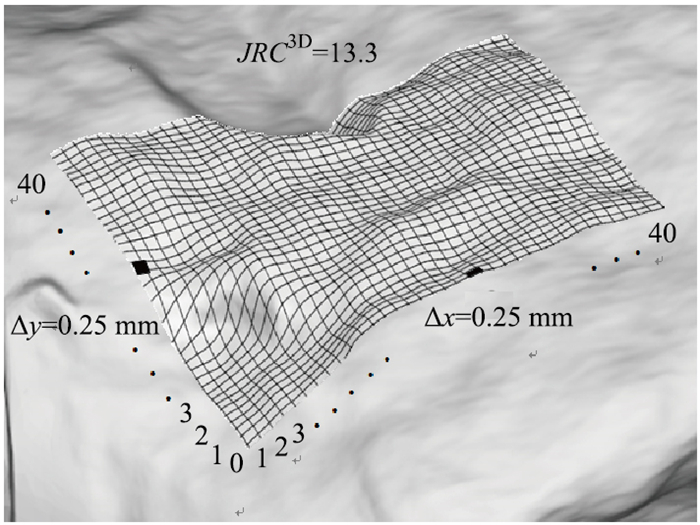
采用三维轮廓面粗糙度评价集料轮廓面的起伏特征,将颗粒破裂面上10 mm×10 mm范围作为局部分析区域(图 7(a))。在集料的三维点阵模型中按Δx=Δy=0.25 mm间隔提取分析区域的特征数据点,应用式(10)计算分析区域表面集料纹理相对起伏高度的均方根特征参数Z2s,代入式(6)得到JRC3D(图 9)。
|
| 图 9 集料表面的三维轮廓面粗糙度 Fig. 9 Three-dimensional profile roughness of aggregate surface |
| |
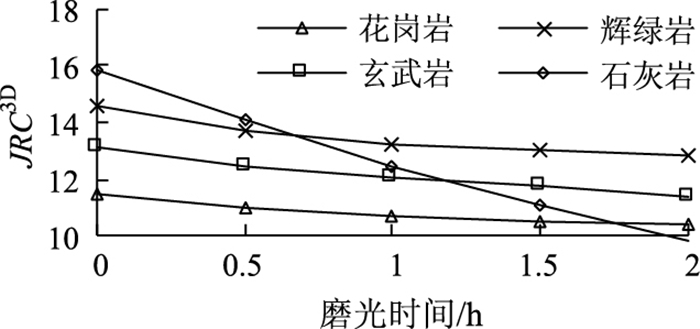
开展集料的磨光试验,检验三维粗糙度指标在表征集料纹理细观层次构造微小变化时的敏感度。以氧化铝含量95%的1000号1级金刚砂作为磨料,使用振动抛光机对同批集料试样分别进行0.5,1.0,1.5,2.0 h的抛光处理,改变分析区域轮廓面的细观构造形态[20]。每时段抛光试验结束后,评价每颗集颗粒表面分析区域的JRC3D,结果见表 5。各岩性集料测试样品在不同抛光时间下粗糙度的变化趋势如图 10所示。
| 抛光时间/h | 样本数 | 花岗岩 | 辉绿岩 | 玄武岩 | 石灰岩 | |||||||||||
| 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | 最大值 | 最小值 | 平均值 | |||||
| 0.0 | 10 | 13.6 | 9.7 | 11.5 | 17.4 | 12.2 | 14.6 | 15.7 | 11.0 | 13.1 | 18.3 | 11.1 | 15.8 | |||
| 0.5 | 10 | 13.1 | 9.5 | 11.0 | 16.5 | 11.7 | 13.7 | 15.1 | 10.5 | 12.4 | 16.01 | 9.63 | 14.1 | |||
| 1.0 | 10 | 12.9 | 9.2 | 10.7 | 15.5 | 11.4 | 13.2 | 14.4 | 10.2 | 12.1 | 14.85 | 8.77 | 12.4 | |||
| 1.5 | 10 | 12.8 | 9.1 | 10.5 | 14.7 | 11.0 | 13.0 | 13.9 | 10.0 | 11.8 | 14.09 | 8.08 | 11.1 | |||
| 2.0 | 10 | 12.5 | 9.2 | 10.4 | 14.6 | 10.7 | 12.8 | 13.3 | 10.0 | 11.4 | 13.50 | 7.11 | 9.8 | |||
|
| 图 10 集料粗糙度的变化趋势 Fig. 10 Variation trend of aggregate roughness |
| |
由试验数据可以看出,抛光试验前石灰岩集料样品破裂面上的平均粗糙度最高,花岗岩最小,玄武岩与辉绿岩居中。随着抛光时间的增加,集料粗糙的纹理表面逐步磨损,体现为不同岩性粗集料表面的粗糙度均随着磨光时间的增加呈下降趋势,其中石灰岩破裂面上的平均粗糙度降幅最大,玄武岩与辉绿岩次之,花岗岩粗糙度降幅最小,表明花岗岩集料表面纹理的耐磨光性能明显优于石灰岩集料,辉绿岩集料与玄武岩的耐磨光性能相近,这与实际工程中路用集料力学指标的衰减规律一致。
在本研究试验条件下,集料轮廓面的三维粗糙度JRC3D≥11.0时,纹理呈现凹凸不平形态,颗粒表面气孔与裂隙较多,有利于沥青与集料在接触面上起到良好的物理吸附作用。使用三维轮廓面粗糙度JRC3D评价集料表面纹理的细观构造变化时具有良好的敏感性,可作为路用集料表面曲率变幅较小破裂面三维粗糙度的评价指标。
4 结论为定量表征路用集料的三维形貌特征,基于三维白光扫描点云数据重构集料三维轮廓面的数字化实体模型,采用6个相互独立的特征参数从不同角度分别评价集料的三维形貌特征,得到以下结论:
(1) 用球度指标可以评价集料形状的紧凑程度,形状因子指标可以表征颗粒的针片形状属性。在本研究试验条件下,SF<0.8时粗集料为扁平片状颗粒,0.80≤SF≤1.20时粗集料为近矩形或近椭球形颗粒,SF>1.2时粗集料为细长针状颗粒。
(2) 用椭球度指标可以从整体角度评价集料的棱角性特征,表面最大曲率可用于识别颗粒的局部棱角特征。在本研究试验条件下,E<0.71时集料表面的尖锐棱角易破裂折断,0.71≤E≤0.88时集料棱角鲜明但不尖锐,E>0.88时集料表面棱角呈磨圆状态。
(3) 用二维粗糙度指标可以分析集料表面轮廓线粗糙度的各向异性特征,用三维粗糙度指标可以评价集料表面纹理的细观构造变化。在本研究试验条件下,JRC3D≥11.0时集料破裂面的表面纹理较为粗糙。
| [1] |
王文真, 申爱琴, 郭寅川, 等. 基于图像分析的粗集料形状特征参数及分布规律[J]. 公路交通科技, 2019, 37(1): 25-31. WANG Wen-zhen, SHEN Ai-qin, GUO Yin-chuan, et al. Shape Feature Parameters and Distribution Rule of Coarse Aggregate Based on Image Analysis[J]. Journal of Highway and Transportation Research and Development, 2019, 37(1): 25-31. |
| [2] |
游志诚, 王亮清, 杨艳霞, 等. 基于三维激光扫描技术的结构面抗剪强度参数各向异性研究[J]. 岩石力学与工程学报, 2014, 33(S1): 3003-3008. YOU Zhi-cheng, WANG Liang-qing, YANG Yan-xia, et al. Anisotropic Research on Shear Strength Parameters of Discontinuity Based on Three-dimensional Laser Scanning Technology[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S1): 3003-3008. |
| [3] |
冯其波, 谢芳, 张斌, 等. 光学测量技术与应用[M]. 北京: 清华大学出版社, 2008. FENG Qi-bo, XIE Fang, ZHANG Bin, et al. Optical Measurement Techniques and Applications[M]. Beijing: Tsinghua University Press, 2008. |
| [4] |
LARKIN K G. Efficien Tnonlinear Algorithm for Envelope Detection in White Lighti Nterferometry[J]. Journal of the Optical Society of America A, 1996, 13(4): 832-843. |
| [5] |
HIRABAYASHI A, OGAWA H, KITAGAWA K. Fast Surface Profiler by White-light Interferometry by Use of a New Algorithm Based on Sampling Theory[J]. Applied Optics, 2002, 41(23): 4876-4883. |
| [6] |
唐志荣, 刘明哲, 蒋悦, 等. 基于典型相关分析的点云配准算法[J]. 中国激光, 2019, 46(4): 173-181. TANG Zhi-rong, LIU Ming-zhe, JIANG Yue, et al. Point Cloud Registration Algorithm Based on Canonical Correlation Analysis[J]. Chinese Journal of Lasers, 2019, 46(4): 173-181. |
| [7] |
崔鑫, 闫秀天, 李世鹏. 保持特征的散乱点云数据去噪[J]. 光学精密工程, 2017, 25(12): 3169-3178. CUI Xin, YAN Xiu-tian, LI Shi-peng. Feature-preserving Scattered Point Cloud Denoising[J]. Optics and Precision Engineering, 2017, 25(12): 3169-3178. |
| [8] |
丁汉, 朱利民, 熊振华. 复杂曲面快速测量、建模及基于测量点云的RP和NC加工[J]. 机械工程学报, 2003, 39(11): 28-37. DING Han, ZHU Li-min, XIONG Zhen-hua. Survey on Coordinate Measurement, Geometric Modeling and RP or NC Code Generation from Measured Data Points[J]. Chinese Journal of Mechanical Engineering, 2003, 39(11): 28-37. |
| [9] |
崔喆, 张生瑞. 基于CT图像的集料三维棱角性计算方法[J]. 交通运输工程学报, 2017, 17(5): 39-49. CUI Zhe, ZHANG Sheng-rui. Computational Method of 3D Aggregate Angularity Based on CT Images[J]. Journal of Traffic and Transportation Engineering, 2017, 17(5): 39-49. |
| [10] |
王伟, 段虎荣, 张德成, 等. 一种求解三维激光扫描后不规则体的体积及表面积方法[J]. 测绘与空间地理信息, 2019, 42(8): 172-175. WANG Wei, DUAN Hu-rong, ZHANG De-cheng, et al. A Method for Solving the Volume and Surface Area of Irregular Body after Three-dimensional Laser Scanning[J]. Geomatics & Spatial Information Technology, 2019, 42(8): 172-175. |
| [11] |
金灿, 汪培松, 杨旭, 等. 基于三维虚拟测量的沥青混合料级配参数分析[J]. 公路交通科技, 2019, 36(8): 1-8. JIN Can, WANG Pei-song, YANG Xu, et al. Analysis on Gradation Parameters of Asphalt Mixture Based on 3D Virtual Measurement[J]. Journal of Highway and Transportation Research and Development, 2019, 36(8): 1-8. |
| [12] |
耿超. 基于图像处理的集料形态特征定量评价[J]. 公路交通科技, 2018, 35(12): 42-47. GENG Chao. Quantitative Evaluation of Morphological Feature of Aggregate Based on Image Processing[J]. Journal of Highway and Transportation Research and Development, 2018, 35(12): 42-47. |
| [13] |
付茹, 胡新丽, 周博, 等. 砂土颗粒三维形态的定量表征方法[J]. 岩土力学, 2018, 39(2): 483-490. FU Ru, HU Xin-li, ZHOU Bo, et al. A Quantitative Characterization Method of 3D Morphology of Sand Particles[J]. Rock and Soil Mechanics, 2018, 39(2): 483-490. |
| [14] |
BARTON N, CHOUBEY V. The Shear Strength of Rock Joints in Theory and Practice[J]. Rock Mechanics, 1977, 10: 1-54. |
| [15] |
TSE R, CRUDEN D M. Estimating Joint Roughness Coefficients[J]. International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts, 1979, 16(5): 303-307. |
| [16] |
陈世江, 朱万成, 王创业, 等. 岩体结构面粗糙度系数定量表征研究进展[J]. 力学学报, 2017, 49(2): 239-256. CHEN Shi-jiang, ZHU Wan-cheng, WANG Chuang-ye, et al. Review of Research Progresses of the Quantifying Joint Roughness Coefficient[J]. Chinese Journal of Theoretical and Applied Mechanics, 2017, 49(2): 239-256. |
| [17] |
BELEM T, HOMAND-ETIENNE F, SOULEY M. Quantitative Parameters for Rock Joint Surface Roughness[J]. Rock Mechanics and Rock Engineering, 2000, 33(4): 217-242. |
| [18] |
POWERS M C. A New Roundness Scale for Sedimentary Particles[J]. Journal of Sedimentary Research, 1953, 23(2): 117-119. |
| [19] |
李燕, 金振奎, 金婷, 等. 岩浆岩砾石磨圆度地质意义的研究[J]. 沉积学报, 2014, 32(2): 189-197. LI Yan, JIN Zhen-kui, JIN Ting, et al. Geological Significance of Magmatic Gravel Roundness[J]. Acta Sedimentologica Sinica, 2014, 32(2): 189-197. |
| [20] |
董文姣. 集料形貌对沥青-集料黏附性影响研究[D]. 扬州: 扬州大学, 2013. DONG Wen-jiao. Resaerch on Effect of Aggregate Morphology on Adhesion between Bitumen and Aggregate[D].Yangzhou: Yangzhou University, 2013. |
 2021, Vol. 38
2021, Vol. 38
