扩展功能
文章信息
- 石志勇, 李倩倩, 王旭东
- SHI Zhi-yong, LI Qian-qian, WANG Xu-dong
- 不同荷载模式下沥青混合料的动态模量依赖模型
- Dynamic Modulus Dependence Model of Asphalt Mixture under Different Load Modes
- 公路交通科技, 2021, 38(2): 9-15, 47
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(2): 9-15, 47
- 10.3969/j.issn.1002-0268.2021.02.002
-
文章历史
- 收稿日期: 2020-05-29
2. 交通运输部公路科学研究院, 北京 100088;
3. 哈尔滨工业大学 交通科学与工程学院, 黑龙江 哈尔滨 150090
2. Research Institute of Highway, Ministry of Transport, Beijing 100088, China;
3. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin Heilongjiang 150090, China
模量是路面结构设计与力学分析的重要参数[1],如何使其取值更加合理可靠一直是困扰世界各国路面设计人员的难点问题之一。沥青混合料作为非均质和各向异性的黏弹性材料,其力学性能受到试验条件、荷载模式和测试方法等多种因素的影响[2-3],获取真实可靠的材料模量较为困难。
事实上,沥青混合料的材料模量是具有多个变量的表达式而非一个定值。关于沥青混合料动态模量表示形式,主要有以下几类研究成果:第1类是建立全面的沥青混合料材料特性及动态模量数据库,并结合美国当地气候环境、试验条件、材料特性等,提出了一系列沥青混合料的动态模量预估模型,其中具有代表性的为Witczak 1-37A模型[4]、改进的Witczak模型[5]、NCHRP 1-40D模型[6]和Hirsch模型[7]等,但该类模型的预测结果与沥青混合料的室内及野外试验结果仅在一定范围、条件下具有较好的相关性,同时存在用于其他地区适用性较差等缺点。人工神经网络(Artificial Neural Network)模型具备一定的数据分析优势,提高了动态模量的预估精度[8-9],因此愈发受到更多关注。第2类是基于沥青混合料线黏弹性理论将荷载作用时间和环境温度采用时温等效原理构造的单一变量的模量主曲线[10],现行我国2017版沥青路面设计规范[11]和美国MEPDG路面设计指南[12]均依据该原理对材料模量取值,此类方法认为模量只与试验温度和扫描频率有关,有悖于沥青混合料的材料荷载依赖性特性,在役沥青路面均受到环境温度和交通荷载耦合作用,忽略荷载的影响,在路面结构力学分析中必然产生较大的误差。第3类是考虑了沥青混合料模量具有荷载依赖性行为,将沥青混合料视作非线黏弹性材料引入应变因素构建了基于温度和应变的沥青混合料弯拉动态模量依赖模型[13-14],该方法相较于第2类方法更为合理,但是没有区分应变作用具有温度敏感区间的现象,导致低温时的模量计算值与实际值误差较大,事实上,低温时沥青混合料可看做线弹性材料,对荷载的依赖性很小甚至可以忽略,因此第3类方法需要进一步完善。第4类方法认为沥青混合料处于三向应力状态之下,将试验温度和围压水平作为主要影响因素归入模量依赖模型之中[15-16],依据该方法可衡量复杂受力状态下沥青混合料的力学性质,但此方法没有考虑轴向应变的影响,且模型复杂,参数难以获取,不利于工程中的实际应用。
在开展沥青路面力学分析时,沥青混合料多采用单轴压缩荷载模式下的动态模量作为结构参数。然而,对于不同的路面病害形式,路面结构内关键位置处的力学响应存在很大的差异,忽视受力模式不同对动态模量的影响会直接在路面结构分析和厚度设计中产生较大的误差,一般而言,沥青混合料在路面结构层中存在压缩、剪切、弯拉、拉伸等受力状态,为了全面准确地描述沥青混合料的力学响应行为,本研究通过开展沥青混合料两点弯拉和三轴围压两种典型荷载模式下的动态模量试验,根据非线黏弹性假设构建了沥青混合料的弯拉和三轴动态模量依赖模型,可较好地表征动态模量的温度和荷载依赖性。该类模型物理意义明确,科学可靠,为沥青混合料动态模量的合理取值提供了一种有效途径。
1 试验设计 1.1 试验材料试验材料选取位于北京通州地区的足尺环道试验路面RIOHTrack两种结构STR1和STR19面层[17]使用的4种沥青混合料AC25(AH-30), AC20(AH-30), AC13(SBS1)和SMA13(SBS1),具体的级配信息汇总于表 1,严格按照标准流程制[18]备所需试件,两点弯拉试件形状类似等腰梯形,试件的上底为(25±1)mm,下底为(56±1)mm,高度为(250±1) mm,厚度为(25±1) mm,两点弯拉试件为圆柱体,试件直径为±100 mm,高度为(150±1) mm。
| 沥青混合料类型 | 各筛孔通过率/% | |||||||||||
| 26.5 | 19 | 16 | 13.2 | 9.5 | 4.75 | 2.36 | 1.18 | 0.6 | 0.3 | 0.15 | 0.075 | |
| AC25(AH-30) | 99.7 | 77.9 | — | 56.8 | 42.8 | 25.9 | 18.5 | 12.9 | 10.4 | 8.2 | 6.6 | 5.0 |
| AC20(AH-30) | — | 100.0 | 95.3 | 72.9 | 52.6 | 30.4 | 21.1 | 14.7 | 12.0 | 9.5 | 7.7 | 5.9 |
| AC13(SBS1) | — | — | 100.0 | 98.0 | 60.6 | 34.8 | 25.4 | 17.7 | 13.4 | 9.9 | 8.8 | 7.1 |
| SMA13(SBS1) | — | — | 100.0 | 97.7 | 54.7 | 24.9 | 16.7 | 14.0 | 12.5 | 11.4 | 11.0 | 9.7 |
1.2 试验方案
根据仪器设备自身具备的条件和试验方法确定相应的试验方案见表 2和表 3,在沥青混合料两点弯拉动态模量试验中,弯拉荷载对试件较为不利,为防止试件的损伤,在低温时不设置高应变水平的试验条件,两种试验均采用应变控制模式。
| 试验温度/℃ | 扫描频率/Hz | 应变水平/(×102 με) |
| 0 | 40, 35, 30, 25, 20, 15, 10 | 30, 60, 90, 120 |
| 5, 10, 15, 20, 25, 30, 35, 40, 45 | 40, 35, 30, 25, 20, 15, 10 | 30, 60, 90, 120, 150 |
| 试验温度/℃ | 扫描频率/Hz | 应变水平/με | 围压水平/kPa |
| 0, 5, 10, 15, 20, 30, 40, 50, 55 | 25, 20, 10, 5, 2, 1, 0.5, 0.2, 0.1 | 20, 40, 60, 80, 100 | 0, 50, 100, 150, 200 |
2 试验结果与分析
沥青混合料是典型的黏弹性材料[19],可根据时温等效原理将其他试验温度或扫描频率的动态模量试验结果平移得到宽温域或宽频率的主曲线以完整地反映材料的力学性能[20],弥补室内试验条件的不足。以10 Hz为基准频率,利用Boltzmann函数进行非线性拟合得到沥青混合料动态模量主曲线,见式(1),为节省篇幅,仅列出部分沥青混合料的动态模量主曲线参数,汇总于表 4和表 5,从表中看出相关系数R2均在0.99以上,拟合效果良好。其中AC25(AH-30)沥青混合料的围压水平为50 kPa,AC20(AH-30)沥青混合料的应变水平为20 με。
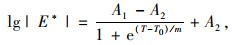
|
(1) |
| 沥青混合料类型 | 试验类型 | 应变水平/(×102 με) | 动态模量主曲线参数 | 相关系数 | ||||
| A1 | A2 | T0 | m | R2 | ||||
| AC25(AH-30) | 两点弯拉 | 30 | 4.653 8 | -5.125 8 | 88.249 7 | 23.262 3 | 0.999 5 | |
| 60 | 4.648 9 | -3.648 7 | 81.214 8 | 22.235 5 | 0.999 5 | |||
| 90 | 4.641 7 | -1.211 6 | 69.468 6 | 20.977 8 | 0.999 5 | |||
| 120 | 4.673 2 | -1.920 7 | 73.281 9 | 22.438 1 | 0.999 4 | |||
| 150 | 4.647 9 | -0.290 8 | 63.470 5 | 21.276 3 | 0.999 4 | |||
| 三轴围压 | 20 | 4.695 9 | 0.044 0 | 74.468 5 | 22.699 2 | 0.998 8 | ||
| 40 | 4.655 7 | 1.443 3 | 61.762 8 | 19.040 5 | 0.999 2 | |||
| 60 | 4.637 1 | 1.858 9 | 57.471 9 | 17.572 6 | 0.998 9 | |||
| 80 | 4.613 6 | 2.172 7 | 54.103 9 | 16.143 7 | 0.998 3 | |||
| 100 | 4.609 9 | 2.350 8 | 52.002 9 | 15.354 9 | 0.996 6 | |||
| 沥青混合料类型 | 围压水平/kPa | 动态模量主曲线参数 | 相关系数 | ||||
| A1 | A2 | T0 | m | R2 | |||
| AC20(AH-30) | 0 | 4.658 5 | 0.380 2 | 69.164 4 | 20.814 5 | 0.998 1 | |
| 50 | 4.650 2 | 0.779 1 | 66.456 2 | 20.210 0 | 0.998 2 | ||
| 100 | 4.678 7 | 1.070 7 | 65.894 2 | 21.629 0 | 0.997 9 | ||
| 150 | 4.636 5 | 1.895 4 | 57.905 5 | 19.125 6 | 0.998 4 | ||
| 200 | 4.621 6 | 2.333 4 | 52.727 0 | 17.785 4 | 0.998 6 | ||
式中,E*为沥青混合料动态模量;A1, A2为与模量有关的回归参数; T0, m为函数模型的形状参数。
图 1为不同应变水平的AC25(AH-30)沥青混合料弯拉(M2F)和三轴(AMPT)动态模量主曲线。从表 4和图 1可知,弯拉和三轴动态模量主曲线总体的变化趋势基本相同,但存在以下差异:

|
| 图 1 AC25(AH-30)不同应变水平的动态模量主曲线 Fig. 1 Master curves of dynamic modulus of AC25(AH-30) with different strain levels |
| |
(1) 三轴动态模量主曲线对应的温度区域更宽广,其曲线的横坐标能延伸到大约76 ℃。两点弯拉试验中试验温度最高只能施加至45 ℃,而三轴围压试验中则能达到55 ℃,此外,两者的主曲线都是以10 Hz为基准频率平移得到的,前者的扫描频率最低为10 Hz,在平移过程中得到的移位因子都为正值,不能向右增加以温度为横坐标的范围,后者的最低扫描频率为0.01 Hz,能得到正负移位因子,从而左右扩大温度横坐标的范围。
(2) 同一横坐标下,三轴动态模量主曲线上各处的斜率均小于弯拉动态模量主曲线,弯拉动态模量对温度的变化更为敏感。这是由于弯拉荷载模式下,梯形梁试件内部主要依靠沥青胶浆间的黏结作用来抵抗拉力[21],温度升高,沥青变软,黏结力显著降低,而圆柱体试件则受压缩作用,试件内部颗粒的嵌挤更加紧密,抵抗变形的能力变强。
(3) 同一条件下,沥青混合料三轴动态模量均大于弯拉动态模量,低温时,两者数值水平较为接近,但随着温度的升高,这种差距变大。同时应变水平增大,弯拉动态模量增大,三轴动态模量则反之,荷载分别起到硬化和软化作用。高温时,沥青混合料动态模量的荷载依赖性显著增强。这是因为弯拉荷载对梯形梁试件较为不利,沥青混合料趋于分离,压缩荷载则使圆柱体试件更为紧密,致使试件刚度更大。低温时,沥青混合料接近于线弹性状态,刚度较大,对外界的荷载作用响应不明显,温度升高,沥青混合料的性状转变为黏弹态甚至黏流态,荷载的影响程度显著加强。在宽温域范围内,温度由低到高,沥青混合料的状态实质上经历了线弹性体-线黏弹性体-非线黏弹性体的转变。
图 2为应变水平20 με下不同围压水平的AC20(AH-30)沥青混合料三轴动态模量主曲线。图中可以看出,随着温度的升高,不同围压水平的沥青混合料动态模量均呈现逐渐减小的趋势,但在高温区域却有明显的差异。当温度较低时,围压水平增大,沥青混合料动态模量之间几乎没有差异,当温度为-10 ℃时,不同围压水平的动态模量最大值与最小值比值为1.03。当温度达到74 ℃时,两者的比值为3.14,可见在高温区域围压水平对AC20(AH-30)沥青混合料的动态模量影响显著[22],这与应变水平的影响规律一致,在进行路面结构设计和力学分析时必须将围压水平纳入到主要影响因素之列。

|
| 图 2 AC20(AH-30)不同围压水平的动态模量主曲线 Fig. 2 Master curves of dynamic modulus of AC20 (AH-30) with different confining pressure levels |
| |
3 沥青混合料动态模量依赖模型的构建 3.1 弯拉动态模量依赖模型的构建
从上述分析可知,两种荷载模式下的沥青混合料动态模量不仅具有显著的温度依赖性,且在高温区域与荷载水平高度相关,此时应将沥青混合料视为非线黏弹性材料。显然式(1)并不能表达这一特性,为了更加准确地描述沥青混合料动态模量的温度和荷载依赖性,需将其归纳到统一的数学方程之中,构造沥青混合料动态模量依赖模型。笔者前期研究发现,式(1)中A2与荷载水平间具有明显的非线性关系,采用指数函数模型可以较好地表征这种关系。因此可将沥青混合料弯拉动态模量对数的最小值A2=a·eb·ε代入式(1),则沥青混合料弯拉动态模量依赖模型见式(2):

|
(2) |
式中,lg|Emax*|为沥青混合料动态模量对数的最大值;ε为应变水平;a,b为与曲线形态有关的回归参数。
根据前节中得到的沥青混合料不同应变水平的弯拉动态模量主曲线数据整理成温度和应变为自变量,动态模量对数为因变量的数据形式,利用式(2)非线性拟合得到模型的各个参数,汇总于表 6,即得到4种沥青混合料考虑荷载温度敏感区间的沥青混合料弯拉动态模量依赖模型,图 3为AC20(AH-30)沥青混合料弯拉动态模量三维主曲面。
| 沥青混合料类型 | a | b | lg|Emax*|/MPa | m | T0 | R2 |
| AC25(AH-30) | 1.503 4 | -0.377 1 | 4.605 9 | 18.377 1 | 54.106 9 | 0.998 8 |
| AC20(AH-30) | 2.313 2 | -0.237 6 | 4.561 0 | 17.111 7 | 45.241 6 | 0.985 9 |
| AC13(SBS1) | 2.318 8 | -0.126 0 | 4.499 7 | 14.519 3 | 31.123 9 | 0.998 5 |
| SMA13(SBS1) | 2.312 7 | -0.134 4 | 4.452 3 | 15.341 0 | 31.057 0 | 0.998 2 |

|
| 图 3 AC20(AH-30)弯拉动态模量主曲面 Fig. 3 Main curved surface of flexural-tensile dynamic modulus of AC20 (AH-30) |
| |
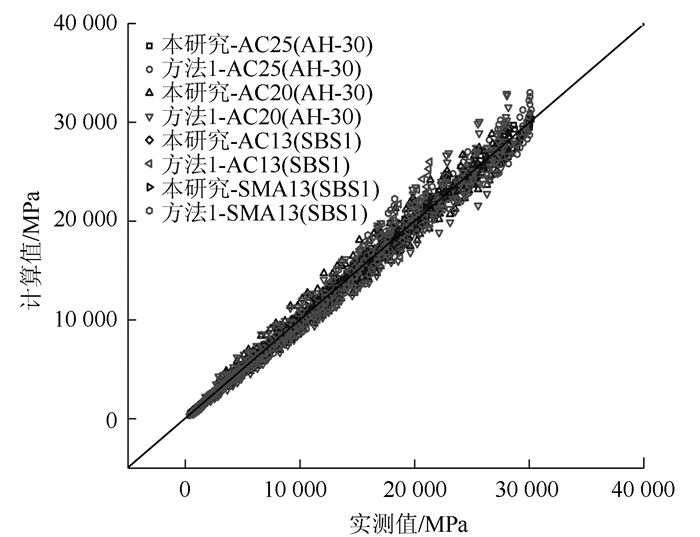
从表 6和图 3中可以看出,基于温度与应变的二元变量的沥青混合料弯拉动态模量的相关系数R2均在0.98以上,拟合效果良好且曲面光滑,该模型可较好地表征沥青混合料弯拉动态模量与温度、应变之间的关系,方法1[13-14]中开展不同应变水平、不同加载频率、不同试验温度下的沥青混合料弯拉动态模量试验;以10 Hz为基准频率,建立不同应变水平温度的沥青混合料动态模量主曲线;将上一步结果整理成自变量为温度和应变水平、因变量为动态模量的数据格式,进行多元回归分析,即得到模型回归参数。本研究模型构建步骤与该方法一致,但考虑了应变水平作用的温度敏感区间,从理论上更具有说服力和合理性。根据两种方法得到的4种沥青混合料弯拉动态模量计算值与实测值的对比结果见图 4。从图中可知,当弯拉模量较小时,通过两种方法得到的4种沥青混合料动态模量都在45°等值线附近,数据点均比较集中,可以较好地与实测值一一对应,但随着弯拉模量的增大,与本研究的模型相比,方法1得到的结果离散效果明显偏大,相对误差增大,甚至有偏离等值线的趋势,已经超过了应变的影响作用。其本质原因是方法1没有考虑到弯拉模量在低温区域几乎不存在荷载依赖性的特征,导致计算结果失真,因此选用本研究的弯拉动态模量依赖模型表征沥青混合料的动态模量变化规律具有优越性。
|
| 图 4 两种方法弯拉动态模量计算值和实测值的对比 Fig. 4 Comparison of calculated and measured values of dynamic modulus of flexural-tensile with 2 methods |
| |
3.2 三轴动态模量依赖模型的构建
我国现行沥青路面设计规范采用单轴压缩动态模量作为路面结构的设计指标,而事实上沥青混合料在实体结构中处于三向压缩受力状态,通过前节的分析可知,在高温范围内,沥青混合料对应变水平和围压水平具有显著的依赖性,不考虑荷载的影响,势必对结构层材料模量取值造成较大的误差,直接影响路面设计的合理性。同样的,在高温区域,对于三轴动态模量而言,应变水平和围压水平均与A2呈现较好的指数关系,为了表征围压水平与应变水平对动态模量的叠加效应,可令沥青混合料三轴动态模量对数的最小值A2=a·eb·ε+c·σ代入式(1),则沥青混合料三轴动态模量依赖模型见式(3):
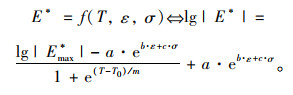
|
(3) |
将数据形式整理成温度、应变和围压为自变量,动态模量对数为因变量的数据形式,利用式(3)非线性拟合得到模型的各个参数,汇总于表 7,即得到4种沥青混合的三轴动态模量依赖模型。
| 沥青混合料类型 | a | b | c | lg|Emax*|/MPa | m | T0 |
| AC25(AH-30) | 1.158 2 | 0.104 8 | 0.119 4 | 4.656 9 | 19.994 2 | 64.408 0 |
| AC20(AH-30) | 1.458 2 | 0.114 8 | 0.129 4 | 4.618 1 | 17.694 2 | 58.408 0 |
| AC13(SBS1) | 2.179 9 | 0.047 6 | 0.073 5 | 4.558 5 | 15.266 7 | 35.505 7 |
| SMA13(SBS1) | 1.475 5 | 0.129 0 | 0.128 3 | 4.406 0 | 16.428 0 | 41.166 9 |
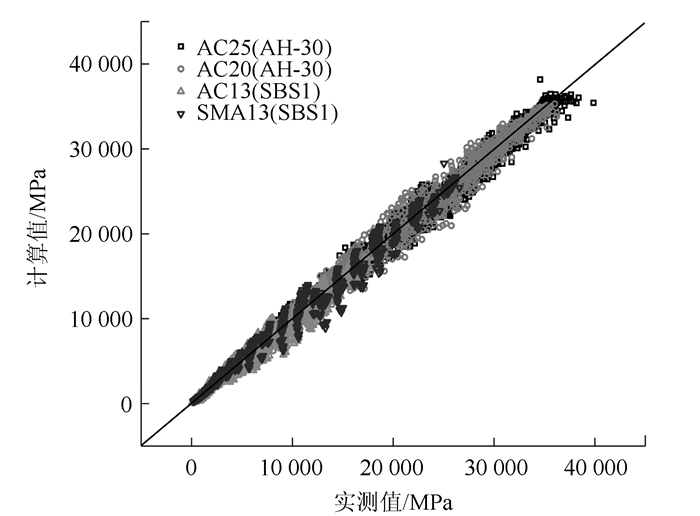
同样的,为了验证沥青混合料三轴动态模量依赖模型的有效性和准确性,根据该模型得到4种沥青混合料三轴动态模量计算值与实测值的对比结果见图 5。从图中可知4种沥青混合料的三轴动态模量计算值均在45°等值线附近,数据点集中离散效果较差,计算值和实测值可以较好地对应,说明该模型可靠度较高,可以准确地描述温度、应变和围压与沥青混合料三轴动态模量的关系。后续应将弯拉和三轴动态模量依赖模型代入实体结构中计算,以验证两种模型的可靠性与适用性。
|
| 图 5 三轴动态模量计算值和实测值的对比 Fig. 5 Comparison of calculated and measured values of triaxial dynamic modulus |
| |
4 结论
(1) 沥青混合料弯拉和三轴动态模量总体的变化趋势基本相同,但两者在主曲线的形态特征和数值水平方面具有明显差异。三轴动态模量主曲线温度区域更为宽广,曲线的斜率更小。相同条件下三轴动态模量大于弯拉动态模量,但对温度的依赖性小于弯拉动态模量。
(2) 沥青混合料动态模量在高温区域内具有显著的荷载依赖性。在高温范围内,应变水平增大,弯拉动态模量显著减小,三轴动态模量则反之,荷载模式对沥青混合料分别起到软化和硬化作用,围压水平和应变水平对三轴动态模量的影响基本一致。宽温度域范围内,温度与荷载耦合作用下,温度由低到高,沥青混合料的状态将发生线性弹性体-线性黏弹性体-非线性黏弹性体的转变。
(3) 考虑荷载作用温度敏感区间的沥青混合料弯拉和三轴动态模量依赖模型,拟合效果良好,可靠度高,可准确描述沥青混合料动态模量的温度、荷载依赖性特性,两种模型为准确获取不同受力状态下的沥青混合料的模量值提供了一种有效途径,后续可用于路面结构计算来验证两种模型的可靠性和适用性。
| [1] |
张晨晨, 王旭东, 钱振东, 等. 半刚性基层材料不同模量试验与分析[J]. 公路交通科技, 2017, 34(6): 53-60. ZHANG Chen-chen, WANG Xu-dong, QIAN Zhen-dong, et al. Test and Analysis on Different Moduli of Semi-rigid Base Material[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 53-60. |
| [2] |
王旭东, 沙爱民, 许志鸿. 沥青路面材料动力特性与动态参数[M]. 北京: 人民交通出版社, 2002. WANG Xu-dong, SHA Ai-min, XU Zhi-hong. Dynamic Characteristics and Dynamic Parameters of Asphalt Pavement Materials[M]. Beijing: China Communications Press, 2002. |
| [3] |
姚祖康. 沥青路面结构设计[M]. 北京: 人民交通出版社, 2011. YAO Zu-kang. Structural Design of Asphalt Pavements[M]. Beijing: China Communications Press, 2011. |
| [4] |
WITCZAK M W, FONSECA O A. Revised Predictive Model for Dynamic (Complex) Modulus of Asphalt Mixtures[J]. Transportation Research Record, 1996, 1540: 15-23. |
| [5] |
BARI J, WITCZAK M W. Development of New Revised Version of the Witczak E Predictive Model for Hot Mix Asphalt Mixtures[J]. Journal of the Association of Asphalt Paving Techonlogists, 2006, 75: 381-423. |
| [6] |
WITCZAK M W, El-BASYOUNY M, El-BADAWY S. Incorporation of the New (2005) E* Predictive Model in the Mepdg, Nchrp 1-40D Final Report[R]. Tempe: Arizona State University, 2007.
|
| [7] |
CHRISTENSEN D W, PELLINEN J T, BONAQUIST R F. Hirsch Model for Estimating the Modulus of Asphalt Concrete[J]. Journal of the Association of Asphalt Paving Technologists, 2003, 72: 97-121. |
| [8] |
GHASEMI P, ASLANI M, ROLLINS D K, et al. Principal Component Neural Networks for Modeling, Prediction, and Optimization of Hot Mix Asphalt Dynamics Modulus[J]. Infrastructures, 2019, 4(3): 53. |
| [9] |
ESFANDIARPOUR S, SHALABY A. Local Calibration of Creep Compliance Models of Asphalt Concrete[J]. Construction and Building Materials, 2017, 132: 313-322. |
| [10] |
WITCZAK M W, REI D, MIRZA W. Development of Revised Predictive Model for the Dynamic (Complex) Modulus of Asphalt Mixtures, Inter-team Technical Report, NCHRP1-37A[R].Washington, D.C.: University of Maryland, 1999.
|
| [11] |
JTG D50-2017, 公路沥青路面设计规范[S]. JTG D50-2017, Specifications for Design of Highway Asphalt Pavement[S]. |
| [12] |
MASON M. Guide for Mechanistic-empirical Design of New and Rehabilitated Pavement Structures, NCHRP 1-37A[R]. Washington, D.C.: Transportation Research Board, 2004.J
|
| [13] |
周兴业, 蒋勇, 王旭东, 等. 基于温度与应变参数的沥青混合料动态模量依赖模型研究[J]. 公路交通科技, 2019, 36(3): 7-13. ZHOU Xing-ye, JIANG Yong, WANG Xu-dong, et al. Study on Dynamic Modulus Dependent Model of Asphalt Mixture Based on Temperature and Strain Parameters[J]. Journal of Highway and Transportation Research and Development, 2019, 36(3): 7-13. |
| [14] |
周维锋. 不同受力模式下沥青混合料动态模量应变依赖特性研究[J]. 重庆交通大学学报: 自然科学版, 2019, 38(9): 57-62. ZHOU Wei-feng. Strain-dependent Model for Complex Modulus of Asphalt Mixture[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2019, 38(9): 57-62. |
| [15] |
赵延庆, 谭忆秋, 于新. 沥青混合料力学性质应力依赖性研究[J]. 华中科技大学学报: 自然科学版, 2010, 38(10): 129-132. ZHAO Yan-qing, TAN Yi-qiu, YU Xin. Stress-dependent Mechanical Behavior of Asphalt Mixtures[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2010, 38(10): 129-132. |
| [16] |
ZHAO Y Q, TANG J M, LIU H. Construction of Triaxial Dynamic Modulus Master Curve for Asphalt Mixtures[J]. Construction and Building Materials, 2012, 37: 21-26. |
| [17] |
王旭东. 足尺路面试验环道路面结构与材料设计[J]. 公路交通科技, 2017, 34(6): 30-37. WANG Xu-dong. Design of Pavement Structure and Material for Full-scale Test Track[J]. Journal of Highway and Transportation Research and Development, 2017, 34(6): 30-37. |
| [18] |
黄优. 沥青混合料梯形梁动态模量试验研究[D]. 长沙: 长沙理工大学, 2015. HUANG You. Experimental Research on Dynamic Modulus of Asphalt Mixture Trapezoid Beam[D]. Changsha: Changsha University of Science and Technology, 2015. |
| [19] |
张肖宁. 沥青与沥青混合料的粘弹力学原理及应用[M]. 北京: 人民交通出版社, 2006. ZHANG Xiao-ning. Principle and Application of Viscoelastic Mechanics of Asphalt and Asphalt Mixture[M]. Beijing: China Communications Press, 2006. |
| [20] |
张晨晨, 钱振东, 王旭东, 等. 基于DMA方法的沥青砂浆动态弯拉黏弹特性[J]. 公路交通科技, 2019, 36(3): 22-28. ZHANG Chen-chen, QIAN Zhen-dong, WANG Xu-dong, et al. Dynamic Flexural-tensile Viscoelastic Property of Asphalt Mortar Based on DMA Method[J]. Journal of Highway and Transportation Research and Development, 2019, 36(3): 22-28. |
| [21] |
黄优, 刘朝晖, 王旭东, 等. 沥青混合料动态模量梯形梁与SPT试验比较研究[J]. 中南大学学报: 自然科学版, 2017, 279(11): 3092-3099. HUANG You, LIU Zhao-hui, WANG Xu-dong, et al. Comparison of HMA Dynamic Modulus Between Trapezoid Beam Test and SPT[J]. Journal of Central South University: Natural Science Edition, 2017, 279(11): 3092-3099. |
| [22] |
赵延庆, 叶勤, 文健. 围压对沥青混合料动态模量的影响[J]. 重庆交通大学学报: 自然科学版, 2007, 118(6): 96-99. ZHAO Yan-qing, YE Qin, WEN Jian. Effects of Confining Pressure on Dynamic Modulus[J]. Journal of Chongqing Jiaotong University: Natural Science Edition, 2007, 118(6): 96-99. |
 2021, Vol. 38
2021, Vol. 38
