扩展功能
文章信息
- 蔡鉴明, 李国栋, 李孝康
- CAI Jian-ming, LI Guo-dong, LI Xiao-kang
- 需求导向的智能快件箱格口数量优化
- Optimization of Compartment Number of Intelligent Self-express Service Machine under Demand Orientation
- 公路交通科技, 2021, 38(1): 151-158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(1): 151-158
- 10.3969/j.issn.1002-0268.2021.01.019
-
文章历史
- 收稿日期: 2019-12-06
近年来,随着我国电子商务行业的迅速发展,快递行业迎来了飞速发展的时期,据国家统计局数据,快递业务完成量从2015年的206亿件增长到了2019年的630亿件,即将进入日均2亿件的时代,这给快递配送尤其是末端配送带来了巨大的压力。智能快件箱作为一种新型快递末端配送模式,能够有效提升配送效率,降低成本,受到了行业和学界的广泛关注。
学者对智能快件箱进行了多方面的研究。在智能快件箱与其他末端配送模式对比方面,王旭坪等[1]研究了在考虑碳税情况下,各种配送模式的成本,并分析其主要的影响因素及各种模式的适用性。Wang等[2]探讨了送货上门、智能快件箱、自助提货点3种配送模式的竞争力,并证明竞争力的主要影响因素包括订单量、人口密度、配送物品类型等。Xing等[3]通过比较分析有人值守式收发货点和无人值守式收发货点在配送成本、特点、效率和用户满意度等方面的差异,研究结果表明后者比前者在成本和效率方面更有优势。杨萌柯等[4]提出了一种以大数据、云计算等技术为基础,以智能快件箱为主,社区便利店为辅的共同配送系统。戢晓峰等[5]针对交通管制下的城市末端物流配送问题建立了双层规划模型,研究了不同管制时间窗下配送企业的运营成本及效率。在智能快件箱选址布局方面,邱晗光等[6]基于双层嵌套logit模型描述了消费者在选择末端交付方式及配送时间窗上的特点,建立了自提柜选址的多目标优化模型。陈义友等[7]提出了一种基于逐渐覆盖的自提点选址模型,计算了不同消费者数量,不同自提点类型下的选址结果。周林等[8]考虑“最后一公里”的配送特征,以系统集成优化的角度对送提一体与终端共享下的多主体共同配送选址—路径问题进行了研究。Deutsch等[9]针对快递柜的选址建立0-1整数规划模型,并设计了3阶段的求解算法。Schwerdfeger等[10]通过引入移动位置快件箱这一概念,并与传统的固定位置快件箱进行比较,结果表明能够通过布置更少的快件箱来满足同等数量用户的需求。施书彪等[11]就快件箱在校园的应用及选址进行了研究。左小德等[12]将粒子群算法引入自助快递包裹箱布点优化研究中,并与穷举法进行了对比。在智能快件箱配送系统优化方面,覃运梅等[13]考虑了基于自动快递机的车辆路径优化问题,并设计了元胞遗传算法对优化模型进行求解。贺冰倩等[14]研究了区域快件收派路线规划,优化了收派流程和路径生成算法。Lachapelle等[15]研究了智能快件箱的布置对城市交通的影响和意义,结果表明能够有效缓解交通拥堵,助力城市实现可持续发展。在智能快件箱效率及用户价值研究方面,Iwan等[16]以波兰一家快件箱运营企业的数据对智能快件箱在解决城市拥堵,提高末端配送效率方面的有效性进行了验证。Vakulenko等[17]对智能快件箱用户价值类型及用户价值创造过程进行了研究,研究结果有一定的开创性。
通过对上述文献的研究发现,目前学者对智能快件箱的研究更多集中在对各种配送模式对比分析、智能快件箱选址布局、智能快件箱收派路线优化等方面,但少有学者针对智能快件箱格口数量优化这一问题进行单独研究。截至2019年底,我国智能快件箱保有量已达41万组。但在行业实际操作中,大部分智能快件箱运营企业在进行布局时往往只注重选址,而格口数量多以经验方式来确定,这导致了格口数量与区域需求量不匹配,进而出现格口不足或大量闲置。智能快件箱的格口数量是在其选址确定以后影响用户使用体验最为关键的因素,因此有必要针对快件箱的格口数量优化问题建立相关模型,从理论上分析一个区域所需要的各种规格格口的最优数量,以此来为智能快件箱运营企业提供参考。
1 智能快件箱格口数量优化模型 1.1 问题描述及符号说明在给定区域内,用户对各种规格包裹的需求量已知,给定各种规格的格口,每种规格格口都有自己的成本和收入,在各种限制条件下,如何确定各种规格格口的数量,才能使得总成本最低,用户满意度水平最高。模型基本假设如下:
(1) 区域内的用户仅在拟设立的快件箱处取件;
(2) 不考虑其他取货方式对用户取件的影响;
(3) 快递员在投递时,不会将小规格快件放入到大规格格口中;
(4) 用户的满意度与自己的包裹能否成功地投递到快件箱中有关;
(5) 快件箱为第三方企业设立,接收来自多家快递企业的包裹;
(6) 快件箱所在地址的面积能够满足快件箱布置要求;
(7) 快递员一天工作时间为8:00—18:00,而用户取件时间为9:00—21:00;
(8) 区域内用户对各种规格包裹的需求总量服从泊松分布。
所用符号定义及说明如下:
xi为第i种规格的快件箱格口数量,即决策变量;I为快件箱规格数;W为观察期天数;desw为观察期内第w天各种规格包裹的需求总量;qwm1i为第w天第m1个时间段i规格格口的空闲量;dwm1i为第w天第m1个时间段快递员送到站点的第i种规格包裹数量;pwm1i为第w天第m1个时间段实际放入快件箱中的第i种规格包裹数量;Dwm2i为第w天第m2个时间段到达站点来取第i种规格包裹的用户数量;c1i为第i种规格格口的单位固定成本;c2i为第i种规格格口的单位变动成本;c3i为因第i种规格格口不足而导致的惩罚成本;c4i为因第i种规格格口闲置带来的损失;Z为总成本;Y表示用户满意度。
根据假设(7),将快递员工作时间分为2个时间段,8时~14时,14时~18时,即m1=1, 2。同时将用户取件时间分为12个时间段,即m2=1, 2, …,12。由于快递员并不是在某一个固定的时间点到达快件箱站点配送,因此将同一时段内到达快件箱站点的包裹视为一个批次。
显然,快件箱格口数量、格口闲置数量、快递员送达站点的包裹数量、实际放入快件箱的包裹数量以及到达站点来取件的用户数量之间有如下关系:
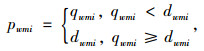
|
(1) |
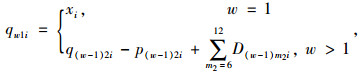
|
(2) |

|
(3) |
在建立模型之前首先需要分析影响快件箱格口需求数量的因素。结合快件箱的实际运作情况,可以得出影响快件箱格口需求数量的因素主要有如下3点:
(1) 快递量:快递量显然是快件箱格口需求数量的决定性影响因素,在不考虑其他影响因素的情况下,快件箱格口需求数量与快递量是正相关的。由于假设区域内的客户仅在拟设立的快件箱处取件,因而此处的快递量仅指用快件箱完成派件的快递包裹数量。
(2) 配送快递中各种规格的比例:同一批次送达快件箱的快递中各种规格的比例将显著影响各种规格格口的具体数量,所占比例越高,则所需格口数量也越多。
(3) 用户取件习惯:指的是用户是准时取件还是延迟取件。理想的情况是快递员将包裹入箱之后,用户即前往站点取件,但是在多数情况下,用户并不能准时取件。当下一批次的包裹到达时,如果快件箱中仍有大量包裹未取,则此时能够入箱的包裹数量会相应减少,而为了达到包裹入箱率的要求,必定会需要更多格口。因此,用户的取件习惯将会影响格口的数量。
基于以上对影响因素的分析及1.1节所设定的参数,建立如下以总成本最小化为目标的优化模型,其中用户满意度水平最高即用户包裹入箱率最高。

|
(4) |
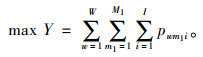
|
(5) |
约束条件为:
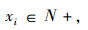
|
(6) |
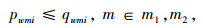
|
(7) |
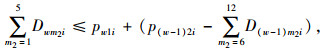
|
(8) |

|
(9) |

|
(10) |
目标函数式(4)由4项构成,分别为各种规格格口固定成本、各种规格格口变动成本、因格口不足导致的惩罚成本以及因格口数量过剩导致的闲置成本。目标函数式(5)表示实际放入的包裹数最大,也即用户满意度最大化。约束式(6)表示决策变量取正整数值。约束式(7)表示每批次放入快件箱的包裹数不应超过快件箱空闲格口数。约束式(8),(9)表示每个配送批次前往站点取件的总人数不应大于快件箱中所有的快递量。约束式(10)表示观察期内空闲格口总数占总格口数的比例不应高于某一确定值α。为了降低模型的求解难度,将目标函数式(5)转化为约束条件,可得式(11),即观察期内总放入快件箱的快递占总需求的比例不得低于某一确定值β。

|
(11) |
上述问题可以简约定义为:在快件箱的格口规格已经确定的前提下,每种格口都有自己的成本和收入,在各种限制条件下,如何选择各种格口的数量,才能使得总成本最低。通过研究问题的本质,可以发现智能快件箱的格口数量优化问题与背包问题有一定的相似性。而背包问题属于经典的NP完全问题,因此需要设计相应的智能优化算法来求解。
群智能优化算法已经被证明在求解大规模背包问题上有较好的效果,而在这其中,粒子群算法(PSO)又由于其易于实现,收敛速度快,且需要调整的参数少,目前在函数优化、神经网络训练等诸多领域已经得到了广泛应用。但粒子群算法也存在着陷入局部最优解无法跳出而早熟收敛的情况,究其原因,主要是粒子在寻优的过程中不断向个体最优和群体最优靠近,进而导致种群中的个体过于相似,算法的局部开发能力较差。针对基本粒子群算法的不足,学者做了诸多改进。Huang等[18]在基本粒子群算法中增加了进化速度控制器,根据粒子群的实际情况,适时地进行放缓或者加速进化操作,增强了算法在不同状况下的适应能力。在综合比较诸多改进算法性能的基础上,采用上述带收敛速度控制器的改进粒子群算法来求解1.2节所提出的模型。
在运用粒子群算法进行求解之前,必须要确定问题的编码方式。考虑智能快件箱格口数量的特性,因此采用实数对粒子进行编码,每个粒子均代表着一种可能的格口需求数量布置方案,粒子的维度即为快件箱不同大小规格种类数量。假设快件箱共有M种规格,粒子群中共有N个粒子,则粒子群可以表示为:

|
(12) |
这是一个N×M的矩阵。根据问题的实际背景,显然每一种规格格口的数量应该要有一个范围。参考实际行业运行情况,将快递包裹量均值d0作为上限,将其1/2作为下限,即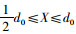
假设某快件箱企业有意在A城市某小区内布置一套快件箱。目前企业委托生产的一套快件箱拥有3种规格的格口,分别是小格口为(34×45×8) cm3,中格口为(34×45×19) cm3,大格口(34×45×29) cm3,调查发现该小区除了符合以上3种规格的快递之外,还有部分快递包裹的长度远远没有达到标准快件箱的34 cm,因此为了充分利用快件箱的空间,有必要增设一些长度小于34 cm的格口。通过调查大量包裹数据以及与部分快递员进行交流,同时考虑到标准制造的重要性,即不宜同时改动标准快件箱的三维,因此增设长度为20 cm的短规格格口。这样一来,某快递企业在该小区设立的快件箱就将有6种尺寸的格口,除了上述的标准快件箱格口外,还有短规格的3种格口,具体尺寸分别为短规格小格口(20×45×8) cm3,短规格中格口(20×45×19) cm3,短规格大格口(20×45×29) cm3。
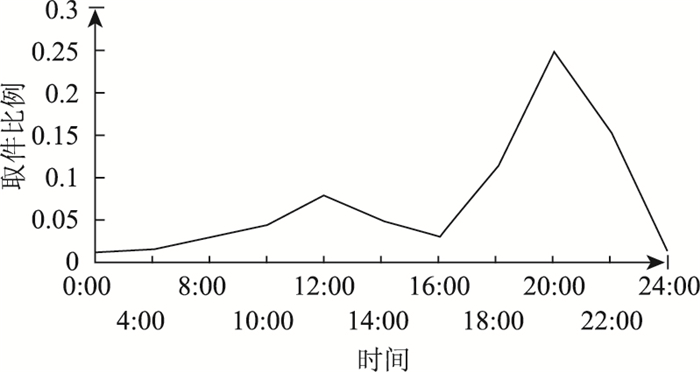
通过调查,该小区快递符合上述6种不同规格格口的比例为[标准大:中:小:短组大:中:小]=[0.09:0.32:0.23:0.17:0.14:0.05];快件箱的建设成本c1i=[569, 373, 157, 334, 219, 92] (元)。快件箱的变动成本主要包括电费、通信费、维护费, 根据现行运行数据,这3项费用一年的总和约为3 000元,则快件箱的单位变动成本c2i=[0.8, 0.5, 0.2, 0.5, 0.3, 0.1](元)。目前该快件箱企业向快递员收取存件费,因而当某种规格的格口数量不足时,以上存件费可视为机会收入损失,具体费用为c3i=[0.6, 0.5, 0.4, 0.5, 0.3, 0.2] (元)。此外,将每种规格格口的折旧视为该种规格格口闲置时的损失,则c4i=[0.09, 0.06, 0.03, 0.05, 0.04, 0.01](元·h)。在以往相关的文献中,都假设用户均匀到达站点取件,但实际上据第三方代收货服务商收货宝在2014年发布的《中国代收货行业发展报告》显示, 如图 1所示,用户取货有明显的时间段,多集中在12:00—14:00以及17:30—20:00。据此,结合假设(7)与实际用户取件行为,确定该小区一天之内12个小时各个时段取件人数的比例p=[0.02:0.03:0.05:0.06:0.12:0.05:0.02:0.03:0.1:0.2:0.25:0.07]。此外,通过实际运行情况中的数据确定约束式(10)和(11)中的参数分别为α=0.1,β=0.85,即平均格口闲置率不得高于10%,平均包裹入箱率不应低于85%。
|
| 图 1 收货宝用户取货规律 Fig. 1 Pick-up habits of users according to Shouhuobao |
| |
以随机生成的方式来模拟未来一段时间内该小区的快递包裹需求量,为此,假设该小区快递包裹量服从均值d0=100的泊松分布,以30天的模拟需求数据来进行计算。同时,模型中内含了一些重要的随机变量,分别是每天两个批次的配送比例、各个批次中各种规格的比例以及每个时段到达站点取件的人数,这些数据均以计算机产生随机数的方式来模拟,而为了尽量减少随机性对结果的影响,以500次独立运行结果的均值作为最终输出。此外,以罚函数的形式处理约束式(10)和(11),在500次独立运行中,若某次未满足约束条件,则加上罚因子(较大的正数),使之无法达到最小。
2.3 计算结果及灵敏度分析以上述粒子群算法求解该算例,其中必要的参数如下:粒子群规模为40,最大迭代次数为500代,惯性权重wei=0.8,学习因子c1=c2=1.5。以下结果均假设用户能够及时前往站点取件。经过迭代求解,最终的结果如表 1所示。
| 规格 | 标准大 | 标准中 | 标准小 | 短组大 | 短组中 | 短组小 | 总和 | 目标函数值 |
| 结果 | 4 | 14 | 10 | 9 | 6 | 2 | 45 | 14 350 |
目前该企业采用的格口需求数量确定方法是经验方法,即在某个地区布置多少格口只参考区域内快递量,多为快递量的60%。由2.2节可知,该企业的快件箱仅有3种规格格口,且每组快件箱各种规格格口之间的比例是固定的,一般由12个标准小格口、8个标准中格口、2个标准大格口组成。因此,按照传统布置方案,该快件箱企业在A城市该小区内布置的快件箱格口数量如表 2所示。
| 规格 | 标准大 | 标准中 | 标准小 | 总和 | 目标函数值 |
| 结果 | 6 | 24 | 36 | 66 | 18 966 |
通过表 1和表 2的结果计算可得相比于传统布局方案,由模型计算得到的方案在成本上降低了24%,整体闲置率下降了20%,收益显著。
由1.2节的分析可知,影响快件箱格口需求数量的因素主要有快递量、送达快件箱的快递中各种规格之间的比例以及用户取件习惯,因而针对以上3种影响因素进行灵敏度分析,以此来定量化描述这3种因素对快件箱格口需求数量的影响。
(1) 快递量灵敏度分析:共设计快递量均值增加10%,20%及减少10%,20%这4种情况,进行独立试验,算法的运行参数同基础求解时的参数,最终结果如表 3所示。
| 规格 | 标准大 | 标准中 | 标准小 | 短组大 | 短组中 | 短组小 | 总和 | 目标函数值 |
| 快递量 | ||||||||
| des+20% | 5 | 16 | 13 | 9 | 8 | 3 | 54 | 16 809 |
| des+10% | 5 | 15 | 12 | 8 | 7 | 3 | 50 | 15 660 |
| des | 4 | 14 | 10 | 9 | 6 | 2 | 45 | 14 350 |
| des-10% | 4 | 13 | 10 | 7 | 5 | 2 | 41 | 13 012 |
| des-20% | 3 | 12 | 8 | 6 | 5 | 2 | 36 | 11 339 |
对表 3的结果进行分析发现各种规格格口需求数量的变化与快递量的变化是不完全一致的。在总量一定的情况下,所占比例越高的格口,其对快递量变化的敏感度越高。具体来说,标准组中格口、小格口、短组中格口的变化幅度大于快递量的变化幅度,而另外3种规格格口需求数量的变化幅度则小于快递量的变化幅度。
(2) 配送快递中各种规格的比例灵敏度分析:该小区原快递符合6种不同规格格口的比例为[标准大:中:小:短组大:中:小]=[0.09:0.32:0.23:0.17:0.14:0.05],现针对每一种规格格口的比例进行灵敏度分析,在规格比例中分别就某一种规格的比例增加10%,20%及减少10%,20%,每次运行保证只有一种规格的比例发生变化。例如标准大格口的比例增加20%,则此时各种规格格口的比值为[标准大:中:小:短组大:中:小]=[0.11:0.31:0.22:0.17:0.14:0.05]。通过算法求解得出的各种规格尺寸格口需求数量如表 4所示。
| 变化/% | 规格 | |||||
| 标准大 | 标准中 | 标准小 | 短组大 | 短组中 | 短组小 | |
| +20 | 5, 14, 10, 8, 6, 2 | 4, 16, 10, 7, 6, 2 | 4, 14, 12, 7, 6, 2 | 4, 14, 10, 9, 6, 2 | 4, 14, 10, 8, 8, 2 | 4, 14, 10, 8, 6, 3 |
| +10 | 5, 15, 10, 8, 6, 2 | 4, 16, 10, 8, 6, 2 | 4, 14, 11, 8, 6, 2 | 4, 15, 11, 9, 6, 2 | 4, 14, 10, 8, 7, 2 | 4, 15, 11, 8, 6, 3 |
| -10 | 4, 15, 10, 8, 6, 2 | 4, 13, 11, 8, 7, 2 | 4, 15, 10, 8, 6, 2 | 4, 15, 11, 7, 6, 2 | 4, 15, 10, 8, 6, 2 | 4, 15, 11, 8, 6, 2 |
| -20 | 3, 15, 11, 8, 6, 2 | 4, 13, 11, 8, 7, 2 | 4, 15, 9, 8, 7, 2 | 4, 15, 11, 6, 7, 2 | 4, 15, 11, 8, 5, 2 | 4, 15, 10, 8, 6, 2 |
对表 4中的结果分析发现配送快递中各种规格比例的变化对不同规格格口需求数量的影响程度并不完全一致,具体而言,标准大格口、短组大格口和短组小格口的需求数量基本不受快递中各种规格比例变化影响,但标准中格口、标准小格口和短组中格口的需求数量受影响较大,且数量变化幅度稍大于这3种规格快递比例的变化幅度。
(3) 用户取件习惯的灵敏度分析:理想情况下,用户在收到取件通知时,将即刻前往快件箱取件,因而针对用户取件习惯的灵敏度分析设置以下几种情形,分别为用户在下一批次包裹送达之前将包裹全部取走,90%的包裹被取走,即延迟取件比例为10%,80%的包裹被取走,70%的包裹被取走,以及一种极端情况下,仅有40%的包裹被及时取走。计算结果如表 5所示。
| 用户延迟取件比例/% | 快件箱格口数量布置方案 |
| 0 | 4, 14, 10, 9, 6, 2 |
| 10 | 5, 16, 12, 9, 7, 3 |
| 20 | 5, 18, 13, 10, 8, 3 |
| 30 | 6, 20, 14, 11, 9, 3 |
| 60 | 10, 35, 25, 18, 15, 5 |
对表 5中的结果分析发现用户取件习惯对格口需求数量也有较大影响,随着用户取件积极性的下降,即越来越多的用户选择延迟取件,这相当于变相的增加了快递量,为了不影响后续用户的取件,快件箱公司不得不布置更多的格口。具体而言,用户延迟取件的比例每增加10%,整体的快件箱格口需求数量将增加12%,但当用户延迟取件的比例增加超过50%,此时用户延迟取件的比例再增加10%,整体快件箱格口需求数量的增加将低于10%。
上述灵敏度分析的结果为快件箱企业在布置快件箱之前的调查工作提供了思路,即在布置快件箱时,除了获得相对准确的区域快递需求量以外,还有快递中各种规格的比例,更为重要的是要调查区域内用户的取件习惯以及具体的延迟取件比例。
3 结论(1) 针对快件箱运营企业采用经验确定方法所导致的同时存在格口不足与闲置的问题,建立了以成本为目标同时考虑用户满意度的优化模型,并且将用户满意度转化为约束条件处理,降低了求解的难度。
(2) 采用性能较优越的带收敛速度控制的粒子群算法来求解模型;算例结果表明,由本模型计算得到的智能快件箱格口数量布置方案在成本上降低了24%,整体闲置率下降了20%,系统优化布置有较大的改进。
(3) 通过对相关影响因素进行灵敏度分析,定量化描述相关因素对格口需求数量的影响幅度,结果表明快递量均值减少10%,格口需求总数将减少约9%,而快递量均值增加10%,格口需求总数将会增加约11%,并且不同规格格口对需求量变化的敏感程度也不相同;标准组大格口、短组大格口和小格口3种规格的需求数量对配送快递中各种规格的比例值变化敏感程度不高,而另外3种随着比例的变化会有明显的波动;用户延迟取件的比例每增加10%,格口需求总数会增加12%左右。
(4) 模型在考虑用户满意度时仅将其与快递入箱率相关联,并未考虑用户取件这一活动本身可能存在的排队现象对用户满意度的影响,因此下一步可以考虑更多影响因素,使模型更加完整。
| [1] |
王旭坪, 詹林敏, 张珺. 考虑碳税的电子商务物流最后一公里不同配送模式的成本研究[J]. 系统管理学报, 2018, 27(4): 776-782. WANG Xu-ping, ZHAN Lin-min, ZHANG Jun. Cost of Different E-logistics "Last Mile" Delivery Mode Considering Carbon Tax[J]. Journal of Systems & Management, 2018, 27(4): 776-782. |
| [2] |
WANG X, ZHAN L, RUAN J, et al. How to Choose "Last Mile" Delivery Modes for E-fulfillment[J]. Mathematical Problems in Engineering, 2014, 2014: 1-11. |
| [3] |
XING Y, GRANT D B, MCKINNON A C, et al. Physical Distribution Service Quality in Online Retailing[J]. International Journal of Physical Distribution & Logistics Management, 2010, 40(5): 415-432. |
| [4] |
杨萌柯, 周晓光. "互联网+"背景下快递末端协同配送模式的构建[J]. 北京邮电大学学报:社会科学版, 2015, 17(6): 45-50. YANG Meng-ke, ZHOU Xiao-guang. Construction of Collaborative Distribution Pattern at the Terminal of Express under the Background of "Internet Plus"[J]. Journal of Beijing University of Posts and Telecommunications:Social Sciences Edition, 2015, 17(6): 45-50. |
| [5] |
戢晓峰, 普永明, 梁斐雯, 等. 交通管制时限条件下城市物流配送优化双层规划模型[J]. 公路交通科技, 2014, 31(12): 145-152. JI Xiao-feng, PU Yong-ming, LIANG Fei-wen, et al. Bi-level Programming Model for City Logistics Distribution Optimization under Time Restrict Condition Caused by Traffic Control[J]. Journal of Highway and Transportation Research and Development, 2014, 31(12): 145-152. |
| [6] |
邱晗光, 周愉峰. 基于嵌套Logit选择模型的城市配送自提柜选址-路径问题[J]. 计算机应用, 2018, 38(2): 582-588. QIU Han-guang, ZHOU Yu-feng. Reception Box Locating-vehicle Routing Problems in Urban Distribution Based on Nested Logit Model[J]. Journal of Computer Applications, 2018, 38(2): 582-588. |
| [7] |
陈义友, 陈以衡. 基于逐渐覆盖的自提点选址模型与算法研究[J]. 计算机应用研究, 2016, 33(8): 2275-2277, 2297. CHEN Yi-you, CHEN Yi-heng. Research on Pickup point Location Model and Algorithm in Presence of Gradual Coverage[J]. Application Research of Computers, 2016, 33(8): 2275-2277, 2297. |
| [8] |
周林, 康燕, 宋寒, 等. 送提一体与终端共享下的最后一公里配送选址:路径问题[J]. 计算机集成制造系统, 2019, 25(7): 1855-1864. ZHOU Lin, KANG Yan, SONG Han, et al. Location-routing Problem for Last Mile Delivery with Simultaneous Home Delivery and Customer's Pickup Based on Terminal Sharing[J]. Computer Integrated Manufacturing Systems, 2019, 25(7): 1855-1864. |
| [9] |
DEUTSCH Y, GOLANY B. A Parcel Locker Network as a Solution to the Logistics Last Mile Problem[J]. International Journal of Production Research, 2018, 56(1/2): 251-261. |
| [10] |
SCHWERDFEGER S, BOYSEN N. Optimizing the Changing Locations of Mobile Parcel Lockers in Last-mile Distribution[J]. European Journal of Operational Research, 2020, 285(3): 1077-1094. |
| [11] |
施书彪, 黄有方, 严伟. 智能柜在校园快递配送中的应用研究[J]. 计算机仿真, 2015, 32(9): 421-424. SHI Shu-biao, HUANG You-fang, YAN Wei. Research on Automatic Logistc Terminal Equipment Application in Campus Express[J]. Computer Simulation, 2015, 32(9): 421-424. |
| [12] |
左小德, 黄钦, 李璨, 等. 基于粒子群算法的自助快递包裹箱布点优化研究[J]. 系统工程, 2018, 36(5): 139-149. ZUO Xiao-de, HUANG Qin, LI Can, et al. The Optimization Research of the Serf-help Delivery Package Box Distribution with Particle Swarm Algorithm[J]. Systems Engineering, 2018, 36(5): 139-149. |
| [13] |
覃运梅, 毛海军, 黑秀玲. 基于自动快递机的快递配送车辆路径优化研究[J]. 公路交通科技, 2015, 32(10): 134-140. QIN Yun-mei, MAO Hai-jun, HEI Xiu-ling. Optimizing of Vehicle Routing for Express Delivery Based on Automatic Parcel Machine[J]. Journal of Highway and Transportation Research and Development, 2015, 32(10): 134-140. |
| [14] |
贺冰倩, 李昆鹏, 成幸幸. 快递企业"最后一公里"快件收派优化方案研究[J]. 运筹与管理, 2019, 28(1): 27-34. HE Bing-qian, LI Kun-peng, CHENG Xing-xing. The Research on the Optimization of Courier Companies "Last-mile" Express Pickup and Delivery Process[J]. Operations Research and Management Science, 2019, 28(1): 27-34. |
| [15] |
LACHAPELLE U, BURKE M, BROTHERTON A, et al. Parcel Locker Systems in a Car Dominant City:Location, Characterisation and Potential Impacts on City Planning and Consumer Travel Access[J]. Journal of Transport Geography, 2018, 71: 1-14. |
| [16] |
IWAN S, KIJEWSKA K, LEMKE J. Analysis of Parcel Lockers' Efficiency as the Last Mile Delivery Solution-The Results of the Research in Poland[J]. Transportation Research Procedia, 2016, 12: 644-655. |
| [17] |
VAKULENKO Y, HELLSTRÖM D, HJORT K. What's in the Parcel Locker? Exploring Customer Value in E-commerce Last Mile Delivery[J]. Journal of Business Research, 2018, 88: 421-427. |
| [18] |
HUANG H, LÜ L, YE S, et al. Particle Swarm Optimization with Convergence Speed Controller for Large-scale Numerical Optimization[J]. Soft Computing, 2019, 23(12): 4421-4437. |
 2021, Vol. 38
2021, Vol. 38
