扩展功能
文章信息
- 陈汨梨, 赵孝进, 邓夕贵, 郑长江, 杜牧青
- CHEN Mi-li, ZHAO Xiao-jin, DENG Xi-gui, ZHENG Chang-jiang, DU Mu-qing
- 不确定条件下的多式联运路径优化
- Multimodal Transport Path Optimization under Uncertain Conditions
- 公路交通科技, 2021, 38(1): 143-150, 158
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(1): 143-150, 158
- 10.3969/j.issn.1002-0268.2021.01.018
-
文章历史
- 收稿日期: 2020-04-17
2. 河海大学 土木与交通学院, 江苏 南京 210098
2. School of Civil and Transportation Engineering, Hohai University, Nanjing Jiangsu 210098, China
多式联运是指货物由一种且不变的运载单元装载,相继以两种及以上运输方式运输,并且在转换运输方式的过程中不对货物本身进行操作的运输形式[1]。与单一道路运输方式相比,在一定条件下,采用多式联运可降低约20%的运输成本[2]。
实际多式联运过程中,受到复杂的社会环境(交通主管部门管理水平影响),多变的交通状况(交通堵塞频繁发生)和个性的托运人时间需求[3]的综合影响,货物运输速度、转运时间以及送达约定时间都可能存在不确定性。目前运输企业大都根据运输经验规划多式联运路径方案,不确定因素可能会导致运输时间的延误或运输费用的损失。因此,对不确定条件下的货物多式联运路径优化研究具有较强的实际工程意义。
国内外学者对不确定条件下的多式联运路径规划问题讨论的侧重点包括运输时间不确定性,运量不确定性,以及客户需求不确定性等方面。Baradaran等[4]分别对确定的运输时间和需求,不确定运输时间和确定需求,以及不确定运输时间与需求3种条件下具有多个硬优先级时间窗口的路径优化问题进行了讨论。Kalinina等[5]建立了以运输时间、成本和碳排放为目标的机会约束模型,研究了不确定送达延误时间条件下,货物多式联运路径方案的选择问题。Goel等[6]以运输成本最小为目标,建立随机需求和随机服务时间条件下带时间窗的车辆路径优化模型,并利用蚁群算法进行模型求解。于雪峤等[7]以总费用最低为目标,构建了基于运量不确定的多式联运网络优化模型,并研究了运量的不确定性,运输路径与节点能力的变化对路径规划产生的影响。李珺等[8]建立混合不确定条件下绿色多式联运路径优化模型,得出考虑不同成本因素的路径优化方案,并探讨了时间、需求和网络服务能力变化对路径优化结果产生的影响。赵祎[9]考虑海铁联运过程中的运输时间、转运时间和客户需求的不确定性,构建了箱流路径随机机会约束规划模型,并采用混合启发式算法求解模型。综上所述,运输过程中的不确定性已引起越来越多国内外学者的关注,至于不确定条件的变化是否对路径优化结果产生影响,以及对于影响能力的评估,目前还没有系统的研究。
本研究考虑了多式联运过程中的不确定性,设计了多式联运路径优化模型,采用K短路算法进行模型求解,并通过灵敏度分析,深入探讨不确定条件的变化对路径优化结果造成的影响。
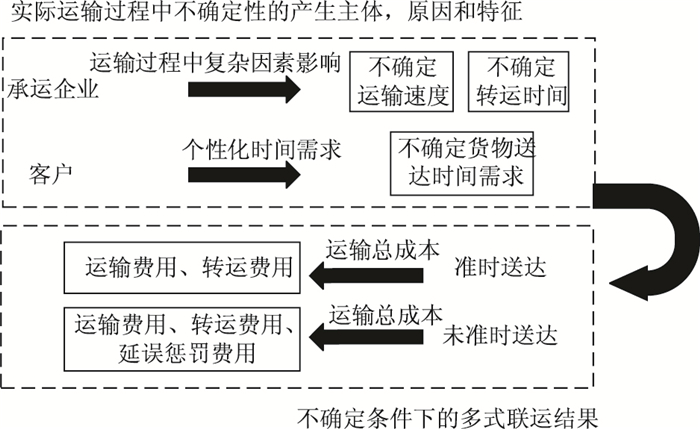
1 问题与模型 1.1 问题描述实际多式联运过程中可能出现的不确定性及成因如图 1所示。基于此,本研究的问题是:不确定条件下,如何在起点与终点之间规划路径方案,使货物满足送达时间约束,并获得最优经济效益。再者,如何评估不确定条件的变化对运输时间和成本造成的影响,为企业提供风险决策支持。为解决以上两个问题,本研究建立了多式联运路径优化模型并进行求解。
|
| 图 1 研究问题描述 Fig. 1 Description of study problem |
| |
1.2 模型假设
构建不确定条件下的多式联运路径优化模型前,需考虑的相关假设条件如下:
(1) 同一批货物运输过程中不可拆分;
(2) 相同运输方式,相邻节点之间仅有1条路径;
(3) 多式联运网络有向无环图,运输路径为简单路径,同一批货物相同节点或路径至多经过1次;
(4) 所有节点都具备货物转运能力,节点上相同运输方式之间的转运费用为0。
1.3 符号说明将多式联运网络抽象为图G=(N, A, M),其中:N为网络中的点集合; A为运输路径集合; M为运输方式集合。不确定条件下的多式联运路径优化模型中的符号及其定义详见表 1。
| 参数 | 定义 |
| h, i, j | 运输节点,h, i, j∈N |
| (h, i) | 运输路径,(h, i)∈A |
| k, l | 货物运输方式,k, l∈M |
| Q/t | 货运总量 |
| NI | 与i点相邻节点集合 |
| M(h, i) | 路径(h, i)运输方式集合,M(h, i)⊆M |
| Tm/h | 货物运输和转运时间 |
| Tod/h | 货物约定送达时间 |
| qi/t | 节点i转运换装能力 |
| Cod/[万元/(t·h)] | 延误惩罚费用 |
| C | 运输总成本 |
| r | 随机模拟次数 |
| R | 随机模拟次数上限 |
| α | 准时送达概率阈值 |
| q(h, i)k/t | k运输模式下运输路径(h, i)通过能力 |
| S(h, i)k/km | k运输模式下运输路径(h, i)距离 |
| v(h, i)k/(km·h-1) | k运输模式下路径(h, i)运输速度 |
| Cik, l/元 | 节点i处从方式k转向方式l的中转费用 |
| Tik, l/h | 节点i从方式k转向方式l的中转时间 |
| C(h, i)k/元 | k运输模式下运输路径(h, i)运输费用 |
| T(h, i)k/h | k运输模式下运输路径(h, i)运输时间 |
| μ=sgn(x) | 符号函数,返回参数的正负。x为数值型参数,x=Tm-Tod。当x < 0时,返回值为-1;当x=0时,返回的函数值为0;当x>0时,返回值为1 |
1.4 模型建立
模型的运输费用与转运费用之和、运输总时间以及延误惩罚费用的计算公式如下:
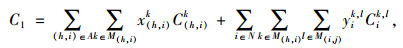
|
(1) |
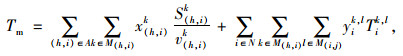
|
(2) |

|
(3) |
式中,货物运输速度为不确定值,导致模型无法求得精确解。因此,本研究结合随机期望值模型[10]与机会约束规划理论[7],将货物是否能够准时送达目的地以概率形式表示,建立不确定条件下的路径优化组合模型,模型的目标函数和约束条件表示为:

|
(4) |
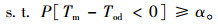
|
(5) |
利用Monte Carlo方法[10],将随机期望值模型转换为混合整数规划模型,以降低模型求解复杂度。Monte Carlo方法能够将所求解的问题同一定的概率模型相联系,用统计方法估计模型的数字特征,从而获得实际问题的近似解。
令r=1, 2, …, R,引入随机向量δr,该向量由不确定变量v(h, i)k的一组样本组成,定义变量h(δr),当路径方案中货物准时送达即Tm-Tod < 0时,h(δr)=1;当Tm-Tod≥0,h(δr)=0。设F'=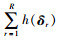
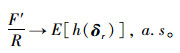
|
h(δr)返回0-1值,P(Tm-Tod < 0)与E[h(δr)]等值。那么,货物准时送达概率值P(Tmr-Tod < 0)可以通过F′/R进行估计;同理,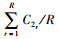
目标函数:
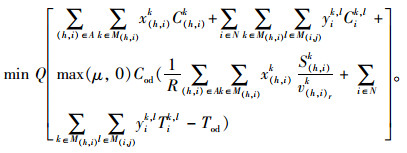
|
(6) |
约束条件:
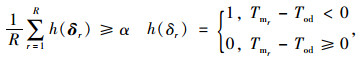
|
(7) |
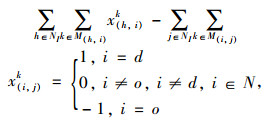
|
(8) |

|
(9) |

|
(10) |

|
(11) |

|
(12) |

|
(13) |

|
(14) |
公式(1)表示运输费用与转运费用之和;公式(2)表示货物运输和转运时间之和;公式(3)表示货物未在指定时间内送达产生的惩罚费用;公式(4)为期望目标函数;公式(5)为送达时间机会约束条件;公式(6)和公式(7)为大数定律转换后的目标函数和约束条件,公式(7)保证货物存在至少α的概率能够准时到达目的地。公式(8)~(14)为公式条件,公式(8)保证相邻运输路径之间货物流量守恒;公式(9)表示x(h, i)k为0-1决策变量,若货物以k方式经过运输路径(h, i),则x(h, i)k=1,否则x(h, i)k=0;公式(10)表示yik, l为0-1决策变量,若在i点发生运输方式的转换,则yik, l=1,否则yik, l=0;公式(11)表示同一物流需求在一条运输路径上采用的运输方式不超过1种;公式(12)表示在一个节点上进行的货物转运环节不超过1次;公式(13)表示任意弧上的货物量小于等于路径的运输能力;公式(14)表示任意转运节点的货物量小于等于其转运能力。
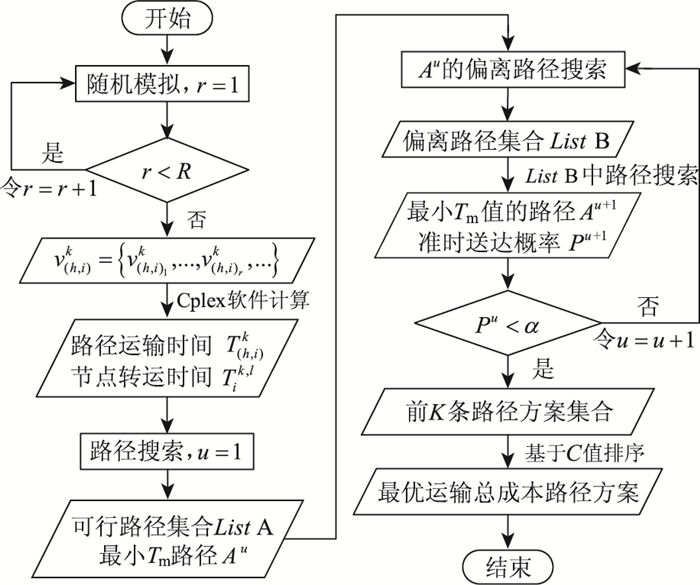
2 求解方法采用K短路算法求解混合整数规划模型,该方法能够降低计算复杂度,突出模型优化结果的特征性,详细的求解流程如图 2所示。
|
| 图 2 求解方法流程图 Fig. 2 Flowchart of solution approach |
| |
模型求解具体流程主要包括以下几个步骤:
步骤1:基础数据收集
收集模型求解的基础数据,包括:节点转运能力;路径服务能力;各运输方式的运输路径里程;单位运价;转运单价。
步骤2:运输速度随机数值生成方法
设各运输方式的速度v(h, i)k服从正态分布N(μ, σ2)[11],μ表示数学期望,决定了速度的均值;σ2表示方差,决定了速度变化的稳定程度,正态分布随机数的产生方法如下:
步骤2.1:产生服从均匀分布U(0, 1)的随机数μ1和μ2;
步骤2.2: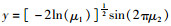
步骤2.3:v(h, i)k=μ+σy。
步骤3:最优路径方案求解
将收集的基础数据与生成的运输速度随机值置入Cplex优化求解器,进行模型参数求解;采用K短路算法筛选符合时间约束运输路径,并输出总成本最优的运输路径方案。K短路算法能够反映总成本最优的路径结果在符合机会约束路径方案集合中的排列次序,即时间优势度[12]。
步骤3.1:参数求解与路径搜索
求解路径运输时间T(h, i)k,节点转运时间Tik, l,路径运输费用以及节点转运费用。对多式联运网络进行路径搜索,输出可行路径集合List A,以运输时间T(h, i)k和转运时间Tik, l之和为边权值,在List A中搜索Tm最小的路径A1。
步骤3.2:机会约束条件下前K条路径筛选
K短路算法指在有向无环图G中,对于给定的起点和终点,输出路径的边权值长度从最短到第K短的路径[13],算法的运行步骤如下:
步骤3.2.1:初始化偏离路径集合List B,令 u=1, 2, …, K,以T(h, i)k和Tik, l之和为边权值,寻找Au所有的偏离路径,逐个添加至List B。偏离路径具有与原路径相同起点,终点与一定数量的公共节点,但在某些节点上偏离了原路径[14]。
步骤3.2.2:从List B中提取最小运输总时间的路径Au+1,同时输出该路径方案的货物准时送达概率Pu+1值。
步骤3.2.3:重复步骤3.2.1至3.2.2共K次。
步骤3.2.4:若第K+1次的输出值PK+1小于α,迭代过程结束,输出前K条符合机会约束的路径方案集合List K。
步骤3.3:输出运输总成本最优的路径方案
根据货物约定送达时间Tod,计算List K中各方案的延误惩罚费用以及运输总成本,并基于运输总成本值排序,输出最优路径方案。
3 实例研究与分析 3.1 参数和相关数据在“一带一路”倡议的推动下,西非几内亚湾沿岸国家与我国的经贸往来日益频繁,跨境跨区域联运走廊的不断完善,多式联运系统的构建迎来了良好的战略机遇期。因此,对西非区域的多式联运路径优化研究与分析具有重要的现实与战略意义。
将区域内无水港的所在城市作为节点,将公、铁、水路网作为运路径,开展多式联运路径优化研究。节点和路径数量分别为19和29,各节点之间不同运输方式路径的里程详见图 3。
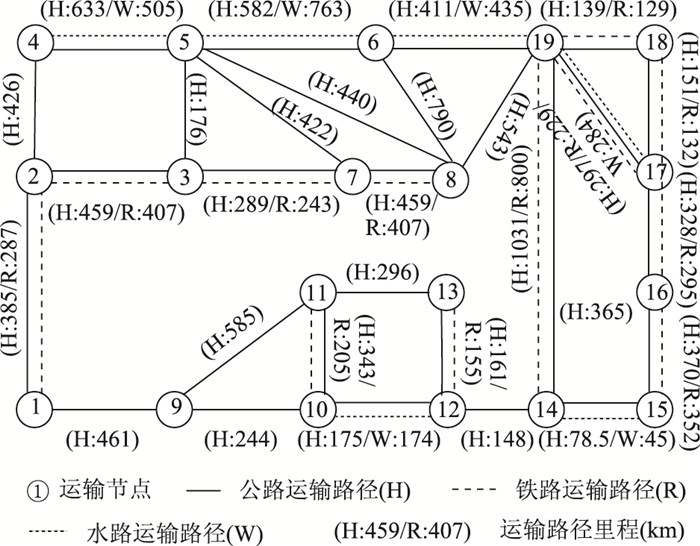
|
| 图 3 西非区域运输网络 Fig. 3 Regional transport network in West Africa |
| |
区域内现有公路等级较低,铁路电气化普及度不高,水路船舶机械化程度低。因此,公路运输速度参照我国三级公路标准,规定货运铁路速度低于40 km/h。3种运输方式的速度服从正态分布,设公路运输速度服从v(h, i)k~N(40, 10),铁路运输速度服从v(h, i)l~N(35, 5),水路运输速度服从v(h, i)m~N(20, 5)。西非物流企业的轴载货汽车等重型运输工具保有量少,因此一次运输作业的载货量上限较低,设本次运输的货物总重量为30 t。节点的最大转运能力和运输路径的最大服务能力都大于货物总重,分别取50 t和70 t。
参照我国物流行业的定价标准,并根据西非区域社会经济发展现状进行适当调整,公路、铁路和水路的运费定价标准如表 2所示。
| 运输方式 | 定价标准/[元/(t·km)] | 备注 | |
| 公路 | 0 < x < 200 | 1.5 | 单位:元/(t·km) x为里程,z1为发到基价,取11.4,z2为运行基价,取0.23。 |
| 200 < x < 500 | 0.75 | ||
| 500 < x < 1 000 | 0.55 | ||
| x>1 000 | 0.35 | ||
| 铁路 | z1+z2×x | ||
| 水路 | 0.03 | ||
转运价格和转运时间的设置参照我国物流企业的定价标准与转运经验,具体数值参见表 3。
| 中转方式 | 转运价格/(元·t-1) | 转运时间/h | |
| 公铁互转 | 6.7 | 公铁 | 铁公 |
| 6 | 4 | ||
| 公水互转 | 9.9 | 公水 | 水公 |
| 5 | 3 | ||
| 铁水互转 | 11.8 | 铁水 | 水铁 |
| 7 | 8 | ||
当货物无法准时到达时,承运公司将支付托运人一定的惩罚费用,惩罚费用的计价方式为超过规定运输时间1 h,支付2%的运输费用与转运费用之和作为惩罚费用,支付阈值为40%。
3.2 优化结果分析取随机次数R=50,运输规定时间Tod=50 h,送达时间约束概率阈值α=60%。利用K短路算法,输出的路径筛选结果如表 4所示,其中,加粗点表示货物转运节点。
| 路径方案 | 运输方式 | 运输时间 | 中转时间 |
| 1-2-3-7-8-19 | 全程公路 | 47.184 | 0 |
| 1-2-3-7-8-19 | 铁-公 | 43.718 | 4 |
| 1-2-3-7-8-19 | 铁-公 | 44.14 | 4 |
| 1-2-3-7-8-19 | 铁-公 | 44.802 | 4 |
| 1-2-3-7-8-19 | 铁-公 | 45.252 | 4 |
| 1-9-10-12-14-19 | 全程公路 | 49.91 | 0 |
| 1-9-10-12-13-16-19 | 全程公路 | 53.106 | 0 |
| 1-9-10-12-13-16-17- 18-19 |
全程公路 | 53.396 | 0 |
| 1-9-10-12-14-16-17-19 | 全程公路 | 53.856 | 0 |
| 1-9-10-12-14-15-16-17- 18-19 |
全程公路 | 54.146 | 0 |
基于运输总成本,对筛选结果进行排序,输出最优运输路径:1-2-3-7-8-19,运输方式为铁路-公路,在Ouagadougou节点进行公铁转运,运输时间为第2短,总费用为1.764万元,其中运输费用为1.762万元,一次转运费用为0.002万元,延误惩罚费用为0元。目前,西非区域内90%的货物都采用全程公路运输方式。与全程公路运输相比,在该路径上开展公铁多式联运,运输时间增加了74.4%的同时,运输总成本降低了125.2%。
3.3 灵敏度分析本节将进行路径优化结果对不确定运输速度、准时送达概率阈值以及不确定运输速度和不确定转运时间的协同灵敏度分析,以探究不同交通状况,不同转运设施条件,以及托运人个性的时间需求,是否会对多式联运最优路径方案的选择造成影响。
3.3.1 优化结果对不确定运输速度灵敏度分析公路的服务能力不足,以及当地运输企业在运营和管理铁路方面经验的欠缺,会影响公、铁运输速度的变化。为了探究不确定运输速度的变化是否会对路径优化结果造成影响,本节设置了1.1~1.4共4个情景。其中,情景1.2降低了公路运输速度的均值,1.3降低了铁路运输速度的均值,1.4降低了公铁运输速度的均值和方差。该区域内影响水运运输速度的因素较少,故不考虑不确定水路运输速度的变化。设随机次数R=50,运输规定时间Tod=50 h,准时送达概率阈值α=60%。各情景不确定值的随机分布以及输出的最优路径方案详见表 5。
| 情景 | 不确定值 | 最优运输路径 | 运输方式 | K |
| 1.1①,④ | v(h, i)k~N(60, 10) v(h, i)l~N(35, 5) |
1-2-3-7-8-19 | 铁-公 | 18 |
| 1.2②,④ | v(h, i)k~N(40, 10) v(h, i)l~N(35, 5) |
1-2-3-7-8-19 | 铁-公 | 2 |
| 1.3②,⑤ | v(h, i)k~N(40, 10) v(h, i)l~N(25, 5) |
1-2-3-7-8-19 | 铁-公 | 7 |
| 1.4③,⑥ | v(h, i)k~N(25, 5) v(h, i)l~N(20, 5) |
1-2-3-7-8-19 | 铁-公 | 4 |
| 注:①公路流量少;②公路流量一般;③公路拥堵;④铁路正点;⑤铁路晚点;⑥铁路严重晚点。 | ||||
调整公路运输速度,铁路运输速度的分布区间并进行对比,得到4组最优路径方案的运输时间与成本如图 4所示。

|
| 图 4 不确定运输速度对优化结果的影响 Fig. 4 Influence of uncertain transport speed on optimization result |
| |
由图 4可知,情景1.2与情景1.1相比,总运输费用的变化不显著,未产生惩罚费用,最优路径方案的选择也相同;情景1.2导致运输总时间略微增加,但最优路径方案的时间优势度明显增强。情景1.3中不确定铁路运输速度期望值出现降低,与情景1.1相比,运输总时间增加约30.6%,总运输费用提高约67.7%,同时产生0.32万元的惩罚费用。而情景1.4中随着公路、铁路运输速度的同时降低,运输总成本再次出现回落。公路运输速度的变化对运输总成本的影响能力相对铁路运输速度较小,但它的变化对K值产生的影响更为显著。随着公铁运输条件的变差,最优路径方案的运输总时间不断增加。在公路通畅,铁路正点情况下(情景1.1),1-2-3-7-8-19这条运输路径,能够取得运输时间与运输成本上的一致最优。
3.3.2 优化结果对货物准时送达概率阈值灵敏度分析货物送达时间机会约束影响承运企业的最优运输路径选择决策,不同程度的机会约束促使其选择运输时间优先或运输成本优先的路径方案。本节设公路运输速度服从v(h, i)k~N(40, 10),铁路运输速度服从v(h, i)l~N(25, 5),水路运输速度服从v(h, i)m~N(20, 5),设置2.1~2.5共5组不同的准时送达时间约束的概率情景,分析不同送达时间约束阈值对路径优化结果的影响关系。取随机次数R=50,运输规定时间Tod=51 h。不同机会约束阈值条件下的路径优化结果如表 6所示。
| 情景 | 情景特征 | 最优运输路径 | 运输方式 |
| 2.1① | 无时间约束条件 | 1-2-4-5-6-19 | 公-水 |
| 2.2 | α=25% | 1-2-3-7-8-19 | 铁-公 |
| 2.3 | α=36% | 1-2-3-7-8-19 | 铁-公 |
| 2.4 | α=50% | 1-2-3-7-8-19 | 铁-公 |
| 2.5② | 严格时间约束条件 | 1-2-3-7-8-19 | 铁-公 |
| 注:①无时间约束:托运人对货物送达时间无要求,亦不会产生惩罚费用;②严格时间约束:硬时间窗,货物指定时间未到达即拒收。 | |||
不同机会约束阈值条件下的惩罚费用,运输总成本和不确定运输时间的变化趋势详见图 5。

|
| 图 5 机会约束阈值对优化结果的影响 Fig. 5 Influence of chance constraint threshold on optimization result |
| |
由优化结果可知,严格时间约束与无时间约束都会导致运费和运输时间出现极值。无时间约束条件下,优化路径选择“公-水”运输,总运输费用为1.71万元,略低于α=25%时的1.764万元,但运输时间要比后者高出约66 h;与α=50%条件下的优化结果相比,严格时间约束条件下的运输费用略高,运输时间略低;3组考虑货物送达时间约束的优化结果显示,惩罚费用和不确定运输时间的变化不显著,随着α值的上升,总运输成本呈线性增长趋势,运输路径选择“铁-公”运输方式。α值的变化过程中,总运输成本随运输时间的降低而增加,各路径方案的运输时间和成本呈现出明显的“此消彼长”的权衡过程。
3.3.3 优化结果对不确定运输速度和转运时间协同灵敏度分析西非区域各转运节点的设施情况与操作人员职业素质参差不齐,公铁、公水、铁水货物转运能力差别较为明显,货物转运时间存在一定的不确定性。不确定运输速度和转运时间都对实际运输过程产生影响,为了探究两者的共同作用对路径优化结果的影响能力,本节尝试对不确定运输速度和转运时间进行协同灵敏度分析。假设货物转运时间服从均匀分布[15],调整货物转运时间服从分布区间,设计3.1~3.5共5组情景。其中,情景3.1转运条件最好,3.2转运条件最差,3.3~3.5中仅公铁、公水、铁水转运条件变差。区间分布信息详见表 7,不确定运输速度的分布区间变化取3.3.1小节中的情景1.1~1.4,不确定运输速度值与转运时间值的随机次数相同,取R=50。
| 情景 | 货物转运时间服从分布 | ||
| 公-铁转运 | 公-水转运 | 铁-水转运 | |
| 3.1① | U~(4, 6) | U~(3, 5) | U~(7, 8) |
| 3.2② | U~(9, 14) | U~(7, 12) | U~(13, 17) |
| 3.3③ | U~(9, 14) | U~(3, 5) | U~(9, 10) |
| 3.4④ | U~(4, 6) | U~(7, 12) | U~(9, 10) |
| 3.5⑤ | U~(4, 6) | U~(3, 5) | U~(13, 17) |
| 注:①公铁水转运设施完好;②公铁水转运设施落后,操作人员素质较低;③公铁转运设施落后,其他转运方式一般;④公水转运设施落后,其他方式一般;⑤水铁转运设施落后,其他方式一般。 | |||
对模型输出结果进行分析后,我们发现,在情景1.1条件下,情景3.1~3.5输出的路径方案与情景1.1一致,不确定转运时间的变化未对路径方案的选择产生影响,情景1.2~1.4条件下输出的路径方案同样未受转运时间的影响。由此可知,不确定运输速度的变化对最优路径方案选择的影响能力大于不确定转运时间。但是,转运时间的变化对运输总成本产生了影响,以情景3.1中的运输总成本作为参照值,情景3.2~3.5的运输总成本变化趋势详见图 6。其中,部分总成本的变化趋势为0是因为延误惩罚费用已达到40%的阈值。结合该变化趋势可知,公铁转运时间不确定性对运输总成本的影响要大于公水转运和铁水转运。另外,不确定转运时间条件下,随着货物转运次数的增多,物流运输总时间将增加,继而产生延误惩罚费用,影响多式联运的经济性。因此,利用各运输方式的高效性或经济性对货物进行1~2次转运,一定程度能够提高综合运输效率,降低物流运输成本。

|
| 图 6 不确定条件协同作用下的成本变化趋势 Fig. 6 Cost change trend under synergy of uncertain conditions |
| |
总的来说,西非区域公路运输服务能力不足,运价相对昂贵,使得该方式在区域多式联运发展中可提升空间不大。而铁路的运输效率高,运价低廉,拥有巨大发展潜力。综合优化结果和区域现状可知,西非区域应当发展以铁路为主导,公路、水路为辅的货物多式联运模式,以进一步提升沿海港口的辐射能力和衔接转换水平,缓解物流服务压力,降低区域综合物流成本。
4 结论本研究考虑了实际多式联运过程中货物运输环节和转运环节出现的不确定性,以及客户个性的时间需求,利用西非区域的综合运输网络验证了提出的模型和求解方法的可行性,并对优化结果展开分析与探讨。总结灵敏度分析结果,得出以下结论:
(1) 不确定条件的变化对最优路径方案选择的影响能力:准时送达概率阈值>不确定运输速度>不确定转运时间。
(2) 准时送达概率阈值的变化会使运输时间和成本产生“权衡”机制。
在未来的研究中,更多运输方式之间的综合运输将会被考虑,以进一步提升多式联运路径优化模型的普适性。另外,基于多目标的多式联运路径规划问题[16-17],运输弧段运输能力不足时的货运量分配问题,以及客户需求不确定情况下,各转运节点货物的拆分与集拼的问题也会被考虑[18],使路径优化结果更加符合实际运输特征。
| [1] |
JT/T 1092-2016, 货物多式联运术语[S]. JT/T 1092-2016, Terminology of Intermodal Freight Transport[S]. |
| [2] |
AGAMEZ-ARIAS A M, MOYANO-FUENTES J. Intermodal Transport in Freight Distribution:A Literature Review[J]. Transport Reviews, 2017, 37(6): 782-807. |
| [3] |
DUAN L, TAVASSZY L A, REZAEI J. Freight Service Network Design with Heterogeneous Preferences for Transport Time and Reliability[J]. Transportation Research Part E:Logistics and Transportation Review, 2019, 124: 1-12. |
| [4] |
BARADARAN V, SHAFAEI A, HOSSEINIAN A H. Stochastic Vehicle Routing Problem with Heterogeneous Vehicles and Multiple Prioritized Time Windows:Mathematical Modeling and Solution Approach[J]. Computers & Industrial Engineering, 2019, 131: 187-199. |
| [5] |
KALININA M, OLSSON L, LARSSON A. A Multi Objective Chance Constrained Programming Model for Intermodal Logistics with Uncertain Time[J]. International Journal of Computer Science Issues, 2013, 10(6): 35-44. |
| [6] |
GOEL R, MAINI R, BANSAL S. Vehicle Routing Problem with Time Windows Having Stochastic Customers Demands and Stochastic Service Times:Modelling and Solution[J]. Journal of Computational Science, 2019, 34: 1-10. |
| [7] |
于雪峤, 郎茂祥, 王伟哲, 等. 考虑模糊需求的多式联运路径优化[J]. 北京交通大学学报, 2018, 42(3): 23-29, 36. YU Xue-qiao, LANG Mao-xiang, WANG Wei-zhe, et al. Multimodal Transportation Routing Optimization Considering Fuzzy Demands[J]. Journal of Beijing Jiaotong University, 2018, 42(3): 23-29, 36. |
| [8] |
李珺, 杨斌, 朱小林. 混合不确定条件下绿色多式联运路径优化[J]. 交通运输系统工程与信息, 2019, 19(4): 13-19, 27. LI Jun, YANG Bin, ZHU Xiao-lin. Path Optimization of Green Multimodal Transportation under Mixed Uncertainties[J]. Journal of Transportation Systems Engineering and Information Technology, 2019, 19(4): 13-19, 27. |
| [9] |
赵祎.随机环境下集装箱海铁联运系统建模与优化研究[D].北京: 北京交通大学, 2019. ZHAO Yi. Research on Modelling and Optimisation of Sea-rail Intermodal Transport System under Stochastic Circumstance[D]. Beijing: Beijing Jiaotong University, 2019. |
| [10] |
刘宝碇, 赵瑞清, 王纲. 不确定规划及应用[M]. 北京: 清华大学出版社, 2003. LIU Bao-ding, ZHAO Rui-qing, WANG Gang. Uncertain Programming with Application[M]. Beijing: Tsinghua University Press, 2003. |
| [11] |
LI M, LIU Z, ZHANG Y, et al. Distribution Analysis of Train Interval Journey Time Employing the Censored Model with Shifting Character[J]. Journal of Applied Statistics, 2017, 44(4): 715-733. |
| [12] |
胡元, 帅宇红. 整车物流运输多式联运与路径优化研究[J]. 交通运输工程与信息学报, 2019, 17(1): 13-18. HU Yuan, SHUAI Yu-hong. Multimodal Transportation and Route Optimization of Vehicle Logistics[J]. Journal of Transportation Engineering and Information, 2019, 17(1): 13-18. |
| [13] |
HU X B, ZHANG C, ZHANG G P, et al. Finding the k Shortest Paths by Ripple-spreading Algorithms[J]. Engineering Applications of Artificial Intelligence, 2020, 87: 103229. |
| [14] |
BOUILLET E, ELLINAS G, LABOURDETTE J F, et al. Path Routing in Mesh Optical Networks[M]. Hoboken: John Wiley & Sons, 2007: 125-137.
|
| [15] |
DAS S, SUGANTHAN P N. Differential Evolution:A Survey of the State-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2010, 15(1): 4-31. |
| [16] |
SALEHI M, JALALIAN M, SIAR M M V. Green Transportation Scheduling with Speed Control:Trade-off between Total Transportation Cost and Carbon Emission[J]. Computers & Industrial Engineering, 2017, 113: 392-404. |
| [17] |
ZHANG W, WANG X, YANG K. Uncertain Multi-Objective Optimization for the Water-rail-road Intermodal Transport System with Consideration of Hub Operation Process Using a Memetic Algorithm[J]. Soft Computing, 2020, 24(5): 3695-3709. |
| [18] |
SUN Y, HRUSOVSKy M, ZHANG C, et al. A Time-dependent Fuzzy Programming Approach for the Green Multimodal Routing Problem with Rail Service Capacity Uncertainty and Road Traffic Congestion[J]. Complexity, 2018, 2018: 1-22. |
 2021, Vol. 38
2021, Vol. 38
