扩展功能
文章信息
- 杨书仁, 丁松
- YANG Shu-ren, DING Song
- 基于应变比的桥梁损伤识别与评估方法
- A Method for Bridge Damage Identification and Evaluation Based on Strain Ratio
- 公路交通科技, 2021, 38(1): 87-96, 111
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(1): 87-96, 111
- 10.3969/j.issn.1002-0268.2021.01.011
-
文章历史
- 收稿日期: 2020-06-17
近年来,桥梁健康监测技术得到了快速发展,越来越多的桥梁尤其是大桥和特大桥安装了健康监测系统,健康监测系统能够全天候采集大量实时监测数据,以期对桥梁结构性能进行实时监测、评估,保证其安全性。但当前健康监测技术仍然存在很多问题,面临诸多挑战,使其无法对桥梁结构
损伤情况进行有效的识别和评估[1],具体表现在以下几个方面:(1)应变传感器数据挖掘与分析不够深入,对海量监测数据的深度挖掘欠缺,造成实测大量数据难以为桥梁安全及损伤评价提供有力支撑[2-3];(2)单一的阈值报警模式在实际交通随机荷载及零漂等因素的作用下,难以反映结构的真实状况,经常发生误报;(3)传感器实际灵敏度系数对测量值存在一定影响,容易造成误判。目前很多学者在桥梁损伤识别的应用方面开展了大量研究工作,提出了利用桥梁动力特性变化进行结构损伤识别[4],柔度矩阵插值法[5-7]、模态应变能法[8]、BP神经网络法[9]及小波分析方法[10-11]等不同类型的损伤识别方法,然而研究表明前两种方法存在诸多不足,而神经网络法也因存在BP网络收敛速度慢,计算资源需求巨大等问题目前难以应用于实际项目。小波分析经过多年的试验研究取得了一些成果,但是距离实际应用仍存在很多需要解决的问题[12]。我们将探讨如何应用既有健康监测系统中现实存在的大量应变传感器采集的数据进行结构的局部损伤识别,通过在桥梁各关键断面安装一定数量的应变传感器,可以对桥梁结构的局部损伤进行有效识别。
我们在大量分析车辆荷载作用下桥梁结构应变响应基础上,综合运用信号处理技术、桥梁结构影响线理论和数据分析理论提出一种基于应变比的损伤识别方法,该方法可以有效消除灵敏度系数带来的测量误差的影响,具有识别精度高,通用性强的特点,可以广泛地适用于各种桥梁的损伤识别和评估,能够实现封闭交通下桥梁损伤快速精准识别与评估和开放交通状态下桥梁损伤定期在线识别,为桥梁健康监测系统的数据分析技术发展和应用提供新的解决方案。
1 基于应变比的损伤识别理论推演理想状态下,我们可以通过对车辆荷载作用下实测应变和理论应变进行分析得到桥梁结构的损伤状况,然而实测应变与车辆荷载的大小、速度有很大关系,由于运营期的车辆轴重和分布是随机的,因此无法直接用应变数据判断测试截面是否发生损伤,导致应变数据的实际应用存在极大的局限性。
1.1 应变比理论以等截面简支梁为例,梁长为L,其坐标xi处的弯矩影响线为:
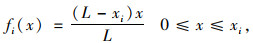
|
(1) |
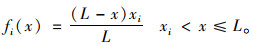
|
(2) |
令中性轴高度为y,弹性模量为E,截面抗弯惯性矩为I,则xi处应变影响线为:
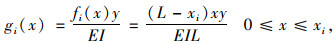
|
(3) |
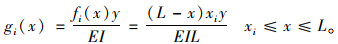
|
(4) |
单位力作用下,xi处梁底产生的最大应变值分别为:
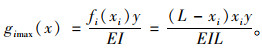
|
(5) |
在相同的荷载F、相同速度下γ,综合考虑应变传感器灵敏度系数误差μi,则xi处实测应变为:
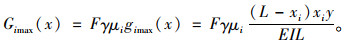
|
(6) |
同理在xj处实测应变为(见图 1):
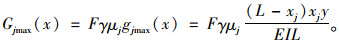
|
(7) |

|
| 图 1 简支梁应变影响线 Fig. 1 Strain influence line of simply supported beam |
| |
则xi,xj处产生的最大应变之比:
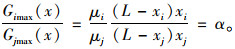
|
(8) |
由于L,xi,xj,μi,μj已知,梁没有损伤的情况下,同一荷载作用下,桥梁各截面测点应变之比α不会改变,即:
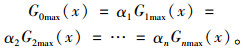
|
(9) |
G0max为基准断面应变,通过监测各截面应变比的变化,可以对桥梁的损伤情况进行识别。
1.2 基于应变比的损伤判据我们将结构平均分成N个单元(与识别精度相关),各单元的刚度为EIi,单位力作用下,第i段最大应变为:
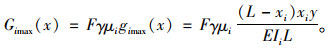
|
(10) |
假设第i段出现了损伤,损伤后截面抗弯惯性矩变为I′i,则其应变最大值为:
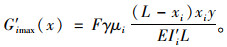
|
(11) |
则损伤前后刚度比可以通过损伤前后相同荷载产生的应变比得到:
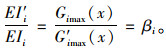
|
(12) |
此时基准断面与损伤断面应变比变为:
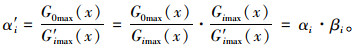
|
(13) |
则断面损伤后的刚度比为:
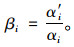
|
(14) |
据此,我们可以从应变比的变化精确识别简支梁的损伤程度。
1.3 刚度退化矩阵目前,健康监测系统主要安装在大桥和特大桥上,桥型涉及到悬索桥、斜拉桥、大跨径拱桥以及大跨径梁式桥等多种类别,其弯矩影响线和应变影响线并不具有简支梁那样的显示表达式,但其总会存在一个数值解[13](见图 2)。我们可以根据此结论对上述算法进行进一步推广。

|
| 图 2 悬索桥边跨跨中和主跨最不利断面弯矩图 Fig. 2 Bending moment diagram of middle section of side span and the most unfavorable section of main span of suspension bridge |
| |
设某桥截面i弯矩影响线为:
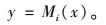
|
(15) |
桥梁在该截面处惯性矩为Ii,中性轴高度为h,弹性模量为E,则其最大应变为:
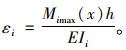
|
(16) |
通常桥梁一般具有多个车道,具有横向刚度,设桥梁车道数为n,为了识别出结构在空间上性能的退化情况可以将其推广得到不同车道下结构应变比矩阵,令C=W(F, γ)代表车辆相关信息(荷载、速度),则应变比矩阵为:
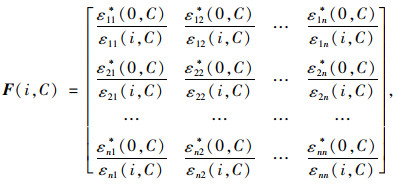
|
(17) |
式中,εpq(i, C)为车辆C在p车道上行驶时第i截面第q车道下传感器的实测应变;εpq*(0, C)为车辆C在p车道行驶时参考断面第q车道下传感器的实测应变。
令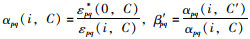
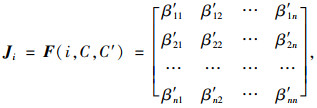
|
(18) |
式中,C为初始应变比所用车辆信息;C′为测试时所用车辆信息。
此时刚度退化矩阵为:
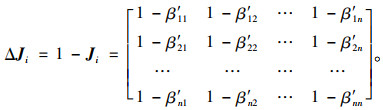
|
(19) |
则第p车道刚度损失指标为:
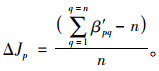
|
(20) |
随着时间的发展,各个车道的刚度会发生变化,结构的性能也会下降。通过对监测数据分析计算出ΔJp,可以对桥梁损伤位置和损伤程度进行评估,对大跨径桥梁的结构性能和寿命进行预测。
1.4 车辆荷载效应分离通过以上分析,我们得到了通过观测车辆荷载作用下桥梁基准断面与各关键断面应变比进行损伤评估的方法。鉴于本方法基于结构静力学推导,因此关键性问题是确保在不同断面捕捉到相同荷载作用下的最大静态效应。车辆荷载激励产生的应变信号是一种包含多种频率组分的复杂信号,基于应变比的损伤识别方法使用的是低频高幅的静态应变信号。动静态信号分离方法主要有傅里叶变换、小波变换[14]、经验模态分解法[15]等技术,小波变换需要根据信号特征选取合适的小波基[16],在实际应用中较为复杂,经验模态分解法需要针对信号实时修正定义局部细节范围,通过迭代进行求解,非常复杂,在健康监测系统上难以进行大规模应用。由于不同截面对于不同阶次的动力响应不同,单纯的光滑处理会使得静态应变失真,从而影响应变比的真实性,特别是当应变幅值不大的时候,因此我们提出采用傅里叶变换和傅里叶反变换对其信号进行处理,得到结构的静态应变响应。该方法模型简单、精度高,能够及时高效的处理车辆荷载产生的应变信号,大大降低了系统的运算负担,提高了其实用性。
将采集到的应变时域信号进行快速傅里叶变换(FFT)转变为频域信号。
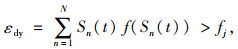
|
(21) |
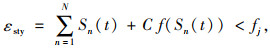
|
(22) |
式中,n=1, 2, 3, …;N为频谱中不同的频率组分;εdy为车辆冲击产生的动态应变组分;εsty为车辆荷载产生的静态应变组分。根据实际频谱分析情况,给出两种静态应变阈值方法,第1种为以主梁第一阶竖弯频率为阈值,第2种为以测点实测信号频谱中基频为阈值。当采集到的实测信号无法反应结构的固有频率时,可以采用实测信号频谱中的基频。
由于傅里叶变换的频率分辨率f0与采样频率fs和采样点数N相关,有以下关系:
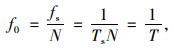
|
(23) |
式中,Ts为采样间隔;T为采样时间,通过提高采样时间,可以得到满足要求的频率分辨率。
通过快速傅里叶变换,我们可以得到足够频率分辨率的频域信号,将信号中的高频低幅组分的幅值设置为0,得到修正后的频域信号。利用傅里叶反变换,将修正后的频域信号进行还原,这样就可有效滤除动态应变的高阶组分,得到结构的静态应变时程信号。
2 基于应变比的损伤识别在监测系统中的应用 2.1 封闭交通下桥梁损伤快速精准识别在桥梁健康监测系统中,我们可以定期使用上述方法在封闭交通状态下,采用标准车辆定期进行桥梁损伤评估,可以得到完备的应变比矩阵和刚度损失矩阵,从而能够实现快速精准识别桥梁损伤,有效降低了大型荷载试验对交通的影响。
为了能够使损伤识别方法更加有效精准,我们对试验参数做了约定。
车辆荷载:测试车辆重量宜选择20~35 t,保持匀速行驶并确保大桥在采样时间段内无其他干扰车辆且测试车辆在单次行驶中不变更车道。
基准断面:本方法的识别需要选取基准断面,基准断面关系到刚度系数的精度,决定了整个损伤识别的准确性。为此,宜选取控制断面以外具有较大荷载响应且无结构性病害的断面作为基准断面,并应定期对其进行病害检查,保证其刚度在监测期内不会发生改变。如果基准断面发生结构性损伤,应对监测数据进行修正,并将此基准断面转变为控制断面,另选无结构性病害断面为基准断面。
传感器选型:为保证在一定范围内捕捉结构裂缝,宜采用长标距FBG传感器,虽然本方法降低了对应变传感器的精度要求,但对其稳定性和线性度要求较高,为了保证监测数据的质量,宜选取同一厂家、同型号、同一批次的传感器,且在安装前务必进行校准。
采样时间:应变传感器信号的频率分辨率与采样时间密切相关,为了能够得到精度良好的静态应变数据采样时间不得低于20 s。
采样频率:采样频率应满足采样定理的要求[17]。
在上述条件下,将桥梁监测系统设定为系统标定模式,应用标准车在测试桥梁各个车道上以相同速度依次通过。在该模式下,系统将自动记录标定时间段内车辆在各条车道上行驶对每个截面不同传感器产生的荷载效应,并计算出车辆在不同车道行驶时测试断面各测点与基准断面对应测点的应变比,组成应变比矩阵及刚度矩阵,并将计算结果作为特征指纹记录在系统数据库内,用于与下一次的试验结果进行对比,并计算出结构的刚度退化矩阵,从而做出结构控制截面是否出现损伤的分析判断。具体流程见图 3。
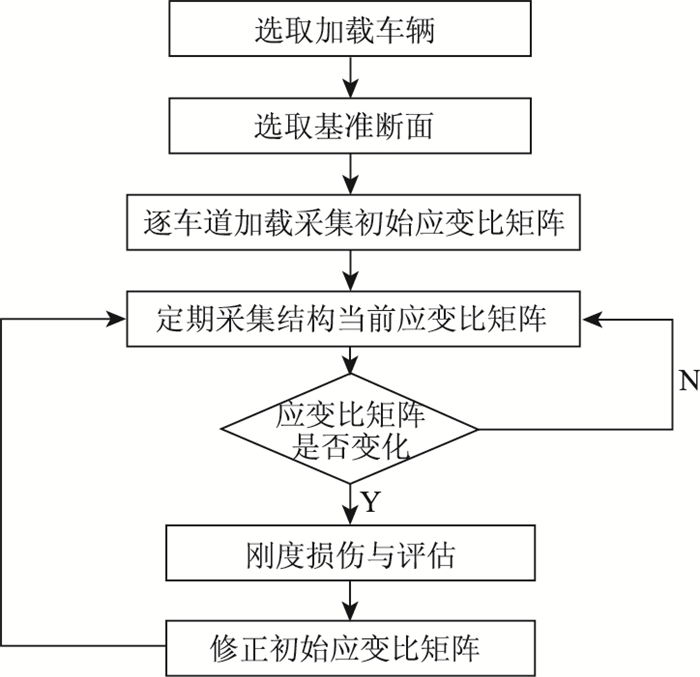
|
| 图 3 封闭交通下桥梁损伤识别程序流程图 Fig. 3 Flowchart of bridge damage identification program under closed traffic condition |
| |
标准车在封闭交通情况下的这种测试分析方法提供了在不进行定期检查以及荷载试验的情况下发现桥梁关键部位技术状况变化的一种方便快捷、高效低费的方法,对于充分利用健康监测系统性能,挖掘潜能具有重要的意义。
2.2 开放交通状态下的损伤识别在桥梁开放交通状态下,由于车辆荷载及其分布具有随机性[18],无法达到设计工况下的条件,因此难以获得理想的应变比矩阵,导致上述方法无法直接对结构损伤情况进行在线定期评估,然而统计数据显示,对于长期运营的桥梁,在一定时期内,其车型占比、行驶车道(轮迹线)会呈现明显的统计规律。以青银线济南黄河大桥为例,重型车辆6月— 9月间下游方向各车道分布统计具有较为一致的规律性(图 4)。
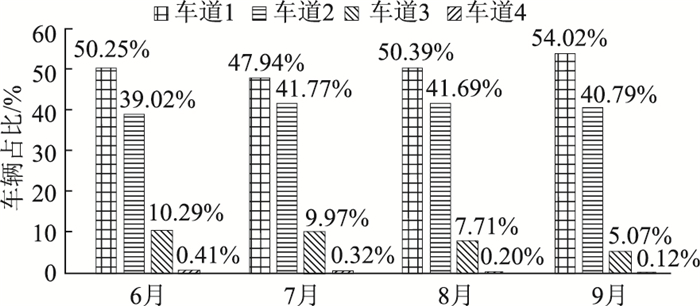
|
| 图 4 济南黄河大桥重型车辆6月-9月下游各车道分布 Fig. 4 Distribution of heavy vehicles in different lanes at downstream of Jinan Yellow River Bridge from June to September |
| |
根据应变比矩阵可知,理想状态下单车通过桥梁固定车道时,某截面测点n的应变比根据车辆所行驶的不同车道得到以下关系:
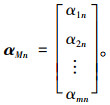
|
(24) |
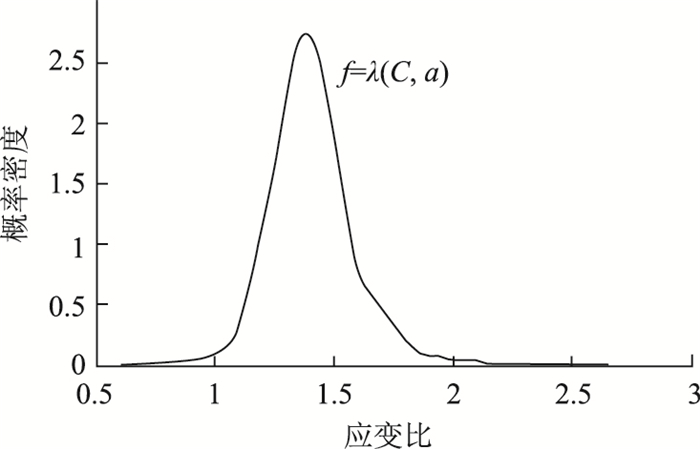
在开放交通条件下,由于车辆在桥上行驶轨迹的随机性,荷载位置信息并不明确。此时上述矩阵难以准确获取,但在无临时交通渠化措施的一定时期内,统计单车过桥时测点的应变比数据,服从某种确定的分布关系(图 5):
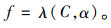
|
(25) |
|
| 图 5 某桥单方向某测点应变比概率密度函数 Fig. 5 Probability density function of strain ratio of a bridge measuring point in one direction |
| |
虽然准确的加载车道无法捕捉,但可以获取车辆行驶方向(上行、下行),此时应变比矩阵变为:
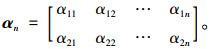
|
(26) |
从概率密度函数可以方便地得到应变比的众值和置信区间,监测数据表明,应变比的众值在正常交通状态下具有高度的稳定性,可以用来定量评估刚度受损情况,当测试截面发生某种损伤时,其应变比的众值对损伤具有较强的敏感性,其众值会随损伤的变化而变化。而置信区间则可以复核有无交通控制措施,当采取临时性交通渠化措施的时候,应变比的置信区间会发生变化,置信区间的稳定可用来剔除临时交通渠化带来的影响,保证数据的可靠性,从而可以在开放交通状态下进行桥梁结构损伤的有效识别。
为保证上述分析方法的实际应用,监测系统应能满足以下功能:
(1) 对应变信号进行实时监测,选取并积累满足条件的应变信号,计算其应变比。
(2) 通过非参数估计求解应变比概率密度函数[19]。
(3) 求解应变比众值和置信区间,通过概率密度函数可以直接获得应变比众值,采用数值方法求解其置信区间。
(4) 观察应变比众值和置信区间是否发生变化,如未发生变化,则进行下一轮观测,否则需通过健康监测系统中部署的全域摄像头记录的影像检查是否存在临时交通管制措施,如果有临时交通管制措施,则直接进行下一周期监测,如果没有则需进行刚度损伤识别并发出预警,修正应变比矩阵后进行下一周期监测。
3 应变比法损伤识别验证 3.1 桥梁概况青银线济南黄河大桥主桥采用独塔双索面扁平钢箱梁斜拉桥,主梁为单箱三室钢箱梁,跨径布置为(60+60+160+386)m,梁高3.5 m,桥面宽度为43.6 m(含布索区及风嘴),桥塔采用倒Y型混凝土索塔,总高197 m,全桥共设96根斜拉索,呈空间双索面扇形分布。大桥于2008年12月26日正式建成通车运营,至今已运行11a。该桥监测系统主梁应变传感器布置如图 6、图 7所示。
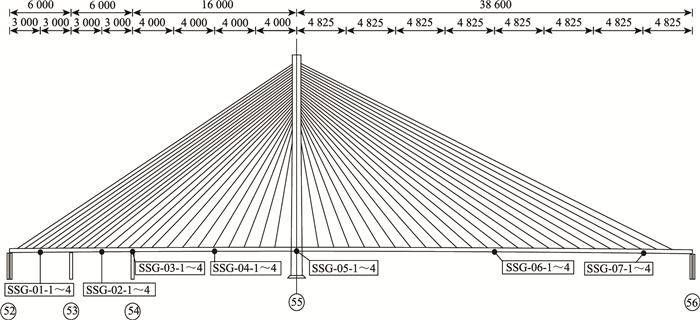
|
| 图 6 济南黄河大桥主桥应变传感器立面布置(单位:cm) Fig. 6 Vertical layout of strain sensors for main bridge of Jinan Yellow River Bridge(unit:cm) |
| |
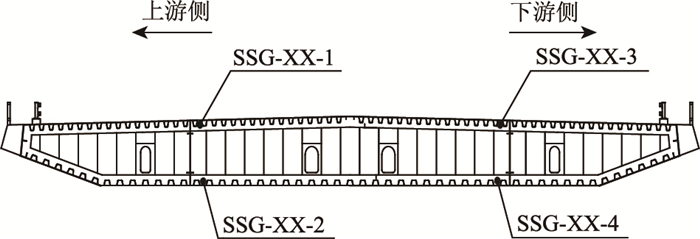
|
| 图 7 济南黄河大桥主桥应变传感器横截面布置图 Fig. 7 Cross-sectional layout of strain sensors for main bridge of Jinan Yellow River Bridge |
| |
3.2 方案设计
为了保证测试效果的可靠性,对方案做以下设计和要求:
基准断面与测试断面:无论是基准断面还是测试断面均选择荷载响应较大截面,本方案基准断面选为边跨跨中即图中SSG-04截面,测试断面选为主跨跨中截面(SSG-06)和主跨最不利截面(SSG-07)。测点选择为上下游钢箱梁底板处共6个监测测点,测试断面与基准断面测点在横截面位置上一一对应。
数据采集:采用光纤光栅解调仪进行数据采集,采样频率设置为20 Hz,保障应变信号能够有效的还原和重构。
数据传输与存储:利用云平台进行数据高效运算与存储见图 8。
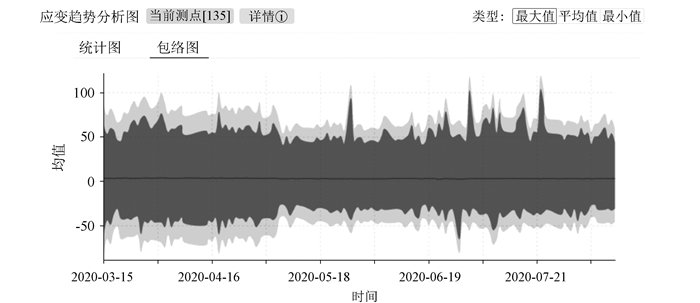
|
| 图 8 济南黄河大桥主桥监测系统SSG-13-8应变测点包络图 Fig. 8 Envelope diagram of SSG-13-8 strain measuring points on Jinan Yellow River Bridge by bridge monitoring system |
| |
样本时间:现场采集2019年9月-2019年12月这4个月的应变响应作为本次分析样本,其中第1个月的应变数据作为初始样本。
3.3 结果分析 3.3.1 应变数据处理青银线济南黄河大桥主桥全长666 m,高速公路最低时速为60 km/h,车辆过桥需要时间最长为40 s,为了保证所选取的应变数据不受多车效应影响以及必要精度,需对应变数据进行自动筛选,保证各测点应变数据在40 s内只有一个波峰,并对采集到的应变时间序列数据按前文1.4节中的方法进行处理得到准确的静态应变响应。
以2019年12月8日某时刻单一荷载作用下的下游侧原始应变时程图(图 9从上至下依次为边跨跨中、主跨跨中、主跨最不利截面)为例,采用前文1.4节所述的方法进行荷载效应分离。
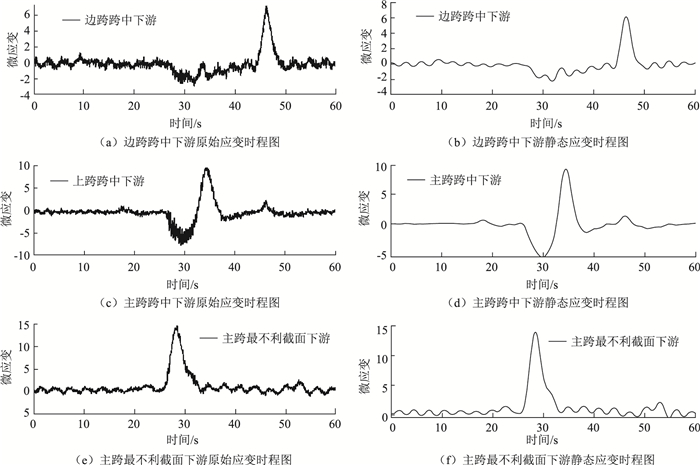
|
| 图 9 应变时程数据处理前后对比图 Fig. 9 Comparison of strain time history data before and after processing |
| |
根据加速度传感器测试数据,主梁一阶竖弯频率为0.34,经过快速傅里叶变换,分别得到了3个测点的频谱图,将频率大于0.34的信号组分幅值设置为0,通过傅里叶反变换即得到结构静态应变组分。通过提取静态应变的峰值,就可以得到准确的应变比。
3.3.2 应变比数据分析对2019年9—12月的应变数据进行分析,将9月份的数据作为初始样本,对10—12月的数据进行分析,对结构在本时间段内的损伤情况进行识别和评估。通过对样本分布的分析得到各测点在各月的概率密度曲线如图 10~图 13所示。
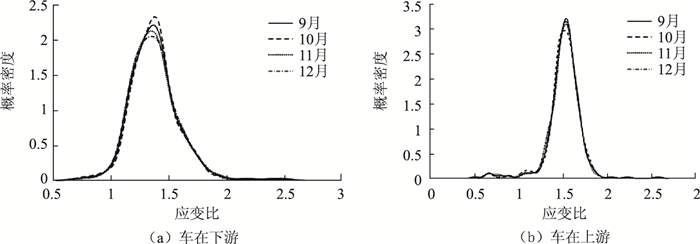
|
| 图 10 主跨跨中下游测点应变比概率密度曲线 Fig. 10 Probability density curves of strain ratio at downstream of middle section of main span |
| |
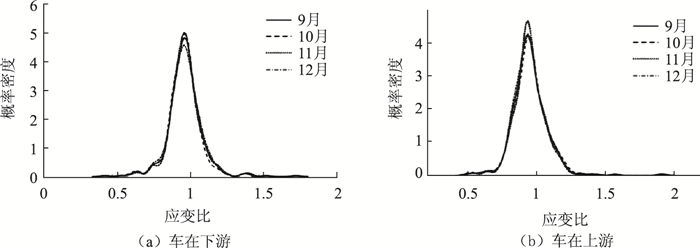
|
| 图 11 主跨跨中上游测点应变比概率密度曲线 Fig. 11 Probability density curves of strain ratio at upstream of middle section of main span |
| |
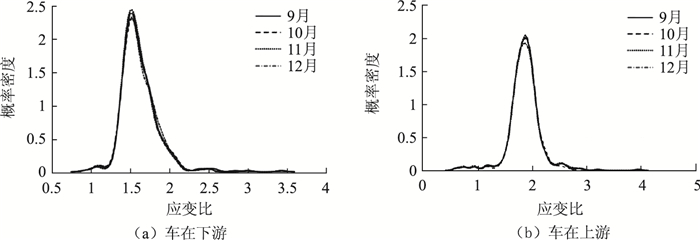
|
| 图 12 主跨最不利截面下游测点应变比概率密度曲线 Fig. 12 Probability density curves of strain ratio at downstream of the most unfavorable section of main span |
| |
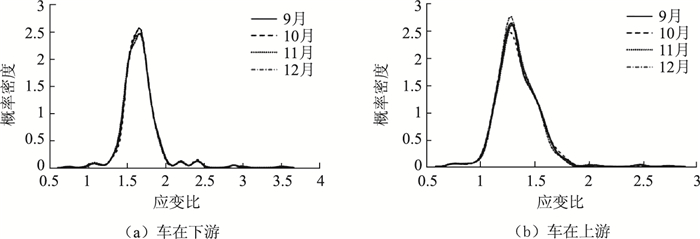
|
| 图 13 主跨最不利截面上游测点应变比概率密度曲线 Fig. 13 Probability density curves of strain ratio at upstream of the most unfavorable section of main span |
| |
通过对概率密度曲线进行积分求解,可以得到测点在各个月份的众值和置信区间,详见表 1。
| 截面 | 测点 | 行车位置 | 众值 | 置信区间 | |||||||
| 9月 | 10月 | 11月 | 12月 | 9月 | 10月 | 11月 | 12月 | ||||
| 主跨跨中 | 上游 | 上游 | 0.937 2 | 0.934 6 | 0.938 1 | 0.935 8 | 0.662 2~2.004 9 | 0.640 5~2.012 8 | 0.700 2~2.000 9 | 0.659 4~2.009 0 | |
| 下游 | 0.991 6 | 0.991 6 | 0.991 4 | 0.989 9 | 0.683 4~1.828 1 | 0.668 9~1.827 7 | 0.682 7~1.829 2 | 0.692 1~1.838 9 | |||
| 下游 | 上游 | 1.522 9 | 1.522 8 | 1.522 8 | 1.531 9 | 0.761 4~2.676 8 | 0.777 0~2.689 2 | 0.752 4~2.690 1 | 0.777 0~2.689 1 | ||
| 下游 | 1.405 1 | 1.405 2 | 1.403 5 | 1.404 2 | 0.975 2~2.698 3 | 0.954 2~2.700 2 | 1.101 0~2.709 0 | 0.986 3~2.715 1 | |||
| 主跨最不利 | 上游 | 上游 | 1.286 5 | 1.281 3 | 1.297 3 | 1.286 2 | 0.985 7~2.882 9 | 0.977 1~2.896 0 | 0.967 5~2.220 8 | 0.985 3~2.883 5 | |
| 下游 | 1.668 1 | 1.667 1 | 1.694 2 | 1.664 8 | 1.205 7~3.671 7 | 1.203 9~3.674 7 | 1.210 4~3.686 2 | 1.199 3~3.682 1 | |||
| 下游 | 上游 | 1.880 9 | 1.878 5 | 1.878 5 | 1.877 2 | 0.951 9~4.110 5 | 0.906 6~4.121 5 | 0.906 4~4.121 7 | 0.864 6~4.127 6 | ||
| 下游 | 1.510 6 | 1.503 1 | 1.510 1 | 1.502 1 | 1.166 2~3.577 2 | 1.154 7~3.593 6 | 1.165 4~3.578 4 | 1.124 1~3.595 9 | |||
由表 1可知4个月内,应变比的置信区间未发生变化,说明此时间段内交通状况未发生明显变化,可以采用众值对结构损伤进行识别。
12月末时主跨跨中截面刚度矩阵为:
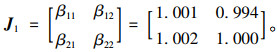
|
(27) |
12月末时主跨最不利截面刚度矩阵为:
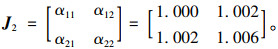
|
(28) |
由于样本存在不确定性,刚度变化在5%范围内,认为桥梁没有发生损伤,通过对刚度变化矩阵的分析,我们可以得出监测期内两个监测截面的刚度变化非常小,经现场核查未发现桥梁损伤迹象。如果应变比的分布规律(众值、置信区间)发生显著变化(图 14),则可以通过本方法迅速对刚度受损情况进行识别和评估。
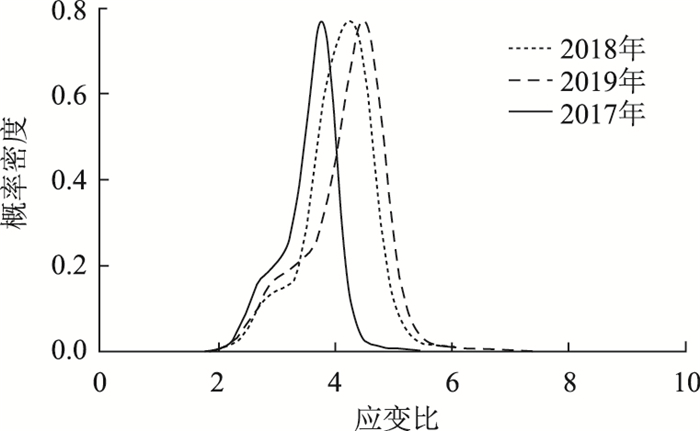
|
| 图 14 某桥梁受损伤断面应变比概率密度曲线 Fig. 14 Probability density curves of strain ratio of damaged section of a bridge |
| |
上述方法对于损伤识别的有效性在国内某连续刚构桥上也得到了验证,该桥控制截面出现了结构性裂缝,我们通过上述方法对裂缝进行监测,结果表明刚度存在逐年降低的趋势,对应的应变比众值分布数据发生了明显偏移,对该桥3 a的定期检查数据显示裂缝有明显开展的趋势,二者结论相吻合。
4 结论结构应变是桥梁健康监测系统的一个重要的监测指标,然而由于实际监测系统难以将荷载与应变响应及理论分析相对应,因此基于应变监测数据的检测结果分析判断难以进行,我们通过研究车辆荷载作用下的应变响应,结合信号处理技术和桥梁影响线理论提出了基于应变比进行结构损伤识别方法,并将其推广应用到开放交通状态下对桥梁损伤的在线识别和评估。通过理论方法的建立及对青银线济南黄河大桥健康监测系统9—12月的监测数据分析、验证,得到结论如下:
(1) 基于应变比的损伤识别和评估方法,解决了应变传感器灵敏度系数精度问题引起的数据分析错误及系统误判,在封闭交通下可以实现桥梁损伤快速精准识别。
(2) 桥梁正常运营过程中,在未采取交通控制措施时,各测点的应变比为确定的概率分布,其概率密度函数与测点位置、交通渠化相关。
(3) 桥梁未受损伤时,各测点的应变比众值和置信区间存在高度的稳定性,可以通过监测数据计算应变比众值对结构损伤进行识别和评估,通过监测置信区间确定是否存在交通控制等现象,保障损伤识别和评估的准确性。
(4) 通过算法集成,可以使整个监测系统高效运行,定期对结构损伤进行分析评价。
综上所述,基于应变比的桥梁局部损伤识别的方法效率高,精度好,通用性强,能够实现封闭交通下桥梁损伤快速精准识别与评估和开放交通状态下桥梁损伤定期在线识别,为在桥梁健康监测系统中利用应变监测数据进行关键部位损伤分析提供了全新的方法。
| [1] |
魏新良, 王震洪. 桥梁健康监测技术发展现状及趋势分析[J]. 铁道工程学报, 2008, 25(9): 44-47. WEI Xin-liang, WANG Zhen-hong. The Current Development Situation and Trend of Monitoring Technology for Bridge Health[J]. Journal of Railway Engineering Society, 2008, 25(9): 44-47. |
| [2] |
孙利民, 尚志强, 夏烨. 大数据背景下的桥梁结构健康监测研究现状与展望[J]. 中国公路学报, 2019, 32(11): 1-20. SUN Li-min, SHANG Zhi-qiang, XIA Ye. Development and Prospect of Bridge Structural Health Monitoring in the Context of Big Data[J]. China Journal of Highway and Transport, 2019, 32(11): 1-20. |
| [3] |
王明俊, 王湛, 陈炳聪, 等. 桥梁健康监测系统发展回顾[J]. 城市道桥与防洪, 2019, 36(11): 53-56. WANG Ming-jun, WANG Zhan, CHEN Bing-cong, et al. Review of Development of Bridge Health Monitoring System[J]. Urban Roads Bridges & Flood Control, 2019, 36(11): 53-56. |
| [4] |
苏彬建.基于动力特性的梁式结构损伤识别研究[D].湘潭: 湘潭大学, 2018. SU Bin-jian. Research on Damage Identification of Beam Structure Based on Dynamic Characteristics[D]. Xiangtan: Xiangtan University, 2018. |
| [5] |
杨华. 基于柔度矩阵法的结构损伤识别[J]. 吉林大学学报:理学版, 2008, 54(2): 242-244. YANG Hua. Structural Damage Identification Based on Flexibility Matrix Method[J]. Journal of Jilin University:Science Edition, 2008, 54(2): 242-244. |
| [6] |
刘庆.基于柔度系数的桥梁结构损伤识别研究[D].天津: 河北工业大学, 2015. LIU Qing. Research on Bridge Structural Damage Identification Based on Compliance Coefficient[D].Tianjin: Hebei University of Technology, 2015. |
| [7] |
孙国, 顾元宪. 连续梁结构损伤识别的改进柔度阵方法[J]. 工程力学, 2003, 20(4): 857-868. SUN Guo, GU Yuan-xian. Improved Flexibility Matrix Method for Damage Identification of Multi-span Beams[J]. Engineering Mechanics, 2003, 20(4): 857-868. |
| [8] |
王锋.基于模态应变能方法的桥梁损伤识别研究[D].长沙: 长沙理工大学, 2006. WANG Feng. Research on Bridge Damage Identification Based on Modal Strain Energy[D].Changsha: Changsha University of Science & Technology, 2006. |
| [9] |
艾叶青, 王根会, 朱尚清. 基于改进的BP神经网络的桥梁结构损伤诊断研究[J]. 兰州交通大学学报:自然科学版, 2005, 24(3): 44-47. AI Ye-qing, WANG Gen-hui, ZHU Shang-qing. Study of Bridge Structure Damage Diagnosis Based on Improved BP Neural Network[J]. Journal of Lanzhou Jiaotong University:Natural Science Edition, 2005, 24(3): 44-47. |
| [10] |
郭健.基于小波分析的结构损伤识别方法研究[D].杭州: 浙江大学, 2004. GUO Jian. Study of Structural Damage Identification Based on Wavelet Analysis[D].Hangzhou: Zhejiang University, 2004. |
| [11] |
蔡正东.基于小波分析的桥梁结构损伤识别方法研究[D].武汉: 武汉理工大学, 2007. CAI Zheng-dong. Research on Bridge Structural Damage Identification Method Based on Wavelet Analysis[D].Wuhan: Wuhan University of Technology, 2007. |
| [12] |
毋淦.基于小波分析的桥梁结构损伤识别研究[D].郑州: 华北水利水电大学, 2016. WU Gan. Research on Bridge Structure Damage Identification Based on Wavelet Analysis[D]. Zhengzhou: North China University of Water Resources and Electric Power, 2016. |
| [13] |
陈静, 葛文璇. 有限元法求解内力影响线[J]. 南通大学学报:自然科学版, 2007, 6(2): 30-33, 37. CHEN Jing, GE Wen-xuan. Calculation of Influence Lines of Internal Forces with Application of Finite Element[J]. Journal of Nantong University:Natural Science Edition, 2007, 6(2): 30-33, 37. |
| [14] |
卢广森.基于改进阈值函数的小波去噪及其优化研究[D].昆明: 昆明理工大学, 2017. LU Guang-sen. Wavelet Denoising and Optimization Based on Improved Threshold Function[D]. Kunming: Kunming University of Science and Technology, 2017. |
| [15] |
石志晓, 李昕, 周晶. 损伤检测的经验模态分解法[J]. 大连理工大学学报, 2005, 45(3): 401-404. SHI Zhi-xiao, LI Xin, ZHOU Jing. Damage Detection Using Empirical Mode Decomposition[J]. Journal of Dalian University of Technology, 2005, 45(3): 401-404. |
| [16] |
罗淼, 姚运萍. 信号降噪中小波基与阈值的选取研究[J]. 机械制造, 2015, 53(12): 42-45. LUO Miao, YAO Yun-ping. An Examination on Selection of Small Porgy and Thresholds during Signal Noise Reduction[J]. Machinery, 2015, 53(12): 42-45. |
| [17] |
刘密歌. 采样定理研究[J]. 西安文理学院学报:自然科学版, 2019, 22(5): 64-68. LIU Mi-ge. Research on Sampling Theorem[J]. Journal of Xi'an University:Natural Science Edition, 2019, 22(5): 64-68. |
| [18] |
吴孟畅.基于随机车流的公路桥车桥耦合振动分析[D].武汉: 华中科技大学, 2018. WU Meng-chang. Coupled Vibration Analysis of Highway Bridge Based on Random Traffic Flow[D].Wuhan: Huazhong University of Science and Technology, 2018. |
| [19] |
朱干江.非参数密度估计在判别分析中的应用[D].南京: 南京信息工程大学, 2007. ZHU Gan-jiang. Application of Non-parametric Density Estimation in Discriminant Analysis[D].Nanjing: Nanjing University of Information, 2007. |
 2021, Vol. 38
2021, Vol. 38
