扩展功能
文章信息
- 王骁帆, 张毅, 刘朝晖
- WANG Xiao-fan, ZHANG Yi, LIU Zhao-hui
- 温湿翘曲对连续配筋混凝土路面配筋设计的影响
- Influence of Temperature and Moisture Warping on Reinforcement Design of CRCP
- 公路交通科技, 2021, 38(1): 33-40
- Journal of Highway and Transportation Research and Denelopment, 2021, 38(1): 33-40
- 10.3969/j.issn.1002-0268.2021.01.005
-
文章历史
- 收稿日期: 2020-02-10
2. 湖南鑫长胜材料科技有限公司, 湖南 长沙 410004;
3. 长沙理工大学 公路养护技术国家工程实验室, 湖南 长沙 410004
2. Hunan Xinchangsheng Materials Technology Co., Ltd., Changsha Hunan 410004, China;
3. State Engineering Laboratory of Highway Maintenance Technology, Changsha University of Science and Technology, Changsha Hunan 410004, China
连续配筋混凝土路面(CRCP)结构强度高、使用寿命长,被广泛运用于港口道路、机场跑道和重工业省份的城际干线[1-2]。配筋设计是CRCP的关键技术,现有研究多聚焦于温缩和干缩效应,较少关注温湿耦合梯度对配筋设计的影响[3-4],配筋指标(横向裂缝的平均间距、纵向钢筋埋置深度处裂缝缝隙的平均宽度和钢筋拉应力)计算值显然偏小。
黄晓明[5]认为CRCP温度翘曲应力的计算可以用同尺寸水泥混凝土板的翘曲应力计算方法,为本研究建模验证提供了理论参考。湿度梯度一般利用等效温度矩的方法进行计算,即将湿度翘曲简化为温度翘曲进行分析[6-14]。张翛[6]计算了湿度梯度作用下,基层类型对配筋设计的影响规律,但他采用的二维有限元模型具有局限性。AASHTO[8]和国内规范[9]假设路面板为均匀混凝土板,忽略了相对湿度对水泥混凝土物理力学性质的影响。Janssen[10]和高原[11]测定了密闭养护条件下,水泥混凝土相对湿度和收缩变形,得到了试件内部的相对湿度变化曲线。Shoukry[12]研究了温湿效应对水泥混凝土模量和泊松比的影响,回归了材料力学性质与相对湿度的相关方程。魏亚[13]和高翔[14]等分析了湿度翘曲机理,但是仍采用均匀板的力学模型。
文章在上述成果的基础上,假设路面板为非均匀板,即考虑了湿度对混凝土材料弹性模量的影响,利用弹性薄板理论和ABAQUS软件,分析了温湿耦合对非均匀CRC板配筋设计的影响规律,成果可以为CRCP设计提供理论借鉴。
1 素混凝土薄板的小挠度翘曲理论 1.1 湿度变形机理和本构方程 1.1.1 自干燥收缩和翘曲变形混凝土板湿度变形包括水泥混凝土的自干燥收缩和相对湿度变化引起的翘曲变形[14]。当路面板与湿度环境相互隔绝时,水泥基胶凝材料仍然会与毛细孔隙自由水发生水化反应,细观上表现为毛细管壁的收缩变形。由于水化硬化属于材料的固有物化属性,故路面板的相对湿度会在全尺寸内均匀降低,引起的变形在宏观上表现为板块沿水平方向的均匀收缩,此类收缩称为自干燥收缩。
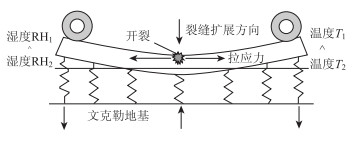
当硬化后的路面板与干燥的大气环境接触时,存在于毛细孔隙中的自由水会从上表面缓慢蒸发,并在上端形成局部干燥区域。若面层底部被基层滞水浸湿,则顶部的干燥区域会与底部的湿润区域形成自上而下的非线性负湿度梯度。路面板相对湿度在深度方向的非线性变化,使其内部各点产生不同程度的毛细管壁收缩变形。当路面板不受任何外部约束时,其内部各点的微元体由于收缩不一致,变形会受到相邻微元体的钳制,呈现翘曲特征。此时,板顶的相对湿度小,收缩变形较大,产生拉应力;板底的相对湿度大,收缩变形小,产生压应力。因此,CRCP在负温湿耦合梯度、均匀温降和车辆荷载的共同作用下,板中位置会自上而下发生疲劳开裂(见图 1)。
|
| 图 1 负温湿耦合梯度和车辆荷载对路面的影响 Fig. 1 Influence of negative coupling gradient of temperature and moisture and traffic loading on pavement |
| |
1.1.2 湿度-应变本构方程
Pickett和魏亚通过自干缩试验[13],提出了水泥基胶凝材料湿度收缩应变与路面板相对湿度的线性本构方程:

|
(1) |
式中,εc为收缩应变;αm为混凝土湿度膨胀系数;n为集料的收缩限制系数,一般取1.68[12];VA为集料的体积含量;RH为相对湿度。
1.1.3 应力-应变本构方程混凝土内部微元体的应变是湿度梯度引起的变形和材料收缩综合作用的结果。假设发生翘曲时,xy截面仍符合平面假设,即γxy=0。根据基尔霍夫假设[15],得到路面板湿度变形的应力-应变本构方程为:
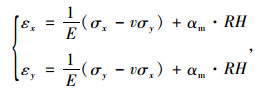
|
(2) |
式中,E为混凝土弹性模量;v为泊松比。
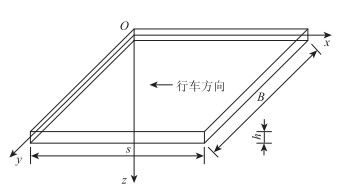
1.2 湿度翘曲应力的直角坐标解答设无限大路面板的体力(自重)忽略不计,其计算模型和坐标系如图 2所示。取行车方向(纵向)为x轴,横向为y轴,深度方向(竖向)为z轴,板厚中心为坐标原点o。板的厚度为h,宽度为B,长度为s。设B与s等价无穷大。规定:拉应力为正;收缩应变为正;引起路面板上翘的力矩为正。
|
| 图 2 直角坐标系和计算模型 Fig. 2 Rectangular coordinate system and calculation model |
| |
当矩形路面板长度和宽度相近时,可假设中性层沿坐标轴方向的曲率χx和χy相等。根据变形几何方程,得:
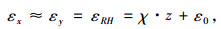
|
(3) |
式中,εRH为湿度翘曲应变;χ为中性层沿坐标方向的曲率;ε0为湿度梯度为零时的残余应变。将式(3)代入本构方程(2),求得路面板的湿度翘曲应力分量为:
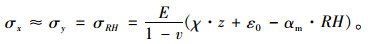
|
(4) |
路面板四周自由翘曲,切应力可忽略不计。又因为四周属于次要边界,根据圣维南原理和静力平衡原则,x=0和x=s处的正应力边界条件(y=0和y=B处的边界条件类似)可等效简化为:
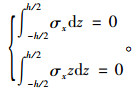
|
(5) |
水泥混凝土的物理力学性质与RH相关,且RH为z的函数。故令E=E(z),v=v(z),αm=αm(z),将式(4)代入式(5),得到ε0和χ。再将ε0和χ的计算公式代入式(4),得到湿度翘曲应力为:

|
(6) |
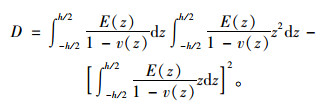
|
(7) |
关于CRCP的翘曲,配筋设计主要考虑板顶受拉的情况[8-9]。故取负温湿耦合梯度来模拟最不利温湿荷载的情况。利用温度矩和湿度矩的概念,使等效温度梯度Te引起的温度收缩变形和湿度梯度引起的湿度收缩变形相等,求解Te。
当路面板不受自重和任何外部约束时,由于χx=χy,则由式(6)和温湿等效原则,得到湿度梯度在单位宽度上引起的湿度矩MRH为:

|
(8) |
式中,MRH为湿度矩。由文献[1]可知,等效温度梯度在单位宽度上产生的温度矩为:

|
(9) |
式中,MT为温度矩;αc为混凝土线膨胀系数;Ec为面层混凝土弹性模量的标准设计值;vc为面层混凝土泊松比的标准设计值;ΔTe为上下板面的等效温差,ΔTe=Te·h。令温、湿梯度产生的截面收缩变形相等,即MRH=MT,则:

|
(10) |
根据文献[12]的水泥混凝土组分和强度试验结果,参考我国现行规范[9],得到有关计算参数为:αc=7.0×10-6/℃,VA=76%,Ec=28 GPa,vc=0.18。混凝土弹性模量E、泊松比v与RH(0~1.0)的相关关系为:

|
(11) |
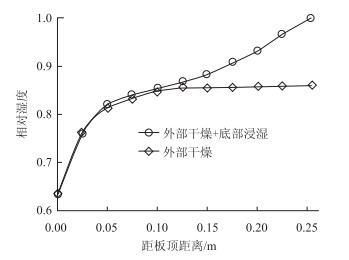
采用相同的水泥混凝土(W/C=0.4),厚度h≈0.25 m。将路面板置于密闭条件下标准养护28 d,模拟外部干燥、外部干燥和底部浸湿耦合的道路湿度环境。将其上表面暴露在RH=50%的环境下,四周与有机玻璃板接触,底部则分别与水h或有机玻璃板接触,再养护28 d。试验过程恒温25 ℃, 用温湿传感器测得路面板内部的相对湿度曲线见图 3。
|
| 图 3 水泥混凝土面板相对湿度分布曲线 Fig. 3 Relative humidity distribution curves of cement concrete slab |
| |
对图 3的两条湿度分布曲线进行拟合,得到RH关于坐标z的回归关系式(12),回归参数的取值(a~f)见表 1。

|
(12) |
| 回归参数 | 外部干燥 | 外部干燥和底部浸湿 |
| a | -31 395 | 0 |
| b | 3 252.7 | 2 157.4 |
| c | 323.19 | -487.74 |
| d | -7.3 | 23.634 |
| e | -4.226 5 | 4.541 9 |
| f | 0.217 4 | 0.566 3 |
| g | 0.854 2 | 0.865 6 |
结合表 1回归参数,联立式(1)、式(8)和式(10)~(12)得到MRH, ΔTe和Te的计算结果(见表 2)。若不考虑RH对材料力学性质的影响,则按文献[13]计算3个参数。
| 计算参数 | 均匀板 | 非均匀板 | |||
| 外部干燥 | 外部干燥底部浸湿 | 外部干燥 | 外部干燥底部浸湿 | ||
| MRH/(kN·m-1) | -12.33 | -24.52 | -13.28 | -27.01 | |
| Δ Te/℃ | -9.60 | -19.08 | -10.34 | -21.02 | |
| Te/(℃·m-1) | -37.79 | -75.13 | -40.70 | -82.74 | |
由表 2可知:相同外部湿度条件下,考虑湿度对材料性质影响的非均匀板的MRH,ΔTe和Te比均匀板大8%~10%。当路面层底部的基层滞水时,MRH,ΔTe和Te会增加1倍。
图 3湿度曲线不可避免受到自干燥的影响。由于自干燥收缩比较均匀,可以假设截面上的自干缩应力分布均匀、合成弯矩为0,测得的RH曲线可用于翘曲变形的计算。
1.3.2 负温度梯度现行规范[9]根据公路环境区划,给出了最大正温度梯度参考值(见表 3),最大负温度梯度Tg则按最大正温度梯度的1/4~1/3选取。
| 公路自然区划 | Ⅱ区、Ⅴ区 | Ⅲ区 | Ⅳ区、Ⅵ区 | Ⅶ区 |
| 最大正温度梯度/(℃·m -1) | 83~88 | 90~95 | 86~92 | 93~98 |
1.4 翘曲应力的计算方法 1.4.1 Westergard公式
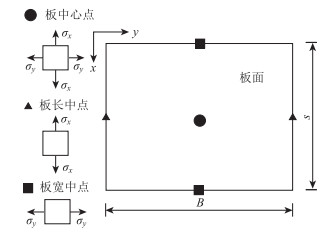
当不计自重和四周约束的无限大矩形薄板置于文克勒地基上时,将等效温度梯度和温度梯度的参考值[9]代入Westergard公式,近似求解有限尺寸板的翘曲应力[5]。该公式也可近似求解有限尺寸板的翘曲应力[5]。式(13)、式(14)为路面板中心点和板边半长(宽)处的最大翘曲应力(见图 4):

|
(13) |

|
(14) |
|
| 图 4 翘曲应力计算点位 Fig. 4 Calculation points for warping stress |
| |
式中,Cx,Cy为素混凝土路面板的翘曲应力系数,根据Bradbury曲线[1]取值;ΔTg为上下板面的温差,ΔTg=Tg·h;σ为σx时,C取Cx;σ为σy时,C取Cy。
1.4.2 现行规范公式现行规范[9]给出了温度和湿度变形完全受约束时的温湿翘曲应力,其计算方法是将温度和湿度应力叠加。具体可参考其附录D公式(D.0.1-2)~公式(D.0.1-5)。设计参数符号与文章基本相同。
2 有限元模拟与验证 2.1 有限元模型 2.1.1 材料参数与几何尺寸以公路区划Ⅱ区某地一级公路的尺寸为例[16]:该试验路面层厚0.25 m;基层厚0.18 m;采用重荷载交通等级;实测横向裂缝间距的分布范围为1~3 m。假设CRCP为路面板断裂后与纵向接缝围成的独立板,取长(裂缝间距)s=3 m、宽(单个行车道宽度)B=3.75 m。钢筋为HRB335:直径ds=16 mm;沿横向排列34根,布置间距107 mm;埋置位置距板顶1/3厚度;纵向配筋率ρ≈0.7%。刚性基层材料为贫混凝土。面层材料采用与前述相同的水泥混凝土(W/C=0.4)。由于基层的热力学性质对面层翘曲影响不大,故将基层视为弹性体。材料的物理力学参数见表 4。
| 材料性质 | 密度/ (kg·m -3) | 弹性模量/ MPa | 泊松比 | 线膨胀系数/ ℃ -1 |
| 钢筋 | 7 800 | 200 000 | 0.28 | 9.0×10 -6 |
| 面层 | 2 270 | 28 000 | 0.18 | 7.0×10 -6 |
| 基层 | 2 350 | 20 000 | 0.15 | N/A |
| 注:N/A表示空白。 | ||||
2.1.2 单元和网格划分
纵向钢筋采用B31(三维2结点线性梁单元),面层和基层采用C3D8R(8结点缩减积分实体单元)。在种子定义和网格尺寸取值时,取CRC板为0.05 m,基层为0.1 m,钢筋为0.025 m,共计28 860个网格。纵筋与面层节点之间植入三向弹簧单元,模拟钢筋和混凝土间的黏结-滑移行为。
2.1.3 荷载与边界条件仅对面层施加温湿耦合梯度,由表 3得Tg=-86/3=-28.67 ℃/m。CRCP所在区域干燥季节的平均相对湿度约为50%,根据表 2得Te=-40.7 ℃/m。碾压式贫混凝土基层与面层的摩阻系数μ参考现行规范取μ=8.5[14],地基的反应模量K=110 MPa/m[4],基层四周和钢筋纵向两端施加法向位移约束。
2.1.4 钢筋和混凝土的界面接触用三向弹簧模拟钢筋与混凝土的黏结-滑移。钢筋与混凝土之间的黏结刚度系数ks=28 MPa/mm[17]。由切应力等效原则,得:

|
(15) |
式中,δx取面层网格长度。则纵向弹簧刚度k=7.037 2×107 N/m。横向弹簧和竖向弹簧的刚度取108 N/m,用于约束钢筋的侧向变形和位移。
2.2 数值模拟的验证对图 4的素混凝土路面板施加温湿耦合梯度(-69.37 ℃/m),将各点的有限元结果和式(13)、式(14)的结果作对比。由表 5可知:对于板中点的最大翘曲应力,有限元解和威斯卡特德解的平均相对误差为3.5%,满足工程精度的要求(相对误差<5%);对于板长(宽)中点的最大翘曲应力,平均相对误差约为8%。越接近板中位置,有限元解的精确度越高,且相对于路面板而言,板边区域的面积所占比例较小。文献[5]认为CRCP温度翘曲应力的计算可以利用同尺寸水泥混凝土板的翘曲应力计算方法。因此,赋予混凝土板温度梯度,利用有限元法分析CRCP的温湿耦合翘曲合理可行。
| 翘曲拉应力/MPa | 板中心点 | 板长中点 | 板宽中点 | |
| σx | σy | σx | σy | |
| Westergaard解 | 0.656 | 1.008 | 0.475 | 0.890 |
| 有限元解 | 0.683 | 1.038 | 0.524 | 0.946 |
3 温湿翘曲对配筋设计的影响
CRCP的配筋指标主要有钢筋应力、横向裂缝间距和缝隙宽度[3]。
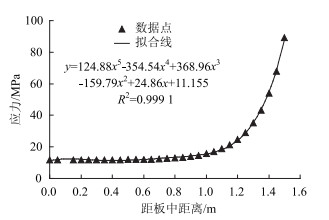
3.1 钢筋应力和缝隙宽度在复杂应力作用下,钢筋等塑性材料的屈服失效一般由形状改变能密度引起,故将Mises应力云图作为钢筋的计算输出结果。计算结果表明,每根纵向钢筋的应力云图几乎相同,且对称于板中截面。取板中钢筋半结构,绘制Mise应力分布如图 5所示:从板中到横向裂缝位置,钢筋的应力逐渐增大,裂缝位置的钢筋应力最大值为89.13 MPa。
|
| 图 5 钢筋Mises应力的纵向分布 Fig. 5 Longitudinal distribution of Mises stress of reinforcement |
| |
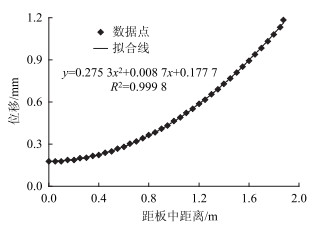
根据黏结滑移理论和对称性,纵向钢筋埋置深度处裂缝缝隙宽度是该位置混凝土板位移(缝隙位移)的两倍[3, 18],由于横向裂缝并不是等间距分布,肖秋明等认为缝隙宽度是缝隙位移的1.4倍[19]。钢筋埋置深度处缝隙位移的横向分布如图 6所示:位移分布规律为二次抛物线形式;板中心的缝隙位移最小,距离板中心越远,缝隙位移越大;钢筋埋深处缝隙的平均位移为0.52 mm。
|
| 图 6 缝隙位移的横向分布 Fig. 6 Transverse distribution of cracking displacement |
| |
3.2 混凝土翘曲应力
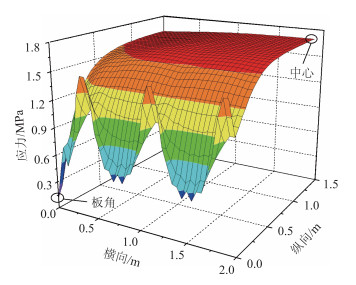
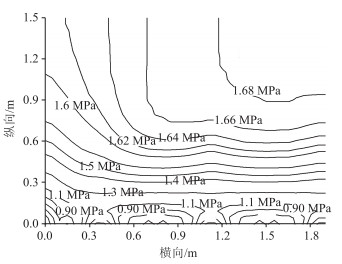
根据湿度变形机理:面层顶部的、混凝土受拉,底部的混凝土受压。混凝土为脆性材料,抗压性能好,其破坏一般由拉应力引起。数值模拟结果表明:主应力云图关于CRC板纵向中线和横向中线对称。因此,取1/4路面板,绘制CRC板顶部的主应力分布和等值线如图 7~8所示。随着临近单元体的钳制力增大,越靠近板中,CRC板顶部拉应力越大,应力变化率越小;横向裂缝附近的钢筋拉应力受到钢筋端部约束的影响,存在应力极值区域;混凝土翘曲应力的最大值为1.69 MPa,且位于CRC板的中心;相邻裂缝间的中部,混凝土拉应力最大,容易发生二次开裂。
|
| 图 7 面层顶部主应力分布 Fig. 7 Distribution of principal stresses at surface course top |
| |
|
| 图 8 面层顶部主应力等值线 Fig. 8 Isogram of principal stresses at surface course top |
| |
将表 2的Te值代入现行规范公式(D.0.1-2)-公式(D.0.1-4),得CRCP混凝土的温度翘曲应力如表 6所示。
| 计算值 | 均匀板 | 非均匀板 | |||
| 外部干燥 | 外部干燥底部浸湿 | 外部干燥 | 外部干燥底部浸湿 | ||
| Te/(℃·m -1) | -37.79 | -75.13 | -40.70 | -82.74 | |
| 应力/MPa | 1.02 | 2.03 | 1.10 | 2.24 | |
3.3 横向裂缝间距与应力、缝隙位移的关系
分别取CRC板长度为1~3 m,其他参数同上,研究横向裂缝间距-钢筋/混凝土最大拉应力、横向裂缝间距-缝隙位移的关系,分析裂缝间距对配筋设计指标的影响规律(见表 7)。由表 7可知:配筋设计指标计算值随着裂缝间距增大而大幅增大。因此,当裂缝间距较大时,温湿翘曲应力和缝隙位移对CRCP结构设计的影响不可忽略。
| 裂缝间距/m | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 |
| 钢筋最大拉应力/MPa | 44.57 | 47.34 | 50.29 | 78.87 | 89.13 |
| 混凝土最大拉应力/MPa | 0.65 | 0.83 | 1.34 | 1.46 | 1.69 |
| 缝隙位移/mm | 0.38 | 0.41 | 0.46 | 0.50 | 0.52 |
4 结论
文章主要关注温湿耦合梯度对配筋设计指标的影响,主要结论有:
(1) 推导了非均匀自由板湿度翘曲应力的解析公式,拟合了路面板内部的相对湿度曲线,计算了等效负温度梯度。相同湿度条件下,非均匀板的等效温度梯度比均匀板大8%~10%。底部浸湿后,非均匀板的等效温度梯度比仅考虑外部干燥的等效温度梯度大1倍。
(2) 将温湿耦合梯度转化为等效温度梯度,代入Westergaard公式和有限元模型,用Westergaard公式验证了有限元建模的合理性。
(3) 温湿耦合梯度作用下,钢筋的拉应力从板中到横向裂缝位置显著增大,最大达到89.13 MPa;混凝土的最大翘曲应力为1.69 MPa,位于面板的中心;钢筋埋深处的缝隙位移沿横向呈二次抛物线分布规律;配筋设计指标的计算值随着横向裂缝间距的增大而增大。
| [1] |
王骁帆, 应正兵, 刘朝晖, 等. 温度场对连续配筋混凝土路面纵向配筋的影响[J]. 公路交通科技, 2017, 34(4): 16-24, 57. WANG Xiao-fan, YING Zheng-bing, LIU Zhao-hui, et al. Effect of Temperature Field on Longitudinal Reinforcement of Continuously Reinforced Concrete Pavement[J]. Journal of Highway and Transportation Research and Development, 2017, 34(4): 16-24, 57. |
| [2] |
LI S, LIU X W, LIU Z H. Interlaminar Shear Fatigue and Damage Characteristics of Asphalt Layer for Asphalt Overlay on Rigid Pavement[J]. Construction and Building Materials, 2014, 68: 341-347. |
| [3] |
葛倩如, 黄志义, 王金昌, 等. BFRP连续配筋复合式路面配筋设计[J]. 浙江大学学报:工学版, 2015, 49(1): 186-192. GE Qian-ru, HUANG Zhi-yi, WANG Jin-chang, et al. Reinforcement Design of Composite Pavement Continuously Reinforced with Basalt Fiber Reinforced Plastics Bars[J]. Journal of Zhejiang University: Engineering Science Edition, 2015, 49(1): 186-192. |
| [4] |
左志武.连续配筋混凝土路面横向裂缝分布和冲断预估研究[D].西安: 长安大学, 2010. ZUO Zhi-wu. Study on Distribution of Transverse Cracks and Pounchout Prediction of Continuously Reinforced Concrete Pavement[D]. Xi'an: Chang'an University, 2010. |
| [5] |
黄晓明, 白桃, 李昶, 等. 连续配筋水泥混凝土路面的温度翘曲应力研究[J]. 同济大学学报:自然科学版, 2011, 39(7): 1026-1030. HUANG Xiao-ming, BAI Tao, LI Chang, et al. Temperature Warping Stress Study on Continuously Reinforced Concrete Pavement[J]. Journal of Tongji University: Natural Science Edition, 2011, 39(7): 1026-1030. |
| [6] |
张翛, 赵鸿铎, 赵队家, 等. 水泥混凝土路面板湿度翘曲应力计算方法[J]. 交通运输工程学报, 2016, 16(1): 1-7. ZHANG Xiao, ZHAO Hong-duo, ZHAO Dui-jia, et al. Calculation Method of Moisture Warping Stress for Cement Concrete Pavement Slab[J]. Journal of Traffic and Transportation Engineering, 2016, 16(1): 1-7. |
| [7] |
权磊, 田波, 冯德成, 等. 水泥混凝土板硬化温度翘曲正向计算方法研究[J]. 土木工程学报, 2016, 49(4): 121-128. QUAN Lei, TIAN Bo, FENG De-cheng, et al. Forward Calculation Method to Determine Built-in Thermal Curling of Concrete Slabs[J]. China Civil Engineering Journal, 2016, 49(4): 121-128. |
| [8] |
AASHTO—2002, Guide for Design of Pavement Structure[S].
|
| [9] |
JTG D40—2011, 公路水泥混凝土路面设计规范[S]. JTG D40—2011, Specifications for Design of Highway Cement Concrete Pavement[S]. |
| [10] |
JANSSEN D J. Moisture in Portland Cement Concrete[J]. Journal of the Transportation Research Board, 1987, 1121: 40-44. |
| [11] |
高原, 张君, 孙伟. 干湿循环下混凝土湿度与变形的测量[J]. 清华大学学报:自然科学版, 2012, 52(2): 144-149. GAO Yuan, ZHANG Jun, SUN Wei. Concrete Deformation and Interior Humidity during Dry-wet Cycles[J]. Journal of Tsinghua University:Science and Technology Edition, 2012, 52(2): 144-149. |
| [12] |
SHOUKRY S N, WILLIAM G W, DOWNIE B, et al. Effect of Moisture and Temperature on the Mechanical Properties of Concrete[J]. Construction & Building Materials, 2011, 25(2): 688-696. |
| [13] |
魏亚. 水泥混凝土路面板湿度翘曲形成机理及变形计算[J]. 工程力学, 2012, 29(11): 266-271. WEI Ya. Mechanism of Moisture Warping and Deformation Calculations in Concrete Pavements[J]. Engineering Mechanics, 2012, 29(11). |
| [14] |
高翔, 魏亚. 水泥混凝土路面板湿度梯度模拟与分析[J]. 工程力学, 2014, 31(8): 183-188. GAO Xiang, WEI Ya. Modeling and Analysis of Moisture Gradients in Concrete Pavements[J]. Engineering Mechanics, 2014, 31(8): 183-188. |
| [15] |
铁摩辛柯S P, 古地尔J N.弹性理论[M].徐芝纶, 译.北京: 人民教育出版社, 1964. TIMOSHENKOS P, GOODIER J N. Elastic Theory[M]. XU Zhi-lun, translated. Beijing: People's Education Press, 1964. |
| [16] |
张翛, 胡圣能, 赵鸿铎, 等. 连续配筋混凝土路面裂缝间距特性[J]. 交通运输工程学报, 2013, 13(4): 1-7. ZHANG Xiao, HU Sheng-neng, ZHAO Hong-duo, et al. Characteristic of Crack Spacing for Continuously Reinforced Concrete Pavement[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 1-7. |
| [17] |
JTG D40—2002, 公路水泥混凝土路面设计规范[S]. JTG D40—2002, Specifications for Design of Highway Cement Concrete Pavement[S]. |
| [18] |
刘朝晖, 王骁帆, 李盛, 等. 温缩和干缩对连续配筋混凝土路面纵向配筋的影响[J]. 中国公路学报, 2016, 29(11): 1-9. LIU Zhao-hui, WANG Xiao-fan, LI Sheng, et al. Influences of Thermal and Drying Shrinkages on Longitudinal Reinforcement in Continuously Reinforced Concrete Pavement[J]. China Journal of Highway and Transport, 2016, 29(11): 1-9. |
| [19] |
肖秋明, 查旭东, 张起森. 连续配筋混凝土路面一维非线性力学分析[J]. 长沙交通学院学报, 2004, 20(3): 20-26. XIAO Qiu-ming, ZHA Xu-dong, ZHANG Qi-sen. One-Dimensional Nonlinear Analysis of Continuously Reinforced Concrete Pavements[J]. Journal of Changsha Communications University, 2004, 20(3): 20-26. |
 2021, Vol. 38
2021, Vol. 38
