扩展功能
文章信息
- 周光伟, 钱长照
- ZHOU Guang-wei, QIAN Chang-zhao
- 张弦桥结构静力分析方法与受力特点研究
- Study on Static Structural Analysis Method and Mechanical Characteristics of String-tensioned Bridge
- 公路交通科技, 2020, 37(12): 63-69
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(12): 63-69
- 10.3969/j.issn.1002-0268.2020.12.009
-
文章历史
- 收稿日期: 2020-03-24
张弦梁结构是近20年发展起来的一种新型组合结构体系,特别适用于大跨度空间结构,并且开展了相关应用研究[1-10]。它由3类基本构件组成,即承受压弯的上弦刚性主梁,承受拉力的下弦索(主缆)和连接二者的受压撑杆组成。由于外部采用简支约束条件,张弦梁结构是一种典型的预应力自平衡结构体系。张弦梁结构主要应用于大跨度工业与建筑结构[11-14],如体育馆、会展中心和航站楼、站台雨棚等屋盖结构,在桥梁结构中应用极少。近年来在城市人行桥设计中开始出现这种结构体系,本研究主要就张弦桥的受力特点进行分析与探讨。
主梁是张弦桥保证车辆行驶、承受人群荷载、提供结构刚度的压弯构件,根据张弦桥的结构特点,一期恒载对主梁不会产生较大的整体弯矩,主梁的弯曲内力主要来自结构二期恒载与活载。由于张弦桥区别于普通的悬索桥,下面基于弹性理论方法和挠度理论方法提出了张弦桥的内力分析方法,推导了主梁在典型工况竖向荷载作用下内力与位移计算公式。
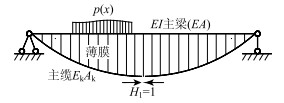
1 弹性理论方法弹性理论是早期中小跨径悬索桥设计采用的设计理论方法,它没有考虑主缆的几何非线性,计算结果偏大,但当主梁刚度较大,跨径较小时,采用弹性理论计算能满足工程设计的要求。张弦桥不同于普通的悬索桥,属于自平衡结构体系,如图 1所示。基于张弦桥的结构受力特点,采用弹性理论方法推导如下。
|
| 图 1 张弦桥弹性理论计算图 Fig. 1 Calculation diagram of elastic theory for string-tensioned bridge |
| |
弹性理论与挠度理论方法的一个基本假定是将等间距布置的撑杆近似视作介于主缆和主梁之间的薄膜,该薄膜只承担竖向支撑力。建立力法方程为:
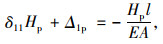
|
(1) |
式中, Δ1p为外荷载p(x)引起的主缆切口两侧的相对水平位移; l为张弦桥计算跨径见图 1。δ11为单位水平力引起的主揽切口两侧的相对水平位移。
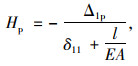
|
(2) |
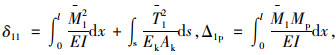
|
(3) |
式中,Hp为二期恒载或活载引起的主缆水平力增量;E为主梁的弹性模量;I为主梁的抗弯惯性矩;Ek为主缆弹性模量;Ak为主缆的截面积;M1,T1分别为单位荷载H1=1作用下主梁产生的弯距及主缆产生的拉力;Mp为外荷载p(x)作用于基本结构上对主梁产生的弯距。
由方程(1)求出赘余力Hp后,就能方便求出主梁任意截面的内力和位移。
2 挠度理论的等代梁方法挠度理论是大跨径悬索桥计算的理论基础,该方法考虑了悬索桥几何非线性的影响。由于挠度理论的非线性方程求解的复杂性,李国豪教授于1941年提出了线性挠度理论的等代梁求解方法[15],近年来在该方法基础上对悬索桥开展了相关研究[16-17]。本研究基于等代梁方法推导了张弦桥的内力与位移的计算方法。
挠度理论的平衡微分方程为:
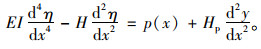
|
(4) |
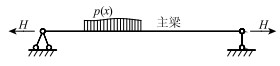
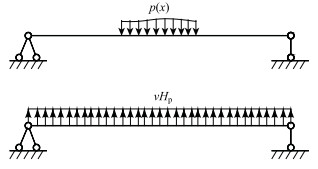
由于张弦桥为自平衡体系,主缆对主梁产生的轴压力刚好与等代梁计算模型中的虚拉力方向相反(如图 2、图 3所示),相互抵消,从而使式(4)变为:
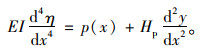
|
(5) |
|
| 图 2 等代梁方法计算模型 Fig. 2 Calculation model of equal-substitute beam method |
| |
|
| 图 3 张弦桥等代梁方法计算模型 Fig. 3 Calculation model of equal-substitute beam method for string-tensioned bridge |
| |
张弦桥下弦主缆成桥后线形(在恒载作用下)一般为二次抛物线,f为矢高,则有:
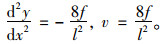
|
(6) |
这时式(5)可以写成如下形式:
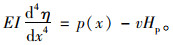
|
(7) |
利用全桥主缆长度变化的水平投影等于主梁受压缩短的长度这一条件有:
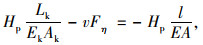
|
(8) |
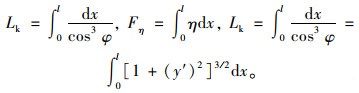
|
(9) |
积分函数按级数展开并取前面两项为:
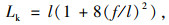
|
(10) |
式中,p(x)为作用在梁上的任意荷载;vHp为作用在整个梁上的均布荷载,其绝对值为vHp。
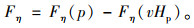
|
(11) |
由均布荷载挠度函数方程求出荷载为vHp的挠度面积为:
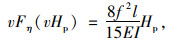
|
(12) |
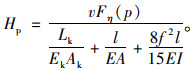
|
(13) |
同样,采用挠度理论方法计算出Hp后,利用公式(5)能方便求出结构的内力与位移。
3 弹性理论与挠度理论方法计算结果比较由上面的分析可知,张弦桥弹性理论与挠度理论方法关键是先求出荷载作用下主缆水平索力增量Hp,后面的内力计算方法均相同。
弹性理论方法中,δ11的计算推导如下:
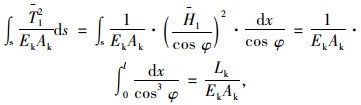
|
(14) |
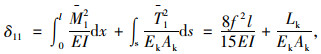
|
(15) |
根据虚功原理,有:
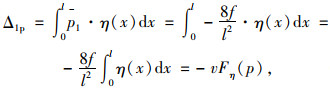
|
(16) |
式中,η(x)为外荷载p(x)的位移函数;p1为单位荷载H1产生的竖向支撑膜力。
把式(15)、式(16)代入式(2),可得
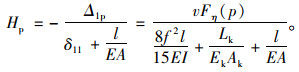
|
(17) |
式(17)与按挠度理论求出的式(13)完全一样,即采用两种方法计算的水平力增量Hp完全相同,上述计算结果证明了张弦桥受力性能接近于线弹性的受力特点,因此和普通悬索桥相比,张弦桥主缆的几何非线性影响较小。
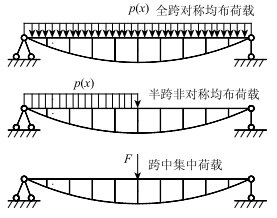
4 典型荷载工况张弦梁内力与位移对于悬索桥静力计算,有3种典型荷载计算工况,即全跨对称均布荷载、半跨非对称荷载以及跨中集中荷载布置工况,如图 4所示。下面推导3种荷载工况下主梁控制截面的内力和位移。
|
| 图 4 典型荷载计算工况 Fig. 4 Typical load calculation cases |
| |
(1) 全跨对称均布荷载
在全跨均布荷载作用下,可以求得其挠度面积为:
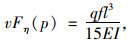
|
(18) |
代入式(17)可得:
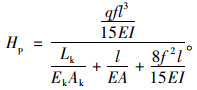
|
(19) |
则跨中处弯矩为:
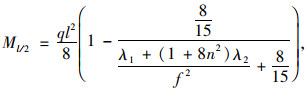
|
(20) |
式中,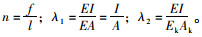
则l/4处弯矩为:
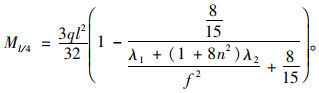
|
(21) |
则跨中处相应位移为:
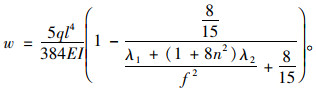
|
(22) |
则l/4处相应位移为:
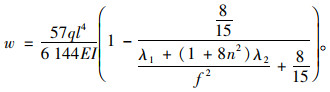
|
(23) |
(2) 半跨非对称均布荷载
在半跨非对称均布荷载作用下,可以求得其挠度面积为:
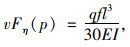
|
(24) |
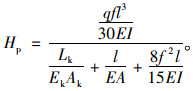
|
(25) |
则跨中处弯矩为:
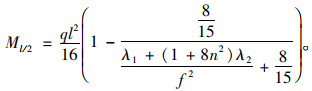
|
(26) |
则l/4处弯矩为:
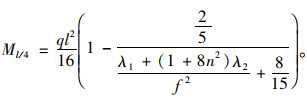
|
(27) |
则跨中处相应位移为:
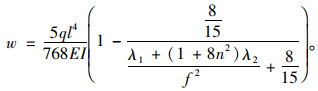
|
(28) |
则l/4处相应位移为:
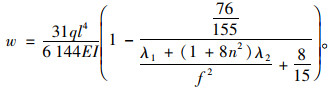
|
(29) |
(3) 跨中集中荷载
在跨中集中荷载F作用下,可以求得其挠度面积为:
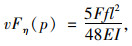
|
(30) |
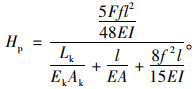
|
(31) |
则跨中处弯矩为:
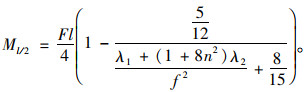
|
(32) |
则l/4处弯矩为:
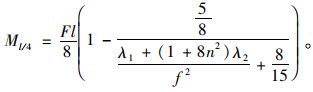
|
(33) |
则跨中处相应位移为:
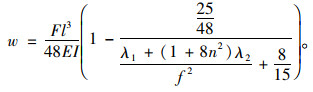
|
(34) |
则l/4处相应位移为:
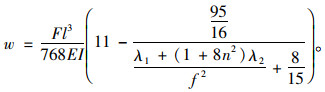
|
(35) |
由张弦桥主梁弯矩与位移推导的公式可知,和普通简支梁桥相比,张弦桥能较大地减小主梁跨中的弯矩与位移,主梁内力与位移的主要影响因素为主缆的矢高f,其他影响因素有主梁截面抗弯刚度与轴向刚度比λ1和主梁截面抗弯刚度与主缆截面轴向刚度比λ2。对于小垂度主缆的张弦桥,一般来说,主梁的矢跨比n影响较小。
对于张弦桥或悬索桥,矢跨比n基本在0.1左右,对于内力与位移来说影响非常小,上述公式可以更加简化,例如式(20)可以简化为:
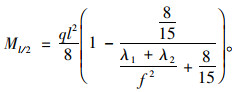
|
(36) |
为了和其他张弦梁分析方法进行比较,本研究采用文献[18]中的算例,张弦梁结构跨度27 m,梁为钢箱梁,其中, E=2.1×105 MPa,A=4.696×104 mm,I=5.006×109 mm4,下弦索为高强钢绞线,其中E=1.9×105 MPa,A=4.808×103 mm。在均布荷载q=27 kN/m作用下,跨中位移计算值在文献中有限元分析为45.92 mm,该文献方法计算值为45.456 mm,本研究方法按公式(22)的计算值为45.79 mm。3种方法计算结果接近完全一致。
5 工程实例分析某市张弦梁人行桥,计算跨径为55 m,矢跨比为1/11,主梁采用扁平钢箱结构,梁高0.8 m,桥面宽度为3 m;主缆基本线形设计为悬链线,主缆共设计10道V形撑杆,撑杆中心间距为5.5 m。该桥建立的MIDAS/ civil有限元模型如图 5所示。

|
| 图 5 张弦桥有限元分析模型 Fig. 5 Finite element analysis model of string-tensioned bridge |
| |
为了验证上述公式推导的正确性,以及比较主缆非线性对结构内力和位移的影响,结构分析采用两种有限元模型:一种是主缆采用弹性的桁架单元(主缆为桁架单元模型),一种是主缆采用非线性索单元(主缆为索单元模型),主梁与V形撑杆均采用空间梁单元,桁架单元模型时采用弹性分析方法,索单元模型采用非线性分析方法。荷载工况为全跨对称均布荷载、半跨非对称均布荷载与跨中集中荷载布置的3种工况。有限元分析与公式计算结果比较如表 1~表 3所示。各计算工况位移偏差值均小于3%;弯矩值偏差除1个值为8.6%外,其他弯矩偏差值均小于5%。
| 主梁弯矩/(kN·m) | 主梁位移/mm | ||||
| 跨中l/2处 | l/4处 | 跨中l/2处 | l/4处 | ||
| 主缆为桁架单元模型 | 624.4 | 457.3 | 82.6 | 58.1 | |
| 主缆为索单元模型 | 625.3 | 457.0 | 82.6 | 58.2 | |
| 公式计算结果 | 635.3 | 476.5 | 80.9 | 57.7 | |
| 主梁弯矩/(kN·m) | 主梁位移/mm | ||||
| 跨中l/2处 | l/4处 | 跨中l/2处 | l/4处 | ||
| 主缆为桁架单元模型 | 312.2 | 609.8 | 41.3 | 41.7 | |
| 主缆为索单元模型 | 312.5 | 609.8 | 41.3 | 41.6 | |
| 公式计算结果 | 317.6 | 635.7 | 40.5 | 41.6 | |
| 主梁弯矩/(kN·m) | 主梁位移/mm | ||||
| 跨中l/2处 | l/4处 | 跨中l/2处 | l/4处 | ||
| 主缆为桁架单元模型 | 1 183.1 | 109.4 | 73.2 | 42.9 | |
| 主缆为索单元模型 | 1 183.7 | 109.4 | 73.2 | 42.9 | |
| 公式计算结果 | 1 192.1 | 100.0 | 71.0 | 42.5 | |
表 1~表 3的结果表明,2种模型计算结果接近一致,和推导公式计算结果偏差较小,计算公式与有限元模型的计算差别主要源于等间距分布的撑杆和理论推导的薄膜假定有关。
常规大跨径悬索桥的一个重要特性是主缆重力刚度效应,即悬索桥的几何非线性效应。为了进一步验证张弦桥的弹性受力特点,将主缆索力增加5倍和10倍分别建立有限元模型进行非线性分析,分析重力刚度对张弦桥结构内力和位移的影响,计算结果如表 4~表 6所示。
| 主梁弯矩/(kN·m) | 主梁位移/mm | ||||
| 跨中l/2处 | l/4处 | 跨中l/2处 | l/4处 | ||
| 主缆为索单元模型 | 625.3 | 457.0 | 82.6 | 58.2 | |
| 5倍主缆索力模型 | 626.3 | 456.6 | 82.5 | 58.1 | |
| 10倍主缆索力模型 | 625.9 | 467.3 | 82.3 | 58.4 | |
| 主梁弯矩/(kN·m) | 主梁位移/mm | ||||
| 跨中l/2处 | l/4处 | 跨中l/2处 | l/4处 | ||
| 主缆为索单元模型 | 312.5 | 609.8 | 41.3 | 41.6 | |
| 5倍主缆索力模型 | 312.8 | 608.6 | 41.3 | 41.6 | |
| 10倍主缆索力模型 | 312.9 | 607.5 | 41.1 | 41.5 | |
| 主梁弯矩/(kN·m) | 主梁位移/mm | ||||
| 跨中l/2处 | l/4处 | 跨中l/2处 | l/4处 | ||
| 主缆为索单元模型 | 1 183.7 | 109.4 | 73.2 | 42.9 | |
| 5倍主缆索力模型 | 1 184.1 | 108.9 | 73.1 | 42.9 | |
| 10倍主缆索力模型 | 1 183.7 | 108.1 | 72.8 | 42.8 | |
表 4~表 6的计算结果表明,3种有限元模型分析结果基本一致,张弦桥主梁弯矩和位移增量与主缆张拉的索力无关,即索力的变化基本没有改变张弦桥的刚度。重力刚度属于几何非线性的范畴,因此,张弦桥主缆非线性影响较小,张弦桥结构具有弹性受力的特点。
6 结论(1) 张弦桥采用弹性理论、挠度理论的等代梁法分析结果相同,从理论上证明了张弦桥结构具有弹性的受力特点。
(2) 基于工程实例的张弦桥有限元分析,验证了本研究推导的主梁内力和位移公式的正确性。
(3) 通过有限元方法验证了主缆索力变化对张弦桥的刚度基本没有影响,张弦桥主缆非线性影响较小,这是张弦桥区别与普通悬索桥的一个重要特点。
| [1] |
沈世钊, 徐崇宝, 赵臣, 等. 悬索结构设计[M]. 2版. 北京: 中国建筑工业出版社, 2006. SHEN Shi-zhao, XU Chong-bao, ZHAO Chen, et al. Suspension Structure Design[M]. 2nd ed. Beijing: China Architecture & Building Press, 2006. |
| [2] |
郭彦林, 田广宇. 索结构体系、设计原理与施工控制[M]. 北京: 科学出版社, 2014. GUO Yan-lin, TIAN Guang-yu. Cable Structure System, Design Principle and Construction Control[M]. Beijing: Science Press, 2014. |
| [3] |
赵宪忠, 陈建兴, 陈以一. 张弦梁结构张拉过程中的结构性能试验研究[J]. 建筑结构学报, 2007, 28(4): 1-7, 50. ZHAO Xian-zhong, CHEN Jian-xing, CHEN Yi-yi. Experimental Study on Structural Performance during Prestressing of Beam String Structure[J]. Journal of Building Structure, 2007, 28(4): 1-7, 50. |
| [4] |
蒋友宝, 黄星星. 张弦梁结构刚度参数分析与优化设计[J]. 广西大学学报:自然科学版, 2015, 40(4): 798-805. JIANG You-bao, HUANG Xing-xing. Parametric Analysis and Design Optimization on Stiffness of Beam String Structure[J]. Journal of Guangxi University:Natural Science Edition, 2015, 40(4): 798-805. |
| [5] |
董宁娟, 赵洪金, 刘海涛. 平面张弦梁结构极限跨度研究[J]. 科学技术与工程, 2014, 14(24): 261-265. DONG Ning-juan, ZHAO Hong-jin, LIU Hai-tao. Ultimate Span Length Analysis for Planar Beam String Structure[J]. Science Technology and Engineering, 2014, 14(24): 261-265. |
| [6] |
李静斌, 洪彩玲, 张哲, 等. 张弦梁结构张拉力确定方法研究[J]. 郑州大学学报, 工学版, 2015, 36(1): 61-65. LI Jing-bin, HONG Cai-ling, ZHANG Zhe, et al. The Inquiry of Tension Method for the Beam String Structure[J]. Journal of Zhengzhou University:Engineering Science Edition, 2015, 36(1): 61-65. |
| [7] |
范栋浩, 杜咏, 盛红梅. 高温下张弦梁结构力学特征解析解[J]. 工程力学, 2016, 33(4): 195-204. FAN Dong-hao, DU Yong, SHENG Hong-mei. Mathematical Calculations for the Characteristics of Beam String Structure in Fire[J]. Engineering Mechanics, 2016, 33(4): 195-204. |
| [8] |
贺拥军, 孙轩, 周绪红. 张弦巨型网格结构动力特性研究[J]. 防灾减灾工程学报, 2016, 36(5): 737-743, 750. HE Yong-jun, SUN Xuan, ZHOU Xu-hong. Research on Dynamic Performance of String Reticulated Mega-structure[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(5): 737-743, 750. |
| [9] |
殷志祥, 岳旭. 基于半波法的双向张弦梁结构索力测试试验研究[J]. 应用力学学报, 2018, 35(4): 880-885, 939. YIN Zhi-xiang, YUE Xu. Study of the Bidirectional Beam String Structure Test of Cable Tension Based on Half-wave Method[J]. Chinese Journal of Applied Mechanics, 2018, 35(4): 880-885, 939. |
| [10] |
李辉进, 廖光明, 柏洁, 等. 基于大位移广义变分的张弦梁理论微分方程近似推导[J]. 科学技术与工程, 2018, 18(5): 276-280. LI Hui-jin, LIAO Guang-ming, BAI Jie, et al. Approximate Derivation of Differential Equations for Beam String Structure's Theory Based on Large Displacement Generalized Variation[J]. Science Technology and Engineering, 2018, 18(5): 276-280. |
| [11] |
汪大绥, 张富林, 高承勇, 等. 浦东国际机场(一期工程)航站楼钢结构研究与设计[J]. 建筑结构学报, 1999, 20(2): 2-8. WANG Da-sui, ZHANG Fu-lin, GAO Cheng-yong, et al. Research and Design of Steel Structure of Shanghai Pudong International Airport Terminal (First Phase of the Project)[J]. Journal of Building Structures, 1999, 20(2): 2-8. |
| [12] |
丁洁民, 何志军. 北京大学体育馆钢屋盖预应力桁架壳体结构分析的几个关键问题[J]. 建筑结构学报, 2006, 27(4): 44-50. DING Jie-min, HE Zhi-jun. Several Key Issues of Structural Analysis of Prestressed Steel Truss Shells Roof of Beijing University Gymnasium[J]. Journal of Building Structures, 2006, 27(4): 44-50. |
| [13] |
张峥, 丁洁民, 李璐. 长沙国际会展中心展厅大跨度下凹形钢屋盖结构选型与设计[J]. 建筑结构, 2020, 50(7): 67-73. ZHANG Zheng, DING Jie-min, LI Lu. Structural System Selection and Design for Large-span Concave Steel Roof of Changsha International Convention and Exhibition Center Hall[J]. Building Structure, 2020, 50(7): 67-73. |
| [14] |
何建平. 银川站张弦梁站台雨棚设计及施工技术研究[J]. 铁道工程学报, 2020, 259(4): 74-78. HE Jian-ping. Research on the Canopy Design and Construction Technology of Platform with Beam String in Yinchuan Station[J]. Journal of Railway Engineering Society, 2020, 259(4): 74-78. |
| [15] |
李国豪. 桥梁与结构理论研究[M]. 上海: 上海科学技术文献出版社, 1983. LI Guo-hao. Research on Bridge and Structure Theory[M]. Shanghai: Shanghai Science and Technology Literature Press, 1983. |
| [16] |
胥润东, 郑凯锋. 悬索桥主缆求解虚拟梁法的改进[J]. 公路交通科技, 2010, 27(1): 84-88. XU Run-dong, ZHENG Kai-feng. Some Improvement on Fictitious Beam Method for Main Cable of Suspension Bridge[J]. Journal of Highway and Transportation Research and Development, 2010, 27(1): 84-88. |
| [17] |
蒋望, 邵旭东, 彭旺虎, 等. 独塔悬索桥基本参数研究[J]. 湖南大学学报:自然科学版, 2011, 38(6): 13-19. JIANG Wang, SHAO Xu-dong, PENG Wang-hu, et al. Research on Suspension Bridges with a Single-tower[J]. Journal of Hunan University:Natural Science Edition, 2011, 38(6): 13-19. |
| [18] |
赵基达, 梁存之. 张弦梁结构的分析与力学性能研究[J]. 建筑科学, 2015, 31(1): 1-6. ZHAO Ji-da, LIANG Cun-zhi. Structural Analysis and Mechanical Behavior Research of Beam String Structures[J]. Building Science, 2015, 31(1): 1-6. |
 2020, Vol. 37
2020, Vol. 37
