扩展功能
文章信息
- 劳俊, 谢伟忠, 刘梦岩, 何家兴, 王瑞林
- LAO Jun, XIE Wei-zhong, LIU Meng-yan, HE Jia-xing, WANG Rui-lin
- 基于轮荷转移的外倾角对操纵稳定性的影响分析
- Analysis on Influence of Camber Angle on Handling Stability Based on Wheel Load Transfer
- 公路交通科技, 2020, 37(11): 130-138
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 130-138
- 10.3969/j.issn.1002-0268.2020.11.016
-
文章历史
- 收稿日期: 2020-03-02
对于操纵稳定性设计领域及对应的相关问题,通常从转向系统、悬架系统K & C及轮胎这几个方面着手分析研究。而4轮定位中的外倾角常常被认为与跑偏和偏磨关系较大[1],而且左右轮能相互抵消,因此常被忽略[2-3]。有涉及的研究[4-5],但无机理解释。
轮胎的极限与轮胎的接触面积相关,外倾角的静态初始值在转弯过程中决定着接触面积的大小。另外,车辆在变向转弯过程中,内外轮会存在轮荷转移[6],而对应轮胎的外倾侧偏刚度也因轮荷的变化而产生左右差异。该差异会形成某向的侧向力,从而影响整车的横摆角速度和侧向加速度的变化,最终影响整车操纵稳定性的指标。
1 外倾角影响机理分析外倾角是指车轮在安装后,其端面向外倾斜,即车轮所处平面和纵向垂直平面间的夹角。轮胎呈现“八”字形张开时称为负外倾,而呈现“V”字形张开时称正外倾。本研究的内容是静态单边外倾角值变化时的性能响应。默认双边外倾角相等。
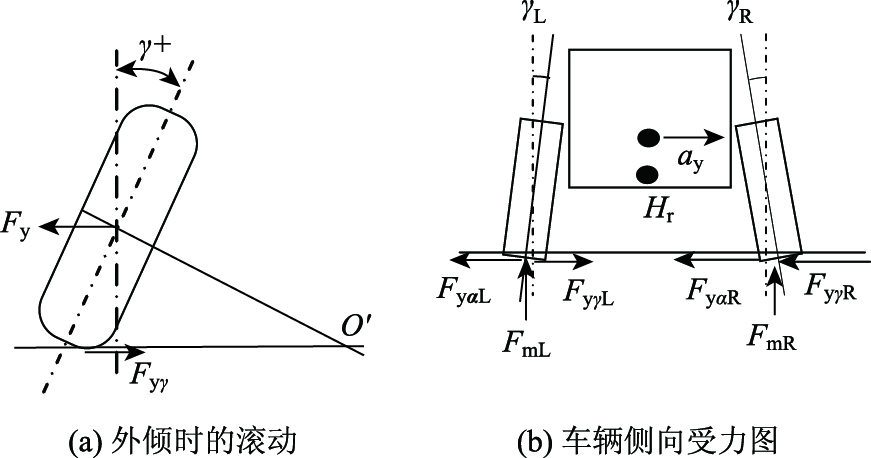
1.1 外倾角作用机理 1.1.1 外倾侧向力当车轮有外倾角γ时,如果将悬架断开,侧向拉力Fy=0,车轮向前滚动,会绕O′点作圆周运动。由于悬架的约束,在拉力Fy的作用下,左右轮只能按给定方向行驶,此时,地面产生与Fy方向相反的侧向反作用力,即为外倾侧向力Fyγ。此时外倾角外倾为正,内倾为负, 见图 1(a)。
|
| 图 1 有外倾时车辆的滚动和侧向受力 Fig. 1 Rolling and lateral forces of vehicle with camber |
| |
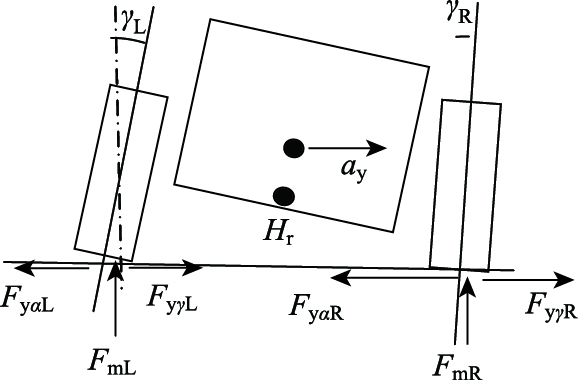
图 1(b)中,γL和γR分别为左右轮的外倾角;ay为车身侧向加速度;Hr为侧倾中心;FyαL和FyαR分别为左右侧轮胎侧偏力;FyγL和FyγR分别为左右轮的外倾侧向力;FmL和FmR分别为左右侧轮胎的垂直载荷。
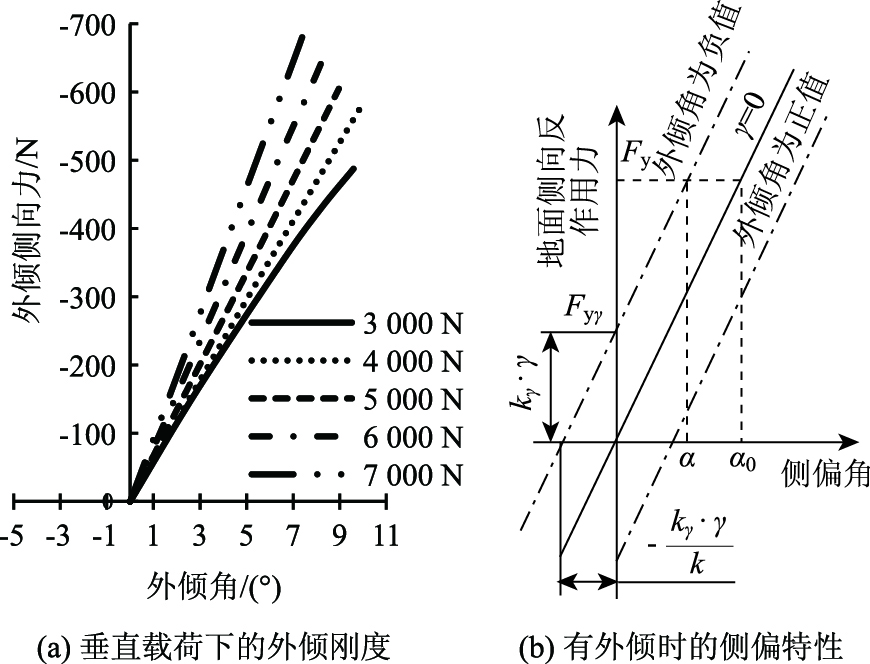
Fyγ为外倾刚度,与γ呈线性关系,Fyγ=kγ·γ,kγ为外倾刚度。外倾刚度与轮胎所受垂直载荷有关,见图 2(a)[7]。受外倾侧向力的影响,轮胎侧偏特性会发生变化,见图 2(b)。
|
| 图 2 垂直载荷下的外侧刚度和有外倾时的侧偏特性 Fig. 2 Lateral stiffness under vertical load and lateral side-slip characteristics when cambered |
| |
此时,地面总的侧向反作用力为:
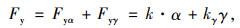
|
(1) |
式中,Fyα为轮胎的轮胎侧偏力;α为轮胎的侧偏角;k为轮胎的侧偏刚度。由此看出,轮胎的侧偏特性会因外倾侧向力的作用产生平移。也可以认为,侧偏角等效变化了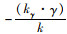
假设某辆车的外倾角为负值,车辆受到侧向力时,假设不考虑悬架变形(即不考虑轮跳、轮跳外倾变化、侧向力外倾变化等),见图 3。一部分重量转移到外侧车轮,这时外侧由侧偏角引起的侧偏力比内侧大。同样,因载荷的转移,静态外倾角引起的外倾侧向力也会比内侧大。
|
| 图 3 车辆外倾受力图 Fig. 3 Forces of cambered vehicle |
| |
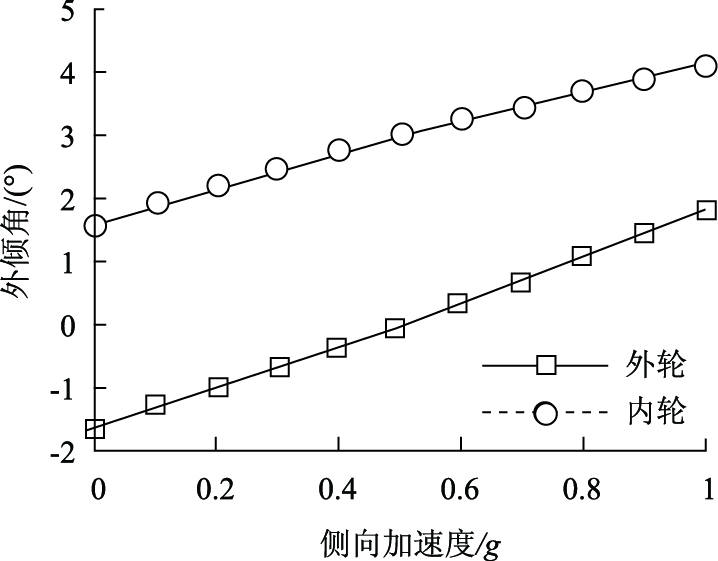
若考虑悬架变形(轮跳、轮跳外倾、侧向力外倾等)后,在较大的侧向加速度时,外轮的外倾会向正方向变化,而内轮的外倾会继续向负方向变化。整体的外倾侧向力会转为指向外端。要保持后轮不甩尾,一般后悬外倾角设置负向较多。图 4是某运动型轿车的后轮外倾角在侧倾时的理论变化曲线。可以看出,起重要作用的外轮在侧向加速度0.5g时,外倾角刚好为零,可以保证该车型在较大侧向加速度时依然有维持较大轮胎接地面积的能力。
|
| 图 4 某运动型轿车外倾角与侧向加速度关系 Fig. 4 Relationship between camber angle and lateral acceleration of a sports car |
| |
1.2 线性二自由度操稳模型
为了便于掌握操纵稳定性的基本特性,研究外倾角的影响,将对一个简化为线性二自由度的汽车模型进行研究[7]。分析中,忽略转向系统的影响,直接以前轮转角作为输入;忽略悬架的作用,认为汽车车厢只作平行于地面的平面运动;在特定条件仿真与试验下,汽车沿x轴的前进速度u视为不变,暂忽略轮荷转移造成的侧偏力影响,忽略外倾侧向力、回正力矩、轮胎锥度力、路面斜度等影响。因此,上述系统只有沿y轴的侧向运动及绕z轴(质心为原点)的横摆运动这两个自由度。
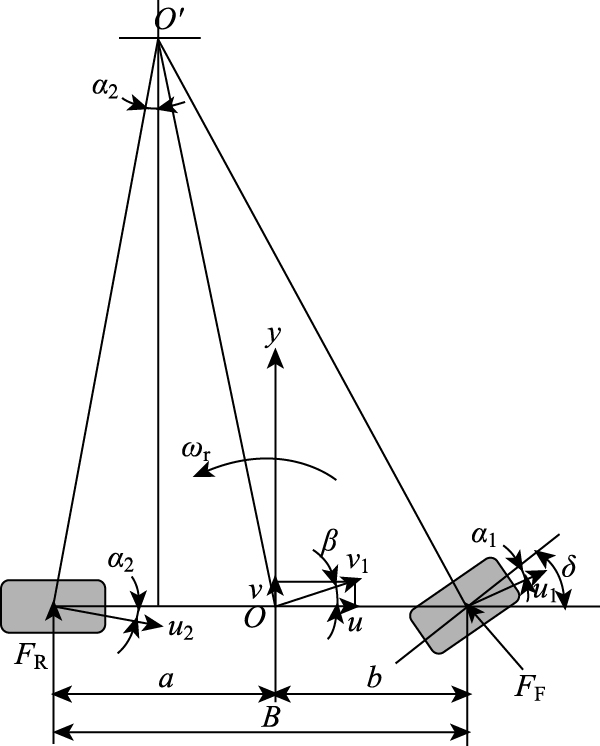
二自由度汽车模型见图 5。其中,车辆质心为O,车辆绕O′转动。前轮心的运动方向u1与车轮朝向形成侧偏角α1;后轮心运动方向与u2与车轮朝向形成侧偏角α2;质心方向速度v1分解后在侧向方向y形成侧向速度v,与车辆前进方向形成车辆前进速度u;车速为u;ωr为摆臂角速度;FF,FR为前、后轮侧偏力;a为前轴到质心的x向距离;b为后轴到质心的x向距离;B为轴距; β为质心的侧偏角,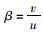
|
| 图 5 二自由度汽车模型 Fig. 5 Two-DOF vehicle model |
| |
整理受力关系并消去α1和α2后,建立以下模型[7]:
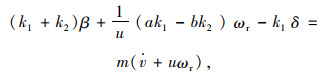
|
(2) |

|
(3) |
式中,m为整车质量;u为车速;ωr为摆臂角速度;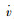

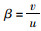
汽车等速行驶时,在前轮角阶跃输入下进入的稳态响应就是等速圆行驶。用常用输入与输入的比值(如前轮转角与侧向加速度之比)来评价稳态响应。这个值称为不足转向度, 以符号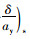
稳态时,横摆角速度ωr为定值。此时
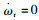

|
(4) |
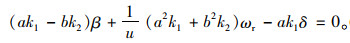
|
(5) |
此时,整车的侧向加速度值ay为uωr,将两式联立消去β,使可求得稳态的不足转向度为:
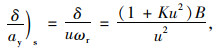
|
(6) |
式中,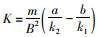
K称为稳定性因数,K增大时,不足转向度增大,反之则减小,是表征汽车稳态响应的重要参数。不足转向度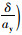
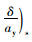
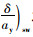
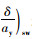
以上模型虽表征了稳态车辆的响应状态,前后轮都采用单轮进行简化,且没有考虑外倾侧向力的作用。如果要考虑外倾角的影响,前后轮必须考虑双轮,而且需加入轮荷转移,这时,需要引入考虑轴荷转移的改进后操稳模型。
1.3 改进后的线性二自由度操稳模型在改进模型前,需假设以下前提:(1)前轮左右转角一致,前束绝对值也一致;(2)只考虑轮荷转移,不考虑侧倾前束及侧向力外倾变化,侧倾对模型的影响可以等效到侧偏刚度中;(3)前后的质心高度、轮距、侧向加速度、车轮气压均一致;(4)侧偏刚度为线性,且随载荷的变化也拟合为线性。因此有图 6所示的改进模型。

|
| 图 6 改进后的二自由度汽车模型 Fig. 6 Improved 2-DOF vehicle model |
| |
改进后的二自由度汽车模型见图 6,其中,γF和γR分别为前后轮的外倾角,以内倾为负(与侧偏力同方向);FFL,FFR,FRL,FRR分别为前左轮、前右轮、后左轮、后右轮的垂向载荷。
侧倾方向的平衡方程组为:
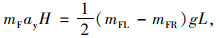
|
(7) |
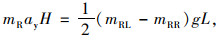
|
(8) |
式中,mFR,mFL,mRR,mRL分别为前右轮、前左轮、后右轮、后左轮的垂向载荷;L为轮距;g为重力加速度;H为质心高;ay为侧向加速度。
由式(7)和式(8),可得轴荷关系为:
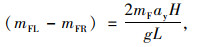
|
(9) |
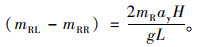
|
(10) |
以前左轮为例,单个车轮的外倾侧向力为:

|
(11) |
式中,FFL为前左轮的垂向载荷;kj为轮胎的基准外倾侧向刚度,表征在某个垂向力作用下的外倾角刚度;km为垂向载荷系数;km与mFL垂向载荷相乘表征对应载荷下的比例;kjkmmFL可以计算mFL载荷下轮胎外倾侧向力值;γF为前轮的外倾角。
二自由度微分方程经改进为:
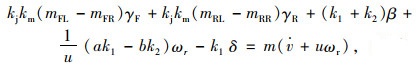
|
(12) |
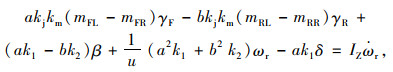
|
(13) |
式中γF和γR分别为前后轮的外倾角,以内倾为负(与侧偏力同方向)。
稳态时,横摆角速度ωr为定值,此时
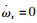

|
(14) |

|
(15) |
将两式联立整理,便可求得稳态的不足转向度为:
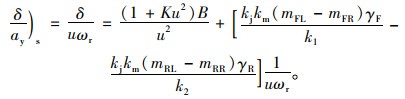
|
(16) |
利用式(9)~(10),且ay=uωr,可得:
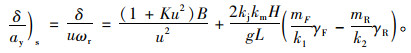
|
(17) |
因侧偏刚度kjkm,k1,k2为负值,所以当前轮单边外倾角γF负向绝对值增加时(内倾方向),不足转向度会下降,车辆趋向转向过度;后轮单边外倾角γR负向绝对值增加时(外倾方向),不足转向度会上升,车辆趋向转向不足。另外,前后轮的外倾角值的敏感度与系数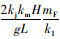
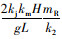
具体机理可概括为:前轮外倾增加,侧偏方向的外倾侧向力随之增加,前轮侧向力也增加;同理,后轮外倾增加,侧偏方向的外倾侧向力随之增加, 后轮侧向力也增加。前轮侧向力增大,转向趋势过度;后轮侧向力增大,转向趋势不足。
2 仿真分析改进的线性二自由度模型由于省略了较多参数,只能表征趋势,计算结果较不准确。因此需要采用动力学仿真软件ADAMS进行整车建模仿真,以确切了解其敏感度。
2.1 模型与工况概述 2.1.1 模型概述采用ADAMS-CAR模块进行分析[9-10],前后悬架按我公司产品A(3厢)和B(SUV)进行搭建,均为前麦弗逊、后4连杆。车身为刚体。配重为前2人,后1人,满油状态。车辆参数见表 1。
| 参数 | 符号 | A | B |
| 整车质量/kg | m | 1 721.5 | 1 805 |
| 前轮心到重心的纵向距离/m | a | 1.2 | 1.15 |
| 后轮心到重心的纵向距离/m | b | 1.6 | 1.55 |
| 质心高/m | H | 566 | 708 |
| 转向传动比/(°/°) | λ | 17.58 | 17.84 |
| 轴距/mm | B | 2 800 | 2 710 |
| 轮距/mm | L | 1 580 | 1 610 |
| 前轴侧偏刚度/(N·rad-1) | k1 | -68 451 | -70 495 |
| 后轴侧偏刚度/(N·rad-1) | k2 | -54 670 | -56 979 |
| 前轮单边前束/(′) | tF | -4 | -2 |
| 后轮单边前束/(′) | tR | 11 | 11 |
| 前轮单边外倾角/(′) | γF | -30 | -30 |
| 后轮单边外倾角/(°, ′) | γR | -1°30′ | -1°30′ |
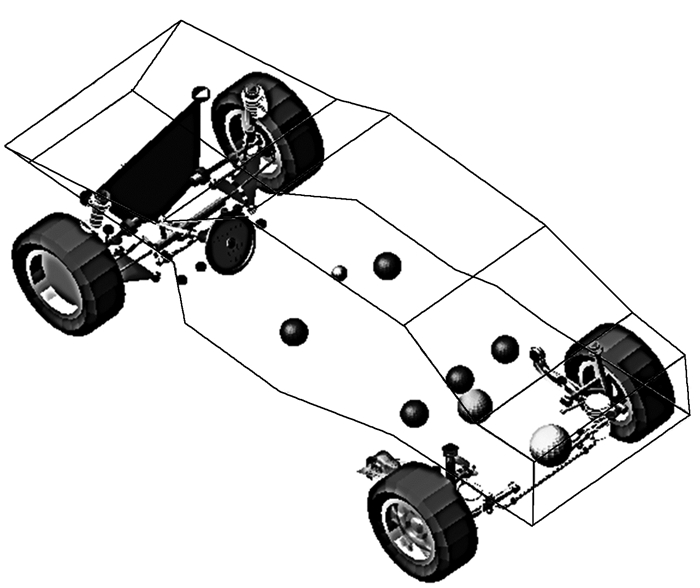
轮胎模型采用PAC模型,PAC模型采用实测轮胎的曲线进行拟合建立。实测工况包含不同载荷时的复合滑移测试工况,把外倾角的影响反映在轮胎模型内,通过类似图 2的方法融合到侧偏刚度曲线中[11-12]。图 7为操纵稳定性仿真模型。
|
| 图 7 操纵稳定性仿真模型 Fig. 7 Handling stability simulation model |
| |
2.1.2 工况概述
进行操稳仿真与试验时,按稳态回转[13]与频率扫描试验[14]工况进行试验。试验方法参考《汽车操纵稳定性试验方法》(GBT 6323—2014)中的“稳态回转试验”及“转向盘中心区转向操纵稳定性试验”,但对方法略作修改。详细描述如下。
稳态回转工况。车辆行驶在半径为40 m轨迹圆上,起步,缓慢而均匀地加速(侧向加速度增量不大于0.2 (m/s2)·s-1, 同时调整方向盘使车辆保持在固定半径圆上,衰减为±0.5 m,直到车辆不能保持在圆周上行驶为止。数据处理:截止频率15 Hz,将单个方向0~0.4g下的数据用最小二乘法线性拟合, 并求得算术平均值后,得出车辆线性范围内的方向盘转角梯度,即不足转向度。该值与第1章中的值同等含义,能表征车辆稳定性。上一章二自由度模型中,是采用车轮转角梯度进行分析的,但考虑实车试验时的难度,采用方向盘转角梯度分析替代,此时,方向盘转角与车轮转角间近似恒定相差1个转向系统的传动比倍率。
频率扫描试验工况。车辆在车速100 km/h下等速行驶,在平直路段开始从中间位置缓慢连续进行方向盘正弦输入,频率范围为0.2~0.3 Hz。以100 Hz采样率导出入计算传递函数,输出0.5 Hz下的横摆角速度与方向盘转角的增益。0.5 Hz能代表大部分驾驶员的使用工况,能表征瞬态时驾驶员的意愿与车辆响应间的关系。值越大,响应越快。
外倾角以表 2形式进行变化,以查看对上述整车参数的影响。原则为单独改变前轮或后轮,保持后轮或前轮的外倾角不变。
| 项目 | 工况 | 位置 | 序列 | ||||
| 1 | 2 | 3 | 4 | 5 | |||
| 中值 | |||||||
| 外倾角 | 1 | 前 | 15′ | -7.5′ | -30′ | -52.5′ | -1°15′ |
| 后 | -1°30′ | ||||||
| 2 | 前 | -30′ | |||||
| 后 | -45′ | -1°7.5′ | -1°30′ | -1°52.5′ | -2°15′ | ||
2.2 仿真过程曲线
直接改变模型中前后轮外倾角的值,通过采用稳态及瞬态的试验模拟工况进行计算。
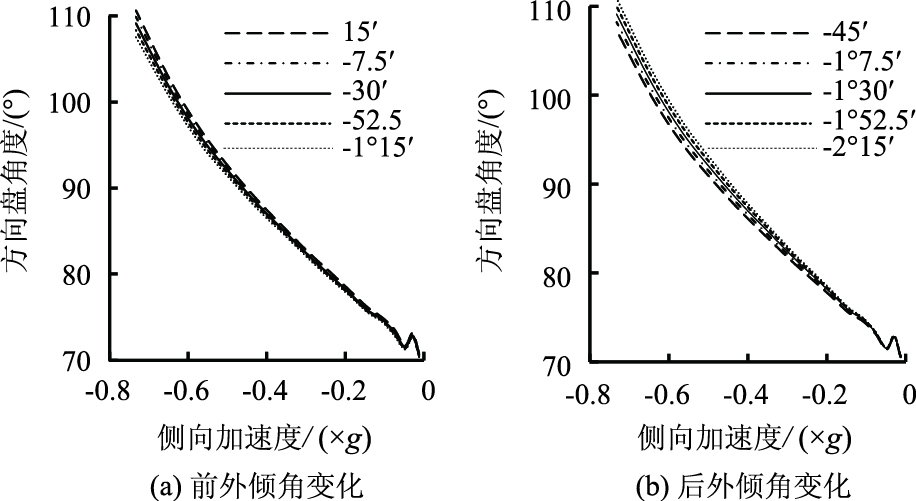
以A车为例,因模型严格对称,所以单边方向盘转角与侧向加速度的曲线如图 8所示。
|
| 图 8 方向盘转角与侧向加速度曲线 Fig. 8 Curves of steering wheel angle vs.lgteral acceleration |
| |
可见,与二自由度模型得出的趋势相同,在同等方向盘转角条件下, 前轮外倾角负向绝对值越大,侧向加速度就越大,表征不足转向度越小;后轮外倾角负向绝对值越大,侧向加速度就越小,表征不足转向度越大。
瞬态扫频试验时,通过对瞬态增益时域曲线的傅立叶变换,平滑后可得横摆角速度增益的频域曲线,如图 9所示。

|
| 图 9 横摆角速度增益与频率曲线 Fig. 9 Curves of yaw rate gain vs.frequency |
| |
可见,与二自由度模型得出趋势相同,整个频段内,前轮外倾角负向绝对值越大,瞬态增益就越大;后轮外倾负向绝对值越大,瞬态增益就越小。图 9中也可发现后外倾角的变化幅度较前外倾角大。
2.3 仿真结果| 车型 | 变量 | 序列 | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 中值 | ||||||
| A车 | 不足转向度/(°·g-1) | 40.44 | 40.02 | 39.55 | 39.05 | 38.69 |
| 瞬态增益/(s-1) | 0.289 | 0.294 | 0.300 | 0.305 | 0.309 | |
| B车 | 不足转向度/(°·g-1) | 39.19 | 38.81 | 38.51 | 38.12 | 37.88 |
| 瞬态增益/(s-1) | 0.283 | 0.286 | 0.289 | 0.291 | 0.294 | |
| 车型 | 变量 | 序列 | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| 中值 | ||||||
| A车 | 不足转向度/(°·g-1) | 37.15 | 38.52 | 39.55 | 40.58 | 41.07 |
| 瞬态增益/(s-1) | 0.323 | 0.310 | 0.300 | 0.289 | 0.283 | |
| B车 | 不足转向度/(°·g-1) | 36.71 | 37.83 | 38.51 | 39.35 | 39.91 |
| 瞬态增益/(s-1) | 0.302 | 0.295 | 0.289 | 0.283 | 0.278 | |
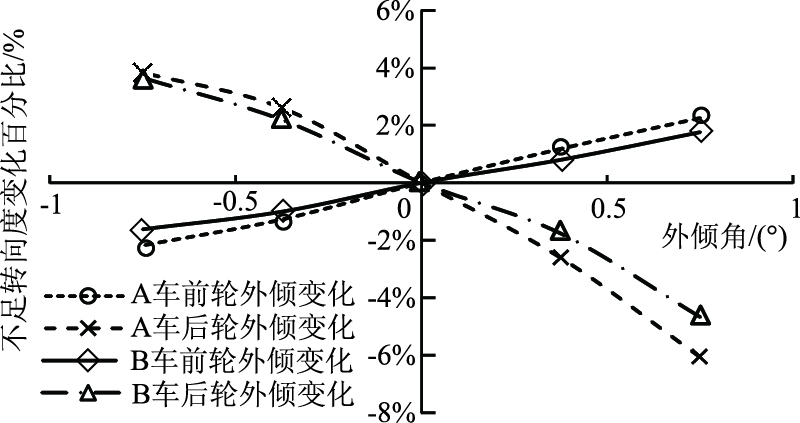
将稳态不足转向度除以中值外倾角的结果值, 前后悬外倾角中值平移归零, 可得到外倾角的不足转向度影响敏感度曲线(图 10)。从图 10中可知,A车与B车的前轮外倾角负向增大时,不足转向度均减小;后轮外倾角负向增大时,不足转向度增大,趋势是与二自由度模型相符的。另外,从两个车型的不足转向度趋势看,后轮的敏感度比前轮要高。
|
| 图 10 外倾角的不足转向度影响敏感度 Fig. 10 Influence sensitivity of camber angle understeer |
| |
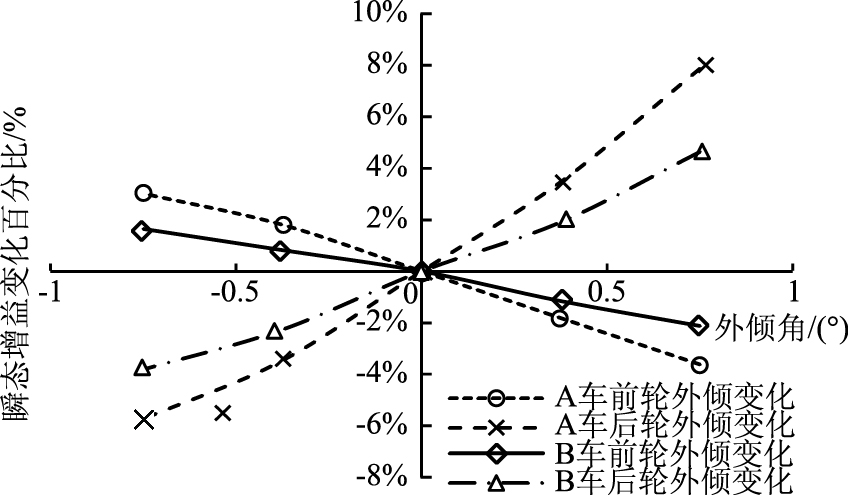
外倾角的瞬态横摆增益影响敏感度曲线见图 11。从图 11中可知,瞬态增益与不足转向度显现相似的趋势。前轮外倾角负向增大时,横摆增益增大;后轮外倾角负向增大时,横摆增益减小。同样,从两个车型的增益趋势看,后轮的敏感度比前轮要高。
|
| 图 11 外倾角的瞬态横摆增益影响敏感度 Fig. 11 Influence sensitivity of camber angle transient yaw gain |
| |
按外倾角变化1′,对应参数的变化百分比计算,得出表 5。
| 车型 | 项目 | 前轮外倾角变化/(%·′-1) | 后轮外倾角变化/(%·′-1) |
| A车 | 不足转向度 | -0.04 | 0.11 |
| 瞬态增益 | 0.04 | -0.15 | |
| B车 | 不足转向度 | -0.05 | 0.09 |
| 瞬态增益 | 0.08 | -0.09 |
从式(17)可看出,后轮外倾影响敏感度相比前轮要低的主要机理与系数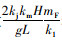


对外倾的影响仿真显示,外倾角(特别是后轮外倾角)对操稳影响较大,因此针对外倾角设计中值需进行实车敏感度试验。
3.1 试验概述采用上文中的A车进行试验验证。按与仿真同样的工况、整车参数、配重条件进行试验。因前轮外倾角无法调整,而且后轮外倾角调整无仿真简化,所以总共只进行3组试验,试验所得外倾角变化矩阵见表 6。
| 项目 | 序列 | 位置 | 1 | 2 | 3 |
| 中值 | |||||
| 外倾角 | 工况1 | 前 | -30′ | ||
| 后 | -1°20′ | -1°30′ | -1°45′ |
试验基本情况见表 7。
| 项目 | 基本状况 |
| 车型 | A车(GAC某款B级轿车) |
| 试验时间 | 2019/08/17—2019/08/21 |
| 试验场地 | 襄阳试验车场 |
| 天气 | 晴朗 |
| 轮胎 | 型号:225/50R17,前后轮胎胎压:220 kPa |
| 配重 | 前排2人+后排设备+90%汽油 |
| 4轮定位调整设备 | 英驰红旗UD |
| 4轮定位调整方式 | 不关注绝对值,只在上个方案测量基础对前束及外倾数值作定量增减 |
| 试验工况 | 参考GBT 6323—2014但有修改的稳态回转试验,频率扫描试验 |
| 试验方案组数 | 3组 |
3.2 试验过程
先对原车未调整的A车进行稳态与瞬态的试验,调整后轮的外倾角。其中,含有偏心螺栓的前束臂与后下臂的多连杆后悬架在调整外倾角时前束角有较大变化,需要同时微调前束臂与后下臂的长度,以在调整外倾角变化的同时保持前束角与原数值相同。
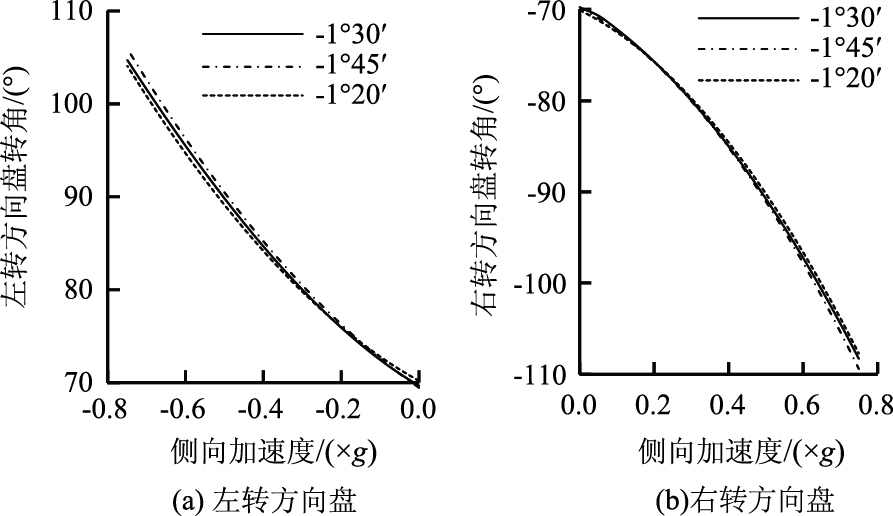
稳态试验时,随着方向盘转角变化,侧向加速度也产生变化。A车向左与向右两组方向盘稳态响应曲线见图 12。
|
| 图 12 A车稳态响应曲线 Fig. 12 Steady state response curves of vehicle A |
| |
可见,由于差值只有1′~15′,影响比较轻微。与仿真的趋势相同,在同等方向盘转角条件下, 外倾角负向绝对值越大,侧向加速度就越小,表征不足转向度越大。
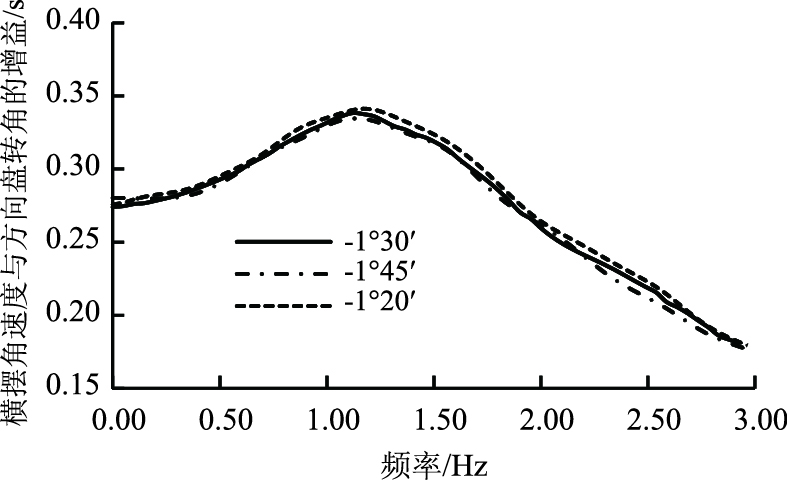
瞬态扫频试验时,通过对瞬态增益时域曲线的傅立叶变换,可得瞬态增益的频域曲线,见图 13。
|
| 图 13 瞬态增益频域曲线 Fig. 13 Frequency domain curve of transient gain |
| |
可见,与仿真趋势相同,整个频段内,外倾负向绝对值越大,瞬态增益就越小。
在稳态试验与瞬态试验后,整理数据得到以下试验对比结果(表 8)。
| 项目 | 后轮外倾角/(%·′-1) | |
| 试验 | 仿真 | |
| 不足转向度 | 0.29 | 0.11 |
| 瞬态增益 | -0.14 | -0.15 |
从操纵稳定性的稳态及瞬态实车试验结果中可见,后轮外倾变化时,整车响应的趋势与仿真是相同的。从数值上看,实车的稳态后轮外倾敏感度比仿真要高,瞬态与仿真接近。这与车辆的车身刚度[16]和后悬K & C[17]的实际参数相关。后轮外倾角的敏感度系数可总结为约0.1%/′~0.2%/′的敏感度。
4 结论从二自由度操纵稳定性模型出发,研究了静态时前后轮单边外倾角对稳态及瞬态的影响机理,并通过仿真和试验验证了其正确性。通过量化敏感度的方式,为设计外倾角以其公差提供了参考依据。
从敏感度与质心高度的强相关性可知,降低质心高度可以有效降低前后外倾角的敏感度,使外倾角绝对值减小,这样可以设计更趋于优化的其他性能,如偏磨[18]、油耗等。另外,前后的轴荷比也会直接影响前后外倾的敏感度比值。前轮外倾对定速跑偏等影响较大,所以,在操稳性能设计时,按后轮外倾值负向绝对值大于前轮的方式进行匹配设计,可有效提高稳定性而不影响其他性能。特别适用于重心较高且前轴较重的SUV车型。
另外,因为外倾角会影响轮胎偏磨、油耗及滑行距离,所以可以在这些性能敏感度较低的或允许的范围内,调整对应的外倾角达到提升操纵稳定性能的目的。同时,对于敏感度较高的后轮,可作为重点的调整方向。
| [1] |
宋年秀, 樊攀, 胡韶文, 等. 基于轮胎磨损的外倾角与前束值匹配研究[J]. 汽车技术, 2015(4): 29-32. SONG Nian-xiu, FAN Pan, HU Shao-wen, et al. A Research on the Matching between Camber Angle and Toe-in Angle Based on Tire Wear[J]. Automobile Technology, 2015(4): 29-32. |
| [2] |
姜军平, 孙福禄, 邓敏敏, 等. 某车型不足转向度偏低原因分析及解决[J]. 农业装备与车辆工程, 2012, 50(6): 16-19, 50. JIANG Jun-ping, SUN Fu-lu, DENG Min-min, et al. A Study on Analysis and Solution to Low Understeer on a Particular Car[J]. Agricultural Equipment & Vehicle Engineering, 2012, 50(6): 16-19, 50. |
| [3] |
王霄锋. 汽车悬架和转向系统设计[M]. 北京: 清华大学出版社, 2015. WANG Xiao-feng. Automotive Suspension and Steering System Design[M]. Beijing: Tsinghua University Press, 2015. |
| [4] |
郑希江, 纪少波, 李淑廷, 等. 独立悬架前轮定位参数对操纵稳定性影响分析[J]. 机械设计与制造, 2019(7): 263-266. ZHENG Xi-jiang, JI Shao-bo, LI Su-ting, et al. Effects Analysis of Front Axle's Alignment Parameters Change on Handling Stability[J]. Machinery Design & Manufacture, 2019(7): 263-266. |
| [5] |
高晋, 杨秀建. 车轮定位角对操纵稳定性指标影响的定量研究[J]. 工程设计学报, 2014, 21(3): 251-258. GAO Jin, YANG Xiu-jian. Quantitative Research of Influence Wheel Alignment Angle on Handling Index[J]. Journal of Engineering Design, 2014, 21(3): 251-258. |
| [6] |
李征, 董益亮, 屈奥斯. 基于轮荷分析的车辆稳态转向特性虚拟仿真[J]. 汽车科技, 2009(6): 53-56. LI Zheng, DONG Yi-liang, QU Ao-si. Virtual Simulation of Vehicle Steady State Steering Characteristics Based on the Analysis of Wheel Load[J]. Automobile Science & Technology, 2009(6): 53-56. |
| [7] |
余志生. 汽车理论[M]. 5版. 北京: 机械工业出版社, 2009. YU Zhi-sheng. Automobile Theory[M]. 5th ed. Beijing: China Machine Press, 2009. |
| [8] |
姜国彬, 赵守月, 劳俊, 等. 汽车行驶稳定性设计体系及应用[J]. 汽车实用技术, 2018(14): 147-153. JIANG Guo-bin, ZHAO Shou-yue, LAO Jun, et al. Vehicle Driving Stability Design Method and Application[J]. Automobile Technology, 2018(14): 147-153. |
| [9] |
周磊, 高龙, 柳强, 等. 基于ADAMS的操纵稳定性分析及优化[J]. 汽车实用技术, 2016(6): 90-99. ZHOU Lei, GAO Long, LIU Qiang, et al. Based on ADAMS, the Steering Stability Analysis and Optimization[J]. Automobile Applied Technology, 2016(6): 90-99. |
| [10] |
张智, 施晓芬, 李俊文. 汽车悬架系统的运动仿真及优化设计[J]. 机械设计, 2015, 32(9): 30-33. ZHANG Zhi, SHI Xiao-fen, LI Jun-wen. Kinematic Simulation and Structural Optimization of Vehicle Suspension[J]. Journal of Machine Design, 2015, 32(9): 30-33. |
| [11] |
王海, 张宏亮, 薛盛兴. 基于TDFT的PAC轮胎模型参数辨识[J]. 汽车实用技术, 2019(7): 62-65. WANG Hai, ZHANG Hong-liang, XUE Sheng-xing. Parameter Identification of PAC Tire Based on TDFT[J]. Automobile Applied Technology, 2019(7): 62-65. |
| [12] |
陈秀梧. 基于TDFT的轮胎模型参数辨识[J]. 轮胎工业, 2017, 37(3): 23-25. CHEN Xiu-wu. Parameter Identification of Tire Model Based on TDFT[J]. Tire Industry, 2017, 37(3): 23-25. |
| [13] |
夏小均, 陈德兵, 姚波, 等. 基于设计参数的转向特性虚拟试验及评价[J]. 汽车零部件, 2019(7): 1-5. XIA Xiao-jun, CHEN De-bing, YAO Bo, et al. Evaluation and Stimulated Test of Steering Performance Based on Designed Parameters[J]. Automobile Parts, 2019(7): 1-5. |
| [14] |
陈娟娟, 王生昌, 刘丹, 等. 乘用车转向性能主观评价与客观评价的相关性[J]. 公路交通科技, 2018, 35(1): 137-141. CHEN Juan-juan, WANG Sheng-chang, LIU Dan, et al. Correlation between Subjective and Objective Evaluations for Steering Performance of Passenger Cars[J]. Journal of Highway and Transportation Research and Development, 2018, 35(1): 137-141. |
| [15] |
陈林, 杨建森, 金剑, 等.悬架K & C特性对操纵稳定性影响的仿真研究[C]//中国汽车工程学会年会论文集.北京: 北京理工大学出版社, 2013: 1501-1505. CHEN Lin, YANG Jian-sen, JIN Jian, et al. Simulation of Influence of Suspension K & C Characteristics on Automotive Handling Stability[C]//Proceedings of SAE-China Annual Congress. Beijing: Beijing Institute of Technology Press, 2013: 1501-1505. |
| [16] |
吴利广, 王晗, 景立新, 等. 某乘用车车身扭转刚度对操纵稳定性的影响[J]. 汽车工程师, 2018(10): 46-49. WU Li-guang, WANG Han, JING Li-xin, et al. Influence of Body Torsion Stiffness on Handling Stability[J]. Auto Engineer, 2018(10): 46-49. |
| [17] |
高金良.悬架K & C特性对操纵稳定性影响分析及前悬架结构优化[D].镇江: 江苏大学, 2019. GAO Jin-liang. Analysis of Influence of Suspension K & C Characteristics on Handling Stability and Structure Optimization of Front Suspension[D]. Zhenjiang: Jiangsu University, 2019. |
| [18] |
宋年秀, 樊攀, 胡韶文, 等. 基于轮胎磨损的外倾角与前束值匹配研究[J]. 汽车技术, 2015(4): 29-32. SONG Nian-xiu, FAN Pan, HU Shao-wen, et al. A Research on the Matching between Camber Angle and Toe-in Angle Based on Tire Wear[J]. Automobile Technology, 2015(4): 29-32. |
 2020, Vol. 37
2020, Vol. 37
