扩展功能
文章信息
- 陶伟, 刘志强, 陈世斌, 郭炎
- TAO Wei, LIU Zhi-qiang, CHEN Shi-bin, GUO Yan
- 基于模糊控制的轮式装载机驾驶室悬架减振设计
- Design of Suspension Damping for Wheel Loader Cab Based on Fuzzy Control
- 公路交通科技, 2020, 37(11): 118-129
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 118-129
- 10.3969/j.issn.1002-0268.2020.11.015
-
文章历史
- 收稿日期: 2020-03-29
2. 农机智能控制与制造技术福建省高校重点实验室, 福建 南平 354300;
3. 江苏大学 汽车与交通工程学院, 江苏 镇江 212013;
4. 长安大学 公路养护装备国家工程实验室, 陕西 西安 710064
2. Key Laboratory of Intelligent Control and Manufacturing Technology of Agricultural Machinery of Fujian Provincial Universities, Nanping Fujian 354300, China;
3. School of Automotive and Traffic Engineering, Jiangsu University, Zhenjiang Jiangsu 212013, China;
4. National Engineering Laboratory for Highway Maintenance Equipment, Chang'an University, Xi'an Shaanxi 710064, China
轮式装载机是工程机械中集铲、装、运、卸于一体的机种,广泛应用于基础设施建设,是机械化施工中的重要一员。装载机在建设工地上进行短途穿梭式作业,施工现场作业环境恶劣,行驶颠簸是正常情况,对装载机产生强烈的振动和冲击,引起结构件的疲劳损坏,影响驾驶员的身心健康。随着用户对操作舒适性要求的不断提高,提高轮式装载机隔振性能已迫在眉睫。
驾驶室的主要功能在于将驾驶员与外界隔离,使得驾驶员免受振动、噪声、灰尘以及其他不利环境因素的影响和干扰。在各种振动激励源的作用下,车架受到来自外部的强烈振动与冲击,而驾驶室悬架系统在传递所有作用在驾驶室与车架之间力和力矩的同时,还可有效隔离来自轮式装载机车架的振动,从而提高驾驶员的作业舒适性[1]。
驾驶室悬架是提高轮式装载机操纵舒适性的有效手段之一,已有大量相关研究报道。2002年,通用汽车公司的Ward进行了多种形式的驾驶室悬置结构对比分析,得出四点式悬置系统具有最佳减振效果的结论[2]。2004年,柳工研制了半主动悬挂装载机CLG858,该装载机利用控制策略分析车身加速度值,把输入电流控制在一定水平来操控悬架系统性能,但由于是外部输入控制悬架系统,可靠性和稳定性较差[3]。2005年,美国路易斯维尔大学的Prater等人对轮式装载机驾驶室悬架系统进行了有限元分析和结构优化,以提高驾驶室NVH性能[4]。东南大学的孙小娟在考虑悬置垂直和水平刚度的基础上,针对轮式装载机驾驶室低频晃动问题,对一个6自由度驾驶室悬架系统进行了优化设计,使座椅垂向振动幅值明显减小[5]。吉林大学的迟春燕等人建立了包含驾驶室悬架的轮式装载机12自由度振动模型,并采用虚拟激励法对装载机行驶平顺性进行了深入研究[6]。兰州城市学院陈翔等人考虑发动机和乘客-座椅系统等因素,建立了4自由度1/4车体动力学模型,设计了参数自整定的模糊PID控制器,发现模糊PID控制器使车辆行驶的平顺性更好[7]。吉林大学的李学飞等人提出了基于装载机行驶路况识别的油气悬架主动控制方法,有效降低了装载机的垂向振动[8]。瑞典皇家理工学院的Rehnberg等人对包含车架隔振系统的轮式装载机平顺性进行了仿真模拟,证实了通过在车轴和车架之间安装悬架系统能够有效降低装载机的低频振动和轮胎动载荷,从而改善作业舒适性和操纵稳定性[9]。
通过综合对比3类悬架各自的性能特点及技术原理可以发现,传统被动悬架由于参数的不可调节,无法满足人们日益增长的悬架性能要求,主动悬架虽然能够大幅提升悬架动态性能,但是成本高、能耗大、作动器设计复杂成为制约其走向工程应用的最大障碍,而且该障碍短期内无法得到有效解决。作为被动悬架与主动悬架之间的折中方案,半主动悬架既能克服传统被动悬架性能参数不可调节的缺点,又相较于主动悬架节约了大量的成本和能耗,具有良好的应用前景[10]。半主动悬架的基本工作原理是:根据运行工况和控制目标对悬架系统的弹簧刚度或减振器阻尼进行一定范围内的自适应调节,从而实现更好的悬架动态性能。通过研究发现,改变悬架刚度与改变减振器阻尼相比较为困难。相反,在传统液压减振器的结构基础上衍生出的阻尼可调实现方案,与之相匹配的各种阻尼控制策略,极大提升了半主动悬架的实际性能,为半主动悬架的推广应用奠定了良好基础。本研究以提高轮式装载机作业舒适性为主要目标,围绕装载机驾驶室半主动悬架系统的振动模型构建及阻尼控制策略设计等方面开展一系列研究,力图在提出新型阻尼可调减振器的基础上,通过设计有效的阻尼控制策略,实现轮式装载机减振性能的进一步提升。
1 减振器的结构组成图 1所示即为本研究所设计的能够实现多种阻尼状态切换的可调阻尼减振器结构示意图,由于压缩室和回弹室之间的油流路径不同,这种阻尼可调减振器能有效地实现4种阻尼模式和8种阻尼状态,满足半主动悬架大范围调节阻尼特性的要求。另外,由于可调阻尼特性是通过控制两个电磁阀的通断状态来实现的,与其他类型的可调阻尼减振器相比,具有结构简单、性能稳定、成本低等优点。因此,本研究将新型减振器应用于轮式装载机驾驶室悬架。在建立包括半主动驾驶室悬架在内的轮式装载机振动模型的基础上,进一步设计了一种根据驾驶室悬架性能指标确定减振模式最佳切换顺序的减振控制策略,以提高轮式装载机的运行舒适性。
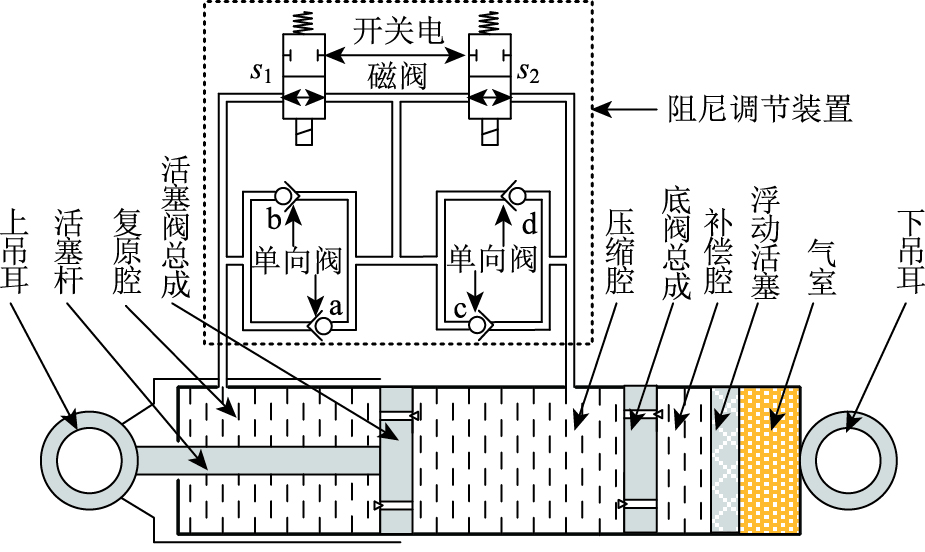
|
| 图 1 阻尼可调减振器结构示意图 Fig. 1 Schematic diagram of shock absorber with adjustable damping |
| |
根据这种结构设计,通过控制两个电磁阀的通断状态,可以很容易地改变压缩室和回弹室之间的油流路径。通过选择4个不同油流压力损失的止回阀,可以获得不同的压缩行程和回弹行程阻尼特性。在上述分析的基础上,减振器实现的4种阻尼模式如表 1所示,其中还给出了电磁阀的通断状态和4种模式的阻尼特性。由于已有文献对不同阻尼模式下的阻尼特性模型和阻尼系数进行了研究,本研究不再重复这些内容,只着重于轮式装载机驾驶室振动模型的建立和阻尼控制策略的设计。
| 阻尼模式 | 电磁阀开关状态 | 减振器工作状态 | |||
| S1 | S2 | 压缩行程 | 复原行程 | ||
| 1 | 打开 | 打开 | 软 | 软 | |
| 2 | 关闭 | 打开 | 软 | 硬 | |
| 3 | 打开 | 关闭 | 硬 | 软 | |
| 4 | 关闭 | 关闭 | 硬 | 硬 | |
2 装载机驾驶室悬架系统分析 2.1 驾驶室悬架系统动力学建模
本研究将装载机动臂油缸和铲斗油缸及其行驶稳定系统分别视为弹簧与阻尼并联的减振系统,从而构建车架与工作装置之间的弹性连接模型。在此基础上,结合装载机振动特性机理,建立整车11自由度振动模型,如图 2所示。11个振动自由度分别为车架的垂向、俯仰、侧倾3个方向的自由度,驾驶室垂向、俯仰、侧倾3个方向的自由度,发动机垂向运动自由度,装载机工作装置等效质量沿左侧动臂油缸轴线和沿左侧铲斗油缸轴线2个方向的自由度以及装载机工作装置等效质量沿右侧动臂油缸轴线和沿右侧铲斗油缸轴线2个方向的自由度。
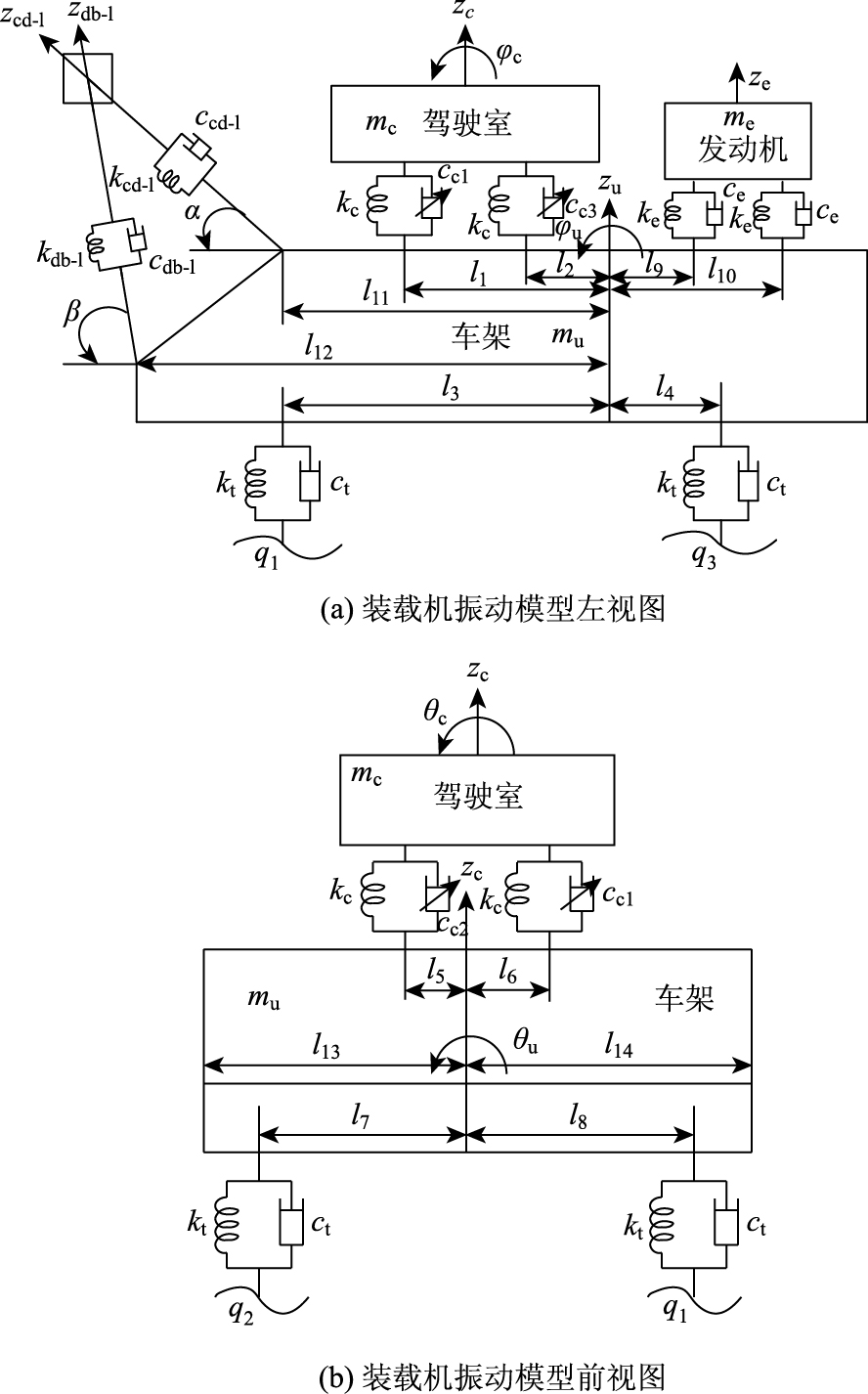
|
| 图 2 装载机驾驶室悬架系统11自由度振动模型 Fig. 2 An 11-DOF vibration model of suspension system of loader cab |
| |
图中,mc,mu和me分别为驾驶室质量、车架质量以及动力总成(发动机)质量;zc和zu分别为驾驶室质心处垂向位移和车架质心处垂向位移;Fe为发动机旋转振动过程中产生的垂向力;ze为发动机质心处垂向位移;ke和ce分别为发动机悬置的刚度和阻尼系数;kc为装载机驾驶室四角处悬架系统的刚度系数; cc1,cc2,cc3以及cc4分别为装载机驾驶室四角处悬架系统的可变阻尼系数;φc和φu分别为装载机驾驶室的俯仰角和车架的俯仰角;θc和θu分别为装载机驾驶室的侧倾角和车架的侧倾角;l1,l2分别为车架质心距驾驶室前悬和驾驶室后悬的垂直距离;l3,l4分别为车架质心距装载机前轮和装载机后轮的垂直距离;l5,l6分别为车架质心距驾驶室左悬和驾驶室右悬的垂直距离;l7,l8分别为车架质心距装载机左轮和装载机右轮的垂直距离;l9,l10分别为车架质心距发动机前悬置和发动机后悬置的垂直距离;l11,l12分别为车架质心距铲斗油缸与车架连接点的纵向垂直距离和距动臂油缸与车架连接点的纵向垂直距离;l13,l14分别为车架质心距铲斗油缸、动臂油缸与车架左侧连接点的垂直距离和距铲斗油缸、动臂油缸与车架右侧连接点的垂直距离;kt和ct分别为装载机轮胎的等效刚度系数和等效阻尼系数;q1,q2,q3以及q4分别为装载机左前、右前、左后以及右后轮处的垂向位移输入;kdb-l和cdb-l分别为左侧动臂油缸的等效刚度系数和等效阻尼系数; kcd-l和ccd-l分别为左侧铲斗油缸的等效刚度系数和等效阻尼系数; zdb-l和zcd-l分别装载机工作装置沿左侧动臂油缸轴线的位移和沿左侧铲斗油缸轴线的位移; α和β分别为动臂油缸轴线和铲斗油缸轴线与水平面的夹角。由于视角原因,图中未列出,但后续建模涉及的参数包括:右侧动臂油缸的等效刚度系数和等效阻尼系数kdb-r和cdb-r,右侧铲斗油缸的等效刚度系数和等效阻尼系数kcd-r和ccd-r,装载机工作装置沿右侧动臂油缸轴线的位移和沿右侧铲斗油缸轴线的位移zdb-r和zcd-r,装载机工作装置沿左侧动臂油缸轴线和沿左侧铲斗油缸轴线的等效质量mdb-l和mcd-l,装载机工作装置沿右侧动臂油缸轴线和沿右侧铲斗油缸轴线的等效质量mdb-r和mcd-r。
根据牛顿运动力学原理,针对轮式装载机振动模型的各个自由度分别进行建模。首先,建立装载机车架垂向振动模型如下:
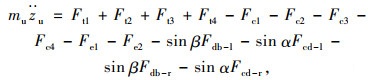
|
(1) |
式中,Ft1,Ft2,Ft3以及Ft4分别为轮式装载机4个轮胎的垂向作用力;Fc1,Fc2,Fc3以及Fc4分别为驾驶室四角处悬架系统的垂向作用力;Fe1和Fe2为发动机前后悬置的垂向作用力;Fdb-l,Fcd-l,Fdb-r以及Fdb-r分别为沿左侧动臂油缸轴线和沿左侧铲斗油缸轴线的作用力以及沿右侧动臂油缸轴线和沿右侧铲斗油缸轴线的作用力。在装载机驾驶室和车架俯仰角和侧倾角均较小的客观前提下,通过力学分析,可得各作用力的具体表达式,其中,4个轮胎的垂向作用力表达式如下[11]:
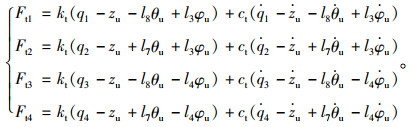
|
(2) |
发动机前后悬置的垂向作用力表达式为:
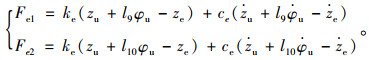
|
(3) |
驾驶室四角处悬架系统的垂向作用力表达式为:
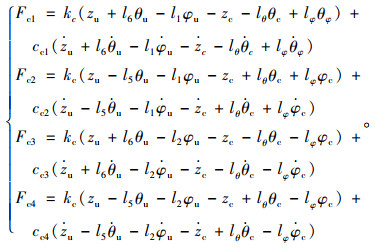
|
(4) |
假设驾驶室质心位于正中间,因此,式中,lφ,lθ分别表示驾驶室前悬与后悬间垂直距离的一半以及左悬与右悬间垂直距离的一半。
沿左侧动臂油缸轴线和沿左侧铲斗油缸轴线的作用力表达式为:
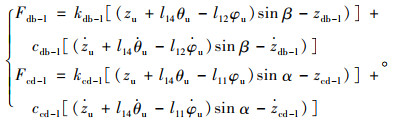
|
(5) |
在上述各作用力求解的基础上,可得装载机车架俯仰和侧倾振动模型的数学方程为:
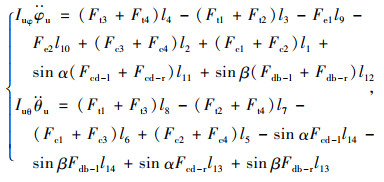
|
(6) |
式中,Iuφ和Iuθ分别为装载机车架的俯仰转动惯量和侧倾转动惯量。
同理,可得描述装载机驾驶室垂向、俯仰及侧倾振动模型的数学方程为:
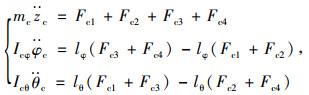
|
(7) |
式中,Icφ和Icθ分别为装载机驾驶室的俯仰转动惯量和侧倾转动惯量。
反映发动机垂向运动自由度的数学方程为:
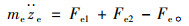
|
(8) |
发动机旋转过程中产生的垂向力Fe是由发动机内部振动产生,视作系统的外部激励,后续将结合发动机工作过程进行建模和分析。
装载机工作装置等效质量沿左侧动臂油缸轴线和沿左侧铲斗油缸轴线2个方向的振动模型以及装载机工作装置等效质量沿右侧动臂油缸轴线和沿右侧铲斗油缸轴线2个方向的振动模型可用下式表示:
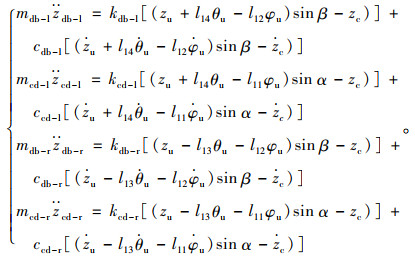
|
(9) |
通过联立上述各式,最终建立含驾驶室悬架系统的轮式装载机11自由度振动模型。驾驶室四角处悬架动行程的具体表达式为:
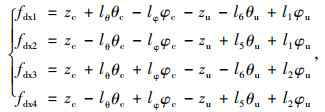
|
(10) |
式中,fdx1,fdx2,fdx3以及fdx4分别为驾驶室四角处的悬架动行程。
2.2 减振器阻尼多状态切换模型建立根据式(4)可知,轮式装载机驾驶室四角处悬架系统的垂向作用力主要通过4个减振器的可变阻尼系数进行调节,通过设计相应的阻尼控制策略,即可实现根据悬架系统振动响应进行减振器阻尼力最优调节的功能,从而改善轮式装载机驾驶室悬架系统的综合性能。为实现减振器阻尼控制策略的有效设计,结合上节完成的减振器阻尼特性试验结果,可进一步建立反映减振器阻尼多状态切换的数学模型。
由阻尼多状态切换减振器的工作原理可知,系统通过控制两个开关电磁阀的通断状态即可实现4种阻尼模式、8种阻尼状态,从而形成各阻尼状态下相应的减振器阻尼系数。因此,针对复原行程和压缩行程,可分别建立减振器阻尼系数与电磁阀开关状态之间的关系式如下:
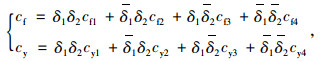
|
(11) |
式中,δ1和δ2分别为反映高速开关电磁阀s1和s2通断状态的逻辑变量,其取值与电磁阀开关状态间存在如下关系:

|
(12) |
式(11)中,cf和cy分别为减振器复原行程和压缩行程的阻尼系数,cf1,cf2,cf3, cf4分别为阻尼模式1, 2, 3, 4中的减振器复原阻尼系数,cy1, cy2, cy3, cy4分别为阻尼模式1, 2, 3, 4中的减振器压缩阻尼系数。结合式(11),可进一步获取装载机驾驶室四角处悬架系统减振器的阻尼系数表达式为:
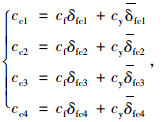
|
(13) |
式中,cc1,cc2,cc3,cc4分别为装载机驾驶室四角处悬架系统的减振器阻尼系数;δfc1,δfc2,δfc3,δfc4分别为反映装载机驾驶室四角处悬架系统减振器处于拉伸行程还是压缩行程的逻辑变量,其取值表达式为:
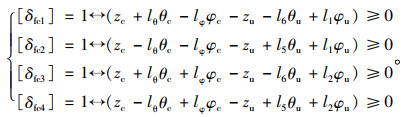
|
(14) |
通过联立式(11)~式(14),即可建立轮式装载机驾驶室悬架系统用阻尼多状态切换减振器阻尼系数与电磁阀开关状态以及减振器具体行程之间的数学关系,为后续在此基础上设计阻尼控制策略奠定了基础。
2.3 驾驶室悬架系统激励建模对于图 2所示的含驾驶室悬架系统的轮式装载机整车11自由度振动模型,系统承受的外部激励除通过4个轮胎传递而来的路面不平度激励外,来自发动机旋转振动产生的冲击对于轮式装载机整车的振动影响也十分明显[12]。因此,为准确反映轮式装载机的实际振动情况,建立了考虑四轮相关特性的路面不平度激励模型。
2.3.1 四轮相关随机路面激励建模四轮相关随机路面激励模型一般是在单轮随机路面模型的基础上进行建立,因此,首先建立单轮随机路面模型[13]。在建立单轮路面不平度激励时域模型时,一般需要在路面谱中引入下截止频率f0,从而得到路面不平度的时域表达式如下:
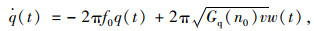
|
(15) |
式中,q(t)为路面不平度时域位移输入;Gq(n0)为与路面等级相关的路面不平度系数几何平均值;v为车辆行进车速;w(t)为均值为零的高斯白噪声。
根据相关标准文件,按功率谱密度可将路面的不平程度分为8级,即A,B,C,D,E,F,G,H级路面,为与8级路面相对应,基于有理函数表达式可将式(15)进一步改写为:
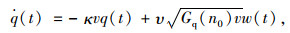
|
(16) |
式中,κ和υ分别为相应的系数。通过与标准路面进行仿真对比,优化系数τ和υ的实际取值,最终获取路面不平度时域数学模型表达式为[14]:
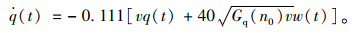
|
(17) |
在前文确定的单轮随机路面时域模型基础上,可根据四轮路面输入的相关特性进一步确定其他车轮的随机路面输入[15]。根据路面对四轮汽车输入谱密度之间的函数关系以及车辆左右轮迹相关函数的近似拟合,可得到左右轮路面输入的相关特性:
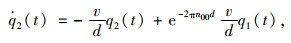
|
(18) |
式中,q1(t)和q2(t)分别为左前轮和右前轮的随机路面时域输入; 左右轮之间的轮距为d; n00为路面空间截止频率,取值为0.01 m-1。
本研究仅考虑车辆匀速直线行驶工况,因此,后轮路面输入与前轮路面输入相比,轨迹应当相同,只是在时间上存在一定滞后。在左前轮路面输入模型的基础上,左后轮路面输入模型q3(t)的数学表达式为:
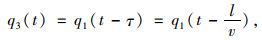
|
(19) |
式中,τ=l/v表示滞后时间,l为前后轴距。式(19)所示为一类纯时间时滞系统,因此,q3(t)与q1(t)之间的传递函数可通过二阶Pade算法近似算出:
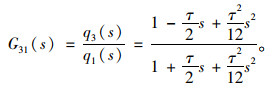
|
(20) |
根据式(20),可以得到前轮和后轮之间的输入相关性的状态空间表达式。在此基础上,可以进一步描述四轮输入相关的状态空间表达式。以C级路面为例,路面不平度系数Gq(n0)为256×10-6 m3,车辆轮距d为2.42 m,轴距l为5.7 m,车速为10 m/s,左前轮和右前轮路面不平度输入如图 3所示。从图 3中可以看出,考虑相关特性的车辆左前轮与右前轮路面不平度输入仿真结果存在较为明显的差异,说明对于建立较为准确的随机路面激励模型考虑四轮相关特性十分必要。
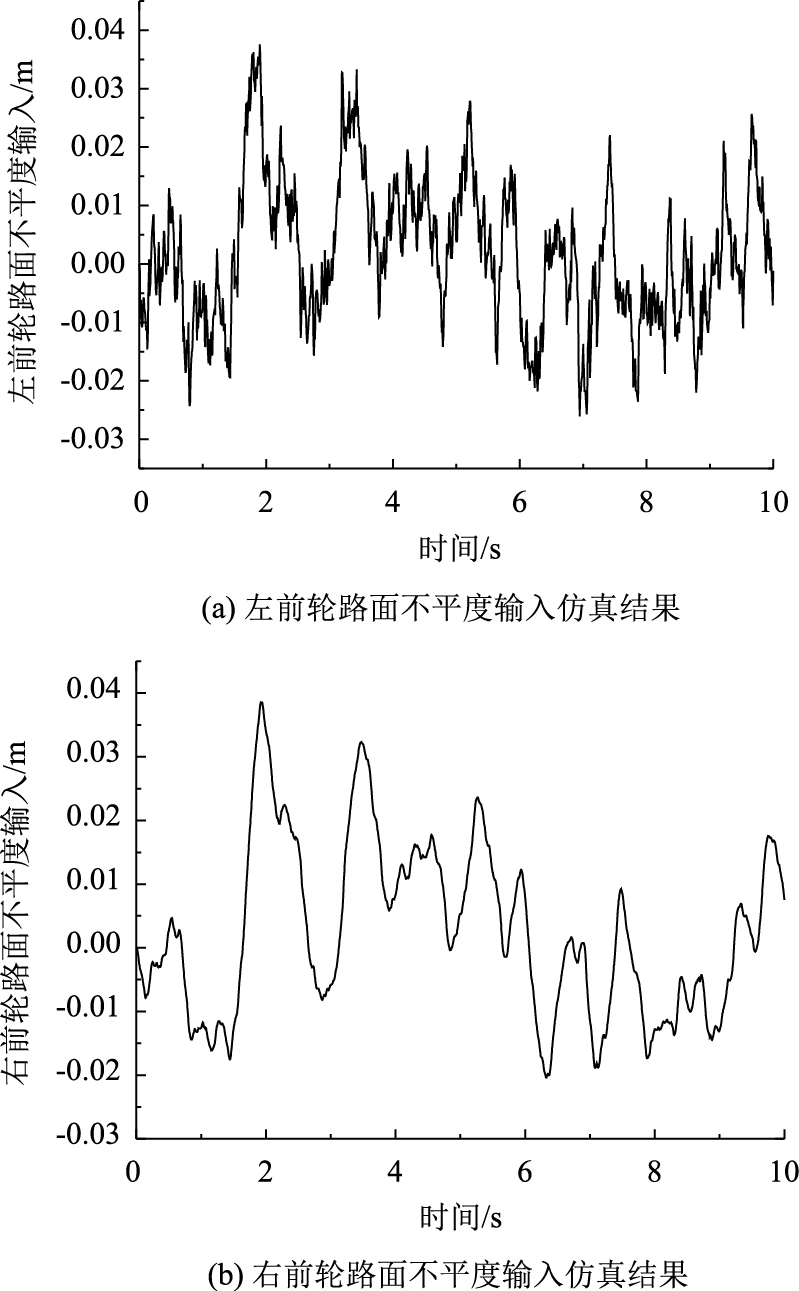
|
| 图 3 C级路面前轮路面不平度输入仿真结果 Fig. 3 Simulation result of C-level road surface roughness in put to front wheels |
| |
2.3.2 发动机振动激励建模
发动机工作循环的周期性以及运动机构的往复性是发动机产生剧烈振动的主要根源[16]。轮式装载机所用发动机为立式四冲程发动机,在对单缸发动机进行受力分析的基础上,综合考虑旋转惯性力和往复惯性力,建立了发动机旋转振动激励模型。
首先对直列四缸发动机旋转惯性力进行计算,沿Z轴和Y轴的旋转惯性力计算如下:
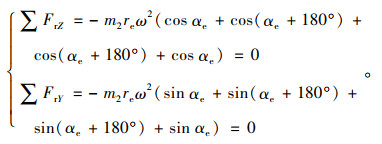
|
(21) |
从方程(21)中可以看出,垂直四冲程发动机在Z轴和Y轴上的转动惯性力等于零,因此在发动机旋转振动激振过程中可以忽略转动惯性力。其次,发动机往复惯性力的计算可分为两部分,其中一阶往复惯性力计算为:
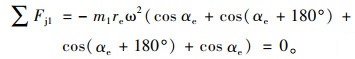
|
(22) |
二阶往复惯性力计算如下:
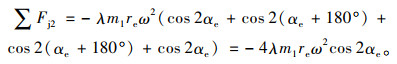
|
(23) |
由式(22)和式(23)可以看出,四缸发动机不对外输出一阶惯性力,只输出二阶惯性力。
通过上述分析,最终可以确定轮式装载机运行过程中,因发动机活塞曲柄连杆机构回转运动与往复运动所产生的惯性力,主要就是等效在活塞销上的质量m1往复运动过程中所产生的二阶惯性力。
3 驾驶室悬架系统阻尼控制策略设计为改善轮式装载机驾驶室垂向振动水平,将悬架动行程控制在合理区间,同时降低驾驶室侧倾角加速度和俯仰角加速度,必须结合减振器的阻尼调节原理及相关控制理论进行轮式装载机驾驶室悬架系统阻尼控制策略设计。为了实现轮式装载机驾驶室悬架系统的阻尼状态控制,采用模糊自适应控制方法。
3.1 模糊控制器设计轮式装载机驾驶室悬架系统阻尼状态控制不仅需要考虑驾驶室的垂向振动及悬架动行程,同时还要兼顾驾驶室俯仰运动和侧倾运动。因此,系统的模糊控制输入量较多,输出量为8个电磁阀的开关状态,也很复杂,故而模糊规则的制定十分困难。针对这一问题,参照传统研究采取的一般处理方式,考虑采用如图 4所示的八板块分解机制进行轮式装载机驾驶室悬架系统阻尼状态整体控制策略设计[17],其设计思想是:首先将驾驶室整体模型视作4个1/4车体模型、前后两个1/2车体模型以及左右两个1/2车体模型的集合,而后针对车体各子板块分别采用模糊控制策略进行减振器阻尼状态设计,最后将抑制驾驶室垂向振动、俯仰振动以及侧倾振动所需的控制量进行叠加,从而得到实现装载机驾驶室悬架整体控制目标所需的最优阻尼状态切换序列[18]。
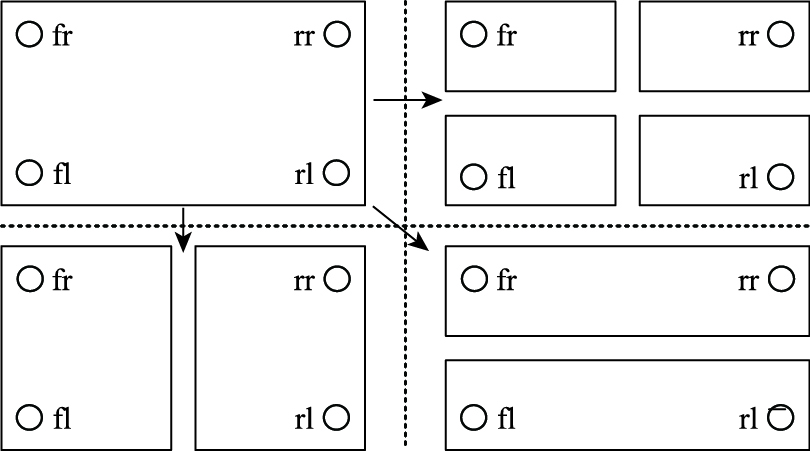
|
| 图 4 八板块分解原理 Fig. 4 Eight-plate decomposition principle |
| |
结合上述控制设计思想,在各子板块阻尼状态控制策略设计的基础上,轮式装载机驾驶室悬架系统阻尼状态模糊控制策略制定方法如下:
(1) 驾驶室悬架垂向振动模糊控制器的输入为驾驶室质心与车架质心之间的垂向位移差值zc-zu及差值变化率,控制器的输出为4个阻尼多状态切换减振器的阻尼状态(各减振器保持一致);
(2) 驾驶室悬架俯仰振动模糊控制器的输入为俯仰角与俯仰角速度,俯仰控制器的输出为前后阻尼多状态切换减振器的阻尼状态(前后减振器分别保持一致);
(3) 驾驶室悬架侧倾振动模糊控制器的输入为侧倾角与侧倾角速度,侧倾控制器的输出为左右阻尼多状态切换减振器的阻尼状态(左右减振器分别保持一致);
(4) 将以上3个子控制器输出的减振器阻尼状态进行合理叠加,即可形成每个减振器最终的阻尼状态。
3.2 驾驶室悬架系统阻尼模糊控制设计在参阅相关文献以及进行大量仿真对比的基础上,装载机驾驶室悬架系统各子控制器的模糊控制策略设计流程如下:
3.2.1 垂向振动模糊控制策略当悬架动行程及其变化趋势满足设计要求时,尽量将减振器的阻尼特性调节为“偏软”,从而降低驾驶室的垂向振动加速度;当悬架动行程及其变化趋势不满足设计要求时,将减振器的阻尼特性调节为“偏硬”,从而保证悬架动行程能够运行在合理范围内,降低悬架撞击限位的概率。
分别采用7个模糊集表示驾驶室悬架动行程及其变化率的模糊状态,相应的模糊子集设置为PB(正大)、PM(正中)、PS(正小)、ZE(零)、NS(负小)、NM(负中)以及NB(负大),模糊控制器的输出应为相应阻尼模式下的开关电磁阀s1和s2的通断状态,为便于实现,这里采用五个模糊集表示电磁阀开关状态的控制趋势,即ZE(闭)、S(小)、M(中)、B(大)、K(开)。
通过前述驾驶室悬架系统垂向振动模糊控制策略设计原则分析以及设置的相应模糊量,可得开关电磁阀s1和s2通断状态的模糊控制规则如表 2和表 3所示。
| E |  |
||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | ZE | ZE | S | M | S | ZE | ZE |
| NM | ZE | S | S | M | S | ZE | ZE |
| NS | B | B | S | K | S | S | S |
| ZE | M | M | K | K | K | M | M |
| PS | B | B | B | K | B | S | S |
| PM | K | K | B | M | B | ZE | ZE |
| PB | K | K | B | M | B | ZE | ZE |
| E |  |
||||||
| NB | NM | NS | ZE | PS | PM | PB | |
| NB | ZE | ZE | B | M | B | K | K |
| NM | ZE | ZE | B | M | B | K | K |
| NS | S | S | B | K | B | B | B |
| ZE | M | M | K | K | K | B | B |
| PS | S | S | S | K | S | B | B |
| PM | ZE | ZE | S | M | S | S | ZE |
| PB | ZE | ZE | S | M | S | ZE | ZE |
3.2.2 俯仰振动模糊控制策略
当驾驶室朝一侧俯仰角及其变化率较大时,应提高该侧减振器的压缩阻尼系数,同时增加另一侧减振器的复原阻尼系数。
分别采用5个模糊集表示驾驶室俯仰角及俯仰角速度的模糊状态,相应的模糊子集设置为PB(正大)、PM(正中)、ZE(零)、NM(负中)以及NB(负大),模糊控制器的输出应为相应阻尼模式下的开关电磁阀s1和s2的通断状态,这里同样采用5个模糊集表示电磁阀开关状态的控制趋势,即ZE(闭)、S(小)、M(中)、B(大)、K(开)。
结合前述驾驶室悬架系统俯仰振动模糊控制策略设计原则及所定义的模糊量,可得驾驶室前悬及后悬减振器开关电磁阀s1和s2通断状态的俯仰模糊控制规则如表 4和表 5所示。
| Valve | s1 | s2 | |||||||||
| E | 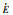 |
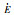 |
|||||||||
| NB | NM | ZE | PM | PB | NB | NM | ZE | PM | PB | ||
| NB | ZE | B | M | M | S | ZE | S | M | M | B | |
| NM | B | B | S | M | M | S | S | S | M | M | |
| ZE | M | S | K] | S | M | M | S | K | S | M | |
| PM | M | M | S | S | S | M | M | S | B | B | |
| PB | B | M | M | S | ZE | S | M | M | B | ZE | |
| Valve | s1 | s2 | |||||||||
| E | 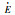 |
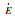 |
|||||||||
| NB | NM | ZE | PM | PB | NB | NM | ZE | PM | PB | ||
| NB | ZE | S | M | M | S | ZE | B | M | M | B | |
| NM | S | S | S | M | M | B | B | S | M | M | |
| ZE | M | S | K | S | M | M | S | K | S | M | |
| PM | M | M | S | B | B | M | M | S | S | S | |
| PB | B | M | M | B | ZE | S | M | M | S | ZE | |
3.2.3 侧倾振动模糊控制策略
驾驶室悬架侧倾振动模糊控制策略的设计依据与俯仰运动相类似,即当驾驶室朝一侧侧倾角及其变化率较大时,应提高该侧减振器的压缩阻尼系数,同时增加另一侧减振器的复原阻尼系数。
定义5个模糊集PB(正大)、PM(正中)、ZE(零)、NM(负中)以及NB(负大)表示驾驶室侧倾角及侧倾角速度的模糊状态;5个模糊集ZE(闭)、S(小)、M(中)、B(大)、K(开)表示电磁阀开关状态的控制趋势。
定义相关模糊量同俯仰振动模糊控制设计,包括模糊控制输入子集、输出子集、模糊控制输入输出论域、输入输出隶属度函数以及解模糊取整处理等,在此基础上,进一步可得轮式装载机驾驶室左悬及右悬阻尼多状态切换减振器开关电磁阀s1和s2通断状态的侧倾模糊控制规则如表 6和表 7所示。
| Valve | s1 | s2 | |||||||||
| E | 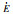 |
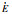 |
|||||||||
| NB | NM | ZE | PM | PB | NB | NM | ZE | PM | PB | ||
| NB | ZE | B | M | M | S | ZE | S | M | M | B | |
| NM | B | B | S | M | M | S | S | S | M | M | |
| ZE | M | S | K | S | M | M | S | K | S | M | |
| PM | M | M | S | S | S | M | M | S | B | B | |
| PB | B | M | M | S | ZE | S | M | M | B | ZE | |
| Valve | s1 | s2 | |||||||||
| E | 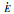 |
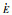 |
|||||||||
| NB | NM | ZE | PM | PB | NB | NM | ZE | PM | PB | ||
| NB | ZE | S | M | M | S | ZE | B | M | M | B | |
| NM | S | S | S | M | M | B | B | S | M | M | |
| ZE | M | S | K | S | M | M | S | K | S | M | |
| PM | M | M | S | B | B | M | M | S | S | S | |
| PB | B | M | M | B | ZE | S | M | M | S | ZE | |
3.2.4 垂向、俯仰及侧倾振动控制量叠加规则
通过上述装载机驾驶室悬架垂向、俯仰及侧倾振动模糊控制策略设计流程可知,各子模块控制设计均会得到每个阻尼多状态切换减振器高速开关电磁阀s1和s2的通断状态,为实现不同控制量的有效叠加,首先确定各控制量的叠加规则为:
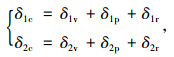
|
(24) |
式中,δ1c为各减振器开关电磁阀s1的控制律叠加结果; δ2c为各减振器开关电磁阀s2的控制律叠加结果; δ1v、δ1p以及δ1r分别为驾驶室悬架垂向、俯仰及侧倾振动模糊控制器输出的开关电磁阀s1通断状态信号; δ2v、δ2p以及δ2r分别为驾驶室悬架垂向、俯仰及侧倾振动模糊控制器输出的开关电磁阀s2通断状态信号。
在式(24)的基础上,为获取各减振器开关电磁阀s1和s2的最终控制信号,进一步设置下述判断准则:
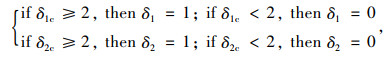
|
(25) |
式中,δ1为各减振器开关电磁阀s1的最终控制信号; δ2为各减振器开关电磁阀s2的最终控制信号; δ1,δ2为1表示电磁阀打开; δ1,δ2为0表示电磁阀关闭。
3.3 模糊控制性能仿真为验证上述基于八板块解耦的轮式装载机驾驶室悬架系统阻尼状态模糊控制策略的实际性能,进一步完成系统控制性能仿真分析。结合建立的装载机四轮相关随机路面激励模型,假定装载机是以10 m/s的速度行驶在D级路面上。控制系统仿真过程中涉及的其他主要参数如表 8所示。
| 参数 | 数值 |
| mc/kg | 19 090 |
| mu/kg | 640 |
| me/kg | 150 |
| kt/(N·m-1) | 392 000 |
| ct/(N·s·m-1) | 3 500 |
| ke/(N·m-1) | 13 580 |
| ce/(N·s·m-1) | 1 400 |
| l1/m | 1.2 |
| l2/m | 0.15 |
| l3/ m | 2.00 |
| l4/m | 1.35 |
| l5/ m | 0.44 |
| l6/m | 0.58 |
| l7/ m | 1.18 |
| l8/m | 1.24 |
| l9/m | 0.21 |
| l10/m | 0.65 |
| l11/m | 1.35 |
| l12/m | 1.7 |
| l13/m | 1.18 |
| l14/m | 1.24 |
| kdb-l, kdb-r/(N·m-1) | 13 500 |
| cdb-l, cdb-r/(N·s·m-1) | 2 050 |
| kcd-l, kcd-r/(N·m-1) | 61 800 |
| ccd-l, ccd-r/(N·s·m-1) | 4 135 |
| β rad | π/3 |
| α/rad | π/4 |
| kc/(N·m-1) | 19 335 |
| λ | 4/3 |
| mdb-l, mdb-r/kg | 180 |
| mcd-l, mcd-r/kg | 260 |
| lφ/m | 0.525 |
| lθ/m | 0.51 |
| Iuφ/(kg·m2) | 15 430 |
| Iuθ/(kg·m2) | 2 500 |
| Icφ/(kg·m2) | 860 |
| Icθ/(kg·m2) | 927 |
| ω/(rad·s-1) | 50π |
| m1/kg | 14.5 |
| re/mm | 0.24 |
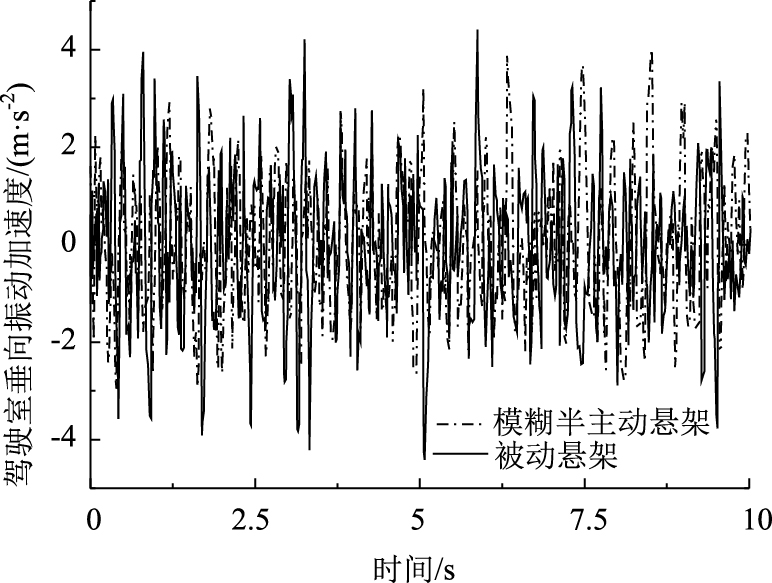
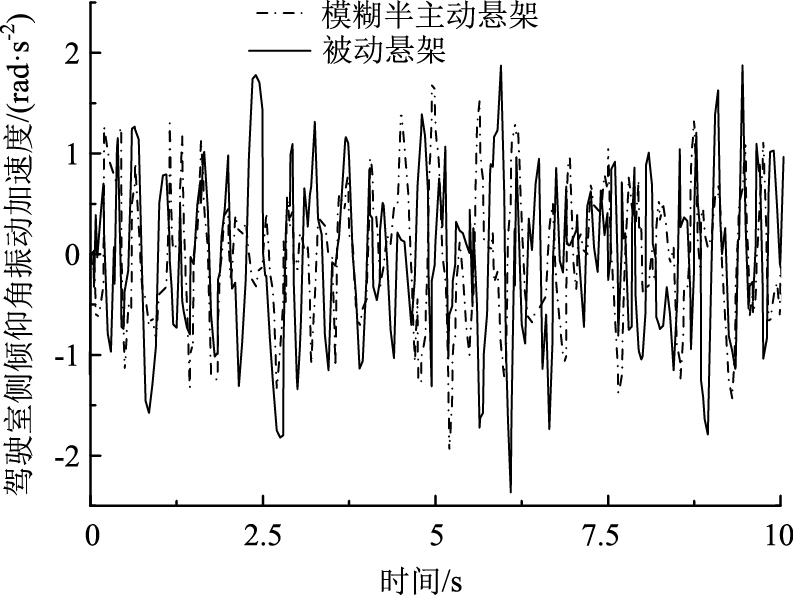
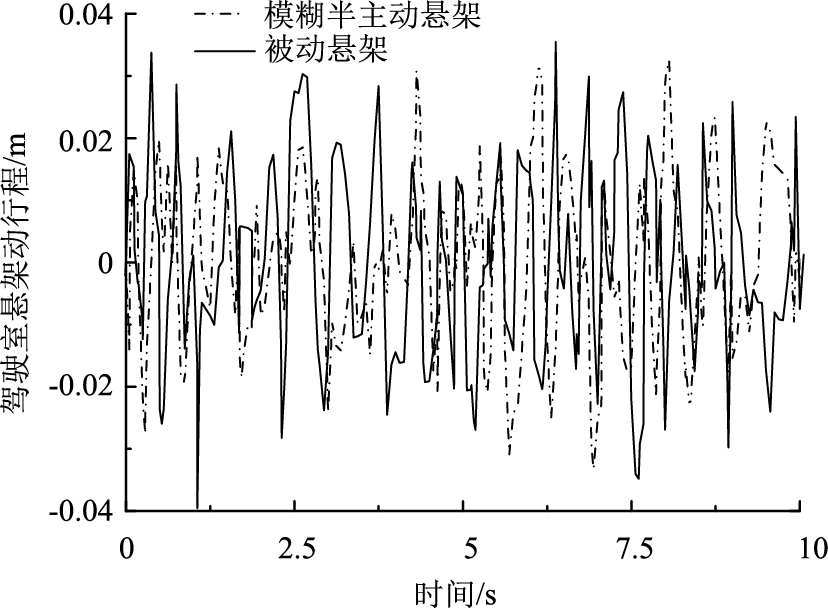
图 5~图 8所示分别为仿真获取的轮式装载机驾驶室垂向振动加速度、驾驶室悬架动行程以及驾驶室俯仰角加速度和侧倾角加速度的仿真结果。从图 5~8中可以明显看出,基于阻尼多状态切换减振器的轮式装载机驾驶室悬架模糊控制策略能够有效改善驾驶室悬架的隔振性能,在不恶化驾驶室悬架动行程的前提下,驾驶室垂向振动加速度、驾驶室俯仰角加速度以及驾驶室侧倾角加速度均有较为明显的改善。
|
| 图 5 模糊控制下的驾驶室垂向振动加速度仿真结果 Fig. 5 Simulation result of cab vertical vibration acceleration under fuzzy control |
| |
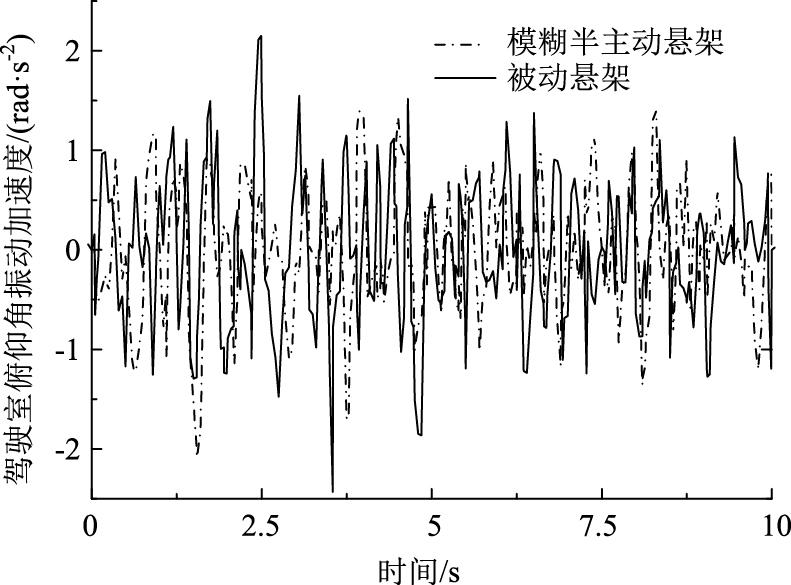
|
| 图 6 模糊控制下的驾驶室俯仰角加速度仿真结果 Fig. 6 Simulation result of cab pitch acceleration under fuzzy control |
| |
|
| 图 7 模糊控制下的驾驶室侧倾角加速度仿真结果 Fig. 7 Simulation result of cab roll acceleration under fuzzy control |
| |
|
| 图 8 模糊控制下的驾驶室悬架动行程仿真结果 Fig. 8 Simulation result of dynamic travel of cab suspension under fuzzy control |
| |
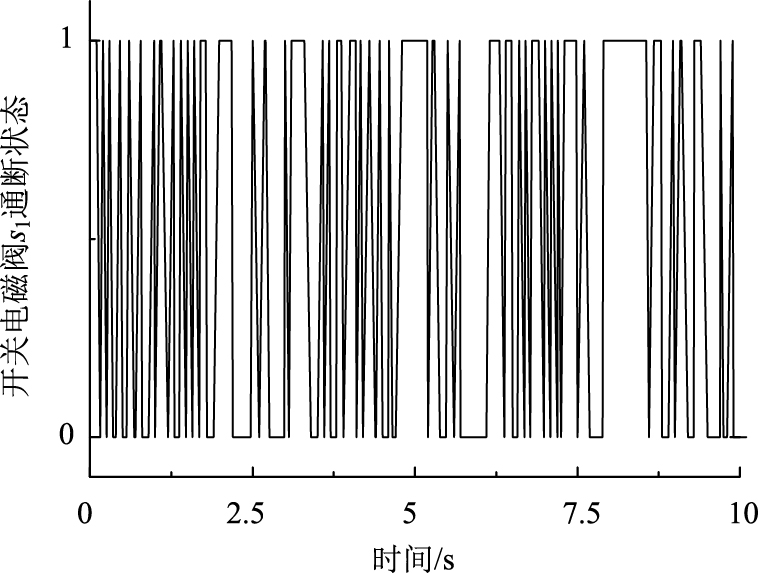
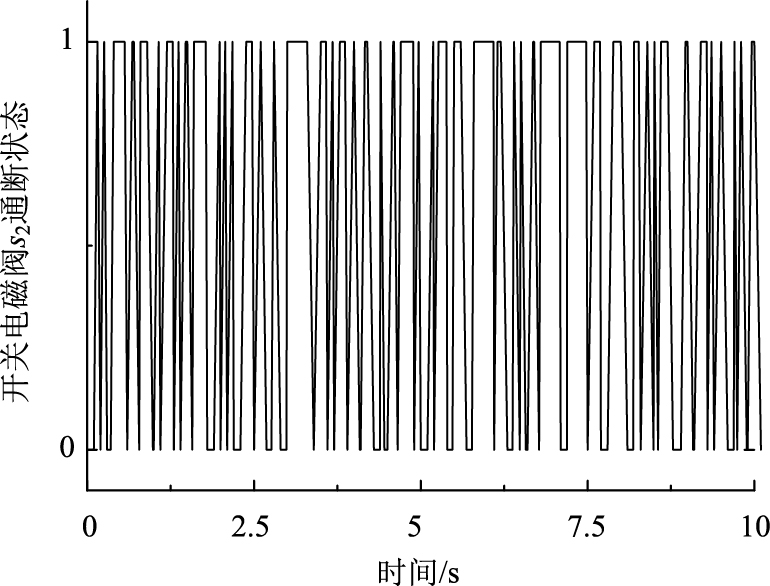
图 9~图 10所示分别为轮式装载机驾驶室悬架四角处阻尼多状态切换减振器开关电磁阀s1和s2的通断状态控制信号,从9图~图 10中可以看出,所设计的模糊控制策略能够根据系统控制目标,实现4个减振器8个开关电磁阀通断状态的直接有效控制,从而有效保障了系统阻尼控制性能。从表 9中可以看出,相较于传统被动悬架,模糊控制使得驾驶室垂向振动加速度均方根值降低了21%,驾驶室俯仰角加速度和侧倾角加速度均方根值分别降低11%和12%,降幅明显优于传统被动悬架,同时驾驶室悬架动行程并未恶化,峰值严格控制在±0.04 m范围之内。
|
| 图 9 模糊控制下的开关电磁阀s1通断状态控制信号 Fig. 9 On-off status control signal of solenoid valve s1 under fuzzy control |
| |
|
| 图 10 模糊控制下的开关电磁阀s2通断状态控制信号 Fig. 10 On-off status control signal of solenoid valve s2 under fuzzy control |
| |
| 仿真结果 | 被动悬架 | 模糊控制 | 降幅 |
| 驾驶室垂向振动加速度/(m·s-2) | 1.432 | 1.136 | 20.6% |
| 驾驶室俯仰角振动加速度/(rad·s-2) | 0.654 | 0.583 | 10.8% |
| 驾驶室侧倾角振动加速度/(rad·s-2) | 0.702 | 0.615 | 12.4% |
| 驾驶室悬架动行程峰值/m | ±0.04 | ±0.034 | 15% |
4 结论
本研究将一种新型四阻尼减振器应用于轮式装载机驾驶室悬架。新型减振器通过控制两个电磁阀的通断状态,可以有效地实现四种阻尼模式和八种阻尼状态,比传统的阻尼可调减振器具有优越性。为实现新型减振器对轮式装载机半主动驾驶室悬架的控制,建立了同时考虑工作装置振动特性、四轮相关随机路面激励和发动机振动激励的轮式装载机11自由度振动模型。在此基础上,设计了模糊控制策略,实现了阻尼模式切换顺序的最优控制。仿真结果表明,采用阻尼多模切换减振器的轮式装载机半主动驾驶室悬架性能得到了显著改善,说明了模糊控制方法的有效性。此外,该控制器还可以直接控制两个电磁阀的开关状态,从而验证了它们解决离散控制问题的能力。因此,后续需要加强工作和改进的方向,是将所提出的减振器及相应的控制方法应用到实际的轮式装载机,通过真机试验结果进一步验证系统的可靠性和稳定性。
| [1] |
张俊红, 李忠鹏, 毕凤荣, 等. 基于板件贡献分析的装载机驾驶室低噪声设计[J]. 振动、测试与诊断, 2016, 36(3): 568-574. ZHANG Jun-hong, LI Zhong-peng, BI Feng-rong, et al. Low Noise Design of Loader Cab Based on Panel Contribution Analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2016, 36(3): 568-574. |
| [2] |
WARD C H. The Application of a New Cab Mounting to Address Cab Shake on the 2003 Chevrolet kodiak and Gmc Topkick[EB/OL]. (2002-11-18)[2019-10-10].https://www.sae.org/publications/technical-papers/content/2002-01-3102.
|
| [3] |
游洁, 郭启华.高速装载机的悬挂减振装置: 中国, ZL03251117.5[P]. 2005-12-28. YOU Jie, GUO Qi-hua. Suspension Damping Device of High Speed Loader, Patent: China, ZL03251117.5[P]. 2005-12-28. |
| [4] |
PRATER G, SHAHHOSSEINI A M, STATE M, et al. Use of Fea Concept Models to Develop Light-truck Cab Architectures with Reduced Weight and Enhanced NVH Characteristics[EB/OL]. (2002-03-04)[2019-10-10].https://www.sae.org/publications/technical-papers/content/2002-01-0369.
|
| [5] |
孙小娟, 张建润. 工程机械驾驶室舒适性设计中的低频隔振优化[J]. 农业工程学报, 2012, 28(21): 44-52. SUN Xiao-juan, ZHANG Jian-run. Optimization of Low-frequency Vibration isolation for Cab Ride Comfort of Construction Machineries[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(21): 44-52. |
| [6] |
CHI C, QIN S, YU D, et al. The Application of Pseudo-Excitation Method to the Ride Comfort Research of Wheel-loader[J]. Applied Mechanics and Materials, 2010, 34-35: 538-543. |
| [7] |
陈翔, 白月飞, 张林燕, 等. 考虑发动机与人椅系统的液压半主动悬架振动控制研究[J]. 公路交通科技, 2011, 28(1): 127-131, 137. CHEN Xiang, BAI Yue-fei, ZHANG Lin-yan, et al. Research on Vibrating Control of Hydraulic Semi-active Suspension Considering Engine and Passenger-seat System[J]. Journal of Highway and Transportation Research and Development, 2011, 28(1): 127-131, 137. |
| [8] |
LI X, LÜ W, ZHANG W, et al. Research on Dynamic Behaviors of Wheel Loaders with Different Layout of Hydropneumatic Suspension[J]. Journal of Vibroengineering, 2017, 19(7): 5388-5404. |
| [9] |
REHNBERG A, EDREN J, ERIKSSON M, et al. Scale Model Investigation of the Snaking and Folding Tability of An Arti-culated Frame Steer Vehicle[J]. International Journal of Vehicle Systems Modelling and Testing, 2011, 6(2): 126-144. |
| [10] |
ZHANG H, WANG E, ZHANG N, et al. Semi-active Sliding Mode Control of Vehicle Suspension with Magneto-rheological Damper[J]. Chinese Journal of Mechanical Engineering, 2015, 28(1): 63-75. |
| [11] |
CHEN M, HU Y, LI C, et al. Performance Benefits of Using Inerter in Semi-active Suspensions[J]. IEEE Transactions on Control Systems Technology, 2015, 23(4): 1571-1577. |
| [12] |
许海亮, 何炼, 何兆才, 等. 考虑路面不平整度因素的车路耦合系统非线性数值模型[J]. 公路交通科技, 2017, 34(8): 23-28. XU Hai-liang, HE Lian, HE Zhao-cai, et al. A Nonlinesr Numerical Model of Vehicle-pavement Coupled System Considering Pavement Roughness[J]. Journal of Highway and Transportation Research and Development, 2017, 34(8): 23-28. |
| [13] |
ARANA C, EVANGELOU S A, DINI D. Series Active Variable Geometry Suspension for Road Vehicles[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1): 361-372. |
| [14] |
李仲兴, 黄建宇, 刘亚威, 等. 白噪声路面不平度时域模型的建立与仿真[J]. 江苏大学学报:自然科学版, 2016, 37(5): 503-506. LI Zhong-xing, HUANG Jian-yu, LIU Ya-wei, et al. Modeling and Simulation on White Noise of Road Roughness in Time Domain[J]. Journal of Jiangsu University:Natural Science Edition, 2016, 37(5): 503-506. |
| [15] |
石晓辉, 蒋欣, 赵军, 等. 不平路面车路耦合动载研究[J]. 中国科技论文, 2018, 13(4): 408-413. SHI Xiao-hui, JIANG Xin, ZHAO Jun, et al. Research on Vehicle-road Coupling Dynamic Load on Uneven Pavement[J]. China Sciencepaper, 2018, 13(4): 408-413. |
| [16] |
李轼.某工程车辆动力总成悬置系统隔振性能优化设计[D].广州: 华南理工大学, 2015. LI Shi. Optimization Design of Vibration Isolation Performance of Powertrain Mounting System of an Engineering Vehicle[D]. Guangzhou: South China University of Technology, 2015. |
| [17] |
陈龙, 黄晨, 江浩斌, 等. 基于悬架效用函数的车身姿态控制[J]. 农业机械学报, 2011, 42(8): 15-19. CHEN Long, HUANG Chen, JIANG Hao-bin, et al. Body Posture Control Based on Suspension Utility Function[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(8): 15-19. |
| [18] |
MASOUDI S, SOLTANPOUR M R, ABDOLLAHI H, et al. Adaptive Fuzzy Control Method for a Linear Switched Reluctance Motor[J]. IET Electric Power Applications, 2018, 12(9): 1328-1336. |
 2020, Vol. 37
2020, Vol. 37
