扩展功能
文章信息
- 王国娟, 吕文红, 高歌, 刘玉洁
- WANG Guo-juan, LÜ Wen-hong, GAO Ge, LIU Yu-jie
- 基于复杂网络的失效公交站点绕行方案研究
- Study on Detour Scheme for Failure of Transit Station Based on Complex Network
- 公路交通科技, 2020, 37(11): 107-117
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 107-117
- 10.3969/j.issn.1002-0268.2020.11.014
-
文章历史
- 收稿日期: 2020-03-27
2. 宿迁市城市规划设计研究院有限公司, 江苏 宿迁 223800
2. Suqian Urban Planning and Design Institute Co., Ltd., Suqian Jiangsu 223800, China
目前,大多数研究采用Space L、Space P和Space R中的一种或几种方法构建单一和复合公交网络模型,对网络站点拓扑特性指标和可靠性展开研究。文献[1-2]构建了无权公交网络,文献[3-6]构建了加权公交网络,文献[7-8]构建了公交—地铁复合网络。上述研究表明城市公交网络站点节点度分布具有明显的小世界和无标度特性。文献[9-10]构建了无权公交换乘网络,文献[11-12]构建了加权复杂运输网络,文献[13-14]构建了公交—地铁加权复合网络。上述研究分别采用不同攻击模式对公交网络站点可靠性展开了研究,得出公交网络具有明显的小世界和无标度特性,复合网络站点可靠性高于单一网络,网络在面对随机攻击时更加脆弱[15-16]。
当前复杂网络在交通运输网络的研究中,对拓扑指标缺乏聚类分析,对公交站点失效后如何采取优化措施亦较少涉及。如能对公交网络站点拓扑特性指标进行聚类分析,找出关键节点并有针对性地进行管理,在站点失效后及时采取合理的绕行措施,将有利于提高公交网络对抗攻击的能力。
1 基于复杂网络的城市公交网络分析 1.1 公交网络模型构建方法本研究采用Space L模型构建方法,以公交线路发车时间间隔倒数为权重构建公交网络模型。此模型以公交站点为网络节点,若两公交站点相邻且经过同一公交线路,则两公交站点间存在一条连边。定义G为公交网络,V,E,W,H分别表示网络的节点、连边、节点权重和连边权重。根据客流量特性,将公交网络划分为早高峰、晚高峰和平峰3个网络,分别用Gm,Ge,Gp表示。
用矩阵形式表示网络拓扑关系,若节点对之间存在连边则矩阵中的元素为1,不存在连边则矩阵中对应元素值为0。假设网络中有N个节点,则定义公交线路网络的邻接矩阵为A为:
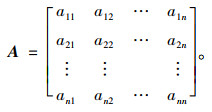
|
(1) |
以早高峰网络为例,阐述公交加权网络模型构建规则。
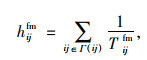
|
(2) |
式中,hijfm为早高峰时段加权网络节点i和j连边权重;Г(ij)为经过节点i与j公交线路的集合;Tijfm为早高峰时段经过节点i和节点j连边公交线路发车时间间隔。
对高峰时段加权公交网络连边权重进行归一化处理则有:
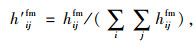
|
(3) |
早高峰公交加权网络连边权为:
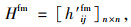
|
(4) |
早高峰加权网络节点权重为:
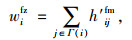
|
(5) |
早高峰公交加权网络节点权重矩阵为:
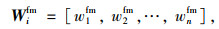
|
(6) |
公交加权网络连边权重向量:
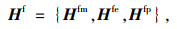
|
(7) |
公交加权网络节点权重向量:
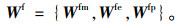
|
(8) |
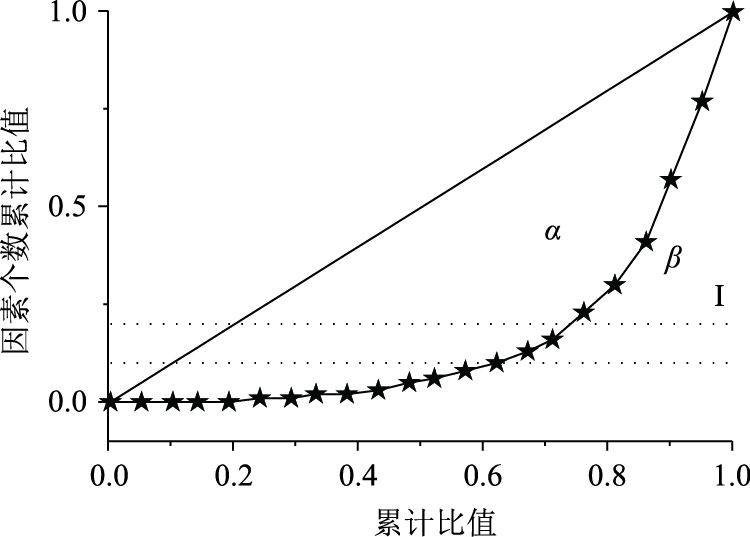
Lorenz曲线能对事件的分布状况进行聚集性分析,并得出热点所在[17]。本研究以公交网络拓扑特性指标为对象,各拓扑特性指标站点个数呈离散分布并趋于集中。聚集系数Q用以描述Lorenz曲线的聚集程度,其值为α/(α+β),其中:α为Lorenz曲线与直线y=x之间的面积,β为Lorenz曲线与x轴之间的面积,如图 1所示。计算公式如下:
|
| 图 1 Lorenz曲线示意图 Fig. 1 Schematic diagram of Lorenz curve |
| |
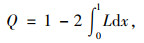
|
(9) |
式中L为Lorenz曲线的函数表达式。
聚集系数越大表示分布越不均匀[18]。Q>0.4时呈聚集性,Q>0.5呈强聚集性。结合ABC管理分类法,根据因素个数累计比值(y轴)将Lorenz曲线分为3个区间,如表 1所示。本研究则以站点个数累计比值(y轴)为分类对象,对各拓扑特性指标分布情况进行分析。
| 累计度分布 | 区间分类 | 研究对象等级 |
| 0.2~1.0 | Ⅰ类 | 主要事物 |
| 0.1~0.2 | Ⅱ类 | 次要事物 |
| 0~0.1 | Ⅲ类 | 更次要事物 |
Lorenz曲线公交网络拓扑特性分析模型求解步骤:
Step 1:将拓扑特性指标按所对应公交站点个数大小进行升序排列。
Step 2:Lorenz曲线x轴获取。
(1) 按照Step 1的顺序,对各拓扑特性指标进行编号;
(2) 计算累计比值:
累计比值=编号/最大编号数;
(3) 累计比值即为Lorenz曲线的x轴。
Step 3:Lorenz曲线y轴获取。
(1) 计算因素个数比值:
站点个数比值=各拓扑指标公交站点个数/公交站点总个数;
(2) 将站点个数比值根据升序排列的次序进行累加,得到站点个数累计比值;
(3) 站点个数累计比值即为Lorenz曲线的y轴。
2 城市公交网络失效站点绕行方案设计公交网络优化主要体现在网络连通性的提高,本研究选取平均路径长度和网络全局效率两个指标衡量公交网络连通性,通过对公交站点绕行前后两指标数值的变化判断网络是否优化:与绕行前网络相比,若绕行后网络平均路径数值变小、网络全局效率数值变大,则表明网络优化后更连通,绕行方案可行。
本研究定义绕行前网络为公交站点失效后不采取绕行方案的网络,此网络为除去失效节点以及与失效节点相连连边后的网络。假设某一小型网络中有10个节点,20条连边,与编号为7的节点相连的连边有3条,则节点7失效后,绕行前网络有9个节点,17条连边。
模型假设:
(1) 绕行网络为采取绕行方案后的网络,为节约运营成本不重新修建公交站点,站点失效后只选择公交网络中已有站点作为绕行站点,绕行后公交网络的站点数为N-1;
(2) 公交线路首末站点不受攻击;
(3) 以公交上行方向为研究对象,规定失效站点的上一站点为前,失效节点的下一站点为后;
(4) 为方便模型计算,网络优化后其他节站权重保持不变,失效站点权重全部分配到绕行站点。
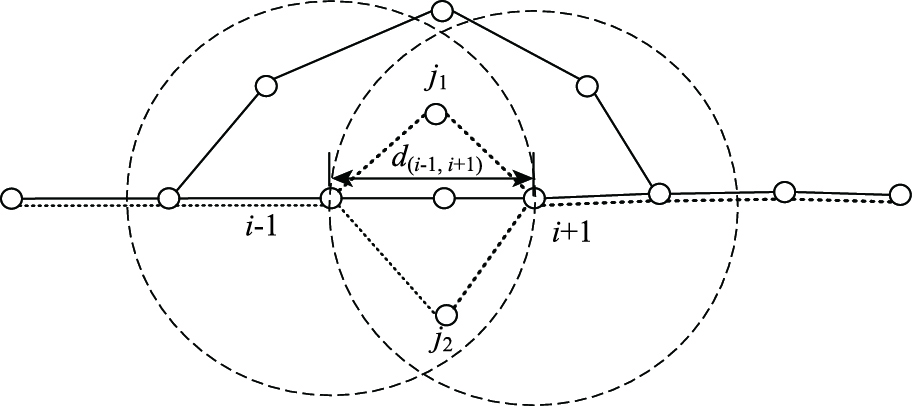
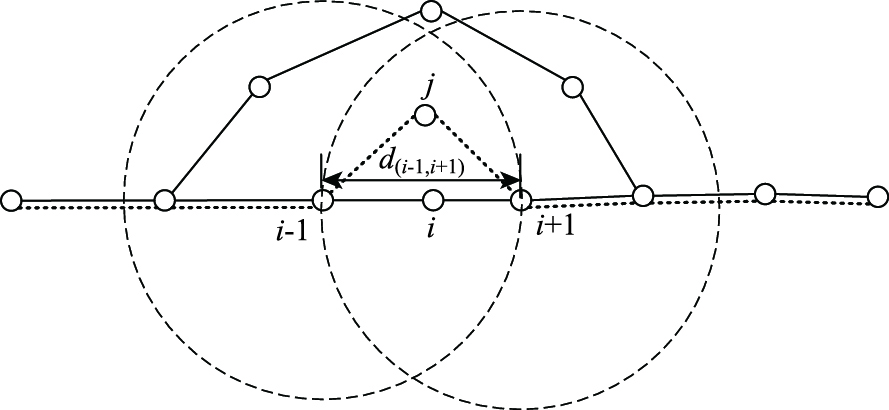
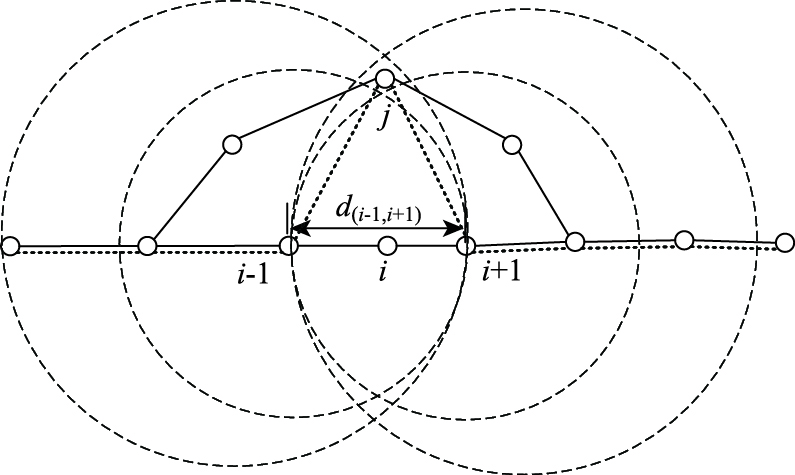
假设节点i为失效站点,节点i-1和i+1为失效站点i的前、后站点,节点j为绕行站点。绕行站点选取过程中既要考虑路径最短,也要考虑与前后站点的位置关系,应尽量选择在前后站点的中间位置,因此设失效站点前后两站点i-1和i+1间直线距离为d(i-1, i+1),分别以节点i-1和节点i+1为圆心,d(i-1, i+1)为半径画圆,两圆重合区域即为选择绕行站点的区域S。节点i-1与j节点间的直线距离为为d(i-1, j),节点j与节点i+1之间的直线距离为d(j, i+1),选取与节点i-1和i+1直线距离和最小的站点作为绕行站点,绕行区域S内,绕行站点有2个、1个和0个绕行站点3类情况。
2.1 绕行区域内存在2个绕行站点若重合区域存在2个最短路径站点,则2个站点同为绕行站点,如图 2所示,实线线段为绕行前线路,虚线线段为绕行后线路。节点j1与节i-1点间的直线距离为d(i-1, j1),节点j1与节点i+1间的直线距离为d(j1, i+1),节点j2与节点i-1间的直线距离为d(i-1, j2),节点j2与节点i+1间的直线距离为d(j2, i+1),则绕行站点j1和j2满足如下条件:
|
| 图 2 绕行区域内存在2个节点 Fig. 2 Two nodes in detour area |
| |
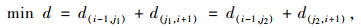
|
(10) |
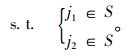
|
(11) |
网络节点度反映节点与其他节点连接关系,节点度值越大表明该节点与其他节点间的联系越密切,连通性越高,可以承担更多的交通负荷。本研究采用节点度值重新分配策略[19-20]分配失效节点权重值,绕行后失效节点i的节点权重按照节点度值重新分配策略分配至节点j1和j2。设失效节点i的权重值为wi,节点j1和j2的权重值为wj1,wj2,节点j1和j2的节点度值为kj1,kj2, 则采用节点度值重新分配策略后节点j1和j2的权重为:
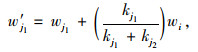
|
(12) |
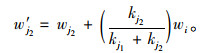
|
(13) |
若重合区域内最短路径站点只有1个,如图 3所示该站点即为绕行站点,实线线段为绕行前线路,虚线线段为绕行后线段,则有绕行站点j满足如下条件:
|
| 图 3 绕行区域内存在1个节点 Fig. 3 One node in detour area |
| |
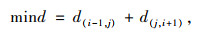
|
(14) |
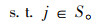
|
(15) |
假设失效前节点i的节点权重为wi, 节点j的权重为wj则有绕行后节点j的权重为:
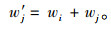
|
(16) |
若重合区域S内无站点,则适当增加半径值,扩大重合区域直至区域内存在最短路径节点,如图 4所示,外侧虚线区域为扩大后的区域,实线线段为绕行前线路,虚线线段为绕行后线段。则有绕行站点j满足如下条件:
|
| 图 4 绕行区域内不存在节点 Fig. 4 No node in detour area |
| |
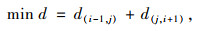
|
(17) |
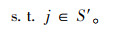
|
(18) |
与S区域内存在站点相同,对于扩大的区域S′同样存在1个绕行节点和存在2个绕行节点两种情况,节点权重w′j由公式(12)、公式(13)和公式(16)计算求得。
3 案例分析本研究以青岛市某区公交网络为例进行分析,区域内有226条公交线路[21],以公交线路发车时间间隔倒数为权重,构建早高峰、晚高峰和平峰公交网络模型见表 2,3个网络均有1 823个节点和2 666条连边。
| 节点度值 | 编号 | 累计比值(x轴) | 站点个数 | 站点个数比值 | 站点个数累计比值(y轴) |
| 17 | 1 | 0.071 4 | 1 | 0.000 5 | 0.000 5 |
| 13 | 2 | 0.142 9 | 1 | 0.000 5 | 0.001 0 |
| 12 | 3 | 0.214 3 | 1 | 0.000 5 | 0.001 0 |
| 11 | 4 | 0.285 7 | 6 | 0.003 3 | 0.004 3 |
| 10 | 5 | 0.357 1 | 8 | 0.004 4 | 0.008 7 |
| 9 | 6 | 0.428 6 | 8 | 0.004 4 | 0.013 1 |
| 8 | 7 | 0.500 0 | 21 | 0.011 5 | 0.024 6 |
| 7 | 8 | 0.571 4 | 36 | 0.019 8 | 0.044 4 |
| 6 | 9 | 0.642 9 | 66 | 0.036 2 | 0.080 6 |
| 1 | 10 | 0.714 3 | 82 | 0.045 0 | 0.125 6 |
| 5 | 11 | 0.785 7 | 110 | 0.060 4 | 0.186 0 |
| 4 | 12 | 0.857 1 | 211 | 0.115 8 | 0.301 8 |
| 3 | 13 | 0.928 6 | 236 | 0.129 5 | 0.431 3 |
| 2 | 14 | 1.000 0 | 1 036 | 0.568 6 | 1.000 0 |
3.1 区域公交网络拓扑特性分析
(1) 节点度
该区域公交站点度值主要分为14类,分别为1,2,…,13和17,公交站点间的节点度值差别较大。累计度服从幂律分布,网络具有小世界特性。
由公式(9)计算可得该区公交站点节点度值分布聚集系数为0.87,大于0.5,呈现强聚集性,由图 5(a)可得Ⅰ类区间的节点度为4,3,2,分别占总数站点的11.57%,12.95%和56.83%。由图 5(b)节点度值为2的公交站点所占比重最大,表明该区大部分公交站点为非换乘站点,此类站点主要分布在郊区及村镇区域,起连接前后两公交站点的作用,换乘便捷性不高;节点度值为1的尽头时公交站点有82个,占总站点数量的4.5%。网络中节点度值大于10的站点只有16个,此类节点为公交枢纽站点,均分布在中心商业区边缘,周围大多分布着度值较大、换乘便捷的公交站点,有利于缓解中心区域交通负荷。
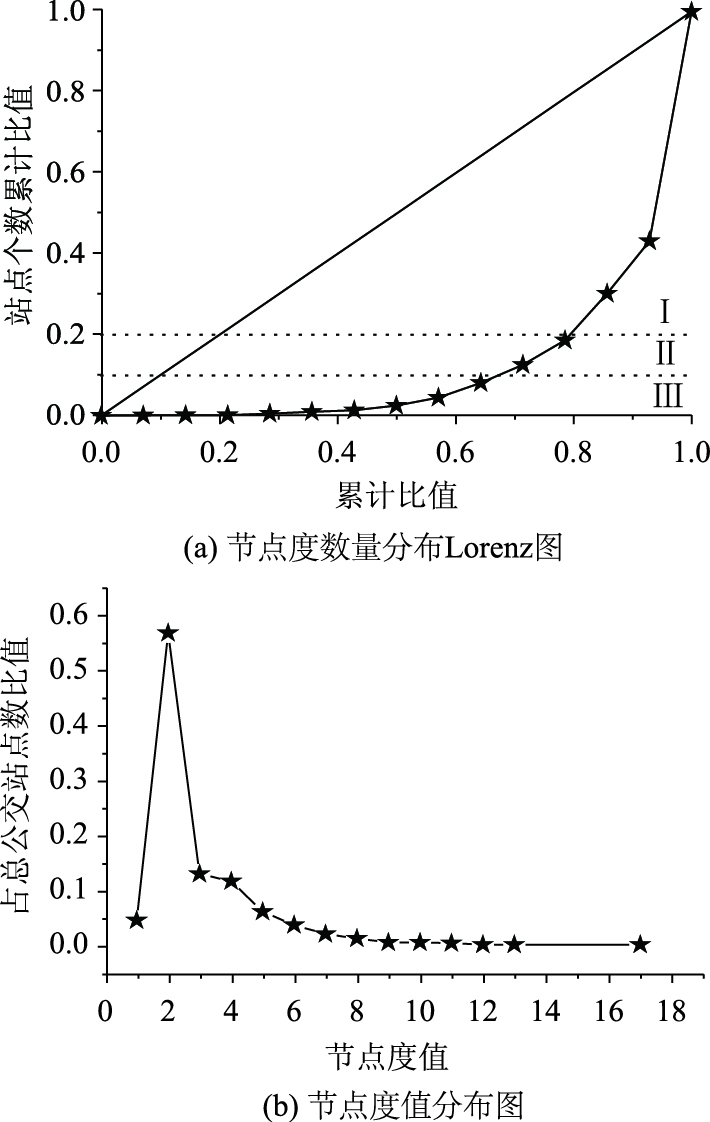
|
| 图 5 节点度值分布图 Fig. 5 Curves of node degree value distribution |
| |
(2) 局部特性分析
考虑相邻及次邻节点的影响,本研究以2阶邻近度这一拓扑指标来衡量公交网络节点局部重要性。对于公交站点而言,2阶邻近度值越大,表明其局部换乘便捷性越高。
如图 6(a)所示,网络节点2阶度值分布集中系数为0.6,呈现强分布性,Ⅰ类区域2阶节点度值为28,22,26,20,24,18,16,2,14,12,6,10,8,4,分别占站点总数量的2.30%,2.47%,2.80%,3.46%,3.68%,3.84%,4.44%,4.88%,5.16%,6.03%,6.14%,7.02%,8.83%,19.14%,如图 6(b)所示2节点度值为4的站点个数最多。由此可得:①青岛市某区域公交网络密度较低,2阶节点度值为4的公交站点最多,约占总节点数的19%,5%的公交站点2阶邻近度值为2,此类公交站点为始发站多分布在郊区、村镇等区域,换乘便捷性差,连通性较低;②2阶邻近度值超过100的站点占总站点数量的1.2%,大多数站点为大型购物中心,其中排名前10的站点为:商城、东新村东、机关东部办事中心、市民服务中心北、世纪商城、西海岸汽车东站、东方华庭、新城吾悦广场、保税港区西门、家佳源,此类节点均布中心商业区。
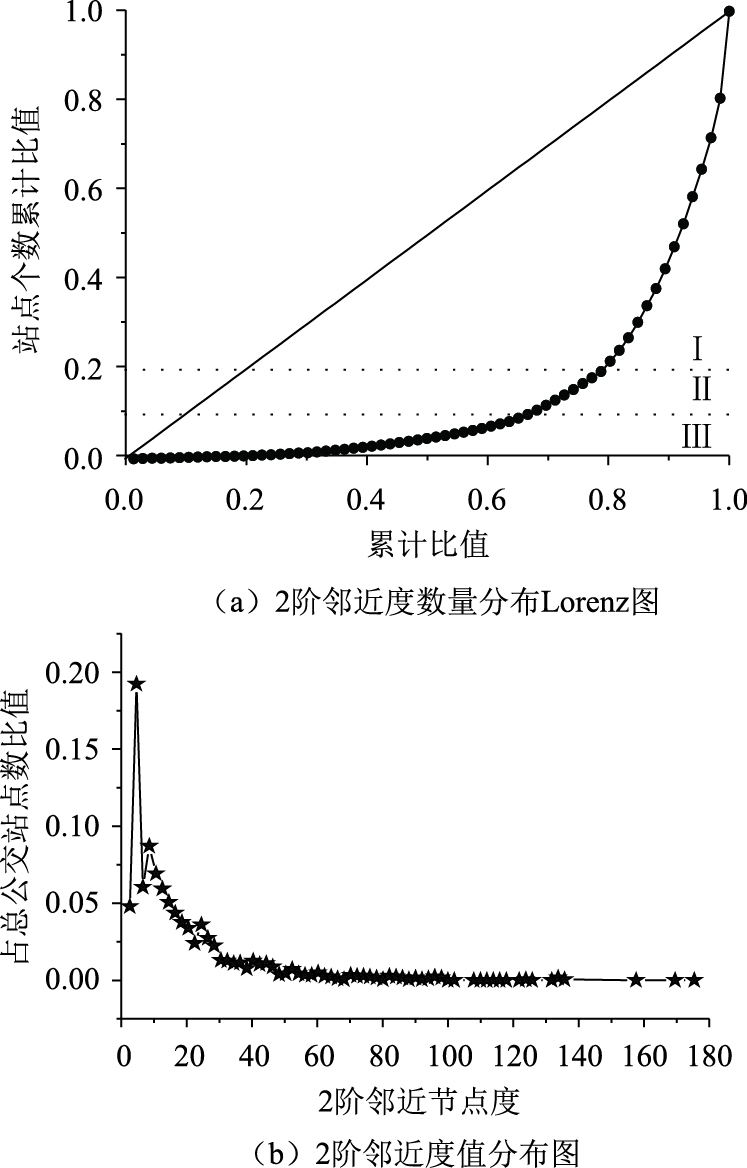
|
| 图 6 2阶邻近度站点分布Lorenz图 Fig. 6 Lorenz curves of 2nd-order proximity degree station distribution |
| |
(3) 中心性分析
点度中心性是网络中刻画节点中心性的最直接指标,在公交网络中若某公交站点与其他很多站点有直接联系,表明该站点处于整个公交网络的中心位置,此站点换乘更便捷,一旦失效后对整个网络的影响也更大。
早高峰、晚高峰和平峰3个时段节点中心度平均值为0.329,0.288,0.179,总和为600.38,525.486,326.154,平方和为502.97,368.239,138.521,最小值为0.011,0.011,0.004,最大值为3.601,3.236,1.959,各值均为早高峰>晚高峰>平峰。
青岛市某区域各时段公交网络相同排名站点的节点中心度值均为早高峰>晚高峰>平峰。这是由于该区域内分布大量的工厂、高校和企事业单位,上班时间较为集中,下班时间较为分散,早高峰时段公交网络节点权重较大,客流量较晚高峰和平峰时段交通流量更为集中,点度中心值反应站点在网络中的重要程度,因此相同排名的节点中心度值:早高峰>晚高峰>平峰。
早高峰时段公交网络节点中心度值范围为0.001~3.601,如表 3所示以0.1为步长将节点中心度值划分为36个区间,由图 7(a)可知公交站点节点中心度值主要分布在[0.8, 0.9),[0.6, 0.7),[0.5, 0.6),[0.4, 0.5),[0.3, 0.4),[0.2, 0.3),[0.1, 0.2)和[0, 0.1)这8个区间,各区间站点个数分别占总站点数的2.14%,3.24%,5.7%,6.8%,8.1%,14.54%,22.87%和27.65%。
| 排序 | 区间 | 站点数 |
| 1 | [0, 0.1) | 504 |
| 2 | [0.1, 0.2) | 417 |
| 3 | [0.2, 0.3) | 265 |
| 4 | [0.3, 0.4) | 146 |
| 5 | [0.4, 0.5) | 124 |
| 6 | [0.5, 0.6) | 104 |
| 7 | [0.6, 0.7) | 59 |
| 8 | [0.7, 0.8) | 36 |
| 9 | [0.8, 0.9) | 39 |
| 10 | [0.9, 1.0) | 23 |
| 11 | [1.0, 1.1) | 14 |
| 12 | [1.1, 1.2) | 19 |
| 13 | [1.2, 1.3) | 11 |
| 14 | [1.3, 1.4) | 8 |
| 15 | [1.4, 1.5) | 5 |
| 16 | [1.5, 1.6) | 8 |
| 17 | [1.6, 1.7) | 9 |
| 18 | [1.7, 1.8) | 2 |
| 19 | [1.8, 1.9) | 4 |
| 20 | [1.9, 2.0) | 0 |
| 21 | [2.0, 2.1) | 7 |
| 22 | [2.1, 2.2) | 2 |
| 23 | [2.2, 2.3) | 3 |
| 24 | [2.3, 2.4) | 4 |
| 25 | [2.4, 2.5) | 3 |
| 26 | [2.5, 2.6) | 0 |
| 27 | [2.6, 2.7) | 0 |
| 28 | [2.7, 2.8) | 3 |
| 29 | [2.8, 2.9) | 0 |
| 30 | [2.9, 3.0) | 1 |
| 31 | [3.0, 3.1) | 0 |
| 32 | [3.1, 3.2) | 1 |
| 33 | [3.2, 3.3) | 0 |
| 34 | [3.3, 3.4) | 0 |
| 35 | [3.4, 3.5) | 1 |
| 36 | [3.5, 3.6) | 1 |
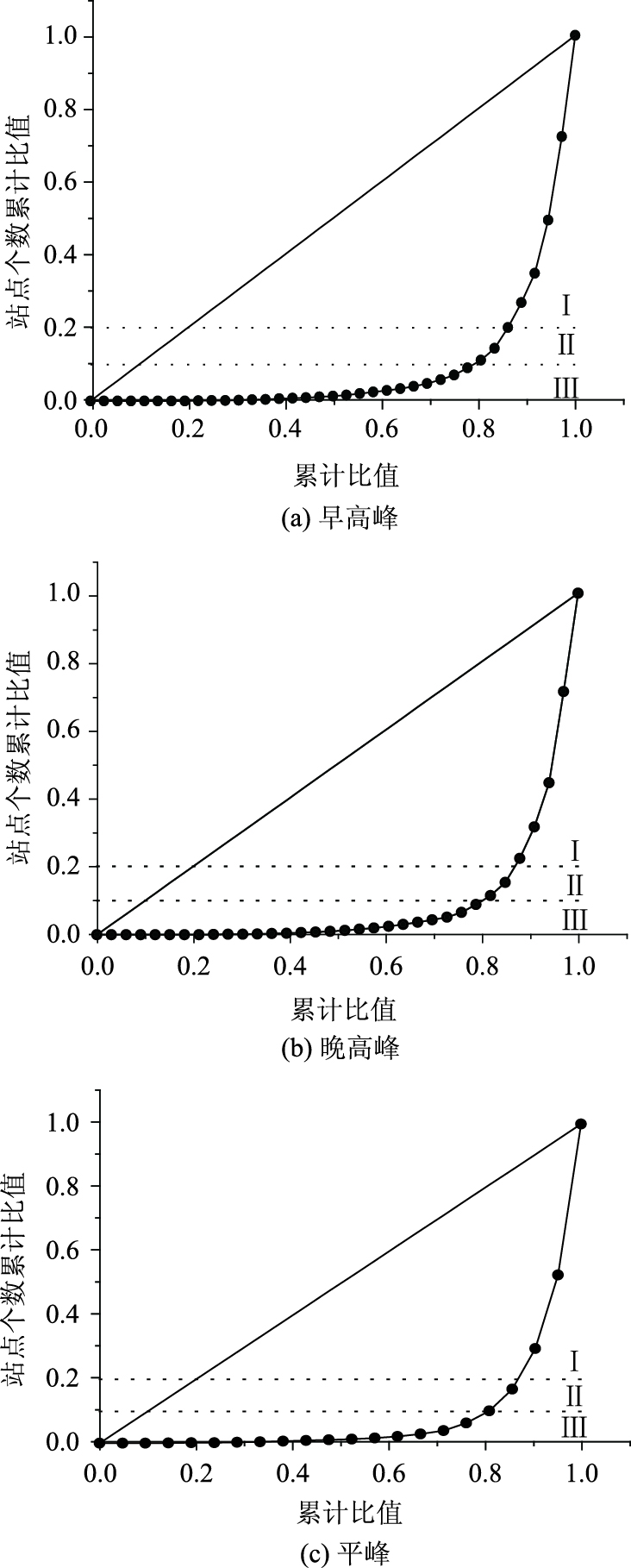
|
| 图 7 节点中心度值站点分布Lorenz图 Fig. 7 Lorenz curve of node centrality value station distribution |
| |
晚高峰时段公交网络节点中心度值范围为0.004~3.236,以0.1为步长将节点中心度值划分为33个区间,由图 7(b)可知公交站点节点中心度值主要分布在[0.4, 0.5),[0.3, 0.4),[0.2, 0.3),[0.1, 0.2)和[0, 0.1)这5个区间,各区间站点个数分别占总站点数的7.02%,9.22%,12.95%,26.71%和28.8%。
平峰时段公交网络节点中心度值范围为0.004~1.959,同样以0.1为步长将点度中心值分为21个区间,由图 7(c)可知公交站点节点中心度值主要分布在[0.2, 0.3),[0.1, 0.2)和[0, 0.1)这3个区间,各区间站点个数分别占总站点数的12.73%,23.04%和47.28%。
综上所述,对于整个区域公交网络而言,大多数公交站点节点中心度值分布在区间[0.2, 0.3),[0.1, 0.2)和[0, 0.1),平均值为0.265,对于相同排名的站点,节点中心度值大小在早高峰、晚高峰和平峰时段呈现明显的分布规律,排序顺序为:早高峰>晚高峰>平峰。
由表 4可知公交网络各时段节点中心度值排序靠前的站点主要分布在商业中心区域和城区边缘新规划区域,此类站点大多分布在商场、高校、政府机构附近,例如同时经过3个时段排名前10的公交站点有:世纪商城、青职学院、东新村东、保税港区西门等。
| 序号 | 站点编号 | 早高峰 | 晚高峰 | 平峰 | ||
| 1 | 319 | 保税港区西门 | 33 | 机关东办公中心 | 33 | 机关东办公中心 |
| 2 | 33 | 机关东办公中心 | 320 | 青职学院 | 341 | 西海岸汽车东站 |
| 3 | 341 | 世纪商城 | 341 | 世纪商城 | 319 | 保税港区西门 |
| 4 | 320 | 青职学院 | 319 | 保税港区西门 | 320 | 青职学院 |
| 5 | 4 | 西海岸医疗中心 | 321 | 武家庄 | 513 | 天目山农贸市场 |
| 6 | 10 | 北船职工公寓 | 51 | 东新村东 | 373 | 王家港 |
| 7 | 321 | 武家庄 | 373 | 王家港 | 328 | 城市桂冠 |
| 8 | 513 | 天目山农贸市场 | 10 | 北船职工公寓 | 51 | 东新村东 |
| 9 | 34 | 西海岸汽车东站 | 332 | 金海岸利群 | 192 | 琅琊台酒厂 |
| 10 | 329 | 丁家河 | 377 | 观海华庭 | 332 | 金海岸利群 |
3.2 区域公交网络站点失效绕行方案设计 3.2.1 绕行站点获取
(1) 失效站点获取
常见城市公共交通网络中地铁与公交站点重合区域大多为交通流量较大的区域,人为造成公交站点失效的常见原因为地铁站点施工,因此本研究在选择失效节点的过程中采用蓄意攻击方式,选择节点度值大的站点进行失效处理,如表 5所示。选取节点度值排名前10的站点作为研究对象,进行线路优化处理,验证模型的可靠性,对于节点度值相同的站点,选取编号较小的站点。
| 序号 | 失效站点编号 | 度值 | 站点名称 | 失效节点权重 | ||
| 早高峰 | 晚高峰 | 平峰 | ||||
| 1 | 50 | 17 | 西海岸汽车总站 | 0.372 2 | 0.358 3 | 0.483 2 |
| 2 | 42 | 13 | 灵山卫公交枢纽站 | 0.785 3 | 0.651 4 | 0.236 5 |
| 3 | 332 | 12 | 金海岸利群 | 1.335 3 | 1.206 1 | 0.701 1 |
| 4 | 33 | 11 | 机关东部办公中心 | 1.450 0 | 1.300 0 | 0.732 6 |
| 5 | 151 | 11 | 市民服务中心北 | 0.488 9 | 0.447 2 | 0.296 9 |
| 6 | 192 | 11 | 琅琊台酒厂 | 0.604 2 | 0.605 6 | 0.377 4 |
| 7 | 319 | 11 | 保税港区西门 | 1.350 0 | 1.226 9 | 0.676 1 |
| 8 | 377 | 11 | 观海华庭 | 0.771 4 | 0.641 3 | 0.676 1 |
| 9 | 551 | 11 | 王台汽车站 | 0.316 7 | 0.300 0 | 0.178 9 |
| 10 | 4 | 10 | 西海岸医疗中心 | 0.441 7 | 0.421 4 | 0.237 4 |
(2) 绕行前、后站点的获取
在确定绕行站点时需要先确定上行线路失效站点前一站点和后一站点的名称及距离,由于只选取一定范围内的公交站点,且公交站点间的距离较远,因此可选用百度地图进行粗略测距。
(3) 绕行站点获取
在确定绕行站点时需要先确定前后站点的名称及距离。以失效站点“西海岸汽车总站”公交站点为例,前后站点距离最近的两公交站点为“唐岛湾小区”和“家佳源”,两站点间直线距最小值为0.579 km,因此则有“西海岸汽车总站”的前一站点为“唐岛湾小区”,后一站点为“家佳源”。分别以前后站点为圆心,两站点间的直线距离为半径画圆选择绕行站点。绕行区域内有“西海岸汽车东站”和“西海岸汽车总站西”两个公交站点,其中“西海岸汽车东站”、“西海岸汽车总站西”到前后站点的直线距离分别为0.214,0.483 km和0.411,0.516 km,则两绕行站点到前后站点距离之和分别为0.697和0.927 km,“西海岸汽车东站”到两前后站点间的距离最小,因此失效站点为“西海岸汽车东站”。其余各失效节点前后站点及绕行站点编号、名称和绕行距离如表 6所示。失效节点的前后站点及绕行站点的编号和名称如表 7所示。
| 失效站点编号 | 绕行站点 | 前站 | 距离/km | 后站 | 距离/km | 总和/km |
| 50 | 西海岸汽车东站 | 唐岛湾小区 | 0.214 | 家佳源 | 0.483 | 0.697 |
| 西海岸汽车总站西 | 0.411 | 0.516 | 0.927 | |||
| 42 | 东方华庭北门 | 瑞海花园 | 0.473 | 东方华庭 | 0.379 | 0.852 |
| 西南村 | 0.806 | 0.294 | 1.100 | |||
| 332 | 爱心农贸市场 | 理工大学新校区 | 0.525 | 泽润金融广场 | 0.277 | 0.802 |
| 美国想象英语 | 0.370 | 0.512 | 0.882 | |||
| 33 | 武夷山市场 | 城市桂冠 | 0.422 | 丁家河 | 1.300 | 1.722 |
| 中治东方大厦 | 0.422 | 1.300 | 1.722 | |||
| 151 | 郝家石桥 | 喜鹊山路 | 0.761 | 金河丽城 | 0.265 | 1.026 |
| 人名医院东 | 0.777 | 0.527 | 1.304 | |||
| 医药公司 | 0.433 | 0.789 | 1.222 | |||
| 192 | 小哨头北 | 小哨头 | 0.493 | 飞宇路 | 0.451 | 0.944 |
| 琅琊台路南 | 0.366 | 0.284 | 0.650 | |||
| 世纪公寓 | 0.439 | 0.732 | 1.171 | |||
| 319 | 卓亭广场 | 五台山路新于家河 | 0.105 | 中国人保财险 | 0.285 | 0.390 |
| 377 | 黄海学院南 | 灵山卫地铁站 | 1.000 | 灵山卫枢纽站 | 0.856 | 1.856 |
| 551 | 同春公司 | 星火集团 | 0.523 | 王台大集 | 0.643 | 1.166 |
| 4 | 西海岸医疗中心北门 | 瑞智精密 | 0.304 | 齐长城 | 0.425 | 0.729 |
| 失效站点编号 | 前站 | 绕行站点 | 后站 | 编号 | ||||
| 名称 | 编号 | 名称 | 编号 | 名称 | ||||
| 50 | 唐岛湾小区 | 436 | 西海岸汽车东站 | 194 | 家佳源 | 370 | ||
| 42 | 瑞海花园 | 540 | 东方华庭北门 | 539 | 东方华庭 | 43 | ||
| 332 | 理工大学新校区 | 7 | 爱心农贸市场 | 515 | 泽润金融广场 | 334 | ||
| 33 | 城市桂冠 | 328 | 武夷山市场 | 327 | 丁家河 | 329 | ||
| 151 | 喜鹊山路 | 150 | 郝家石桥 | 982 | 金河丽城 | 152 | ||
| 192 | 小哨头 | 175 | 琅琊台路南 | 872 | 飞宇路 | 873 | ||
| 319 | 五台山路新于家河 | 475 | 卓亭广场 | 318 | 中国人保财险 | 324 | ||
| 377 | 灵山卫地铁站 | 1 745 | 黄海学院南 | 841 | 灵山卫枢纽站 | 42 | ||
| 551 | 星火集团 | 549 | 同春路 | 673 | 王台大集 | 548 | ||
| 4 | 瑞智精密 | 429 | 西海岸医疗中心北门 | 657 | 齐长城 | 430 | ||
3.2.2 绕行后指标计算
在计算绕行后公交网络最短路径长度和网络全局效率之前,首先获得优化后公交网络拓扑连边权重。若原网络中节点j与前后站点i-1或i+1存在连边,则优化后的站点j与站点i-1或i+1存在连边,优化后网络绕行站点与连边的权重值为h′j, i+1= 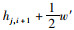
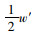
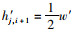
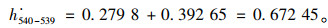
|
(19) |
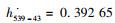
| 序号 | 绕行后连边权重 | 绕行后连边权重 | |||||||
| 连边 | 早 | 晚 | 平 | 连边 | 早 | 晚 | 平 | ||
| 1 | 436-194 | 0.181 60 | 0.179 15 | 0.241 60 | 194-370 | 0.181 60 | 0.179 15 | 0.241 60 | |
| 2 | 540-539 | 0.672 45 | 0.551 20 | 0.259 25 | 539-43 | 0.392 65 | 0.325 70 | 0.118 25 | |
| 3 | 7-515 | 0.667 65 | 0.603 05 | 0.350 55 | 515-334 | 0.667 65 | 0.603 05 | 0.350 55 | |
| 4 | 328-327 | 1.391 70 | 1.216 70 | 0.674 60 | 327-329 | 0.725 00 | 0.650 00 | 0.366 30 | |
| 5 | 150-982 | 0.244 45 | 0.223 60 | 0.148 45 | 982-152 | 0.244 45 | 0.223 60 | 0.148 45 | |
| 6 | 175-872 | 0.302 10 | 0.302 80 | 0.188 70 | 872-873 | 0.352 10 | 0.312 80 | 0.205 40 | |
| 7 | 475-318 | 0.675 00 | 0.613 45 | 0.338 05 | 318-324 | 0.675 00 | 0.613 45 | 0.338 05 | |
| 8 | 1745-841 | 0.385 70 | 0.320 65 | 0.338 05 | 841-42 | 0.485 70 | 0.403 98 | 0.383 50 | |
| 9 | 549-673 | 0.158 35 | 0.150 00 | 0.089 45 | 673-548 | 0.158 35 | 0.150 00 | 0.089 45 | |
| 10 | 429-675 | 0.220 85 | 0.210 70 | 0.118 70 | 657-430 | 0.220 85 | 0.210 70 | 0.118 70 | |
公式(11)、公式(12)和公式(14)计算求得绕行站点连边权重,如表 9所示。
| 序号 | 早高峰节点权重 | 晚高峰节点权重 | 平峰节点权重 | |||||
| 绕行前 | 绕行后 | 绕行前 | 绕行后 | 绕行前 | 绕行后 | |||
| 1 | 0.412 5 | 0.784 7 | 0.355 6 | 0.713 9 | 0.355 6 | 0.740 8 | ||
| 2 | 0.363 1 | 1.148 4 | 0.281 0 | 0.932 4 | 0.281 0 | 0.390 0 | ||
| 3 | 0.208 3 | 1.543 6 | 0.166 7 | 1.372 8 | 0.166 7 | 0.796 6 | ||
| 4 | 1.416 7 | 2.866 7 | 1.266 7 | 2.566 7 | 1.266 7 | 1.490 9 | ||
| 5 | 0.438 0 | 0.926 9 | 0.366 7 | 0.813 9 | 0.366 7 | 0.540 9 | ||
| 6 | 0.116 7 | 0.720 9 | 0.116 7 | 0.722 3 | 0.116 7 | 0.460 7 | ||
| 7 | 1.583 3 | 2.933 3 | 1.426 9 | 2.653 8 | 1.426 9 | 1.454 1 | ||
| 8 | 0.193 6 | 0.965 | 0.179 2 | 0.820 5 | 0.179 2 | 0.773 4 | ||
| 9 | 0.366 7 | 0.683 4 | 0.328 1 | 0.628 1 | 0.328 1 | 0.393 1 | ||
| 10 | 0.250 0 | 0.691 7 | 0.200 0 | 0.621 4 | 0.200 0 | 0.337 4 | ||
计算结果如表 10和表 11所示。表 10中与绕行前相比,早高峰、晚高峰和平峰时段绕行后公交网络平均最短路径长度均变小,表明绕行后公交网络越紧密,网络性能提升。
| 序号 | 失效编号 | 绕行编号 | 早高峰 | 晚高峰 | 平峰 | |||||
| 绕行前 | 绕行后 | 绕行前 | 绕行后 | 绕行前 | 绕行后 | |||||
| 1 | 50 | 194 | 13.729 08 | 13.650 53 | 13.727 45 | 13.648 99 | 13.792 91 | 13.649 00 | ||
| 2 | 42 | 539 | 13.730 42 | 13.710 21 | 13.729 33 | 13.714 33 | 13.729 33 | 13.699 45 | ||
| 3 | 332 | 515 | 13.559 23 | 13.452 45 | 13.559 23 | 13.498 72 | 13.559 23 | 13.544 49 | ||
| 4 | 33 | 327 | 13.634 73 | 13.589 72 | 13.634 72 | 13.453 45 | 13.634 73 | 13.579 24 | ||
| 5 | 151 | 982 | 13.545 86 | 13.445 24 | 13.545 85 | 13.528 93 | 13.545 86 | 13.476 82 | ||
| 6 | 192 | 872 | 13.557 49 | 13.547 99 | 13.557 48 | 13.444 78 | 13.557 49 | 13.498 72 | ||
| 7 | 319 | 318 | 13.605 72 | 13.443 21 | 13.605 71 | 13.554 32 | 13.605 72 | 13.600 12 | ||
| 8 | 377 | 841 | 13.547 89 | 13.512 14 | 13.547 89 | 13.459 01 | 13.547 89 | 13.423 87 | ||
| 9 | 551 | 673 | 13.534 44 | 13.444 21 | 13.601 82 | 13.598 87 | 13.601 82 | 13.577 82 | ||
| 10 | 4 | 657 | 13.547 83 | 13.541 12 | 13.547 83 | 13.478 91 | 13.547 83 | 13.489 21 | ||
| 序号 | 失效编号 | 绕行编号 | 早高峰 | 晚高峰 | 平峰 | |||||
| 绕行前 | 绕行后 | 绕行前 | 绕行后 | 绕行前 | 绕行后 | |||||
| 1 | 50 | 194 | 3.419 2 | 3.419 3 | 1.774 6 | 1.776 7 | 3.610 2 | 3.610 1 | ||
| 2 | 42 | 539 | 3.521 1 | 3.529 8 | 1.751 2 | 1.752 4 | 3.521 7 | 3.597 8 | ||
| 3 | 332 | 515 | 1.585 0 | 1.587 3 | 1.585 0 | 1.585 5 | 3.543 7 | 3.548 0 | ||
| 4 | 33 | 327 | 1.536 2 | 1.536 3 | 1.536 2 | 1.536 3 | 3.452 2 | 3.453 0 | ||
| 5 | 151 | 982 | 1.585 9 | 1.586 1 | 1.789 4 | 1.790 0 | 3.518 2 | 3.519 4 | ||
| 6 | 192 | 872 | 1.594 4 | 1.600 2 | 1.784 4 | 1.784 9 | 3.595 0 | 3.595 1 | ||
| 7 | 319 | 318 | 1.583 6 | 1.583 7 | 1.775 9 | 1.776 2 | 3.564 4 | 3.564 7 | ||
| 8 | 377 | 841 | 1.604 1 | 1.605 2 | 1.795 6 | 1.796 5 | 1.795 6 | 1.796 0 | ||
| 9 | 551 | 673 | 1.606 9 | 1.607 2 | 1.760 3 | 1.760 5 | 3.539 5 | 3.539 8 | ||
| 10 | 4 | 657 | 1.604 1 | 1.605 3 | 1.797 3 | 1.797 4 | 3.592 1 | 3.592 4 | ||
如表 11所示,除平峰时段编号为50的站点“西海岸汽车总站”,绕行前后公交网络全局效率均为3.610 2无变化之外,其余绕行站点在早高峰、晚高峰和平峰时段公交网络全局效率均提高。这是由于“西海岸汽车总站”站点失效后绕行节点为“西海岸汽车东站”,由表 4可知“西海岸汽车东站”在平峰时段为节点中心度值排名前3站的关键站点,交通负荷较大,“西海岸汽车总站”站点失效后站点权重分配到“西海岸汽车东站”,使得这一站点权重大幅度增加,因而网络效率没有提升。进一步研究中选择到前后两站点距离次小的“西海岸汽车总站”作为新的绕行站点,绕行后平均最短路径长度由13.792 91变为13.700 89,网络全局效率由3.610 2变为3.610 3数值在增大,绕行方案可行。
4 结论本研究以青岛市某区域公交网络为例,结合ABC管理法,构建了基于Lorezen曲线的公交网络拓扑特性指标分析模型,并在拓扑特性指标研究的基础上设计了公交网络优化方案。通过对节点度,2阶节点度、中心性等指标的分析,得出该区公交网络具有明显的小世界性,各时段对于相同排名的站点,节点中心度值大小为早高峰>晚高峰>平峰;选取节点度值排名前10的公交站点作为失效站点,研究绕行方案的可靠性,研究结果表明设计的优化方案可以有效提高公交网络的连通性。
| [1] |
李英, 周伟, 郭世进. 上海公共交通网络复杂性分析[J]. 系统工程, 2007, 25(1): 38-41. LI Ying, ZHOU Wei, GUO Shi-jin. An Analysis of Complexity of Public Transportation Network in Shanghai[J]. Systems Engineering, 2007, 25(1): 38-41. |
| [2] |
张琳, 傅白白, 殷增超. 城市公交网络拓扑特性与鲁棒性实证研究[J]. 山东建筑大学学报, 2015, 30(3): 243-248. ZHANG Lin, FU Bai-bai, YIN Zeng-chao. Empirical Research on Topological Properties and Robustness of Urban Public Transit Network[J]. Journal of Shandong Jianzhu University, 2015, 30(3): 243-248. |
| [3] |
高红艳, 刘飞, 钱郁. 公共交通网络的复杂性及其优化:以宝鸡市为例[J]. 长安大学学报:自然科学版, 2018, 38(5): 146-153, 181. GAO Hong-yan, LIU Fei, QIAN Yu. Complexity and Optimization of Public Transit Network:Taking Baoji for Example[J]. Journal of Chang'an University:Natural Science Edition, 2018, 38(5): 146-153, 181. |
| [4] |
冯慧芳, 李彩虹, 王瑞. 河谷型城市公交网络脆弱性研究:以兰州市为例[J]. 交通运输系统工程与信息, 2016, 16(1): 217-222. FENG Hui-fang, LI Cai-hong, WANG Rui. Vulnerability Study for Public Transport Network of Valley City:Case of Lanzhou[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(1): 217-222. |
| [5] |
刘锐, 严宝杰, 黄志鹏. 公共交通的局域世界演化网络模型[J]. 公路交通科技, 2010, 27(3): 108-113. LIU Rui, YAN Bao-jie, HUANG Zhi-peng. Local-world Evolving Network Model for Public Transport[J]. Journal of Highway and Transportation Research and Development, 2010, 27(3): 108-113. |
| [6] |
赵国锋, 苑少伟, 慈玉生. 城市路网的复杂网络特性和鲁棒性研究[J]. 公路交通科技, 2016, 33(1): 119-124, 146. ZHAO Guo-feng, YUAN Shao-wei, CI Yu-sheng. Analysis of Complex Network Property and Robustness of Urban Road Network[J]. Journal of Highway and Transportation Research and Development, 2016, 33(1): 119-124, 146. |
| [7] |
罗艺, 钱大琳. 公交-地铁复合网络构建及网络特性分析[J]. 交通运输系统工程与信息, 2015, 15(5): 39-44. LUO Yi, QIAN Da-lin. Construction of Subway and Bus Transport Networks and Analysis of the Network Topology Characteristics[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(5): 39-44. |
| [8] |
LI X H, GUO J Y, GAO C, et al. Network-based Transportation System Analysis:A Case Study in a Mountain City[J]. Chaos, Solitons & Fractals, 2018, 107: 256-265. |
| [9] |
朱中华. 重庆公交线路复杂网络性质研究[J]. 科技创新与应用, 2014(14): 57. ZHU Zhong-hua. Study on Nature of Complex Network of Bus Lines in Chongqing[J]. Technology Innovation and Application, 2014(14): 57. |
| [10] |
朱中华, 杨德刚. 公交系统复杂网络抗毁性分析:以重庆市公交换乘网络为例[J]. 重庆师范大学学报:自然科学版, 2014, 31(1): 89-93. ZHU Zhong-hua, YANG De-gang. Analysis of Survivability of the Bus Complex Network in Chongqing[J]. Journal of Chongqing Normal University:Natural Science Edition, 2014, 31(1): 89-93. |
| [11] |
YANG Y H, LIU Y X, ZHOU M X, et al. Robustness Assessment of Urban Rail Transit Based on Complex Network Theory:A Case Study of the Beijing Subway[J]. Safety Science, 2015, 79: 149-162. |
| [12] |
WANG X G, KOU Y, DERRIBLE S, et al. Multi-criteria Robustness Analysis of Metro Networks[J]. Physica A:Statistical Mechanics and Its Applications, 2017, 474(10): 19-31. |
| [13] |
彭景新.南京市区公交、地铁加权复合网络建模与实证分析[D].南京: 南京邮电大学, 2017. PENG Jing-xin. Modeling and Empirical Analysis of Bus and Subway Weighted Composite Network in Nanjing[D]. Nanjing: Nanjing University of Posts and Telecommunications, 2017. |
| [14] |
强添纲, 赵明明, 裴玉龙. 城市多模式交通网络的复杂网络特性与鲁棒性研究[J]. 交通信息与安全, 2019, 37(1): 65-71. QIANG Tian-gang, ZHAO Ming-ming, PEI Yu-long. An Analysis of Characteristics of Complex Network and Robustness in Harbin Multi-mode Traffic Network[J]. Journal of Transport Information and Safety, 2019, 37(1): 65-71. |
| [15] |
吕文红, 王国娟, 王鹏飞. 协同共享视角下城市交通治理的伦理途径[J]. 昆明理工大学学报:社会科学版, 2017, 17(6): 42-46. LÜ Wen-hong, WANG Guo-juan, WANG Peng-fei. Ethical Approach to Urban Traffic Governance from the Perspective of Collaborative Commons[J]. Journal of Kunming University of Science and Technology:Social Science Edition, 2017, 17(6): 42-46. |
| [16] |
吕文红, 王国娟, 王鹏飞. 基于复杂网络的交通运输网络可靠性研究进展[J]. 科学技术与工程, 2019, 19(24): 26-33. LÜ Wen-hong, WANG Guo-juan, WANG Peng-fei. A Review on Reliability of Transportation Network Based on Complex Network Theory[J]. Science Technology and Engineering, 2019, 19(24): 26-33. |
| [17] |
黄一洲. Lorenz曲线在反恐情报分析中的应用研究:以中国及周边国家的恐怖袭击分析为例[J]. 净月学刊, 2017(6): 87-95. HUANG Yi-zhou. Application of Lorenz Curve in Counter Terrorism Intelligence Analysis:A Case Study of Terrorist Attacks in China and Neighboring Countries[J]. Jingyue Journal, 2017(6): 87-95. |
| [18] |
王东方.城市公交复杂网络的节点重要性及稳定性研究[D].西安: 长安大学, 2018. WANG Dong-fang. Study on Nodes' Importance and Stability of Urban Public Transport Complex Networks[D]. Xi'an: Chang'an University, 2018. |
| [19] |
黄光球, 谢蓉. 考虑节点过载的碳排放空间关联系统级联失效模型[J]. 计算机应用, 2019, 39(6): 1829-1835. HUANG Guang-qiu, XIE Rong. Cascading Failure Model of Carbon Emission Spatial Correlation System Considering Load Overload[J]. Journal of Computer Applications, 2019, 39(6): 1829-1835. |
| [20] |
傅杰, 邹艳丽, 谢蓉. 基于复杂网络理论的电力网络关键线路识别[J]. 复杂系统与复杂性科学, 2017, 14(3): 91-96. FU Jie, ZOU Yan-li, XIE Rong. The Critical Lines Identification of the Power Grids Based on the Complex Network Theory[J]. Complex Systems and Complexity Science, 2017, 14(3): 91-96. |
| [21] |
青岛市统计局.青岛市2018年国民经济和社会发展统计公报[EB/OL]. (2019-03-19)[2019-05-10]. http://qdtj.qingdao.gov.cn/n28356045/n32561056/n32561072/190319133354050380.html. Qingdao Municipal Bureau of Statistics. Qingdao Municipal Statistical Bulletin of National Economic and Social Development in 2018[EB/OL]. (2019-03-19)[2019-05-10]. http://qdtj.qingdao.gov.cn/n28356045/n32561056/n32561072/190319133354050380.html. |
 2020, Vol. 37
2020, Vol. 37
