扩展功能
文章信息
- 曹堉, 王成, 杨岳铭, 徐江涛
- CAO Yu, WANG Cheng, YANG Yue-ming, XU Jiang-tao
- 基于贝叶斯网络的城市道路交通拥堵多原因自动实时识别
- Multi-cause Automatic Real-time Recognition of Urban Road Traffic Congestion Based on Bayesian Network
- 公路交通科技, 2020, 37(11): 89-97
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 89-97
- 10.3969/j.issn.1002-0268.2020.11.012
-
文章历史
- 收稿日期: 2019-12-24
目前,在交通拥堵的问题中多从两个方面研究:(1)判断识别某道路是否发生拥堵。例如:李宇轩等[1]利用支持向量机构建了对拥堵状态和非拥堵状态识别的分类器;李桂毅等[2]通过分析管制扇区交通时空拥挤特征,基于雷达航迹数据建立了多扇区交通拥挤识别模型。(2)拥堵发生后采取措施的有效性[3-4]。而这两个问题的连接处即寻找发生交通拥堵的具体原因对于解决交通拥堵也至关重要。在此问题中,安萌等[5]从路网结构出发,分析了重庆市路网系统的特征和缺陷,延伸到对重庆市路网格局下特有的节点型拥堵进行成因和特征分析,但该分析是城市级宏观静态的,无法落实到具体的某条城市道路。王潇[6]基于故障树理论建立了城市交通拥堵致因分析模型。Wang等[7]根据M/M/1的排队模型,测量平均到达率、平均服务率和队列长度等参数,在此基础上根据各交叉口的繁忙率和空闲率分析了道路交通拥堵的原因,没有进行自动实时识别。
目前对于拥堵原因的分析识别研究中,遇到拥堵情况后多凭当时的具体情况及道理信息以主观经验分析拥堵原因,自动化程度低、主观性强、实时性差。而道路的拥堵原因是动态实时、复杂多变的。人工进行主观判断费时、费力、效率不高,延长了拥堵的持续时间,因此根据道路工作状态下交通可观测变量对交通拥堵原因进行自动实时识别就尤为必要。
本研究将贝叶斯网络引入城市道路交通拥堵的原因识别中,提出了一种基于贝叶斯网络的城市道路交通拥堵多原因自动实时识别方法。贝叶斯网络通过图形化的方法来表示,克服了基于规则的系统所具有的概念上和计算上的许多困难,并且擅长描述学习变量间的因果关系,能够充分利用领域知识和样本数据的信息,在交通拥堵的判别[8]、交通事故的自动识别[9-10]等方面的运用上效果显著。本研究运用贝叶斯网络, 首先对城市道路交通的动态可观测变量和多个拥堵原因之间的关系进行系统的机理分析和仿真验证,从而构建贝叶斯网络结构,再以获取的实测历史数据进行参数学习训练,得到完整的贝叶斯网络模型。最后,将该道路工作状态下的交通可观测变量输入该贝叶斯网络模型,就能同时自动实时识别出交通拥堵的多个原因。
1 基于贝叶斯网络的城市道路交通拥堵原因识别模型的构建 1.1 城市道路交通拥堵多原因识别问题的形式化描述问题模型:道路的交通拥堵多原因识别是要根据研究区域范围内有关的城市道路交通状态可观测变量{a1, a2, a3, …, an},判断出交通拥堵原因的0-1离散类型{c1, c2, c3, …, cm}。该问题的难点在于:城市道路交通状态可观测变量{a1, a2, a3, …, an}与交通拥堵原因的离散类型{c1, c2, c3, …, cm}之间存在复杂的因果关系,1个城市道路交通拥堵的原因发生会引发多个城市道路交通状态可观测变量值的变化;同时,1个城市道路交通状态可观测变量值的变化,可能是多个城市道路交通拥堵的原因共同发生作用后的结果。且多个交通拥堵原因可以单独发生,也可以同时发生。
但对于该道路,已经采集了一些历史数据作为辅助数据集,拟将交通状态可观测变量{a1, a2, a3, …, an}的历史数据{a1h, a2h, a3h, …, anh}作为输入,拥堵原因的离散类型{c1, c2, c3, …, cm}的历史数据{c1h, c2h, c3h, …, cmh}作为输出,训练得到城市道路交通拥堵原因识别预测模型。然后应用在工况下,将工况下交通状态可观测变量{a1w, a2w, a3w, …, anw}作为输入,输入到城市道路交通拥堵原因识别的预测模型中,模型的输出{ 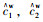
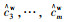
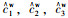
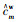
值得注意的是,由于交通拥堵原因{c1, c2, c3, …, cm}是0-1型离散类型,多个交通拥堵原因可以单独发生,也可以同时发生。因此,该问题转化为一个数据驱动的多分类问题。
1.2 道路拥堵原因类型城市道路交通系统是由人、车、路、环境4个部分组成。其中车辆作为道路上的主要交通工具,因此是交通拥堵的关键因素。行人作为交通的主要参与者,其行为也对城市道路交通产生重大影响。道路和环境对道路使用者有着直接的影响[11]。系统的各个部分都与交通拥堵紧密相关。
但由于固定的因素状态无法通过数据变化来反映,所以本研究只考虑非固定因素,即不考虑道路缺陷。另外,考虑到模型可用性和数据的可获得性,因此对于交通环境因素仅考虑信号配时不合理和停车占道现象,对其他问题,如天气情况及交通事故因素,由于数据缺乏可靠来源,难以获取,因此本研究模型中暂不考虑。
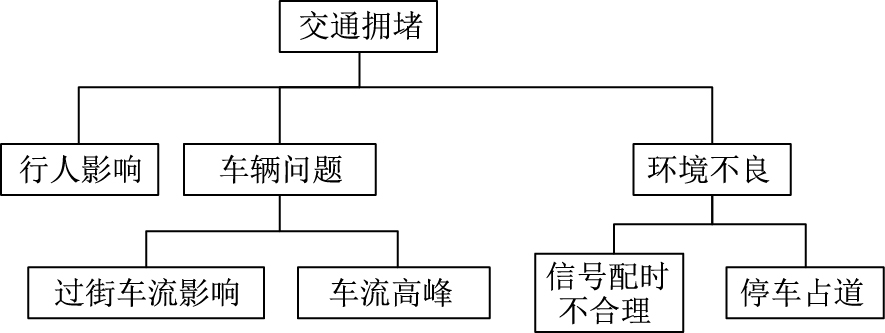
同时,对交通拥堵原因节点进行调整,将车辆问题向下细化变为过街车流影响、车流高峰2个类别。因此,重点研究行人影响、过街车流影响、车流高峰、信号配时不合理及停车占道这5个原因类型(如图 1所示)。需要注意的是,交通拥堵发生时,5种原因类型相互独立,可能有1种或多种原因类型同时发生。
|
| 图 1 调整后的交通拥堵原因类别 Fig. 1 Adjusted traffic congestion cause categories |
| |
1.3 可观测交通状态变量
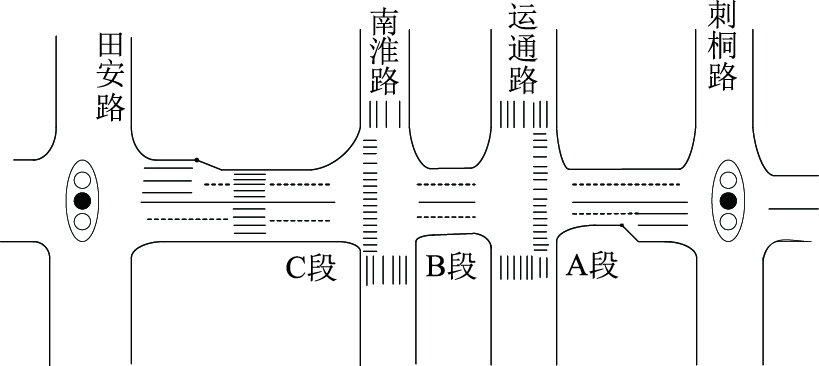
针对本研究的5个原因类型,参考福建省泉州市泉秀街(刺桐路至田安路方向)的路段情况,将部分道路分为A, B, C 3段,其道路结构如图 2所示。根据道路监控视频,路段上可观测的交通状态变量见表 1。为了满足建模要求,需要将连续变量处理为离散变量,各变量的设置同见表 1。
|
| 图 2 泉秀街道路结构示意图 Fig. 2 Schematic diagram of road structure of Quanxiu Street |
| |
| 变量 | 符号 | 变量取值 |
| A段停车让行次数 | a1 | 1. [0, 4]; 2: (4, 6]; 3. (6, 8]; 4. (8, +∞) |
| B段停车让行次数 | a2 | 1. [0, 4]; 2. (4, 6]; 3. (6, 8]; 4. (8, +∞) |
| C段停车让行次数 | a3 | 1. [0, 4]; 2. (4, 6]; 3. (6, 8]; 4. (8, +∞) |
| 左转车流二次排队 | a4 | 1.存在; 2.不存在 |
| 直行车流二次排队 | a5 | 1.存在; 2.不存在 |
| A段第1车道车流量 | a6 | 1. [0, 40); 2. [40, 50); 3. [50, +∞) |
| A段第2车道车流量 | a7 | 1. [0, 30); 2. [30, 40); 3. [40, +∞) |
| B段第1车道车流量 | a8 | 1. [0, 35); 2. [35, 45); 3. [45, +∞) |
| B段第2车道车流量 | a9 | 1. [0, 30); 2. [30, 40); 3. [40, +∞) |
| C段第1车道车流量 | a10 | 1. [0, 35); 2. [35, 45); 3. [45, +∞) |
| C段第2车道车流量 | a11 | 1. [0, 25); 2. [25, 35); 3. [35, +∞) |
| A段人行横道流量 | a12 | 1. [0, 50); 2. [50, 70); 3. [70, +∞) |
| B段人行横道流量 | a13 | 1. [0, 115); 2. [115, 140); 3. [140, +∞) |
| C段人行横道流量 | a14 | 1. [0, 100); 2. [100, 120); 3. [120, +∞) |
| 运通路通过车流量 | a15 | 1. [0, 7]; 2. (7, 10]; 3. (10, 13]; 4. (13, +∞) |
| 南淮路通过车流量 | a16 | 1. [0, 7]; 2. (7, 10]; 3. (10, 13]; 4. (13, +∞) |
| 左转流入车流量 | a17 | 1. [0, 20]; 2. (20, 30]; 3. (30, +∞) |
| 右转流入车流量 | a18 | 1. [0, 10]; 2. (10, 20]; 3. (20, +∞) |
| 直行流入车流量 | a19 | 1. [0, 30]; 2. (30, 40]; 3. (40, +∞) |
| 左转流出车流量 | a20 | 1. [0, 20]; 2. (20, 30]; 3. (30, +∞) |
| 直行流出车流量 | a21 | 1. [0, 20]; 2. (20, 30]; 3. (30, +∞) |
| A段两车道流量差 | a22 | 1. [0, 15]; 2. (15, 20]; 3. (20, +∞) |
| B段两车道流量差 | a23 | 1. [0, 10]; 2. (10, 15]; 3. (15, +∞) |
| C段两车道流量差 | a24 | 1. [0, 15]; 2. (15, 20]; 3. (20, +∞) |
1.4 贝叶斯网络构建
构建贝叶斯网络的过程分为结构学习和参数学习两个步骤。结构学习主要是确定贝叶斯网络的节点和节点间的链接关系,从而获得贝叶斯网络结构。贝叶斯网络结构构建有两种方法:(1)通过对样本数据的学习,使用结构学习算法自动得到贝叶斯网络结构[12];(2)根据专家知识确定贝叶斯网络的变量节点及变量间的依赖关系。第1种方法需要有足够的样本数据为前提,而第2种方法在相关专业知识比较重要、变量间关系明显、缺少数据的情况下非常有效[13]。所以通过专家知识事先确定,而不使用贝叶斯结构学习得到的贝叶斯网络结构,只是通过样本进行参数学习,可大大降低对训练样本的要求。可见第2种方法更加适用于本研究建立交通拥堵原因识别的贝叶斯网络。
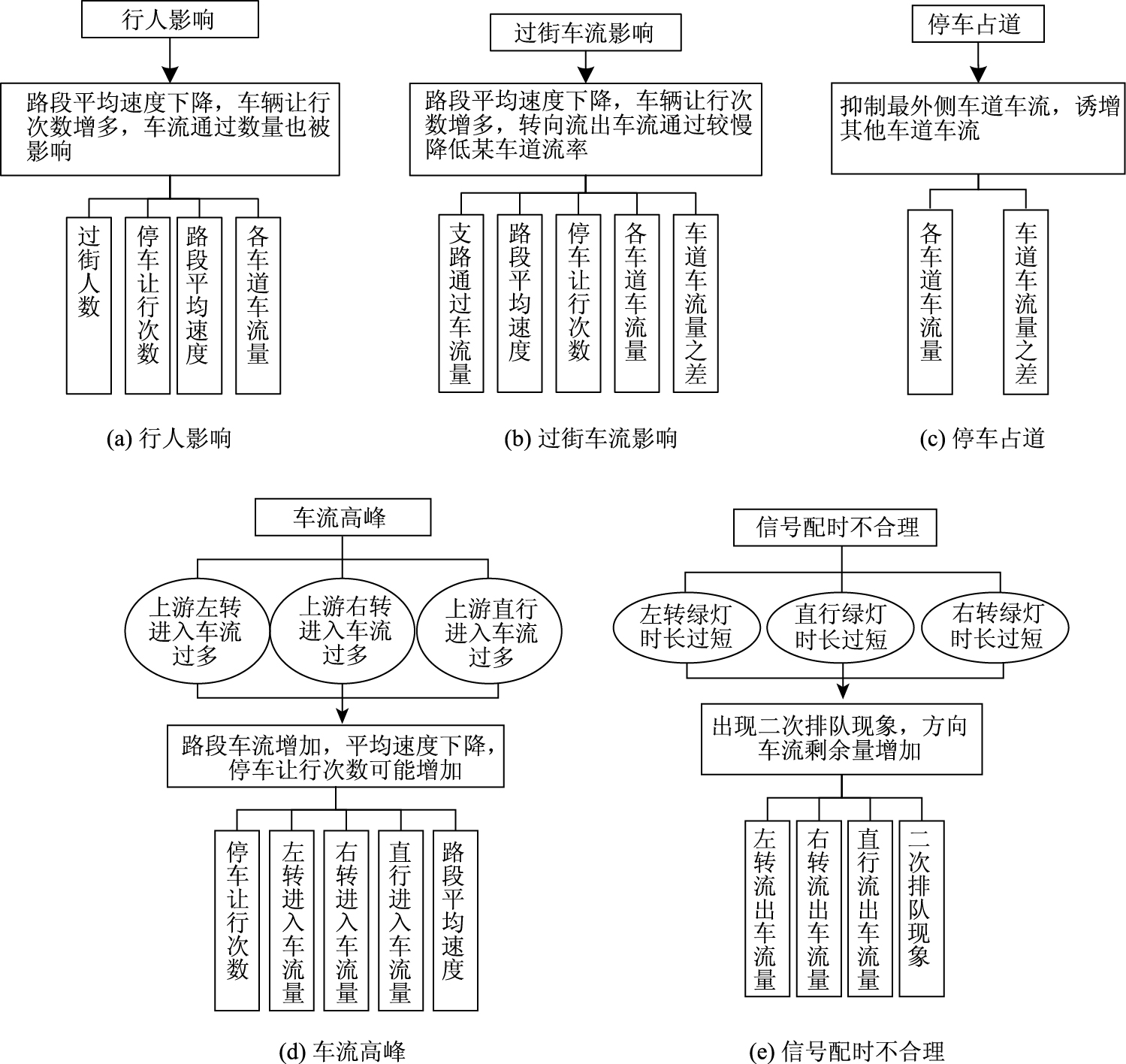
1.4.1 确定网络结构对本研究的5种拥堵类型进行详细分析,贝叶斯网络在解决这类问题上有着较突出的优点。行人影响主要指行人分散过街情况,分散过街次数增加理论上造成停车让行次数增多[14]、路段的平均速度下降及单位时间内的车流通过数量降低[15]。车流高峰主要表现为单位时间内路段的进入车流过多,造成车速下降,同时也可能会因为更加密集的车流使得让行次数也增加[16]。停车占道(路边停车)则会造成该车道后续车流停车等待或变换车道行驶,在单位时间内最外侧车道通过车流下降,其他车道车流增多,车道流量差明显变化[17]。信号配时不合理主要是某方向上绿灯时间过长导致该方向已无车通过,而其他方向车流排队时长过长或某方向上绿灯过短,造成该方向上还存在过多的剩余车流量未流出即车辆二次排队现象严重[18]。而车道流量之差在不同方向车流就存在一定的差值,并且通过固定的绿灯放行时间难以较好地显示信号配时不合理问题,主要以剩余排队车流和方向上的流出量来反映。过街车流的增多造成的影响与行人影响类似[19],但本研究的“过街车流”不仅包括从与主路相交的支路流出的车流,还包括从主路转向支路的车流,因此若主路左右转车辆流出受阻也会降低单位时间内的车流通过数量。根据以上系统的理论分析得出的节点关系结构如图 3所示。
|
| 图 3 节点影响关系及数据类型 Fig. 3 Node influence relationships and data types |
| |
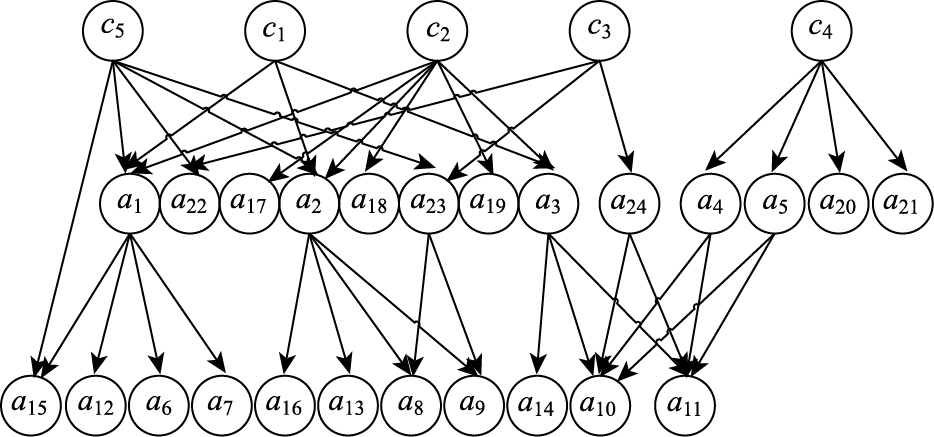
由于实际上引发一次拥堵的原因可能是单个也可能是多个,因此分别单列原因类型节点。本模型的网络结构搭建基于专家知识,根据图 3的分析结果及表 1中所示变量,以变量作为贝叶斯网络的节点用符号表示,相互间的影响关系为连接线,构建如图 4所示的贝叶斯网络结构。根据道路的实际情况和监控视频,可以观测并统计出表 1中的数据。由于视频无法得到速度信息,本试验暂不考虑速度变量。其中,c1至c5分别代表行人影响、车流高峰、停车占道、信号配时不合理和过街车流影响5种原因类型。需要注意的是,交通拥堵发生时,5种原因类型相互独立,可能有1种或者多种原因类型同时发生。
|
| 图 4 交通拥堵原因识别贝叶斯网络结构 Fig. 4 Bayesian network structure for traffic congestion cause recognition |
| |
1.4.2 确定网络参数
对于该道路,已经采集了一些历史数据作为辅助数据集,在确定贝叶斯网络结构后,可以利用辅助数据集进行贝叶斯网络的参数学习。参数学习方法主要有贝叶斯方法、极大似然估计方法,在此不多论述其原理。在进行结构构建和参数学习后,一个完整的贝叶斯网络就构建完成,并可应用到城市道路交通拥堵原因识别的预测中。
2 应用实例的试验验证 2.1 应用对象和数据说明应用对象为福建省泉州市泉秀街,其示意图如图 2所示。原始数据取自2019年2月25日至3月3日每天17:40—19:30晚高峰的监控视频(此期间无特殊天气及交通事故情况)。数据以每5 min间隔统计1次,每条数据包含表 1中的所有变量和专家手工标注的道路拥堵原因类型,排除由于原始视频出现问题导致的数据缺失和无交通拥堵发生情况,可得154条有效数据。
2.2 拥堵原因识别准确率评价指标采用n折交叉验证重复n次试验,选取平均值来表征平均识别准确率,对模型预测准确度进行检验。拥堵原因识别准确率为:
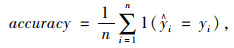
|
(1) |
式中,n为试验次数;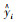
本试验运用MATLAB里的FullBNT-1.0.4工具箱,将各节点及节点关系网络构建完毕后,将各节点的先验分布取Dirichlet分布,采用贝叶斯方法进行参数学习[10]。根据实际采集的数据更新其条件概率表直至数据全部使用完毕,得到参数学习结果。采用工具箱中联结树推理引擎,用所输入的证据求解后验概率,获得最大可能解释。
本研究采用BPNN(反向传播神经网络)、ML-KNN(多标签k近邻算法)及多标签岭回归作为对比试验,其中BPNN隐含层节点设置为13个,最大训练次数设置为300次,最多验证失败次数设置为50次,ML-KNN最近邻为15个,多标签岭回归正则化系数0.01。
2.4 贝叶斯网络结构的试验结果和分析 2.4.1 网络结构模型验证试验结果在与交通拥堵有关的各个因素影响下,本模型的参数学习部分结果见表 2。
| 节点 | 取值 | 父节点 | 取值 | 概率 |
| c1 | 1 | — | — | 0.421 6 |
| 2 | — | — | 0.578 4 | |
| c2 | 1 | — | — | 0.696 1 |
| 2 | — | — | 0.303 9 | |
| c3 | 1 | — | — | 0.101 3 |
| 2 | — | — | 0.898 7 | |
| c4 | 1 | — | — | 0.238 6 |
| 2 | — | — | 0.761 4 | |
| c5 | 1 | — | — | 0.343 1 |
| 2 | — | — | 0.656 9 | |
| a22 | 1 | c5, c3 | 1, 1 | 0.490 2 |
| 1 | 1, 2 | 0.718 5 | ||
| 1 | 2, 1 | 0.333 3 | ||
| 1 | 2, 2 | 0.803 1 | ||
| 2 | 1, 1 | 0.019 6 | ||
| 2 | 1, 2 | 0.185 2 | ||
| 2 | 2, 1 | 0.250 4 | ||
| 2 | 2, 2 | 0.146 6 | ||
| 3 | 1, 1 | 0.490 2 | ||
| 3 | 1, 2 | 0.096 3 | ||
| 3 | 2, 1 | 0.416 2 | ||
| 3 | 2, 2 | 0.023 3 |
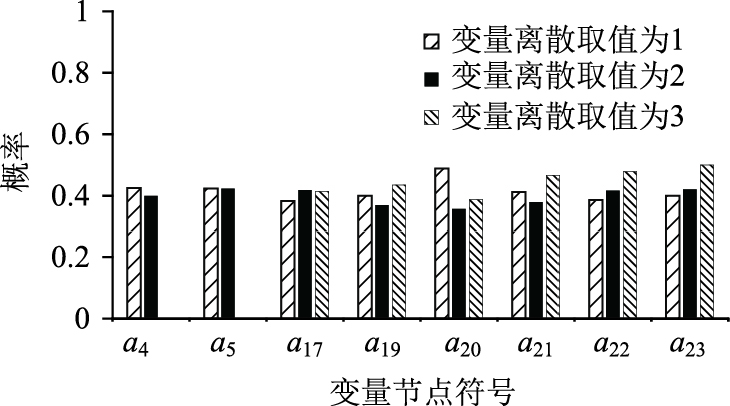
利用联合树算法对拥堵原因进行贝叶斯网络的部分节点进行推理分析, 得到图 5、图 6。
|
| 图 5 一些节点对行人影响的影响 Fig. 5 Influence of some nodes on pedestrian influence |
| |
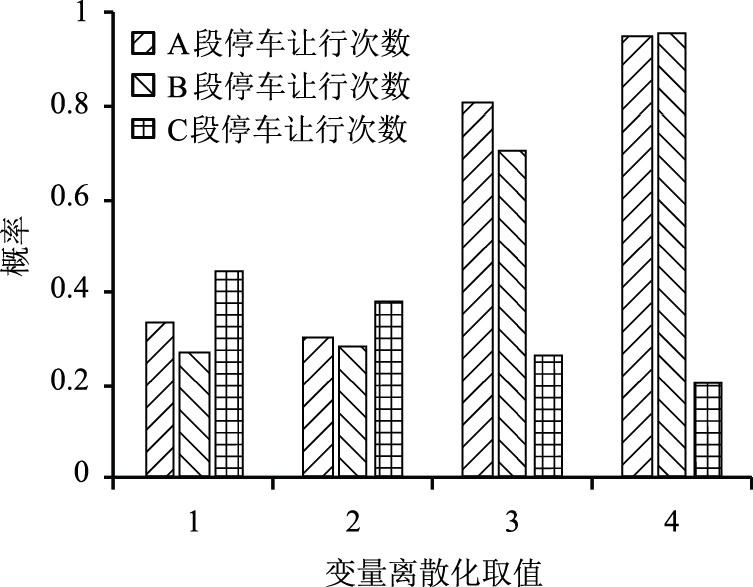
|
| 图 6 停车让行次数对行人影响的影响分析 Fig. 6 Analysis of influence of parking times on pedestrian influence |
| |
同时,使用vissim仿真软件构建了1个类似图 2但路段中仅有1条支路的基础路段模型,针对行人影响、车流高峰、停车占道、信号配时不合理及过街车流影响5种拥堵原因类型,在初始条件相同的情况下分别调整过街行人数量(在仿真模型中将人数转化为分散过街次数)、车流流入量、路边停车发生次数、同一个进口道3个方向上的绿灯时长、过街车流数量,进行3个时段的连续仿真(每5 min为1个时段),详细内容见表 3~表 7。
| 路段流入车流量/ (veh·h-1) | 仿真时段 | 行程时间/s | 停车让行次数/次 | 平均行程时间/s | 平均停车让行次数/次 |
| 750 | 1 | 34.9 | 5 | 34.60 | 5.66 |
| 2 | 34.7 | 2 | |||
| 3 | 34.2 | 10 | |||
| 900 | 1 | 37.0 | 6 | 37.33 | 8.33 |
| 2 | 34.5 | 5 | |||
| 3 | 40.5 | 14 | |||
| 1 050 | 1 | 38.7 | 12 | 39.07 | 10.00 |
| 2 | 35.3 | 6 | |||
| 3 | 43.2 | 12 |
| 绿灯或信号周期时长/s | 仿真时段 | 排队车辆数/veh | 车流通过数/veh | 平均排队车辆数 | 平均车流通过数/veh |
| 10/80 | 1 | 71 | 33 | 78.66 | 42.33 |
| 2 | 87 | 46 | |||
| 3 | 78 | 48 | |||
| 20/80 | 1 | 37 | 77 | 39.00 | 87.00 |
| 2 | 39 | 97 | |||
| 3 | 41 | 87 | |||
| 40/80 | 1 | 27 | 71 | 26.67 | 84.00 |
| 2 | 28 | 93 | |||
| 3 | 25 | 88 |
| 过街行人数量/(人·h-1) | 仿真时段 | 行程时间/s | 停车让行次数/次 | 路段车流量/(veh·h-1) | 平均行程时间/s | 平均停车让行次数/次 | 平均路段车流量/(veh·h-1) |
| 240 | 1 | 34.9 | 5 | 48 | 34.60 | 5.67 | 55.33 |
| 2 | 34.7 | 2 | 55 | ||||
| 3 | 34.2 | 10 | 63 | ||||
| 400 | 1 | 35.5 | 7 | 50 | 38.27 | 8.67 | 53.33 |
| 2 | 40.5 | 9 | 51 | ||||
| 3 | 38.8 | 10 | 59 | ||||
| 600 | 1 | 41.6 | 12 | 43 | 46.70 | 13.00 | 53.67 |
| 2 | 51.2 | 11 | 57 | ||||
| 3 | 47.3 | 16 | 61 |
| 路边停车设置 | 仿真时段 | 停车前方 | 停车后方 | 停车前方车道平均车流量之差/(veh·h-1) | 停车后方车道平均车流量之差/(veh·h-1) | |||
| 第1车道车流量/(veh·h-1) | 第2车道车流量/(veh·h-1) | 第1车道车流量/(veh·h-1) | 第2车道车流量/(veh·h-1) | |||||
| 无 | 1 | 41 | 41 | — | — | 1.33 | — | |
| 2 | 49 | 46 | — | — | ||||
| 3 | 50 | 51 | — | — | ||||
| 有 | 1 | 61 | 21 | 70 | 11 | 28.00 | 63.00 | |
| 2 | 58 | 37 | 79 | 15 | ||||
| 3 | 62 | 39 | 84 | 18 | ||||
| 过街车流量/(veh·h-1) | 仿真时段 | 行程时间/s | 停车让行次数/次 | 第1车道车流量/(veh·h-1) | 第2车道车流量/(veh·h-1) | 两车道车流量之差/(veh·h-1) | 平均行程时间/s | 平均停车让行次数/次 | 平均路段车流量/(veh·h-1) |
| 100 | 1 | 35.1 | 5 | 27 | 21 | 6 | 34.67 | 6.00 | 55.00 |
| 2 | 34.7 | 3 | 30 | 25 | 5 | ||||
| 3 | 34.2 | 10 | 35 | 27 | 8 | ||||
| 200 | 1 | 34.9 | 5 | 28 | 21 | 7 | 35.23 | 7.00 | 55.00 |
| 2 | 35.8 | 5 | 31 | 23 | 8 | ||||
| 3 | 35.0 | 11 | 34 | 28 | 6 | ||||
| 300 | 1 | 37.7 | 5 | 30 | 24 | 6 | 37.17 | 7.67 | 57.00 |
| 2 | 37.9 | 6 | 31 | 24 | 7 | ||||
| 3 | 35.9 | 12 | 35 | 27 | 8 |
2.4.2 网络结构模型验证结果分析
由表 3~表 7可以发现,随着不同变量的数据改变,一些交通状态(即可观测变量)也发生了不同程度的量值变化。对于行人影响原因类型,发生变化的数据有过街人数、停车让行次数、路段平均速度(根据行程时间转化)、路段车流量;车流高峰时停车让行次数、路段平均速度和流入车流改变;发生停车占道时各车道流量差异明显;信号配时不合理时,交叉口进口道车流流出受限,二次排队现象增加;过街车流影响时各车道流量、过街车数不同。根据仿真结果可知,与本研究构建的网络结构基本符合。
由图 5可知,对于在本研究构建的网络结构中与行人影响原因类型无直接关系的节点,其随变量状态的改变而改变的概率大小幅度不大,或没有发现有规律性的变化,没有表现出明显的相关关系。因此,从推理分析的数据上看,本研究构建的网络结构具有一定的合理性。
根据图 6的推理分析结果可知,对于行人影响原因类型,随着A段或B段停车让行次数的增加,概率也随之增大,因此,若A段或B段停车让行次数较多,则发生行人影响拥堵类型的可能性增加。而C段停车让行次数的增加却没提升发生行人影响拥堵类型的可能性,说明在C段使停车让行增多的原因大部分不是行人影响。可见,若在实际应用中使用本模型分析出发生了行人影响的拥堵原因类型,则后续可以重点对A段及B段实施缓堵措施,使措施更加具有针对性。本研究的贝叶斯网络共构建了5种拥堵原因,由于篇幅原因,本研究仅列出部分结果。
2.5 拥堵原因识别精度的试验结果和分析 2.5.1 模型识别精度试验结果本研究根据观测到的证据(即变量状态),通过本模型分析识别每次拥堵发生的原因类型,即若观测到的证据为a1=2,a2=1,a3=1,a4=1,a5=2,a6=2,a7=3,a8=2,a9=3,a10=2,a11=2,a12=1,a13=2,a14=1,a15=1,a16=2,a17=2,a18=3,a19=2,a20=2,a21=2,a22=1,a23=1,a24=1,根据推理引擎得最大可能为c1=2,c2=1,c3=2,c4=1,c5=2,而实际值为c1=2,c2=1,c3=2,c4=1,c5=2,则推理的结果与实际情况相符,此次拥堵的发生的原因为车流高峰(c2)及信号配时不合理(c4)。本研究构建的模型与对比模型对行人影响、车流高峰、停车占道、信号配时不合理和过街车流影响这5个类型,在n为10的交叉验证下,分析结果的拥堵原因平均识别准确率见表 8。
| 拥堵类型 | 因果贝叶斯网络 | BPNN | ML-KNN | 多标签岭回归 |
| 行人影响 | 71.65 | 56.55 | 69.49 | 71.65 |
| 车流高峰 | 81.65 | 71.88 | 74.39 | 80.31 |
| 停车占道 | 86.90 | 86.16 | 89.49 | 92.67 |
| 信号配时不合理 | 95.33 | 89.49 | 74.55 | 92.00 |
| 过街车流影响 | 77.41 | 64.55 | 72.08 | 74.24 |
2.5.2 模型识别精度试验结果分析
从表 8的对比试验结果可以发现,5种类型的拥堵原因使用因果贝叶斯网络模型的识别准确率都高于BPNN模型的识别准确率,但在停车占道这个原因上的识别准确率略低于ML-KNN和多标签岭回归。本研究模型的“停车占道”拥堵类型的准确率较低,这是由于本试验获取的这一类型的数据过于缺乏导致,而以概率为基础的贝叶斯网络无足够的数据支撑从而影响了模型的精度,增加数据量有助于提升准确率。
本模型对其他4种拥堵类型的对比试验结果都表现良好,说明使用本模型对城市道路交通拥堵原因分析识别是有效的。
试验仅采集了154条有效数据,还需要采用十折交叉验证方法将其划分为训练集和测试集,否则训练样本数太少会影响基于贝叶斯网络的城市道路交通拥堵多原因识别的准确率。
3 结论本研究针对寻找发生拥堵的具体原因的问题,基于理论推导及仿真手段进行系统的分析拥堵变量,对交通拥堵建立分析树,根据变量间的相互关系构建贝叶斯网络结构,建模时选择了5个常见的引发交通拥堵的原因,通过实际数据进行采用贝叶斯方法进行参数学习。所建模型对于不同城市道路交通拥堵原因的分析与判断识别具有一定的实用性及借鉴意义。
今后将对拥堵原因影响可观测交通状态的变量进行更深入的探究,使贝叶斯网络结构更加完善精确,同时可考虑从历史数据中利用结构学习方法获得贝叶斯网络的结构,对本研究利用专家知识所构建的网络结构的正确性进行验证。采用更多多分类模型的评价指标评价贝叶斯网络方法,以识别交通拥堵多原因的精度。由于数据的获取限制,本研究只采用了视频信息能获得的交通状态作为可观测交通状态变量,拥堵的影响变量还有很多(例如路段所处位置、天气情况和交通事故等),可用以进一步完善模型结构,分析其对拥堵的敏感程度,做变量选择,并获取更多的数据量,进一步提高预测精度。
| [1] |
李宇轩, 韦凌翔, 陈红, 等. 基于支持向量机的城市快速路交通拥堵识别方法[J]. 交通工程, 2018, 18(1): 43-47. LI Yu-xuan, WEI Ling-xiang, CHEN Hong, et al. Traffic Congestion Pattern Recognition in Urban Expressway Based on Support Vector Machine[J]. Journal of Transportation Engineering, 2018, 18(1): 43-47. |
| [2] |
李桂毅, 胡明华, 郑哲. 基于FCM-粗糙集的多扇区交通拥挤识别方法研究[J]. 交通运输系统工程与信息, 2017, 17(6): 141-146. LI Gui-yi, HU Ming-hua, ZHENG Zhe. Multi-sector Traffic Congestion Identification Method Based on FCM-rough Sets[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(6): 141-146. |
| [3] |
MENELAOU C, KOLIOS P, TIMOTHEHOU S, et al. Controlling Road Congestion via a Low-complexity Route Reservation Approach[J]. Transportation Research Part C:Emerging Technologies, 2017, 81: 118-136. |
| [4] |
马亚锋.基于出入流率匹配的区域交通拥挤测度与控制研究[D].成都: 西南交通大学, 2018. MA Ya-feng. Research on Regional Traffic Congestion Measurement and Control Based on Inflow and Outflow Rate Matching[D].Chengdu: Southwest Jiaotong University, 2018. |
| [5] |
安萌, 祝烨, 杨强, 等. 基于路段流量均衡控制的节点拥堵治理研究:以重庆市为例[J]. 交通工程, 2018, 18(5): 46-52, 64. AN Meng, ZHU Ye, YANG Qiang, et al. Traffic Congestion Management Research Basedon Coordinated Control:A Case Study in Chongqing[J]. Journal of Transportation Engineering, 2018, 18(5): 46-52, 64. |
| [6] |
王潇, 王武宏, 毛琰, 等. 大城市交通拥堵致因的故障树分析[J]. 交通信息与安全, 2012, 30(2): 127-130. WANG Xiao, WANG Wu-hong, MAO Yan, et al. Fault Tree Analysis of Urban Traffic Congestion Causes[J]. Journal of Transport Information and Safety, 2012, 30(2): 127-130. |
| [7] |
WANG F Y, YE C M, LI Y. Study on Reasons and Countermeasures of Traffic Congestion of Urban Road Based on the Queuing Models[C]//2013 International Conference on Computational and Information Sciences. Shiyan: IEEE, 2013: 1855-1858.
|
| [8] |
MONDAL M, REHENA Z. Identifying Traffic Congestion Pattern Using K-means Clustering Technique[C]//20194th International Conference on Internet of Things: Smart Innovation and Usages, Ghaziabad. India: IEEE, 2019: 1-5.
|
| [9] |
XU H G, ZHANG H Y, ZONG F. Bayesian Network-Based Road Traffic Accident Causality Analysis[C]//2010 WASE International Conference on Information Engineering. Beidaihe: IEEE, 2010: 413-417.
|
| [10] |
赵金宝, 邓卫, 王建. 基于贝叶斯网络的城市道路交通事故分析[J]. 东南大学学报:自然科学版, 2011, 41(6): 1300-1306. ZHAO Jin-bao, DENG Wei, WANG Jian. Bayesian Network-based Urban Road Traffic Accidents Analysis[J]. Journal of Southeast University:Natural Science Edition, 2011, 41(6): 1300-1306. |
| [11] |
KUZMINSKI P, EISELE J S, GARBER N, et al. Improvement of Highway Safety Ⅰ:Identification of Causal Factors through Fault-tree Modeling[J]. Risk Analysis, 1995, 15(3): 293-312. |
| [12] |
王静云.几类概率图模型结构学习算法研究[D].西安: 西安电子科技大学, 2018. WANG Jing-yu. Research on Several Types of Probability Graph Model Structure Learning Algorithms[D]. Xi'an: Xidian University, 2018. |
| [13] |
俞娉婷, 刘振元, 陈学广. 基于贝叶斯网络的一种事故分析模型[J]. 中国安全生产科学技术, 2006, 2(4): 45-50. YU Ping-ting, LIU Zhen-yuan, CHEN Xue-guang. A Bayesian Network Approach to Accident Analysis[J]. Journal of Safety Science and Technology, 2006, 2(4): 45-50. |
| [14] |
张珩, 徐寅峰, 吴腾宇. 行人从众过街对机动车流延误影响分析[J]. 系统工程学报, 2016, 31(4): 536-544. ZHANG Heng, XU Yin-feng, WU Teng-yu. Research on Traffic Delay Caused by Pedestrians' Group Psychology[J]. Journal of Systems Engineering, 2016, 31(4): 536-544. |
| [15] |
崔曼, 薛惠锋, 陈福振, 等. 行人穿越道路对交通运行拥堵预测仿真[J]. 计算机仿真, 2018, 35(2): 81-84. CUI Man, XUE Hui-feng, CHEN Fu-zhen, et al. Simulation of Traffic Congestion Prediction for Pedestrian Crossing Road[J]. Computer Simulation, 2018, 35(2): 81-84. |
| [16] |
孙亚南.道路交通拥塞环境下车辆运行规律分析[D].昆明: 昆明理工大学, 2016. SUN Ya-nan. Analysis of Vehicle Running Rule in Road Traffic Congestion Environment[D].Kunming: Kunming University of Science and Technology, 2016. |
| [17] |
冯伟.路边停车对路段交通流的影响研究[D].北京: 北京交通大学, 2008. FENG Wei. Study on Influence of Roadside Parking on Traffic Flow[D].Beijing: Beijing Jiaotong University, 2008. |
| [18] |
LI Z F, ELEFTERIADOU L, RANKA S. Signal Control Optimization for Automated Vehicles at Isolated Signalized Intersections[J]. Transportation Research Part C:Emerging Technologies, 2017, 49: 1-18. |
| [19] |
俞敏健.无信号T型公路平面交叉口支路与主路交通流相互作用研究[D].南京: 东南大学, 2015. YU Min-jian. Study on Interaction between Traffic Flows of Signalless T-shaped Highway Intersection and Main Road[D].Nanjing: Southeast University, 2015. |
 2020, Vol. 37
2020, Vol. 37
