扩展功能
文章信息
- 翟晓亮, 朱青, 钱程, 朱乐东
- ZHAI Xiao-liang, ZHU Qing, QIAN Cheng, ZHU Le-dong
- 山区峡谷大跨度钢桁梁悬索桥抗风性能研究
- Study on Wind-resistance Performance of Steel Truss Girder Suspension Bridges in Mountainous Canyon
- 公路交通科技, 2020, 37(11): 56-62
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 56-62
- 10.3969/j.issn.1002-0268.2020.11.008
-
文章历史
- 收稿日期: 2019-12-24
2. 同济大学 土木工程防灾国家重点实验室, 上海 200092;
3. 同济大学 土木工程学院, 上海 200092
2. State Key Laboratory of Disaster Reduction in Civil Engineering, Tongji University, Shanghai 200092, China;
3. School of Civil Engineering, Tongji University, Shanghai 200092, China
随着桥梁跨径不断增大,桥梁结构变得更柔,抗风稳定性问题也更为突出。伴随着世界,特别是我国近年来大跨度、超大跨度桥梁的建设,桥梁抗风研究也不断成熟,并朝着精细化的方向发展。但是,以往国内外大跨度桥梁多数是跨海、海湾、大江、大河的, 传统的桥梁抗风研究也主要针对此类地区的风场特性展开。近年来,随着我国山区高速公路的快速发展,作为交通设施关键节点的山区大跨度桥梁建设得到了高速发展。当桥址位于山区峡谷时,桥位处风场受局部地形影响剧烈。为了得到桥址处的风环境特性,通常需要地形模型风洞试验、CFD分析、或者现场实测。目前针对山区峡谷地形桥址风环境的研究和数据还比较少。
胡峰强等[1]通过桥址区地形模型风洞试验确定了北盘江大桥的设计基准风速和相关的风特性参数。孙毅等[2]为了研究平均和脉动风速在山地中的空间分布规律,进行了10个不同坡度和高度的三维轴对称山体模型的边界层风洞试验。朱乐东等[3]采用相控阵声雷达风廓线仪对该桥桥址区的风剖面进行了实测。李永乐等[4]采用CFD计算软件对某深切峡谷桥址处的风场进行了研究。韩艳等[5-6]通过CFD分析得到了澧水大桥所在峡谷桥址处的风环境。王云飞等[7]就复杂山区水库蓄水对跨水库桥梁桥址处的风环境影响进行了数值模拟研究。遆子龙等[8]还研究了地表粗糙度对山区峡谷地形风场的影响。
既有研究结果表明,山区峡谷地形风环境具有强烈的三维特性,相较于常规平坦地貌桥梁,其所处风环境主要有以下几个特点:(1)风场沿桥跨方向分布不均匀;(2)风剖面的指数模型已不适用;(3)来流风攻角的范围通常较大;(4)来流风速和风参数严重依赖于来流风向;(5)可能存在较强紊流。(6)通常没有合适的风速实测数据,其设计风速需要根据附件测点进行换算[9-10]。因此如果用规范中的常规方法得出的设计风速进行抗风检验,可能得到不安全的结果[11-12]。
以上这些特殊的风场特性,比如大攻角、大紊流度等都会影响山区桥梁的抗风性能[13-14]。如何合理确定复杂山区地形中桥梁的设计风参数,并针对山区地形特殊风场特性进行桥梁抗风设计是目前我国桥梁抗风研究的重要挑战之一,也是山区大跨度悬索桥设计的关键。
目前大跨度悬索桥加劲梁采用的断面形式主要有空间桁架、单箱钢箱梁及中央开槽钢箱梁等形式,当桥梁处于山区峡谷地区时,考虑地形条件以及施工因素,空间钢桁架梁是悬索桥加劲梁断面的首选形式。虽然桁架加劲梁扭转刚度大,透风性能好,但是仅桁架加劲梁本身往往很难满足气动稳定性要求。特别是在大风攻角下,桥梁的气动性能降低比较剧烈,颤振临界风速往往很低;在加劲梁截面形式已定的情况下,采用适当的被动气动措施来改善主梁的颤振稳定性能往往是一种最可靠的途径[15]。因此研究桁架加劲梁悬索桥气动稳定措施具有重要的理论和实际应用价值。在钢桁梁加劲的悬索桥中,日本明石海峡桥采用了桥面下侧设置中央稳定板和带开孔格栅桥面的方案提高了大桥的颤振稳定性[16],四渡河大桥采用了钢桁梁中部设置水平翼板的方案提高了气动稳定性。
以跨越独木河峡谷钢桁梁悬索桥——贵黄高速阳宝山特大桥为背景,首先进行了桥址地貌风环境风洞试验研究,分析其风场特性,给出了其颤振临界风速的确定方法;继而通过大攻角范围的弹簧悬挂节段模型试验,研究了该桥的颤振性能,并提出了改善大攻角下颤振性能的气动措施。
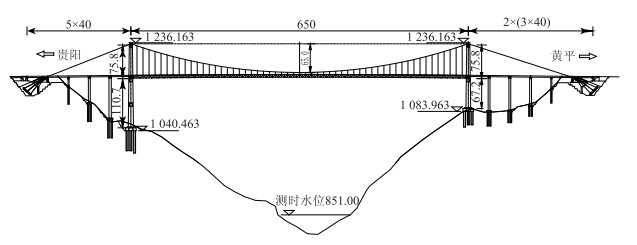
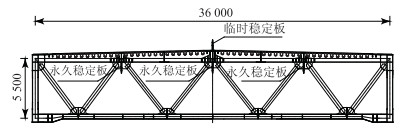
1 工程背景[17]阳宝山特大桥位于贵定县新巴镇和德新镇境内,是贵黄高速公路的控制性工程。主桥为单跨650 m钢桁梁悬索桥(如图 1所示),主缆计算跨度为(170+650+210)m,主缆垂跨比为1/10。大桥主梁采用板桁结合体系,钢桁梁包括钢桁架和正交异性钢桥面板两部分。主桁架为带竖腹杆的华伦式结构,主桁桁高5.5 m,桁宽36 m(如图 2所示)。初始设计断面中没有图 2中所示的气动稳定板,气动稳定板是依据风洞试验结果而设,设置目的是提高断面在较大负攻角下的颤振性能。
|
| 图 1 主桥总体布置图(单位:m) Fig. 1 Overall layout of main bridge (unit: m) |
| |
|
| 图 2 主梁截面图(单位:cm) Fig. 2 Section of main girder (unit: cm) |
| |
阳宝山特大桥桥址处为高原峡谷地貌,桥址附近10 km直径范围内地形图如图 3所示,图中央直线代表桥址。10 km直径范围内最低处海拔约800 m,最高处海拔约1 400 m,桥面距水面约316 m。桥址各面几乎皆有山岭遮挡,其中正东和西南两个方向的山地最高,最高海拔约1 400 m。西南方向海拔约1 400 m的山峰离桥址的距离只有约2 km。正南偏东方向遮挡的山岭最矮,最高海拔只有1 150m左右,与阳宝山大桥主梁海拔高度相当。

|
| 图 3 桥址附近10 km直径地形 Fig. 3 Terrain of 10 km diameter around bridge site |
| |
桥址周围复杂的地形对桥址处的风场有决定性的影响。阳宝山特大桥采用地形模型风洞试验来得到桥址处的设计风参数。
2 地形模型风洞试验与设计风参数确定 2.1 地形模型风洞试验概况阳宝山特大桥桥址地形模型风参数风洞试验在同济大学土木工程防灾国家重点实验室TJ-3大型边界层风洞中进行。该风洞是一座闭口竖向回流式低速风洞,试验段尺寸为宽15 m、高2 m、长14 m。模型比例为1:2 500,用于地形模拟的模型核心区直径10 km。地形模型由KT板层叠而成,每层的形状根据地形等高线确定。每层KT板的厚度为5 mm,对应实际地形高差为12.5 m。为更好地模拟地形模型的边界,在10 k范围以外采用约60°斜坡来过渡到地面(见图 4)。模型底面相当于海拔851 m(水面高度),地形模型风洞阻塞度约为4%。试验来流接近于均匀流,即平均风速沿高度基本没有变化,且湍流度 < 0.5%,来流平均风速为10 m/s。

|
| 图 4 风洞中的地形模型 Fig. 4 Terrain model in wind tunnel |
| |
风速测量系统采用澳大利亚某公司的100系列眼镜蛇探头及配套控制、数据采集设备。在试验中对主梁高度跨中,以及贵阳、黄平两侧四分点处的三维风速时程进行测量,然后计算风攻角、风偏角以及平均风速。在试验中,地形模型被固定在同济大学TJ-3风洞的转盘上,通过转盘转动对地形模型进行不同风向角来流作用下的风参数测试。试验风向角的范围为0°~360°,间隔10°。阳宝山特大桥主梁纵轴线法向与正北正南方向的夹角约为6°,因此增加了6°和186°两个风向角。这样总计有38个风向角。试验中将正北方向定义为0°风向角。
2.2 地形模型风洞试验结果测量结果显示,3个测点风速较大的风向均是北偏西和南偏东方向。该风向基本是沿峡谷走向,而且周围山峰较矮。而西南和正东方向山峰最高,对来流的遮挡效应最为明显,因此该风向主梁高度处风速最低。
主梁高度3个测点测得的风攻角差异较大,不少风向贵阳侧和黄平侧四分点测得的风攻角反号。这说明来流风攻角受地形影响而沿跨向分布非常不均匀。黄平侧测点测得的最大负攻角达到-20°左右。黄平侧测点和跨中测得的最大正攻角都达到+9°左右。
由于风攻角的范围非常大,而且最大平均风速随着风攻角的增大而明显减小,因此不能对全部风攻角范围设置统一的设计基准风速和颤振检验风速,而应该针对不同的风攻角范围取不同的值。
首先需要对不同风攻角范围的风速大小进行统计。表 1所列的是桥面高度不同风攻角范围内的3个测点所得的最大相对风速比,即各测点所有风向角下的最大平均风速和试验梯度风速的比值。由于试验在均匀流场中进行,因此在风速不再随高度增加而变化的高度测得的风速即为试验梯度风速。
| 风攻角范围 | 最大相对风速比 | |||
| 跨中 | 黄平侧四分点 | 贵阳侧四分点 | 最不利 | |
| -25°≤α<-20° | — | 0.21 | — | 0.21 |
| -20°≤α<-15° | 0.23 | 0.23 | 0.30 | 0.30 |
| -15°≤α<-10° | 0.60 | 0.71 | 0.52 | 0.71 |
| -10°≤α<-5° | 0.28 | 0.80 | 0.68 | 0.80 |
| -5°≤α<-3° | 0.76 | 0.83 | 0.75 | 0.83 |
| -3°≤α≤+3° | 0.81 | 0.81 | 0.79 | 0.81 |
| +3°<α≤+5° | 0.56 | 0.51 | 0.52 | 0.56 |
| +5°<α≤+9° | 0.51 | 0.34 | — | 0.51 |
对于试验测得的风偏角≤20°的情况,直接按试验测得的相对风速比作为设计风速的取值依据;对于风偏角>20°的情况, 对试验测得风速按风偏角进行正交分解,即将试验测得的相对风速比乘以风偏角的余弦作为设计风速的取值依据。
在跨中位置,±3°风攻角范围的风速最大,相对风速比为0.81;总体而言,在±3°以外,风速随攻角增大而减小。两侧四分点在正攻角时的风速都小于跨中。黄平侧四分点在负攻角时的风速大于跨中,而且在-15°~+3°范围内,风速都较大,相对风速一直保持在0.7~0.8。各测点在-15°以下攻角时测得的相对风速都比较小,小于0.3。
由此可见,最大风速并不一定出现在跨中,四分点的最大风速可能相对更大,而且四分点处测得的风攻角绝对值通常也比跨中大。由于作用在两个四分点之间的近跨中梁段上的风致静、动力荷载对桥梁风致响应起主要作用,因此,需要综合考虑3个测点测得的风参数。偏于保守地对3个测点取最大的相对风速以后,在-10°~+3°风攻角范围内,最大相对风速都在0.8以上;在-15°~-10°风攻角范围内,最大相对风速为0.71;在+3°~+9°风攻角范围内,最大相对风速在0.5~0.6之间。试验测得的桥面高度最大顺风向和竖向紊流度分别为19.1%和13.5%。
2.3 设计基准风速和颤振临界风速计算地形模型试验结果显示,桥址处在某些来流方向下风攻角较大,显著超过通常考虑的±3°风攻角,而且在风攻角较大时的最大风速有时并不小于风攻角在±3°范围内的最大风速。因此,需根据不同的风攻角范围分别考虑设计基准风速和颤振检验风速。在桥梁运营期间,沿跨向风速分布不均匀,出于安全性考虑,应该偏于保守地对于不同风攻角下的设计风速取不同测点的最大值。但是,在此之前,首先要建立起风洞试验风速和实际桥址处风速的对应关系。本研究按照梯度风速等效原则推导了试验中各测点的风速与桥址附近气象站基本风速的关系。
试验中每个测点风速对应的实际风速为:
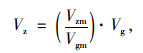
|
(1) |
式中,Vz为实际高度Z处的实际风速;Vzm为模型高度zm处测得的平均风速;Vg为实际的梯度风速;Vgm为模型试验中的梯度风速。
要最终得到Vz,需要先确定实际桥址处的梯度风速Vg。根据《公路桥梁抗风设计规范》(JTG/T D60-01—2004)[18]中的全国基本风速分布图和全国各气象台站的基本风速值,桥位西侧贵阳市基本风速(B类地貌地面或水面以上10 m高度处,100年重现期的10 min平均年最大风速)为25.3 m/s;桥位东侧凯里市基本风速为24.8 m/s,桥位北侧遵义市基本风速为24.9 m/s。因此,该桥所在地区的基本风速(标准B类场地、10 m高度处、100 a重现期、10 min平均风速)可以按照相邻城市风速取最大值为:V10=25.3 m/s。
标准B类地貌幂指数为αB=0.16、边界层厚度HG, B=350 m,因此桥址上空梯度风速取贵阳上空梯度风速为:
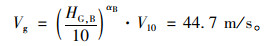
|
(2) |
然后通过对各测点桥面高度处风速测试,即可根据式(1)得到桥面高度处的设计基准风速。
阳宝山特大桥主跨长650 m,考虑风速的脉动影响及水平相关特性的无量纲修正系数μf可参照《公路桥梁抗风设计规范》,按D类地表类别取为1.36。考虑风洞试验误差及设计、施工中不确定因素的综合安全系数K=1.2,则100 a重现期成桥运营状态颤振检验风速为:
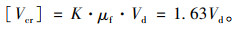
|
(3) |
阳宝山特大桥实桥梯度风速为44.7 m/s,根据模型试验梯度风和实桥梯度风成比例的原则以及模型试验得出的不同风攻角风速比。可以求得不同风攻角范围实桥跨中和四分点的设计基准风速和颤振临界风速,列于表 2。
| 风攻角范围 | 设计基准风速 | 颤振检验风速 |
| -20°≤α<-15° | 13.4 | 21.9 |
| -15°≤α<-10° | 31.7 | 51.7 |
| -10°≤α<-5° | 35.8 | 58.3 |
| -5°≤α<-3° | 37.1 | 60.5 |
| -3°≤α≤+3° | 36.2 | 59.0 |
| +3°<α≤+5° | 25.0 | 40.8 |
| +5°<α≤+9° | 22.8 | 37.2 |
在±3°风攻角范围内,颤振检验风速为59.0 m/s;在-5°~-3°风攻角范围内的检验风速更大,达到60.5 m/s;-10°~-5°风攻角范围内检验风速也很大,有58.3 m/s;15°~-10°风攻角范围内检验风速依然达到51.7 m/s。其他风攻角范围内颤振检验风速相对较低。
因此,需要对主梁在-15°~+9°风攻角范围内的颤振性能进行检验。
3 颤振稳定性检验和气动措施节段模型测振试验在汕头大学边界层风洞中进行。汕头大学边界层风洞是一座回流式低速风洞,风洞主试验段宽3 m、高2 m、长20 m。主梁节段模型的缩尺比取为λL=1/60,模型的总长度为1.70 m,竖弯频率2.22 Hz,扭转频率5.32 Hz。通过大攻角范围节段模型风洞试验,研究了原断面和增加了中央气动稳定板(如图 5所示)断面的颤振性能。

|
| 图 5 风洞中的节段模型 Fig. 5 Sectional model in wind tunnel |
| |
试验风攻角范围为-15°~+9°,间隔2°~3°,具体值见表 3。试验得到的原断面和增加中央气动稳定板断面的颤振临界风速也列于表 3。
| 攻角/ (°) | 检验风速/ (m·s-1) | 临界风速/(m·s-1) | 富余度/% | |||
| 原断面 | 有稳定板 | 原断面 | 有稳定板 | |||
| 9 | 37.2 | 56.6 | 58.5 | 52.15 | 57.26 | |
| 7 | 37.2 | 57.6 | 67.2 | 54.84 | 80.65 | |
| 5 | 40.8 | 86.4 | 86.4 | 111.76 | 111.76 | |
| 3 | 40.8 | 86.4 | 86.4 | 111.76 | 111.76 | |
| 0 | 59 | 86.4 | 86.4 | 46.44 | 46.44 | |
| -3 | 59 | 81.6 | 86.4 | 38.31 | 46.44 | |
| -5 | 60.5 | 72 | 83.3 | 19.01 | 37.69 | |
| -7 | 58.3 | 64.8 | 69.8 | 11.15 | 19.73 | |
| -9 | 58.3 | 61 | 62.6 | 4.63 | 7.38 | |
| -11 | 51.7 | 57.1 | 61.2 | 10.44 | 18.38 | |
| -13 | 51.7 | 55.7 | 59.4 | 7.74 | 14.89 | |
| -15 | 51.7 | 55.7 | 57.6 | 7.74 | 11.41 | |
原断面主梁的颤振临界风速在-3°~+5°风攻角范围内都超过80 m/s;此外随着攻角绝对值的增大,断面颤振临界风速逐渐降低。由于颤振检验风速也随着攻角绝对值下降,原断面主梁在-3°~+9°风攻角范围内相较于检验风速的富余度超过40%, 即在小攻角和所有正攻角下的颤振临界风速都有较为充足的富余度。但是在较大的负攻角下,颤振临界风速富余度较低,在-9°攻角下仅有4.63%,在-13°和-15°攻角下为7.74%。虽然试验得到的颤振临界风速值都满足检验要求,但是考虑到试验的不确定性,太小的富余度可能不足以充分保证大跨度桥梁的颤振安全性,有必要进一步研究能提高颤振临界风速的气动措施供实际工程中参考选用。
研究过程中采用在主梁桥面板下方设置3道气动稳定板的方法提高断面的颤振稳定性能。经过方案比选,最优的稳定板高度为82.8 cm,约为主梁高的15%。设置了稳定板后的主梁断面在负攻角下颤振性能有了一定改善。临界风速富余度在-9°攻角下提高到了7.38%,在-13°和-15°攻角下分别提高到了14.89%和11.41%。
本研究还通过节段模型风洞试验对设置中央稳定板前后的主梁断面的涡振性能进行了检验。结果显示,在以上风攻角范围内,设计风速以下都没有观测到涡激共振现象。
4 结论通过地形模型风洞试验和主梁节段模型风洞试验对阳宝山特大桥的桥址风环境和主梁抗风性能进行了系统研究,根据研究结果得出以下结论。
(1) 受峡谷地形影响,阳宝山特大桥桥址处两个四分点之间的风攻角可能很大,最大负攻角达到-20°左右,最大正攻角达到+9°左右。由于风攻角的范围非常大,而且最大平均风速随着风攻角的增大而明显减小,因此不能对全部风攻角范围设置统一的设计基准风速和颤振检验风速,而应该针对不同的风攻角范围取不同的值。
(2) 阳宝山特大桥主梁高度跨中和两侧四分点测得的风攻角差异较大,说明来流风攻角受地形影响而沿跨向分布非常不均匀。最大风速并不一定出现在跨中。由于作用在两个四分点之间的近跨中梁段上的风致静、动力荷载对桥梁风致响应起主要作用,因此,需要综合考虑3个测点测得的风参数进行设计风速取值。阳宝山特大桥设计时取3个点的最大值。
(3) 根据梯度风速等效原则建立了试验所测风速和桥址附近气象站基准风速的关系,并根据不同的风攻角区间确定了设计基准风速和颤振临界风速的取值。然后通过弹簧悬挂节段模型试验,研究了主梁断面在大攻角范围内的颤振性能,发现主梁断面在较大负攻角下颤振临界风速较低,相对颤振检验风速富余度很小,不到5%。为确保结构安全,设计最终采用了“主梁桥面板下方设置3道纵向永久稳定板+桥面上中央分隔带处设置1道施工期临时稳定板”的方式用以提高主梁建设及运营期的颤振性能。
| [1] |
胡峰强, 陈艾荣, 王达磊. 山区桥梁桥址风环境试验研究[J]. 同济大学学报:自然科学版, 2006, 34(6): 721-725. HU Feng-qiang, CHEN Ai-rong, WANG Da-lei. Experimental Study of Wind Field in Bridge Site Located in Mountainous Area[J]. Journal of Tongji University:Natural Science Edition, 2006, 34(6): 721-725. |
| [2] |
孙毅, 李正良, 黄汉杰, 等. 山地风场平均及脉动风速特性试验研究[J]. 空气动力学学报, 2011, 29(5): 593-599. SUN Yi, LI Zheng-liang, HUANG Han-jie, et al. Experimental Research on Mean and Fluctuating Wind Velocity in Hilly Terrain Wind Field[J]. Acta Aerodynamica Sinica, 2011, 29(5): 593-599. |
| [3] |
朱乐东, 任鹏杰, 陈伟, 等. 坝陵河大桥桥位深切峡谷风剖面实测研究[J]. 实验流体力学, 2011, 25(4): 15-21. ZHU Le-dong, REN Peng-jie, CHEN Wei, et al. Investigation on Wind Profiles in the Deep Gorge at the Balinghe Bridge Site via Field Measurement[J]. Journal of Experiments in Fluid Mechanics, 2011, 25(4): 15-21. |
| [4] |
李永乐, 蔡宪棠, 唐康, 等. 深切峡谷桥址区风场空间分布特性的数值模拟研究[J]. 土木工程学报, 2011, 44(2): 116-122. LI Yong-le, CAI Xian-tang, TANG Kang, et al. Study of Spatial Distribution Feature of Wind Fields over Bridge Site with a Deep-cutting Gorge Using Numerical Simulation[J]. China Civil Engineering Journal, 2011, 44(2): 116-122. |
| [5] |
沈炼, 韩艳, 蔡春声, 等. 山区峡谷桥址处风场实测与数值模拟研究[J]. 湖南大学学报:自科科学版, 2016, 43(7): 16-24. SHEN Lian, HAN Yan, CAI Chun-sheng, et al. Experiment and Numerical Simulation for Wind Field of a Long-span Suspension Bridge Located in Mountainous Canyon[J]. Journal of Hunan University:Natural Science Edition, 2016, 43(7): 16-24. |
| [6] |
HAN Y, SHEN L, XU G J, et al. Multiscale Simulation of Wind Field on a Long Span Bridge Site in Mountainous Area[J]. Journal of Wind Engineering & Industrial Aerodynamics, 2018, 177: 260-274. |
| [7] |
王云飞, 汪斌, 李永乐. 复杂山区水库蓄水影响下的库区桥址风特性数值模拟研究[J]. 福州大学学报, 2017, 45(4): 466-471. WANG Yun-fei, WANG Bin, LI Yong-le. Numerical Simulation of Wind Characteristics over Bridge Site in Complicated Mountains under the Influence of Reservoir Water Storage[J]. Journal of Fuzhou University:Natural Science Edition, 2017, 45(4): 466-471. |
| [8] |
遆子龙, 李永乐, 廖海黎. 地表粗糙度对山区峡谷地形桥址区风场影响研究[J]. 工程力学, 2017, 34(6): 84-92. TI Zi-long, LI Yong-le, LIAO Hai-li. Effect of Ground Surface Roughness on Wind Field over Bridge Site with a Gorge in Mountainous Area[J]. Engineering Mechanics, 2017, 34(6): 84-92. |
| [9] |
庞加斌, 宋锦忠, 林志兴. 山区峡谷桥梁抗风设计风速的确定方法[J]. 中国公路学报, 2008, 21(5): 39-44. PANG Jia-bin, SONG Jin-zhong, LIN Zhi-xing. Determination Method for Wind-resistant Design Wind Speed of Mountainous-valley Bridge[J]. China Journal of Highway and Transport, 2008, 21(5): 39-44. |
| [10] |
王凯, 廖海黎, 李明水, 等. 山区峡谷桥梁设计基准风速的确定方法[J]. 西南交通大学学报, 2013, 48(1): 29-35. WANG Kai, LIAO Hai-li, LI Ming-shui, et al. Determination Method for Basic Design Wind Speed of Mountainous-valley Bridge[J]. Journal of Southwest Jiaotong University, 2013, 48(1): 29-35. |
| [11] |
RAUPACH M R, FINNIGAN J J. The Influence of Topography on Meteorological Variables and Surface-atmosphere Interactions[J]. Journal of Hydrology, 1997, 190(3/4): 182-213. |
| [12] |
CARPENTER P, LOCKE N. Investigation of Wind Speeds over Multiple Two-dimensional Hills[J]. Journal of Wind Engineering & Industrial Aerodynamics, 1999, 83(1/2/3): 109-120. |
| [13] |
孙芳锦, 梁爽. 考虑流固耦合作用的大跨度桥梁风振响应研究[J]. 公路交通科技, 2015, 32(7): 84-91. SUN Fang-jin, LIANG Shuang. Study on Wind-induced Viberation Responses of Long-span Bridge Considering Fluid-solid Coupling[J]. Journal of Highway and Transportation Research and Development, 2015, 32(7): 84-91. |
| [14] |
白桦, 姬乃川, 张亮亮, 等. 紊流风特性参数对近流线形桥梁表面风压分布影响[J]. 公路交通科技, 2019, 36(1): 70-77. BAI Hua, JI Nai-chuan, ZHANG Liang-liang, et al. Influence of Turbulent Wind Characteristic Parameters on Wind Pressure Distribution on Approximate Streamlined Bridge Surface[J]. Journal of Highway and Transportation Research and Development, 2019, 36(1): 70-77. |
| [15] |
李春光, 张志田, 陈政清, 等. 桁架加劲梁悬索桥气动稳定措施试验研究[J]. 振动与冲击, 2008, 27(9): 40-43, 181. LI Chun-guang, ZHANG Zhi-tian, CHEN Zheng-qing, et al. Experimental Study on the Aerodynamic Stability Measure of a Suspension Bridge with Truss Stiffening Girder[J]. Journal of Vibration and Shock, 2008, 27(9): 40-43, 181. |
| [16] |
KITAGAWA M. Technology of the Akashi Kaikyo Bridge[J]. Structural Control & Health Monitoring, 2010, 11(2): 75-90. |
| [17] |
中交第一公路勘察设计研究院有限公司.贵阳至黄平高速公路阳宝山特大桥施工图[R].西安: 中交第一公路勘察设计研究院有限公司, 2018. CCCC First Highway Consultants Co., Ltd. Construction Drawing of Yangbaoshan Bridge on Guiyang-Huangping Expressway[R]. Xi'an: CCCC First Highway Consultants Co., Ltd., 2018. |
| [18] |
JTG/T D60-01-2004, 公路桥梁抗风设计规范[S]. JTG/T D60-01-2004, Wind-resistant Design Specification for Highway Bridges[S]. |
 2020, Vol. 37
2020, Vol. 37
