扩展功能
文章信息
- 关振长, 毛顺飞, 张淑宝, 徐惠明
- GUAN Zhen-chang, MAO Shun-fei, ZHANG Shu-bao, XU Hui-ming
- 基于BBM非饱和土本构模型的高填路堤沉降特性
- Settlement Characteristics of High-filled Embankment Based on Unsaturated Soil Constitutive Model
- 公路交通科技, 2020, 37(11): 31-38
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 31-38
- 10.3969/j.issn.1002-0268.2020.11.005
-
文章历史
- 收稿日期: 2019-09-17
2. 漳州厦蓉高速扩建工程有限公司, 福建 漳州 363000
2. Zhangzhou Xiamen-Chengdu Expressway Extension Engineering Co., Ltd., Zhangzhou Fujian 363000, China
随着我国高速公路建设向山岭重丘地区发展,高填路堤因其建设成本低、施工难度小,且能有效利用挖方弃土等优点,而被广泛运用。而控制高填路堤的沉降量、保证高填路堤的稳定性,是保证其工程建设质量与安全的关键所在。
许多学者采用数值模拟方法对高填路堤沉降特性展开了相关研究。杨静[1]依托新疆某高速公路工程,在ABAQUS数值平台上采用MC本构模型分析了路基拓宽对其沉降的影响,结果表明拓宽后最大竖向位移呈倒钟形分布,主要出现在新路基一侧。郑建斌[2]在Geostudio平台上采用MC本构模型对软土地区路基沉降进行数值模拟研究,结果表明地基回弹模量对路基沉降有很大的影响,路基顶面沉降值随地基回弹模量的增大而减小。李自强[3]在ABAQUS数值平台上采用MCC本构模型对深厚软土区的沉降问题展开研究,结果表明由于防护堤沉降量过大,将会影响其上部建构筑物安全,建议在防护堤施工前进行地基处理。占鑫杰[4]依托连云港淤泥地基工程实例,在FLAC3D数值平台上采用MCC本构模型分析了不同涂抹效应参数对地基表面沉降的影响,结果表明当涂抹区渗透系数减小,涂抹半径增大时,地基固结沉降速率变缓。
综上所述,目前基于数值模拟的路堤沉降特性分析,大多采用MC, MCC等常规本构模型[5-7],仅能考虑完全饱和或完全干燥的情况。但实际上高填路堤所用填料多为非饱和土,常规本构模型未考虑非饱和土中基质吸力的影响,其计算分析结果不够准确。因此,以厦蓉高速公路漳州段高填路堤工程为背景,基于BBM非饱和土本构模型,在FLAC3D数值平台上分析其沉降变形,并与常规MCC本构模型的计算结果相比照,为高填路堤沉降特性的研究提供参考。
1 MCC本构模型英国剑桥大学Roscoe和Schofield[8]于20世纪中叶,在对正常固结黏土和弱超固结黏土进行大量三轴试验的基础上,提出了一种等向硬化的弹塑性本构模型,称之为修正剑桥(MCC)本构模型。其核心是提出了临界状态线和状态边界面的概念。该模型通过等向三轴压缩试验和常规三轴压缩试验,采用相关联流动法则建立起屈服函数f(σ)和势函数g(σ)的数学方程式。20世纪60年代末,Burland教授进一步引入弹性偏应变不为0的修正,并使其屈服函数得以完善,在p-q坐标系中其屈服面呈椭圆状,在主应力空间中则为椭球状体。
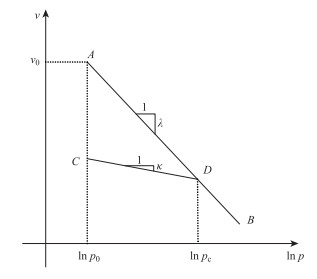
由各向等压固结试验(即q=0情况)可得到孔隙比e与平均应力p之间的关系。以比体积v为纵坐标,ln p为横坐标,绘制如图 1所示固结曲线。该曲线称之为正常固结线,简称NCL,其中AB为压缩固结曲线,CD为回弹再压缩曲线,λ, κ分别为加载、卸载曲线的斜率。
|
| 图 1 v-ln p固结曲线 Fig. 1 v-ln p consolidation curve |
| |
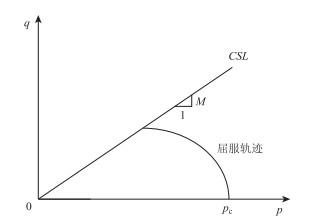
Roscoe通过常规三轴压缩试验证明,无论是排水剪切、不排水剪切或其他任何应力路径试验都具有相同的破坏轨迹(即临界破坏线CSL),在p-q平面上是一条过原点的直线,如图 2所示。临界破坏线CSL的表达式为q=Mp,其中M为该直线的斜率,也称为临界状态有效应力比。椭圆型屈服曲线为土体从开始受剪直到破坏的屈服轨迹,每一个确定的p值对应一条屈服轨迹;其最大屈服轨迹的水平半轴为pc/2,竖向半轴为Mpc/2,椭圆中心在(pc/2,0)位置。
|
| 图 2 p-q平面上的屈服轨迹 Fig. 2 Yield trajectory in p-q plane |
| |
进一步地,以p,v,q为坐标建立三维空间,将土体三轴试验破坏时的p-q-v对应关系描绘在三维空间中,该关系唯一且表示为一条空间曲线,其在p-q面上的投影即为CSL线,该曲线称之为空间临界状态线。由空间临界状态线,v-p平面NCL线,p-q平面屈服轨迹以及v轴所围成的空间曲面既表示土体状态边界面。该曲面以下为弹性区,以上不可达到,故可根据p-q-v关系所处位置作为判别是否屈服的标准,并由此建立相应的屈服准则。
MCC本构模型是目前岩土工程界广泛应用的弹塑性本构模型之一,其参数λ,κ,pc,M,μ,G, p0和v0都具有明确的物理意义,且容易由常规土工试验获取,详见表 1。
| 符号 | 意义 |
| λ | 等向三轴压缩试验得到的v-ln p加载曲线的斜率,表征土体加载时的刚度 |
| κ | 等向三轴压缩试验得到的v-ln p回弹曲线的斜率,表征土体卸载或再加载时的刚度 |
| pc | 其应力历史中所受过的最大有效应力 |
| M | 常规三轴压缩试验在q-p坐标下临界破坏线的斜率 |
| μ | 泊松比 |
| G | 剪切模量 |
| p0 | 正常固结曲线(v-ln p曲线)上的初始点,通常取标准大气压 |
| v0 | 正常固结曲线(v-ln p曲线)上的初始点,通常取标准大气压下初始孔隙比e0+1 |
2 BBM非饱和本构模型
基于临界状态理论建立的MCC本构模型标志着现代土力学理论的发端,被广泛应用于各类土工计算中。但该本构主要是针对饱和土而建立的,而实际工程中遇到的土体大多处于非饱和状态,黄土、膨胀土、残积土、人工填土以及地下水位以上的土,都是典型的非饱和土。基质吸力s的存在是非饱和土区别于饱和土的重要原因,因此如何考虑基质吸力的影响,是建立非饱和土本构模型的关键所在。
2.1 BBM本构模型及其参数Alonso[9]等基于试验结果提出不同吸力下非饱和土体积变化与应力的关系,并将此变化融入到修正剑桥模型中,于20世纪90年代建立了BBM非饱和土本构模型[10]。与其他弹塑性本构模型一样,BBM本构模型也将土体变形分为弹性变形和塑性变形,采用平均净应力p,偏应力q,基质吸力s这3种应力变量,在应力空间中以屈服面(SI,LC,CSL)来划分弹性空间与塑性空间。
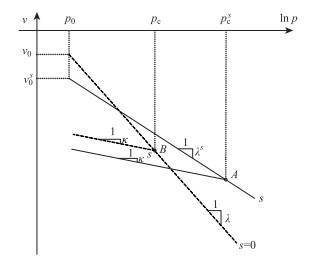
在各向等压(即q=0)应力状态下,仍以v-ln p曲线来描述非饱和土的应力状态(如图 3所示),加载曲线的斜率λ随基质吸力s的增大而减小,当s=0时(即饱和土)斜率λ达到最大。对于s=0和给定s的两个土样,分别在A, B两点屈服,所对应的屈服应力为先期固结压力pc和pcs。为保证模型中弹性部分保持平衡,BBM中回弹曲线的斜率κ认为与s无关。
|
| 图 3 饱和与非饱和土的压缩曲线 Fig. 3 Compression curves of saturated and unsaturated soils |
| |
Alonso等认为,屈服点A和屈服点B之间(即pc和pcs之间)存在如下的函数关系。
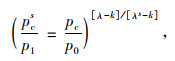
|
(1) |
式中λs随基质吸力s变化的经验公式为:
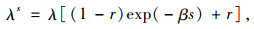
|
(2) |
式中, r为与土体最大刚度有关的常数; β为控制土体刚度λ随基质吸力s增长速率的参数。
式(1)定义了每个吸力值对应特定的屈服应力pcs,这些点在p-s应力平面中组成了一条屈服曲线,吸力的增加会导致先期固结应力增加,且在土体吸湿过程中会有体积坍塌的现象发生,因此这条屈服曲线被命名为LC(loading-collapse)屈服曲线。
当吸力s<sc时,土体处于弹性变形状态,当s>sc时,土体将产生塑性变形。sc为屈服与否的分界点,其实际意义与最大先期固结应力相似,为土体应力历史上的最大吸力值。将其绘在p-s平面内,为一条水平线,称之为SI(suction-increase)屈服曲线,相应的屈服函数为:
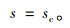
|
(3) |
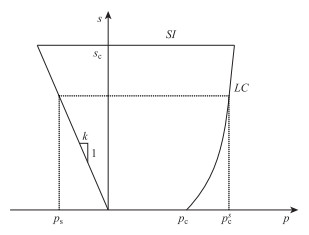
LC和SI屈服曲线在p-s平面上如图 4所示。
|
| 图 4 p-s平面上的屈服线 Fig. 4 Yield curve on p-s plane |
| |
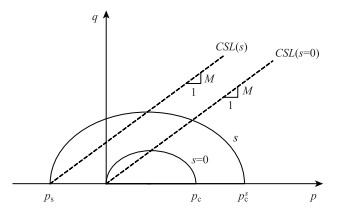
BBM模型中,其p-q平面的屈服轨迹借鉴了MCC模型中的屈服轨迹,即特定吸力下非饱和土的屈服轨迹为椭圆[11],因此BBM模型中p-q平面上的屈服轨迹如图 5所示。M仍为临界状态线(CSL)的斜率,且其大小保持不变,与土体是否处于饱和状态无关。ps是特定吸力下临界状态线在p轴上的截距,BBM模型认为吸力的存在会使土体黏聚力发生变化,且变化关系呈线性正相关,即ps=ks,k为反映黏聚力随吸力变化的常数。p-q平面上椭圆型屈服轨迹的最大水平半轴为(pcs-ps)/2,最大竖向半轴为M(pcs-ps)/2,椭圆中心位于点((pcs+ps)/2,0)。
|
| 图 5 空间屈服面在p-q平面上的投影 Fig. 5 Projection of spatial yield surface on p-q plane |
| |
BBM模型基于饱和土临界状态概念和增量塑性理论,能较好地反映非饱和土的主要应力-应变特征,其所需参数及物理意义如表 2所示。
| 符号 | 意义 |
| λ | 与p0相关的饱和土的压缩指数,与MCC相同 |
| κ | 与p0相关的弹性回弹系数,与MCC相同 |
| p0 | 初始应力,与MCC相同 |
| m | 泊松比,与MCC相同 |
| G | 剪切模量,与MCC相同 |
| M | 临界状态线的斜率,与MCC相同 |
| Pc | 饱和土的先期最大固结应力,与MCC相同 |
| λs | 考虑基质吸力的非饱和土压缩指数,与MCC类似 |
| κs | 考虑基质吸力的弹性回弹系数,与MCC类似 |
| pcs | 考虑基质吸力的非饱和土先期最大固结应力,与MCC类似 |
| β | 控制土体刚度λ随基质吸力s增长速率的参数 |
| r | 与土体最大刚度相关的常数 |
| k | 反映黏聚力随基质吸力变化的常数 |
| sc | 先期最大基质吸力 |
2.2 基质吸力的成因及确定方法
非饱和土与饱和土的主要区别在于土中存在第三相,即气相[12]。严格来说非饱和土中的水与气体的分界面,由于其性质的特殊性应被视为另一独立的相,称为收缩膜。正是由于收缩膜的存在,土中水可以有不同的应力值。与大气接触处的水压为0,而与收缩膜弯液面接触处的水压小于气接触处,即土中孔隙水压力uw为负值,说明土中水是处于承受拉应力的状态。弯液面两边孔隙气压力ua大于孔隙水压力uw,一般情况下孔隙气压力等于大气压,而ua与uw的差值称为基质吸力s[13]。
基质吸力反映以土的结构、土粒成分、孔隙分布形态等土的基质对土中水的吸持作用。基质吸力随土中含水量增加而降低,饱和土体所有孔隙已被水占据而没有吸水能力,即基质吸力为零。基质吸力是描述非饱和土力学性质的重要参数,亦是研究BBM本构模型的关键所在。常见基质吸力的测试方法包括为直接法和间接法两大类:其中直接测试方法有压力板仪法、张力计法、轴平移法;间接测试方法有湿度计法、滤纸法等。土体吸力与含水率间的关系曲线称之为土水特征曲线(SWCC),它能够反映非饱和土的强度、渗透性及持水能力等的基本性质,是研究非饱和土的重要纽带[14]。
另一方面,基质吸力也可通过理论计算得到,可根据弯液面表面内外差的Young-Laplace公式和弯液面表面蒸气压的Kelvin公式,推导出基质吸力的理论计算公式如下[15]:
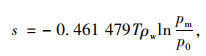
|
(4) |
式中, ρw为水的密度; T为绝对温度; pm为T温度下弯液面的蒸气压; p0为T温度下平液面的蒸气压。由式(4)可见,基质吸力与非饱和土中水-气体系的温度、孔隙水的密度和孔隙气的相对湿度有关。
2.3 BBM本构模型数值平台上的实现在FLAC3D数值模拟平台中,可通过FISH语言对MCC模型的一些参数(λ,v0,pc)进行修正,考虑基质吸力s的影响,使其变为BBM模型的参数λs,v0s,pcs,其转换公式如下所示[16-17]。
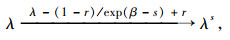
|
(5) |
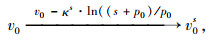
|
(6) |
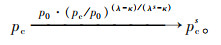
|
(7) |
根据BBM非饱和本构模型,在FLAC3D数值平台上对厦蓉高速公路漳州段高填路堤填筑全过程展开数值模拟,以分析其沉降变形特性。
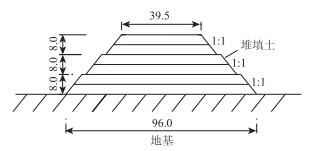
3.1 工程背景厦蓉高速公路漳州段,其线位呈南东-北西向展布,设计速度为80 km/h;双向8车道,整体式路基宽度39.5 m,单侧分离整幅4车道宽度为19.75 m。线路穿越地形起伏、地势条件复杂、相对高差较大的地段,为解决局部地区弃方量大,达到平衡填挖,沿线设有多处高填路堤段。其典型设计横断面示意图如图 6所示。堆填体高度共24 m,分为3阶,每阶堆填坡度均为1:1;每阶又分为4层堆填并碾压密实,每层堆高为2 m。
|
| 图 6 高填路堤典型设计横断面示意图(单位:m) Fig. 6 Schematic diagram of typical designed cross-section of high-filled embankment (unit: m) |
| |
3.2 数值模型
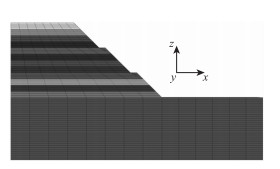
根据上述典型设计断面,考虑对称性,取右半侧高填路堤,建立相应的数值模型如图 7所示。原地基及上部堆填体均为六面体实体单元,共计68 200个单元,67 365个节点。其中原地基横向边界取3~5倍路基净宽,则X方向共计100 m;下部边界取3~5倍路堤沉降影响范围,则Z方向共计44 m;Y方向选取目标断面前后各20 m范围,共计40 m。边界条件为:顶面取自由边界,侧面与底面为法向位移约束边界。
|
| 图 7 数值模型网格划分示意图 Fig. 7 Schematic diagram of meshing in numerical model |
| |
原地基采用常规摩尔-库伦(MC)本构模型,堆填体则分别采用BBM或MCC本构模型。依据《工程地质手册》[18]及厦蓉高速公路(漳州段)设计文件,其本构参数具体取值如表 3所示。
| 参数 | MC | MMC | BBM |
| γ/(kN·m-3) | 20 | 18.6 | 18.6 |
| K/MPa | 5e3 | — | — |
| G/MPa | 3e3 | 29 | 29 |
| μ | 0.31 | 0.31 | |
| c/kPa | 60 | 4.86 | 4.86 |
| φ/(°) | 35 | 26.8 | 26.8 |
| M | — | 1.05 | 1.05 |
| λ或λs | — | 0.015 | 0.013 7 |
| κ | — | 0.01 | 0.01 |
| ν0或ν0s | — | 2 | 1.945 |
| P0/MPa | — | 0.1 | 0.1 |
| β /MPa-1 | — | — | 0.125 |
| r | — | — | 0.26 |
| s/MPa | — | — | 0.102 |
3.3 工况与测点
根据高填路堤的施工过程,沿填土高度每2 m堆填并压实一层,堆填总高度24 m,共计12个工况, 如表 4所示。同时,在路堤中部沿填土高度每隔4 m布置一个沉降监测点,共计6个监测点,观察其分层沉降随施工步的变化规律。
| 工况 | 堆载高度/m | 堆高对应z坐标 | 监测点坐标 |
| 1 | 2 | 20-22 | 测点1:z=21 m |
| 2 | 2 | 22-24 | |
| 3 | 2 | 24-26 | 测点2:z=25 m |
| 4 | 2 | 26-28 | |
| 5 | 2 | 28-30 | 测点3:z=29 m |
| 6 | 2 | 30-32 | |
| 7 | 2 | 32-34 | 测点4:z=33 m |
| 8 | 2 | 34-36 | |
| 9 | 2 | 36-38 | 测点5:z=37 m |
| 10 | 2 | 38-40 | |
| 11 | 2 | 40-42 | 测点6:z=41 m |
| 12 | 2 | 42-44 |
4 高填路堤的沉降特性分析
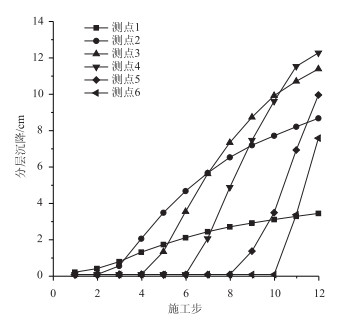
原地基采用MC本构,堆填体采用BBM非饱和土本构模型,根据数值模拟结果,绘制高填路堤分层沉降随施工步的变化规律,如图 8所示。
|
| 图 8 分层沉降随施工步的变化规律(BBM本构模型) Fig. 8 Stratified settlement varying with construction steps (BBM constitutive model) |
| |
首先比较各分层测点沉降的变化率,其变化率从底部(测点1)到顶部(测点6)呈现逐步增大的规律。这说明在相同荷载增量作用下,堆填体分层沉降的变化率与下伏可压缩层(堆填体自身)的厚度有关,其下伏层越厚,分层沉降变化率越大。
再比较各分层测点的最终沉降量,路堤底部所承受的上覆荷载最大,但其下伏可压缩层很薄,因此路堤底部(测点1)的分层沉降最小,仅为3.4 cm。同理,路堤顶部虽然下伏可压缩层较厚,但其承担的上覆荷载较小,故路堤顶部(测点6)的分层沉降也不大,约为6.9 cm。而路堤中部既承受了较大的上覆荷载,下伏也有较厚的可压缩层,因此最大分层沉降发生在路堤中部(测点4),达到12.3 cm。
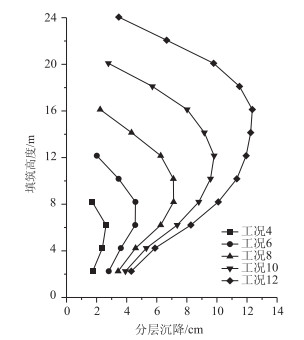
进一步地绘制各分层测点沉降量沿填土高度的分布规律,如图 9所示。各分层测点的沉降量在高程上呈中间大、两头小的规律,且随着施工步的进行,该规律愈发明显。上述结论与分层沉降结果相一致,也与李占锋[19]等的相关研究成果一致。
|
| 图 9 分层沉降沿高程的分布规律(BBM本构模型) Fig. 9 Distribution of stratified settlement along elevation (BBM constitutive model) |
| |
5 与MCC模型的对比
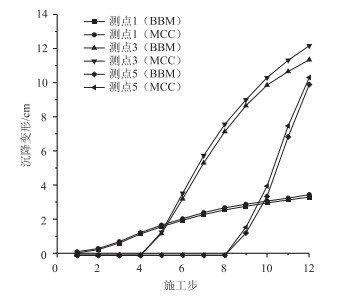
原地基仍采用MC本构,堆填体采用MCC饱和土本构模型,根据数值模拟结果,绘制高填路堤分层沉降随施工步的变化规律,如图 10所示。为了更好体现与前述BBM本构计算结果的区别,图中仅列出测点1,3,5的分层沉降。
|
| 图 10 分层沉降随施工步的变化规律(MCC与BBM对比) Fig. 10 Stratified settlement varying with construction steps (comparison between MCC and BBM) |
| |
由图 10可知,采用两种本构计算所得各测点分层沉降变化规律基本一致。但采用MCC本构计算所得的路堤分层沉降略大,以路堤中部测点3为例,其最终沉降量达到12.1 cm,比采用BBM本构的计算结果(11.2 cm)略大8%。
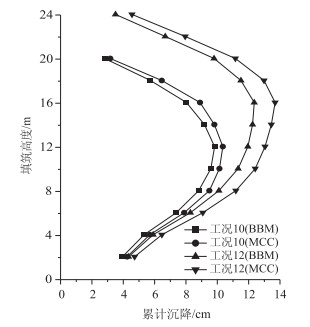
同样地,绘制各分层测点沉降量沿填土高度的分布规律,如图 11所示。为了便于与前述BBM本构计算结果进行对比,图中仅列出工况10和工况12的情形。
|
| 图 11 分层沉降沿高程的分布规律(MCC与BBM对比) Fig. 11 Distribution of stratified settlement along elevation (comparison between MCC and BBM) |
| |
由上图可知,采用两种本构模型计算所得的分层沉降沿填土高度分布规律基本一致,呈现出中间大、两头小的规律。但采用MCC本构计算所得的路堤分层沉降整体上均大于前者,以工况12为例,其路堤中部测点4的最终沉降量达到13.7 mm,比采用BBM本构的计算结果(12.3 mm)略大11.4%。
究其原因,BBM本构模型考虑了非饱和土基质吸力s的影响,并通过基质吸力s对饱和土MCC本构中的一些参数(λ,v0,pc)进行修正,使其沉降计算量与分布规律更符合工程实际。上述结果与前人采用饱和与非饱和弹黏塑性本构模型,对高填路堤填筑过程展开数值模拟的结论相一致[20]。
6 结论以厦蓉高速公路漳州段高填路堤工程为背景,基于BBM非饱和土本构模型,在FLAC3D数值平台分析了路堤堆填体自身的分层沉降特性。同时与常规MCC饱和土本构模型的计算结果相比照,得到主要结论如下:
(1) 无论采用BBM非饱和土本构模型或是MCC饱和土本构模型,其计算所得路堤自身的分层沉降量,均沿填土高度呈现出中间大、两头小的分布形态。与底部及上部相比,路堤中部既承受了较大的上覆荷载,也下伏有较厚的可压缩层,因此最大分层沉降发生在路堤中部。
(2) BBM本构充分考虑了非饱和土基质吸力的影响,并通过基质吸力对MCC本构中的一些参数进行修正,其计算所得沉降量整体上略小于MCC本构的计算结果,其沉降计算量与分布规律更符合工程实际。
| [1] |
杨静. 基于ABAQUS软件对路基拓宽沉降规律的分析[J]. 中国公路, 2018(15): 96-97. YANG Jing. Analysis of Subgrade Widening Settlement Law Based on ABAQUS Software[J]. China Highway, 2018(15): 96-97. |
| [2] |
郑建斌. 软土地区路基沉降数值分析[J]. 中国公路, 2018(6): 98-99. ZHENG Jian-bin. Numerical Analysis of Subgrade Settlement in Soft Soil Area[J]. China Highway, 2018(6): 98-99. |
| [3] |
李自强. 有限元二次开发的山区软土区地基沉降量计算方法[J]. 云南水力发电, 2016, 32(6): 65-69. LI Zi-qiang. The Foundation Settlement Calculation Method in Mountainous Soft Soil Areas Based on the Finite Element Secondary Development[J]. Yunnan Water Power, 2016, 32(6): 65-69. |
| [4] |
占鑫杰, 高长胜, 朱群峰, 等. 连云港港区深厚淤泥地基筑堤数值分析[J]. 岩土工程学报, 2017, 39(11): 2109-2115. ZHAN Xin-jie, GAO Chang-sheng, ZHU Qun-feng, et al. Numerical Analysis of Breakwater Construction on Soft Clay in Harbor Area of Lianyungang Port[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(11): 2109-2115. |
| [5] |
曹海莹, 窦远明. 上硬下软型双层路基应力扩散特征及工程应用[J]. 公路交通科技, 2012, 29(2): 29-34. CAO Hai-ying, DOU Yuan-ming. Characteristics of Dry Crust's Stress Dispersion in Two-layer Roadbed and Its Engineering Application[J]. Journal of Highway and Transportation Research and Development, 2012, 29(2): 29-34. |
| [6] |
李林峰. 基于位移反分析的拓宽路基差异沉降预测[J]. 公路交通科技, 2015, 32(1): 57-62. LI Lin-feng. Prediction of Differential Settlement of Widened Subgrade Based on Displacement Back Analysis[J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 57-62. |
| [7] |
赵志峰, 邵光辉, 杨小平. 单侧高填土道路加宽工程的稳定性及变形实测[J]. 公路交通科技, 2013, 30(9): 33-37. ZHAO Zhi-feng, SHAO Guang-hui, YANG Xiao-ping. Stability and Measurement of Deformation in Widening of Unilateral High Filled Road[J]. Journal of Highway and Transportation Research and Development, 2013, 30(9): 33-37. |
| [8] |
ROSCOE K H, SCHOFIELD A N, WROTH C P. On the Yielding of Soils[J]. Geotechnique, 1958, 8(1): 22-53. |
| [9] |
ALONSO E E, GENS A, JOSA A. A Constitutive Model for Partially Saturated Soils[J]. Geotechnique, 1990, 40(3): 405-430. |
| [10] |
ALONSOE E, 杨代泉. 非饱和土弹塑性应力应变特性模拟[J]. 岩土工程学报, 1995(6): 42-51. ALONSO E E, YANG Dai-quan. Elasto-plastic Modelling for the Stress and Strain Behaviour of Unsaturated Soil[J]. Chinese Journal of Geotechnical Engineering, 1995(6): 42-51. |
| [11] |
李涛, 史世波. 含统一屈服面的非饱和黏性土弹塑性本构模型[J]. 北京工业大学学报, 2011, 37(11): 1684-1691. LI Tao, SHI Shi-bo. Elastoplastic Constitutive Model for Unsaturated Cohesive Soils with a Unified Yield Surface[J]. Journal of Beijing University of Technology, 2011, 37(11): 1684-1691. |
| [12] |
包承纲. 非饱和土的性状及膨胀土边坡稳定问题[J]. 岩土工程学报, 2004, 26(1): 1-15. BAO Cheng-gang. Behavior of Unsaturated Soil and Stability of Expansive Soil Slope[J]. Journal of Geotechnical Engineering, 2004, 26(1): 1-15. |
| [13] |
何秋奇.基于土水特征曲线的非饱和橡胶颗粒改良粉煤灰土强度研究[D].长春: 吉林大学, 2018. HE Qiu-qi. Study on Strength in Unsaturated Fly Ash Soil Modified by Rubber Crumbs Based on Soil-water Characteristic Curve[D]. Changchun: Jilin University, 2018. |
| [14] |
白福青, 刘斯宏, 袁骄. 滤纸总吸力吸湿曲线的率定试验[J]. 岩土力学, 2011, 32(8): 2336-2340. BAI Fu-qing, LIU Si-hong, YUAN Jiao. Calibration Test for Total Suction Wetting Curve of Filter Paper[J]. Rock and Soil Mechanics, 2011, 32(8): 2336-2340. |
| [15] |
姚海林. 关于基质吸力及几个相关问题的一些思考[J]. 岩土力学, 2005, 26(1): 67-70. YAO Hai-lin. Some Considerations about the Concept of Matric Suction and Questions Related to Matric Suction[J]. Rock and Soil Mechanics, 2005, 26(1): 67-70. |
| [16] |
史世波.具有统一屈服面的非饱和粘性土弹塑性本构模型[D].北京: 北京交通大学, 2008. SHI Shi-bo. An Elasto-plastic Constitutive Model for Unsaturated Cohesive Soils with a Unified Yield Surface[D]. Beijing: Beijing Jiaotong University, 2008. |
| [17] |
陈育民. FLAC/FLAC3D基础与工程实例[M]. 北京: 中国水利水电出版社, 2013. CHEN Yu-min. FLAC/FLAC3D Foundation and Engineering Examples[M]. Beijing: China Water & Power Press, 2013. |
| [18] |
工程地质手册编写委员会. 工程地质手册[M]. 北京: 中国建筑工业出版社, 2002. Engineering Geology Handbook Editorial Committee. Engineering Geology Handbook[M]. Beijing: China Architecture & Building Press, 2002. |
| [19] |
李占锋. 山区高填路堤沉降特征研究[J]. 公路工程, 2019, 44(2): 169-172. LI Zhan-feng. Study on Settlement Characteristics of High Fill Embankment in Mountain Area[J]. Highway Engineering, 2019, 44(2): 169-172. |
| [20] |
周芊妤.基于弹粘塑性本构的高填方路堤沉降计算理论及工程应用[D].湘潭: 湘潭大学, 2018. ZHOU Qian-yu. Calculation Thoery and lts Engineering Application of Settlement of High-filled Embankment Based on Elasto-viscoplastic Constitutive Model[D]. Xiangtan: Xiangtan University, 2018. |
 2020, Vol. 37
2020, Vol. 37
