扩展功能
文章信息
- 李吉祥, 范晨光, 李彦达
- LI Ji-xiang, FAN Chen-guang, LI Yan-da
- 共振碎石机振动机理及参数研究
- Study on Vibration Mechanism and Parameters of Resonance Stone Crusher
- 公路交通科技, 2020, 37(11): 15-21
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(11): 15-21
- 10.3969/j.issn.1002-0268.2020.11.003
-
文章历史
- 收稿日期: 2019-09-17
水泥路面共振碎石化技术是旧水泥路面碎石化改造及再生利用的一项关键工程技术。由于其高效环保的施工特点,已经成为目前旧水泥路面最有效的改造方法。作为共振破碎机进行碎石作业的核心系统,共振系统工作端的响应输出受共振梁各结构参数、激振器频率及激振力大小等因素的影响。在共振系统的设计过程中,可以通过控制共振系统结构参数的方法来控制系统频率及响应。因此,针对共振系统的力学建模和理论分析,可以加深对共振碎石化机械工作原理和系统性能的认识。
随着对混凝土路面的大量修复的需要,共振碎石化技术的自主研发和产业化需求日益迫切。美国的共振机械有限公司(RMI)是目前国际上唯一掌握共振碎石化核心技术并研发出共振式道路破碎机用于现场施工的企业。1980年,Raymond等[1-2]申请了共振试验台架的专利,对共振式道路破碎机共振梁的支撑节点位置及激振频率展开研究,并申请了共振式道路破碎机的发明专利。国内研究起步较晚。徐海[3]结合多体系统动力学理论知识,运用虚拟样机技术,对共振破碎机振动系统进行了动力学仿真研究。Zhang等[4]基于共振式路面破碎车共振系统的结构,给出了破碎机的共振频率和振幅的参数模型。基于比例泵空马达,建立了频率调节的控制模型,针对共振系统模型中的不确定参数设计了一套自适应的算法,从而得出各个参数的自适应规律,利用Lyapunov函数,验证了频率的输入的规律。李万莉等[5]通过经典力学方法在理论上建立了共振梁受迫振动的动力学模型,并利用振型叠加法对此动力学方程进行求解,但并没有给出求解结果及各项系统参数对共振频率的影响。黄家善等[6]釆用控制器得到了破碎机的电气系统。晏星凡[7]以反求理论为理论基础,运用多刚体多力学、智能优化和有限元等技术,对破碎机的振动系统进行了反求仿真分析,获得了1组设计参数,在这组参数下,动力学模型的分析结果跟原型机结果相近,并且能满足平顺性要求。纪秀业[8]借助仿真分析技术,对共振破碎机的车架结构进行设计研究,进一步完善了对车架的优化设计。王晓友[9]建立了刚柔耦合的虚拟样机模型,研究了整梁柔性化和分段柔性化对振动特性的影响,并研究了激振器不同的频率时路面的响应特性。李盛等[10]研究了不同频率和行进速度对共振碎石化整体破碎效果的影响,发现共振破碎机行进速度对破碎粒径大小、回弹模量和弯沉值的大小均有影响。
比较来看, 国内对共振碎石化技术的研究并不深入,虽然部分企业开始了共振碎石化机械的应用,但是一直还处在道路施工技术摸索阶段[11-18],目前尚缺乏对共振系统振动机理及其参数控制的完整动力学理论分析及参数研究的文献报道。本研究根据共振碎石化机械的特点,建立共振系统的动力学模型,并推导其运动微分方程,利用假设模态法离散,计算系统固有频率及强迫振动响应,研究各系统参数对固有特性及响应特性的影响。
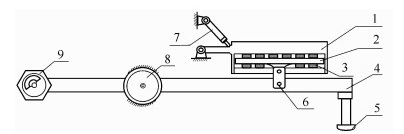
1 共振系统运动方程的建立 1.1 共振系统的模型及简化共振破碎机通过控制激振端的振动频率,使共振大梁带动锤头产生振动。当振动频率等于或接近水泥混凝土路面的固有频率时,在锤头作用下,激励路面板块产生共振,当混凝土路面强迫响应超过混凝土颗粒间最大摩擦力时,混凝土内部产生剪切破环,从而达到破碎路面的效果。目前,常用的共振碎石化机械的共振系统结构简图如图 1所示[3]。
|
| 图 1 共振结构示意图 Fig. 1 Schematic diagram of resonance structure 1—配重体; 2—承载体; 3—减振材料; 4—共振梁; 5—碎锤头; 6—吊耳; 7—举升油缸; 8—橡胶减震器; 9—激振器 |
| |
由于共振大梁振动时产生弯曲变形,为方便动力学方程建模,做出如下简化[3]:
(1) 将共振梁视为等截面梁。忽略吊耳及橡胶减振器部位的铰接孔对梁横向弯曲刚度的影响。
(2) 忽略激振器及锤头的细节,将其简化为集中质量块,分别位于共振梁的两边。
(3) 与共振梁连接的支承部分简化为弹簧。
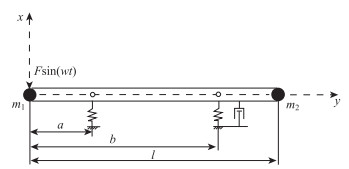
简化后的动力学模型如图 2所示,Fsin(wt)为外激励,激振器和破碎锤头分别简化为共振梁两端的集中质量m1及m2,共振大梁支承部分简化为弹簧,等效刚度分别为k1, k2,在锤头端的等效弹簧处加一阻尼器,阻尼系数为c。以m1为原点建立坐标系,共振大梁总长度为l,a为原点到第1个弹簧的距离,b为原点到第2个弹簧的距离。
|
| 图 2 简化后的共振系统动力学模型 Fig. 2 Simplified dynamic model of resonance system |
| |
1.2 共振系统的动力学方程推导
结合实际的共振碎石机,将系统的振动分为两部分,分别为刚体振动和弹性体振动。共振系统的动力学方程应同时包含两部分的振动。首先计算刚体振动阶段的固有频率和模态,再通过假设模态法离散系统方程,最后计算响应。
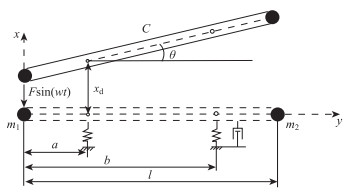
1.2.1 刚体振动固有频率的推导与计算共振系统的刚体振动分为刚体平移和刚体转动两部分。设系统做刚体平移的竖向位移为xd,做刚体转动的角度为θ,C为共振梁的质心,如图 3所示。
|
| 图 3 共振梁的刚体振动示意图 Fig. 3 Schematic diagram of rigid body vibration of resonance beam |
| |
考虑梁上的附加质量及弹性支撑,系统做刚体振动的动能及势能可表示为:
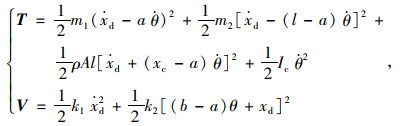
|
(1) |
式中,T为系统的动能;V为系统的势能;m1为激振端质量;m2为锤头端质量;ρ为共振大梁的密度;A为大梁截面积;k1为激振端弹簧等效刚度;k2为锤头端弹簧等效刚度;xc为质心距离原点的长度,xc= 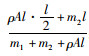
由拉格朗日方程,
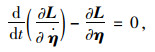
|
(2) |
式中,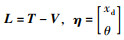
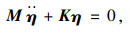
|
(3) |
式中,
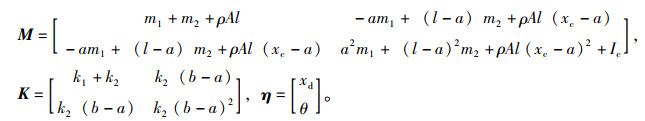
|
将式(2)整理成标准特征值问题可得:
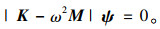
|
(4) |
通过特征值分析,即可求出系统做刚体振动时的两阶固有频率ω及模态ψ,分别为ω1和ω2,ψ1和ψ2。
1.2.2 共振系统运动方程设y(x, t)为梁的横向位移,梁上作用有单位长度分布力q(x, t),根据文献[10]得到系统横向振动偏微分方程为:
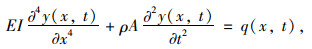
|
(5) |
式中EI为共振大梁的抗弯刚度。
设共振梁的第i阶振型函数为ψi(x),系统的响应可表示为:
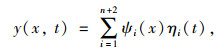
|
(6) |
式中, ηi(t)为广义坐标,当i=1,2时,ψ1和ψ2是上一小节中计算得到的刚体振动阶段的模态, η1(t),η2(t)为相应的广义坐标。当i≥3时,假设其模态为两端自由梁的模态[18],表示为:
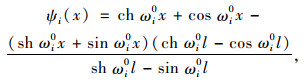
|
(7) |
式中, ωi0为对应阶次的固有频率,可表示为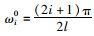
然后列出系统共振运动时的动能和势能为:
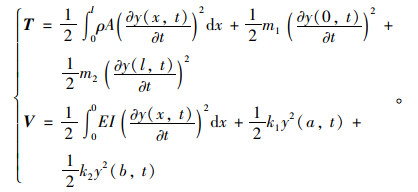
|
(8) |
将系统响应代入整理可得:
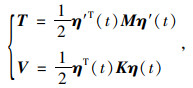
|
(9) |
式中,η′(t)为广义坐标对时间的一阶偏导;质量矩阵和刚度矩阵分别为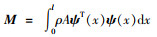
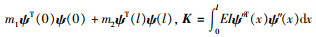
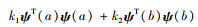
由于结构一旦确定且材料不变的情况下,结构阻尼的变化是十分小的,所以为了研究阻尼比对共振大梁的影响,在锤头端弹簧处加有一个阻尼器,其阻尼系数定为c1,以此作为整个系统的阻尼。所以阻尼矩阵即可表示为:
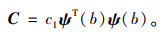
|
(10) |
采用式(5)离散后的系统运动方程的一般矩阵形式:
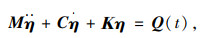
|
(11) |
式中,Q(t)为广义外力,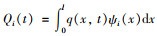
激振器通过偏心质量块旋转产生激振力。激振力F的大小可表示为[3]:
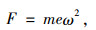
|
(12) |
式中,e为转子质心的偏心半径;m为转子的质量;ω为外激励频率。
由于激振力是作用于梁激振端的集中力,故需要将集中力转变为分布力进行表示。引入狄拉克函数δ(x-xi),其中xi为集中力作用点的坐标,则广义力表示为:
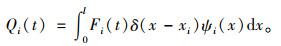
|
(13) |
由此,将连续系统振动问题离散为多自由度系统振动问题。
2 系统响应求解忽略阻尼,求解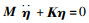
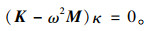
|
(14) |
解得ωi为系统第i阶固有频率,κi为对应特征向量。
设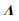
设η=Aq,代入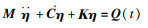
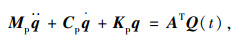
|
(15) |
式中第i个方程为:
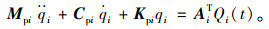
|
(16) |
两端同除以Mpi,并令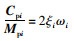
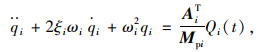
|
(17) |
式中ξi为振型阻尼比,可以求得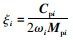
又因为Qi(t)=Pi(t)sin(ωt),其中Pi(t)为同一频率的简谐激振力,所以式(15)可写为:
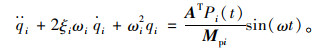
|
(18) |
由单自由度强迫振动的结论,主坐标下的稳态解为:
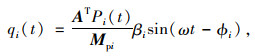
|
(19) |
式中,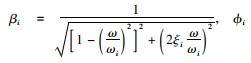
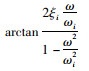
所以,可以得到:
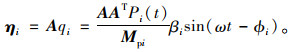
|
(20) |
系统的响应为:
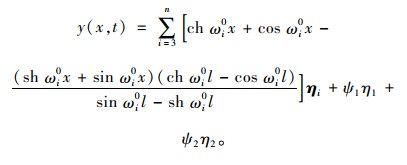
|
(21) |
根据文献[3]中数据进行计算:振动梁长度l=3.85 m,截面宽b=0.5 m,截面高h=0.15 m,激振端集中质量m1=300 kg;锤头集中质量m2=100 kg;材料弹性模量E=2.1×1011 Pa;材料密度ρ=7 850 kg/m3;激振器参数,转子质心半径e=56 mm;转子质量m=23 kg;激振频率35~53 Hz。在满足精度要求的前提下,为简化计算,取n=5。
共振碎石机工作过程中,要求锤头的振动频率为35~53 Hz。当共振碎石机的固有频率与激振力的频率相近时,才能实现共振碎石机的最佳工作状态。由式(12)求得系统前5阶固有频率,如表 1所示。
由表 1可以发现,固有频率与文献[3]中对比,低阶误差很小,在5阶频率开始出现误差,考虑是由于模态选取数量较少产生的误差,由于共振碎石机的工作频率在35~53 Hz之间,故可忽略高阶频率的误差。此外,系统做刚体振动时的固有频率非常小,实际的振动过程中以弹性振动为主,与文献[10]对比后发现,共振碎石机频率和行进速度较佳组合为:振动频率为48 Hz,共振时行进速度为1.3 km/h。与计算结果的43.06 Hz误差不大,较为可信。
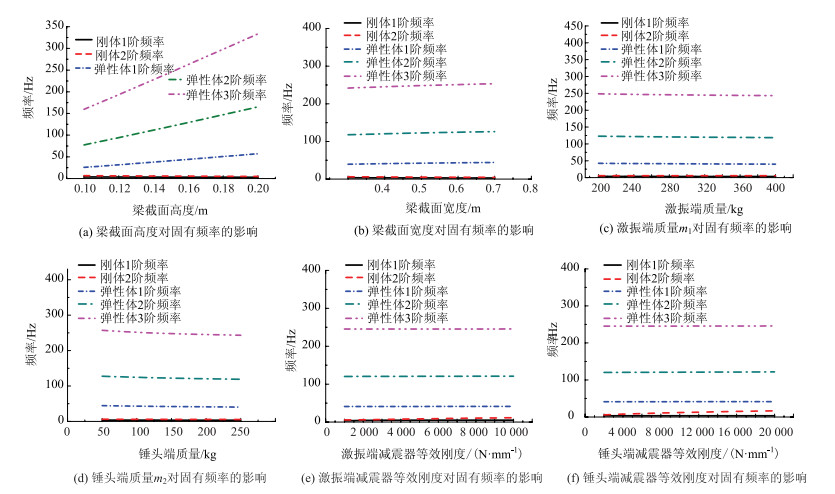
3.2 系统参数对固有频率的影响共振系统的频率与系统的结构参数有密切关系。通过改变系统结构参数,可以对系统固有频率进行控制。共振大梁截面高度及宽度、激振端质量、锤头端质量、激振端和锤头端减振器等效刚度等都可能会对系统固有频率产生影响。图 4(a)~(f)分别给出了各个参量对系统的固有频率的影响。
|
| 图 4 系统结构参数对固有频率的影响 Fig. 4 Influence of system structure parameters on natural frequency |
| |
可以看出,共振梁截面高度及宽度、激振端质量、锤头端质量、激振端和锤头端减振器等效刚度等参数都会对系统固有频率产生影响。其中,系统各阶固有频率随着共振梁截面宽度、截面高度的增大而增大,随着激振端质量、锤头质量的增大而减小;增大激振端减振器等效刚度,系统各阶固有频率增大;增大锤头端减振器等效刚度,系统各阶固有频率也将增大。对比可见,共振梁截面高度的变化对系统模态的影响最为显著,可以通过控制共振梁截面高度来有效改变梁的各阶频率。
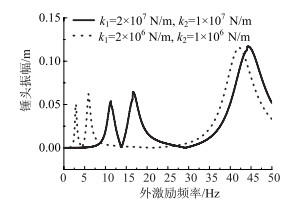
3.3 外界激振频率对锤头端振幅的影响激振力的频率及大小是由激振器提供的。改变激振器激振频率会引起锤头振幅的改变。选取了两阶刚体模态及第3阶弹性体模态所求得的锤头端响应关系,并且使用不同的弹簧减震器刚度值进行对比,如图 5所示。
|
| 图 5 外激励频率与锤头振幅的关系曲线 Fig. 5 Curves of external excitation frequency vs. hammerhead amplitude |
| |
在激振器结构确定的情况下,激振力的频率逼近系统固有频率时,锤头振幅变大。所以在激振力频率接近系统固有频率的情况下,对能量的利用更为高效。
3.4 阻尼系数对锤头端振幅的影响取阻尼器的阻尼系数为变量,研究其阻尼系数对共振大梁锤头振幅的影响。由前文可知:ξi= 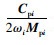
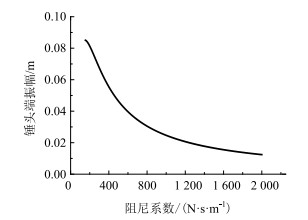
图 6为系统以弹性振动1阶固有频率发生共振时的共振大梁阻尼系数取值与锤头振幅的关系。可以看出,随着阻尼系数的增大,锤头的振幅也逐渐变小,与阻尼影响振动衰减一致。
|
| 图 6 阻尼器的阻尼系数与锤头振幅的关系曲线 Fig. 6 Curve of damping coefficient of damper vs. hammerhead amplitude |
| |
4 结论
本研究从共振大梁的刚体振动和弹性振动出发,建立了共振碎石机共振大梁的动力学模型。基于假设模态法,求解了系统参数对其固有频率及强迫响应的影响,对工程应用上更好地理解共振碎石机的振动原理起到了积极的作用,填补了目前共振碎石机振动机理理论计算的空白,着重研究了系统参数对共振频率的影响,结论如下:
(1) 在本研究的参数下,系统做刚体振动时的固有频率分别为3.35,5.87 Hz,不在共振碎石机的工作频率范围内,计算获得的工作频率为43.06 Hz,发生在弹性振动阶段,共振大梁的梁高在0.1~0.16 m区间内时为最佳工作频率,有助于工程应用中控制共振梁的固有频率。
(2) 当外激励频率接近共振大梁的固有频率时发生共振,锤头的振幅会变大,且弹簧刚度越大,发生共振的频率越高,此时对能量的利用率更为高效。
(3) 阻尼系数在200~2 000 (N·s)/m范围内变化时,最大锤头振幅为0.084 m,其对锤头振幅的影响呈反比趋势,与阻尼影响振动衰减一致。
| [1] |
GURRIES R A. Resonant System Support: US, 4320807[P].1982-03-23.
|
| [2] |
GURRIES R A. Resonantly Driven Pavement Crusher: US, 4402629[P].1983-09-06.
|
| [3] |
徐海.共振破碎机振动系统的动力学仿真研究[D].武汉: 武汉理工大学, 2012. XU hai. Dynamic Simulation Study of Vibration System of Resonance Crusher[D]. Wuhan: Wuhan University of Technology, 2012. |
| [4] |
ZHANG P J, JIANG X H. Adaptive Backstepping Control Based upon DRFNN for RCRBV[J]. Advanced Materials Research, 2011, 403-408: 5082-5087. |
| [5] |
李万莉, 刘鹏. 共振梁受迫振动的动力学建模与求解[J]. 建设机械技术与管理, 2014, 27(1): 101-103. LI Wan-li, LIU Peng. The Dynamics Modeling and Solving of the Resonance Beam with Forced Vibration[J]. Construction Machinery Technology and Management, 2014, 27(1): 101-103. |
| [6] |
黄家善, 黄靖, 张平均. 水泥路面共振式破碎车的控制系统设计与分析[J]. 福建师范大学学报:自然科学版, 2010, 26(6): 64-68. HUANG Jia-shan, HUANG Jing, ZHANG Ping-jun. Design and Analysis of Control System for RCPBV[J]. Journal of Fujian Normal University:Natural Science Edition, 2010, 26(6): 64-68. |
| [7] |
晏星凡.基于仿真和优化方法的共振破碎机振动系统反求研究[D].成都: 西南交通大学, 2008. YAN Xing-fan. Reverse Research on Vibration System of Resonance Crusher Based on Simulation and Optimization Method[D]. Chengdu: Southwest Jiaotong University, 2008. |
| [8] |
纪秀业.共振式道路破碎机车架设计与研究[D].武汉: 武汉理工大学, 2011. JI Xiu-ye. Frame Design and Research of Resonance Road Crusher[D]. Wuhan: Wuhan University of Technology, 2011. |
| [9] |
王晓友.共振破碎机车路耦合的动力学仿真研究[D].武汉: 武汉理工大学, 2013. WANG Xiao-you. Dynamic Simulation Research on Vehicle-road Coupling of Resonant Crusher[D]. Wuhan: Wuhan University of Technology, 2013. |
| [10] |
李盛, 马永波, 刘朝晖, 等. 共振碎石化控制参数和结构模量研究[J]. 内蒙古公路与运输, 2019, 169(1): 5-8. LI Sheng, MA Yong-bo, LIU Zhao-hui, et al. Study on Control Parameters and Structural Modulus of Resonance Crushedization[J]. Highway & Transportation in Inner Mongolia, 2019, 169(1): 5-8. |
| [11] |
刘增晖. 共振碎石化在水泥混凝土路面改造中的应用[J]. 山西建筑, 2015, 41(23): 142-143. LIU Zeng-hui. The Application of Resonance Broken Petrochemical Technology in Cement Concrete Pavement Reconstruction[J]. Shanxi Architecture, 2015, 41(23): 142-143. |
| [12] |
周祖兰. 碎石化技术在旧水泥混凝土路面改造施工中的应用[J]. 筑路机械与施工机械化, 2018, 35(9): 105-108. ZHOU Zu-lan. Application of Rubblization Technology in Reconstruction of Existing Cement Concrete Pavement[J]. Road Machinery and Construction Mechanization, 2018, 35(9): 105-108. |
| [13] |
黄琴龙, 陈达豪, 凌建明, 等. 共振碎石化在上海水泥混凝土路面改建中的成效[J]. 长沙理工大学学报:自然科学版, 2008, 5(2): 103-106. HUANG Qin-long, CHEN Da-hao, LING Jian-ming, et al. Performance of Rubblization on Jointed Concrete Pavement Rehabilitation in Shanghai[J]. Journal of Changsha University of Science and Technology:Natural Science Edition, 2008, 5(2): 103-106. |
| [14] |
高璇, 吴彦. 共振碎石化技术在水泥混凝土路面养护中的应用[J]. 交通世界, 2018(8): 40-41, 47. GAO Xuan, WU Yan. Application of Resonance Crushedization Technology in Cement Concrete Pavement Maintenance[J]. Transpo World, 2018(8): 40-41, 47. |
| [15] |
陈可弟.全浮动式共振破碎机振动系统动力学性能研究[D].徐州: 中国矿业大学, 2019. CHEN Ke-di. Research on Dynamic Performance of Vibration System of Full-floating Resonance Crusher[D]. Xuzhou: China University of Mining and Technology, 2019. |
| [16] |
曹征磊. 共振碎石化技术在旧水泥路面改造施工中的应用[J]. 交通世界, 2019(5): 28-29. CAO Zheng-lei. Application of Resonance Crushedization Technology in Reconstruction of Old Cement Pavement[J]. Transpo World, 2019(5): 28-29. |
| [17] |
熊雪明. 共振碎石化技术在双港大街改造中的应用[J]. 城市道桥与防洪, 2019(7): 59-60, 64, 11. XIONG Xue-ming. Application of Resonance Rubblization Technology in Reconstruction of Shuanggang Street[J]. Urban Road Bridge and Flood Control, 2019(7): 59-60, 64, 11. |
| [18] |
倪振华. 振动力学[M]. 西安: 西安交通大学出版社, 1988. NI Zhen-hua. Vibration Mechanics[M]. Xi'an: Xi'an Jiaotong University Press, 1988. |
 2020, Vol. 37
2020, Vol. 37
