扩展功能
文章信息
- 潘兵宏, 赵悦彤, 温长鹏, 杨婵君, 梅杰
- PAN Bing-hong, ZHAO Yue-tong, WEN Chang-peng, YANG Chan-jun, MEI Jie
- 基于驾驶人视觉特性和停车视距的公路平面交叉角度研究
- Study on Highway Intersection Angle Based on Driver's Visual Characteristics and Stopping Sight Distance
- 公路交通科技, 2020, 37(10): 118-126
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(10): 118-126
- 10.3969/j.issn.1002-0268.2020.10.013
-
文章历史
- 收稿日期: 2019-10-16
平面交叉(以下简称平交)作为道路相交节点,交通信息复杂,车辆运行存在较多冲突点,事故频发,尤其是无信号控制平交,由于缺乏信号灯管控,导致路权分配不明,使得无信号平交成为道路安全的短板,统计表明,在平交发生的事故中,有70%发生在无信号平交[1]。无信号平交根据交叉角度可划分为正交和斜交两种形式,交叉角度直接影响平交的安全性和经济性。一方面,交叉角度影响交叉面积,随角度减小,部分转弯象限交叉面积逐渐增大,车辆穿越冲突区域时间增加,不利于平交的经济与安全;另一方面,角度过小,会影响处于锐角象限驾驶人的通视效果[2]。我国《公路路线设计规范》(JTG D20—2017)(以下简称《路线规范》)[3]指出:平交应尽量正交,一般情况,锐角交叉角度(简称交角)应不小于70°,条件困难时,应不小于45°;而《公路路线设计规范》(JTG D20—2006)[4]规定:在条件困难时,应不小于60°;对于条件困难时的最小交叉角度值的变更,在条文中没有给出解释,且对不同设计速度道路的平交交角没有细分。美国《A Policy on Geometric Design of Highways and Streets》 (简称AASHTO)[5]指出:平交的冲突取决于驾驶人的判断、反应、驾驶能力;对于无信号平交,速度是影响驾驶人决策的关键因素[6]。驾驶人行为受驾驶人信息获取能力制约,80%以上的道路信息获取渠道为视觉[7],因此,本研究结合驾驶人视觉特性,根据平交视距的要求,探究不同设计速度下相交道路平交交角最小值。
关于平交斜交交角,基于事故频率与平交几何特性、交通量、交通组织方式关系的广义线性模型研究指出,斜交平交受视距和穿越距离影响使得事故频发[8],斜交交角越小, 平交形状越狭长,直行车辆通过时间越长,对转弯车辆行驶影响越大,而采取增大锐角象限转弯半径,会使形状更为狭长[9],斜交可能导致车身阻碍锐角象限驾驶人视线,对于停车让行交叉口70°~75°的交角有助于改善视线[10];针对畸形平交存在的问题,常采用交通组织优化方法,并通过仿真验证优化措施的有效性[11],当畸形平交视距受限时,可通过限速来增加驾驶人视角[12],或利用磁感线圈与单片机建立一种辅助方法进行处理[13]。文献[14-15]研究了平交视距长度优化取值,建立验算平交视距的三维模型[16],基于驾驶人视认性,通过仿真试验可获得驾驶人感知反应时间,进而计算斜交平交视距[17]。国内研究均基于规范给出的斜交交角最小值,探究斜交带来的不利影响,并修正斜交情况下,视距三角形中采用的停车视距;但忽视了《路线规范》对交角最小值界定模糊,没有探究平交交角最小取值的合理性。本研究通过分析驾驶人视觉特性,研究被交路驾驶人行车动态视野处于极大值情况下,针对一般视距三角形,分析求解平交交角计算方法,并结合规范,分析模型中关键参数的取值,进而确定不同设计速度道路相交时交角最小值。
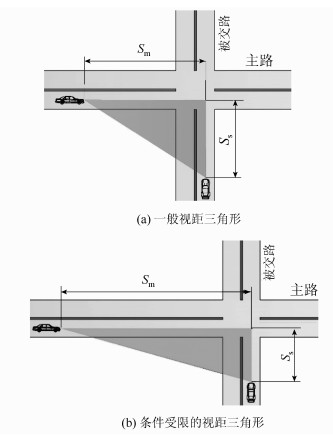
1 平交相交角度的影响因素 1.1 平交视距三角形无信号控制平交需保证在视距三角形内主路、被交路上的通视性,视距三角形由停车视距夹平交交角组成。根据平交选址是否受到地形、特殊构造物等条件限制,可以划分为一般视距三角形与条件受限的视距三角形, 分别如图 1(a)、图 1(b)所示。
|
| 图 1 视距三角形 Fig. 1 Sight triangles |
| |
对于满足条件的一般视距三角形,正交平交驾驶人在行驶至决策点(即停车视距起点)时,会判断视野范围内有无车辆,然后采取减速让行或直接通过等措施,保证行驶安全。平交斜交时,处于锐角象限驾驶人视野会受限,由于主路设计速度大于等于被交路设计速度,故主路停车视距Sm大于等于被交路停车视距Ss,根据三角形几何原理,边长较长的边对应较大内角,在驾驶人行驶至决策点,被交路驾驶人动视野范围先达到极大值,故在驾驶人视野范围处于极大值时,平交角度极小值由被交路驾驶人视野决定。
对于条件受限的视距三角形如图 1(b)所示,对应被交路停车让行的平交[3],被交路驾驶人决策点至冲突点距离Ss为5~7 m,主路驾驶人决策点至冲突点距离应满足安全交叉停车视距Sm。《公路项目安全性评价规范》(JTG805—2015)指出:停车让行平交,位于被交路驾驶人行驶过程为先在决策点附近停车,当主路出现可接受间隙时,次路车辆伺机通过。被交路驾驶人伺机时,处于静止状态,其眼部动视野范围可到达静止状态下极大值62°[18], 再配合头部及身体扭转,因而驾驶人视野可覆盖视距三角形范围,故研究对象为一般视距三角形。
1.2 驾驶人动态视野驾驶人动态视野,指在行驶时,驾驶人头部固定的前提下,通过眼球自由转动,驾驶人能够看到的视野范围。试验结果表明动视野取值与车辆行驶速度密切相关[19-21],随着车辆行驶速度提高,动视野可见区域缩小,见表 1。
| 行驶速度/(km·h-1) | 40 | 60 | 70 | 80 | 95 |
| 视野/(°) | 100 | 86 | 70 | 60 | 40 |
经回归分析,视野极值与行驶速度呈显著线性关系,如式(1)所示。此时R2=0.985,t检验结果表明回归系数和常数的p值均小于0.05。公路设计速度取值范围为20~100 km/h,采用公式(1)计算得到不同设计速度下驾驶人动视野,见表 2,可知在20 km/h时驾驶人视野在水平范围达到最大值左右各61°, 小于人机工程学人眼视野范围极值62°[23]。
| 设计速度/(km·h-1) | 20 | 30 | 40 | 60 | 80 | 100 |
| 视野/(°) | 122 | 112 | 100 | 86 | 60 | 40 |
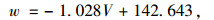
|
(1) |
式中, w为人眼双侧动视野范围;V为行驶速度。
1.3 驾驶人头部扭转特性车辆行驶过程中,驾驶人通过视觉获取信息的过程,是眼球与头部转动共同作用的结果。动视野获取信息范围受限时,驾驶人会自然转动头部,以获取所需信息。文献[18, 22-23]指出,头部自然转动角度界限取左右各45°为宜。在考虑驾驶人头部转动的情况下,可得到不同速度下驾驶人单侧视野极值, 见表 3。因此可把单侧视野极值作为驾驶人在平交处的单侧视野范围,超过此范围,将影响驾驶人对平交范围内交通状况信息的获取,不利于驾驶员做出正确的判断。
| 设计速度/(km·h-1) | 20 | 30 | 40 | 60 | 80 | 100 |
| 单侧视野/(°) | 106 | 101 | 95 | 88 | 75 | 65 |
2 平交最小交角计算模型 2.1 被交路车辆直行时最小交角计算模型
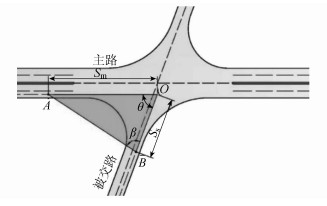
主、被交路驾驶人均处于斜交锐角象限,当被交路车辆直行,主路与被交路直行车辆存在冲突点O。为确保行车安全,应确保驾驶人在看到冲突车辆后,均能在O点前安全停车。考虑临界情况如图 2所示,假定被交路驾驶人在决策点B处单侧视野达到极大值为β, OB为被交路的停车视距Ss(按表 4取值),当主路上距离OA恰好等于停车视距值Sm(按表 4取值)时,对应平交交叉角度θ取极小值。在三角形AOB中,根据正弦定理求出OA关于θ的表达式,如公式2所示。由于不利于驾驶人观察的情况是锐角象限,故θ的取值范围为(0, 90°)。
|
| 图 2 被交路车辆直行平交角度 Fig. 2 Intersection angle of vehicle going straight on crossed road |
| |
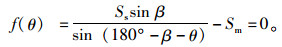
|
(2) |
图 2中相交道路停车视距计算公式根据AASHTO[5]如公式(3)所示。我国交叉口视距三角形两相交道路的停车视距(又称引道视距)与一般路段相同,没有考虑车辆驶近交叉口减速行为;而美国交叉口附近的停车视距区别于一般路段,考虑了驾驶人在驶近交叉口的减速行为。为贴合实际行驶情况、保障安全,同时适用于我国现有交叉口设计情况,在计算交叉口停车视距时,不对道路设计速度折减,但减速度取值考虑在交叉口减速时的最大值4.51 m/s2[24],如公式(4)所示, 纵向摩阻系数根据《澳大利亚道路设计指南》取0.46[25],计算取整后停车视距结果见表 4。
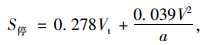
|
(3) |
式中, a为减速度,4.51 m/s2;t为反应时间,取2.5 s[3](判断时间1.5 s、运行时间1.0 s);
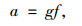
|
(4) |
式中,g为重力加速度,9.8 m/s2;f为纵向摩擦系数,0.46。
| 速度/(km·h-1) | 15 | 20 | 25 | 30 | 40 | 60 | 80 | 100 |
| 停车视距/m | 15 | 20 | 25 | 30 | 40 | 75 | 110 | 160 |
利用二分法求出使得公式(2)成立的θ值,被交路车辆直行斜交角度计算结果见表 5。
| 主路设计速 度/(km·h-1) |
20 | 30 | 40 | 60 | 80 | 100 | |
| 被交路设 计速度/ (km·h-1) |
80 | — | — | — | — | 30° | 63° |
| 60 | — | — | — | 不限 | 50° | 64° | |
| 40 | — | — | 不限 | 53° | 64° | 71° | |
| 30 | — | 不限 | 32° | 56° | 63° | 68° | |
| 20 | 不限 | 35° | 46° | 60° | 64° | 67° | |
从表 5可知:《路线规范》[3]规定,一般情况下平交交叉角度值应不小于70°,基本满足不同设计速度道路相交时斜交角度计算最小值要求;当主路设计速度较高时,斜交平交交叉角度最小值比《路线规范》[3]规定的条件困难时最小值大;而速度不超过40 km/h,规范规定的条件困难时交角最小值基本满足计算得到的最小值。主、被交路设计速度相同时,设计速度为60 km/h及以下路段斜交角度不受驾驶人视野范围限制,因为此时视距三角形为等腰三角形,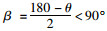
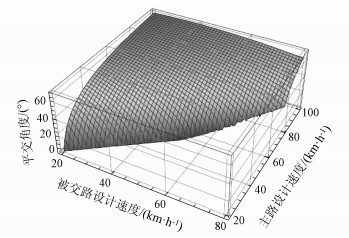
主、被交路设计速度不同,斜交交角计算值不同,为进一步探究交角与设计速度之间变化关系,将停车视距计算公式(3)代入式(2),得到相交道路设计速度与斜交交角之间的具体关系,见公式5,绘制交角θ与主、被交路设计速度之间的三维图像,如图 3所示。
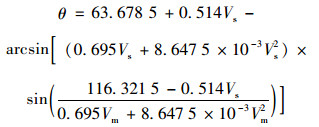
|
(5) |
式中,Vs为被交路设计速度;Vm为主路设计速度;θ为平交交角。
|
| 图 3 被交路车辆直行平交角度与设计速度关系 Fig. 3 Relationship between intersection angle of vehicle going straight on crossed road and design speed |
| |
从图 3可知:当被交路速度一定时,交叉角度最小值随主路设计速度增大而逐渐增大,且增大幅度随主路设计速度增大而减小。当主路设计速度在80~100 km/h,交叉角度随被交路运行速度增大,先增大后减小,在被交路设计速度为40 km/h时,取极大值,且被交路设计速度与40 km/h差值越大,下降幅度越显著;当主路设计速度低于80 km/h时,交叉角度最小值随被交路设计速度增大而逐渐增大,且增大幅度随被交路设计速度增大而增大。
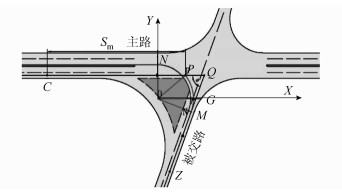
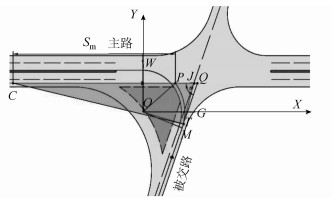
2.2 被交路车辆左转时最小交角计算模型当被交路车辆左转,与主路直行车辆存在冲突,其中主路最外侧直行车道与被交路左转最内侧车道为该种情况下的最不利冲突, 如图 4所示,主路和被交路单车道宽分别表示为l1和l2,主路车道数n1,中间带宽度μ1。ZP为被交路车辆行驶轨迹,CP为主路车辆行驶轨迹(假定为道路中线),ZM与CP延长线交于点Q,∠CQZ为平交角度θ,被交路中间带右侧边线与主路中间带左侧边线导圆角,形成的部分轨迹圆为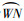
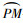
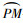
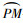
|
| 图 4 被交路车辆左转平交角度 Fig. 4 Intersection angle of vehicle turning left on crossed road |
| |
(1) 被交路行车视距小于左转曲线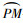
当被交路驾驶人在转弯段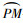
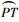
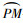
|
图 5 被交路行车视距小于左转曲线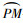 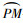 |
| |
车辆在转弯段行驶的速度取值根据《路线设计规范》[3], 见表 6。当左转弯车速取最大时,对应单侧视野极值最小,由表 3可知为101°,由于101°>90°,故被交路驾驶人观测主路冲突车辆位置位于第一象限时,单侧视野极值β一定能够覆盖∠CTJ。当驾驶人位于第二象限时,计算模型如下,P点坐标:
| 左转速度/(km·h-1) | 15 | 20 | 25 | 30 |
| 最小半径/m | 15 | 20 | 25 | 30 |
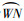
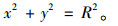
|
(6) |
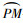
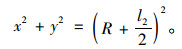
|
(7) |
直线PQ所在直线表达式为:
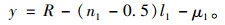
|
(8) |
由式(7)、式(8)联立得P点的坐标:
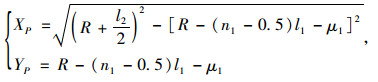
|
(9) |
C点坐标表示为:
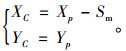
|
(10) |
因为∠GOT=∠WOP+∠POT-90°,∠POT为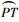
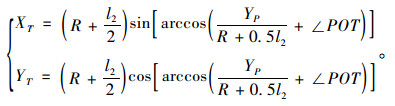
|
(11) |
在△OTC中,根据余弦定理得:
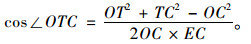
|
(12) |
因为被交路驾驶人观测角∠CTJ=90°+∠OTC,而∠OTC与平交交角θ无关,故单侧视野极值β能否覆盖视距三角形,与平交交角θ无关,即此时驾驶人视野不会限制平交交角。
(2) 被交路行车视距大于等于左转曲线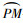
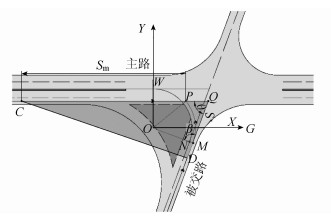
当被交路驾驶人在直行段ZM观测主路冲突车辆, 如图 6所示,假设观测点为D,D为ZM上任意一点,Z点为被交路车辆开始减速对应位置。被交路驾驶人在驶近交叉口左转前,即使主路不存在潜在冲突车辆,为保障行车安全,驾驶人会减速至左转弯半径对应左转速度(表 6),由于驾驶人观测点位置存在个体差异,故在计算平交角度时,驾驶人观测点D是任意的,被交路驾驶人在D点速度取值范围为[R, Vs], Vs为被交路设计速度,计算D点速度从最小值到最大值对应的平交交角θ。情况2中P点坐标与情况1相同。
|
图 6 被交路行车视距大于等于左转曲线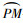 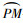 |
| |
由四边形内角和定理得∠WON=180°-θ,因为x轴y轴相互垂直,求得M点坐标与x轴夹角∠GON=90°-θ, 根据三角函数求得M点坐标:
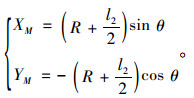
|
(13) |
根据QM斜率k=tan θ,求得Q点坐标:
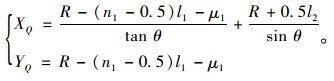
|
(14) |
由两点坐标距离公式求得QM, CQ:
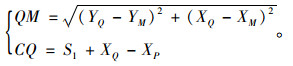
|
(15) |
根据坐标反算圆心角,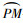
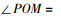
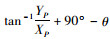
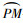
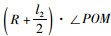
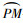
在三角形QCM中,根据正弦定理求出CQ关于θ的表达式(16),利用二分法求满足条件θ,并验证求得θ带入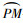
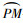
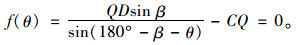
|
(16) |
根据《路线规范》[3],各级公路中间带宽度,车道数及宽度取值依据见表 7,各参数取值代入被交路车辆左转平交角度计算模型,分别计算R取15,20,25,30 m时,被交路驾驶人在观测点D速度从最小值,以步长1变化到最大值时对应平交交角最小值,根据计算结果取平交交角最小值中的最大值作为主、被交路设计速度既定情况下,保障平交视距三角形通视的最小角度(表 8)。并绘制主、被交路设计速度一定,被交路驾驶人观测主路冲突车辆D点速度及位置变化对于平交交角的影响趋势图,如图 7所示。
| 公路等级 | 一级公路 | 二级公路 | 三、四级公路 | |||||
| 设计速度/(km·h-1) | 100 | 80 | 60 | 80 | 60 | 40 | 30 | 20 |
| 车道宽度/m | 3.75 | 3.75 | 3.5 | 3.75 | 3.5 | 3.5 | 3.25 | 3.0 |
| 车道数 | 4 | 2 | 2 | |||||
| 中间带宽/m | 3.5 | 3 | 3 | 无 | 无 | 无 | 无 | 无 |
| 主/被交路设计速度/(km·h-1) | R=15 m | R=20 m | R=25 m | R=30 m | |||||
| θ | VD | θ | VD | θ | VD | θ | VD | ||
| 主路一级公路 | 100/80 | 70 | 38 | 70 | 40 | 71 | 42 | 70 | 43 |
| 100/60 | 70 | 38 | 70 | 40 | 71 | 42 | 70 | 45 | |
| 100/40 | 70 | 38 | 70 | 40 | 71 | 40 | 70 | 40 | |
| 100/30 | 69 | 30 | 70 | 30 | 70 | 30 | — | — | |
| 100/20 | 69 | 15 | — | — | — | — | — | — | |
| 80/80 | 66 | 17 | 66 | 24 | 66 | 31 | 66 | 37 | |
| 80/60 | 66 | 17 | 66 | 24 | 66 | 31 | 66 | 37 | |
| 80/40 | 66 | 17 | 66 | 24 | 66 | 31 | 66 | 37 | |
| 80/30 | 66 | 17 | 66 | 24 | — | — | — | — | |
| 80/20 | 66 | 17 | — | — | — | — | — | — | |
| 60/60 | 62 | 18 | 60 | 26 | 59 | 34 | 58 | 41 | |
| 60/40 | 62 | 18 | 60 | 26 | 59 | 34 | — | — | |
| 60/30 | 62 | 18 | 60 | 26 | — | — | — | — | |
| 60/20 | 62 | 18 | — | — | — | — | — | — | |
| 主路二级公路 | 80/80 | 67 | 25 | 68 | 32 | 68 | 38 | 69 | 44 |
| 80/60 | 67 | 25 | 68 | 32 | 68 | 38 | 69 | 44 | |
| 80/40 | 67 | 25 | 68 | 32 | 68 | 38 | — | — | |
| 80/30 | 67 | 25 | — | — | — | — | — | — | |
| 80/20 | — | — | — | — | — | — | — | — | |
| 60/60 | 62 | 26 | 61 | 34 | 61 | 41 | 61 | 47 | |
| 60/40 | 62 | 26 | 61 | 34 | — | — | — | — | |
| 60/30 | 62 | 26 | — | — | — | — | — | — | |
| 60/20 | — | — | — | — | — | — | — | — | |
| 主路三四级公路 | 40/40 | 50 | 29 | 47 | 38 | — | — | — | — |
| 40/30 | 50 | 29 | — | — | — | — | — | — | |
| 40/20 | — | — | — | — | — | — | — | — | |
| 30/30 | — | — | — | — | — | — | — | — | |
| 30/20 | — | — | — | — | — | — | — | — | |
| 20/20 | — | — | — | — | — | — | — | — | |
注:表格中—表示计算得到的θ不满足验证条件,即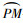 ≤Ss。 ≤Ss。 |
|||||||||
|
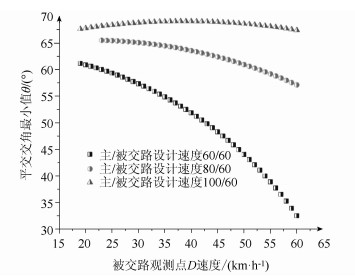
| 图 7 被交路车辆观测点速度不同时对应左转平交角度 Fig. 7 Intersection angle of vehicle turning left on crossed road at different speeds at observing point |
| |
图 7表征主、被交路设计速度一定,被交路驾驶人在观测点D行驶速度不同时,对应平交交角最小值变化趋势。当被交路设计速度一定,主路设计速度小于100 km/h,平交交角最小值随观测点速度变大而逐渐降低;而主路设计速度为100 km/h时,平交交角最小值随观测点速度变大先增加后降低。当被交路设计速度改变,主路设计速度仍取上述3种情况,变化趋势与被交路设计速度为60 km/h相同。
由表 8可知,主被交路设计速度一定,主路设有中间带道路比不设中间带道路的平交交角最小值小,说明设置中间带在一定程度上可提高平交范围的通视性, 但影响幅度较小。在主、被交路设计速度及道路等级一定情况下,增大左转弯半径,被交路驾驶人在D点观测到主路冲突车辆时速度VD增大,但增大左转半径对于改善平交口视距条件没有必然联系。当且仅当被交路设计速度降低,其他条件不变时,平交交角最小值降低,但下降幅度较小,故将表 7进行简化如表 9所示。
| 主路等级 | 三、四级 | 二级 | 一级 | |||||
| 主路设计速度/ (km·h-1) |
20 | 30 | 40 | 60 | 80 | 100 | 60 | 80 |
| 平交交角θ/(°) | — | — | 50 | 62 | 69 | 71 | 62 | 66 |
2.3 平交锐角最小值
根据表 9计算后化简结果,结合表 5被交路直行视距计算的平交交角,两者取大值得到公路平交交角最小值θ。出于方便施工考虑,将交角最小值取整为整5或整10 m,最终得到满足驾驶人视野范围的不同设计速度下平交角度锐角最小值,见表 10。从表 10可知:平交交叉角度最小值取值范围为35°~75°;平交交角与主路设计速度相关。根据《路线设计规范》[3]规定:平交交角在条件困难时,应不小于45°,在一般情况下,应不小于70°。与表 10对比,可知平交交角若想在任何情况下均能保障视距三角形通视性,应将70°变为75°。
| 主路设计速度/(km·h-1) | 20 | 30 | 40 | 60 | 80 | 100 |
| 平交交角θ/(°) | — | 35 | 50 | 65 | 70 | 75 |
3 结论
驾驶人在通过平交冲突区域时,其感知、判断和反应能力是避免车辆冲突的关键,应确保驾驶人在平交范围内视线良好。本研究基于平交视距三角形,根据驾驶人动态视觉特性,以驾驶人位于平交决策点处视野区域覆盖视距三角形为条件,分别建立被交路车辆直行和左转时平交角度计算模型,并采用规范中道路横断面设计指标的建议值,利用二分法求解出满足驾驶人视野范围的不同设计速度下平交角度锐角最小临界值。研究表明当主路设计速度大于等于40 km/h,被交路左转为限制平交交角最小值主要情况,其余情况受主路车辆直行限制,平交交角与主路设计速度、驾驶人在观测点D时的速度密切相关。创新点如下:
(1) 基于驾驶人位于平交决策点处的视野范围和一般视距三角形,建立了被交路车辆直行和左转交叉角度最小值计算模型。
(2) 被交路车辆直行情况下,平交交角与主、被交路设计速度关系如下:被交路速度一定,交叉角度最小值随主路设计速度增大而增大。当主路设计速度在80~100 km/h,交叉角度随被交路运行速度增大,先增后减,被交路设计速度为40 km/h时,取极大值;当主路设计速度低于80 km/h时,交叉角度最小值随被交路设计速度增大而增大。
(3) 被交路车辆左转情况下,主被交路设计速度一定,主路设有中间带道路比不设中间带道路的平交交角最小值小,说明设置中间带在一定程度上可提高平交范围的通视性。在主、被交路设计速度及道路等级一定情况下,增大左转弯半径,被交路驾驶人观测到主路冲突车辆时速度增大,但增大左转半径对于改善平交口视距条件没有必然联系。
(4) 提出了平交斜交时,保证锐角象限驾驶人视线良好的不同设计速度下公路斜交最小交角建议值。
研究成果细化了我国平交最小交角的规定,但研究只考虑了主、被交路线形都是直线的情况,考虑平交纵坡较缓,忽略了纵坡对视距的影响,今后将进一步研究主要道路平面线形为圆曲线情况,并计算纵坡为3%时停车视距修正对平交交角的影响。
| [1] |
张国强, 亓玉礼, 张清源. 无信号公路平交口次路进口道机动车运行研究[J]. 武汉理工大学学报:交通科学与工程版, 2014, 38(6): 1221-1225. ZHANG Guo-qiang, QI Yu-li, ZHANG Qing-yuan. Study on Motor Vehicle Operation on Minor Road Approach at Non-signalized At-grade Intersection of Highways[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2014, 38(6): 1221-1225. |
| [2] |
日本道路公团. 日本高速公路设计要领[M]. 西安: 陕西旅游出版社, 1991.
|
| [3] |
JTG D20-2017, 公路路线设计规范[S]. JTG D20-2017, Design Specifications for Highway Alignment[S]. |
| [4] |
JTG D20-2006, 公路路线设计规范[S]. JTG D20-2006, Design Specifications for Highway Alignment[S]. |
| [5] |
AASHTO. A Policy on Geometric Design of Highways and Streets[M].Washington, D.C.: American Association of State Highway and Transportation Officials, 2011.
|
| [6] |
LIU M, LU G, WANG Y, et al. Analyzing Drivers' Crossing Decisions at Unsignalized Intersections in China[J]. Transportation Research Part F:Traffic Psychology and Behaviour, 2014, 24: 244-255. |
| [7] |
袁伟, 付锐, 郭应时, 等. 驾驶员视觉搜索模式模糊聚类评价方法[J]. 中国公路学报, 2011, 24(1): 103-108. YUAN Wei, FU Rui, GUO Ying-shi, et al. Fuzzy Clustering Evaluation Method for Driver's Visual Search Mode[J]. China Journal of Highway and Transport, 2011, 24(1): 103-108. |
| [8] |
HALL R D. Accidents at Four-arm Single Carriageway Urban Traffic Signals, No.CR65[R]. Crowthorne, UK: Transport Research Laboratory, 1986.
|
| [9] |
徐家钰, 梁家民. X形交叉口的改善[J]. 上海公路, 1997(2): 25-31. XU Jia-yu, LIANG Jia-min. Improvement of X-shaped Intersection[J]. Shanghai Highways, 1997(2): 25-31. |
| [10] |
GATTIS J, LOW S T. Intersection Angle Geometry and the Driver's Field of View[J]. Transportation Research Record, 1998, 1612: 10-16. |
| [11] |
秦焕美, 关宏志, 赵红征, 等. 基于仿真的畸形交叉口交通组织优化研究[J]. 交通信息与安全, 2010, 28(4): 43-48. QIN Huan-mei, GUAN Hong-zhi, ZHAO Hong-zheng, et al. Simulation-based Traffic Organization Optimization for Irregular Intersections[J]. Journal of Transport Information and Safety, 2010, 28(4): 43-48. |
| [12] |
李薇, 张志伟, 李兴庆, 等. 公路X形交叉口通行安全与效率研究[J]. 中外公路, 2016, 36(1): 321-325. LI Wei, ZHANG Zhi-wei, LI Xing-qing, et al. Research on Safety and Efficiency of Highway X-shaped Traffic[J]. Journal of China & Foreign Highway, 2016, 36(1): 321-325. |
| [13] |
文渊, 周扬, 韩如碧, 等. 一种解决无信号控制交叉口视距不良的辅助控制方法[J]. 公路交通科技, 2012, 29(增1): 44-49. WEN Yuan, ZHOU Yang, HAN Ru-bi, et al. An Auxiliary Control Method to Overcome Inappropriate Sight Span[J]. Journal of Highway and Transportation Research and Development, 2012, 29(S1): 44-49. |
| [14] |
袁浩, 史桂芳, 黄晓明, 等. 停车视距制动模型[J]. 东南大学学报:自然科学版, 2009, 39(4): 859-862. YUAN Hao, SHI Gui-fang, HUANG Xiao-ming, et al. Braking Model of Stopping Sight Distance[J]. Journal of Southeast University:Natural Science Edition, 2009, 39(4): 859-862. |
| [15] |
刘浪, 白彬, 燕南, 等. 基于驾驶员视认性的山区双车道公路交叉口停车视距计算[J]. 重庆交通大学学报:自然科学版, 2017, 36(5): 98-103. LIU Lang, BAI Bin, YAN Nan, et al. Calculation on Stopping Sight Distance of Two-lane Mountainous Highway Intersection Based on Driver's Visual Characteristics[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2017, 36(5): 98-103. |
| [16] |
袁浩, 程建川, 黄晓明. 交叉口视距的三维模型研究[J]. 公路交通科技, 2007, 24(12): 136-139. YUAN Hao, CHENG Jian-chuan, HUANG Xiao-ming. Research on Three-dimensional Model of Intersection Sight Distance[J]. Journal of Highway and Transportation Research and Development, 2007, 24(12): 136-139. |
| [17] |
郭忠印, 刘天龙, 周小焕. 基于驾驶人视认性的畸形交叉口安全视距计算[J]. 华东交通大学学报, 2012, 29(3): 46-50. GUO Zhong-yin, LIU Tian-long, ZHOU Xiao-huan. A Safety Sight Distance Calculation in the Skewed Intersection Based on the Driver's Observation Features[J]. Journal of East China Jiaotong University, 2012, 29(3): 46-50. |
| [18] |
吕杰锋, 陈建新, 徐进波. 人机工程学[M]. 北京: 清华大学出版社, 2009. LÜ Jie-feng, CHEN Jian-xin, XU Jin-bo. Human Engineering[M]. Beijing: Tsinghua University Press, 2009. |
| [19] |
赵炳强. 驾驶人动态视觉特征及其影响[J]. 公路交通科技, 1998, 15(1): 102-104. ZHAO Bing-qiang. Driver's Dynamic Visual Characters and Its Effects[J]. Journal of Highway and Transportation Research and Development, 1998, 15(1): 102-104. |
| [20] |
潘兵宏, 赵一飞, 梁孝忠. 动视觉原理在公路线形设计中的应用[J]. 长安大学学报:自然科学版, 2004, 24(6): 20-24. PAN Bing-hong, ZHAO Yi-fei, LIANG Xiao-zhong. Application of Dynamic Vision Theory in Highway Alignment Design[J]. Journal of Chang'an University:Natural Science Edition, 2004, 24(6): 20-24. |
| [21] |
许金良, 王荣华, 冯志慧, 等. 基于动视觉特性的高速公路景观敏感区划分[J]. 交通运输工程学报, 2015, 15(2): 1-9. XU Jin-liang, WANG Rong-hua, FENG Zhi-hui, et al. Classification of Expressway Landscape Sensitive Zone Based on Dynamic Visual Characteristics[J]. Journal of Traffic and Transportation Engineering, 2015, 15(2): 1-9. |
| [22] |
项英华. 人类工效学[M]. 北京: 北京理工大学出版社, 2008. XIANG Ying-hua. Ergonomics[M]. Beijing: Beijing Institute of Technology Press, 2008. |
| [23] |
SAE J985-2004, Vision Factors Considerations in Rearview Mirror Design[S].
|
| [24] |
杨永红, 吴传海, 葛婷. 山区高速公路超车道小客车停车视距安全性[J]. 长安大学学报:自然科学版, 2014, 34(5): 42-48. YANG Yong-hong, WU Chuan-hai, GE Ting. Safety of Stop Sight Distance of Freeway Passing Lane for Passenger Car in Mountainous Area[J]. Journal of Chang'an University:Natural Science Edition, 2014, 34(5): 42-48. |
| [25] |
FANNING R, VEITH G, WHITEHEAD M, et al. Guide to Road Design Part 3: Geometric Design[M]. Sydney: NSW, 2016.
|
 2020, Vol. 37
2020, Vol. 37
