扩展功能
文章信息
- 杨雅勋, 杨福利, 陈东
- YANG Ya-xun, YANG Fu-li, CHEN Dong
- 改进响应面法在桥梁结构有限元模型修正中的应用
- Application of Improved Response Surface Method in Modification of Bridge Structure FE Model
- 公路交通科技, 2020, 37(10): 83-91, 133
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(10): 83-91, 133
- 10.3969/j.issn.1002-0268.2020.10.009
-
文章历史
- 收稿日期: 2019-11-06
2. 上海市政工程设计研究总院(集团)有限公司天津分公司 天津 300042
2. Tianjin Branch, Shanghai Municipal Engineering Design General Institute(Group) Co., Ltd., Tianjin 300042, China
采用有限元模型对工程结构分析已成为现在工程设计必不可少的环节。模型建立过程中的多种因素的简化、截面尺寸误差、材料性能参数、连续介质离散化的精度及施工过程中某些不确定因素的影响等都会使初始有限元模型计算结果与实测结果存在偏差[1]。因此,务必考虑对初始有限元模型修正,使其与桥梁实际受力性能一致。
国内外已对有限元模型修正进行了一系列的研究,提出了几种模型修正方法,主要有矩阵修正法、灵敏度法和响应面法等[2]。矩阵修正法将质量矩阵、刚度矩阵作为修正对象对有限元模型进行修正,但复杂结构的矩阵不容易得出,且修正后的矩阵往往不具有稀疏、对称的性质,丧失了其物理意义[3-5]。灵敏度法对于修正参数选取有较大随机性和单一性,每次迭代必须调用程序计算,计算量较大,修正效率低[6-8]。响应面法由于其精确性和高效性在优化设计、可靠度分析和有限元模型修正中得到广泛应用[9-11]。
本研究对传统响应面法进行改进,并将改进后响应面法应用到一座系杆拱桥的有限元模型修正中,以铺装层的厚度及各构件的弹性模量和密度为待修正参数,采用F检验法寻找显著性高的参数,通过函数拟合构造响应面模型,再根据试验数据,在响应面内优化求解,得到最优解对有限元模型进行修正。在响应面法的基础上,利用成桥荷载试验数据对一座系杆拱桥模型进行修正,修正前后误差明显降低,验证了该方法在系杆拱桥模型修正中的有效性。
1 基于响应面法的有限元模型修正理论 1.1 修正参数及响应参数的选取通常选择材料的弹性模量、密度、泊松比阻尼比、摩擦系数、支座刚度等作为待修正参数。当基于动力测试数据对模型进行修正时,响应值通常为模态振型和模态频率,当基于静力测试数据对模型进行修正时,响应值通常为挠度和应变。
1.2 试验设计与参数显著性检验以有限的试验次数获得最有效的试验数据的关键在于试验设计,样本数据的增加能够使模型的精确度提高,但大量的数据会使计算效率显著降低[12]。因此,在不影响精度的前提下,选择最具代表性的样本数据是试验设计的中心原则。D-最优设计是一种基于最小化协方差矩阵|(X′X)-1|的计算机随机生成的设计,在拟合响应面模型时,其样本个数为n=(k+1)(k+2)/2(k为待修正参数的数量),与其他试验设计相比,具有较高的精度且试验次数少[12]。
参数显著性检验是对参数响应值进行方差分析,结合F检验法,挑选显著性高的参数。其基本原理是将总离差平方和分解为由各个试验因素引起的离差平方和SSA和试验数据本身偏差引起的离差平方和SSE,然后,构造服从F分布的统计量FA:通过计算出的FA值进行假设检验,判定参数的显著性。
统计量:
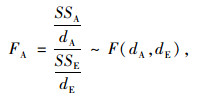
|
(1) |
式中,dA为因素自由度数,dE为偏差自由度数。在方差分析中,对于给定的显著性水平α,当F≥F1-α(nc, ne)即P≤α时,则称该因素对其影响显著;否则,该因素对响应值的影响不显著。
1.3 改进响应面法对于修正参数较多,输入值和响应值之间存在高度非线性的问题,传统响应面法构造的响应面模型往往精度不高,所以更适合局部模型的建立,而径向基函数的方法可用于全局显式模型的建立[13]。改进响应面法是将二阶多项式与径向基函数相结合作为响应面的模型函数, 旨在提高模型与实际结构在参数取值的全局范围内的契合度,提高模型修正的精度。
根据最佳一致理论中的哈文条件的等价定义[14],径向基函数是未知函数唯一的最佳一致逼近形式[13]。根据不同的径向基函数的函数近似结果,发现对不同类型的测试函数、高斯函数的均方根误差均较小,说明高斯径向基函数具有良好的拟合适应性、较高的精度和应用的广泛性[15]。所以,选择高斯函数作为径向基函数,随着空间维数的增加,计算量呈线性增长,对模型的非线性模拟适应能力强[16-19]。因此, 将多项式函数和径向基函数相结合作为响应面函数,形成混合响应面[20-23],即改进响应面法。
传统响应面法一般选用二阶多项式作为响应面模型函数式[24],其函数形式如式(2);对传统响应法进行改进,在二阶多项式后增加高斯函数项,旨在提高响应面拟合精度,其方程形式如式(3):
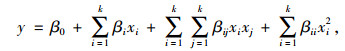
|
(2) |

|
(3) |
式中,xi∈[xil, xiu],xil, xiu为待修正参数的取值下限和取值上限;β0,βi,βii,βij为组成响应面模型的多项式系数;ai为高斯函数待定系数; ‖x-xi‖表示实测值到第i个样本均值的范数; σ为高斯函数宽度参数。
文献[13]通过大量的数值算例验证,总结出σ取值的经验公式:
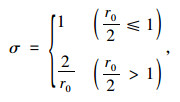
|
(4) |
式中r0为设计空间内最远两点的距离。
检验响应面拟合程度可靠性的标准有:
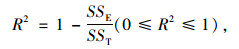
|
(5) |
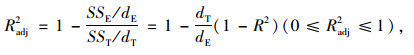
|
(6) |
式中,dE为偏差的自由度;dT为总自由度;SSE为误差的离差平方和;SST为总离差平方和;R2和Radj2的值越靠近1,响应面的可靠性越高。
1.4 优化求解构造目标函数对响应面模型进行优化求解[25]。目标函数表达式如式(7):
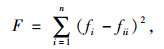
|
(7) |
式中,fi为响应面模型的计算值,fii为结构的实测值。在参数取值区间内,当目标函数F取最小值时,得到参数最优解,即修正后的参数取值。
2 有限元模型修正 2.1 工程概况与有限元模型建立贵州岑巩黄弓大桥为(52+70+52) m的三跨系杆拱桥,拱轴线为二次抛物线,主拱矢高14 m。主拱圈和纵梁均为2 m×1.2 m的矩形截面,中横梁为1.35 m×0.8 m的矩形截面,横撑为1.2 m×1 m的内八角形箱形截面,均为钢筋混凝土材料;吊杆采用消除预应力镀锌高强钢丝束。材料参数见表 1。根据桥梁的结构信息,采用ANASYS建立主桥的有限元模型如图 1所示。

|
| 图 1 黄弓大桥有限元模型 Fig. 1 Finite element model of Huanggong Bridge |
| |
| 结构 | 材料 | 弹性模量/(×1010 Pa) | 密度/(kg·m-3) |
| 拱肋 | C40混凝土 | E1=3.25 | D1=2 549 |
| 纵梁 | C50混凝土 | E2=3.45 | D2=2 549 |
| 横梁 | C40混凝土 | E3=3.25 | D3=2 549 |
| 吊杆 | 高强钢丝 | E4=20.5 | D4=7 850 |
2.2 静动载试验 2.2.1 静载试验
按照作用效应等效的原则进行荷载试验,获得主拱圈跨中和纵梁跨中各测点的数据。为保证其合理有效性,按影响线的最不利位置进行加载,并保证各截面的加载效率在0.95~1.05之间,本次静载试验共采用4辆35T的三轴加载车,设置4个工况:
(1) 工况1:L/2拱肋、纵梁截面最大正弯矩中载工况;
(2) 工况2:L/2拱肋、纵梁截面最大正弯矩偏载工况。
(3) 工况3:L/4拱肋、纵梁截面最大正弯矩中载工况;
(4) 工况4:L/4拱肋、纵梁截面最大正弯矩偏载工况。
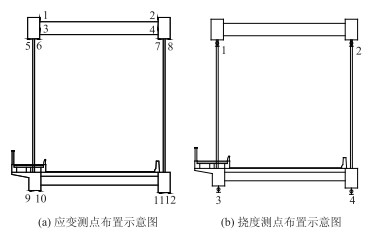
荷载试验中应变和挠度测点布置图如图 2所示,现场实验如图 3所示。测试多组数据取平均值并进行处理,消除沉降影响,由于残余应变和残余挠度在合理范围内,消除残余应变和残余挠度,得到各工况下的应变和挠度测试数据见表 2。
|
| 图 2 荷载试验测点布置示意图 Fig. 2 Schematic diagram of arrangement of measuring points in load test |
| |

|
| 图 3 现场荷载试验 Fig. 3 Field load test |
| |
| 测点 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 工况1 | 计算值/με | -32 | -37 | -13 | -14 | 16 | 19 | 21 | 20 | 49 | 54 | 60 | 55 |
| 实测值/με | -23 | -27 | -9 | -10 | 11 | 14 | 17 | 16 | 33 | 40 | 42 | 37 | |
| 工况2 | 计算值/με | -23 | -47 | -10 | -20 | 14 | 18 | 24 | 22 | 39 | 50 | 71 | 74 |
| 实测值/με | -17 | -34 | -8 | -14 | 10 | 13 | 17 | 17 | 28 | 35 | 47 | 52 | |
| 工况3 | 计算值/με | -71 | -64 | -12 | -8 | 46 | 59 | 51 | 51 | 69 | 95 | 90 | 87 |
| 实测值/με | -45 | -33 | -10 | -5 | 31 | 33 | 33 | 32 | 51 | 54 | 55 | 53 | |
| 工况4 | 计算值/με | -60 | -71 | -8 | -10 | 36 | 55 | 62 | 52 | 56 | 74 | 110 | 104 |
| 实测值/με | -35 | -40 | -7 | -7 | 24 | 34 | 35 | 33 | 34 | 52 | 64 | 62 | |
| 测点 | d1/mm | d2/mm | d3/mm | d4/mm | |
| 工况1 | 计算值 | 3.65 | 3.71 | 6.44 | 6.67 |
| 实测值 | 3.14 | 3.15 | 5.41 | 5.54 | |
| 工况2 | 计算值 | 3.18 | 4.53 | 5.31 | 7.71 |
| 实测值 | 2.64 | 3.86 | 4.27 | 6.66 | |
| 工况3 | 计算值 | 7.71 | 8.14 | 10.36 | 10.62 |
| 实测值 | 6.36 | 7.01 | 8.97 | 9.15 | |
| 工况4 | 计算值 | 6.86 | 8.69 | 9.70 | 12.48 |
| 实测值 | 5.94 | 7.42 | 7.79 | 10.53 | |
2.2.2 动载试验
采用行车激励的方法对桥梁进行动力测试,使用加速度传感器进行数据收集。在主桥的拱肋L/2截面和桥面L/2截面的拱肋上缘和桥面分别布置测点,测试结构振动频率。以一辆35T的激励车分别以15,30,45 km/h速度对桥梁进行激励,采集多组数据并进行处理,对比个阶模态对数据进行处理后得到各阶频率实测值,并将实测值与计算值对比见表 4。
| 项目 | 自振频率/Hz | 相对误差/% | |
| 初始计算值 | 实测值 | ||
| 一阶频率 | 1.740 | 1.99 | -12.95 |
| 二阶频率 | 2.481 | 2.88 | -13.82 |
| 三阶频率 | 3.199 | 3.61 | -11.28 |
| 四阶频率 | 3.828 | 4.22 | -9.28 |
2.3 有限元模型修正 2.3.1 修正参数及响应值选取
对本桥结构特点进行分析,得出可能造成模型与实桥存在偏差的因素有:材料特性参数、几何尺寸,边界条件等。研究中模型是根据施工图建立的,截面几何尺寸误差较小,桥墩与纵梁简支连接,桥墩变形对频率响应影响较小,但施工过程中标高控制误差的存在会使成桥后的桥面铺装层厚度产生误差,以材料参数和桥面铺装层厚度作为修正对象,在设计值上下20%内进行取值,参数及修正范围见表 5。
| 因子 | 参数描述 | 修正范围 |
| A | 拱肋弹性模量E1/(×1010 Pa) | [2.6,3.9] |
| B | 拱肋密度D1/(kg·m-3) | [2 039.2,3 058.8] |
| C | 纵梁密度D2/(kg·m-3) | [2 039.2,3 058.8] |
| D | 纵梁弹性模量E2/(×1010 Pa) | [2.76,4.14] |
| E | 横梁密度D3/(kg·m-3) | [2 039.2,3 058.8] |
| F | 横梁弹性模量E3/(×1010 Pa) | [2.6,3.9] |
| G | 吊杆密度D4/(kg·m-3) | [6 280,9 420] |
| H | 吊杆弹性模量E4/(×1010 Pa) | [16, 24] |
| J | 桥面铺装层厚度T/cm | [14.4,21.6] |
2.3.2 试验设计与参数显著性分析
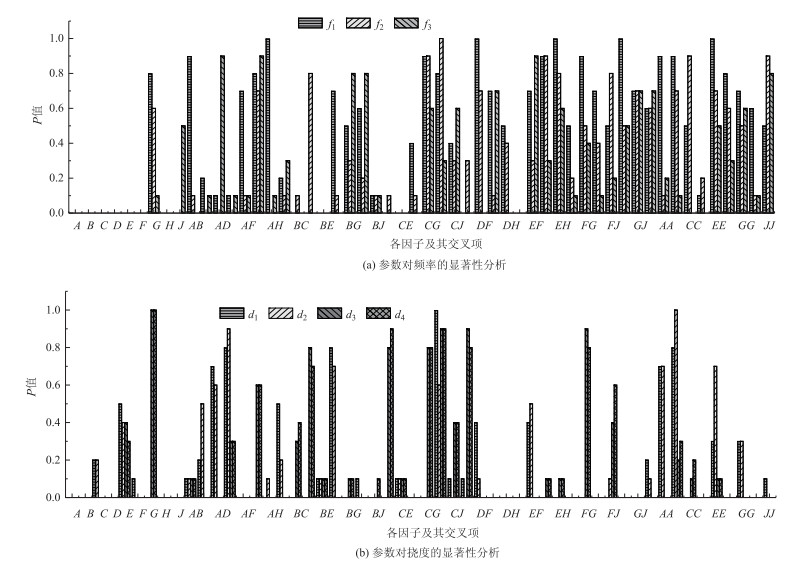
根据实桥的结构特点与本次模型修正的目的,选择工况1作用下拱顶截面挠度d1,d2, 纵梁跨中挠度d3,d4及前三阶频率f1,f2,f3作为响应值进行试验设计。由于待修正参数较多,按照取最少样本点获得最有效的数据原则,选择D-最优准则的计算机生成设计。试验设计得到65个(55个设计试验点+5个不匹配点+5个最佳重复点)随机样本点见表 6,将样本点数据代入有限元模型得到响应值见表 7,并进行方差分析。根据各参数类型及其对应显著水平值得显著性分析图,如图 4所示:
|
| 图 4 参数显著性分析 Fig. 4 Parameter significance analysis |
| |
| 样本 | 待修正参数 | ||||||||
| E1/(×1010 Pa) | D1/(kg·m-3) | E2/(×1010 Pa) | D2/(kg·m-3) | E3/(×1010 Pa) | D3/(kg·m-3) | E4/(×1010 Pa) | D4/(kg·m-3) | T/cm | |
| 1 | 3.9 | 2 931.3 | 2.82 | 3 058.8 | 3.9 | 3 058.8 | 16 | 9 420 | 14.4 |
| 2 | 3.9 | 2 159.6 | 4.14 | 3 058.8 | 2.6 | 2 039.2 | 24 | 6 280 | 21.6 |
| … | … | … | … | … | … | … | … | … | … |
| 64 | 2.6 | 2 263.1 | 4.14 | 2 039.2 | 2.6 | 2 039.2 | 16 | 8 583.55 | 14.4 |
| 65 | 3.9 | 2 039.2 | 2.76 | 2 039.2 | 3.5 | 2 758.95 | 24 | 6 280 | 21.6 |
| 样本 | 响应值 | ||||||
| f1/Hz | f2/Hz | f3/Hz | d1/mm | d2/mm | d3/mm | d4/mm | |
| 1 | 2.436 8 | 3.377 5 | 3.815 2 | 3.93 8 | 3.940 | 6.298 | 6.442 |
| 2 | 2.992 3 | 3.901 9 | 4.363 1 | 2.994 | 2.999 | 5.807 | 5.983 |
| … | … | … | … | … | … | … | … |
| 64 | 3.129 1 | 3.771 7 | 4.609 5 | 3.909 | 3.913 | 6.799 | 6.984 |
| 65 | 2.763 2 | 3.909 6 | 4.451 7 | 3.456 | 3.457 | 5.937 | 6.086 |
本次分析中设置显著性水平为0.05,当p∈[0, 0.001]时,该参数影响高度显著;当P∈(0.001, 0.05],该参数影响显著;当P∈(0.05, 1]时,该参数影响不显著。参数对频率的显著性分析结果表明,主效应中E1,D1,E2,D2对前三阶频率影响高度显著,E3,D3,E4对前三阶频率影响显著;大部分参数交互项和二次项对前三阶频率影响不显著。参数对挠度的显著性分析结果表明,主效应中弹性模量对挠度影响高度显著;部分参数的交互作用对挠度影响显著,主要为各构件弹性模量交互项;纵梁弹性模量二次项, 纵梁密度二次项对挠度影响高度显著,其他二次项分别对d1,d2,d3,d4的显著性有不同程度的影响。桥面铺装层厚度对挠度影响高度显著,分析原因,主要为铺装层层厚度在一定程度上改变了桥梁的整体刚度。
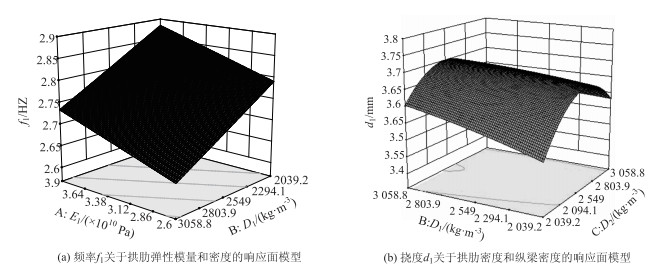
2.3.3 响应面拟合先对影响的不显著参数予以排除,再根据样本点响应值,采用含高斯函数项的二次多项式进行拟合,得到响应面模型。由于响应面的模型较多,下面仅给出f1关于E1,D1响应面模型和d1关于D1,D2的响应面模型如图 5。R2和Radj2的计算值见表 8,其值均接近于1,说明响应面的拟合效果较好。
|
| 图 5 部分响应面模型 Fig. 5 Partial response surface models |
| |
| 准则 | f1/Hz | f2/Hz | f3/Hz | d1/mm | d2/mm | d3/mm | d4/mm |
| R2 | 0.999 9 | 0.999 8 | 1 | 0.999 5 | 0.999 8 | 1.000 | 1.000 0 |
| Radj2 | 0.999 4 | 0.999 7 | 0.999 8 | 0.999 4 | 0.995 7 | 0.999 9 | 1.000 0 |
2.3.4 优化求解
将设计参数代入响应面模型得到计算值,构造计算值与实测值目标函数并进行优化求解,采用粒子群优化算法求解,得到修正后的参数见表 9。将修正后的全部参数代入有限元模型计算,得到频率和挠度的计算值并与实测值进行对比见表 10。
| 类型 | E1/Hz | D1/(g·m-3) | E2/Hz | D2/(g·m-3) | E3/Hz | D3/(g·m-3) | E4/Hz | D4/(g·m-3) | T/cm |
| 初始值 | 3.25 | 2 549 | 3.45 | 2 549 | 3.25 | 2 549 | 2.0 | 7 850 | 18 |
| 修正后 | 3.78 | 2 319 | 4.08 | 2 612 | 3.71 | 2 606 | 2.13 | 7 824 | 18.7 |
| 偏差/% | 16.31 | -9.02 | 18.26 | 2.47 | 14.15 | 2.24 | 6.50 | -0.33 | 3.89 |
| 类型 | 初始值/Hz | 实测值/Hz | 修正值/Hz | 初始相对误差/% | 修正后相对误差/% |
| f1 | 1.740 | 1.99 | 1.983 | -12.56 | -0.35 |
| f2 | 2.481 | 2.88 | 2.862 | -13.85 | -0.62 |
| f3 | 3.199 | 3.61 | 3.582 | -11.39 | -0.78 |
| 类型 | 初始值/mm | 实测值/mm | 修正值/mm | 初始相对误差/% | 修正后 <相对误差/% |
| d1 | 3.652 | 3.14 | 3.183 | 16.31 | 1.37 |
| d2 | 3.711 | 3.15 | 3.176 | 17.81 | 0.83 |
| d3 | 6.442 | 5.41 | 5.507 | 19.08 | 1.79 |
| d4 | 6.674 | 5.54 | 5.621 | 20.47 | 1.46 |
由表 9可以发现,有限元模型修正后,各构件的弹性模量均增大,吊杆的弹性模量较初始值增加了0.065倍;拱肋、纵梁、横梁的弹性模量值较初始值都增加了0.14倍以上;铺装层厚度比初始值增加了约0.04倍,拱肋的密度较初始值则减少了0.09倍,其余各构件密度较初始值变化不大,均在0.03倍之内。分析原因可能为:(1)拱肋结构、纵梁、横向联系中钢筋的存在增大了构件的弹性模量,而初始有限元模型中未考虑钢筋的影响;(2)施工中使用的水泥或者混凝土标号高于设计值;(3)拱肋浇注过程中振捣不完全,造成密实度降低。修正后的弹性模量可视为各钢筋混凝土构件的整体弹性模量,反映了各构件的实际刚度。
由表 10可以发现,修正后的频率响应值误差由初始的13%左右降到1%以内,修正后的挠度响应值误差由20%降至1.8%以内,在可接受的范围内。结果表明:响应面法可以实现对系杆拱桥结构有限元模型修正,且精度能满足工程要求。
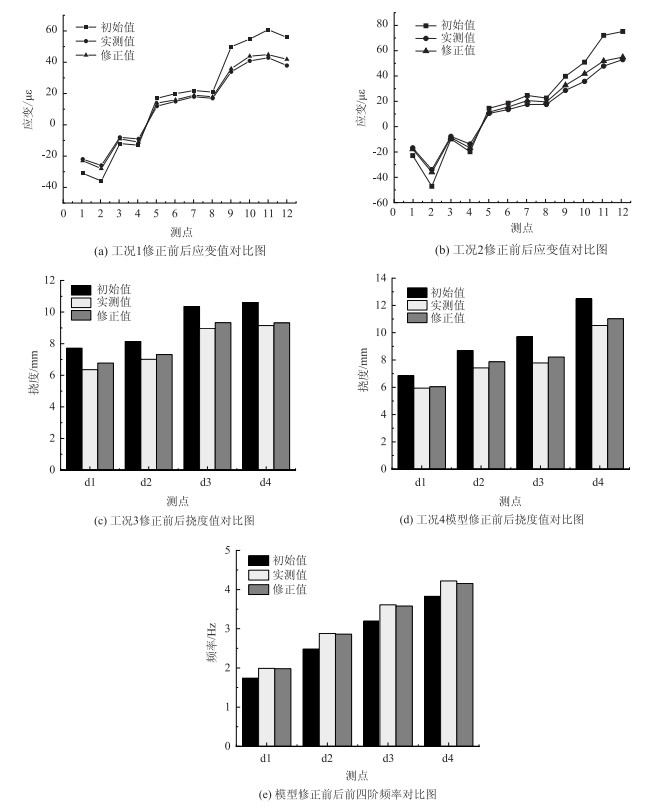
2.3.5 结构静动力响应验证将原有限元模型中的参数改为修正值,计算不同工况下的响应值,并与实测值对比,图 6表明,修正后的有限元模型响应值与实测值偏差明显降低。
|
| 图 6 模型修正前后计算结果对比图 Fig. 6 Comparison of calculation results before and after model correction |
| |
3 结论
以贵州岑巩黄弓大桥为例,结合静动力测试数据,采用改进响应面法,对该桥的有限元模型进行了修正,得到以下几点结论:
(1) 利用统计学原理,结合径向基函数,将传统响应面法进行改进,增加了对模型非线性模拟的适应性,提高了响应面的拟合精度。基于静动力测试数据在响应面内优化求解,以修正参数进行D-最优试验设计,避免了采样点的主观性,降低了样本点采集数量,提高了样本点质量;缩减有限元模型的调用频率,模型修正的效率提高。
(2) 建立了贵州岑巩黄弓大桥有限元模型,结合静动力测试数据得到对挠度的主要响应因素为弹性模量E二次项效应,并将铺装层厚度作为修正参数,分析得出铺装层厚度对频率影响不显著,对挠度影响高度显著。因此,在今后的分析中铺装层厚度对桥梁的静力特性的影响不可忽略。
(3) 利用改进的响应面法修正后的系杆拱桥有限元模型,其计算值更接近于实测值,频率误差由原来的13%左右降至1%以内,挠度误差由原来的20%左右降至1.8%以内,在结构静动力响应验证中,修正后有限元模型的响应值与实测值相吻合,为以后的桥梁结构受力性能再分析、承载能力评估等提供了基准有限元模型,对桥梁服役期内的健康监测与结构损伤识别具有重要意义与实用价值。
| [1] |
李辉, 丁桦. 结构动力模型修正方法研究进展[J]. 力学进展, 2005, 35(2): 170-180. LI Hui, DING Hua. Progress in Model Updating for Structural Dynamics[J]. Advances in Mechanics, 2005, 35(2): 170-180. |
| [2] |
梁鹏, 李斌, 王秀兰, 等. 基于桥梁健康监测的有限元模型修正研究现状与发展趋势[J]. 长安大学学报:自然科学版, 2014, 34(4): 52-61. LIANG Peng, LI Bin, WANG Xiu-lan, et al. Present Research Status and Development Trend of Finite Element Model Updating Based on Bridge Health Monitoring[J]. Journal of Chang'an University:Natural Science Edition, 2014, 34(4): 52-61. |
| [3] |
BERMAN A, FLANNELLY W G. Theory of Incomplete Models of Dynamic Structures[J]. AIAA Journal, 1971, 9(8): 1481-1487. |
| [4] |
ZHAO W, FAN F, WANG W, et al. Non-linear Partial Least Squares Response Surface Method for Structural Reliability Analysis[J]. Reliability Engineering & System Safety, 2017, 161: 69-77. |
| [5] |
PARK W, KIM H K, JONGCHIL P. Finite Element Model Updating for a Cable-stayed Bridge Using Manual Tuning and Sensitivity-based Optimization[J]. Structural Engineering International, 2012, 22(1): 14-19. |
| [6] |
韩建平, 骆勇鹏. 基于响应面法的结构有限元模型静动力修正理论及应用[J]. 地震工程与工程振动, 2013, 33(5): 128-137. HAN Jian-ping, LUO Yong-peng. Static and Dynamic Finite Element Model Updating of Structures Based on Response Surface Method:Theory and Application[J]. Journal of Earthquake Engineering and Engineering Vibration, 2013, 33(5): 128-137. |
| [7] |
SANAYEI M, KHALOO A, GUL M, et al. Automated Finite Element Model Updating of a Scale Bridge Model Using Measured Static and Modal Test Data[J]. Engineering Structures, 2015, 102: 66-79. |
| [8] |
REN W, CHEN H. Finite Element Model Updating in Structural Dynamics by Using the Response Surface Method[J]. Engineering Structures, 2010, 32(8): 2455-2465. |
| [9] |
宗周红, 高铭霖, 夏樟华. 基于健康监测的连续刚构桥有限元模型确认(Ⅰ):基于响应面法的有限元模型修正[J]. 土木工程学报, 2011, 44(2): 90-98. ZONG Zhou-hong, GAO Ming-lin, XIA Zhang-hua. Finite Element Model Validation of the Continuous Rigid Frame Bridge Based on Structural Health Monitoring Part I:FE Model Updating Based on the Response Surface Method[J]. China Civil Engineering Journal, 2011, 44(2): 90-98. |
| [10] |
FANG S E, ZHANG Q H, REN W X. An Interval Model Updating Strategy Using Interval Response Surface Models[J]. Mechanical Systems and Signal Processing, 2015, 60/61: 909-927. |
| [11] |
FANG S E, PERERA R. A Response Surface Methodology Based Damage Identification Technique[J]. Smart Materials and Structures, 2009, 18(6): 1-14. |
| [12] |
何为, 唐斌, 薛卫东. 优化试验设计方法及数据分析[M]. 北京: 化学工业出版社, 2012. HE Wei, TANG Bin, XUE Wei-dong. Optimization Test Design Method and Data Analysis[M]. Beijing: Chemical Industry Press, 2012. |
| [13] |
隋允康, 宇慧平. 响应面方法的改进及其对工程优化的应用[M]. 北京: 科学出版社, 2011. SUI Yun-kang, YU Hui-ping. Improvement of Response Surface Methodology and Its Applications to Engineering Optimization[M]. Beijing: Science Press, 2011. |
| [14] |
于志玲, 张阳. 最佳一致逼近理论中哈尔(Haar)条件的等价定义[J]. 南开大学学报:自然科学版, 2006, 39(3): 101-103. YU Zhi-ling, ZHANG Yang. The Equivalent Definition of Haar Condition in Best Uniform Approximation Theory[J]. Acta Scientiarum Naturalium Universitatis Nankaiensis, 2006, 39(3): 101-103. |
| [15] |
郁胜, 周林仁. 基于径向基函数响应面方法的超大跨悬索桥有限元模型修正[J]. 铁道科学与工程学报, 2014, 11(1): 1-9. YU Sheng, ZHOU Lin-ren. Finite Element Model Updating of Large Suspension Bridge Based on Radial Basis Function Response Surface[J]. Journal of Railway Science and Engineering, 2014, 11(1): 1-9. |
| [16] |
陆征然, 张茂胜, 郭超. 基于随机有限元的修正剑桥模型可靠性研究[J]. 沈阳建筑大学学报:自然科学版, 2018, 34(4): 703-710. LU Zheng-ran, ZHANG Mao-sheng, GUO Chao. Reliability Analysis of Modified Cambridge Model Based on Stochastic Finite Elements Methods[J]. Journal of Shenyang Jianzhu University:Natural Science Edition, 2018, 34(4): 703-710. |
| [17] |
陈喆, 何欢, 陈国平, 等. 考虑不确定性因素的有限元模型修正方法研究[J]. 振动工程学报, 2017, 30(6): 921-928. CHEN Zhe, HE Huan, CHEN Guo-ping, et al. The Research of Finite Element Model Updating Method Considering the Uncertainty[J]. Journal of Vibration Engineering, 2017, 30(6): 921-928. |
| [18] |
杜进生, 张天能, 周赤伟. 基于二阶泰勒级数展开和风驱动优化算法的结构有限元模型修正[J]. 建筑结构学报, 2019, 40(2): 206-214. DU Jin-sheng, ZHANG Tian-neng, ZHOU Chi-wei. Updating of Finite Element Model of Structures Using Second-order Taylor Expansions and Wind Driven Optimization[J]. Journal of Building Structures, 2019, 40(2): 206-214. |
| [19] |
杨荷.基于改进响应面法的水布垭面板堆石坝材料参数反演与分析[D].武汉: 武汉大学, 2017. YANG He. Inversion and Analysis of Material Parameters of Shuibuya CFRD Based on Improved Response Surface Method[D]. Wuhan: Wuhan University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10486-1017195785.htm |
| [20] |
SHAN D, LI Q, KHAN I, et al. A Novel Finite Element Model Updating Method Based on Substructure and Response Surface Model[J]. Engineering Structures, 2015, 103: 147-156. |
| [21] |
ASTROZA R, EBRAHIMIAN H, CONTE J P, et al. Performance Comparison of Kalman-based Filters for Nonlinear Structural Finite Element Model Updating[J]. Journal of Sound and Vibration, 2019, 438: 520-542. |
| [22] |
胡星星, 裘乐淼, 张树有, 等. 基于混合响应面法的滚压成型回弹角预测控制及应用[J]. 浙江大学学报:工学版, 2013, 47(11): 2010-2019. HU Xing-xing, QIU Le-miao, ZHANG Shu-you, et al. Application of a Hybrid RSM for Springback Predictive Control in Roll Forming[J]. Journal of Zhejiang University:Engineering Science Edition, 2013, 47(11): 2010-2019. |
| [23] |
张松涵, 高芳清, 张伟伟. 基于组合函数响应面的桥梁有限元模型修正[J]. 重庆交通大学学报:自然科学版, 2015, 34(5): 18-24. ZHANG Song-han, GAO Fang-qing, ZHANG Wei-wei. Bridge Finite Element Model Updating Based on Combination Function Response Surfaces[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2015, 34(5): 18-24. |
| [24] |
张挣鑫, 刘黔会, 黄方林. 面向桥梁工程的响应面技术在有限元模型修正中的应用探讨[J]. 公路工程, 2018, 43(4): 145-149. ZHANG Zheng-xin, LIU Qian-hui, HUANG Fang-lin. Research on Response Surface Technique for Bridge Engineering in Finite Element Model Correction[J]. Highway Engineering, 2018, 43(4): 145-149. |
| [25] |
彭涛, 田仲初, 张建仁, 等. 基于多目标优化的混凝土斜拉桥静动力有限元模型修正[J]. 振动与冲击, 2018, 37(21): 108-116. PENG Tao, TIAN Zhong-chu, ZHANG Jian-ren, et al. Static and Dynamic Finite Element Model Updating for a Concrete Cable-stayed Bridge Based on Multi-objective Optimization[J]. Journal of Vibration and Shock, 2018, 37(21): 108-116. |
 2020, Vol. 37
2020, Vol. 37
