扩展功能
文章信息
- 杨晓华, 李嘉璐, 李斌, 张莎莎
- YANG Xiao-hua, LI Jia-lu, LI Bin, ZHANG Sha-sha
- 高填方路堤下钢波纹管涵受力与变形特征离心模型试验
- Centrifugal Model Test on Force and Deformation Characteristics of Corrugated Steel Pipe Culvert under High-filled Embankment
- 公路交通科技, 2020, 37(10): 74-82
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(10): 74-82
- 10.3969/j.issn.1002-0268.2020.10.008
-
文章历史
- 收稿日期: 2019-10-12
钢波纹管涵洞是采用钢波纹状管或由弧形钢波纹状板通过现场吊装、螺栓拼接形成的一种涵洞结构形式。轴向纵波的存在,使填土荷载产生的应力应变在钢波纹管涵的轴向、径向同时分布,充分发挥钢材的抗拉、抗压、抗剪性能[1]。此外,由于其自身的柔性大、强度高、运输便捷、施工简便、适应地基与基础变形能力强、绿色环保等优良的工程特性,在公路工程中具有广泛的应用前景[2]。
目前,国内外针对钢波纹管涵的受力特性、力学性能、土压力计算、工程应用等方面进行了大量研究。在北美、澳大利亚、西欧以及日本等国家,都将钢波纹管涵广泛应用于公路工程中,并制定了相关的技术规范,包含设计、制造及施工安装等方面[3-4]。Kjartanson等对波纹管涵进行了足尺试验研究,表明上覆填土能显著提高波纹管的纵向刚度[5]。Machelski等通过对钢波纹板涵结构的荷载试验研究,得出了钢波纹板涵结构的设计计算方法[6]。李祝龙通过现场施工数据及室内数值分析,研究了在不同荷载作用下,不同直径、不同板厚、不同波形参数的钢波纹管涵的受力情况[7-10]。Yeau等、Sezenl等通过现场试验,研究了钢波纹管涵在静态和动态荷载下的挠度变化[11-12]。潘春风等通过室内试验和数值模拟对比分析了不同荷载下钢波纹管涵的力学特性和变形规律[13]。褚夫蛟等通过现场测试及数值模拟,研究了不同填土高度情况下大直径钢波纹管涵的轴向、环向应变,管体土压力及横向、竖向变形情况[14]。冯忠居等通过室内模型试验和现场试验,研究了钢波纹管涵在填土荷载作用下的力学特性、管周土压力及涵管变形规律[15-16]。廖鑫通过现场试验及数值模拟,研究了高填方下钢波纹管涵在施工阶段的受力特性和变形规律[17]。刘百来等通过数值模拟、现场试验等手段,研究了斜交、低填、大直径钢波纹管涵的内壁应变及周围土压力分布规律[18-19]。张东山等研究了钢波纹管涵在实际工程中的应用[20-21]。魏瑞等通过Spangler管-土相互作用模型,推导了管涵垂直土压力、变形的计算公式和涵土相对刚度系数的计算公式[22-24]。
综上可知,国内外针对高填方路堤下钢波纹管涵在路堤填筑高度、与路堤主线夹角及涵管直径变化时,其受力特性和变形规律的研究较少,未进行离心模型试验研究。基于此,本研究依托山西榆次龙白-祁县城赵段高速公路钢波纹管涵工程,采用离心模型试验技术,以路堤中部和路肩断面钢波纹管涵作为研究对象,对高填方路堤典型工况下钢波纹管涵洞的受力和变形特性进行系统的分析研究,对钢波纹管涵的工程设计和施工参数选取具有重要地工程意义。
1 钢波纹管涵离心模型试验设计 1.1 土工离心模型试验技术指标本试验采用长安大学TLJ-3型土工离心机,规格为60 g·t,有效半径2.0 m,最大加速度200g。离心试验模型箱尺寸为700 mm(长)×360 mm(宽)×500 mm(高)。根据离心模型试验箱的大小、钢波纹管涵的尺寸、路堤填筑高度以及离心模型试验原理,试验离心加速度定为40g,相似关系见表 1,离心试验模型尺寸为原型的1/40。
| 物理量 | 模型/原型 | 试验取值 |
| 长度、位移 | 1/n | 1/40 |
| 加速度 | n | 40 |
| 弹性模量 | 1 | 1 |
| 应力应变 | 1 | 1 |
| 时间 | 1/ n2 | 1/1 600 |
1.2 钢波纹管涵模型及填土材料特性
在几何相似的基础上,为了保证钢波纹管涵离心试验模型与原型结构的受力和变形特性一致,离心试验模型材料的选取由原型结构的轴向刚度EA、弯曲刚度EI及其对地基产生的压应力控制。离心试验模型采用强度相似的轧制铝,板厚0.3 mm,屈服强度约235 MPa,三瓣拼装,波形参数为200 mm×55 mm(波距×波高)。分别制作了直径为7.5,9.0,11.0 cm的钢波纹管涵模型,模拟了原型结构直径为3.0,3.6,4.4 m的钢波纹管涵。
涵顶填方对钢波纹管涵的影响主要是其荷载的影响,所以在进行离心模型试验时,涵顶50 mm范围内,模型填土与原型填土完全一致,最大干密度为1.93 g/cm3,最佳含水率为12.3%,压实度为0.96;而50 mm以上范围,由于离心模型试验箱的限高,考虑模型填土主要与原型荷载大小一致,采用重量一致的荷载板;涵底布设12.5 mm厚的砂砾垫层,砂砾粒径不大于10 mm,压实度为0.96;涵底地基黄土厚度为225 mm,压实度为0.96。工况1离心模型试验箱如图 1(a)所示。

|
| 图 1 离心试验模型(单位:mm) Fig. 1 Centrifugal test model(unit:mm) |
| |
1.3 试验工况设计
为研究黄土地区高填方路堤典型工况下钢波纹管涵结构的受力特性和变形规律,共设计了5种试验工况,具体工况见表 2。工况2离心试验模型示意图如图 1(b)所示,模型均以半幅路堤为模拟对象。
| 试验工况 | 路堤填筑高度H/cm | 与路堤主线夹角φ/(°) | 钢波纹管涵直径D/cm | 模拟工况 |
| 工况1 | 35 | 50 | 7.5 | 与依托工程里程桩号K2+510.5原型结构一致 |
| 工况2 | 35 | 30,75,90 | 7.5 | φ改变,其余不变 |
| 工况3 | 35 | 90 | 9.0,11.0 | D改变,其余不变,模拟3.6 m,4.4 m |
| 工况4 | 40,50 | 90 | 7.5 | H改变,其余不变,模拟16 m,20 m |
| 工况5 | 65 | 90 | 7.5 | 模拟路堤填筑高度26 m |
1.4 试验程序及其测试方法
配土:试验填土采用黄土,碾压后过2 mm筛,按照最佳含水率配水,闷料24 h备用。
分层填土和埋置钢波纹管涵洞:首先,根据离心试验模型箱的尺寸和设定的压实度计算出每层所需土样质量,称土后装入模型试验箱并摊铺均匀,用击实工具将土样从两边向中间击实,击实过程中用直尺测量已装入土样高度,以保证其达到设定压实度。其次,待达到一定标高时铺设砂砾垫层埋入钢波纹管涵。最后,涵顶按照第一道工序继续填土,涵顶50 mm以上,放置相应的荷载板。
测试断面及测试元件:离心试验模型的应变测试选取路堤中部和路肩处两个断面,每个断面选取涵顶、涵侧和涵底3个测点,每个测点分别测试波峰的轴向、环向应变和波谷的轴向、环向应变4个应变值,测点布置示意图见图 2。应变测试采用bq120-5aa型电阻应变片,采用细毛笔在应变片反面均匀刷胶,粘贴在打磨好的测试位置并反复调整,以保证应变片的位置粘贴准确,并采用硅酮密封胶抹平密封应变片,以防止应变片脱落和受损,影响各测点应变值的准确性,应变片的粘贴与防护如图 3所示。

|
| 图 2 测点布置示意图 Fig. 2 Schematic plots of measuring points |
| |

|
| 图 3 应变片的粘贴与防护处理 Fig. 3 Sticking and protection of strain gauges |
| |
1.5 工程依托
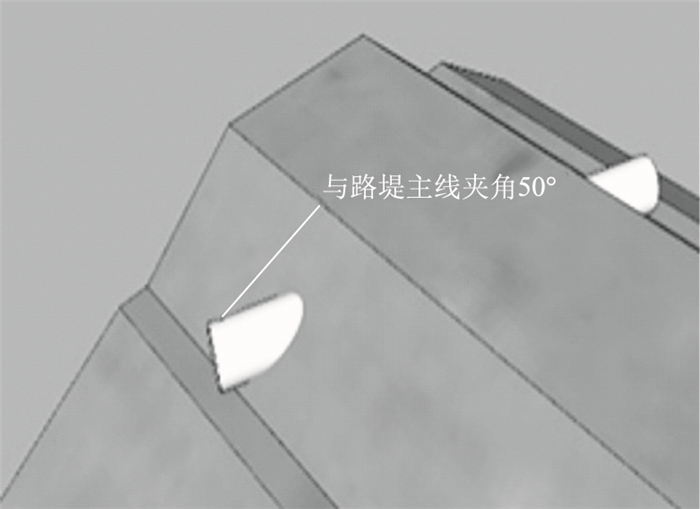
试验依托工程的钢波纹管涵位于山西榆次龙白至祁县城赵高速公路,现场场地地形及依托工程示意图如图 4~图 5所示,钢波纹管涵直径3.0 m,波形采用200 mm×55 mm,其与路堤主线夹角为50°,涵顶路堤填筑高度14 m,涵管周围填筑土均为湿陷性黄土。

|
| 图 4 现场场地地形 Fig. 4 Site topography |
| |
|
| 图 5 钢波纹管涵洞工程示意图 Fig. 5 Schematic diagram of steel corrugated pipe culvert project |
| |
2 钢波纹管涵结构受力与变形特性分析 2.1 工况1下钢波纹管涵应力应变分析
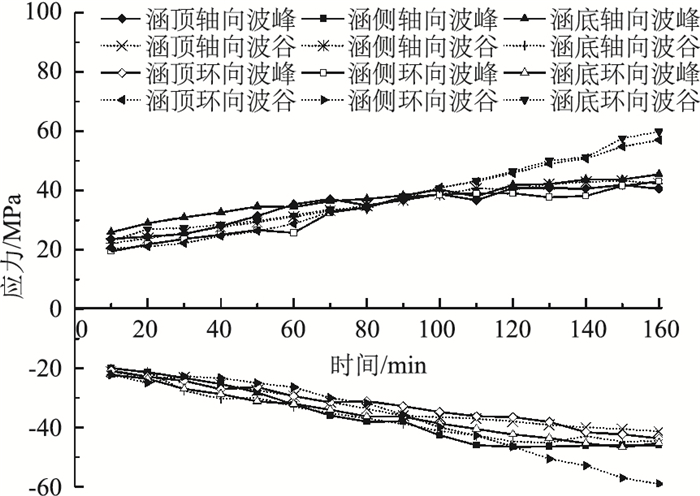
通过对工况1模拟里程桩号K2+510.5路段原型工况下的离心模型试验结果整理可知,当离心加速度达到40g后,钢波纹管涵受力特性随时间变化曲线如图 6~图 7所示。可以看出,在原型路堤填筑高度为14 m时,钢波纹管涵各测点轴向、环向应力随时间增加大致呈线性增加的趋势,增大趋势逐渐变缓。涵顶、涵侧及涵底不同位置处变化规律基本一致,同一位置处波峰和波谷的轴向应力(或环向应力)呈拉、压相反的变化规律,波峰(或波谷)的轴向应力与环向应力亦呈拉、压相反的变化规律。
|
| 图 6 路堤中部各测点轴向、环向应力随时间变化曲线 Fig. 6 Curves of axial & circumferential stresses at each measuring point on middle of embankment varying with time |
| |
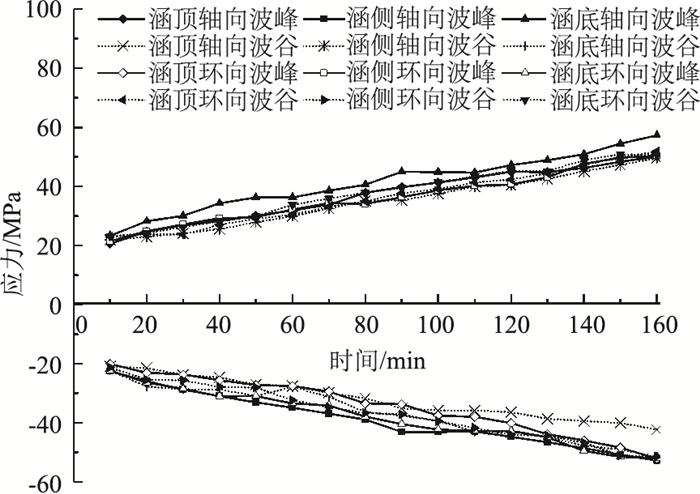
|
| 图 7 路肩处各测点轴向、环向应力随时间变化曲线 Fig. 7 Curves of axial & circumferential stresses at each measuring point on shoulder varying with time |
| |
由表 3可知,路堤中部钢波纹管涵的轴向和环向最大拉应力、拉应变分别为45.51 MPa,216.71 με(涵底波峰)和59.85 MPa,285.00 με(涵底波谷);轴向和环向最大压应力、压应变分别为-45.97 MPa,-218.90 με(涵底波谷)和-59.06 MPa,-281.24 με(涵底波峰)。由于路肩处的路堤填筑高度较小,路肩处的最大环向拉、压应力应变小于路堤中部的环向拉、压应力应变,拉、压应力应变最大值分别为51.85 MPa,246.90 με和-52.16 MPa,-248.38 με;路肩处的最大轴向拉、压应力应变值比路堤中部对应值略大,分别为57.26 MPa,272.67 με和-52.82 MPa,-251.52 με,分布位置与路堤中部一致,表明纵波的存在可以使上覆荷载分布更加均匀。钢波纹管涵拉、压应力大小相当,波峰波谷应力相互协调,共同承担上覆荷载,能充分发挥钢材的力学性能。且涵管各测点的应力远远小于钢材的屈服强度235 MPa,因此原型钢波纹管涵结构满足设计使用要求。
| 试验工况 | 影响因素 | 最大拉应力/MPa | 最大拉应变/με | 最大压应力/MPa | 最大压应变/με | |||||||
| 轴向 | 环向 | 轴向 | 环向 | 轴向 | 环向 | 轴向 | 环向 | |||||
| 工况1 | 路堤中部 | 45.51 | 59.85 | 216.71 | 285.00 | -45.97 | -59.06 | -218.90 | -281.24 | |||
| 路肩位置 | 57.26 | 51.85 | 272.67 | 246.90 | -52.82 | -52.16 | -251.52 | -248.38 | ||||
| 工况2 | φ=30° | 35.19 | 34.46 | 167.60 | 164.07 | -35.17 | -34.01 | -167.52 | -161.95 | |||
| φ=50° | 37.17 | 36.86 | 177.00 | 175.54 | -36.18 | -36.68 | -172.28 | -175.51 | ||||
| φ=75° | 39.80 | 40.72 | 189.50 | 193.91 | -39.37 | -40.20 | -187.46 | -191.43 | ||||
| φ=90° | 43.20 | 45.57 | 205.70 | 217.00 | -42.99 | -45.92 | -204.72 | -218.65 | ||||
| 工况3 | D=9.0 cm | 38.70 | 41.05 | 184.27 | 195.48 | -41.59 | -37.04 | -198.04 | -176.36 | |||
| D=11.0 cm | 48.18 | 49.30 | 229.41 | 234.74 | -53.86 | -43.20 | -256.45 | -205.70 | ||||
| 工况4 | H=40 cm | 30.94 | 35.77 | 147.29 | 170.33 | -54.98 | -32.91 | -261.80 | -156.74 | |||
| H=50 cm | 42.09 | 41.42 | 200.42 | 197.25 | -62.47 | -47.99 | -297.46 | -228.52 | ||||
| 工况5 | H=65 cm | 251.89 | 247.91 | 1 199.49 | 1 180.52 | -302.65 | -287.22 | -1 441.17 | -1 367.72 | |||
2.2 工况2下钢波纹管涵应力应变分析
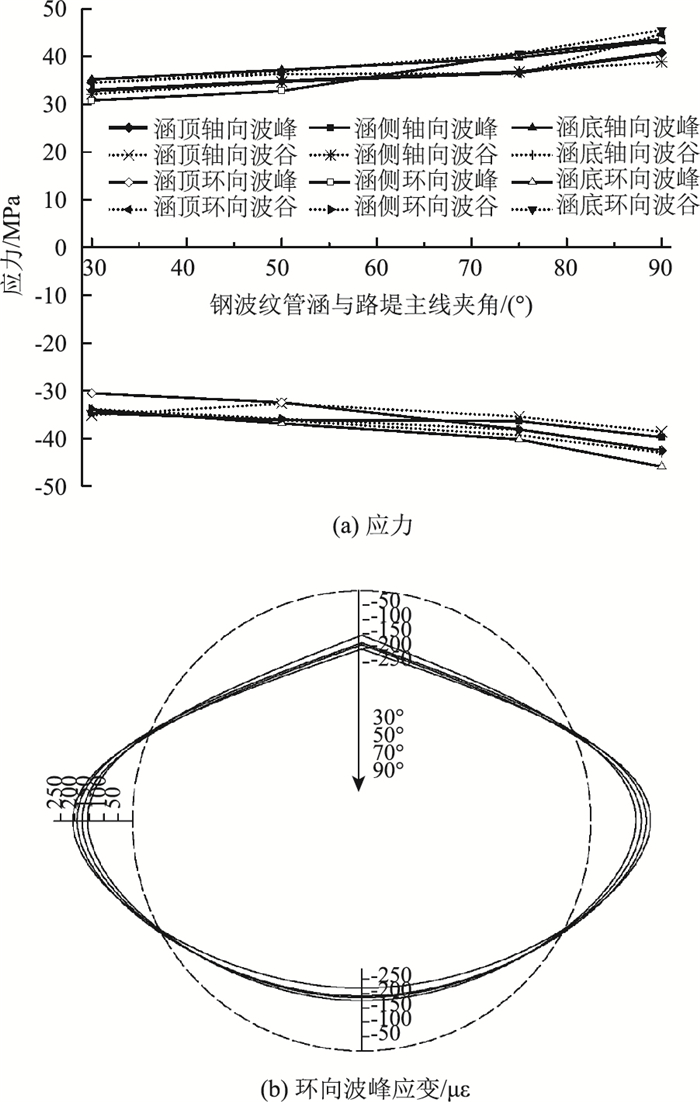
在工况2条件下,路堤填筑高度(14 m)和钢波纹管涵直径(3.0 m)一定时,路堤中部钢波纹管涵离心试验模型各测点应力、环向波峰应变随其与路堤主线夹角变化的规律如表 3和图 8所示。图 8(b)中数字表示钢波纹管涵与路堤主线夹角,虚线仅示意钢波纹管涵的横截面。从图中可以看出,钢波纹管涵各测点轴向、环向应力随其与路堤主线夹角的增大呈缓慢增大的趋势。当钢波纹管涵与路堤主线夹角为30°时,路堤中部钢波纹管涵各测点轴向、环向应力最小,轴向、环向拉应力及拉应变最大值分别为35.19 MPa,167.60 με(涵底波峰)和34.46 MPa,164.07 με(涵底波谷);轴向、环向压应力及压应变最大值分别为-35.17 MPa,-167.52 με(涵底波谷)和-34.01 MPa,-161.95 με(涵底波峰)。当钢波纹管涵与路堤主线夹角为90°时,路堤中部钢波纹管涵各测点轴向、环向应力最大,轴向、环向拉应力及拉应变最大值为43.20 MPa,205.70 με和45.57 MPa,217.00 με;轴向、环向压应力及压应变最大值分别为-42.99 MPa,-204.72 με和-45.92 MPa,-218.65 με,最大拉、压应力应变分布位置与夹角为30°时一致。最大拉、压应力分别增长了29.50%和30.57%。这是因为钢波纹管涵与路堤主线夹角趋于正交,直接影响了涵侧轴向、环向应力应变的分布情况,进而导致涵底处所受到的拉、压应力增大。上述结果表明,合理选择钢波纹管涵与路堤主线夹角对钢波纹管受力性状的改善具有一定的意义。
|
| 图 8 路堤中部各测点应力应变随涵管与路堤主线夹角变化曲线 Fig. 8 Curves of stress and strain at each measuring point on middle of embankment varying with angle between culvert and embankment main line |
| |
考虑钢波纹管涵的最不利受力状态,工况3~5选取钢波纹管涵与路堤主线呈90°进行研究。
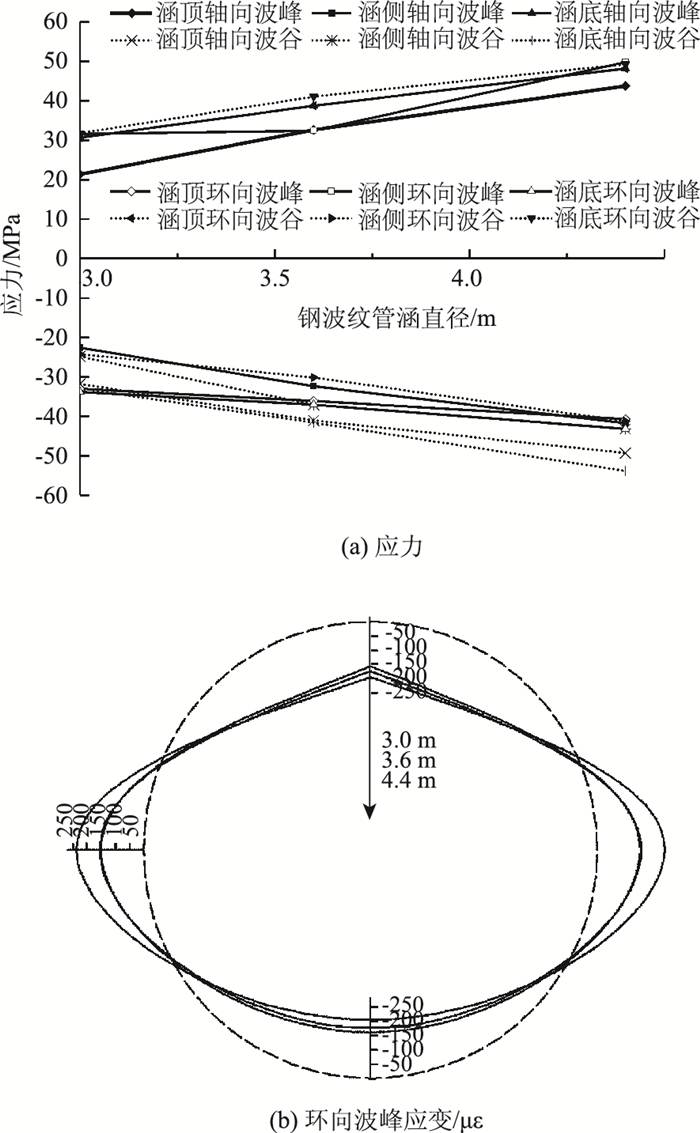
2.3 工况3下钢波纹管涵应力应变分析在工况3条件下,钢波纹管涵路堤填筑高度(14.0 m)和其与路堤主线夹角(90°)一定时,路堤中部钢波纹管涵离心试验模型各测点应力、环向波峰应变随其直径变化的规律如图 9所示。
|
| 图 9 路堤中部钢波纹管涵各测点应力应变随涵管直径变化规律 Fig. 9 Stress and strain at each measuring point of steel corrugated pipe culvert in middle of embankment varying with culvert diameter |
| |
由表 3和图 9分析可得,路堤中部钢波纹管涵各测点应力随其直径的增大呈逐渐增大趋势。当涵管直径为3.6 m时,轴向、环向拉应力及拉应变最大值分别为38.70 MPa,184.27 με(涵底波峰)和41.05 MPa,195.48 με(涵底波谷);轴向、环向压应力及压应变最大值分别为-41.59 MPa,-198.04 με(涵底波谷)和-37.04 MPa,-176.36 με(涵底波峰)。当涵管直径为4.4 m时,拉应力、拉应变最大值分别为48.18 MPa,229.41 με(轴向)和49.30 MPa,234.74 με(环向);压应力、压应变最大值分别为-53.86 MPa,-256.45 με(轴向)和-43.20 MPa,-205.70 με(环向),应力应变分布位置与涵管直径为3.6 m时一致。当钢波纹钢涵直径由3.0 m增大至3.6 m,4.4 m时,最大拉应力分别增长了29.11%,55.05%;最大压应力分别增长了26.25%,63.49%。这表明,涵管直径较大时,上部有效土柱自重较大,钢波纹管涵受力较大。同时大直径钢波纹管涵因材料变形,通过变形将部分涵顶填土荷载转移到周围土体,对上覆荷载能起到一定的卸载作用,降低了涵顶土压力,有利于钢波纹管涵与周围土体的相互作用。
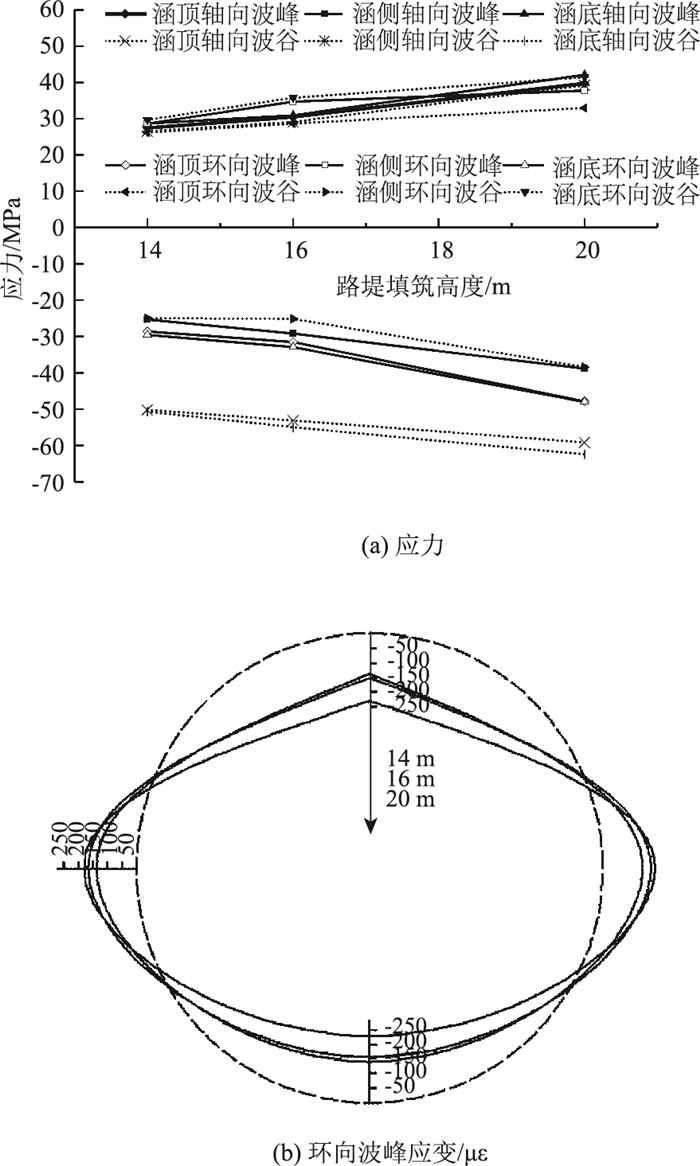
2.4 工况4下钢波纹管涵应力应变分析在工况4条件下,钢波纹管涵直径(3.0 m)和其与路堤主线夹角(90°)一定时,路堤中部钢波纹管涵离心试验模型各测点应力、环向波峰应变随路堤填筑高度变化的规律如图 10所示。
|
| 图 10 路堤中部各测点应力应变随路堤填筑高度变化曲线 Fig. 10 Curves of stress and strain at each measuring point on middle of embankment varying with embankment filling height |
| |
由表 3和图 10分析可得,路堤中部钢波纹管涵各测点的应力随路堤填筑高度的增加大致呈线性增长趋势。当路堤填筑高度为16 m时,轴向、环向拉应力及拉应变最大值分别为30.94 MPa,147.29 με(涵底波峰)和35.77 MPa,170.33 με(涵底波谷);轴向、环向压应力及拉应变最大值分别为-54.98 MPa,-261.80 με(涵底波谷)和-32.91 MPa,-156.74 με(涵底波峰)。当路堤填筑高度为20 m时,轴向、环向最大拉、压应力分布位置与路堤填筑高度为16 m时一致,轴向应力应变最大值分别为42.09 MPa,200.42 με和-62.47 MPa,-297.46 με;环向应力应变最大值分别为41.42 MPa,197.25 με和-47.99 MPa,-228.52 με。当路堤填筑高度由14 m增大16 m,20 m时,钢波纹管涵各测点最大拉应力分别是原型工况下的1.21倍、1.40倍,最大压应力分别是原型工况下的1.08倍、1.23倍。这是由于随填土高度的增加,作用在涵管上部的荷载增大。随填土荷载的增大,钢波纹管涵对涵侧土体产生的鼓胀变形加剧,涵管趋于水平椭圆形,结构与周围填土协调受力和变形。
上述结果表明,在涵顶上部填土荷载产生的应力不超过钢波纹管涵屈服极限时,其受力状态尚处于弹性受力阶段,应力随路堤填筑高度的增加大致呈线性增大的趋势。若在此基础上继续增加路堤填筑高度,应力会继续保持线性增长,但是当填土荷载对钢波纹管涵产生的应力超过钢材的屈服极限时,结构进入屈服状态,变形急剧增加,不利于钢波纹管涵的正常使用。因此通过继续增加路堤填筑高度来研究钢波纹管涵的受力特征与变形规律具有重要的意义,基于此可得涵顶的最大路堤填筑高度,实现其功能的最大化,有利于其设计、施工技术的推广应用。
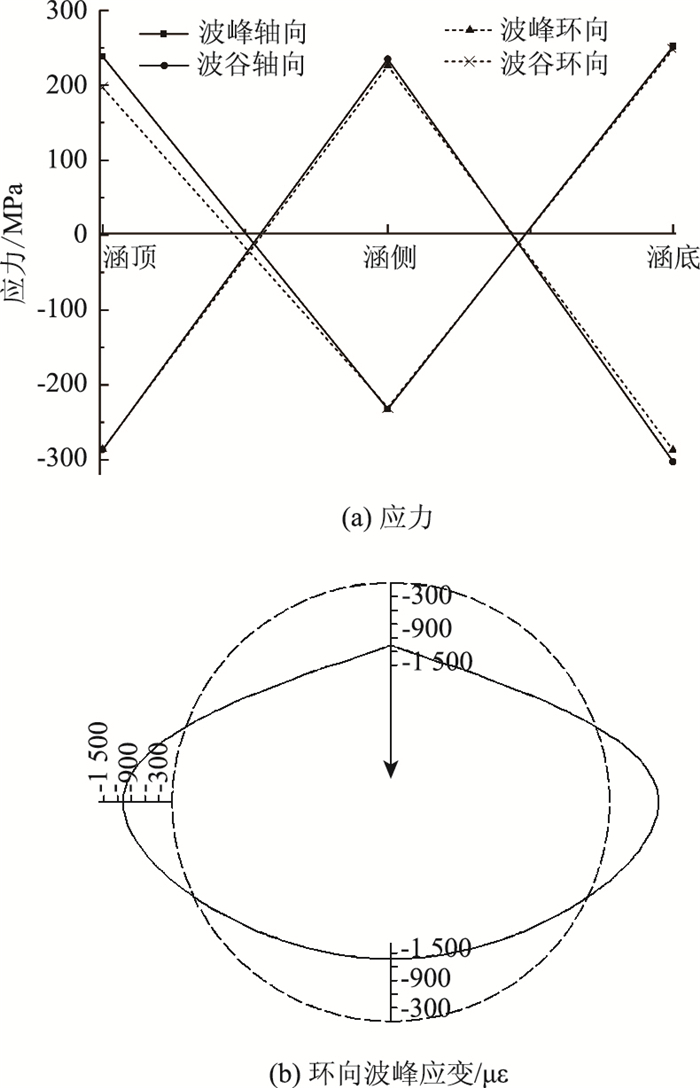
2.5 工况5下钢波纹管涵应力应变分析在工况4条件下,逐级增加路堤填土高度,直至钢波纹管涵进入屈服状态。由表 3和图 11分析可得,当路堤填筑高度为26 m时,最大拉、压应力应变出现在涵底波峰、涵底波谷位置处,应力值分别为251.89 MPa,-302.65 MPa,应变量分别为1 199.49 με,-1 441.17 με,相比路堤填筑高度为20 m时,最大拉、压应变分别提高了498.50%和384.50%,表明此时钢波纹管涵产生塑性变形,进入屈服状态,涵顶的最大路堤填筑高度不应超过26 m。
|
| 图 11 路堤填筑高度为26 m时各测点应力应变 Fig. 11 Stress and strain at each measuring point when embankment filling height is 26 m |
| |
3 结论
本研究依据钢波纹管涵离心模型试验结果,针对钢波纹管涵与路堤主线夹角、路堤填筑高度和钢波纹管涵直径等不同工况下的受力与变形特性开展了研究,主要得出以下结论:
(1) 钢波纹管涵轴向(或环向)最大拉、应力出现在涵底位置,轴向最小拉、压应力常出现在涵侧波谷、涵顶波谷位置,环向最小拉、应力常出现在涵侧波峰、涵顶波峰位置。在钢波纹管涵波峰涵顶、涵侧及涵底不同位置处,波峰(或波谷)的轴向应力、环向应力呈拉、压相反的变化规律,波峰和波谷的轴向应力(或环向应力)亦呈拉、压相反的变化规律。这表明由于轴向纵波的存在,钢波纹管涵轴向、环向共同承担上覆填土荷载,涵管拉、压应力相互协调,能充分发挥钢材的力学性能。
(2) 原型工况下,钢波纹管涵最大拉、压应力为59.85 MPa和-59.06 MPa,远远小于钢材的屈服强度235 MPa,表明钢波纹管涵尚处于弹性受力阶段,满足设计使用要求。
(3) 路堤填筑高度(14 m)和钢波纹管涵直径(3 m)一定时,各测点应力应变随其与路堤主线夹角的增大呈缓慢增大的趋势,其与路堤主线夹角为50°,70°,90°时,最大拉、压应力分别是夹角为30°的1.06,1.16,1.29倍和1.04,1.14,1.31倍。这表明在钢波纹管涵设计过程中,应充分考虑其与路堤主线夹角对涵管受力性状的改善作用。
(4) 钢波纹管涵与路堤主线正交,路堤填筑高度(14 m)一定时,各测点应力应变随涵管直径的增大呈逐渐增大趋势,涵管直径由3.0 m增大至3.6 m,4.4 m时,最大拉应力分别增长了29.11%,55.05%;最大压应力分别增长了26.25%,63.49%。这表明涵管直径较大时,其上部有效土柱自重较大,钢波纹管涵受力较大。
(5) 钢波纹管与路堤主线正交,涵管直径(3 m)一定时,路堤填筑高度为14~20 m,涵管各测点应力、应变随涵洞上方填土高度的增加大致呈线性增大趋势,钢波纹管处于弹性受力阶段。当填筑高度为26 m时,最大拉、压应力应变分别为251.89 MPa,1 199.49 με和-302.65 MPa,-1 441.17 με,钢波纹管涵进入塑性状态。这表明此工况下,钢波纹管涵涵顶的路堤填筑高度不应超过26 m。
(6) 钢波纹管涵轴向刚度EA、弯曲刚度EI一定时,随涵管直径的增大,路基填筑高度降低;随其与路堤主线夹角趋于正交,路堤填筑高度降低,但涵管两侧水平位置处应力趋于相等呈对称分布。
| [1] |
刘刚.高填方路堤下钢波纹管涵洞受力与变形特性研究[D].西安: 长安大学, 2012. LIU Gang. Study on Stress and Deformation Characteristics of Steel Corrugated Pipe Culvert under High Embankment[D]. Xi'an: Chang'an University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10710-1013018027.htm |
| [2] |
李斌.钢波纹管涵洞受力和变形特性离心模型试验研究[D].西安: 长安大学, 2014. LI Bin. Centrifugal Model Test Study on Force and Deformation Characteristics of Corrugated Steel Pipe Culverts[D]. Xi'an: Chang'an University, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10710-1014071562.htm |
| [3] |
Corrugated Steel Pipe Institute, American Iron and Steel Institute. Handbook of Steel Drainage & Highway Construction Products[M]. .
|
| [4] |
CAN/CSA-S6-00, Canadian Highway Bridge Design Code[S].
|
| [5] |
KJARTANSON B H, LOHNES R A, KLAIBER F W, et al. Full-scale Filed Test of Uplift Resistance of Corrugated Metal Pipe Culvert[J]. Transportation Research Record, 1995, 1514: 74-82. |
| [6] |
MACHELSKI C, ANTONISZYN G, MICHALSKI B. Live Load Effects on a Soil-steel Bridge Founded on Elastic Supports[J]. Studia Geotechnica et Mechanica, 2006, 28(2/3/4): 65-82. |
| [7] |
李祝龙.公路钢波纹管涵洞设计与施工技术研究[D].西安: 长安大学, 2006. LI Zhu-long. Study on Design and Construction Technology of Highway Corrugated Steel Pipe Culverts[D]. Xi'an: Chang'an University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-11941-2006163392.htm |
| [8] |
李祝龙, 刘百来, 李自武. 钢波纹管涵洞力学性能现场试验研究[J]. 公路交通科技, 2006, 23(3): 79-82. LI Zhu-long, LIU Bai-lai, LI Zi-wu. Field Mechanical Performance Test of Corrugated Steel Culvert[J]. Journal of Highway and Transportation Research and Development, 2006, 23(3): 79-82. |
| [9] |
李祝龙. 公路钢波纹管涵洞设计与施工技术[M]. 北京: 人民交通出版社, 2007. LI Zhu-long. Design and Construction Technology of Corrugated Pipe Culvert in Highway[M]. Beijing: China Communications Press, 2007. |
| [10] |
李祝龙, 曹彪, 梁养辉, 等. 管拱型钢波纹管涵洞有限元计算分析[J]. 重庆交通大学学报:自然科学版, 2016, 35(4): 29-34, 39. LI Zhu-long, CAO Biao, LIANG Yang-hui, et al. Finite Element Analysis of Arch-shaped Steel Corrugated Tubular Culvert[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2016, 35(4): 29-34, 39. |
| [11] |
YEAU K Y, SEZEN H, FOX P J. Load Performance of In Situ Corrugated Steel Highway Culverts[J]. Journal of Performance of Constructed Facilities, 2009, 23(1): 32-39. |
| [12] |
SEZEN H, YEAU K Y, FOX P J. In-situ Load Testing of Corrugated Steel Pipe-arch Culverts[J]. Journal of Performance of Constructed Facilities, 2008, 22(4): 245-252. |
| [13] |
潘春风, 季文玉. 青藏线金属波纹管涵洞室内试验研究[J]. 铁道建筑, 2006(8): 28-30. PAN Chun-feng, JI Wen-yu. Indoor Experimental Study on Culvert Made of Metal Rappled Tube Used on Qinghai-Tibet Railway Line[J]. Railway Engineering, 2006(8): 28-30. |
| [14] |
褚夫蛟, 曾水生, 方文富, 等. 高填方大直径钢波纹管涵洞力学特性[J]. 东北大学学报:自然科学版, 2016, 37(9): 1338-1342. CHU Fu-jiao, ZENG Shui-sheng, FANG Wen-fu, et al. Mechanical Properties of Large-sized Corrugated Steel Pipe Culvert under High Embankment Filled[J]. Journal of Northeastern University:Natural Science Edition, 2016, 37(9): 1338-1342. |
| [15] |
乌延玲, 冯忠居, 王彦志, 等. 钢波纹管涵洞受力与变形特性现场试验分析[J]. 西安建筑科技大学学报:自然科学版, 2011, 43(4): 513-516. WU Yan-ling, FENG Zhong-ju, WANG Yan-zhi, et al. Field Force and Deformation Characteristic Test of Corrugated Steel Pipe Culvert[J]. Journal of Xi'an University of Architecture and Technology:Natural Science Edition, 2011, 43(4): 513-516. |
| [16] |
冯忠居, 乌延玲, 贾彦武, 等. 钢波纹管涵洞受力与变形特性模拟试验研究[J]. 岩土工程学报, 2013, 35(1): 187-192. FENG Zhong-ju, WU Yan-ling, JIA Yan-wu, et al. Model Tests on Force and Deformation Characteristics of Corrugated Steel Pipe Culvert[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(1): 187-192. |
| [17] |
廖鑫.高填土大跨径钢波纹管涵的力学性能与设计方法研究[D].长沙: 湖南大学, 2014. LIAO Xin. Study on Mechanical Property and Design Method of High-backfill and Long-span Corrugated Steel Pipes[D]. Changsha: Hunan University, 2014. http://cdmd.cnki.com.cn/article/cdmd-10532-1014300580.htm |
| [18] |
刘云春.斜交低填大孔径钢波纹管涵内壁应变规律研究[D].西安: 西安工业大学, 2017. LIU Yun-chun. Study on Strain Law of Inner Wall of Skew Low-filled Large Diameter Corrugated Steel Pipe Culvert[D]. Xi'an: Xi'an Technological University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10702-1017195042.htm |
| [19] |
窦艳宁.斜交低填大孔径钢波纹管涵土压力分析[D].西安: 西安工业大学, 2017. DOU Yan-ning. Study on Skew Low-filled and Large Diameter Corrugated Steel Pipe Culvert Earth Pressure[D]. Xi'an: Xi'an Technological University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10702-1017195024.htm |
| [20] |
张东山, 王宪国. 大直径钢波纹管涵在多雨山区公路的应用[J]. 筑路机械与施工机械化, 2016, 33(10): 75-78. ZHANG Dong-shan, WANG Xian-guo. Application of Corrugated Steel Culvert with Large Diameter of Highway in Rainy Mountain Area[J]. Road Machinery and Construction Mechanization, 2016, 33(10): 75-78. |
| [21] |
赵国虎, 齐宏学, 王志宏. 公路建设钢波纹管涵设计与施工关键技术分析[J]. 公路, 2017, 62(8): 107-112. ZHAO Guo-hu, QI Hong-xue, WANG Zhi-hong. Analysis on Key Technologies for Design and Construction of Corrugated Steel Culverts for Highway Construction[J]. Highway, 2017, 62(8): 107-112. |
| [22] |
魏瑞, 曹周阳, 顾安全, 等. 高填方钢波纹管涵垂直土压力计算[J]. 交通运输工程学报, 2018, 18(3): 74-83. WEI Rui, CAO Zhou-yang, GU An-quan, et al. Calculation of Vertical Earth Pressure of High-fill Steel Corrugated Pipe Culvert[J]. Journal of Traffic and Transportation Engineering, 2018, 18(3): 74-83. |
| [23] |
魏瑞, 曹周阳, 顾安全. 高填方大直径钢波纹管涵减荷试验[J]. 长安大学学报:自然科学版, 2018, 38(3): 1-9. WEI Rui, CAO Zhou-yang, GU An-quan. Load Reduction Experimental of High Fill Soil Large Diameter Corrugated Steel Pipe Culvert[J]. Journal of Chang'an University:Natural Science Edition, 2018, 38(3): 1-9. |
| [24] |
魏瑞, 曹周阳, 顾安全. 高填方钢波纹管涵变形计算及涵土相对刚度系数研究[J]. 公路交通科技, 2018, 35(4): 67-76, 92. WEI Rui, CAO Zhou-yang, GU An-quan. Calculation of Deformation of High-filling Steel Corrugated Pipe Culvert and Study on Culvert Soil Relative Stiffness Coefficient[J]. Journal of Highway and Transportation Research and Development, 2018, 35(4): 67-76, 92. |
 2020, Vol. 37
2020, Vol. 37
