扩展功能
文章信息
- 张俊, 张晓德, 王文珊
- ZHANG Jun, ZHANG Xiao-de, WANG Wen-shan
- 沥青路面疲劳损伤理论研究综述
- Review of Studies on Asphalt Pavement Fatigue Damage Theory
- 公路交通科技, 2020, 37(10): 1-11
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(10): 1-11
- 10.3969/j.issn.1002-0268.2020.10.001
-
文章历史
- 收稿日期: 2019-02-19
目前沥青路面结构设计所用方法主要是力学-经验法[1],该法的基本原理是利用层状弹性力学理论,计算出路面最危险部位的应力、应变,然后通过疲劳分析建立这些指标与路面材料疲劳寿命、永久变形之间的关系,进而通过控制这些指标实现路面结构设计。力学-经验法能反映结构层厚度、模量大小等因素对路面疲劳寿命的影响,相比传统经验方法有明显进步,但是,随着交通量的日益增长和更多路面结构形式及材料种类的出现,力学-经验法的不足日益突出[2]:(1)按沥青层层底弯拉应力或应变控制设计的思想,与路面实际受力不符。对于半刚性基层路面而言,基层模量一般较大,沥青层层底一般处于受压状态,因此,路面实际受力与弯拉疲劳导致破坏的设计思想不符。(2)按容许弯沉控制设计后,即使是基层层底,其弯拉应力或应变一般都能满足验算要求,所以按层底弯拉疲劳控制设计的思想,实际不能起到控制作用。(3)沥青混合料的力学和疲劳特性受温度和加载速率的影响很大,而且表征混合料模量的定义繁多,彼此之间物理意义、测试结果相差甚大,而该法对进行路面应力分析和疲劳验算所用的模量、容许弯拉应力或应变等参数并未给出明确规定,实际选用多为不同温度、加载速率下测试结果的简单平均,分析结果存在很大随意性。
以上不足使得该法难以有效指导半刚性基层沥青路面结构设计,路面实际使用寿命与设计寿命相去甚远,设计人员实际设计时多以经验为主,所以,研究一种能克服当前路面设计理论的不足、能体现路面结构与其使用性能之间的关系、能反映路面使用性能随其使用年限发展演化规律的新设计和计算理论,是当前沥青路面分析与计算研究面临的重要课题。
疲劳损伤力学是专门研究材料在重复荷载作用下,其内部应力、应变、刚度及损伤等指标随加载次数的增加而发展演变的规律的一个固体力学分支,其在描述材料疲劳破坏过程中力学性能的演变等方面具有突出优势,受到力学界的广泛重视和推崇[3]。
沥青路面在车辆荷载和环境因素的重复作用下,性能逐渐劣化最终发生破坏的过程,是一种典型的疲劳损伤现象[4-10],采用疲劳损伤力学研究其受力与性能演化,具有其他力学理论所难以比拟的优势,因此,疲劳损伤力学兴起不久,就引起道路工程专家的广泛关注,并围绕其在沥青路面领域的应用开展了大量工作[11-24]。
但就疲劳损伤力学在道路领域的研究与应用现状来看,目前较为系统地介绍沥青路面疲劳损伤理论的文献较少,仍有较多人对疲劳损伤理论的基础概念和基本原理不甚清楚,研究中动辄称之为损伤,混淆了损伤的基本概念。另外,损伤力学理论自20世纪70—80年代发展至今,已取得长足进步,在沥青路面领域亦取得丰硕成果,因此,有必要对其进行系统梳理,及时向广大工作者介绍该理论的最新进展。同时,随着疲劳损伤理论在沥青路面领域的不断进展,新的问题不断涌现,梳理和剖析这些问题、为后续研究者指明新的切入点,亦有助该理论在沥青路面领域的进步。
鉴于以上背景,本研究从疲劳损伤力学基本理论、沥青路面疲劳损伤理论研究现状、存在的问题等方面入手,对沥青路面疲劳损伤理论进行综述,以求明晰疲劳损伤理论基本概念、及时介绍该理论在路面领域的最新进展和主要成果,同时探讨当前研究存在的主要问题,指出沥青路面疲劳损伤研究新的切入点。
1 疲劳损伤力学基本原理 1.1 疲劳损伤力学简介损伤力学于20世纪70—80年代兴起,其宗旨是研究材料受力过程中其内部产生的损伤,以及这些损伤对材料力学性能的影响[3]。
损伤力学研究对象(即损伤类型)包括弹塑性损伤、蠕变损伤、疲劳损伤、腐蚀损伤及辐射损伤等,其中,疲劳损伤专指因外荷载的重复作用而引起的损伤,相应专门研究疲劳损伤的力学称之为疲劳损伤力学。
1.2 疲劳损伤力学的主要内容(1) 损伤变量
研究材料的损伤演化规律时,需要定义一个不可逆的场变量来描述材料损伤的发展演化状态,这个场变量称之为损伤变量[25]。损伤变量的定义有很多种,合理的定义既要能恰当体现材料的损伤状态,又要便于试验测量,因此,定义一个合适的损伤变量是该理论的关键。
在经典损伤力学中,常用损伤前后材料模量的劣化来定义损伤:

|
(1) |
式中,D为损伤变量;E为无损材料的模量;E′为损伤后材料的模量。
(2) 损伤演化方程
损伤演化方程是一个损伤变量和加载次数、应力应变及环境影响变量之间的公式,用来描述材料损伤随循环加载次数增加而累积演化的规律,反映一次加载能给工程结构造成多大损伤及多次循环加载造成的损伤如何累积和演化,是疲劳损伤力学的核心[3]。
损伤演化方程一般具有如下形式:
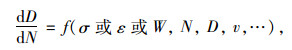
|
(2) |
式中,N为循环加载次数;σ,ε为应力和应变;W为耗散能;v为反映环境影响因素的变量。
当边界条件给定后,对以上微分形式的损伤演化方程进行积分,即可得到损伤变量的表达式:
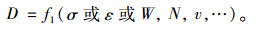
|
(3) |
当损伤变量D=1时,即可得疲劳寿命N=Nf的表达式:

|
(4) |
式中Nf为疲劳寿命。
(3) 损伤-本构方程
损伤-本构方程用来描述受损材料的应力-应变关系,是疲劳损伤力学的又一关键内容。损伤-本构方程的建立方法有多种,最经典的是利用应变等效原理来建立,即任何损伤材料的本构关系与无损时的形式相同,只要将其中的Cuachy应力替换为有效应力而应变保持不变即可。
例如,一维线弹性材料的损伤-本构关系可表示为:
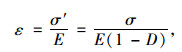
|
(5) |
式中,ε为应变;σ′为有效应力;E为弹性模量;σ为Cauchy应力,又叫名义应力;D为损伤,其表达式由损伤演化方程给出。
(4) 求解工程结构的应力、应变和损伤场
求解疲劳损伤力学的基本方程包括下列方程,下标i, j, k分别为3个直角坐标中的坐标之一:

|
(6) |
式中,σij为应力分量;Bi为体力分量。

|
(7) |
式中,ui为位移分量;εij为应变分量。
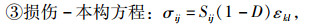
|
(8) |
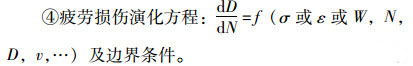
|
(9) |
与弹塑性力学相比,疲劳损伤力学的基本方程只多了损伤演化方程,本构方程也变成了损伤-本构方程,因此,对于疲劳损伤理论来说,其关键就是建立损伤演化方程和损伤-本构方程。当这两个方程给定后,剩下问题就是研究如何在给定的边界条件下求解以上方程。对于少数简单的边界条件,可尝试采用解析方法求解,其余情况一般采用耦合损伤的有限元方法。
2 沥青路面疲劳损伤力学研究现状 2.1 损伤变量如前所述,定义一个合理又便于试验测量的损伤变量是研究疲劳损伤理论的前提。目前定义沥青混合料损伤变量的方法大致有两种,一种是从细观层次出发来建立损伤变量,另一种则是从混合料宏观性能入手建立损伤变量。
从细观层次来看,沥青混合料内部含有大量微观缺陷,这些微观缺陷的数量、大小和取向反映了损伤状态,因此,当利用CT、扫描电镜、X射线衍射等手段获得这些微观缺陷分布、演变的定量数据后,便可用来定义沥青混合料的损伤变[26-28]。
从细观层次定义损伤变量,概念清楚,直观易懂,但是其力学意义不够明确,不易建立其与材料力学性能之间的联系,所以从宏观角度出发,利用混合料宏观力学性能的改变来定义损伤变量为大多数专家学者所采用。如损伤力学发展初期,用弹性模量的劣化定义损伤的方法获得广泛应用[29-30];且随着损伤理论的不断发展,又有新的损伤变量定义产生,如关宏信等、Park等研究沥青混合料黏弹性损伤时采用耗散能定义损伤变量,朱洪洲等研究沥青混合料疲劳与蠕变损伤耦合时,采用复数模量定义损伤变量,均取得了较好结果。
总的来说,损伤变量的定义存在一定主观任意性。就目前研究结果来看,利用CT等细观技术建立的损伤变量方法,虽然直观易懂,但却不便与材料的宏观力学性能相联系,而从沥青路面疲劳损伤力学的最终研究目的来看,利用沥青混合料力学的劣化改变来定义损伤的方法,显然更便于实际的损伤分析和计算。
2.2 损伤演化方程如前所述,损伤演化方程是疲劳损伤力学的核心内容,建立一个能恰当描述材料损伤演化累积规律的数学模型,是疲劳损伤研究的一个关键。损伤演化方程是损伤变量和加载次数、应力应变及环境影响变量之间的一个数学公式,回答了给定环境下某确定应力或应变的加载作用能给结构造成多大损伤,或结构完全疲劳破坏需要多少次加载。
对于沥青混合料的损伤演化方程而言,其危险部位的应力或应变主要取决于路面结构与车辆轴重,损伤大小反映了混合料模量的衰减(即路面的损坏状态),加载次数则对应交通量或使用年限,环境变量主要是温度和加载频率(车辆行驶速度),因此,合理的沥青混合料损伤演化方程,可以严格体现路面性能与路面结构、材料、车辆荷载和使用年限、环境变量之间的关系,比起当前路面设计理论具有明显进步。
2.2.1 代表性损伤演化方程及其建立方法就目前已有结果来看,建立损伤演化方程的方法主要有4种,分别是:细观方法、宏观方法(又称唯象学方法)、能量方法和基于概率分布的方法,因此,本节关于损伤演化方程研究现状的介绍也从这4个方面入手。
(1) 细观方法
损伤的经典定义即为材料中的大量微观缺陷,因此,研究这些微观缺陷的分布和损伤之间的关系,是建立损伤演化方程的重要方法。如谢涛[31]建立了CT数和损伤演化率的数学表达式;李芬等基于分形维数和孔隙率的概念定义了损伤变量,建立了其与疲劳加载次数的关系曲线;杨军则利用声发射和扫描电镜研究了沥青混合料的细观损伤等等。
细观方法可以直观描述和解释材料损伤演化的过程和机理,建立的损伤演化方程一般也能较好地描述材料疲劳破坏过程的细观现象,但从实际应用角度,人们更关心损伤演化过程中材料的宏观力学性能和使用寿命,因此,采用唯象的宏观力学方法建立损伤演化方程的方式更为广大研究人员所接受。
(2) 宏观力学方法(唯象学方法)
宏观力学方法注重材料损伤演化过程中宏观力学性能的演变,不穷究其细观层次的损伤机理,其最终目的是解决实际工程结构的疲劳损伤问题,而不是解释其损伤机理。
采用宏观方法建立的损伤演化方程中,最经典的当属Miner准则:

|
(10) |
式中,D为损伤变量; N为加载次数; Nf为疲劳应力σ作用下材料的疲劳寿命。
Miner准则认为损伤只与加载次数有关,且与加载次数呈线性关系,多次损伤线性累加,各个循环之间互不影响。Miner准则简单易懂,应用广泛,在沥青路面领域应用较多,但忽略了疲劳损伤的非线性效应,无法考虑加载历史对损伤演化的影响,因而其适用性受到一些专家学者的质疑。
而能考虑损伤的非线性累积和演化,又被广泛应用且采用宏观方法建立的经典损伤演化方程则是Chaboche模型[32]:
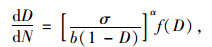
|
(11) |
式中, f(D)为损伤度的函数;α,b为材料参数,b与试验平均加载应力有关。f (D)有两种形式:f (D)= (1-D)-β,β为材料参数;f (D)= [1-(1-D)1+α]β。
Chaboche模型依据不可逆热力学导出,属于非线性损伤演化模型。该模型具有严格的理论背景,能体现荷载大小、加载顺序对材料损伤演化的影响,在我国沥青路面疲劳损伤分析中广泛应用[33-36]。但Chaboche模型最初主要用于金属材料,不能体现加载速率(或频率)对材料损伤演化特性的影响,将其直接用于沥青混合料显然不甚理想。鉴于此,Zhang[4-5]对该模型进行了修正,提出了一个能体现加载频率影响的沥青混合料损伤演化模型,通过大量试验标定了频率的影响指数,取得了较好效果。该模型表达式为:

|
(12) |
式中,σa为疲劳应力幅值;f为加载频率;α,β,γ,b均为材料参数。
(3) 能量法
黏弹性理论认为,材料疲劳加载直至破坏过程中,外力所做的功转变为两种形式:一种以可逆的弹性势能形式存在,卸载后释放出来;另一种则由于黏滞作用而耗散,以耗散能的形式存在,不可恢复,并导致材料性能的劣化而产生损伤。基于此认识,Schapery[17]首先提出基于能量耗散的损伤演化理论,即材料疲劳破坏过程中,损伤的演化速率与能量的耗散速率有对应关系,即:
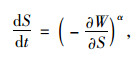
|
(13) |
式中,S为反映损伤状态的内变量;W为应变能密度函数;α为材料参数;t为时间。
据此理论,Schapery,Little,Kim等[37-46]对沥青混合料的损伤演化规律进行了分析,并利用弹性-黏弹性的对应准则和时温等效原理,建立了相应的疲劳损伤模型。
这些工作中,以Kim研究的VECD模型最具代表性,其模型经大量室内试验和试验路观测表明,能较好地反映沥青路面的疲劳损伤性能(图 1),在沥青路面疲劳损伤领域拥有广泛影响。

|
| 图 1 VECD模型预测疲劳损伤与美国联邦公路局加速加载路面实测开裂的对比[38] Fig. 1 Comparison between fatigue damage predicted by VECD model and measured crack on FHWA accelerated loading pavement |
| |
Schapery模型基于耗散能的演化模型,物理意义明确、理论依据较充分,能够考虑沥青混合料的黏弹性特点对其损伤演化特性的影响,可认为是目前沥青混合料损伤演化模型的代表。我国很多专家学者在研究沥青路面疲劳损伤时也采用该模型,如张俊[47]采用广义Maxwell和Burgers模型,给出沥青混合料耗散能的解析表达式,然后利用能量耗散理论建立疲劳损伤的演化模型,取得了较好效果。
(4) 基于概率分布的方法
按照损伤的经典定义,损伤就是材料内部存在的大量微观缺陷。虽然缺陷的大小、分布各不相同,但从连续介质力学角度来看,可认为这些缺陷是连续分布的,且服从概率分布f (ε),因此有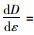
一般情况下,取分布函数f (ε)为Weibull分布,此时损伤演化方程转变为如下形式:
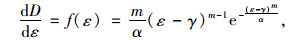
|
(14) |
式中,α,m,γ分别为微缺陷的尺度参数、形状参数和位置参数。
按照概率分布的方法建立损伤演化方程的方法,最早在岩石、混凝土等领域得到广泛应用。由于沥青混合料和岩石、混凝土在很多方面颇具相似之处,因此,关于沥青路面疲劳损伤理论的研究,很多也采用了概率分布的方法建立损伤演化方程[48-51]。
2.2.2 损伤演化方程建立方法评述以上4种方法均在沥青路面疲劳损伤领域研究中得到了较广泛的应用,尤其是Chaboche模型,在当前沥青路面疲劳损伤分析中最为常见。但以Chaboche模型为代表的、基于宏观力学性能衰变思想建立的损伤演化方程,主要源于金属材料疲劳损伤领域,由于其着重于材料宏观力学性能与其损伤之间的联系,因此用于具体工程损伤分析有便利之处,但对于沥青混凝土,黏性对其宏观性能有着重要影响,这点则是当前Chaboche等宏观力学模型所不能反映的,因此尝试在该类损伤演化方程中引入黏性的影响变量,将是该方向的一个具有重要实际意义的工作。
而基于细观技术和概率分布理论建立的损伤演化方程,最早多用于岩石、混凝土等领域。这类材料的细观孔隙、微裂隙大小、分布和发展对其宏观力学特性有重要影响,这点和沥青混凝土颇为类似,因此,采用该类方法建立的损伤演化方程,对揭示沥青混合料的疲劳损伤机理应有较好意义。但对沥青路面而言,人们更加关心其损伤大小与混合料或路面宏观力学性能之间的关系,因此,采用细观和概率分布原理建立的沥青混合料损伤演化方程的方法,在疲劳损伤分析及与路面性能相联系等方面具有较大局限。
至于基于能量耗散原理建立损伤演化模型的方法,其初衷就是用于描述黏弹性材料的损伤演化特性,因此其用于沥青混合料损伤研究更具内在优势。正因如此,国外较早开展沥青路面疲劳损伤模型研究的Park,Little,Kim,在研究沥青混合料损伤演化规律时均采用能量耗散原理建立损伤演化模型。可以预见,在今后较长一段时间内,利用能量耗散原理研究沥青混合料的损伤演化特性,将是这一领域的重要方向。
同时,考虑到路面孔隙水压、温度、老化等环境因素对沥青路面性能的重要影响,在以上代表性损伤演化方程中引入环境因素的影响变量,对于研究沥青路面的疲劳损伤规律来说亦具有重要意义。
2.3 损伤-本构方程由于损伤的产生,受损材料的本构关系不同于无损材料,而且随着损伤的增加,受损材料的本构关系也不断发生变化,所以,损伤分析所用本构方程须耦合并能体现损伤演化对其应力-应变关系影响的变量,即采用损伤-本构方程。
损伤本构方程的建立方法主要有两种,一种是利用前面介绍的应变等效原理,另一种是根据不可逆热力学导出。由于应变等效原理概念清晰、简便易懂,且关于无损材料本构关系的研究也较为充分,因此,目前建立沥青混合料损伤-本构方程多采用应变等效原理[52-55]。
采用应变等效原理建立损伤-本构方程,前提要先给出一个能较好地描述无损材料应力应变关系的本构方程。对于沥青混合料来说,人们早已认识到它是一种典型的黏弹塑性材料,在温度较低、外加荷载较小、施加频率较高时,其弹性和黏弹性表现比较明显;而当温度较高、荷载较大、频率较低时塑性和黏塑性则表现突出。所以在沥青混合料力学研究初期,人们多采用Maxwell模型或广义Maxwell模型来描述沥青混合料的黏弹性质,甚至为简便起见,线弹性Hooke模型也被用于损伤分析。但随着研究的持续深入,更多研究表明Burgers模型以及修正的Burgers模型在描述沥青混合料的黏弹性时能取得更好结果,虽然Burgers模型并不能描述应变曲线的第3阶段,但由于从实际角度出发应变曲线第3阶段的工程意义并不明显,所以Burgers模型获得了广泛认可。
但在夏季重载路段和平面交叉路口,沥青混合料的塑性特点更加明显,此时路面的车辙现象往往比较突出,如果仍旧采用以Burgers模型为基础的黏弹性模型来描述沥青混合料的应力应变关系,结果往往不尽人意,所以,发展新的能够反映沥青混合料黏塑性特点的黏弹塑性本构模型有实际意义。基于此,很多学者通过在Burgus模型或VanDerPoel模型中串联黏塑性元件,得到不同的非线性黏弹塑性本构方程,并与不同的损伤演化方程相结合得出沥青混合料的黏弹塑性损伤-本构方程,取得了良好效果。有必要指出的是,虽然非线性黏弹塑性本构方程在刻画沥青混合料复杂力学行为时表现出了明显优势,但其本构方程待定参数甚多,参数的拟合标定往往并不简单,从而限制了黏弹塑性本构方程的应用和发展,所以实际研究中,以Burgurs模型为代表的黏弹性模型具有实用价值。
至于另一种以不可逆热力学为基础导出损伤-本构方程的方法,由于过程相对繁琐、力学推导和数学演绎相对复杂,且其力学概念也没有等效应变原理清晰易懂,因此实际应用并不多。
纵观以上现状可知,采用应变等效原理,并以Burgers黏弹性模型为基础而改进的沥青混合料损伤本构关系研究,目前已取得较多进展。所建立的损伤-本构模型,不仅能描述沥青混合料的黏弹性、黏弹塑性等复杂力学行为,还能体现加载间歇、沥青损伤自愈等对其损伤-本构关系的影响,基本上较好地描述了损伤状态下沥青混合料的应力应变关系。
需指出的是,沥青路面承受的外荷载主要是车辆动态循环荷载,因此沥青混合料损伤-本构方程应能反映动态循环荷载作用下的应力应变关系,而目前众多损伤-本构关系的研究则多以静态荷载为主,能够反映动态循环荷载作用下沥青混合料损伤与其本构关系特点的研究尚不多见,这也是今后沥青混合料损伤本构关系研究应加以注意的问题。
2.4 疲劳损伤求解方法当沥青混合料的损伤-本构方程、损伤演化方程建立后,剩下工作便是如何应用数学和力学方法来求解实际路面结构的应力、应变和损伤场,即疲劳损伤分析,并建立这些指标与路面结构、加载次数、环境条件(如温度)之间的关系,进而指导路面设计。
虽然沥青路面疲劳损伤理论目的是明确的,理论也基本完备,但其实际的损伤分析和计算却并不简单。到目前为止,也只能对个别简单边界条件进行解析,稍复杂的边界需借助损伤力学-有限元方法,而且即使是数值方法也主要针对简单工况的分析,距离实际应用还有一定距离。这些疲劳损伤计算研究中,较早的、较为系统的给出疲劳损伤力学求解方法的是张行等[3],他们在《金属构件应用疲劳损伤力学》一书中,分别提出了疲劳裂纹形成和扩展过程的损伤力学分析方法,并给出了能对裂纹形成和扩展过程进行全寿命分析的损伤力学-有限元-附加力法。虽然该著作并不针对沥青路面领域,但其分析方法却对沥青路面疲劳损伤问题的求解产生了重要影响,后续较早采用损伤力学原理对沥青混合料的损伤场、疲劳寿命进行分析计算的研究,也基本采用了此著作所述方法。此后,采用疲劳损伤理论求解沥青路面损伤场、疲劳寿命的研究逐渐开展起来,不仅分析了车辆荷载作用下路面的损伤场,还能计算温度应力引发损伤导致的温缩裂缝现象[56],研究对象也没有局限于沥青路面,桥面铺装、机场道面采用疲劳损伤理论也取得了一定成果。
就目前沥青路面疲劳损伤计算所用方法来看,采用耦合损伤的有限元方法占据了绝大多数。该方法通过在每个计算步中修改单元刚度矩阵和其他有限元计算参数的方法,来体现损伤对材料性能的劣化影响,在每个计算步长中则采取和普通有限元一样的算法。计算步长可用加载次数也可用损伤,以加载次数作为计算步长比较直观,实现相对简单,但耗费机时;而以损伤作为步长则正相反,机时耗费较少但实现相对困难,而且对于疲劳损伤有限元计算而言,单元划分数一般较大,尤其是三维有限元计算,其单元划分数量对计算机时有着重大影响。近年来许多专家学者所提倡的细观数值方法,更是对计算效率、计算机硬件提出了巨大挑战,研究采用大型计算机对沥青路面进行疲劳损伤力学细观数值分析,将是今后该方向发展的一个热点。
除了采用损伤力学-有限元数值方法计算沥青混合料的疲劳损伤外,解析方法在损伤分析和计算领域也占有重要地位。虽然解析方法模型和边界比较单一,但其结果可靠,可为实际工程问题提供方向性的指导,因此,解析方法在沥青路面疲劳损伤计算领域历来受到重视。如唐雪松等[57]提出了一种模拟疲劳裂纹扩展的特征单元失效模式,对沥青混合料小梁试件的疲劳裂纹形成和扩展寿命进行了分析,而张俊[58]则在此基础上,对实际沥青路面的疲劳寿命进行了解析,且与实测结果吻合较好。刘振清[33]从力学近似法角度对钢桥面沥青铺装体系的疲劳损伤特性进行了分析。这些工作均为解析法分析和计算沥青混合料的疲劳损伤工作起到积极促进作用。但是目前关于解析法计算沥青路面损伤的研究,所采用模型和边界条件均比较简单,距离实用尚有较大距离,所以,开展更多的、与沥青路面实际工况更加接近的疲劳损伤解析研究,具有重要研究意义。
3 需进一步关注的问题(1) 虽然目前就沥青混合料损伤-本构和损伤演化模型的研究已取得了很多富有成效的成果,但当前研究多以一维损伤为主,能够描述混合料三维损伤-本构关系和损伤演化规律的研究还很少见到。
(2) 目前沥青路面疲劳损伤研究主要集中在混合料的损伤-本构关系方面,对于混合料的疲劳损伤演化方程这一核心工作,目前成果明显不足。时至今日,损伤分析所用演化模型仍以Miner准则、Chaboche模型、Schapery模型等损伤力学兴起之初,研究金属材料损伤时提出的经典损伤演化模型为主。这些模型用于沥青路面损伤分析虽取得了丰富成果,但不足也显而易见,因此,建立一个能较好体现沥青混合料的黏弹特性显著、温度敏感、沥青老化敏感、加速速率敏感等特点的损伤演化模型,是沥青路面疲劳损伤研究与应用的实际需求。
另外,对于饱水沥青路面,车辆荷载引起的超孔隙水压力对路面损伤演化的影响不亚于车辆荷载本身,所以,研究路面孔隙水压对沥青混合料损伤演化特性的影响,尝试在损伤演化方程中引入孔隙水压力的变量,建立一个能反映孔隙水压力对混合料损伤影响的演化方程具有现实意义。
(3) 沥青混合料为典型的黏弹或黏弹塑性材料,除了损伤演化模型要考虑其黏性影响外,采用黏弹性分析路面应力应变,更是对损伤计算结果具有重要影响,而这一工作目前在国际范围内才刚刚开始。
(4) 目前沥青路面疲劳损伤分析多采用有限元方法,虽然该法能够考虑较复杂的工况,但其分析过程较为复杂,不便于广大研究者掌握,结果也往往不具普适性。与数值方法相反,解析法的分析结果一般比较可靠,合理简化后的计算模型往往能为实际工程问题提供方向性的指导,但由于解析方法对研究人员数理基础提出较高要求,导致实际研究中采用解析方法分析和计算路面损伤的研究较为少见。因此,对沥青路面实际问题合理简化,建立典型的路面计算模型,采用解析方法分析路面疲劳损伤,并与数值方法、室内外试验研究相结合,对于促进沥青路面疲劳损伤理论的发展具有重要意义。
(5) 沥青路面疲劳损伤求解多采用有限元数值方法,但由于沥青混合料体积组成的非均匀性和随机性特点对其宏观性能有重要影响,以及常规均质各向同性有限元在反映这些特点对路面损伤影响方面存在固有缺陷,因此,沥青路面疲劳损伤分析须采用能体现空隙、级配等细观结构特性的细观数值模型,方能正确反映混合料疲劳损伤的演化累积规律,这也是今后沥青路面疲劳损伤分析应持续开展的工作之一。
相应大规模的细观疲劳损伤分析,对计算机规模的巨大需求,也使得沥青路面大规模的科学计算工作具有实际价值。
4 结论(1) 疲劳损伤理论符合沥青路面疲劳破坏现象的力学本质。将其用于路面分析与计算,能够反映路面性能与车辆荷载、路面结构和材料、环境及使用时间之间的关系,相比现行设计理论,该理论具有明显的先进性。
(2) 沥青路面疲劳损伤理论的主要内容是:建立能恰当反映沥青混合料主要力学特点的损伤演化方程和损伤-本构方程,并利用所建方程对合理简化后的路面结构进行应力、应变和损伤分析。
(3) 沥青路面疲劳损伤的后续研究,宜在混合料三维损伤-本构关系,能反映混合料黏弹特性、孔隙水压、温度和加载速率对损伤影响的演化方程,解析法求解路面损伤场,大规模细观数值计算等方面投入更多精力。
| [1] |
孙立军. 铺面工程学[M]. 上海: 同济大学出版社, 2012: 157-159. SUN Li-jun. Pavement Engineering[M]. Shanghai: Tongji University Press, 2012: 157-159. |
| [2] |
孙立军, 许志军, 陈子建. 沥青路面的行为函数[J]. 同济大学学报:自然科学版, 2003, 31(5): 558-561. SUN Li-jun, XU Zhi-jun, CHEN Zi-jian. Behavior Modeling for Asphalt Pavements[J]. Journal of Tongji University:Natural Science Edition, 2003, 31(5): 558-561. |
| [3] |
张行, 赵军. 金属构件应用疲劳损伤力学[M]. 北京: 国防工业出版社, 1998: 2-11. ZHANG Hang, ZHAO Jun. Applied Fatigue Damage Mechanics of Metallic Structural Members[M]. Beijing: National Defense Industry Press, 1998: 2-11. |
| [4] |
ZHANG J, WANG Y D, SU Y. Fatigue Damage Evolution Model of Asphalt Mixture Considering Influence of Loading Frequency[J]. Construction and Building Materials, 2019, 218: 712-720. |
| [5] |
ZHANG J, LI Z, CHU H, et al. A Viscoelastic Damage Constitutive Model for Asphalt Mixture under the Cyclic Loading[J]. Construction and Building Materials, 2019, 227: 116631. |
| [6] |
ZHANG J, SABOURI M, GUDDATIA M N, et al. Development of a Failure Criterion for Asphalt Mixtures under Fatigue Loading[J]. Road Materials and Pavement Design, 2013, 14(S2): 1-15. |
| [7] |
ZHANG J, SU Y, ZHANG X, et al. Experimental Investigation on the Effect of Loading Frequency on the Fatigue Damage Characteristic of Asphalt Mixture[J]. International Journal of Pavement Research and Technology, 2019, 12(5): 478-485. |
| [8] |
张俊, 李志伟. 循环荷载作用下沥青混合料的黏弹塑性损伤本构模型[J]. 东北大学学报:自然科学版, 2019, 40(10): 1496-1503. ZHANG Jun, LI Zhi-wei. Viscoelastic-plastic Damage Constitutive Model of Asphalt Mixture under Cyclic Loading[J]. Journal of Northeastern University:Natural Science Edition, 2019, 40(10): 1496-1503. |
| [9] |
WANG Y D, GHANBARI A, UNDERWOOD B S, et al. Development of a Performance-volumetric Relationship for Asphalt Mixtures:[J]. Transportation Research Record, 2019, 2673: 416-430. |
| [10] |
WANG Y D, KESHAVARZI B, KIM Y R. Fatigue Performance Prediction of Asphalt Pavements Using FlexPAVETM, the S-VECD Model, and DR Failure Criterion[J]. Transportation Research Record, 2018, 2672: 217-227. |
| [11] |
郑健龙, 吕松涛. 沥青混合料非线性疲劳损伤模型[J]. 中国公路学报, 2009, 22(5): 21-28. ZHENG Jian-long, LÜ Song-tao. Nonlinear Fatigue Damage Model for Asphalt Mixtures[J]. China Journal of Highway and Transport, 2009, 22(5): 21-28. |
| [12] |
周志刚, 张清平, 袁秀湘. 沥青混凝土弯曲疲劳试验疲劳损伤分析[J]. 中南大学学报:自然科学版, 2011, 42(6): 1743-1751. ZHOU Zhi-gang, ZHANG Qing-ping, YUAN Xiu-xiang. Fatigue Damage Analysis of Asphalt Mixture Specimen during Cyclic Bending Test[J]. Journal of Central South University:Science and Technology Edition, 2011, 42(6): 1743-1751. |
| [13] |
沙爱民, 贾侃, 李小刚. 半刚性基层材料的疲劳特性[J]. 交通运输工程学报, 2009, 9(3): 29-33. ShA Ai-min, JIA Kan, LI Xiao-gang. Fatigue Performances of Semi-rigid Base Course Materials[J]. Journal of Traffic and Transportation Engineering, 2009, 9(3): 29-33. |
| [14] |
单丽岩, 谭忆秋, 许亚男, 等. 应力、应变控制模式下沥青疲劳损伤演化规律[J]. 中国公路学报, 2016, 29(1): 16-21. SHAN Li-yan, TAN Yi-qiu, XU Ya-nan, et al. Fatigue Damage Evolution Rules of Asphalt under Controlled-stress and Controlled-strain Modes[J]. China Journal of Highway and Transport, 2016, 29(1): 16-21. |
| [15] |
关宏信, 郑健龙, 张起森. 沥青混合料的黏弹性疲劳损伤模型研究[J]. 力学与实践, 2007, 29(2): 50-53. GUAN Hong-xin, ZHENG Jian-long, ZHANG Qi-sen. Viscoelastic Fatigue Damage Model of Bituminous Mixture[J]. Mechanics in Engineering, 2007, 29(2): 50-53. |
| [16] |
朱洪洲, 黄晓明. 沥青混合料疲劳性能关键影响因素分析[J]. 东南大学学报:自然科学版, 2004, 34(2): 260-263. ZHU Hong-zhou, HUANG Xiao-ming. Analysis of Key Influential Factors of Asphalt-mixture Fatigue Property[J]. Journal of Southeast University:Natural Science Edition, 2004, 34(2): 260-263. |
| [17] |
PARK S W, SCHAPERY R A. A Viscoelastic Constitutive Model for Particulate Composite with Growing Damage[J]. International Journal of Solids & Structures, 1997, 34(8): 931-947. |
| [18] |
KIM Y R, LEE H J, LITTLE D N. Fatigue Characterization of Asphalt Concrete Using Viscoelasticity And Continuum Damage Theory[J]. Journal of the Association of Asphalt Paving Technologists, 1997, 66: 520-569. |
| [19] |
MUN S. Numerical Computation in the Viscoelastoplastic Continuum Damage of Hot Mix Asphalt Concrete[J]. Fatigue & Fracture of Engineering Materials & Structures, 2009, 32(12): 995-1003. |
| [20] |
郑健龙, 马健, 吕松涛, 等. 老化沥青混合料粘弹性疲劳损伤模型研究[J]. 工程力学, 2010, 27(3): 116-123. ZHENG Jian-long, MA Jian, LÜ Song-tao, et al. Research on Viscoelastic Fatigue Damage Model of Aging Asphalt Mixtures[J]. Engineering Mechanics, 2010, 27(3): 116-123. |
| [21] |
谭忆秋, 赵立东, 蓝碧武, 等. 沥青混合料冻融损伤模型及寿命预估研究[J]. 公路交通科技, 2011, 28(6): 1-6. TAN Yi-qiu, ZHAO Li-dong, LAN Bi-wu, et al. Research on Freeze-thaw Damage Model and Life Prediction of Asphalt Mixture[J]. Journal of Highway and Transportation Research and Development, 2011, 28(6): 1-6. |
| [22] |
DANIEL J S, KIM Y R. Development of a Simplified Fatigue Test and Analysis Procedure Using a Viscoelastic Continuum Damage Model[J]. Journal of the Association of Asphalt Paving Technologists, 2002, 71: 619-650. |
| [23] |
张久鹏, 黄晓明. 沥青混合料永久变形的弹黏塑-损伤力学模型[J]. 东南大学学报:自然科学版, 2010, 40(1): 185-189. ZHANG Jiu-peng, HUANG Xiao-ming. Viscoelastoplastic-damage Mechanics Model of Permanent Deformation in Asphalt Mixture[J]. Journal of Southeast University:Natural Science Edition, 2010, 40(1): 185-189. |
| [24] |
孙志林, 卓斌, 廖中平. 沥青路面非线性疲劳损伤特性及应力状态演变规律[J]. 中南大学学报:自然科学版, 2014, 45(2): 576-580. SUN Zhi-lin, ZHUO Bin, LIAO Zhong-ping. Nonlinear Fatigue Damage Characteristics and Stress Evolution Law of Asphalt Pavement[J]. Journal of Central South University:Science and Technology Edition, 2014, 45(2): 576-580. |
| [25] |
余寿文, 冯西桥. 损伤力学[M]. 北京: 清华大学出版社, 1997: 10-17. YU Shou-wen, FENG Xi-qiao. Damage Mechanics[M]. Beijing: Tsinghua University Press, 1997: 10-17. |
| [26] |
李之达, 陈智军, 李芬. 沥青混凝土路面水破坏的疲劳损伤模型研究[J]. 武汉理工大学学报:交通科学与工程版, 2009, 33(1): 5-8. LI Zhi-da, CHEN Zhi-jun, LI Fen. Research on Fatigue Damage Model of Water Damage to Asphalt Concrete Pavement[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering Edition, 2009, 33(1): 5-8. |
| [27] |
蒋泽中, 张华, 谢涛, 等. 基于图像技术的沥青混合料细观损伤演化研究[J]. 公路交通科技, 2009, 26(2): 27-37. JIANG Ze-zhong, ZHANG Hua, XIE Tao, et al. Research on Meso-damage Evolution of Asphalt Mixtures Based on Image Technology[J]. Journal of Highway and Transportation Research and Development, 2009, 26(2): 27-37. |
| [28] |
石妍, 彭尚仕, 闫小虎, 等. 水泥乳化沥青混凝土细观损伤及微观性能[J]. 建筑材料学报, 2014, 17(1): 177-186. SHI Yan, PENG Shang-shi, YAN Xiao-hu, et al. Meso-damage and Micro-properties of Cement Emulsified Asphalt Concrete[J]. Journal of Building Materials, 2014, 17(1): 177-186. |
| [29] |
ALOBAIDI I, HOARE D J. The Development of Pore Water Pressure at the Subgrade-subbase Interface of a Highway Pavement and Its Effect on Pumping of Fines[J]. Geotextiles & Geomembranes, 1996, 14(2): 111-135. |
| [30] |
CARO S, MASAD E, SÁNCHEZ-SILVA M, et al. Stochastic Micromechanical Model of the Deterioration of Asphalt Mixtures Subject to Moisture Diffusion Processes[J]. International Journal for Numerical & Analytical Methods in Geomechanics, 2011, 35(10): 1079-1097. |
| [31] |
谢涛.基于CT实时观测的沥青混合料裂纹扩展行为研究[D].成都: 西南交通大学, 2006. XIE Tao.Study on Crack Propagation Behavior of Asphalt Mixtures Based on CT Real Time Observation[D].Chengdu: Southwest Jiaotong University, 2006. http://cdmd.cnki.com.cn/Article/CDMD-10613-2007019935.htm |
| [32] |
CHABOCHE J L, LESNE P M. A Non-linear Continuous Fatigue Damage Model[J]. Fatigue & Fracture of Engineering Materials & Structures, 2010, 11(1): 1-17. |
| [33] |
刘振清, 黄卫, 刘清泉, 等. 钢桥面沥青混合料铺装体系疲劳特性的损伤力学分析[J]. 土木工程学报, 2006, 39(2): 117-121. LIU Zhen-qing, HUANG Wei, LIU Qing-quan, et al. Damage Mechanics on the Fatigue Characteristics of Asphalt Mixture Surfacing for Steel Bridge Decks[J]. China Civil Engineering Journal, 2006, 39(2): 117-121. |
| [34] |
李盛, 李宇峙, 刘朝晖. 刚柔复合式路面沥青层温度疲劳损伤及开裂研究[J]. 工程力学, 2013, 30(10): 122-127. LI Sheng, LI Yu-zhi, LIU Zhao-hui. Research on Temperature Fatigue Damage and Cracking in Asphalt Layer of Rigid-flexible Composite Pavement[J]. Engineering Mechanics, 2013, 30(10): 122-127. |
| [35] |
吕松涛. 基于非线性疲劳损伤的沥青路面轴载换算[J]. 工程力学, 2012, 29(10): 268-274. LÜ Song-tao. Axle Load Conversion of Asphalt Pavement Based on Nonlinear Fatigue Damage[J]. Engineering Mechanics, 2012, 29(10): 268-274. |
| [36] |
孙志林, 黄晓明. 考虑层间接触的沥青路面非线性疲劳损伤特性分析[J]. 中南大学学报:自然科学版, 2012, 43(6): 2385-2389. SUN Zhi-lin, HUANG Xiao-ming. Nonlinear Fatigue Damage Characteristics Analysis of Asphalt Pavement Considering Interlayer Contact[J]. Journal of Central South University:Science and Technology Edition, 2012, 43(6): 2385-2389. |
| [37] |
CARO S, MASAD E, BHASIN A, et al. Micromechanical Modeling of the Influence of Material Properties on Moisture-induced Damage in Asphalt Mixtures[J]. Construction and Building Materials, 2010, 24(7): 1184-1192. |
| [38] |
NOROUZI A.Investigation of Specimen Geometries for the VECD Model and Calibration of the LVECD Program for Fatigue Cracking Performance of Asphalt Pavements[D].Raleigh: North Carolina State University, 2015.
|
| [39] |
WANG Y, KIM Y R. Development of a Pseudo Strain Energy-based Fatigue Failure Criterion for Asphalt Mixtures[J]. International Journal of Pavement Engineering, 2019, 20(10): 1182-1192. |
| [40] |
UNDERWOOD B S, YUN T, KIM Y R, et al. Experimental Investigations of the Viscoelastic and Damage Behaviors of Hot-mix Asphalt in Compression[J]. Journal of Materials in Civil Engineering, 2011, 23(4): 459-466. |
| [41] |
DANIEL J S, KIM Y R. Development of a Simplified Fatigue Test and Analysis Procedure Using a Viscoelastic Continuum Damage Model[J]. Journal of the Association of Asphalt Paving Technologists, 2002, 71: 619-650. |
| [42] |
YUN T, UNDERWOOD B S, KIM Y R. Time-temperature Superposition for HMA with Growing Damage and Permanent Strain in Confined Tension and Compression[J]. Journal of Materials in Civil Engineering, 2010, 22(5): 415-422. |
| [43] |
LEE H J, KIM Y R. Viscoelastic Continuum Damage Model of Asphalt Concrete with Healing[J]. Journal of Engineering Mechanics, 1998, 124(11): 1224-1232. |
| [44] |
KIM Y R, LITTLE D N, LYTTON R R. Use of Dynamic Mechanical Analysis (DMA) to Evaluate the Fatigue and Healing Potential of Asphalt Binders in Sand Asphalt Mixtures[J]. Journal of the Association of Asphalt Paving Technologists, 2002, 71: 176-206. |
| [45] |
LEE H J, KIM Y R. Viscoelastic Constitutive Model for Asphalt Concrete under Cyclic Loading[J]. Journal of Engineering Mechanics, 1998, 124(1): 32-40. |
| [46] |
UNDERWOOD B S, KIM Y R, GUDDATI M N.Characterization and Performance Prediction of ALF Mixtures Using a Viscoelastoplastic Continuum Damage Model[C]//Proceedings of the Technical Sessions 2006 Annual Meeting.Savannah, US: AAPT, 2006: 577-636.
|
| [47] |
张晓德, 张俊.基于能量法沥青混合料疲劳损伤演化特性和模型[D].沈阳: 东北大学, 2017. ZHANG Xiao-de, ZHANG Jun.Fatigue Damage Evolution Characteristics and Model of Asphalt Mixture Based on Energy Method[D].Shenyang: Northeastern University, 2017. |
| [48] |
郑健龙, 吕松涛, 田小革. 基于蠕变试验的沥青粘弹性损伤特性[J]. 工程力学, 2008, 25(2): 193-196. ZHENG Jian-long, LÜ Song-tao, TIAN Xiao-ge. Viscoelastic Damage Characteristics of Asphalt Based on Creep Test[J]. Engineering Mechanics, 2008, 25(2): 193-196. |
| [49] |
郑健龙. 基于结构层寿命递增的耐久性沥青路面设计新思想[J]. 中国公路学报, 2014, 27(1): 1-7. ZHENG Jian-long. New Structure Design of Durable Asphalt Pavement Based on Life Increment[J]. China Journal of Highway and Transport, 2014, 27(1): 1-7. |
| [50] |
刘俊卿, 李倩, 李红孝. 基于统计损伤理论的沥青混合料的蠕变模型[J]. 公路交通科技, 2014, 31(8): 13-18. LIU Jun-qing, LI Qian, LI Hong-xiao. A New Creep Model of Asphalt Mixture Based on Statistical Damage Theory[J]. Journal of Highway and Transportation Research and Development, 2014, 31(8): 13-18. |
| [51] |
邵腊庚, 周晓青, 李宇峙, 等. 基于直接拉伸试验的沥青混合料粘弹性损伤特性研究[J]. 土木工程学报, 2005, 38(4): 125-128. SHAO La-geng, ZHOU Xiao-qing, LI Yu-zhi, et al. A Study on the Viscoelastic and Damage Characteristics of Asphalt Mixture Based on Pure Tension Test[J]. China Civil Engineering Journal, 2005, 38(4): 125-128. |
| [52] |
张久鹏, 黄晓明, 马涛. 沥青混合料损伤蠕变特性及模型研究[J]. 岩土工程学报, 2008, 30(12): 1867-1871. ZHANG Jiu-peng, HUANG Xiao-ming, MA Tao. Damage-creep Characteristics and Model of Asphalt Mixture[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(12): 1867-1871. |
| [53] |
曾国伟, 杨新华, 白凡, 等. 沥青砂粘弹塑蠕变损伤本构模型实验研究[J]. 工程力学, 2013, 30(4): 249-253. ZENG Guo-wei, YANG Xin-hua, BAI Fan, et al. Experimental Researches on a Visco-elastoplastic Creep Damage Constitutive Model of Asphalt Mastic[J]. Engineering Mechanics, 2013, 30(4): 249-253. |
| [54] |
YE Y, YANG X, CHEN C. Experimental Researches on Visco-elastoplastic Constitutive Model of Asphalt Mastic[J]. Construction & Building Materials, 2009, 23(10): 3161-3165. |
| [55] |
朱浩然, 孙璐, 朱耀庭. 基于热力学的沥青混合料粘弹-粘塑性损伤本构模型[J]. 中国公路学报, 2013, 26(3): 57-64. ZHU Hao-ran, SUN Lu, ZHU Yao-ting. Viscoelastic-viscoplastic Damage Constitutive Model Based on Thermodynamics for Asphalt Mixtures[J]. China Journal of Highway and Transport, 2013, 26(3): 57-64. |
| [56] |
王金昌, 赵颖华, 孙雅珍. 沥青混凝土路面表面裂缝的疲劳变温损伤分析[J]. 中国公路学报, 2001, 14(2): 6-8. WANG Jin-chang, ZHAO Ying-hua, SUN Ya-zhen. Fatigue Damage Analysis of Surface Cracked Asphalt Pavement under Varying Temperature[J]. China Journal of Highway and Transport, 2001, 14(2): 6-8. |
| [57] |
唐雪松, 蒋持平, 郑健龙, 等. 沥青混合料疲劳过程的损伤力学分析[J]. 应用力学学报, 2000, 17(4): 92-98. TANG Xue-song, JIANG Chi-ping, ZHENG Jian-long, et al. Damage Mechanical Analysis for Fatigue Failure Process of Bituminous Mixtures[J]. Chinese Journal of Applied Mechanics, 2000, 17(4): 92-98. |
| [58] |
曾攀, 张俊.基于弯曲小梁疲劳寿命解析的沥青路面使用寿命计算模型[D].沈阳: 东北大学, 2018. ZENG Pan, ZHANG Jun.A Service Life Prediction Model for Asphalt Pavement Based on Fatigue Life of Curved Beams Analysis[D].Shenyang: Northeastern University, 2018. |
 2020, Vol. 37
2020, Vol. 37
