扩展功能
文章信息
- 崔洪军, 赵锐, 朱敏清, 李霞
- CUI Hong-jun, ZHAO Rui, ZHU Min-qing, LI Xia
- 基于熵率的公交乘客出行重复性度量方法
- A Method for Measuring Repeatability of Bus Passenger Travel Based on Entropy Rate
- 公路交通科技, 2020, 37(9): 97-103, 112
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(9): 97-103, 112
- 10.3969/j.issn.1002-0268.2020.09.013
-
文章历史
- 收稿日期: 2020-03-27
在城市基础设施日趋完善的今天,人们的出行变得更加多元化, 随之对出行规律的研究也逐渐成为热门。研究方法多为通过对出行者时空变化进行有效地考量继而总结出规律。
Alfred等[1]、Ma等[2]利用时空关联理论分别分析了智能卡乘客在指定车站的乘降数量及关联行程、针对北京智能卡出行者的出行时空特性规律进行了研究。Kusakabe T等[3-4]对地铁出行乘客的智能卡数据加以研究进而得到出行者的出行时空关联性信息。Ordóñez等[5]对出行活动进行聚类,并利用分层选择模型对为期7天的连续出行活动进行了分析。张晚笛等[6]基于多时间粒度对乘客的地铁出行规律进行了研究。杨光[7]对快速公交乘客的出行时空规律特征进行了研究。Sang、Gordon、Nassir、Weng等基于智能卡数据对出行目的、出行链进行了分类研究[8-11]。由此可知,学者多注重研究出行者连续多日的出行习惯及行为,继而总结出规律,同时需要大量连续的研究数据做以支撑。
1 出行重复性乘客出行有着很强的时空关联性;同时,在一定的时间阈值内,出行者因个体需要,会反复访问某一地点并在此地点逗留近似时长。本研究将此定义为出行的重复性,即:一定时间跨度内,出行者访问某一地点并逗留相近时长的反复程度称为出行重复性。出行重复性可衡量出行者的出行偏好,在出行规律推算中有着重要的意义,但要在冗杂的数据中准确分析所选个体的出行规律时即需对出行重复性进行合理度量。在此有必要说明,本研究的重复性度量是对乘客出行重复程度的度量,研究乘客出行的重复程度可以辅助分析其出行规律,并可为交管部门提供交通线路优化的第一手数据材料。
2 出行重复性度量 2.1 出行序列生成度量出行重复性首先需要对乘客多日的出行进行合理化排序。乘客的出行可链化为一系列出行序列,而出行序列中又包含了诸多出行关键特征事件,例如:地点、模式、路线、活动类型、活动持续时间等。这些特征事件的维度变化并不是独立的[12-14],如:一个乘客对出行方式及线路的选择会影响到他的出行起始时间和出行持续时间;而探究序列的要点在于对各关键特征事件进行合理排序。
本研究将出行序列用数学方法呈现,通过排列关键特征事件顺序来定义出行序列。将每名乘客在多日的出行活动看作一个随机过程,该过程用以表示特征事件的发生频率及发生次序。设给定乘客个体u出行所对应的随机过程为Xu,在该过程中产生的特征事件为随机变量Xu。同时假设每个特征事件均为一个离散变量x,该变量来自个体u出行时产生的可能出行特征事件集Eu,并以此识别特征事件的唯一性;当且仅当两个特征事件具有相同的事件属性组合时,二者的x值相同。对于x∈Eu,Xu具有离散概率分布p(x)=P{Xu=x}。
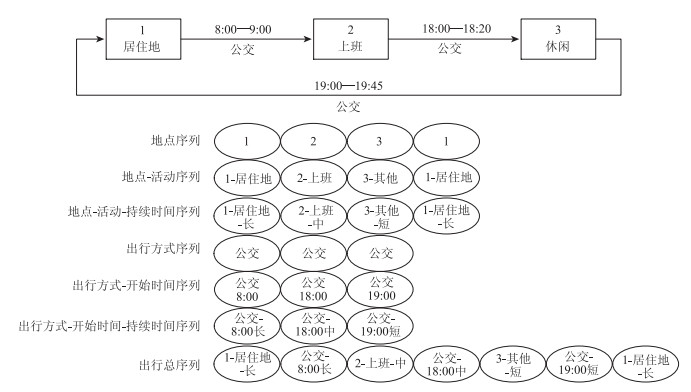
为避免冗余表达,本研究省略下标u,其中数学符号表示对象均为单个出行个体。随机过程X={…, X-1, X0, X1, X2,…}为随机变量Xi的有序集合,特征事件i与j间有序集合的任意有限出行序列可用有序子集Xij={Xi, Xi+1, …, Xj-1, Xj}表示,其中,-∞ < i≤j < +∞, Xij⊂X。为了一致性和计算方便,笔者假设所有事件属性均是离散的。图 1展示了如何利用特征事件将乘客一天的出行活动链化表示。笔者通过划分活动持续时长将出行活动划分为3类:长持续时间(大于10 h)、短持续时间(小于2 h)及中等持续时间(介于2~10 h之间)。同时,通过长(大于30 min)和短(小于30 min)两个维度划分行程持续时间。这样,各出行活动序列变得更加细化,特征事件得以凸显。
|
| 图 1 出行序列示意图 Fig. 1 Schematic diagram of travel sequences |
| |
2.2 下车地点确定
本研究针对公交乘客的出行重复性进行研究。在国内大多城市中,公交车辆的收费方式为一票制,即只存在上车刷卡的数据,而乘客下车的站点数据无法直接得到。因此,要生成完整的乘客公交出行序列需要推算下车站点信息。本研究根据多日乘车数据,基于经典出行链方法对下车站点数据进行推断,以得到乘客的下车站点信息,进而为后续出行地点状态的标定奠定基础。
乘客在日常出行中,往往以居住地为起点,经过一天中一系列的出行活动后返回起始居住地点, 同时,在这一系列的出行活动中又多以各行程间首尾顺次相接作为典型特征。因此,可将乘客的出行活动看做一个链状结构,即出行链,通过以下3个基本假设对算乘客的下车站点信息:
(1) 在同一出行日中,同一乘客的前一次出行终点为其紧邻下一次出行的起点;
(2) 在同一出行日中,乘客最后一次出行的终点为其当日首次出行的起点;
(3) 在客观条件不变的情况下,乘客总是选取离自己最近的乘车站点开始下一段行程。
依照以上3个假设,可推算出绝大部分乘客的下车站点信息,其准确率为93%[15]。
2.3 出行地点状态标定本研究侧重于公交乘客出行的重复性,同时也因数据源的局限性,只对公交出行乘客的出行数据进行了分析。现实生活中,乘客可能采用公交、轨道交通等复合出行方式,继而会影响到本研究对于乘客出行目的地的判断。因而,针对此问题,本研究将可推算下车站点的出行即视为一次完整的出行。如该乘客在推断的下车站点下车后采用了非公交的其他交通出行方式到达下一目的地,笔者则将其目的地一概划入上文推算得到的下车站点中,而逗留时间起始值也按照该乘客在该站点下车的时间计算。简言之:在乘客下车后,当无法判断其是否还采用了其他非公交出行方式到达他处时即认为乘客在下车地点附近停留,并以此记录逗留时长。基于该理论方法,可尽可能地减少因数据局限性引发的对于乘客出行规律以及公交出行需求的判断误差。
将乘客的出行地点状态进行标定,其中状态1, 2…依照乘客出行的逗留时间予以划分。具体描述如表 1所示。
| 状态 | 相关描述 |
| -1 | 由于无行程记录,乘客出行地点不能推断 |
| 0 | 不能推断乘客起讫点,出行地点无法推断 |
| 1 | 乘客所在的第1个且滞留时间最长的地点 |
| 2 | 乘客所在的第2个且滞留时间次长的地点 |
| … | 出行者所在的乘客位于地点… |
在此,以某持卡人出行记录为例,其2018年1月1日—2018年2月1日的部分出行记录如表 2所示。
| 交易时间 | 线路名 | 站点名称 |
| 2018-1-1 6:31 | 2路 | 北国商城 |
| 2018-1-1 10:22 | 2路 | 胸科医院 |
| 2018-1-2 6:54 | 2路 | 北国商城 |
| 2018-1-2 10:26 | 2路 | 胸科医院 |
| 2018-1-3 6:31 | 2路 | 水务集团 |
| 2018-1-3 6:49 | 2路 | 北国商城 |
| 2018-1-3 10:49 | 2路 | 胸科医院 |
| 2018-1-4 15:05 | 2路 | 北国商城 |
| 2018-1-6 6:25 | 2路 | 市城管委 |
| 2018-1-6 10:25 | 2路 | 水务集团 |
| 2018-1-6 11:08 | 27路 | 老年病医院 |
以出行地点状态为依据将其出行特征序列进行排序, 故可将此持卡人在2018年1月1日—2018年2月1日期间的出行序列简化为(1, 2, 1, 2, 3, 1, 2, 1, 4, 3, 5), 基于简化的出行序列可对乘客每一出行地点的出行概率p(x)进行计算,同时也将出行序列以数学方法进行了表述,为后续出行重复性的度量做好准备。
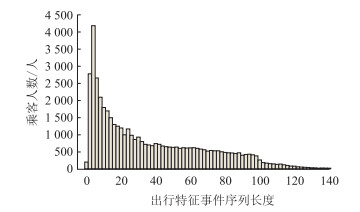
以收集到的2018年1月1日—2018年2月1日石家庄公交智能卡乘客出行数据为例,将乘客的出行记录进行链化处理,依照前文所述方法将出行序列进行整理后得到如图 2所示的46 923名乘客的出行特征事件序列分布情况。其中横坐标所示的出行特征事件序列长度指乘客出行中的地点状态累计排列长度。
|
| 图 2 出行特征事件序列长度分布 Fig. 2 Distribution of travel characteristics event sequence lengths |
| |
3 度量方法
如前文所述,本研究将出行者个体多日的出行特征事件看作随机过程X,以此来度量出行序列。随机过程X中不同的特征属性可提供关于个人出行的不同规律信息,集合E中的关键特征事件个数表达了出行活动的多样性, 而概率分布p(x)则可表现个人出行活动的频率。下面针对以上诸多性质,介绍其推算方法,并以此来度量出行重复性。
3.1 出行序列的信息熵无论出行特征属性如何排序,首先均应核算出行序列的重复程度。在前文给定的假设下,随机过程X(即出行特征序列)的规律性完全由概率分布p(x)决定。通常情况下:一个规律性的出行过程会产生更为确定且更易估计的出行规律结果。在信息论中,一个过程的随机性或不可预测性可以用信息熵来衡量。信息熵以比特(bits)为单位,其可度量每次预测随机变量时所需的平均信息,即基于现有信息推测乘客今后出行潜在访问地点所需的信息量值。
当x∈E时,具有概率分布p(x)=P{X=x}的随机变量X的信息熵H(X)可用公式(1)表示。其中X为出行序列中被看做随机变量的乘客访问地点状态,E为给定个体出行时所有可能的特征事件集合。
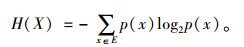
|
(1) |
对于乘客出行的地点序列而言,信息熵为考量出行地点在研究时段中被出行者访问概率的方差,当乘客只有一个备选访问地点时,其出行序列的信息熵为0。而当乘客出行地点随出行时段分布越均匀时,其出行序列的信息熵就越大,出行重复性越高。
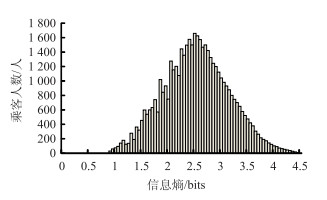
将上述46 923名乘客出行特征序列的信息熵按照式(1)计算后,分布情况如图 3所示。其中,信息熵分布的均值为2.53 bits。
|
| 图 3 智能卡乘客出行序列的信息熵分布 Fig. 3 Distribution of information entropies of smart card passengers' travel sequence |
| |
3.2 出行序列熵率
尽管信息熵可以较好地度量出行序列中乘客访问某一地点的重复性,但却不能良好地反映随时间变化时该乘客访问某一出行地点的重复程度。与此同时,特征事件Xi的条件概率分布也取决于事件Xi-1,Xi-2的分布结果(p(Xi|Xi-1, Xi-2, …)≠p(Xi)),即出行地点排列的先后顺序。因此,笔者在此引入熵率来度量出行的重复性。
熵率能够反映出行序列中各出行访问地点的排列顺序对出行重复性的影响情况。随机过程X的熵率H′(X)定义为当子序列X1n随n逐渐增大时其信息熵H(X)的收敛速率,以式(2)表示。其中,H(X1, X2, X3, …, Xn)为由子序列X1,X2,…,Xn(即前文标定的地点状态序列)定义的联合变量序列X1n的熵率。
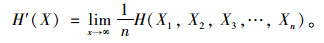
|
(2) |
由文献[16-17]可知:在所有平稳随机过程中此极限必存在,且等于式(3)所示,其中pn为长度n的子地点状态序列的联合分布概率。
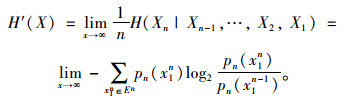
|
(3) |
结合式(2)、(3)可知,熵率测算的是随机过程X中每一新产生的特征事件占之前特征事件信息熵的平均值, 即反映了在乘客的出行地点状态序列中,该乘客每新增一个访问地点,对其整体地点序列信息熵的影响变化情况。出行序列熵率的上界为该出行序列信息熵的值,而当出行地点状态序列中乘客新访问的地点可完全由先前的地点状态决定时(p(Xi=x|Xi-1, Xi-2, …)=1),其熵率为0。
通俗来讲,熵率是一系列事件中产生新生信息多少的度量,先前数据中存有的信息越多,可提供给后续数据分析的信息就越多,而可供挖掘的新信息就越少,相应的,其熵率就越小。因而熵率可用来度量乘客的出行重复性,出行序列的熵率越小,则该乘客的出行重复性越高,出行规律性越强。
3.3 熵率的计算有限序列的熵率在计算时存在很大难度:由式(3)可知,熵率是由序列X1n中未知的联合分布概率pn构成的函数,一般方法为在序列X1n中观察相应符号在表达式中出现的组合频率来推算pn, 但当组合长度增加时此法便难以实施。在计算熵率时通常使用数据压缩方法来规避对pn的计算,本研究基于Burrows-Wheeler转换对熵率进行计算[16]。
BWT分为两步,首先,长度为n的有限地点状态序列X1n依次循环右移,每次循环移动一位;其次,对循环移位后的n个字符按字母表顺序排列,将每一个排序后的字符最后一个字母提取出来便组成了新的序列。表 3以序列banana#为例展示了其转换过程, 详细叙述参见参考文献[18],因篇幅原因此处不再赘述。
| 序号 | 循环转换 | 循环转换后排序 | 转换后序列 |
| 1 | banana# | #banana | annb#aa |
| 2 | #banana | a#banan | |
| 3 | a#banan | ana#ban | |
| 4 | na#bana | anana#b | |
| 5 | ana#ban | banana# | |
| 6 | nana#ba | na#bana | |
| 7 | anana#b | nana#ba |
在任一平稳随机过程X中,通过BWT均可将有限记忆序列转化为分段形式的无记忆序列,通过这一过程可推算出原始序列过程的熵率。将变换后的序列分割为等长的s段,根据式(4)估计每段的结果分布。其中,Ns(x)为字符x在段落s中出现的次数,而每一段s的信息熵由式(5)得到;q为字符出现次数的估计值,最后通过每一段信息熵的均值求得随机过程X即乘客出行序列的熵率,由式(6)表示。
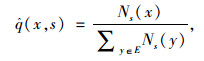
|
(4) |
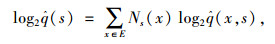
|
(5) |
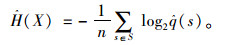
|
(6) |
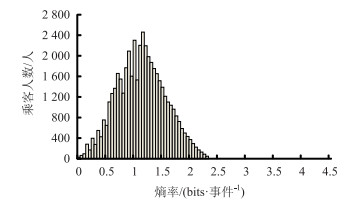
将上述46 923名乘客出行特征序列的熵率按上述方法计算后,分布情况如图 4所示。其中,熵率分布的均值为1.13 bits/事件。
|
| 图 4 智能卡乘客出行序列熵率分布 Fig. 4 Distribution of entropy rates of smart card passengers' travel sequence |
| |
由上文可知,如不考虑事件发生顺序所提供的信息,乘客的出行序列排序结果几乎与公平掷骰子结果一致(掷骰子的信息熵为2.6 bits,而所研究乘客出行序列的信息熵均值为2.53 bits)。若一个人只在家庭和工作地(p(home)=p(work)=0.5)之间出行,则其熵为1 bits,等同于抛硬币所产生结果的信息熵(信息熵为1 bits)。而熵率是考虑了事件发生顺序时信息熵的值, 文中考虑乘客的出行地点序列及目的地逗留持续时间。结合图 3、图 4可观察到:出行序列的信息熵与熵率二者均值之差为1.4 bits,意味着考虑乘客出行事件的发生顺序可使乘客出行重复性度量时的不确定性显著降低,并有助于出行规律的推算。
4 应用与效果分析以石家庄公交智能卡出行数据为例,介绍该方法的实际应用。分别选取编号为A、B、C、D的4名持卡人2018年1月1日—2018年2月1日期间的出行信息,将其出行记录按照本研究所述方法进行排列,计算得到以上4人的出行序列信息的信息熵及熵率值如表 4所示。
| 乘客序号 | 1 | 2 | 3 | 4 |
| 信息熵 | 2.712 | 2.543 | 2.658 | 1.593 |
| 熵率 | 1.024 | 1.165 | 1.212 | 0.549 |
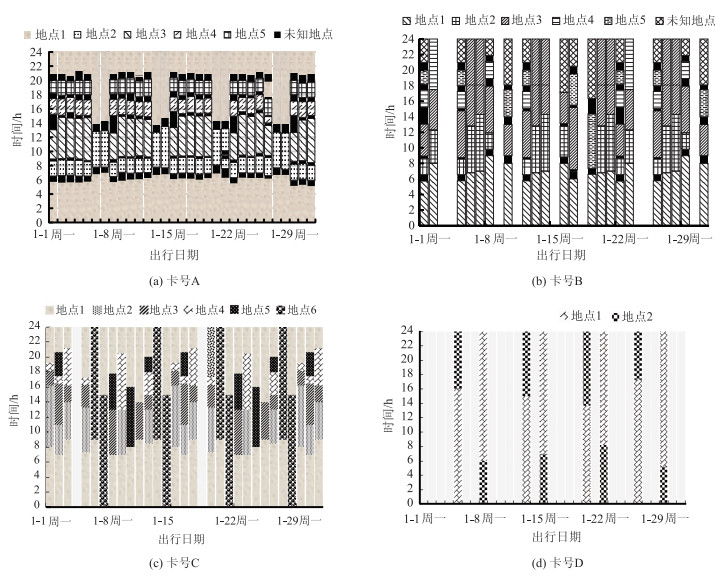
根据不同地点的出行序列分布情况,结合乘客活动的持续时间,可得到其出行序列分布情况分别如图 5所示。图中不同纹理图案表示该乘客的不同出行地点。
|
| 图 5 乘客出行活动序列 Fig. 5 Travel sequence of passengers |
| |
由图 5(a)可知,该持卡乘客1月内访问5个出行地点的次数几乎相同,工作日时段,该乘客固定的已知出行地点为5个,而周末时多为2个;其在每周一13:00—15:00时左右均会产生未知出行。出行地点访问顺序较为一致。此外,虽此用户的多日出行活动并不完全一致,但呈现出明显规律,其出行重复性较强,此结论可通过熵率在研究数据均值以下而得以佐证。
图 5(b)、5(c)直观来看并无规律性可言,但由出行序列的信息熵均在均值以上可知,两位持卡用户的出行较为规律。仔细分析图像可见,图 5(b)用户间隔两周的出行序列显示出重复性,即:第4周与第1周重复,第2周与第5周重复。基于本研究的重复性度量方法,有理由相信:该用户1月第3周的出行在接下来的日历周期中会有较大的可能出现重复。而图 5(c)用户在1月第1,3,5周及第2、4周的出行分别显示出重复性,单数周与双数周的出行需求并不一致,但总体却呈现出规律性。
图 5(d)展示了通过熵率测量而得到的另一个出行重复性度量实例。该乘客的出行模式在研究期间一直持续,却并不是严格意义上的周期性重复,因而常规出行链模型可能无法捕捉到其间断性的出行规律,但基于本研究提出的出行重复性度量方法,可明确地捕捉到数据集中此用户的出行规律性。由图可知,在4种不同的情况下,该乘客由主要位置(深色格纹)出行至次要位置(浅色斜纹),并在1~2天后进行反向出行。查阅ADCs系统数据可知,浅色斜纹所示位置区域临近石家庄北站,该乘客可能在此处离开石家庄度过周末;该用户在周五或周六离开,并在接下来一周的周一返回。
通过上述4名持卡人的出行记录及经由本研究所述方法计算后可分析得到乘客的出行规律信息。基于该方法,在可获得的研究数据较为有限的情况下可通过乘客的出行重复性判断其出行规律特征,并依此推断其今后一定时段内的出行需求。与此同时,基于乘客出行序列的信息熵及熵率可对新增出行信息的多少进行度量评价,因此,结合其概率特性,使用该法可对乘客今后一段时间内的出行进行预测。
此外,由本研究的出行序列与时间分布信息图可看出乘客在具体某一地点的停留时间,通过分析大量持卡人的出行数据可得到公交站点的上下客人数及各站点的载客高峰时段,结合本研究的出行重复性可对公交线路进行站点选址、线路密度安排、车辆时间间隔优化等一系列交通规划管理工作。
5 结论(1) 对出行重复性概念进行了定义及阐述。
(2) 用数学方法结合随机过程对乘客的多日出行片段进行链化排序,对乘客出行地点进行状态标定,得到了度量出行重复性所需的基于地点状态的乘客出行序列。
(3) 利用信息熵及熵率对乘客的出行重复性进行度量。信息熵是对概率分布方差的考量,其分布越均匀,相应的信息熵就越大,出行重复性就越高;而熵率作为对事件中新生信息产生量的度量,可更好地表现随机事件随时间变化时事件的重复程度,新生信息越少,其熵率就越小,出行的重复性越高。
(4) 结合石家庄智能卡乘客的出行数据,通过4名乘客的出行实例分析了本研究所述方法的实用效果,利用出行序列图表直观地反映了乘客研究时段内出行的重复性,同时,该法为以少量研究数据推算较长周期内乘客的出行规律提供了新思路。
| [1] |
ALFRED C K, CHAPLEAU R. Enriching Archived Smart Card Transaction Data for Transit Demand Modeling[J]. Transportation Research Record, 2008, 2063: 63-72. |
| [2] |
MA X L, WU Y J, WANG Y H, et al. Mining Smart Card Data for Transit Riders' Travel Patterns[J]. Transportation Research Part C:Emerging Technologies, 2013, 36: 1-12. |
| [3] |
KUSAKABE T, ASAKURA Y. Behavioural Data Mining of Transit Smart Card Data:A Data Fusion Approach[J]. Transportation Research Part C:Emerging Technologies, 2014, 46: 179-191. |
| [4] |
KUSAKABE T, IRYO T, ASAKURA Y. Estimation Method for Railway Passengers' Train Choice Behavior with Smart Card Transaction Data[J]. Transportation, 2010, 37(5): 731-749. |
| [5] |
MEDINA S A O. Inferring Weekly Primary Activity Patterns Using Public Transport Smart Card Data and a Household Travel Survey[J]. Travel Behaviour and Society, 2018, 12: 93-101. |
| [6] |
张晚笛, 陈峰, 王子甲, 等. 基于多时间粒度的地铁出行规律相似性度量[J]. 铁道学报, 2018, 40(4): 9-17. ZHANG Wan-di, CHEN Feng, WANG Zi-jia, et al. Similarity Measurement of Metro Travel Rules Based on Multi-time Granularities[J]. Journal of the China Railway Society, 2018, 40(4): 9-17. |
| [7] |
杨光.快速公交乘客出行的时空规律特征研究[D].成都: 西南交通大学, 2017. YANG Guang. Research on Temporal and Spatial Characteristics of Bus Rapid Transit[D]. Chengdu: Southwest Jiaotong University, 2017. |
| [8] |
LEE S G, HICHMAN M. Trip Purpose Inference Using Automated Fare Collection Date[J]. Public Transport, 2014, 6(2): 1-20. |
| [9] |
GORDON J B, KOUTSOPOULOS H N, WILSON N H M, et al. Automated Inference of Linked Transit Journeys in London Using Fare-transaction and Vehicle Location Data[J]. Transportation Research Record, 2013, 2343: 17-24. |
| [10] |
NASSIR N, HICHMAN M, MA Z L. Activity Detection and Transfer Identification for Public Transit Fare Card Data[J]. Transportation, 2015, 42(4): 1-23. |
| [11] |
WENG X X, LIU Y X, SONG H B, et al. Mining Urban Passengers' Travel Patterns from Incomplete Data with Use Cases[J]. Computer Networks, 2018, 134: 116-126. |
| [12] |
HANSON S, HUFF O J. Assessing Day-to-day Variability in Complex Travel Patterns[J]. Transportation Research Record, 1982, 891: 18-24. |
| [13] |
HANSON S, HUFF O J. Systematic Variability in Repetitious Travel[J]. Transportation, 1988, 15: 111-135. |
| [14] |
HUFF O J, HANSON S. Repetition and Variability in Urban Travel[J]. Geographical Analysis, 1986, 18(2): 97-114. |
| [15] |
BARRY J J, FREIMER R, SLAVIN H. Use of Entry-only Automatic Fare Collection Data to Estimate Linked Transit Trips in New York City[J]. Transportation Research Record, 2009, 2112: 53-61. |
| [16] |
CAI H, KULKARNI S R, VERDU S. Universal Entropy Estimation Viablock Sorting[J]. IEEE Transactions on Information Theory, 2004, 50(7): 1551-1561. |
| [17] |
GAO Y, KONTOYIANNIS I, BIENENSTOCK E. Estimating the Entropy of Binary Time Series:Methodology, Some Theory and a Simulation Study[J]. Entropy, 2008, 10(2): 71-99. |
| [18] |
ADJEROH D, BELL T, MUKHERJEE A. The Burrows-wheeler Transform:Data Compression, Suffix Arrays, and Pattern Matching[M]. Boston: Springer, 2008.
|
 2020, Vol. 37
2020, Vol. 37
