扩展功能
文章信息
- 范一平
- FAN Yi-ping
- 压力型预应力锚索受力特性数值分析
- Numerical Analysis on Mechanical Characteristics of Pressure-type Prestressed Anchor Cable
- 公路交通科技, 2020, 37(9): 34-40
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(9): 34-40
- 10.3969/j.issn.1002-0268.2020.09.005
-
文章历史
- 收稿日期: 2020-04-23
山区公路修建过程中不可避免会遇到大量高填深挖工程,特别是一些高陡边坡需要采用大吨位锚固支护才能维持其稳定性[1-2]。工程中拉力型锚索的锚固体以受拉为主并在端部产生应力集中,从而容易导致锚固体拉裂破坏,时常无法满足边坡防护的锚固承载力要求。压力型锚索筋材连接于锚固体远端(远离孔口端)的承载体上,锚索受拉时筋材将荷载传递至承载体上并将其转化为对锚固体的压力,再通过锚固体与围岩之间的剪应力将荷载传递到稳定的岩土体中。由于锚固体的抗压强度远高于其抗拉强度,因而压力型锚索受力机制更加合理,在工程中也逐渐得到应用和发展[3-4]。
虽然压力型锚索在我国各类工程中得到大量应用,且国内学者对其工作机制、破坏模式、设计方法等方面也开展了大量研究工作[5-9],但由于压力型锚索承载能力受众多因素影响,设计计算理论尚不完善,远不能满足工程实践需要。本研究选取山西省吉河高速某处路堑岩质边坡作为试验场地开展了现场测试,在试验数据基础上采用有限差分软件建立了三维数值计算模型,对压力型锚索受力特性及影响因素进行了分析探讨,可为今后类似工程设计和施工提供技术参考。
1 现场试验 1.1 工程概况本次试验地点位于吉县至河津高速公路,地貌属于喀斯特侵蚀剥蚀中、低山区,地层岩性以寒武系下统馒头组、中统张夏组及上统凤山组灰岩、白云质灰岩、白云岩、泥灰岩及页岩,奥陶系下统亮甲山组及中统下马家沟组灰岩、白云质灰岩、泥灰岩及白云岩为主,岩层产状平缓,溶蚀现象发育,深挖路段边坡稳定性较差,工程建议对其进行防护治理。为确定工程所在边坡地层中压力型锚索的极限承载力及受力特性,分析锚索的荷载位移曲线,以及为建立数值模型提供相关参数,在工程现场开展了锚索张拉试验。
|
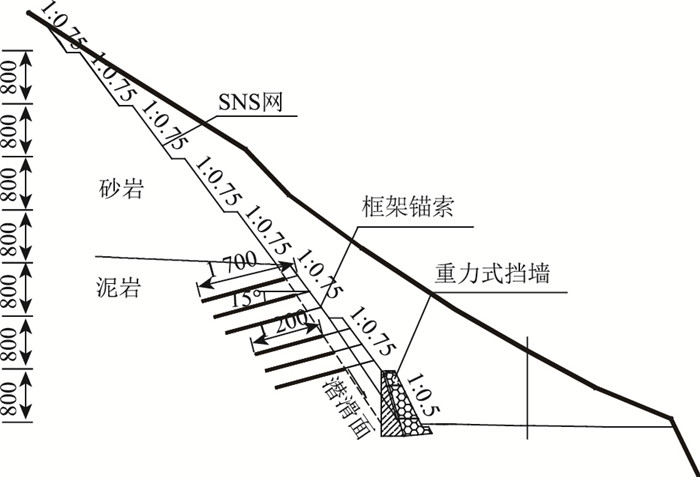
| 图 1 边坡支护及锚索布置(单位:cm) Fig. 1 Slope support and arrangement of anchor cables(unit: cm) |
| |
1.2 测试内容
本次试验锚索孔直径130 mm,锚索为2束1 860 MPa级高强度低松弛无黏结钢绞线(单束钢绞线直径15.24 mm,横截面积A=139 mm2),锚索锚固段采用M40砂浆灌注,分别在锚索的锚固体内部布设了混凝土应变计,以及在锚索孔口处布设了锚索轴力计,仪器安装如图 2所示。试验采用干钻法施工,采用空压机高压风吹清孔,避免用水清孔造成的岩屑遇水形成浆体附着在孔壁上形成润滑层,降低锚固性能[10-11]。钻孔过程中揭露地层表明,该地层岩质较为破碎,强度较低,吹出岩粉为浅灰青色,夹杂部分黄色粉末。

|
| 图 2 压力型锚索监测试验方案(单位:mm) Fig. 2 Monitoring test scheme of pressure-type prestressed cable(unit: mm) |
| |
1.3 试验结果分析
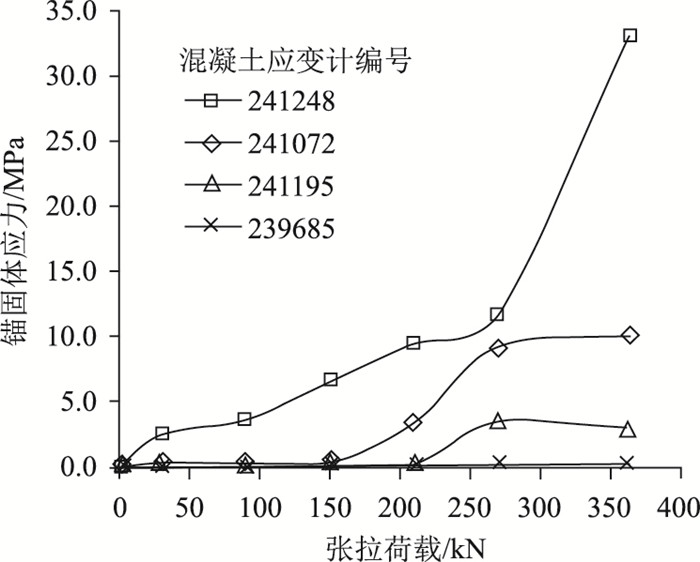
试验得到锚索极限荷载为363 kN,图 3为锚固体应力随张拉荷载的变化规律,从图中可以看出,锚固体底部应力随张拉荷载变化最大,特别是在达到锚索极限荷载时,其迅速增大到33 MPa,接近M40砂浆的极限抗压强度,锚固体抗压强度得到充分发挥,此时锚头位移持续增加,但张拉荷载不再继续增大;同时从图中还可以看出,在张拉荷载达到150 kN时,距锚固体底部0.75 m的混凝土应变计(241072)读数才开始持续增大,而最远端的混凝土应变计(239685)读数直至锚索达到极限荷载时都基本维持不变。从监测结果来看,该锚索破坏属于锚固体应力在张拉荷载作用下超过了其自身的承载能力,锚固体局部承压破坏,导致锚索的承载能力下降、轴向位移增大,计算得出锚索破坏时锚固体底部位移达到57.26 mm。
|
| 图 3 压力型锚索锚固体应力分布规律 Fig. 3 Distribution of stresses of anchorage body for pressure-type anchor cables |
| |
2 数值模拟分析 2.1 建立模型
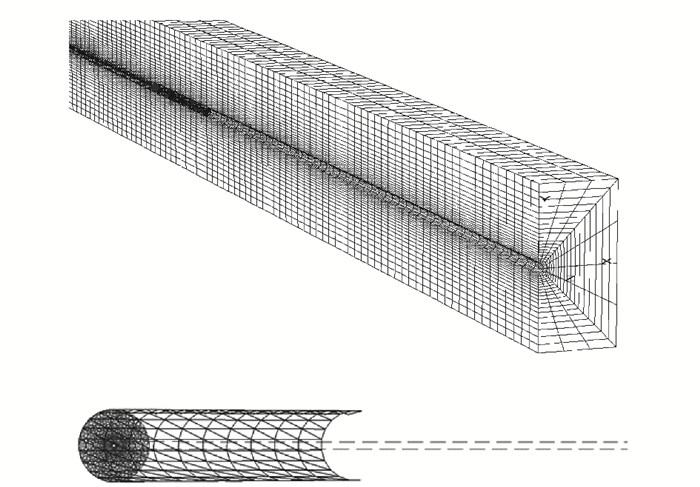
本研究采用有限差分软件FLAC3D建立压力型锚索数值计算模型,其中钢绞线采用锚索(Cable)单元模拟,承载板采用壳(Shell)单元模拟,砂浆体和岩土体之间的接触面,采用接触面(Interface)单元来模拟[12-15]。计算模型以锚索体为中心,垂直于锚索平面取3.0 m×3.0 m建立网格,锚固体标准长度2.5 m,自由段长度15.0 m,锚固体底部岩土体厚5.0 m,锚索孔径130 mm。根据试算,荷载在岩土体内部传递范围较小,模型只在四周施加侧向约束;由于只对锚固体及深层岩土体内部进行力学分析,因此只在模型临空面及锚索端部施加z方向约束。模型如图 4所示。为简化锚索预应力施加过程,直接将张拉荷载施加于锚索单元,模型中锚索、砂浆体和岩土体都不计自重。
|
| 图 4 压力型锚索数值模型 Fig. 4 Numerical model of pressure-type prestressed cable |
| |
2.2 计算参数
由于压力分散型预应力锚索采用无黏结钢绞线,锚索与锚固体之间摩擦作用力基本可以忽略不计。FLAC模型中的Cable单元同时考虑了钢绞线和锚固体的作用,此时可将Cable单元全长都按自由段考虑(cg=0),忽略锚固体环面厚度t,但锚固体仍采用实体单元模拟,因此将Cable单元中关于Grout的参数都设为小值。无黏结锚索选用碳素钢材质钢绞线,其中3 000 kN级及以下级别锚索采用公称直径d=15.20 mm(7ø5)、强度等级为1 860 MPa(270级)的低松弛钢绞线。
模型中锚固体和围岩材料均采用线弹性本构模型,锚固体与围岩之间设置接触单元,根据现场试验数据结果求出接触单元剪切刚度Kg为17.5 MPa/m,黏结强度可取锚固体与围岩之间单轴抗压强度较小值的一半。模型材料参数取值如表 1、表 2所示。
| 锚索弹性模量/Pa | 锚固体黏结强度/(N·m-1) | 锚固体摩擦角/(°) | 锚固体剪切刚度/Pa | 锚固体周长/m | 锚索截面积/mm2 | 锚索屈服强度/N |
| 195E9 | 0 | 1 | 0 | 0.048 | 140 | 220E3 |
| 材料 | 弹性模量/Pa | 泊松比 | 黏聚力/Pa | 内摩擦角/(°) |
| 围岩 | 3.0E9 | 0.32 | 60.0E3 | 19.0 |
| 锚固体 | 28.0E9 | 0.28 | 200.0E3 | 26.0 |
| 接触面 | 230.0E3 | 19.0 |
3 数值模拟结果分析 3.1 压力型岩锚应力分布特征
对锚索单元施加220 kN的预应力,研究锚固体及围岩应力分布情况,并根据模拟结果推算出锚固体与围岩界面剪应力分布规律。
图 5是锚固体轴向应力云图,从图中可以看出,在锚固段底部有明显的轴向应力集中现象,最大压应力达到13.65 MPa,远小于灌注锚固体所用M40水泥砂浆的抗压强度,其后锚固体轴向应力沿轴向逐渐减小。同时,由于承载板相对锚固体刚度较大,因此锚固体底部压应力分布较为均匀。

|
| 图 5 锚固体轴向应力云图(单位: MPa) Fig. 5 Nephogram of axial stress of anchorage body (unit: MPa) |
| |
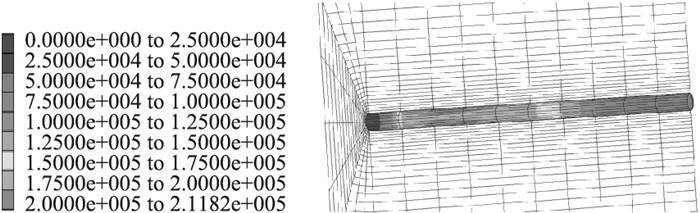
图 6为围岩与锚固体接触面剪应力分布云图,从图中可以看出界面剪应力呈抛物线形分布,峰值位于距承载板约40 cm处,且低于接触面剪应力极限值。这是因为围岩与锚固体接触面上的剪应力与二者相对位移成正比,围岩在锚固体端部会产生较大变形,其后随着应力扩散作用变形逐渐减小,因此在该部位围岩与锚固体间协调变形,接触面剪应力也随之呈抛物线形分布。
|
| 图 6 围岩与锚固体接触面剪应力云图(单位: MPa) Fig. 6 Nephogram of shearing stress of interface between surrounding rock and anchorage body(unit: MPa) |
| |
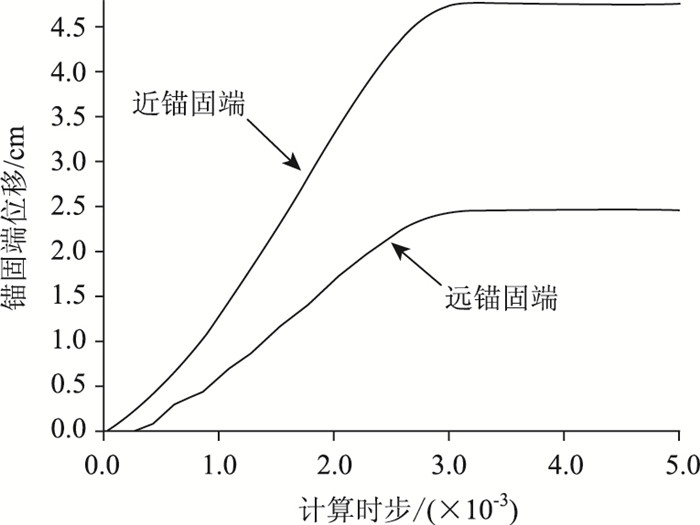
从锚固端位移曲线图(图 7)可以看出,近锚固端与远锚固端的位移差值即为锚固体发生的压缩变形,其值是在逐步增大的,最大值达到2.5 cm,其后锚固体位移及变形趋于定值,受力也达到平衡状态。
|
| 图 7 锚固体端部位移曲线 Fig. 7 Displacement curves of anchorage body end |
| |
3.2 压力型锚索工作特性参数分析 3.2.1 锚固体弹性模量的影响
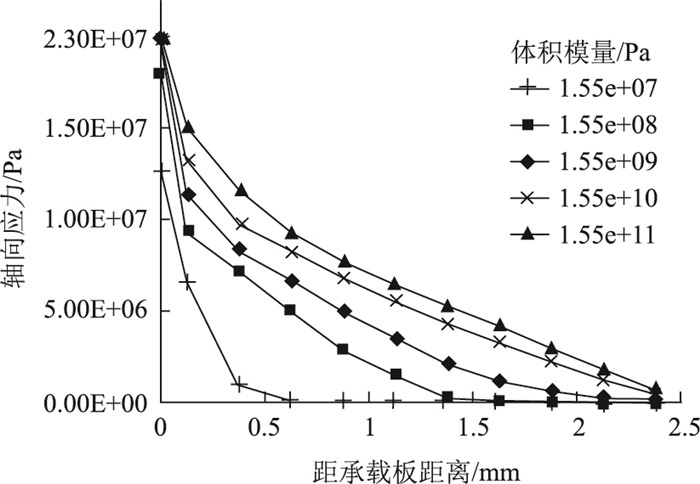
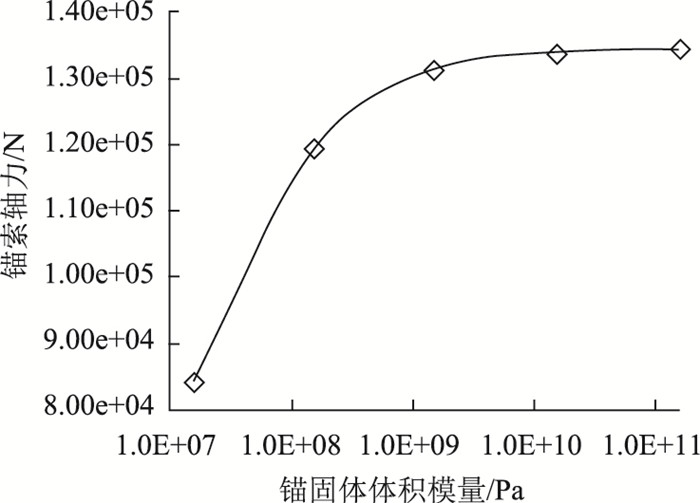
图 8为不同刚度锚固体的轴向应力曲线,从图中可以看出,锚固体刚度越大,作用在锚固端处的轴向应力也越大,轴向应力分布也越均匀。这是由于在相同压力下,大刚度锚固体变形较小,其锚索产生的预应力损失也较小,从图 9也可以看出,锚索轴力是随着锚固体体积模量的增加而逐渐增大的,但在锚固体刚度较小的情况下,其压缩变形以及侧向变形都较大,围岩对其约束作用增强,其径向应力也会随之增大,使得围岩与锚固体接触面上极限摩阻力增大,因此在锚固体端部,其轴向应力会迅速减小。
|
| 图 8 不同刚度的锚固体轴向应力分布曲线 Fig. 8 Axial stress distribution curves of anchorage body with different stiffnesses |
| |
|
| 图 9 锚固体体积模量与锚索预应力关系曲线 Fig. 9 Curve of bulk modulus of anchorage body vs. prestress of anchor cable |
| |
3.2.2 围岩弹性模量的影响
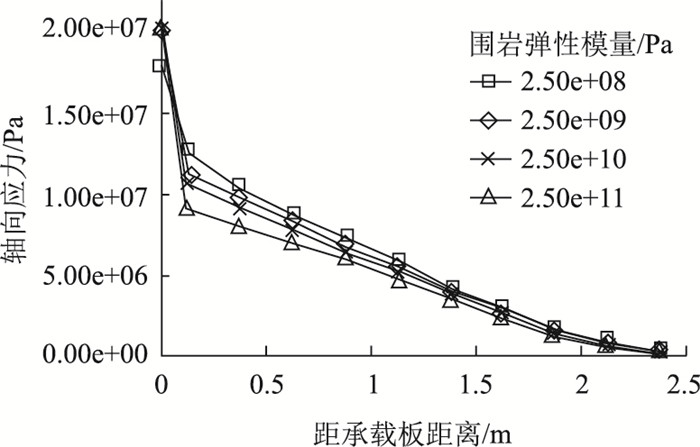
围岩岩质直接决定着预应力锚索的承载能力,围岩岩质越好,其弹性模量、黏聚力等力学性能也越高。图 10为围岩弹性模量对锚固体轴向应力分布的影响,从图中可以看出,随着围岩弹性模量的增大,锚固体端部应力有所增大,而且其近锚固端轴向应力减小幅值也较大,表明该部位锚固体与围岩之间界面的剪应力较大,围岩对锚固体的侧向约束作用得到增强,其后随着距锚固端距离的增加,轴向应力的减小幅值也逐渐趋于平缓。
|
| 图 10 不同围岩模量的锚固体轴向应力分布曲线 Fig. 10 Axial stress distribution curves of anchorage body with different surrounding rock moduli |
| |
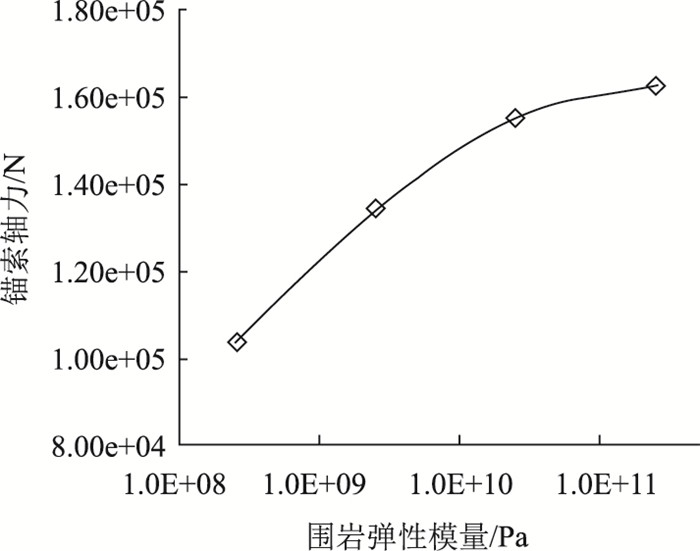
图 11显示了围岩弹性模量对锚索预应力的影响情况,可以看出锚索预应力随围岩弹性模量的增大而增大,这是因为随着围岩弹性模量的增加,围岩与锚固体之间的相对位移也会随之增大,从而有利于锚固体压应力迅速向围岩四周扩散。在此作用下,锚固体自身压缩变形及位移都会随之减小,由此引起的预应力损失也会得到控制[10]。因此,在实际工程中将锚索锚固段设置在围岩等级较好部位或采用劈裂注浆以提升围岩整体性,可以有效降低锚索预应力损失,保证支护效果[16-17]。
|
| 图 11 围岩模量与锚索预应力关系曲线 Fig. 11 Curve of modulus of surrounding rock vs. prestress of anchor cable |
| |
3.2.3 锚孔直径的影响
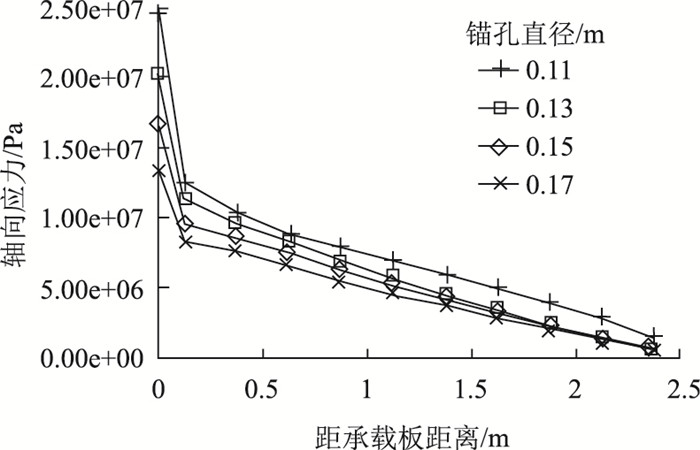
图 12为锚固体直径对其轴向应力的影响,可以看出在相同锚索预应力的情况下,随着锚固体直径及相应承载面积的增大,锚固端应力随之减小。但从锚固体轴向应力减小趋势看,锚固体直径越小,轴向应力降低幅值反而越大,特别是在近锚端,该趋势最为明显,说明该部位锚固体剪应力较大。这是由于小直径锚固体会受到较大的轴向应力,其径向应力也会随之增大,围岩对其约束作用增强,使得围岩与锚固体之间的摩阻作用得到充分发挥,但同时也降低了压应力锚索的安全储备。
|
| 图 12 不同直径锚固体轴向应力分布曲线 Fig. 12 Axial stress distribution curves of anchorage body with different diameters |
| |
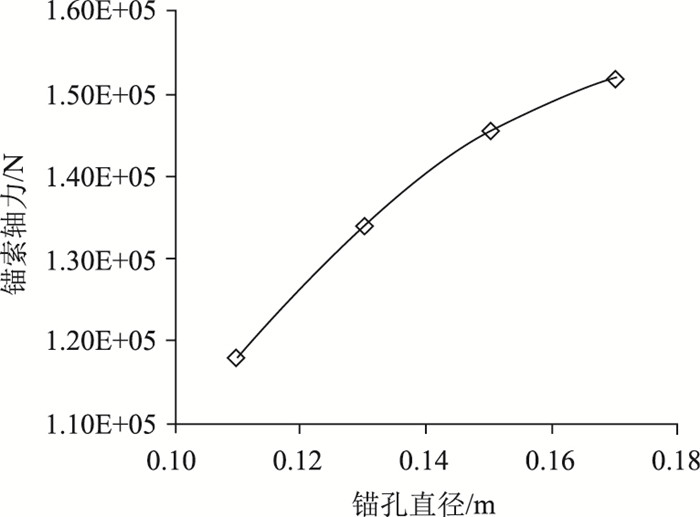
从孔径与锚索预应力关系变化曲线(图 13)还可以看出,锚索预应力随锚孔直径的减小而大幅减小,这是由于锚固体与围岩之间摩阻作用的充分发挥是建立在二者之间发生较大相对位移基础上的,小直径锚固体承压端受到更大的初始压力,其位移及自身的压缩变形都会对预应力锚索造成更大的预应力损失,从而降低了预应力锚索的锚固效应[18]。
|
| 图 13 锚固体直径与锚索预应力关系曲线 Fig. 13 Curve of diameter of anchorage body vs. prestress of anchor cable |
| |
3.2.4 接触刚度的影响
接触面法向刚度和切向刚度是反映接触面力学性质的重要参数,是接触的两表面抵抗变形的能力。本模型中接触面法向刚度是切向刚度的1.5倍,在保持其他条件不变的情况下,改变这两个参数,可以分析接触面刚度对锚索锚固性能的影响。
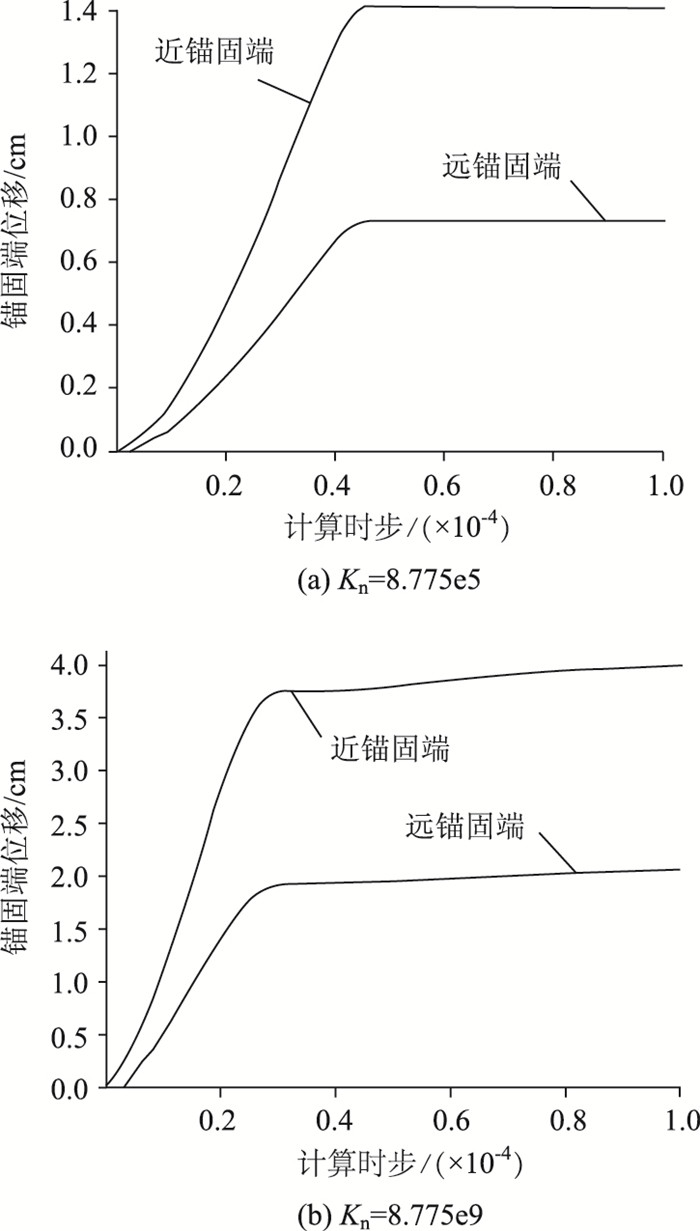
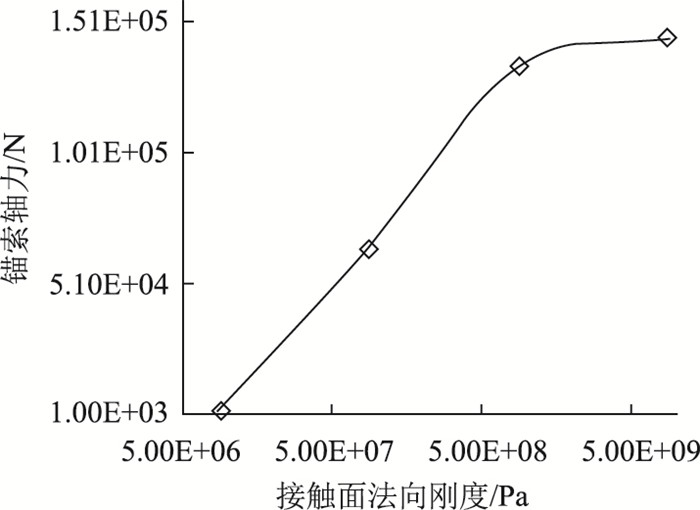
由图 14锚固体端部位移曲线可见,当接触刚度较小时,锚固体将产生较大刚体位移,图 14(a)中最大位移达到14.1 cm,可以近似认为锚固体被拔出,锚索预应力基本全部损失,而图 14(b)中最大位移只有4.15 cm。从接触面法向刚度与锚索预应力关系变化曲线(图 15)也可以看出,随着接触面刚度的增加,锚索预应力迅速增大,但当刚度增大到一定程度后,锚固体位移不再随接触刚度的增加而大幅减小,锚索预应力增加幅度也不再明显。
|
| 图 14 不同接触刚度锚固体端部位移曲线 Fig. 14 Displacement curve of anchorage body end with different contact stiffnesses |
| |
|
| 图 15 接触面法向刚度与锚索预应力关系曲线 Fig. 15 Curve of normal stiffness of contact surface vs. prestress of anchor cable |
| |
4 结论
本研究建立了压力型锚索的三维数值模型,分析了模型的特点以及压力型锚索作用机理,并对各种条件下的压力型锚索受力特性进行了对比,主要结论如下:
(1) 用壳单元模拟压力型锚索的承载板,并且将锚索单元全长都按自由段考虑(cg=0),忽略锚固体环面厚度t,可以得到较好的模拟效果;
(2) 锚固体与围岩接触面上的剪应力呈抛物线形分布,峰值位于距离承载板约40 cm处;
(3) 接触面相对位移由锚固体弹性压缩和刚体位移构成,随着锚固体和围岩刚度、锚孔直径,以及接触面剪切刚度的增大,由钢绞线松弛造成的锚索预应力损失幅值会随之降低,支护效果有效提升。
| [1] |
张永兴, 饶枭宇, 唐树名, 等. 预应力锚索注浆体与岩石黏结界面抗剪强度试验[J]. 中国公路学报, 2008, 21(6): 1-6. ZHANG Yong-xing, RAO Xiao-yu, TANG Shu-ming, et al. Experiment on Shear Strength of Cementation Plane between Grout and Rock in Prestressed Anchor[J]. China Journal of Highway and Transport, 2008, 21(6): 1-6. |
| [2] |
PHILLIPS S H E. Factors Affecting the Design of Anchorages in Rock[R]. London: Cementation Research Ltd., 1970.
|
| [3] |
段少杰. 黏结式预应力锚索加固围岩优越性数值分析[J]. 中国水能及电气化, 2015(9): 63-66. DUAN Shao-jie. Numerical Value Analysis on Superiority of Adhesive Pre-stressed Anchor Cable Reinforcement Surrounding Rock[J]. China Water Power & Electrification, 2015(9): 63-66. |
| [4] |
KRISHNAN S. Structural Design and Behavior of Prestressed Cable Domes[J]. Engineering Structures, 2020, 209: 110294. |
| [5] |
周德培, 刘世雄, 刘鸿. 压力分散型锚索设计中应考虑的几个问题[J]. 岩石力学与工程学报, 2013, 32(8): 1513-1519. ZHOU De-pei, LIU Shi-xiong, LIU Hong. Some Problems to be Considered in Design for Compression Dispersion-type Anchor Cables[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(8): 1513-1519. |
| [6] |
周德培, 刘鸿, 冯君. 压力分散型锚索单元锚体间的应力影响[J]. 岩土工程学报, 2012, 34(10): 1765-1771. ZHOU De-pei, LIU Hong, FENG Jun. Stress Influence between Unit Anchor Bodies for Compression Dispersion-type Anchored Cables[J]. Chinese Journal of Geotechnical Engineering, 2012, 34(10): 1765-1771. |
| [7] |
盛宏光.压力分散型锚索锚固性能与设计方法研究[D].成都: 成都理工大学, 2003. SHENG Hong-guang. Study on Anchorage Performance and Design Method of Compression Dispersion-type Anchor[D]. Chengdu: Chengdu University of Technology, 2003. http://d.wanfangdata.com.cn/Thesis/Y599092 |
| [8] |
KIM N K. Performance of Tension and Compression Anchors in Weathered Soil[J]. Jounal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1138-1150. |
| [9] |
KILLIC A, YASAR E, ATIS C D. Effect of Bar Shape on the Pull-out Load Capacity of Fully Grouted Rock Bolt[J]. Tunnelling and Underground Space Technology, 2003, 18(1): 1-6. |
| [10] |
张永兴, 饶枭宇, 唐树名, 等. 预应力锚索注浆体与岩石黏结界面抗剪强度试验[J]. 中国公路学报, 2008, 21(6): 1-6. ZHANG Yong-xing, RAO Xiao-yu, TANG Shu-ming, et al. Experiment on Shear Strength of Cementation Plane between Grout and Rock in Prestressed Anchor[J]. China Journal of Highway and Transport, 2008, 21(6): 1-6. |
| [11] |
CECS 22-2005, 岩土锚杆索技术规程[S]. CECS22-2005, Technical Specification for Ground Anchors[S]. |
| [12] |
Itasca Consulting Group Inc. FLAC3D, Fast Lagrangian Analysis of Continua in 3 Dimension, User's Manual[M]. Version 2.0. Minneapolis: Itasca Consulting, Group Inc, 1997.
|
| [13] |
丁秀丽, 盛谦, 韩军, 等. 预应力锚索锚固机理的数值模拟试验研究[J]. 岩石力学与工程学报, 2002, 21(7): 980-988. DING Xiu-li, SHENG Qian, HAN Jun, et al. Numerical Simulation Testing Study on Reinforcement Mechanism of Prestressed Anchorage Cable[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(7): 980-988. |
| [14] |
雷金山, 阳军生, 王安正, 等. 压力分散型锚索锚固段受力特性分析[J]. 铁道科学与工程学报, 2010, 7(3): 60-64. LEI Jin-shan, YANG Jun-sheng, WANG An-zheng, et al. Mechanical Analysis on Anchoring Segment of Pressure-dispersive Cable[J]. Journal of Railway Science and Engineering, 2010, 7(3): 60-64. |
| [15] |
顾培英, 邹庆, 邓昌, 等. 饱和粉砂土中压力分散型锚杆摩阻力试验[J]. 水利水运工程学报, 2009(2): 78-81. GU Pei-ying, ZOU Qing, DENG Chang, et al. Test study on Frictional Resistance of Compression Dispersive Prestressed Anchor in Saturated Mealy Sand[J]. Hydro-Science and Engineering, 2009(2): 78-81. |
| [16] |
张发明, 赵维炳, 刘宁, 等. 预应力锚索锚固荷载的变化规律及预测模型[J]. 岩石力学与工程学报, 2004, 23(1): 39-43. ZHANG Fa-ming, ZHAO Wei-bing, LIU Ning, et al. Long-term Performance and Load Prediction Model of Prestressed Cables[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(1): 39-43. |
| [17] |
尤春安. 压力型锚索锚固段的受力分析[J]. 岩土工程学报, 2004, 26(6): 828-831. YOU Chun-an. Mechanical Analysis on Anchorage Segment of Pressure-type Cable[J]. Chinese Journal of Geotechnical Engineering, 2004, 26(6): 828-831. |
| [18] |
FUJITA K, UEDA K, KUSABUKA M, et al. A Method to Predict the Load-displacement Relationship of Ground Anchors[C]//Proceedings of the 9th International Conference on Soil Mechanics and Foundation Engineering. Tokyo: The Japanese Society of Soil Mechanics and Foundation Engineering, 1977: 58-62. http://www.researchgate.net/publication/320284932_A_method_to_predict_the_load-displacement_relationship_of_ground_anchors
|
 2020, Vol. 37
2020, Vol. 37
