扩展功能
文章信息
- 刘斌, 赵天舒, 张冉霞
- LIU Bin, ZHAO Tian-shu, ZHANG Ran-xia
- 基于改进PCA-Logistic模型对个人汽车保有量预测
- Prediction of Private Car ownership Based on Improved PCA-Logistic Model
- 公路交通科技, 2020, 37(8): 136-143
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(8): 136-143
- 10.3969/j.issn.1002-0268.2020.08.017
-
文章历史
- 收稿日期: 2020-01-03
随着我国经济健康持续发展,社会收入水平不断提高,城市化步伐逐渐加快,我国的个人汽车保有量在连年攀升[1]。个人汽车保有量是指公安交通管理部门按照《机动车注册登记工作规范》,已注册登记领有民用车辆牌照的全部私人汽车数量,也可以称为私人或私家的汽车拥有量。根据《中国统计年鉴》[2-5],1985年我国个人汽车保有量只有约28万辆,随着改革开放的深入进行,我国汽车工业目前进入全面高速发展阶段,2003年我国个人汽车保有量首次突破1 000万辆。2006年,个人汽车保有量突破2 000万辆,仅3年时间数量翻了一番。2013年我国个人汽车保有量突破了1亿辆。截止到2018年,我国个人汽车保有量超过2亿辆。
个人汽车带给我们方便的同时,也为我们的生活带来了一系列问题,如道路拥堵、交通事故频发,停车困难、停车位昂贵,能耗严重、环境污染加剧,交通设施更替加速等。通过对个人汽车保有量的预测,可以为城市道路交通规划工作的展开提供数据支撑,为政府对交通设施建设的投资成本预算提供依据[6]。
对于汽车保有量的预测,国外学者首先做了较多的研究,提出了许多模型,比如基于集合模型的Comperta模型[7]、基于非集合模型的多项Logit模型及多项Probit模型等,这些模型基于当地的人口、社会等数据信息,已经成功应用于发达国家。近年来国外学者也对印度等发展中国家汽车保有量建立模型进行了分析,Dash等提出分段线性多项Logit模型对印度个人汽车保有量进行了研究[8]。Shaygan等对伊朗的汽车保有量模型进行了综述性分析,指出需要对已有模型进行更多改进才可适用于当地城市[9]。从中可以看出国外预测模型存在一定的区域性,由于国外汽车文化和经济水平与国内相差较大,所以难以直接将其应用于国内的个人汽车保有量分析[10-11]。
国内的汽车保有量预测研究起步较晚,同样也提出了许多模型与方法。陈勇和孔峰利用BP神经网络建立了具有时间序列预测模型对我国私人汽车保有量进行了分析和预测[12]。朱开永等利用灰色系统理论建立私家车保有量预测模型对某地区1996—2007年私家车保有量分析[13]。张雪伍和常晋义通过主成分分析法将影响汽车保有量因子间的重复信息进行消除,建立了PCA-BP神经网络预测模型对南京市1978—2005年的汽车保有量进行分析,并对未来南京市汽车保有量进行预测[11]。王传鑫等基于改进密度峰值聚类方法研究了不同地区间私人汽车保有量影响因素的差异性,为研究的两类地区私人汽车发展提供一定的参考[14]。蒋艳梅和赵文平建立了分别基于遗传算法和非线性最小二乘法的Logistic模型,对我国汽车保有量进行了预测,并和其他文献进行对比,结果表明Logistic模型预测私人汽车保有量的精确度比其他模型高[15]。张兰怡和胡喜生等通过对影响汽车保有量的8个指标进行主成分分析,得到了综合经济发展值的预测方程,并采用Logistic模型预测福建省2020年汽车保有量[16]。任玉珑等基于传统Logistic模型和以灰色理论为基础的极差格式的Logistic模型为基础,建立了以误差标准差为权重的Logistic组合模型对我国汽车保有量进行预测,得出了到2020年我国汽车保有量达到2.35亿辆的结论[17]。
通过对国内外相关文献进行整理可以发现,汽车保有量的发展趋势比较符合随时间变化呈S型变化的Logistic模型,同时许多研究都是通过分析影响汽车保有量的因素进行展开。主成分分析法可以通过“线性”降维技术将多个影响因素尽可能压缩为少数几个代表性综合指标,再结合Logistic模型可以对汽车保有量进行分析和预测。但在实际应用中,影响因素可能存在非线性关系,尤其是对于时间跨度较长的数据,直接用传统主成分分析的线性方法会影响降维效果,进而影响预测精度[18]。因此,本研究使用对数变换法对传统主成分分析法进行了改进,结合Logistic模型,提出了改进PCA-Logistic模型,并对我国个人汽车保有量进行分析和预测。通过实证分析结果可以表明,改进PCA-Logistic模型可以消除数据之间的非线性影响,使得模型的模拟精度更高。
1 模型建立 1.1 改进的主成分分析法传统的主成分分析法是一种“线性”降维方法,如果变量间存在非线性关系,会导致降维效果不明显,因此需要对传统主成分分析法进行改进。常见的改进方法有均值法、对数变换法和平方根变换等,对原始影响因素数据进行分析,发现其随着时间呈现类似指数形式的变化趋势,于是改进方法采用对数变换法,以达到更好的降维效果。具体步骤如下[18]:
(1) 对原始数据进行对数变换:设原始数据矩阵为X=(xij)n×p,令yij=ln xij,对数变换后矩阵为:Y=(yij)n×p,其中i=1, 2, …, n; j=1, 2, …, p。
(2) 以yij作为新的数据代替原始数据,并对其进行标准化处理,以消除各个特征在数量级或量纲上的影响,公式如下:
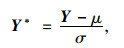
|
(1) |
式中,μ为各个指标数据的平均值; σ为各个指标数据的标准差。
(3) 根据标准化矩阵,计算其协方差矩阵,计算公式为:
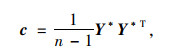
|
(2) |
式中,c为协方差矩阵; n为数据指标的元素个数; Y*为标准化的数据。
(4) 根据协方差矩阵计算特征值与特征向量,并将特征值从大到小进行排列。
(5) 计算主成分贡献率及累积贡献率,并根据计算结果提取主成分。通常选取累积贡献率在85%以上的对应成分作为主成分。
1.2 Logistic模型Logistic方程由比利时数学家P.F.Verhulst在1838年首次提出,它是描述因变量随时间变动趋势的模型,能较好地描述某些呈现S型曲线增长的现象,并已经广泛应用于农业、经济学、医学等领域。对于产品市场扩展分析,采用美国Edwin Mansfield提出的Logistic模型微分方程为[19]:
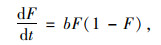
|
(3) |
式中,b为常数;F=y(t)/m,它是t时刻市场汽车保有量y(t)与市场最大保有量m的比值。
由分离变量法求解式(3)得:
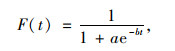
|
(4) |
式中, a为常数。最终得t时刻汽车保有量为:
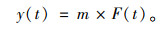
|
(5) |
结合前面两个方法,提出改进PCA-Logistic模型。首先选取影响我国个人汽车保有量的几个代表性因素作为评价指标,将原始数据进行对数转换,以消除非线性的影响,再进行标准化处理以消除量纲或数量级上的差异。然后再利用SPSS软件中的降维因子分析模块对其进行改进的主成分分析,确定主成分,并计算主成分得分。
根据主成分贡献率及累计贡献率的计算结果,选择第一主成分FAC1_1作为自变量,个人汽车保有量作为因变量,对其进行Logistic模型回归分析,由于没有采用时间序号作为自变量,对公式(4)进行等价变换,最终采取的模型方程为:
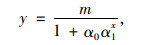
|
(6) |
式中,α0和α1为待求参数。采用非线性最小二乘法进行参数求解,首先选取合适的最大个人汽车保有量m作为固定值,然后给出参数α0和α1初始值进行迭代求解,迭代算法为麦夸特法。
2 实证分析 2.1 变量选取与数据来源通过文献资料的搜集与整理可以发现[20],影响我国个人汽车保有量变化的因素有多种,如经济因素,包括人均GDP、居民收入、经济产业结构、居民消费水平等;社会因素,包括城市人口、城市化率、失业率、拥塞成本等;环境因素,包括公路网规模、基础设施完善度等。考虑长期完整数据的可获得性,选取了城市人口、城市化水平、人均GDP、居民消费水平、公路里程、第一产业生产值所占比重、第二产业生产值所占比重、第三产业生产值所占比重这8个代表性的影响因素进行分析。我国个人汽车保有量及其影响因素的样本数据见表 1,选取区间为1985—2018年,统计数据均来源于《中国统计年鉴》[2-5]。
| 年份 | 时间 序号t | 城市人口 数P1/万 | 城市化水平 P2/% | 人均GDP P3/元 | 居民消费水 平P4/元 | 公路里程 P5/km | 第一产业所 占比P6/% | 第二产业所 占比P7/% | 第三产业所 占比P8/% | 个人汽车保有 量Y/万辆 | 个人汽车保有 量占比/% |
| 1985 | 1 | 25 094 | 23.71 | 866 | 440 | 942 400 | 28.1 | 42.6 | 29.3 | 28.49 | 8.87 |
| 1986 | 2 | 263 66 | 24.52 | 973 | 497 | 962 800 | 26.8 | 43.4 | 29.8 | 34.71 | 9.59 |
| 1987 | 3 | 27 674 | 25.32 | 1 123 | 565 | 982 200 | 26.5 | 43.2 | 30.3 | 42.29 | 10.36 |
| 1988 | 4 | 28 661 | 25.81 | 1 378 | 714 | 999 600 | 25.4 | 43.4 | 31.2 | 60.42 | 13.01 |
| 1989 | 5 | 29 540 | 26.21 | 1 536 | 788 | 1 014 300 | 24.7 | 42.4 | 32.9 | 73.12 | 14.30 |
| 1990 | 6 | 30 195 | 26.41 | 1 663 | 831 | 1 028 300 | 26.7 | 40.9 | 32.4 | 81.62 | 14.80 |
| 1991 | 7 | 31 203 | 26.94 | 1 912 | 932 | 1 041 100 | 24.2 | 41.4 | 34.5 | 96.04 | 15.84 |
| 1992 | 8 | 32 175 | 27.46 | 2 334 | 1 116 | 1 056 700 | 21.4 | 43.0 | 35.6 | 118.2 | 17.09 |
| 1993 | 9 | 33 173 | 27.99 | 3 027 | 1 393 | 1 083 500 | 19.4 | 46.1 | 34.5 | 155.77 | 19.05 |
| 1994 | 10 | 34 169 | 28.51 | 4 081 | 1 833 | 1 117 800 | 19.5 | 46.1 | 34.4 | 205.42 | 21.81 |
| 1995 | 11 | 35 174 | 29.04 | 5 091 | 2 330 | 1 157 000 | 19.7 | 46.7 | 33.7 | 249.96 | 24.03 |
| 1996 | 12 | 37 304 | 30.48 | 5 898 | 2 789 | 1 185 800 | 19.4 | 47.0 | 33.6 | 289.67 | 26.33 |
| 1997 | 13 | 39 449 | 31.91 | 6 481 | 3 002 | 1 226 400 | 18.0 | 47.0 | 35.0 | 358.36 | 29.40 |
| 1998 | 14 | 41 608 | 33.35 | 6 860 | 3 159 | 1 278 500 | 17.2 | 45.7 | 37.1 | 423.65 | 32.11 |
| 1999 | 15 | 43 748 | 34.78 | 7 229 | 3 346 | 1 351 700 | 16.1 | 45.3 | 38.6 | 533.88 | 36.74 |
| 2000 | 16 | 45 906 | 36.22 | 7 942 | 3 721 | 1 679 800 | 14.7 | 45.4 | 39.8 | 625.33 | 38.87 |
| 2001 | 17 | 48 064 | 37.66 | 8 717 | 3 987 | 1 698 000 | 14.1 | 44.7 | 41.3 | 770.78 | 42.77 |
| 2002 | 18 | 50 212 | 39.09 | 9 506 | 4 301 | 1 765 200 | 13.4 | 44.3 | 42.3 | 968.98 | 47.19 |
| 2003 | 19 | 52 376 | 40.53 | 10 666 | 4 606 | 1 809 800 | 12.4 | 45.5 | 42.1 | 1219.23 | 51.16 |
| 2004 | 20 | 54 283 | 41.76 | 12 487 | 5 138 | 1 870 700 | 13.0 | 45.8 | 41.2 | 1 481.66 | 55.00 |
| 2005 | 21 | 56 212 | 42.99 | 14 368 | 5 771 | 3 345 200 | 11.7 | 46.9 | 41.4 | 1 848.07 | 58.49 |
| 2006 | 22 | 58 288 | 44.34 | 16 738 | 6 416 | 3 456 999 | 10.7 | 47.4 | 41.9 | 2 333.32 | 63.10 |
| 2007 | 23 | 60 633 | 45.89 | 20 505 | 7 572 | 3 583 715 | 10.4 | 46.7 | 42.9 | 2 876.22 | 65.99 |
| 2008 | 24 | 62 403 | 46.99 | 24 121 | 8 707 | 3 730 164 | 10.3 | 46.8 | 42.9 | 3501.39 | 68.66 |
| 2009 | 25 | 64 512 | 48.34 | 26 222 | 9 514 | 3 860 823 | 9.9 | 45.7 | 44.4 | 4 574.91 | 72.84 |
| 2010 | 26 | 66 978 | 49.95 | 30 876 | 10 918 | 4 008 229 | 9.6 | 46.2 | 44.2 | 5 938.71 | 76.12 |
| 2011 | 27 | 69 079 | 51.27 | 36 403 | 13 133 | 4 106 387 | 9.5 | 46.1 | 44.3 | 7 326.79 | 78.31 |
| 2012 | 28 | 71 182 | 52.57 | 40 007 | 14 698 | 4 237 508 | 9.5 | 45.0 | 45.5 | 8 838.6 | 80.84 |
| 2013 | 29 | 73 111 | 53.73 | 43 852 | 16 190 | 4 356 218 | 9.4 | 43.7 | 46.9 | 10 501.68 | 82.88 |
| 2014 | 30 | 74 916 | 54.77 | 47 203 | 17 777 | 4 463 913 | 9.2 | 42.7 | 48.1 | 12 339.36 | 84.53 |
| 2015 | 31 | 77 116 | 56.1 | 50 251 | 19 397 | 4 577 296 | 8.8 | 40.9 | 50.2 | 14 099.1 | 86.58 |
| 2016 | 32 | 79 298 | 57.35 | 53 980 | 21 227 | 4 696 263 | 8.6 | 39.8 | 51.6 | 16 330.22 | 87.92 |
| 2017 | 33 | 81 347 | 58.52 | 59 201 | 22 902 | 4 773 468 | 7.9 | 40.4 | 51.6 | 18 515.11 | 88.56 |
| 2018 | 34 | 83 137 | 59.58 | 64 644 | 25 002 | 4 846 531 | 7.2 | 40.7 | 52.2 | 20 574.93 | 88.57 |
2.2 改进的主成分分析
应用SPSS22.0计算软件,对我国个人汽车保有量的影响因素按以下步骤提取主成分:
(1) 将原始数据进行对数变换处理。
(2) 将变换后的8个影响因素标准化处理后,再进行主成分分析,得到解释的总方差见表 2。
| 成分 | 初始特征值/% | 提取载荷平方和/% | |||||
| 总计 | 方差 | 累积 | 总计 | 方差 | 累积 | ||
| 1 | 6.865 | 85.812 | 85.812 | 6.865 | 85.812 | 85.812 | |
| 2 | 1.017 | 12.718 | 98.531 | 1.017 | 12.718 | 98.531 | |
| 3 | 0.078 | 0.981 | 99.512 | ||||
| 4 | 0.029 | 0.357 | 99.869 | ||||
| 5 | 0.006 | 0.073 | 99.942 | ||||
| 6 | 0.004 | 0.054 | 99.996 | ||||
| 7 | 0.000 | 0.003 | 99.999 | ||||
| 8 | 0.000 | 0.001 | 100.000 | ||||
由表 2可以看到,第一主成分的特征值为6.865,其方差占总方差比为85.812%,对个人汽车保有量影响占主要作用,根据主成分选择标准,将原来的8个影响因素用这一个主成分来代替。
(3) 成分得分系数矩阵见表 3。根据表 3可以写出第一主成分的因子表达式为:
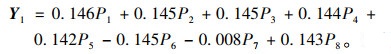
|
(7) |
| 影响因素 | 成分 | |
| 1 | 2 | |
| 城市人口数P1 | 0.146 | 0.015 |
| 城市化水平P2 | 0.145 | -0.013 |
| 人均GDP P3 | 0.145 | 0.063 |
| 居民消费水平P4 | 0.144 | 0.047 |
| 公路里程P5 | 0.142 | -0.017 |
| 第一产业所占比重P6 | -0.145 | -0.059 |
| 第二产业所占比重P7 | -0.008 | 0.981 |
| 第三产业所占比重P8 | 0.143 | -0.100 |
根据上述表达式对标准化后的数据进行计算,计算后的第一主成分FAC1_1相关数据见表 4。
| 序号 | FAC1_1 |
| 1 | -1.625 51 |
| 2 | -1.530 95 |
| 3 | -1.443 12 |
| 4 | -1.328 14 |
| 5 | -1.224 21 |
| 6 | -1.228 22 |
| 7 | -1.089 58 |
| 8 | -0.959 64 |
| 9 | -0.882 86 |
| 10 | -0.795 24 |
| 11 | -0.738 36 |
| 12 | -0.648 14 |
| 13 | -0.517 85 |
| 14 | -0.385 18 |
| 15 | -0.263 09 |
| 16 | -0.097 |
| 17 | 0.008 21 |
| 18 | 0.109 15 |
| 19 | 0.187 25 |
| 20 | 0.217 07 |
| 21 | 0.439 55 |
| 22 | 0.543 91 |
| 23 | 0.657 27 |
| 24 | 0.725 67 |
| 25 | 0.825 8 |
| 26 | 0.903 26 |
| 27 | 0.978 53 |
| 28 | 1.059 12 |
| 29 | 1.141 4 |
| 30 | 1.216 96 |
| 31 | 1.320 68 |
| 32 | 1.401 69 |
| 33 | 1.470 19 |
| 34 | 1.551 38 |
2.3 主成分分析法改进前后的主成分回归曲线比较
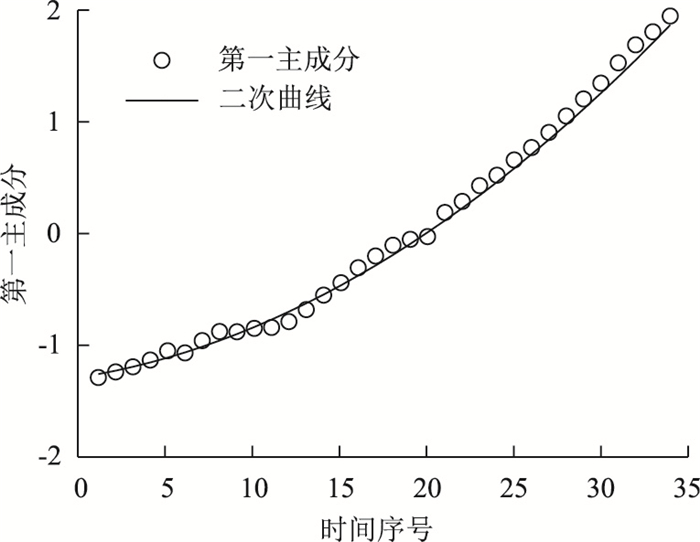
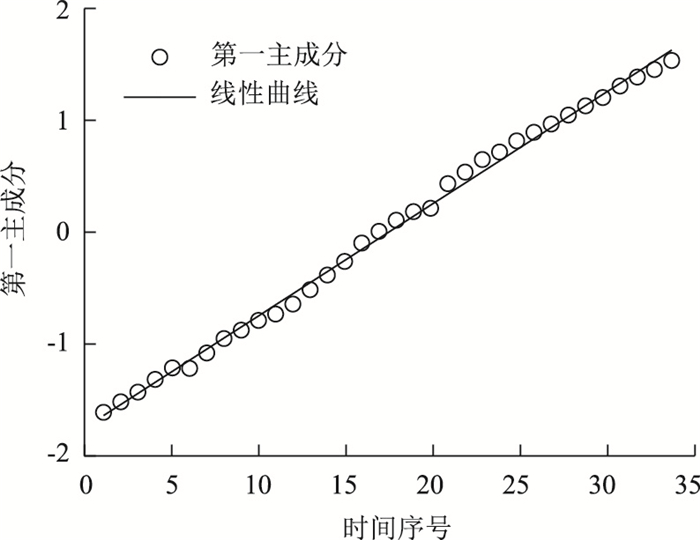
利用1985-2018年之间我国个人汽车保有量的影响因素原始数据,采用传统主成分分析法进行分析。图 1与图 2分别表示用传统主成分分析法与改进主成分分析法拟合得到的第一主成分FAC1_1与时间序号的回归曲线,从两个图可以看出传统主成分分析法的回归曲线与时间几乎呈现二次非线性关系,而改进主成分分析法得到的回归曲线和时间几乎呈现线性关系。由于主成分分析方法更适用于线性结构数据,可以看出通过改进主成分分析法消除了数据之间的非线性关系,更符合主成分分析法的原则,从而有利于提高预测的准确性。
|
| 图 1 传统主成分分析法的第一主成分FAC1_1与时间序号的回归曲线 Fig. 1 Regression curve of 1st principal component FAC1_1 vs. time serial number by conventional PCA |
| |
|
| 图 2 改进主成分分析法的第一主成分FAC1_1与时间序号的回归曲线 Fig. 2 Regression curve of 1st principal component FAC1_1 vs. time serial number by improved PCA |
| |
利用线性回归模型可得改进主成分分析法的第一主成分FAC1_1与时间序号t之间的回归公式为:
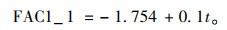
|
(8) |
利用Logistic模型对第一主成分FAC1_1和个人汽车保有量进行回归分析,由于最大汽车保有量m具有不确定性,需要提前进行估算。对m的估算方法大致有3种,分别是直接选取最大值法、专家判断法和纯粹数学推导法。本研究采用专家判断法确定个人汽车最大保有量m。根据文献[21],国家信息中心信息资源部主任徐长明认为,汽车保有量最高可达4.5亿辆。根据表 1中个人汽车保有量占比的历年数据,可以看出该比值一直呈增长趋势,1985年为8.87%,2018年为88.57%,为了合理地预估我国个人汽车保有量极限,本研究假设其极限占比为90%,计算得出我国个人汽车最大保有量为4.05亿辆,则原公式(6)变为:
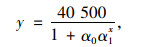
|
(9) |
令α0和α1的初始值为1,利用计算工具SPSS22.0对样本数据进行Logistic非线性回归,得到的参数估计结果见表 5。
| 参数 | 估算 | 标准错误 | 95%置信区间 | |
| 下限值 | 上限 | |||
| a | 68.515 | 3.118 | 62.163 | 74.866 |
| b | 0.064 | 0.003 | 0.059 | 0.069 |
| R2=1-(残差平方和)/(已更正的平方和)=0.998 | ||||
根据表 5可得到拟合程度的相关系数为R2=0.998。当R2越接近于1,表明回归曲线与数据越接近,可以看出得到的Logistic回归曲线拟合程度非常高,最后曲线方程为:
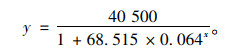
|
(10) |
同样根据上述步骤,利用传统PCA-Logistic模型对我国个人汽车保有量进行回归分析,得到的参数估计结果见表 6,此时R2=0.996<0.998,说明改进PCA-Logistic模型的回归曲线拟合程度更好,会使预测结果更准确。
| 参数 | 估算 | 标准错误 | 95%置信区间 | |
| 下限值 | 上限值 | |||
| a | 22.971 | 1.099 | 20.731 | 25.210 |
| b | 0.194 | 0.006 | 0.181 | 0.206 |
| R2=1-(残差平方和)/(已更正的平方和)=0.996 | ||||
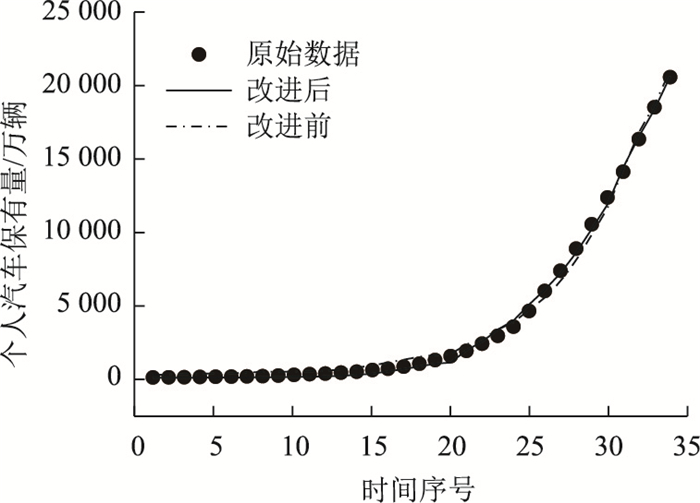
图 3是主成分分析法改进前后通过Logistic模型得到的个人汽车保有量预测曲线与实际汽车保有量数据点的比较,横坐标为时间序号。由图可以看出,在2007年之前,传统PCA-Logistic模型得到的个人汽车保有量预测数据曲线要高于实际个人汽车保有量数据点,而在2007年之后,其又低于实际个人汽车保有量数据点。而改进PCA-Logistic得到的个人汽车保有量数据曲线更接近实际个人汽车保有量数据点,这也再次证明改进主成分分析法有利于提升Logistic回归曲线的拟合度,并提高预测的准确度。
|
| 图 3 主成分分析法改进前后Logistic模型的预测值与实际值对比 Fig. 3 Comparison of predicted and actual values obtained by Logistic model before and after PCA improvement |
| |
2.5 个人汽车保有量预测
为了预测我国2019—2024年的个人汽车保有量,将对应时间序号代入公式(8)中得相应的FAC1_1值,再将所得结果代入Logistic模型公式(10),可得2019—2024年个人汽车保有量预测值见表 7。
| 年份 | 个人汽车保有量/万辆 |
| 2019 | 25 893.1 |
| 2020 | 28 350.6 |
| 2021 | 30 553.5 |
| 2022 | 32 470.0 |
| 2023 | 34 094.8 |
| 2024 | 35 441.9 |
经过预测,我国个人汽车保有量在2021年可能会突破3亿。2019年实际个人汽车保有量为22 635万辆,发现预测值大于实际值,这可能是因为近来年国家为了缓解交通拥挤压力而实施的限购限号等政策延缓了汽车保有量的高速增长,说明国家政策会短期性的影响个人汽车保有量的变化。
3 结论通过对数变换法对传统主成分分析法进行了改进,并结合Logistic模型,提出了改进PCA-Logistic模型。采用改进主成分分析法对影响我国个人汽车保有量的8个代表性主要因素进行“非线性”降维处理并提取主成分,利用Logistic回归模型研究主成分与汽车保有量之间的关系。
通过将PCA-Logistic模型改进前后得到的估计结果进行对比,发现改进PCA-Logistic模型可以有效地消除长时间跨度的数据之间的非线性关系,得到的线性主成分回归曲线更符合主成分分析法原则,同时也有效地提高Logistic模型回归的拟合度,从而更准确地预测未来我国个人汽车保有量。经过预测,我国个人汽车保有量在2021年可能会突破3亿。
本研究在提取主成分时仅仅对影响因素进行分析,没有考虑其与汽车保有量之间的关系,也没有考虑国家政策对汽车保有量的影响,后续工作会考虑更多的影响因素进行分析,从而对汽车保有量进行更合理的评价。
| [1] |
李绍仪. 迎接汽车社会, 中国准备好了吗?[J]. 汽车观察, 2010(10): 79. LI Shao-yi. Is China Ready to Embrace the Automobile Society?[J]. Automobile Observer, 2010(10): 79. |
| [2] |
国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 1985. National Bureau of Statistics. China Statistical Yearbook[M]. Beijing: China Statistics Press, 1985. |
| [3] |
国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2003. National Bureau of Statistics. China Statistical Yearbook[M]. Beijing: China Statistics Press, 2003. |
| [4] |
国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2006. National Bureau of Statistics. China Statistical Yearbook[M]. Beijing: China Statistics Press, 2006. |
| [5] |
国家统计局. 中国统计年鉴[M]. 北京: 中国统计出版社, 2018. National Bureau of Statistics. China Statistical Yearbook[M]. Beijing: China Statistics Press, 2018. |
| [6] |
严筱.低碳交通背景下中国新能源汽车的市场扩散研究[D].武汉: 中国地质大学, 2016. YAN Xiao. Research on Market Diffusion of New Energy Vehicles in China under Background of Low-carbon Transportation[D]. Wuhan: China University of Geosciences, 2016. |
| [7] |
DARGAY J, GATELY D. Income's effect on Car and Vehicle Ownership, Worldwide:1960-2015[J]. Transportation Research Part A:Policy and Practice, 1999, 33(2): 101-138. |
| [8] |
DASH S, VASUDEVAN V, SINGH S K. A Piecewise Linear Multinomial Logit Model of Private Vehicle Ownership Behaviour of Indian Households[J]. Transportation in Developing Economies, 2016, 2(2): 1-10. |
| [9] |
SHAYGAN M, MAMDOOHI A, MASOUMI H E. Car Ownership Models in Iran:A Review of Methods and Determinants[J]. Transport and Telecommunication Journal, 2017, 18(1): 45-59. |
| [10] |
崔凯俊.居民家庭小汽车保有量影响因素分析与预测建模[D].北京: 北京交通大学, 2019. CUI Kai-Jun. Analysis and Predictive Modeling on Influencing Factors of Resident Family Car Ownership[D]. Beijing: Beijing Jiaotong University, 2019. http://cdmd.cnki.com.cn/Article/CDMD-10004-1019214825.htm |
| [11] |
张雪伍, 常晋义. PCA-BP在城市汽车保有量预测中的应用研究[J]. 计算机仿真, 2012, 29(12): 376-379. ZHANG Xue-wu, CHANG Jin-yi. Research on Urban Car Ownership Prediction Based on PCA-BP Neural Network[J]. Computer Simulation, 2012, 29(12): 376-379. |
| [12] |
陈勇, 孔峰. BP神经网络预测全国私人汽车拥有量[J]. 计算技术与自动化, 2003, 22(3): 67-70. CHEN Yong, KONG Feng. Application of BP Neural Network to Forecast Possession of Private Automobile[J]. Computing Technology and Automation, 2003, 22(3): 67-70. |
| [13] |
朱开永, 周圣武, 娄可元, 等. 基于私家车保有量预测与调控的灰色模型研究[J]. 中国矿业大学学报, 2008, 37(6): 868-872. ZHU Kai-yong, ZHOU Sheng-wu, LOU Ke-yuan, et al. Research on Grey Model about Forecast and Control for Total Number of Private Cars[J]. Journal of China University of Mining & Technology, 2008, 37(6): 868-872. |
| [14] |
王传鑫, 袁永生, 周铭华. 基于改进密度峰值聚类的私人汽车保有量影响因素分析[J]. 计算技术与自动化, 2019, 38(1): 122-125. WANG Chuan-xin, YUAN Yong-sheng, ZHOU Ming-hua. Analysis of Influence Factors of Private Car Ownership Based on Improved Density Peak Clustering[J]. Computing Technology and Automation, 2019, 38(1): 122-125. |
| [15] |
蒋艳梅, 赵文平. Logistic模型在我国私人汽车保有量预测中的应用研究[J]. 工业技术经济, 2010, 29(11): 99-104. JIANG Yan-mei, ZHAO Wen-ping. Application Research of Logistic Model in Private Car Ownership Prediction in China[J]. Journal of Industrial Technological Economics, 2010, 29(11): 99-104. |
| [16] |
张兰怡, 胡喜生, 陈清耀, 等. 基于PCA-Logistic回归的汽车保有量预测研究[J]. 重庆交通大学学报:自然科学版, 2017, 36(5): 104-109. ZHANG Lan-yi, HU Xi-sheng, CHEN Qing-yao, et al. Prediction of Car Ownership Based on Principal Component Analysis and Logistic Regression[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2017, 36(5): 104-109. |
| [17] |
任玉珑, 陈容, 史乐峰. 基于Logistic组合模型的中国民用汽车保有量预测[J]. 工业技术经济, 2011, 30(8): 90-97. REN Yu-long, CHEN Rong, SHI Yue-feng. Prediction of Civil Vehicles' Possession Based on Combined Logistic Model[J]. Journal of Industrial Technological Economics, 2011, 30(8): 90-97. |
| [18] |
曲双红, 李华, 李刚. 基于主成分分析的几种常用改进方法[J]. 统计与决策, 2011(5): 155-156. QU Shuang-hong, LI Hua, LI Gang. Several Improved Methods Based on Principal Component Analysis[J]. Statistics and Decision, 2011(5): 155-156. |
| [19] |
MANSFIELD E, HENSLEY C. The Logistic Process:Tables of the Stochastic Epidemic Curve and Applications[J]. Journal of the Royal Statistical Society Series B:Methodological, 1960, 22(2): 332-337. |
| [20] |
陈璇璇.人口、资源与环境视角下的汽车保有量影响因素研究[D].北京: 首都经济贸易大学, 2008. CHEN Xuan-xuan. Study on Influence Factors of Car Ownership from Perspective of Population, Resource and Environment[D]. Beijing: Capital University of Economics and Business, 2008. http://cdmd.cnki.com.cn/Article/CDMD-11912-2008083158.htm |
| [21] |
姜靖, 戴慧兰.汽车保有量首次破亿, 我国到底能承载多少汽车[N].科技日报, 2011-09-26(1). JIANG Jing, DAI Hui-lan. Car Ownership Exceeds 100 Million for the First Time, How Many Cars Can Our Country Holds?[N]. Science and Technology Daily, 2011-09-26(1). |
 2020, Vol. 37
2020, Vol. 37
