扩展功能
文章信息
- 石州, 罗彦斌, 陈建勋, 刘伟伟, 武云飞
- SHI Zhou, LUO Yan-bin, CHEN Jian-xun, LIU Wei-wei, WU Yun-fei
- 木寨岭公路隧道大变形综合评价预测
- Comprehensive Evaluation and Prediction of Large Deformation of Muzhailing Highway Tunnel
- 公路交通科技, 2020, 37(8): 90-98, 158
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(8): 90-98, 158
- 10.3969/j.issn.1002-0268.2020.08.012
-
文章历史
- 收稿日期: 2019-11-21
近年来,复杂地质条件下的隧道工程诸如鹧鸪山公路隧道、祁连山铁路隧道、木寨岭铁路隧道、天坪铁路隧道等一大批重点建设项目相继建成通车。木寨岭公路隧道、大瑞铁路高黎贡山隧道等重点项目正在如期建设。隧道工程建设未来的发展方向呈现出大跨度、特长、深埋等特点,安全高效地穿越高应力软岩地区面临巨大挑战,特别是在高地应力软弱破碎地层,隧道大变形灾害尤为突出,严重制约隧道工程的建设和发展。对于隧道设计和施工,合理地预测和评价隧道变形级别并进行分级管理,以避免大变形灾害的发生就显得尤为必要。对此,众多学者开展了隧道大变形分级预测的研究,试图确定各种指标以及相应的临界值,对隧道大变形进行预测。现有的软岩隧道大变形分级预测方法主要有经验方法和半经验半定量法。半经验半定量法按照分级指标又可分为单指标强度应力法、相对变形量法和多指标或综合指标法。Singh[1],Geol,Jimenez和Recio等学者基于岩石质量指标,利用统计数据,提出了预测挤压变形的临界隧道埋深经验公式。Muirwood首次提出强度应力比来评价隧道的挤压变形,后被Nakano[2]用来预测日本软岩隧道挤压变形,其后Jethwa等[3]、Aydan等[4]、Barla[5]、陈子全等[6]也均根据岩体强度与原始地应力(或垂直应力)的比值来预测隧道可能发生的挤压变形。喻渝[7]根据初始地应力与围岩抗压强度的比值来预测大变形。Bhasin等[8]提出根据岩体切向应力与岩石强度的比值来预测隧道可能发生的挤压变形。Saari[9]建议采用隧道切向应变强度作为评价岩石挤压程度的指标,提出采用最终变形量的1%作为识别挤压变形的临界值。根据Goel[10]和Sakurai[11]的研究,当隧道在无支护条件下变形量超过总变形量的1%时,即认为隧道发生了大变形。Hoek[12]根据应变率将软岩隧道变形分为无挤压变形、轻微挤压变形、中等挤压变形、严重挤压变形和极严重挤压变形。Singh等[13]根据该指标将围岩挤压变形程度分为微弱挤压、中等挤压和高度挤压。张祉道[14]依据洞壁相对位移,将软岩隧道变形分为轻度、中等和严重等3个级别。黄兴等[15]指出当围岩挤压变形与开挖半径间的比值≥1%,且挤压变形与扩挖间隙的比值≥1时,产生挤压大变形。根据这2个指标,将TBM围岩挤压变形划分为无挤压变形、轻微挤压变形、中等挤压变形、严重挤压变形和非常严重挤压变形5个等级。Aydan等[4]将该指标作为判断隧道挤压变形程度的依据,认为围岩总变形和弹性变形与岩石的室内试验结果是对应的,因此利用岩石室内试验获得的应力-应变曲线中应变硬化阶段、屈服阶段、应变软化阶段的极限应变与弹性极限应变的比值作为预测挤压变形程度的评判标准,将隧道围岩挤压程度划分为无挤压、轻度挤压、中度挤压、严重挤压和最严重挤压5个级别。Hoek等[16]提出用强度应力比与隧道应变率双指标,将大变形分为无支护问题、轻微挤压、严重挤压、非常严重挤压、极严重挤压5个等级。刘志春[17]等结合乌鞘岭隧道提出综合系数,综合考虑了围岩的相对变形、强度应力比、原始地应力和弹性模量等几个因素。徐林生等[18]根据隧道估判变形量和相对变形,将公路隧道围岩大变形分为1级、2级和3级。李国良等[19]结合兰渝铁路软岩隧道提出在设计阶段以隧道洞壁相对位移和岩体强度应力比作为分级指标,将挤压大变形分为3个等级,根据岩体强度应力比进行大变形预测,在施工阶段以变形量和变形速率作为分级指标。孟陆波等[20]以影响大变形发生的8个主要因素作为综合分级指标,提出基于模糊层次综合评价的大变形预测方法,将大变形分为无大变形、轻微大变形、中等大变形和强烈大变形4类。任洋等[21]以岩石单轴抗压强度、主应力值、强度应力比和弹性模量4个因素作为综合分级指标,采用可拓学理论和层次分析法,将大变形也分为无大变形、轻微大变形、中等大变形和强烈大变形。
以上研究中众多分级预测指标是基于设计阶段岩石的物理力学性质提出的,施工阶段这些参数指标获得较难,准确性不高。例如,相对变形量法[9-10, 12]等理论中隧道洞壁相对位移一般适用于以水平变形为主的隧道;层次分析法[20]、强度应力比法[2-4]等理论中的岩体单轴抗压强度、极限应变等分级指标多需要通过岩石室内试验得出,而目前典型的软岩隧道大变形多发生于破碎、强度低及易风化的碳质板岩、绿泥石片岩和千枚岩等地层,对于这类薄层或破碎围岩,往往无法取得扰动软弱围岩岩芯进行室内试验,而且相应的地应力测试也难以开展。关于软弱围岩地层中的地应力量测的准确度历来存在较大的争议,可拓学理论[21]、Jethwa[3]等研究理论的指标中采用的地应力在软弱松散围岩现场量测准确度不高。现有的大变形灾害预测与评价方法多为勘测和设计阶段的研究,对于薄层或破碎岩体大变形现场快速预测具有较大的局限性。对此,需要确定适用于薄层软弱破碎岩体大变形的综合评价指标,并提出施工阶段大变形现场快速预测与评价方法。
本研究依托兰州至海口国家高速公路(G75)木寨岭公路隧道工程,提出基于施工阶段快速判识理念的软岩大变形分级预测的模糊层次分析法。通过将模糊层次分析法与在隧道施工现场快速获得的一系列与岩体结构特征及岩体完整性特征相关的评价指标相结合,快速准确地对软岩隧道大变形进行定量分级预测。以期为软弱破碎围岩隧道大变形综合评价预测提出一种方法。
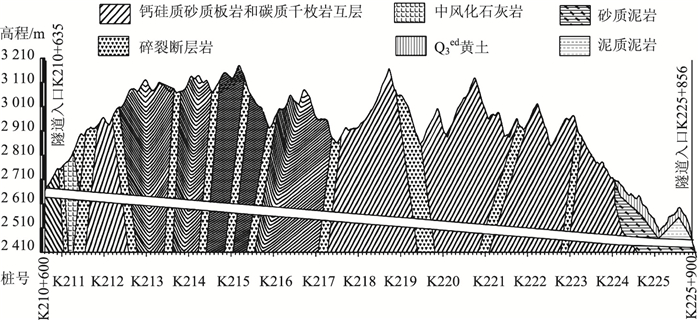
1 工程概况木寨岭公路隧道是兰州—海口国家高速公路(G75)渭源—武都段的一个重点工程。隧道采用两个单向孔四车道的设计结构,隧道左洞长15.231 km,右洞长15.173 km,最大埋深629 m。隧道整体穿越了6种地层结构,围岩岩性主要以钙硅质砂质板岩和碳质千枚岩互层岩体为主,纵断面如图 1所示。沿隧道依次布置3个斜井,其中1号、2号、3号斜井长度分别为1 633,1 814,1 265 m。
|
| 图 1 木寨岭公路隧道地质纵断面 Fig. 1 Geological longitudinal profile of Muzhailing Highway Tunnel |
| |
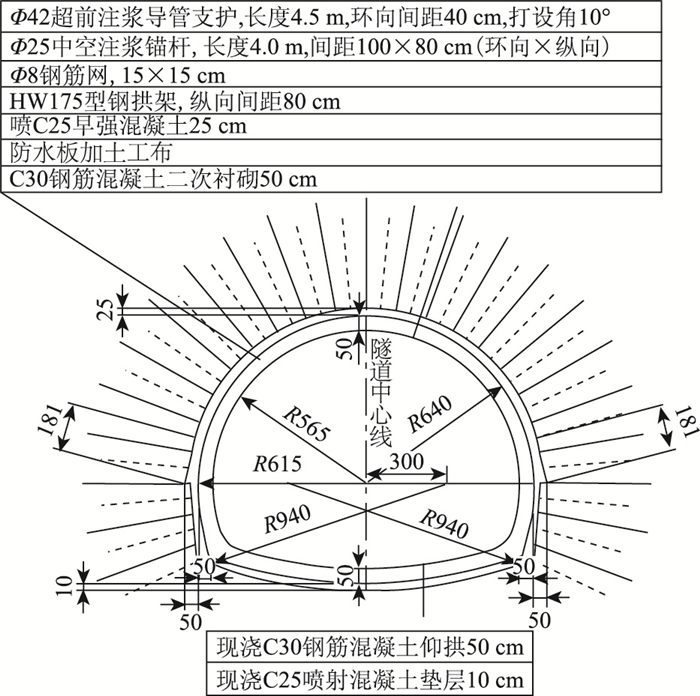
木寨岭公路隧道自开工建设以来,发生了不同程度的大变形灾害问题,特别是木寨岭公路隧道2号斜井、3号斜井换拱率高达30%,造成工期延缓、工程造价剧增,严重威胁隧道施工人员安全。本研究选取的隧道变形段衬砌属于SVC型衬砌结构,支护结构参数如图 2所示。隧道地应力测试结果表明K214+085段钻孔的5个测段最大主应力值为12.14~18.76 MPa,最小主应力值为7.34~11.61 MPa,最大主应力方向为39.6°。K218+400段钻孔的3个测段最大主应力值为11.37~17.98 MPa,最小主应力值为6.80~10.06 MPa,最大主应力方向为34.1°,测量结果与区域地应力场分析结果较吻合。测试钻孔附近以水平构造应力作用为主,属于走滑断层应力状态,最大水平主应力方向与隧洞轴线方向大致相同,均为北东东(NEE)方向。
|
| 图 2 SVC型衬砌结构设计(单位:cm) Fig. 2 Design of SVC type lining structure (unit: cm) |
| |
2 模糊层次综合评价法
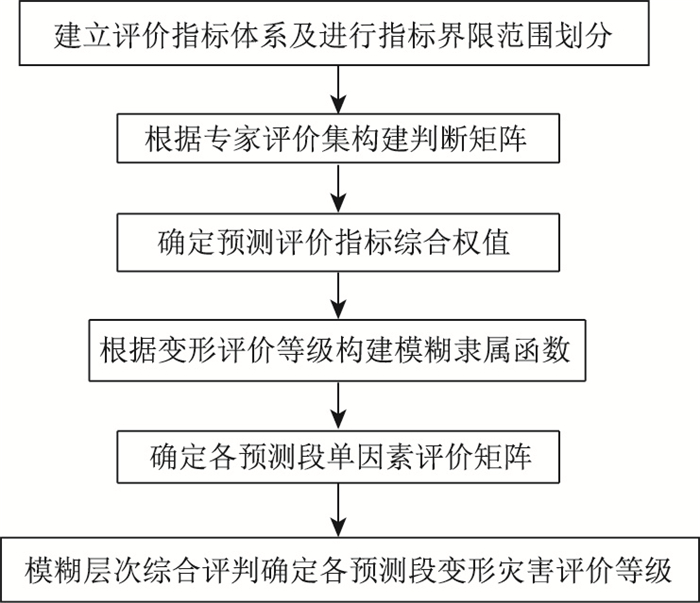
模糊层次综合评价法是一种基于模糊数学和层次分析的综合评价法[22]。该方法根据模糊数学的隶属度理论把定性评价转化为定量预测,建立了定性与定量相统一、模糊数学与层次结构相结合的评价模型,对受到多种因素制约的事物或对象做出总体评价。步骤如图 3所示。
|
| 图 3 模糊数学和层次分析综合评价法流程图 Fig. 3 Flowchart of fuzzy of comprehensive evaluation method of fuzzy mathematics and AHP |
| |
2.1 建立预测指标评价体系
根据预测评价的目标和要求,选取合适的评价指标并分析各因素之间的关系,建立整个评价指标体系的层次结构模型,确定各评价因子基于不同变形等级的分布范围及指标界限值。
2.2 建立指标判断矩阵基于层次分析法,根据专家评分机制采用1~9标度确定各层次指标量化关系,构建评价指标重要性程度判断矩阵。
2.3 确定预测指标综合权值计算某层所有因素对于总目标相对重要性的组合权重,进行层次总排序:
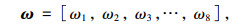
|
(1) |
式中ωi(i=1~8)为各影响因素所对应的权值。
2.4 建立评价指标集与评价集在评价指标体系的基础上,采用模糊数学的方法建立指标集和评价集:
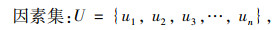
|
(2) |
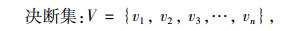
|
(3) |
式中ui和vi分别为因素集和决断集中的元素。
2.5 单因素模糊综合评判在建立评价指标集和评价集后,利用隶属函数实现指标集到评价集的模糊变换,第i个元素ui的模糊评价矩阵为R=(rij)n×m。
单因素模糊矩阵表示为:
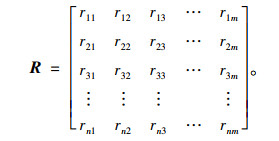
|
(4) |
通过预测指标综合权重集和模糊矩阵R计算得到综合评价集B:
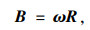
|
(5) |
式中,B=[B1, B2, …, Bn],Bn为评价对象第n评价级别的隶属度。
最后根据最大隶属度原则,确定各预测段变形综合评价等级。
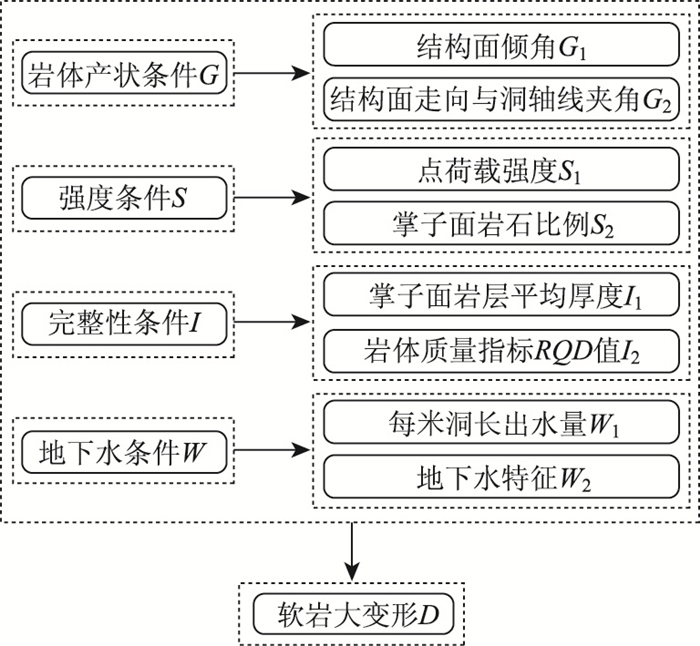
3 大变形模糊层次综合预测 3.1 预测评价指标选取木寨岭公路隧道工程实践表明,岩层产状、岩石强度、岩体完整性及地下水条件是软岩隧道大变形致灾的主控因子,且围岩变形与隧道的赋存环境密切相关,属于工程软岩范畴。本研究根据定性划分和定量指标相结合的原则,构造隧道软岩大变形指标评价体系,指标层次结构如图 4所示。
|
| 图 4 预测指标层次结构 Fig. 4 Hierarchical structure of predictive indicators |
| |
(1) 岩层产状:包括结构面倾角及结构面走向与洞轴线夹角。木寨岭公路隧道围岩岩性主要为质软的碳质千枚岩和质硬的钙硅质砂质板岩,两类岩石以互层状、不同比例和不同厚度组合分布,各向异性更加突出,岩层走向与隧道开挖方向的夹角多变,倾角也缓陡起伏,造成围岩不同程度和不同模式的变形和失稳。
(2) 岩石强度:包括点荷载强度及掌子面软岩比例。木寨岭公路隧道岩石强度试验结果表明,砂质板岩强度较高,属于较硬岩,可完整取芯测得其单轴饱和抗压强度,经过统计分析岩体单轴抗压强度Rc平均值为56.3 MPa。而碳质千枚岩强度较低,点荷载试验修正后的点荷载强度值Is(50)平均值为0.11 MPa,属于软岩,耐崩解试验加水浸泡0.5 h时试样崩解已达到60%以上,加水浸泡2 h后岩石试样崩解已基本完成。试验取样时不易直接取得完整岩心样本,单轴抗压强度的获取存在难度。点载荷试验因其仪器轻便、操作简易、适用性强的优势能较好地适应木寨岭公路隧道地层,克服碳质千枚岩无法获取单轴抗压强度的不足。软弱破碎岩体的含量(主要为软弱的碳质千枚岩所占比例)直接影响着岩体的强度。
(3) 岩体完整性:包括掌子面岩层平均厚度和岩石质量指标RQD值。围岩的完整性是影响隧道围岩开挖稳定性的重要因素。岩体完整性指数Kv和岩体体积节理数Jv是评价隧道岩体完整性的常用指标,但在软弱、薄层、裂隙岩体中,很难准确、快速地得到。木寨岭公路隧道地层结构破碎,属于碎裂结构,围岩自稳能力差,开挖后极容易松动坍塌,牵引后方岩体松弛变形。用掌子面岩层的平均厚度从横断面内评价岩体的完整性,用RQD值从隧道纵向评价岩体的完整性,将二者综合起来,能更加全面和准确地评价围岩的完整性。
(4) 地下水条件:包括开挖每延米洞长出水量和地下水特征。木寨岭隧道地下水整体不发育,但偶有富水的储水带。地下水对围岩的软化作用明显,尤其是碳质千枚岩遇水2 h接近完全泥化崩解,丧失强度。同时,地下水增加围岩自重、润滑层理,会加剧大变形的发生。
3.2 各指标综合权重分析基于木寨岭隧道围岩大变形各影响因素的统计规律及变形特性分析,根据Hoek、孟陆波和李天斌等[6, 12, 20-21]对影响软岩大变形各指标的研究及专家打分,通过采用Saaty[23]判断矩阵标准度及其倒数的标度方法,将层次结构图各层中的因子对上一层次目标的相对重要性进行两两比较,构造判断矩阵,如表 1~表 5所示。将各层级指标单权值与所属类别权值进行整合,得出8个评价指标关于隧道变形的综合权值集合,如表 6所示。
| G | G1 | G2 |
| G1 | 1 | 3 |
| G2 | 1/3 | 1 |
| 各指标 综合 排序 | G-W权值分布 | 各指标 综合 权值 | |||
| G | S | I | W | ||
| 0.122 | 0.418 | 0.418 | 0.042 | ||
| G1 | 0.75 | 0 | 0 | 0 | 0.091 |
| G2 | 0.25 | 0 | 0 | 0 | 0.031 |
| S1 | 0 | 0.75 | 0 | 0 | 0.314 |
| S2 | 0 | 0.25 | 0 | 0 | 0.104 |
| I1 | 0 | 0 | 0.667 | 0 | 0.279 |
| I2 | 0 | 0 | 0.333 | 0 | 0.139 |
| W1 | 0 | 0 | 0 | 0.5 | 0.021 |
| W2 | 0 | 0 | 0 | 0.5 | 0.021 |
3.3 大变形分级及评价指标分级
根据木寨岭隧道不同级别大变形段监控量测结果,通过数据统计及理论分析,将隧道变形划分为5个等级:极严重大变形(变形量1 000~3 000 mm)、严重大变形(变形量800~1 000 mm)、中等大变形(变形量500~800 mm)、轻微大变形(变形量200~500 mm)、无大变形(变形量0~200 mm)。
基于木寨岭公路隧道不同级别大变形各分级指标的统计特征,参照《工程岩体分级标准》(GB/T 50218—2014)[24]、《公路隧道设计规范》(JTG 3370. 1—2018)[25]、《铁路隧道设计规范》(TB-1003—2016)[26]和《铁路挤压性围岩隧道技术规范》(Q/CR 9512—2019)[27]中各指标的分级范围,结合先前关于软岩大变形分级指标的研究[17, 28],提出了各评价指标相对于不同级别大变形的界限及分布范围,如表 7所示。
| 评价指标 | 岩层产状条件 | 强度条件 | 完整性条件 | 地下水条件 | ||||||||
| 结构面倾 角/(°) | 结构面走向与 洞轴线夹角/(°) | 点荷载 强度/MPa | 软岩比 例/% | 掌子面岩层 平均厚度/cm | RQD/% | 每米洞长出水量/ [L·(min·m)-1] | 地下水 特征 | |||||
| 各评价指标相对于不同级别大变形的界限及分布范围 | 极严重大变形 | < 30 | < 30 | < 0.1 | >80 | < 10 | < 25 | >12.5 | 涌流状出水 | |||
| 严重大变形 | 30~45 | 30~40 | 0.1~0.5 | 70~80 | 10~20 | 25~50 | 7.5~12.5 | 淋雨状出水 | ||||
| 中等大变形 | 45~60 | 40~50 | 0.5~1.5 | 60~70 | 20~30 | 50~75 | 2.5~7.5 | 线流状出水 | ||||
| 轻微大变形 | 60~75 | 50~60 | 1.5~3.5 | 50~60 | 30~50 | 75~90 | 1~2.5 | 潮湿状出水 | ||||
| 无大变形 | >75 | >60 | >3.5 | < 50 | >50 | >90 | < 1 | 点滴状出水 | ||||
3.4 隶属函数构造
在大变形综合模糊评测中,采用梯形隶属函数对各参评因子的隶属度进行计算。根据各影响因子的特点将其分为以下两类。
第1类:所选取的指标需要进行定性分析,无法定量的对其进行评价(如地下水特征),其隶属函数采用特征函数来进行研究:
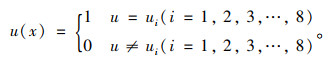
|
(6) |
第2类:所选取的指标可进行精确量化,可定量分析其变化及发展规律(如点荷载强度等),根据各评价指标的的界限范围,可确定隶属函数。本研究所列隶属函数为降半阶梯型函数分布,对于升半阶梯型分布的评价因子,在分析时将评价分级及隶属度分布按相反方向分析即可。相应指标的隶属函数如表 8所示。
上述区间隶属度函数中,ui(x)为各评价指标因子对应于不同变形级别的隶属函数;x为各评价指标的实际值;a1,a2,a3,a4分别为各评价指标对应于不同变形等级的基准界限值。
3.5 变形预测与工程验证通过监控量测和现场试验获取木寨岭公路隧道5个变形预测段的8个评价指标值,如表 9所示。
| 条件 | 变量 | 位置 | ||||
| 2号斜井 | 2号斜井 | 2号斜井 | 2号斜井 | 3号斜井 | ||
| 预测段桩号 | ||||||
| XK1+105 | XK1+554 | XK1+643 | XK1+684 | XK0+701 | ||
| 岩层产状 | 结构面倾角/(°) | 69 | 62 | 50 | 53 | 43 |
| 结构面走向与洞轴线夹角/(°) | 42 | 36 | 14 | 20 | 34 | |
| 强度 | 点荷载强度/MPa | 0.09 | 0.27 | 0.13 | 0.13 | 1.07 |
| 掌子面软岩比例/% | 68 | 76 | 78 | 82 | 67 | |
| 完整性 | 掌子面岩层平均厚度/cm | 11 | 12 | 12 | 10 | 27 |
| RQD/% | 27 | 57 | 52 | 48 | 31 | |
| 地下水 | 每米洞长出水量/[L·(min·m)-1] | 0.9 | 0.9 | 2 | 1.9 | 5.4 |
| 地下水特征 | 潮湿状出水 | 点滴状出水 | 点滴状出水 | 线流状出水 | 点滴状出水 | |
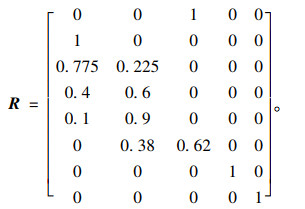
将上述预测段的指标值代入隶属函数计算得出预测指标模糊矩阵,进而根据综合权值计算预测段各变形等级隶属度。以XK1+643为例,该段的隶属度计算如下。
预测指标单因素模糊矩阵:
|
各预测指标的综合权值:
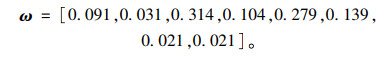
|
该预测段各大变形级别的隶属度:
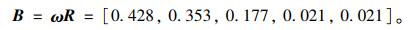
|
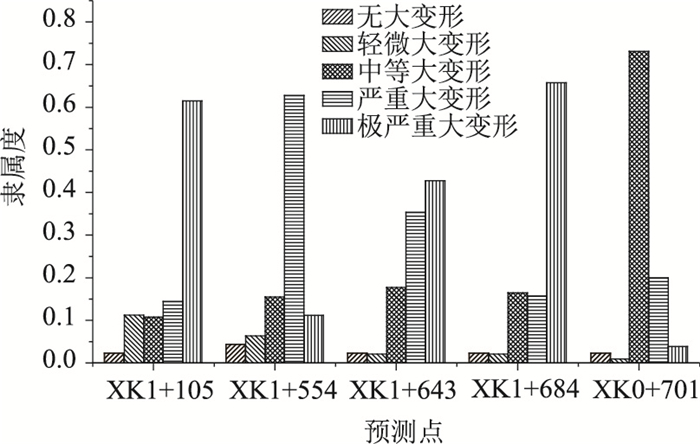
类似地,可计算出其他预测段的隶属度,结果如图 5所示。
|
| 图 5 各预测段隶属度柱状图 Fig. 5 Histogram of membership degree of each prediction segment |
| |
由图 5可得,各预测段最大隶属度分别为0.615,0.628,0.428,0.657,0.731。根据最大隶属度原则,各预测段变形等级分别为极严重大变形、严重大变形、极严重大变形、极严重大变形、中等大变形。
3.6 不同预测方法对比分别采用本研究方法和强度应力比法[3, 6]及其他模糊综合评价法[20]对上述木寨岭公路隧道5个桩号段的变形进行预测,由于文献[20]虽对大变形进行了分级,但并未划定各级别变形分级范围,因此不同级别变形的分布范围参照本研究的分布范围取值。预测结果如表 10和图 6所示。
| 预测点桩号 | 强度应力比 | 实际变形级别和变形值/mm | 本研究预测结果 | 孟陆波法 | Jethwa法 | 陈子全法 |
| XK1+105 | 0.67 | 极严重/1 149 | 极严重/(1 000~3 000) | 无/(0~200) | 轻微 | 轻微/(100~300) |
| XK1+554 | 0.35 | 严重/883 | 严重/(800~1 000) | 轻微/(200~500) | 中等 | 中等/(300~500) |
| XK1+643 | 0.32 | 极严重/2 733 | 极严重/(1 000~3 000) | 轻微/(200~500) | 中等 | 严重/(500~800) |
| XK1+684 | 0.32 | 极严重/1 171 | 极严重/(1 000~3 000) | 轻微/(200~500) | 中等 | 严重/(500~800) |
| XK0+701 | 0.75 | 中等/705 | 中等/(500~800) | 无/(0~200) | 轻微 | 轻微/(100~300) |
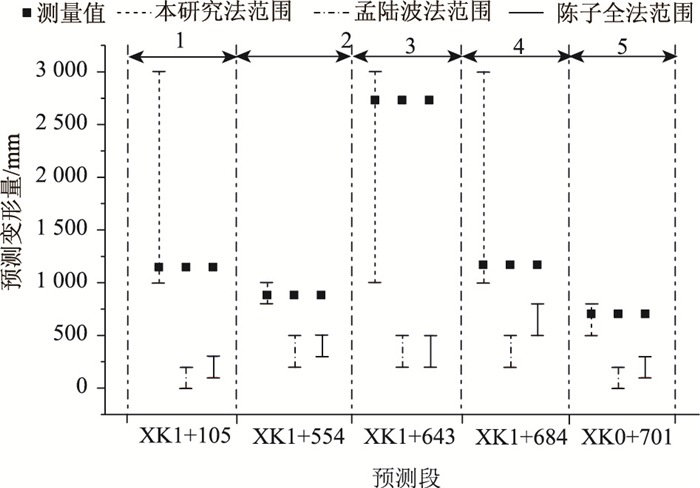
|
| 图 6 不同预测方法预测结果对比分析 Fig. 6 Comparative analysis of prediction results of different prediction methods |
| |
由图 6可知,预测段围岩大变形实测值均处于本方法预测的大变形分布范围内。而其他两种方法预测精确度不高,实际变形量超过陈法和孟法预测范围上限值的变形量最大可达上限值的2.4倍和4.4倍。分析上述对比结果,可得以下几点:
(1) 木寨岭公路隧道在施工过程中,岩层产状成为影响围岩稳定性的重要因素,强度应力法等预测方法虽考虑了岩石的强度、完整性等,却未考虑岩石产状对软弱破碎围岩大变形的影响。
(2) 软岩大变形受多因素控制,是一种非常复杂的与时间有关的弹黏塑性变形,其他预测方法仅根据单评价指标或较少的评价指标去预测大变形,显然无法应对大变形的复杂性。
(3) 木寨岭公路隧道的变形量较大,变形范围远超普通大变形隧道,其他预测方法的变形分级已无法满足木寨岭公路隧道的实际变形情况,普适性较差。
(4) 木寨岭公路隧道岩性结构属于砂质板岩和碳质千枚岩软硬互层岩石,不是单一岩性,且隧道的大变形不只由软弱碳质千枚岩的岩性控制,同时还受岩层组合结构复合控制。其他预测方法多是基于单一岩性,故应用于木寨岭公路隧道大变形预测时准确度不高。
(5) 其他预测方法中的大多数评价指标均是现场取样后由室内试验获得,然而隧道内大变形区域的应力场极其复杂,试验样本取样后的应力状态相比于原位应力场有较大变化,其相应的指标与原位岩层中实际值有一定区别,这种区别导致了预测结果与实际情况有所偏差。
4 结论(1) 结合木寨岭公路隧道大变形统计情况,基于模糊综合评价法和层次分析法,提出了适用于软弱破碎围岩隧道施工阶段大变形分级预测的模糊层次综合评价方法。
(2) 选取岩层产状、强度、完整性和地下水作为大变形的分级和评价指标。为了充分考量4类指标对大变形的影响,共选取了结构面走向与洞轴线夹角、结构面倾角、点荷载强度、掌子面软岩比例、掌子面岩层平均厚度、岩体RQD值、每延米洞长出水量、地下水特征8项指标对大变形进行分级预测。同时,根据木寨岭隧道变形的统计结果,将隧道大变形分为无大变形、轻微大变形、中等大变形、严重大变形和极严重大变形5个等级,并提出了8项指标对应于不同大变形级别的界限和分布范围。
(3) 本预测方法在木寨岭公路隧道变形段的工程实践表明,该方法的工程适用性强、准确度高。将本研究方法与陈子全法、孟陆波法和Jethwa法应用于木寨岭公路隧道5个变形段进行比较分析,得到实际变形量超过陈法和孟法预测范围上限值的变形量最大可达上限值的2.4倍和4.4倍。
| [1] |
SINGH B, JETHWA J L, DUBE A K. Correlation between Observed Support Pressure and Rock Mass Quality[J]. Tunnelling and Underground Space Technology, 1992, 7(1): 59-74. |
| [2] |
NAKANO R. Geotechnical Properties of Mudstone of Neogene Tertiary in Japan with Special Reference to the Mechanism of Squeezing Swelling Rock Pressure in Tunneling[C]//Proceedings of the International Symposium of Soil Mechanics. Oaxaca: [s.n.], 1979: 75-92.
|
| [3] |
JETHWA J L, SINGH B, SINGH B. Estimation of Ultimate Rock Pressure for Tunnel Linings under Squeezing Rock Conditions:A New Approach[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1984, 22(1): 21. |
| [4] |
AYDAN O, AKAGI T, KAWAMOTO T. The Squeezing Potential of Rocks Around Tunnels:Theory and Prediction[J]. Rock Mechanics and Rock Engineering, 1993, 26(2): 137-163. |
| [5] |
BARLA G. Squeezing Rocks in Tunnels[J]. ISRM News Journal, 1995, 2(3/4): 44-49. |
| [6] |
陈子全, 何川, 吴迪, 等. 高地应力层状软岩隧道大变形预测分级研究[J]. 西南交通大学学报, 2018, 53(6): 1237-1244. CHEN Zi-quan, HE Chuan, WU Di, et al. Study of Large Deformation Classification Criterion for Layered Soft Rock Tunnels under High Geostress[J]. Journal of Southwest Jiaotong University, 2018, 53(6): 1237-1244. |
| [7] |
喻渝. 挤压性围岩支护大变形的机理及判定方法[J]. 世界隧道, 1998(1): 46-51. YU Yu. Serious Deformation of Surrounding Rock in Squeezing Ground[J]. World Tunnel, 1998(1): 46-51. |
| [8] |
BHASIN R, GRIMATAD E. The Use of Stress-strength Relationships in the Assessment of Tunnel Stability[J]. Tunnelling and Underground Space Technology, 1996, 11(1): 93-98. |
| [9] |
SAARI K. Analysis of Plastic Deformation (Squeezing) of Layers Intersecting Tunnels and Shafts in Rock[D]. Berkeley: University of California, 1982.
|
| [10] |
GOEL R K. Correlations for Predicting Support Pressures and Deformations in Tunnels[D]. Nagpur, India: Nagpur University, 1994.
|
| [11] |
SAKURAI S. Lessons Learned from Field Measurements in Tunneling[J]. Tunnelling and Underground Space Technology, 1997, 12(4): 453-460. |
| [12] |
HOEK E. Big Tunnels in Bad Rock[J]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(9): 726-740. |
| [13] |
SINGH B, GEOL R K. Rock Mass Classification: A Practical Approach in Civil Engineering[M].[S. l.]: Elsevier Science Ltd., 1999: 128-135.
|
| [14] |
张祉道. 关于挤压性围岩隧道大变形的探讨和研究[J]. 现代隧道技术, 2003, 40(2): 5-12. ZHANG Zhi-dao. Discussion and Study on Large Deformation of Tunnel in Squeezing Ground[J]. Modern Tunnelling Technology, 2003, 40(2): 5-12. |
| [15] |
黄兴, 刘泉声, 刘滨, 等. TBM围岩挤压大变形特性分析与等级划分[J]. 采矿与安全工程学报, 2015, 32(2): 260-266. HUANG Xing, LIU Quan-sheng, LIU Bin, et al. Study on the Properties of TBM Surrounding Rock Large Squeezing Deformation and Its Grading[J]. Journal of Mining and Safety Engineering, 2015, 32(2): 260-266. |
| [16] |
HOEK E, MARINOS P. Predicting Tunnel Squeezing Problems in Weak Heterogeneous Rock Masses[J]. Tunnels & Tunnelling International, 2000, 32(11): 45-51. |
| [17] |
刘志春, 朱永全, 李文江, 等. 挤压性围岩隧道大变形机理及分级标准研究[J]. 岩土工程学报, 2008, 30(5): 690-697. LIU Zhi-chun, ZHU Yong-quan, LI Wen-jiang, et al. Mechanism and Classification Criterion for Large Deformation of Squeezing Ground Tunnels[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 690-697. |
| [18] |
徐林生, 李永林, 程崇国. 公路隧道围岩变形破裂类型与等级的判定[J]. 重庆交通学院学报, 2002, 21(2): 16-19. XU Lin-sheng, LI Yong-lin, CHENG Chong-guo. Judging of the Deformation-cracking Type and Grade about Surrounding Rock of Highway Tunnel[J]. Journal of Chongqing Jiaotong University, 2002, 21(2): 16-19. |
| [19] |
李国良, 刘志春, 朱永全. 兰渝铁路高地应力软岩隧道挤压大变形规律及分级标准研究[J]. 现代隧道技术, 2015, 52(1): 62-68. LI Guo-liang, LIU Zhi-chun, ZHU Yong-quan. On the Large Squeezing Deformation Law and Classification Criteria for the Lanzhou-Chongqing Railway Tunnels in Soft and High Geostress Rocks[J]. Modern Tunnelling Technology, 2015, 52(1): 62-68. |
| [20] |
孟陆波, 李天斌, 龚勇. 基于模糊层次综合评判的大变形预测方法[J]. 成都理工大学学报:自然科学版, 2010, 37(2): 195-200. MENG Lu-bo, LI Tian-bin, GONG Yong. Large Deformation Forecasting Method Based on Fuzzy Hierarchical Integrated Evaluation[J]. Journal of Chengdu University of science and Technology:Natural Science Edition, 2010, 37(2): 195-200. |
| [21] |
任洋, 李天斌. 基于层次分析的可拓学理论围岩大变形预测方法及应用[J]. 现代隧道技术, 2011, 48(4): 6-12. REN Yang, LI Tian-bin. Application of Large Deformation Forecast Method for Surrounding Rocks Based on Hierarchical Analysis and Extension Theory[J]. Modern Tunnelling Technology, 2011, 48(4): 6-12. |
| [22] |
谢季坚, 刘承平. 模糊数学方法应用[M]. 武汉: 华中科技大学出版社, 2000. XIE Ji-jian, LIU Cheng-ping. Application of Fuzzy Mathematics Method[M]. Wuhan: Huazhong University of Science and Technology Press, 2000. |
| [23] |
SAATY T L. The Analytic Hierarchy Process 2nd ed[M]. New York: McGraw-Hill, 1988.
|
| [24] |
GB/T 50218-2014, 工程岩体分级标准[S]. GB/T 50218-2014, Standard for Engineering Classification of Rock Mass[S]. |
| [25] |
JTG 3370.1-2018, 公路隧道设计规范[S]. JTG 3370.1-2018, Specifications for Design of Highway Tunnels[S]. |
| [26] |
TB-1003-2016, 铁路隧道设计规范[S]. TB-1003-2016, Code for Design of Railway Tunnel[S]. |
| [27] |
Q/CR 9512-2019, 铁路挤压性围岩隧道技术规范[S]. Q/CR 9512-2019, Code for Tunneling in Squeezing Rocks[S]. |
| [28] |
铁道第一勘察设计院.乌鞘岭隧道岭脊地段复杂应力条件下的变形控制技术研究阶段成果总报告[R].兰州: 铁道第一勘察设计院, 2004. No.1 Survey and Design Institute of Railway. General Report on Research Result of Deformation Control Technology under Complex Stress Conditions in Ridge Section of Wushaoling Tunnel[R]. Lanzhou: No.1 Survey and Design Institute of Railway, 2004. |
 2020, Vol. 37
2020, Vol. 37

