扩展功能
文章信息
- 柏雪松, 李俊峰, 祁小博, 陈红旗, 刘红岩
- BAI Xue-song, LI Jun-feng, QI Xiao-bo, CHEN Hong-qi, LIU Hong-yan
- 落石冲击棚洞结构的动力响应研究
- Study on Dynamic Response of Shed-tunnel Structure under Rockfall Impact
- 公路交通科技, 2020, 37(8): 73-80
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(8): 73-80
- 10.3969/j.issn.1002-0268.2020.08.010
-
文章历史
- 收稿日期: 2019-06-19
2. 中国地质环境监测院, 北京 100081;
3. 中国地质大学(北京) 工程技术学院, 北京 100083
2. China Institute for Geo-environmental Monitoring, Beijing 100081, China;
3. School of Engineering & Technology, China University of Geosciences(Beijing), Beijing 100083, China
崩塌落石是我国山区最为严重的自然地质灾害之一[1-2]。近年来,由于我国西部山区矿产资源的大力开发,基础设施建设不断增加,落石灾害事件的发生频率也随之增加,对山区的交通安全造成了严重影响。国内外的学者们已对落石进行了一定研究,并取得了诸多成果,主要集中在落石的运动特性[3]、落石的冲击力计算[4]、落石灾害的防护结构[5]及对落石灾害的风险评估[6]。
国内外诸多学者对于落石冲击力进行了研究, 如日本道路协会[7]、杨其新等[8]、Labiouse等[9]、Pichle等[10]进行了多次落石试验,并根据试验结果提出了计算落石冲击力的经验公式。国内的冲击力计算方法所得结果为落石冲击力的平均值,结果偏小。日本道路协会和瑞士计算方法结果较为接近实际,但这两种方法未考虑缓冲垫层厚度及冲击角度对落石冲击力的影响。Plassiard等[11]通过离散单元法模拟落石冲击防护堤的过程。叶四桥等[12]指出目前落石冲击力计算方法存在一定差异,并且相对实际工程中的落石最大冲击力偏小。Zhang等[13]结合法向和切向的恢复系数,提出了落石冲击的计算公式。王林峰等[14]通过室内试验研究了6种不同因素对落石冲击力的影响规律。
棚洞结构在落石灾害防治中起到了重要作用,因此,国内外诸多学者对棚洞结构在落石冲击下的动力响应进行了研究。Calvetti等[15-16]通过对落石不同下落高度冲击棚洞结构的试验,分析了冲击力在垫层中的扩散机制及棚洞结构的动力响应。王静峰等[17]应用ANSYS/LS-DYNA有限元软件并结合模型试验对EPS复合垫层的抗冲击性能进行了研究。Ouyang等[18]提出了一种新型的棚洞防护系统,采用土工格栅加筋土和聚苯乙烯泡沫(EPS)作为棚洞防护材料。
从研究现状来看,数值模拟法较其他方法具有计算快捷、可方便模拟多种工况等优点。因此,近些年来,国内外许多学者应用数值软件对落石冲击问题进行了研究,但少有学者综合考虑冲击力时程曲线、冲击深度时程曲线和Mises等效动应力时程曲线等对落石冲击棚洞结构的动力响应特征进行系统的分析。为此,本研究应用动力有限元软件ANSYS/LS-DYNA,通过分析上述时程曲线,探究落石质量、下落高度、冲击角度及形状这4个因素对冲击作用下棚洞结构动力响应的影响。
1 模型建立 1.1 有限元模型王广坤[19]所开展的落石模型试验与本研究课题十分相符,故利用其试验结果对本研究数值模拟的合理性进行验证。
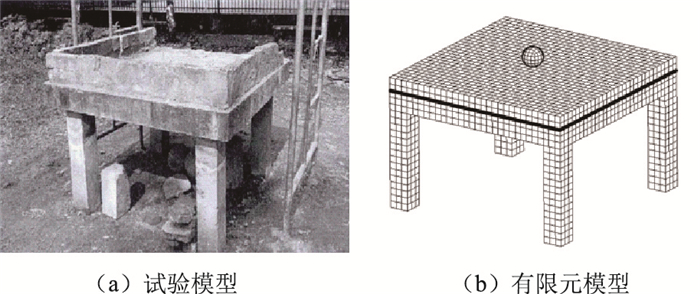
王广坤所做试验模型如图 1(a)所示,由试验平台、砂垫层、落石3部分组成。试验平台由顶板和4个角柱组成,顶板尺寸为1.5 m×1.5 m×0.15 m,角柱尺寸为0.15 m×0.15 m×0.75 m,砂垫层厚度为0.1 m。王广坤在模型试验中设置5种不同落石质量,为简化落石冲击过程并便于对比分析,通过改变球体落石直径来对落石质量进行控制,工况1~5中保持其他条件不变,仅改变落石质量分别为3.56,8.88,11.57,16.6,21.84 kg,对应落石直径分别为0.15,0.20,0.22,0.25,0.27 m。试验平台和落石均为C30混凝土浇注而成。为了与其试验结果进行对比分析,本研究所建的有限元模型、材料参数及工况条件与该试验保持一致。
|
| 图 1 试验模型及有限元模型 Fig. 1 Test model and FE model |
| |
建立相应的有限元模型见图 1(b),垫层四周设置位移约束、角柱底部设置全约束。
1.2 材料参数由于落石刚度远远大于缓冲垫层土体刚度,因此将落石视为刚体模型,在保证计算结果合理性的同时,还可以大大减少计算时间。缓冲垫层土体采用Drucker-Prager模型[19-21],其参数见表 1。
| 材料 | 弹性模量/MPa | 泊松比 | 内摩擦角/(°) | 黏聚力/kPa |
| 落石 | 30 000 | 0.3 | — | — |
| 土垫层 | 40 | 0.37 | 25 | 30 |
| 混凝土单向拉伸屈服极限为1.43 MPa。 | ||||
试验平台混凝土采用Holmquist-Johnson-Cook(HJC)模型[22-23],主要适用于大应变、大应变率和高静水压力的情况,具体参数见表 2。其中,C30混凝土单向拉伸屈服极限为1.43 MPa。
| 密度/(kg·m-3) | 剪切模量/GPa | 规范化黏聚强度 | 规范化压力硬化系数 | 应变速率系数 | 压力硬化指数 | 单轴抗压强度/MPa | |
| 2 400 | 1.15 | 0.75 | 1.65 | 0.007 | 0.61 | 48 | |
| 抗拉强度/MPa | 参考应变率 | 断裂最小塑性应变 | 规范化最大强度 | 弹性极限压力/MPa | 弹性极限体应变 | 压实压力/GPa | |
| 4 | 1 | 0.01 | 7 | 16 | 0.001 | 0.8 | |
| 压实体应变 | 损伤变量参数 | 压力常数 | 失效类型 | ||||
| D1 | D2 | K1/GPa | K2/GPa | K3/GPa | |||
| 0.1 | 0.04 | 1 | 85 | -171 | 208 | 0.1 | |
2 计算结果分析
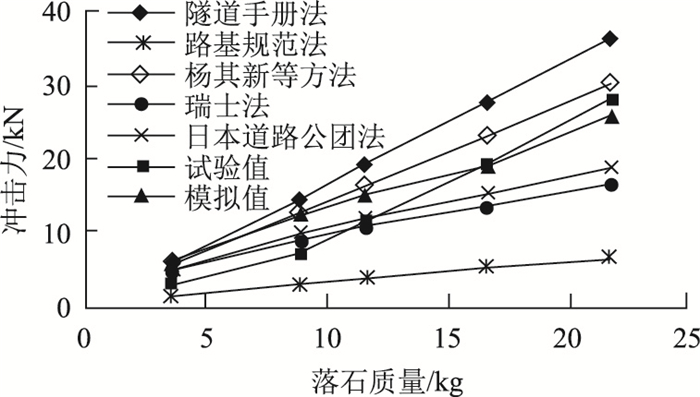
将本研究最大冲击力的计算结果与试验值、代表性计算方法的结果进行对比,以验证模拟结果的准确性。对比情况如图 2所示。可以看出:(1)落石冲击力随落石质量的增加呈近似线性增长。(2)隧道手册法和杨其新等方法计算的落石冲击力最大,原因是这2种方法受垫层厚度影响较大,而试验中的垫层厚度较小,仅为0.1 m。(3)路基规范法所得到的冲击力是所有方法中最小的。(4)当落石质量为3.56,8.88,11.57 kg时,计算的模拟值与杨其新算法计算结果基本相等;当落石质量为16.65,21.84 kg时,模拟值与试验值十分接近。(5)各个计算方法所得落石最大冲击力相差可达5~6倍之多,主要原因是,国内外学者们根据不同的理论基础,结合各自试验数据结果,同时综合考虑不同影响因素,从而推导出不同的冲击力计算公式,使冲击力的计算结果产生差异,并且各个方法对落石质量因素的敏感性也有所差别。
|
| 图 2 落石最大冲击力对比 Fig. 2 Comparison of rockfall maximum impact force |
| |
综上所述,通过与试验数据及代表性冲击力计算方法对比分析,可以验证本研究数值模型的合理性和计算结果的准确性。
3 落石冲击棚洞结构的动力响应为了进一步系统地分析讨论落石质量、下落高度等因素对冲击作用的影响规律,在模型形状保持不变的基础上将其体积进行扩大,落石直径为0.8 m、质量为670.2 kg,垫层厚度为1 m,4个角柱尺寸为0.5 m×0.5 m×5 m,混凝土板尺寸为5 m×5 m×0.5 m。垫层上表面的中心处为落石冲击深度监测点,混凝土板下表面的中心处为棚顶Mises等效动应力监测点。
3.1 不同落石质量本节中讨论不同落石质量对冲击作用的影响规律。为了方便建模计算和更符合实际情况,通过改变落石直径来对落石质量进行控制。落石直径设置为0.4,0.6,0.8,1.0 m,对应质量分别为83.8,282.7,670.2,1 309.0 kg。
3.1.1 冲击力对比分析不同落石质量对冲击力时程曲线的影响情况如图 3所示。该时程曲线具有相似的形状,呈脉冲状变化。冲击力在落石发生碰撞瞬间急剧增大达到最大值,随后快速减小,在产生一次振荡后减小为0。随着落石质量的增加,最大冲击力从111.19 kN增至638.52 kN,冲击时间从0.021 s增至0.054 s。分析表明,当落石质量在一定范围内变化时,落石冲击力、冲击过程时长与质量呈正相关。

|
| 图 3 冲击力时程曲线 Fig. 3 Time-history curves of impact force |
| |
3.1.2 冲击深度对比分析
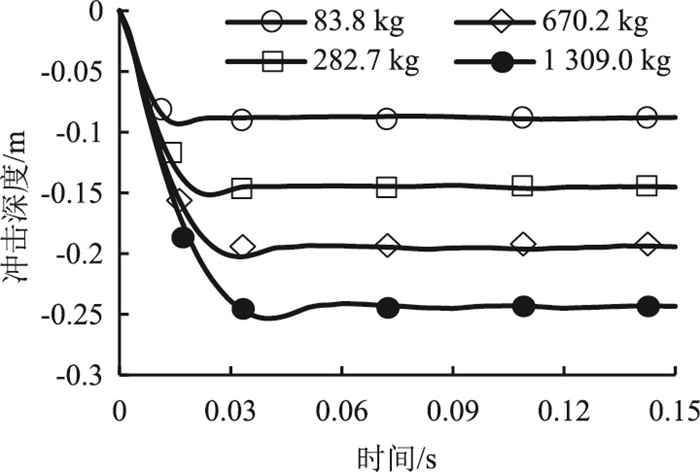
不同落石质量冲击深度时程曲线对比情况如图 4所示。该时程曲线具有相似的形状,冲击深度在落石发生碰撞的瞬间迅速增大达到峰值,其后垫层发生回弹变形并稳定不再变化。垫层土体为弹塑性材料,在冲击力的作用下,冲击深度达到最大值后会有微小恢复变形,但由于土体发生了一定的塑性变形,从而无法恢复至初始状态,也因此具有良好的耗能作用,起到保护棚洞的效果。当落石质量从83.8 kg增至1 309.0 kg时,最大冲击深度随之增加,从-0.093 m增至-0.253 m。分析表明,冲击深度与落石质量呈正相关。
|
| 图 4 冲击深度时程曲线 Fig. 4 Time-history curves of penetration depth |
| |
3.1.3 Mises等效动应力对比分析
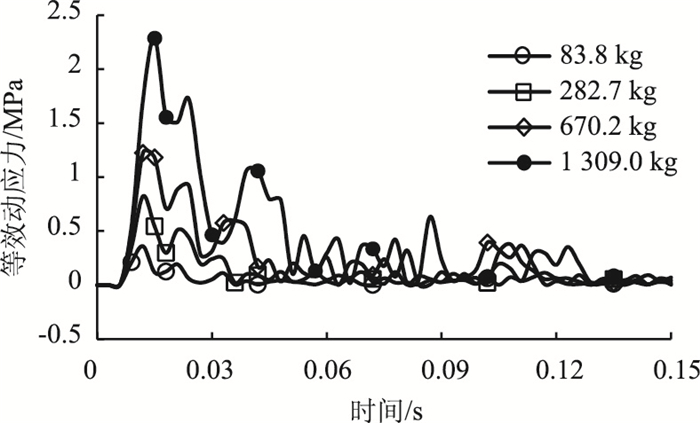
不同落石质量对Mises等效动应力的影响如图 5所示。该时程曲线变化趋势大致相同。曲线在起始阶段为0,是因为冲击力经垫层传递至棚顶需要一定时间,Mises等效动应力在极短时间内达到最大值,随后曲线呈波动式减小并趋于稳定。随着落石质量的增加,Mises等效动应力逐渐增大,当落石质量为1 039.0 kg时,Mises等效动应力最大为2.287 MPa,大于1.43 MPa(C30混凝土单向拉伸的屈服极限),此时应对棚洞结构进行一定的安全防护。分析表明,棚顶Mises等效动应力与落石质量呈正相关,且随着落石质量的增加,等效动应力时程曲线的振荡幅度更明显。
|
| 图 5 Mises等效动应力时程曲线 Fig. 5 Time-history curves of Mises equivalent dynamic stress |
| |
3.2 不同下落高度
为讨论不同下落高度对冲击作用的影响,下落高度设置为5,10,15,20 m。
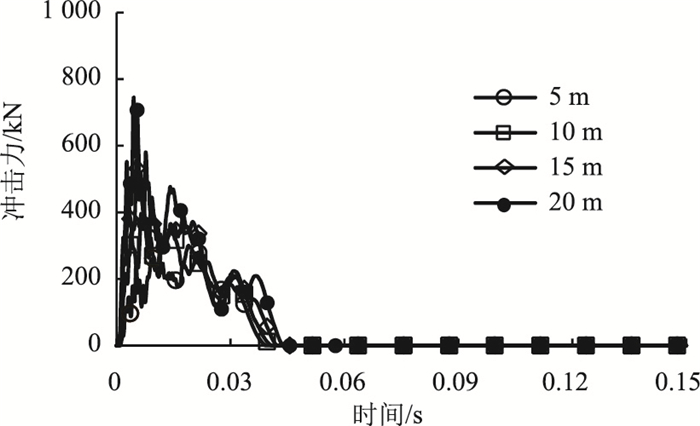
3.2.1 冲击力对比分析不同下落高度时的冲击力时程曲线对比情况如图 6所示。该时程曲线具有相似的形状,呈脉冲状变化。冲击力在落石发生碰撞瞬间急剧增大达到最大值,随后迅速减小为0。下落高度从5 m增至20 m时,落石最大冲击力从279.16 kN增至744.95 kN,冲击时间略有增加,从0.040 s增至0.044 s。分析表明,落石冲击力与下落高度呈正相关,但落石下落高度对冲击时间的影响不大。
|
| 图 6 冲击力时程曲线 Fig. 6 Time-history curves of impact force |
| |
3.2.2 冲击深度对比分析
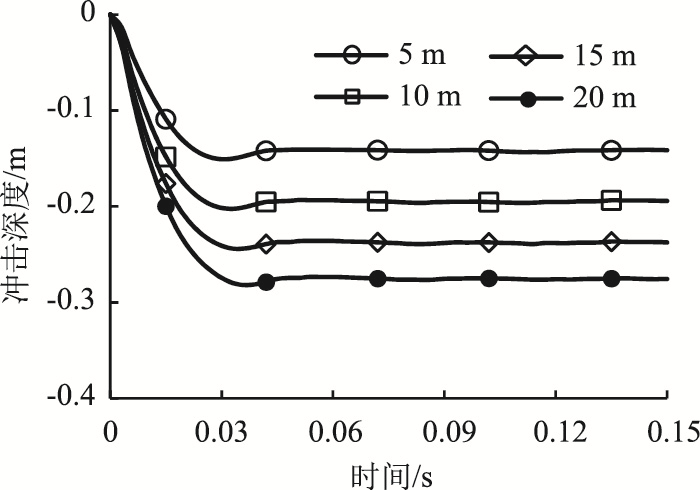
不同下落高度时的冲击深度时程曲线对比情况如图 7所示。该时程曲线具有相似的形状,冲击深度在落石发生碰撞的瞬间迅速增大达到最大,其后垫层发生回弹变形并稳定不再变化。垫层土体为弹塑性材料,在落石冲击力的作用下,冲击深度达到最大之后会有微小恢复变形,但由于土体发生了一定的塑性变形,从而无法恢复至初始状态,也因此具有良好的耗能作用,起到保护棚洞的效果。当下落高度从5 m增至20 m时,最大冲击深度从-0.151 m增至-0.282 m。分析表明,冲击深度与下落高度呈正相关。
|
| 图 7 冲击深度时程曲线 Fig. 7 Time-history curves of penetration depth |
| |
3.2.3 Mises等效动应力对比分析
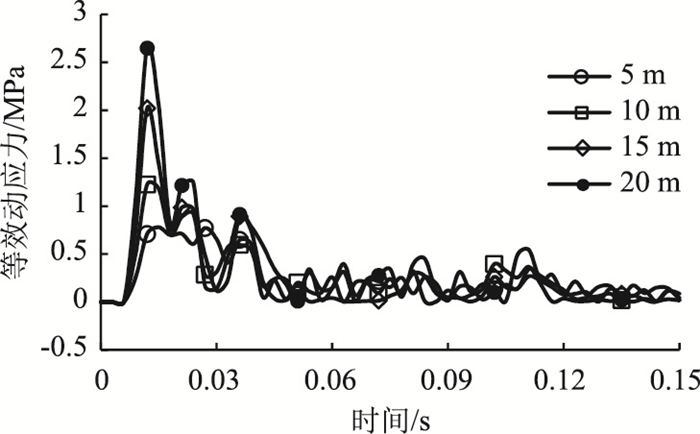
不同下落高度对Mises等效动应力的影响如图 8所示。该时程曲线变化趋势大致相同。曲线在起始阶段为0,是因为冲击力经垫层传递至棚顶需要一定时间,Mises等效动应力在极短时间内达到最大值,随后曲线呈波动式减小,逐渐趋于稳定。随着下落高度的增加,棚顶Mises等效动应力从0.779 MPa增至2.648 MPa,下落高度为15 m和20 m时的等效动应力大于1.43 MPa(C30混凝土单向拉伸的屈服极限),此时应对棚洞结构进行一定的安全防护。分析表明,棚顶Mises等效动应力与下落高度呈正相关,且随着下落高度的增加,曲线的振荡幅度更明显。
|
| 图 8 Mises等效动应力时程曲线 Fig. 8 Time-history curves of Mises equivalent dynamic stress |
| |
3.3 不同冲击角度
为讨论不同冲击角度对冲击作用的影响,冲击角度设置为30°,45°,60°,90°(落石初速度方向与垫层平面的夹角)。
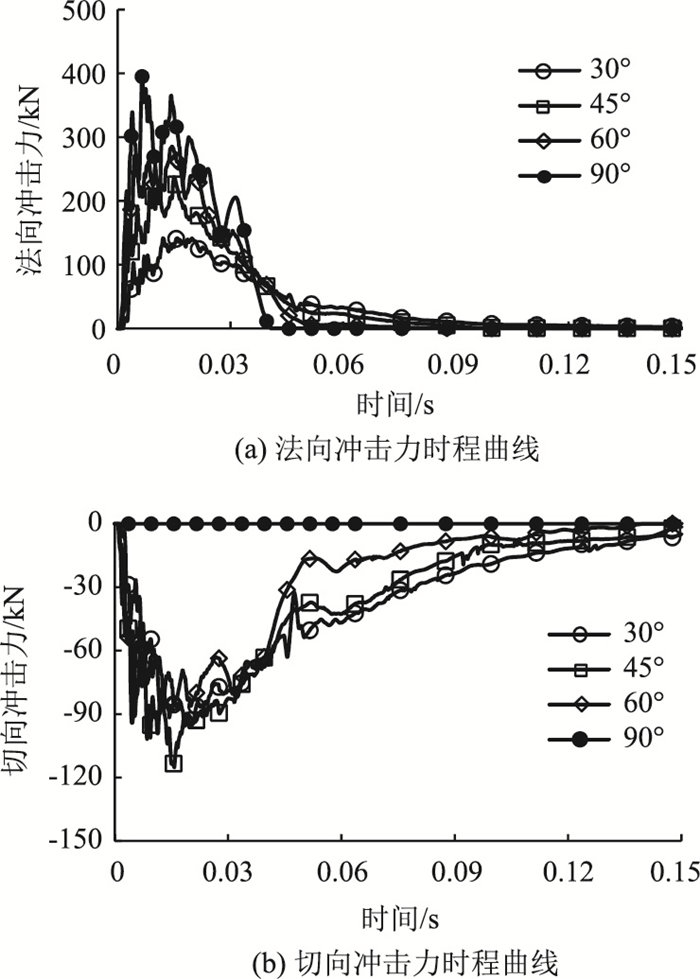
3.3.1 冲击力对比分析不同冲击角度对法向冲击力时程曲线的影响如图 9(a)所示。该时程曲线具有相似的形状,呈脉冲状变化。法向冲击力在落石发生碰撞瞬间急剧增大达到最大值,随后快速减小为0。当冲击角度从30°增至90°时,法向冲击力从141.80 kN增至395.12 kN。冲击角度为90°时,冲击时间最短为0.041 s,并且随着冲击角度的减小,冲击时间不断增加。分析表明,法向冲击力与冲击角度呈正相关,垂直冲击时的冲击持续时间最短。
|
| 图 9 冲击力时程曲线 Fig. 9 Time-history curves of impact force |
| |
不同冲击角度对切向冲击力时程曲线的影响如图 9(b)所示。该时程曲线具有相似的形状,切向冲击力在落石发生碰撞瞬间急剧增大达到峰值(正负表示方向),随后快速减小。当冲击角度为45°时,切向冲击力最大为-115.28 kN;当冲击角度为30°和60°时,切向冲击力分别为-95.79,-94.10 kN,二者大小基本相等。分析表明,随着冲击角度的增加,切向冲击力先增大后减小,当冲击角度为45°时,切向冲击力最大。
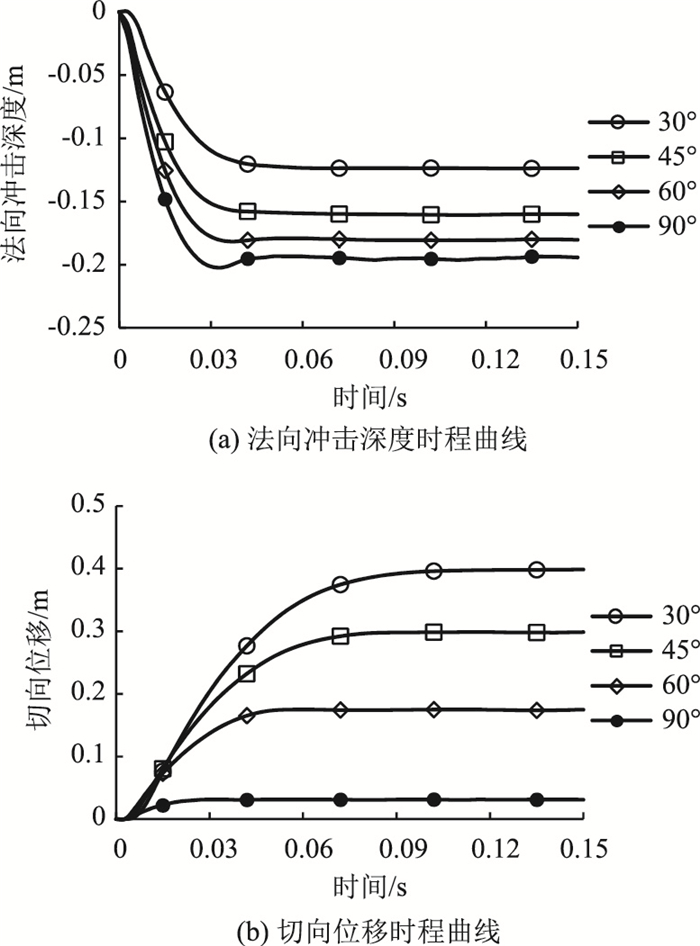
3.3.2 冲击深度对比分析不同冲击角度对法向冲击深度时程曲线的影响如图 10(a)所示。该时程曲线具有相似的形状,法向冲击深度在落石发生碰撞的瞬间迅速增大达到最大,其后垫层发生回弹变形并稳定不再变化。垫层土体为弹塑性材料,在落石冲击力的作用下,冲击深度达到最大之后会有微小恢复变形,但由于土体发生了一定的塑性变形,从而无法恢复至初始状态,也因此具有良好的耗能作用,起到保护棚洞的效果。当冲击角度从30°增至90°时,法向冲击深度从-0.124 m增至-0.202 m。分析表明,法向冲击深度与冲击角度呈正相关。
|
| 图 10 冲击深度时程曲线 Fig. 10 Time-history curves of penetration depth |
| |
不同冲击角度对切向位移的影响情况如图 10(b)所示。当冲击角度从30°增至90°时,所产生的最大切向位移由0.399 m减至0.031 m。冲击角度为90°时也产生微小切向位移,主要原因是:在冲击垫层土体的过程中,落石会将冲击点附近的土体向四周挤压。分析表明,土体的切向位移与冲击角度呈负相关。
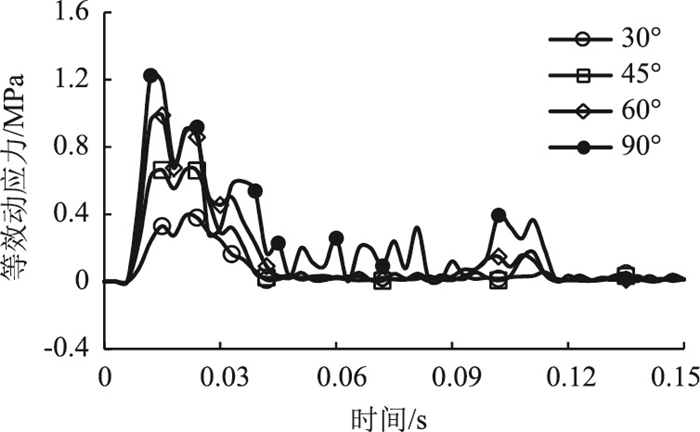
3.3.3 Mises等效动应力对比分析冲击角度对Mises等效动应力的影响如图 11所示。该时程曲线变化趋势大致相同。曲线在起始阶段为0,是因为冲击力经垫层传递至棚顶需要一定时间,Mises等效动应力在极短时间内达到最大值,随后曲线呈波动式减小,逐渐趋于稳定。当冲击角度从30°增至90°时,棚顶Mises等效动应力从0.392 MPa增至1.225 MPa,均小于1.43 MPa(C30混凝土单向拉伸的屈服极限),棚洞较安全。分析表明,棚顶Mises等效动应力与冲击角度呈正相关,且随着冲击角度的增加,等效动应力时程曲线的振荡幅度更明显。
|
| 图 11 Mises等效动应力时程曲线 Fig. 11 Time-history curves of Mises equivalent dynamic stress |
| |
3.4 不同落石形状
下面讨论落石质量相同的条件下,不同落石形状对冲击作用的影响。设落石形状分别为球体、立方体、长方体。球体直径为0.8 m,立方体边长为0.64 m,长方体为1.02 m×0.52 m×0.52 m。对冲击的接触面做如下假定:选取立方体0.64 m×0.64 m的面、长方体1.02 m×0.52 m的面。
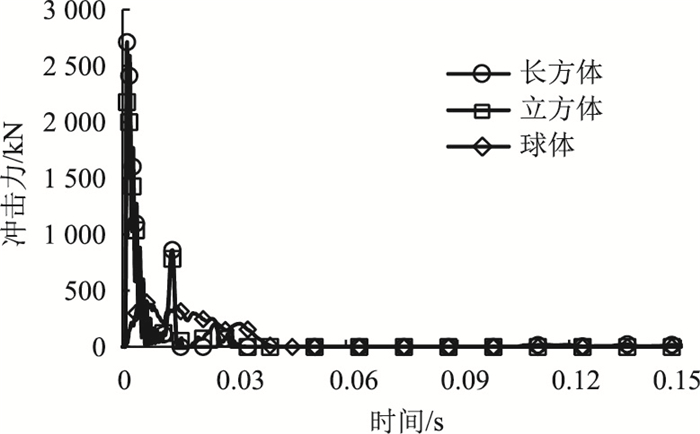
3.4.1 冲击力对比分析不同落石形状对冲击力时程曲线的影响如图 12所示。该时程曲线变化趋势大致相同,冲击力大、冲击时间短。球体落石的冲击力较小,冲击时间较长。长方体落石的最大冲击力为2 710.99 kN,球体落石的最大冲击力为395.12 kN,二者相差6.8倍;长方体落石的冲击时间为0.015 s,为球体落石冲击时间的1/3左右。球体落石的接触面积从0逐渐增加,相较而言,长方体落石和立方体落石要大得多(其中长方体落石最大)。因此,冲击碰撞的瞬间,长方体落石和立方体落石的冲击力时程曲线变化更为剧烈、冲击时间也较短。分析表明,不同落石形状对最大冲击力及冲击时间有较大的影响。
|
| 图 12 冲击力时程曲线 Fig. 12 Time-history curves of impact force |
| |
3.4.2 冲击深度对比分析
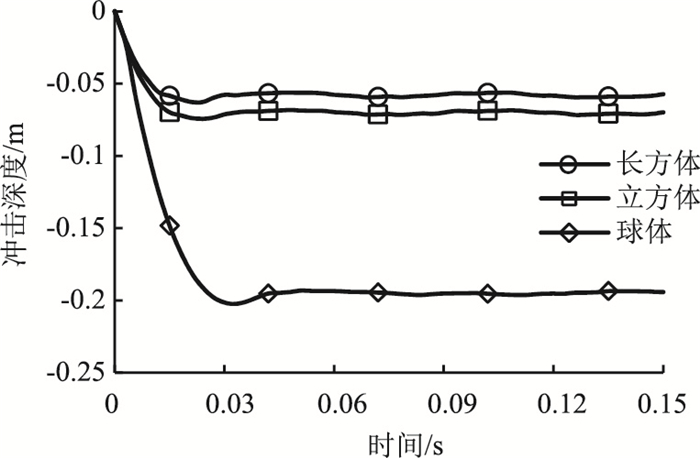
不同落石形状对冲击深度时程曲线的影响如图 13所示。相对于球体落石,长方体落石和立方体落石所产生的冲击深度小得多,仅为球体落石的1/3左右,垫层土体回弹现象不明显,同时冲击持续时间也相对较短。主要原因是长方体落石和立方体落石的初始接触面积远大于球体的初始接触面积。分析表明,落石形状对冲击深度有较大的影响。
|
| 图 13 冲击深度时程曲线 Fig. 13 Time-history curves of penetration depth |
| |
3.4.3 Mises等效动应力对比分析
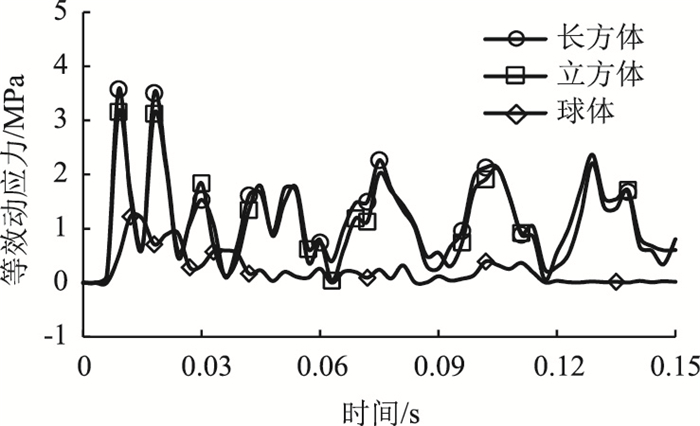
不同落石形状对Mises等效动应力的影响如图 14所示。长方体落石和立方体落石的棚顶Mises等效动应力时程曲线形状相似,在落石碰撞后Mises等效动应力急剧增大到峰值,随后呈振荡式减小。与这两种落石形状相比,球体落石的Mises等效动应力相对较小,且变化相对缓慢。长方体落石和立方体落石的最大等效动应力分别为3.574,3.159 MPa,均大于1.43 MPa(C30混凝土单向拉伸的屈服极限),此时应对棚洞结构进行一定的安全防护。由于球体落石所产生的冲击力相对长方体落石和立方体落石小、冲击时间也相对较长,因此棚顶Mises等效动应力比较小。
|
| 图 14 Mises等效动应力时程曲线 Fig. 14 Time-history curves of Mises equivalent dynamic stress |
| |
4 结论
(1) 落石冲击力、冲击持续时间、冲击深度和棚顶Mises等效动应力与落石质量呈正相关。
(2) 落石冲击力、冲击深度及棚顶Mises等效动应力与落石下落高度呈正相关;冲击持续时间略微增加,但影响比较小。
(3) 不同冲击角度情况下,在法向方向,落石冲击力和冲击深度与冲击角度呈正相关。在切向方向,切向位移与冲击角度呈负相关。切向冲击力随冲击角度的增加先增大后减小,当冲击角度为45°时,切向冲击力最大。
(4) 长方体落石和立方体落石所产生的冲击力是球体的5~7倍,棚顶Mises等效动应力是球体的2~3倍,而冲击深度却仅为球体的1/3左右。
| [1] |
陈洪凯, 唐红梅, 叶四桥. 危岩防治原理[M]. 北京: 地震出版社, 2006. CHEN Hong-kai, TANG Hong-mei, YE Si-qiao. Prevention Principle of Perilous Rock[M]. Beijing: Seismological Press, 2006. |
| [2] |
DORREN L K A, SEIJMONSBERGEN A C. Comparison of Three GIS-based Models for Predicting Rockfall Runout Zones at a Regional Scale[J]. Geomorphology, 2003, 56(1): 49-64. |
| [3] |
AZZONI A, LA BARBERA G L, ZANINETTI A. Analysis and Prediction of Rockfalls Using a Mathematical Model[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1995, 32(7): 709-724. |
| [4] |
LABIOUSE V, HEIDENREICH B. Half-scale Experimental Study of Rockfall Impacts on Sandy Slopes[J]. Natural Hazards and Earth System Sciences, 2009, 9(6): 1981-1993. |
| [5] |
陈江, 夏雄. 金温铁路危石治理中柔性防护技术应用研究[J]. 岩石力学与工程学报, 2006, 25(2): 312-317. CHEN Jiang, XIA Xiong. Research on Application of Flexible Protection Technique to Jinhua-Wenzhou Railway Rock Fall Treatment[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(2): 312-317. |
| [6] |
GUPTA N K, IQBAL M A, SEKHON G S. Effect of Projectile Nose Shape, Impact Velocity and Target Thickness on the Deformation Behavior of Layered Plates[J]. International Journal of Impact Engineering, 2008, 35(1): 37-60. |
| [7] |
KAWAHARA S, MURO T. Effects of Dry Density and Thickness of Sandy Soil on Impact Response due to Rockfall[J]. Journal of Terramechanics, 2006(43): 329-340. |
| [8] |
杨其新, 关宝树. 落石冲击力计算方法的试验研究[J]. 铁道学报, 1996, 18(1): 101-106. YANG Qi-xin, GUAN Bao-shu. Test and Research on Calculating Method of Falling Stone Impulsive Force[J]. Journal of the China Railway Society, 1996, 18(1): 101-106. |
| [9] |
LABIOUSE V, DESCOEUDRES F, MONTANI S. Experimental Study of Rock Sheds Impacted by Rock Blocks[J]. Structural Engineering International, 1996, 6(3): 171-176. |
| [10] |
PICHLER B, HELLMICH C, MANG H A. Impact of Rocks onto Gravel Design and Evaluation of Experiments[J]. International Journal of Impact Engineering, 2005, 31(5): 559-578. |
| [11] |
PLASSIARD J, DONZE F. Rockfall Impact Parameters on Embankments:A Discrete Element Method Analysis[J]. Structural Engineering International, 2009, 19(3): 333-341. |
| [12] |
叶四桥, 陈洪凯, 唐红梅. 落石冲击力计算方法的比较研究[J]. 水文地质工程地质, 2010, 37(2): 59-63. YE Si-qiao, CHEN Hong-kai, TANG Hong-mei. Comparative Research on Impact Force Calculation Methods for Rockfalls[J]. Hydrogeology & Engineering Geology, 2010, 37(2): 59-63. |
| [13] |
ZHANG G C, TANG H M, XIANG X, et al. Theoretical Study of Rockfall Impacts Based on Logistic Curves[J]. International Journal of Rock Mechanics and Mining Sciences, 2015, 78: 133-143. |
| [14] |
王林峰, 唐红梅, 唐芬, 等. 基于正交设计的不同垫层落石冲击力试验研究[J]. 中国铁道科学, 2017, 38(5): 16-21. WANG Lin-feng, TANG Hong-mei, TANG Fen, et al. Experimental Study of Rockfall Impact Force with Different Cushion Based on Orthogonal Design[J]. China Railway Science, 2017, 38(5): 16-21. |
| [15] |
CALVETTI F. Rockfall Shelters Covered by Granular Layers[J]. European Journal of Environmental and Civil Engineering, 2011, 15(S1): 73-100. |
| [16] |
CALVETTI F, DI PRISCO C. Rockfall Impacts on Sheltering Tunnels:Real-scale Experiments[J]. Geotechnique, 2012, 62(10): 865-876. |
| [17] |
王静峰, 赵鹏, 袁松, 等. 复合垫层钢棚洞抵抗落石冲击性能研究[J]. 土木工程学报, 2018, 51(增2): 7-13. WANG Jing-feng, ZHAO Peng, YUAN Song, et al. Numerical Study on Impact Resistance of Steel Shed Gallery with Composite Cushion[J]. China Civil Engineering Journal, 2018, 51(S2): 7-13. |
| [18] |
OUYANG C J, LIU Y, WANG D P, et al. Dynamic Analysis of Rockfall Impacts on Geogrid Reinforced Soil and EPS Absorption Cushions[J]. KSCE Journal of Civil Engineering, 2018, 23: 37-45. |
| [19] |
王广坤.抗落石冲击棚洞结构研究[D].重庆: 重庆交通大学, 2014. WANG Guang-kun. Research on Shed Structure for Rockfall Impact[D]. Chongqing: Chongqing Jiaotong University, 2014. http://www.cqvip.com/QK/97829A/201505/664796923.html |
| [20] |
王爽, 周晓军, 姜波, 等. 落石冲击下隧道大跨度棚洞的动力响应数值分析与抗冲击研究[J]. 爆炸与冲击, 2016, 36(4): 548-555. WANG Shuang, ZHOU Xiao-jun, JIANG Bo, et al. Numerical Analysis of Dynamic Response and Impact Resistance of a Large-span Rock Shed in a Tunnel under Rockfall Impact[J]. Explosion and Shock Waves, 2016, 36(4): 548-555. |
| [21] |
何思明, 沈均, 吴永. 滚石冲击荷载下棚洞结构动力响应[J]. 岩土力学, 2011, 32(3): 781-788. HE Si-ming, SHEN Jun, WU Yong. Rock Shed Dynamic Response to Impact of Rock-fall[J]. Rock and Soil Mechanics, 2011, 32(3): 781-788. |
| [22] |
HOLMQUIST T J, JOHSON G R, COOK W H. A Computational Constitutive Model for Concrete Subjected to Large Strains, High Stain Rates and High Pressures[C]//The 14th International Symposium on Ballistics. Quebec City: [s. n.], 1993: 591-600.
|
| [23] |
陈驰, 刘成清, 陈琳雅, 等. 落石作用于钢筋混凝土棚洞的冲击力研究[J]. 公路交通科技, 2015, 32(1): 102-109. CHEN Chi, LIU Cheng-qing, CHEN Lin-ya, et al. Study on Impact Force of Rock-fall onto Rock Shed Tunnel[J]. Journal of Highway and Transportation Research and Development, 2015, 32(1): 102-109. |
 2020, Vol. 37
2020, Vol. 37
