扩展功能
文章信息
- 赵品, 荣学亮, 叶见曙
- ZHAO Pin, RONG Xue-liang, YE Jian-shu
- 承托设置对波形钢腹板箱梁桥面板横向内力的影响
- Influence of Support Setting on Transverse Internal Force in Deck of Box Girder Bridge with Corrugated Steel Webs
- 公路交通科技, 2020, 37(8): 41-47
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(8): 41-47
- 10.3969/j.issn.1002-0268.2020.08.006
-
文章历史
- 收稿日期: 2015-12-03
2. 东南大学 交通学院, 江苏 南京 210096
2. School of Transportation, Southeast University, Nanjing Jiangsu 210096, China
当组合梁的混凝土翼板采用普通钢筋混凝土板时,为了提高组合梁的正截面抗弯承载能力及节约钢材,可设置混凝土承托[1]。承托的设置对箱梁的结构性能是有一定影响的,不仅可以提高截面的抗弯、扭刚度,减少扭转剪应力和畸变应力;同时可使桥面板支点刚度加大,力线过渡比较均匀,减小次内力[2]。
承托对箱梁受力的影响已有一定研究:我国公路桥规中提到的与梁肋整体连接的板,计算弯矩时其计算跨径可取为两肋间的净距加板厚,但不大于两肋中心之间的距离。即在桥规的规定中已经考虑了承托构造对桥面板内力计算的影响,但是仅为简便计算规定。文献[3-4]针对考虑隅角点承托刚性影响的薄壁直线/曲线箱梁进行了空间计算分析,将箱梁板件视为板梁,隅角处承托视为梁元,提出了考虑承托刚性影响薄壁直线/曲线箱梁空间计算的板梁有限单元法。但是仅采用了电算方法,尚未采用试验方法进行验证。
对于波形钢腹板箱梁桥面板而言,从自身构造上来讲波形钢腹板与承托这两类因素均会对桥面板横向受力产生一定影响[5-6]。波形钢腹板箱梁的腹板受力特性不同于混凝土腹板,基于上述因素,承托的设置将会对桥面板的横向内力产生怎样的影响。本研究将在此基础上以室内试验、有限元分析结合理论推导来探讨混凝土桥面板承托的设置对桥面板受力的影响。
1 波形钢腹板箱梁模型试验分别制作了2片单箱双室波形钢腹板试验梁,分为桥面板不加承托和加承托。将两片梁的相关试验数据进行对比,研究承托设置对波形钢腹板箱梁桥面板横向内力的影响。
1.1 试验梁试验梁总长3 500 mm,计算跨径3 300 mm,不加承托和加承托的试验梁跨中断面见图 1(a)~(b)。顶、底板宽分别为1 800,1 400 mm,顶、底板厚度分别为80,70 mm,其中80 mm为顶板不考虑承托的厚度。

|
| 图 1 横断面尺寸及承托大样图(单位:mm) Fig. 1 Dimensions of cross-section and detail drawing of support (unit:mm) |
| |
波形钢腹板采用Q235C钢板,厚度为2.0 mm,折叠角度37.0°,波高24 mm,波长144 mm。钢腹板与混凝土顶板、底板的连接采用在钢腹板上下端插入穿透钢筋与混凝土顶板、底板的构造钢筋绑扎在一起来构成整体。
承托的尺寸如图 1(c)~(d)所示,无论边腹板还是中腹板处的承托高度均为40 mm。梁高为450 mm,与不加承托的试验梁高相等。承托的截面尺寸有以下规定:混凝土承托的高度不应大于混凝土翼板厚度的1.5倍;承托外形轮廓应在由连接件根部起的45°线界限以外[1]。试验梁的承托尺寸符合要求。
试验梁的加工在实验室完成,按照设计的图纸,试验梁的制作过程如图 2所示。

|
| 图 2 试验梁制作流程 Fig. 2 Production process of test girder |
| |
(1) 首先搭设底板的模板,在底板模板内布置钢筋。(2)根据钢腹板的位置将其定位,并绑扎端横隔板处的钢筋。(3)浇注底板混凝土。(4)待底板混凝土干燥之后搭设顶板、横隔板处的模板,并绑扎顶板钢筋和抗剪连接件处钢筋。(5)浇注顶板和横隔板处混凝土;由于翼缘较宽,混凝土用量较大,为避免翼缘板的模板损坏,在翼缘底部及端部布设相应木板做支撑。
待混凝土浇注完毕后进行了养护。由于时值冬季,温度较低,在试验梁的顶板上覆盖薄毯将有助于提高混凝土养护的温度。
根据试验目的,需在混凝土顶、底板钢筋及钢腹板上粘贴相应的应变片,所以在试验梁的施工过程中应根据施工进程准时布设。
为验证承托的设置对于混凝土桥面板横向内力及其有效分布宽度的影响,横向加载工况的分类为中腹板处加载(工况Ⅰ)、A-A截面加载即边腹板、中腹板间的桥面板跨中位置加载(工况Ⅱ)、边腹板处加载(工况Ⅲ)3种工况,加载的最大吨位分别为40,25,20 kN,各分级加载值均为5 kN。加载工况见图 1(a)。
为测得箱梁的横向内力分布曲线,分别在箱梁边腹板、中腹板间的桥面板横向跨中位置、悬臂长度的1/2位置、悬臂翼缘端部及腹板与顶板相交部位下由跨中向支座沿纵向每隔20 cm布设应变片,见图 3。在试验梁的支点和跨中布置有竖向位移计。采用TDS静态应变读数仪读取应变,东华静态应变读数仪读取位移[7]。

|
| 图 3 应变片布置(单位:mm) Fig. 3 Layout of strain gauges (unit:mm) |
| |
1.2 承托对于波形钢腹板箱梁桥面板受力的影响
本节就加承托、不加承托的相应结果进行比较,以此检测承托设置对桥面板横向内力的影响。以下将加承托与不加承托的试验结果进行比较,试验结果分为箱梁挠度和桥面板横向内力两项。
(1) 承托对箱梁挠度的影响
由图 4可知3种工况下挠度值与荷载值呈线性比例关系,挠度值随着荷载值的增大而线性增大;加承托时的箱梁挠度较不加承托时的相应值均有一定程度的减小。进而由表 1可知3种工况下对应于最大加载值作用下的挠度值,加承托时较不加承托时分别减少了14.6%,12.4%,14.6%,上述差值大都接近15%。

|
| 图 4 跨中断面加载时跨中断面箱梁挠度的对比 Fig. 4 Comparison of deflections of box girder at mid-span when mid-span is under loading |
| |
| 加载方式 | 加载工况 | 差值/% | |
| 不加承托/mm | 加承托/mm | ||
| 中腹板处加载 | 0.410 | 0.350 | 14.6 |
| A-A截面加载 | 0.322 | 0.282 | 12.4 |
| 边腹板处加载 | 0.313 | 0.267 | 14.6 |
(2) 承托对桥面板横向内力的影响
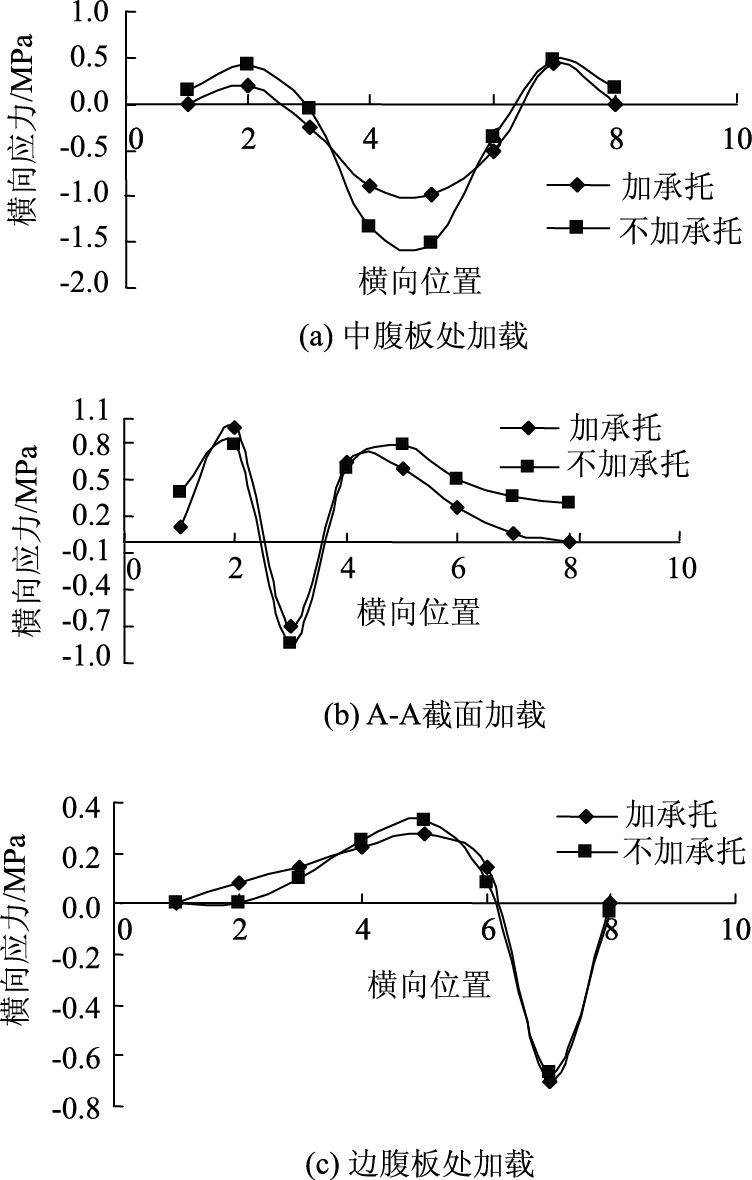
从图 5可知桥面板加承托、不加承托的箱梁跨中断面桥面板横向应力分布规律相同,只是前者较后者的数值有一定程度的减小。以中腹板处加载为例,其中腹板位置处的横向应力值分别减少13.3%,10.2%。
|
| 图 5 跨中位置的横向应力值对比 Fig. 5 Comparison of lateral stresses at mid-span |
| |
可见由于试验梁桥面板设置了承托,使其抗弯刚度增大,降低了箱梁的挠度,同时也降低了桥面板横向应力值。
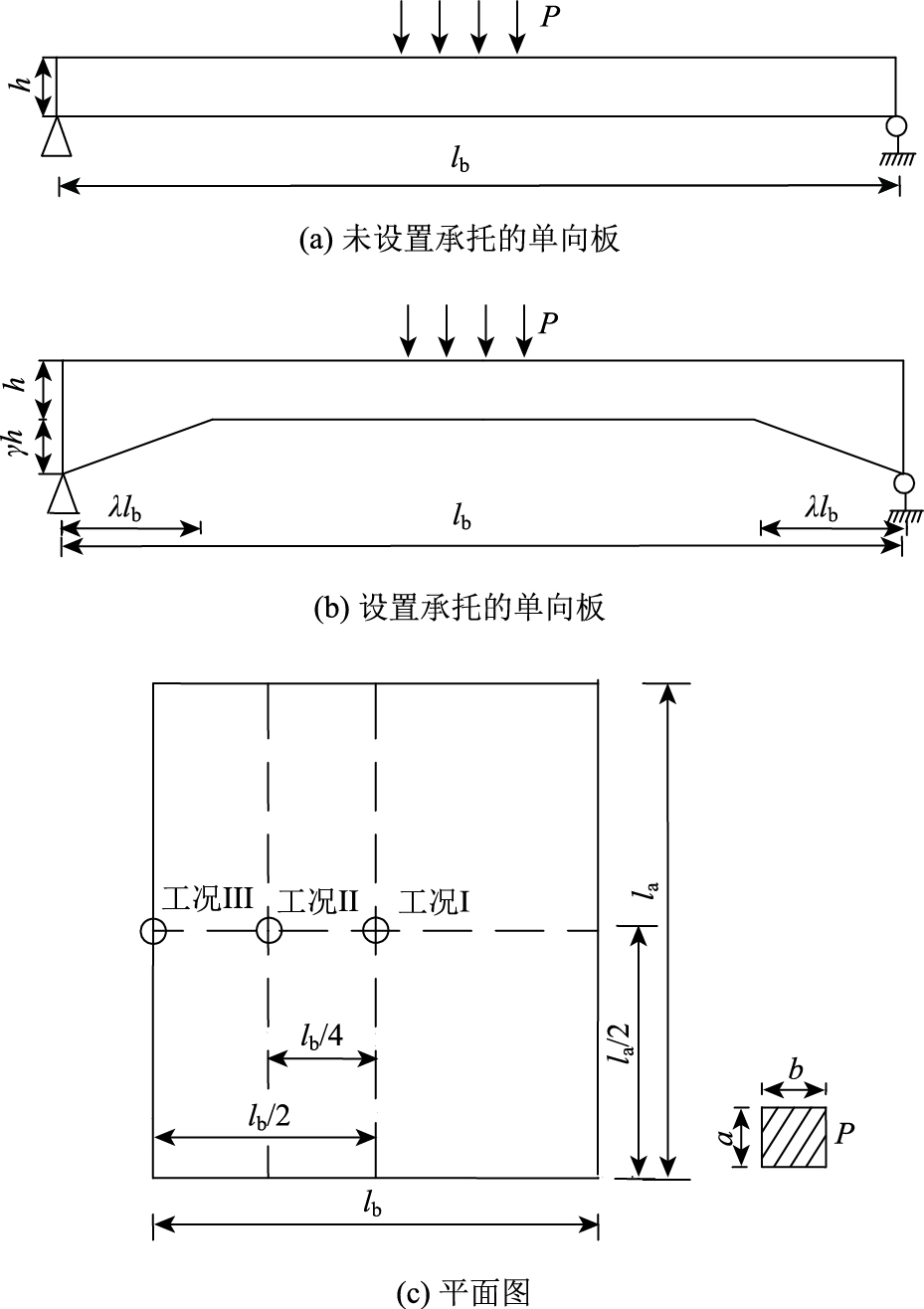
2 加设承托的混凝土桥面板有效分布宽度及横向内力计算研究 2.1 加设承托的混凝土板有效分布宽度研究将上述不加承托和加承托试验梁中单室箱梁桥面板的横断面尺寸作为板的短跨方向尺寸,则图 6(a)~(b)中的lb=570 mm,h=80 mm,γh=λlb=40 mm。长跨方向la取为2 m,则la/lb>2,满足单向板的要求[8]。
|
| 图 6 桥面板示意图 Fig. 6 Schematic diagram of bridge deck |
| |
以加承托和不加承托的混凝土简支板为对象,分别将荷载置于图 6(c)所示位置,分为工况Ⅰ、工况Ⅱ、工况Ⅲ,3种工况采用同一均布荷载值p=P/(a×b)=250 kN/m;其中a, b分别为试验中千斤顶作用下的条形钢板平面尺寸200 mm×200 mm。采用有限元法对板的有效分布宽度进行计算,有限元模型中混凝土板采用实体单元Solid95模拟,在单向板的支座处约束UX,UY,UZ,这3个方向的线位移,其中横向为X轴,竖向为Y轴,纵向为Z轴[9],结果见表 2。
| 加载位置 | 单向板 | ||
| 不加承托 | 加承托 | 差值/% | |
| 板跨中 | 1.18 | 1.12 | 5.1 |
| 靠近板的支撑处 | 1.31 | 1.23 | 6.1 |
| 在板的支撑处 | 0.98 | 0.93 | 5.1 |
通过上述分析可知加设承托与否对板的有效分布宽度影响很小,加承托与不加承托的单向板在上述3种加载位置下的有效分布宽度差值仅为5%。
2.2 加设承托的混凝土桥面板横向内力计算研究[10]承托设置的影响参数即变截面杆件的形常数及载常数[10-12]已有大量的表格可查,其充分考虑了承托尺寸对桥面板横向内力值的影响。结构力学方法未考虑扭转、畸变等的影响[13],但是为了分析承托设置对箱梁桥面板横向内力的影响,仅以结构力学[14]方法作为近似方法。
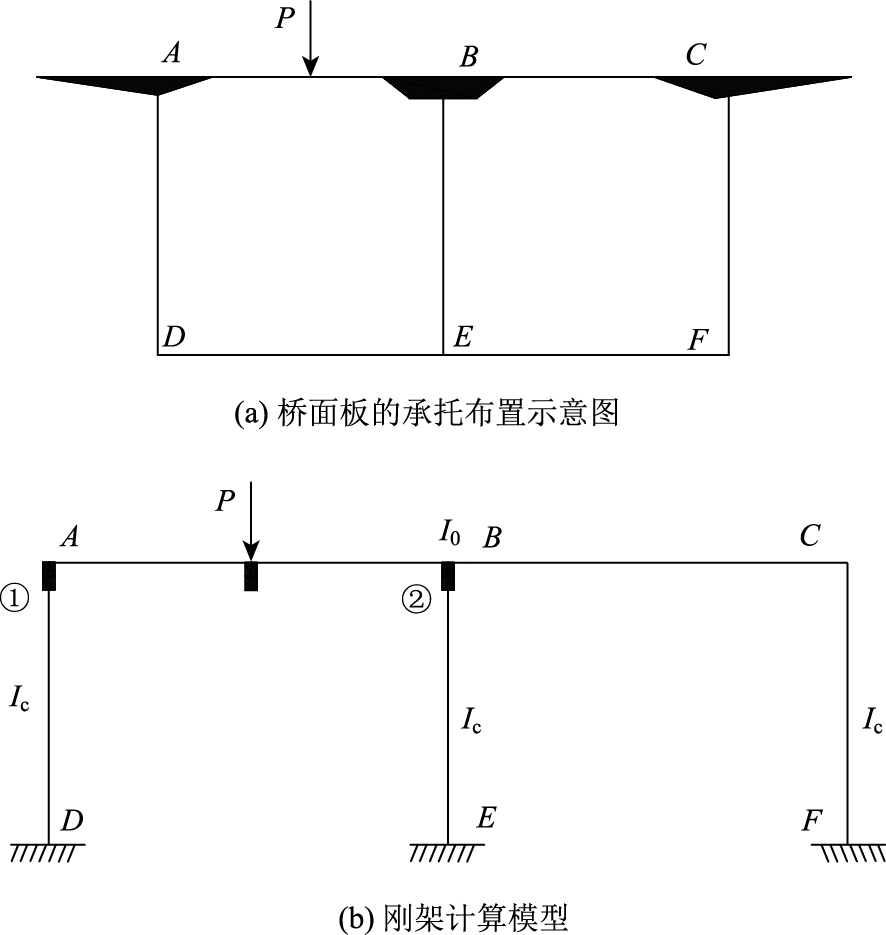
本节将基于上述理论及数据资料,比较试验梁承托设置与否对箱梁桥面板横向内力值的影响。以加承托的试验梁在偏载下的横向内力求解为对象,采用结构力学中的刚架模型,见图 7。
|
| 图 7 计算模型 Fig. 7 Calculation model |
| |
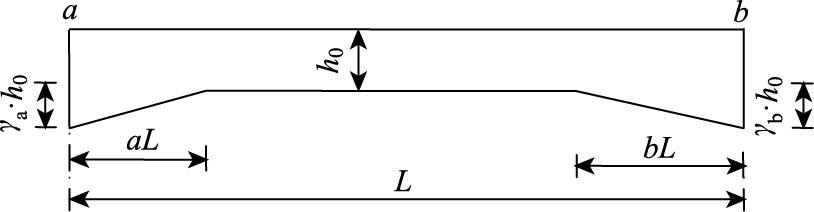
试验梁中单室桥面板的承托设置见图 8,图中a,b为承托的两端。
|
| 图 8 承托设置及符号标示 Fig. 8 Support setting and symbols |
| |
(1)形常数及载常数
AB跨:a=0.07,b=0.12;ra=0.5,rb=0.5。
根据以上数据,查文献[11]附录得:
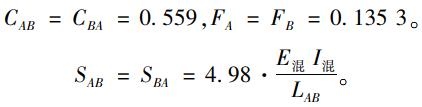
|
(1) |
则固端力矩:

|
(2) |
BC跨:(无荷载作用)
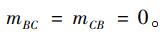
|
(3) |
AD跨:按上端有承托,下端无承托计算。
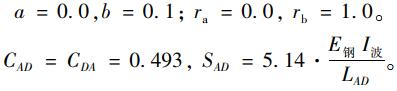
|
(4) |
BE跨:

|
(5) |
(2)分配系数
设AB跨线刚度E混I混/LAD=1,则各杆转动刚度相对值为:

|
(6) |

|
(7) |
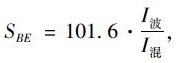
|
(8) |
其中:
I混=4.444×10-5 m3,I波=2.581×10-8×m3。
分配系数求得如下:

|
式中,ra,rb为梁两端A与B的腋深度之比; LAB为AB胯长度; CAB, CBA为梁两端A与B的传递系数; SAB, SBA为梁两端A与B的转动刚度相对值; FA, FB为梁两端A与B的固定端力矩系数; E混,E钢,I混,I波分别为混凝土、波形钢腹板的弹性模量及其各自的横向抗弯惯性矩[15-16],其中I混指的是未加承托部分的混凝土桥面板横向抗弯惯性矩。
上述参数求出之后,按照结构力学中的力矩分配法[17-18]计算得出的结果见表 3,同时将不加承托的相应结果示于表 3。
| 位置 | 横向应力值 | ||
| 不加承托 | 加承托 | 差值/% | |
| 承托① | 1.29 | 1.14 | 11.6 |
| 荷载处 | 1.36 | 1.22 | 10.3 |
| 承托② | 1.30 | 1.16 | 10.8 |
由表 3可知加承托与不加承托时的桥面板横向内力值大约相差10%,可见承托的设置对桥面板横向内力值存在一定的影响,不可忽略。
由于计算模型的差异,采用结构力学方法计算的结果与实际箱梁模型结果存在一定差异。但是综合试验结果和力学分析结果,加设承托与否对桥面板受力的影响一致,且影响值均在10%以上。
3 结论(1) 由于桥面板承托的设置增强了箱梁的抗弯刚度,其箱梁挠度、桥面板横向应力值较不加承托时同一工况下的相应值均有一定程度的减小,可见承托的施加对波形钢腹板箱梁桥面板的受力是有一定影响的。
(2) 针对承托的设置对桥面板有效分布宽度及横向内力的影响,得出以下结论。
① 承托的设置对板的有效分布宽度影响很小,加承托与不加承托的单向板在文中所述3种加载工况下的有效分布宽度误差均约为5%。
② 承托的设置对波形钢腹板箱梁桥面板的受力存在一定影响,约为10%。
(3) 对于波形钢腹板箱梁而言,从自身构造上来讲波形钢腹板与承托这两类因素均会对桥面板横向受力产生一定影响,不可忽略。
| [1] |
朱聘儒. 钢-混凝土组合梁设计原理[M]. 北京: 中国建筑工业出版社, 2006. ZHU Pin-ru. Design Principle of Steel-concrete Composite Girder[M]. Beijing: China Communications Press, 2006. |
| [2] |
范立础. 桥梁工程[M]. 北京: 人民交通出版社, 2002. FAN Li-chu. Bridge Engineering[M]. Beijing: China Communications Press, 2002. |
| [3] |
王荣辉, 周建春. 考虑隅角点承托刚性影响薄壁曲线箱梁的空间计算分析[J]. 土木工程学报, 2002, 35(6): 66-72. WANG Rong-hui, ZHOU Jian-chun. Spatial Analysis of Curved Thin-walled Box Girder Considering the Stiffness Effects of Box Corner[J]. China Civil Engineering Journal, 2002, 35(6): 66-72. |
| [4] |
邱波, 王荣辉, 刘光栋. 考虑隅角点承托刚性影响薄壁箱梁的空间计算分析[J]. 中国公路学报, 2003, 16(1): 50-53. QIU Bo, WANG Rong-hui, LIU Guang-dong. Spatial Computational Analysis of Considering Rigidity of Box Corner Reinforcement Part for Thin-walled Box Girder[J]. China Journal of Highway and Transport, 2003, 16(1): 50-53. |
| [5] |
钟新谷, 舒小娟, 张昊宇. 预应力混凝土箱梁横向框架效应有限元分析[J]. 计算力学学报, 2013, 30(4): 549-533. ZHONG Xin-gu, SHU Xiao-juan, ZHANG Hao-yu. Finite Element Analysis on Transversal Frame-effect of Prestressed Concrete Box-girder Bridge[J]. Chinese Journal of Computational Mechanics, 2013, 30(4): 549-533. |
| [6] |
赵品, 叶见曙. 波形钢腹板箱梁桥面板横向内力计算的框架分析法[J]. 东南大学学报:自然科学版, 2012, 42(5): 940-944. ZHAO Pin, YE Jian-shu. Frame Analysis Method of Transverse Internal Force in Bridge Deck of Box Girders with Corrugated Steel Webs[J]. Journal of Southeast University:Natural Science Edition, 2012, 42(5): 940-944. |
| [7] |
李立峰, 侯立超, 孙君翠. 波形钢腹板抗剪性能的研究[J]. 湖南大学学报:自然科学版, 2015, 42(11): 56-63. LI Li-feng, HOU Li-chao, SUN Jun-cui. Research on Shear Mechanical Property of Corrugated Steel Webs[J]. Journal of Hunan University:Natural Science Edition, 2015, 42(11): 56-63. |
| [8] |
JOHNSON R P, CAFOLLA J. Corrugated Webs in Plate Girders for Bridges[J]. Structures and Buildings, 1997, 122(2): 157-164. |
| [9] |
姚玲森. 桥梁工程[M]. 北京: 人民交通出版社, 2008. YAO Ling-sen. Bridge Engineering[M]. Beijing: China Communications Press, 2008. |
| [10] |
方志, 郑辉, 刘双阳. 基于塑性分析的钢筋混凝土箱梁悬臂板横向受力有效分布宽度[J]. 土木工程学报, 2012, 45(3): 35-41. FANG Zhi, ZHENG Hui, LIU Shuang-yang. Plastic Analysis of the Lateral Effective Width of Cantilever Slabs of Reinforced Concrete Box-girders[J]. China Civil Engineering Journal, 2012, 45(3): 35-41. |
| [11] |
蔡方荫. 变截面刚构分析[M]. 上海: 上海科学技术出版社, 1962. CAI Fang-yin. Analysis on Variable Sectional Rigid Frame[M]. Shanghai: Shanghai Science and Technology Press, 1962. |
| [12] |
清华大学建筑工程系. 结构力学[M]. 北京: 中国建筑工业出版社, 1974. Architectural Engineering Department of Tsinghua University. Structural Mechanics[M]. Beijing: China Architecture & Building Press, 1974. |
| [13] |
ELGAALY M, SESHADRI A. Girders with Corrugated Webs under Partial Compressive Edge Loading[J]. Journal of the Structural Engineering, 1997, 123(6): 783-791. |
| [14] |
赵品, 荣学亮, 叶见曙. 波形钢腹板箱梁桥面板横向内力计算方法研究[J]. 同济大学学报:自然科学版, 2019, 47(4): 467-474. ZHAO Pin, RONG Xue-liang, YE Jian-shu. Calculation Method of Transverse Internal Force in Bridge Deck of Box Girder with Corrugated Steel Webs[J]. Journal of Tongji University:Natural Science Edition, 2019, 47(4): 467-474. |
| [15] |
郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 北京: 人民交通出版社, 2008. GUO Jin-qiong, FANG Zhen-zheng, ZHENG Zhen. Design Theory of Box Girder[M]. Beijing: China Communications Press, 2008. |
| [16] |
方志, 郑辉, 刘双阳. 基于塑性分析的钢筋混凝土箱梁悬臂板横向受力有效分布宽度[J]. 土木工程学报, 2012, 45(3): 35-41. FANG Zhi, ZHENG Hui, LIU Shuang-yang. Plastic Analysis of the Lateral Effective Width of Cantilever Slabs of Reinforced Concrete Box-girders[J]. China Civil Engineering Journal, 2012, 45(3): 35-41. |
| [17] |
赵品, 荣学亮, 叶见曙. 波形钢腹板组合箱梁横向受力有效分布宽度研究[J]. 湖南大学学报:自然科学版, 2016, 43(7): 105-110. ZHAO Pin, RONG Xue-liang, YE Jian-shu. Research on the Lateral Effective Width of Composite Box-girders with Corrugated Steel Webs[J]. Journal of Hunan University:Natural Science Edition, 2016, 43(7): 105-110. |
| [18] |
赵品, 叶见曙. 波形钢腹板单箱多室箱梁横向受力分析[J]. 哈尔滨工程大学学报, 2018, 39(6): 1109-1115. ZHAO Pin, YE Jian-shu. Transverse Force Study of Single Box Multi-chamber with Corrugated Steel Webs[J]. Journal of Harbin Engineering University, 2018, 39(6): 1109-1115. |
 2020, Vol. 37
2020, Vol. 37
