扩展功能
文章信息
- 吴晋武, 张海峰, 冉旭东
- WU Jin-wu, ZHANG Hai-feng, RAN Xu-dong
- 基于数据约减和支持向量机的非参数回归短时交通流预测算法
- Nonparametric Regressive Short-term Traffic Flow Forecast Algorithm Based on Data Reduction and SVM
- 公路交通科技, 2020, 37(7): 129-134
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(7): 129-134
- 10.3969/j.issn.1002-0268.2020.07.017
-
文章历史
- 收稿日期: 2019-06-25
2. 北京空间科技信息研究所, 北京 100094;
3. 天津大学 管理与经济学部, 天津 300072;
4. 深圳市易行网交通科技有限公司, 广东 深圳 518057
2. Beijing Institute of Space Science and Technology Information, Beijing 100094, China;
3. School of Management and Economics, Tianjin University, Tianjin 300072, China;
4. Shenzhen e-Traffic Technology Co., Ltd., Shenzhen Guangdong 518057, China
城市路网的交通流系统具有非线性、时变等特性。对于预测时间小于15 min的短时预测,不仅要考虑状态变量、控制变量与预测流量之间的映射关系,而且也要考虑流量的时变特性。采样时间越短(<5 min)时,各种干扰因素对流量预测的影响也就越强,当空间位置、道路环境越复杂且在高峰时段时,其交通流量的不确定性愈为突出,而且会受到许多因素的影响,因此,交通流短时预测算法一直是智能交通中的重要研究领域[1-6]。尽管近年来深度学习方法得到了极大的重视[3-6],但非参数回归方法在交通流预测中仍然能发挥不错的作用[7],这是因为非参数回归方法以交通流量存在自重复性和时间连续性的特点为前提,通过构造模式库直接从历史数据中提取原因与结果的映射,在数据量足够的情况下精度较高,而且具有很高的鲁棒性,能够较好地应对短时交通流的非线性和不确定性。与深度学习方法相比,非参数回归方法对数据类型和数据质量的要求不高,不需要复杂的模型构建和训练过程,对前期数据准备和硬件要求低,在实际的交通流预测任务中实用性更强。尤其在现阶段交通大数据来源多(包括检测器、视频、信令等)、数据量大且实时性强、但数据质量参差不齐的背景下,非参数回归算法可以在不对现有软硬件进行大幅修改的条件下融入现有智能交通系统体系,提供性能较好的交通预测能力。
非参数回归方法因其自身的众多优点,一直是交通流预测领域中的重要方法。Clark等[8]将单变量预测扩展到多变量预测,并讨论了选择近邻个数、数据可迁移性等问题。Kim[9]考虑了历史状态对于非参数回归预测特征向量的影响,提高了预测效果。张晓利[10]提出了一种基于小波分析与神经网络的交通流量预测方法,针对多维神经网络映射学习极易产生维数灾难问题给出了有效的解决方法。Turochy[11]在非参数回归预测中考虑交通状态信息,提高了算法的预测精度。张晓利等[12]提出了一种结合主成分分析和组合神经网络的交通流量预测方法,并且证明了其结果优于BP网络的优势。Zheng[13]在非参数回归预测中的结果生成阶段引入线性主成分方法,提高了预测精度。张晓利等[14]利用聚类算法和平衡二叉树建立案例数据库,提出了一种基于平衡二叉树的K-邻域非参数回归(KNN-NPR)方法,提高了预测的精度和实时性。
然而,在实际交通流量预测任务中,若采用非参数回归方法的标准过程会产生其他问题。首先,当数据量巨大,特别是在历史数据积累较多的情况下,数据匹配时间过长,无法满足预测实时性要求。其次,数据维数高,容易产生维数灾难问题,导致无法匹配到合乎要求的相似模式,使预测失败。此外,在基于搜索到的相似模式进行预测时,对预测变量直接进行平均,会带来一定的预测误差。针对以上缺陷,在一般K-邻域非参数回归算法基础上,进行了如下改进:(1)使用减法模糊聚类(Subtraction Fuzzy Clustering,FCM)方法,对历史数据进行聚类,使用聚类中心点数据而不是所有数据构造模式库,可大大减少模式库的数据量。(2)采用主成分分析(PCA)方法降低模型的维度,可克服模式匹配速度较慢、无关维度干扰问题。(3)融合支持向量机方法,运用搜索到的K个模式估计最终待预测变量的值。运用仿真系统生成的实时大流量数据进行测试,发现改进后的算法能够有效提升非参数回归预测的实时性,并提高预测精度。
1 计算方法与算法框架非参数回归方法本身脱胎于混沌理论,是基于模式识别并且依靠数据驱动的智能方法。它不需要为历史数据建立近似模型和大量参数估计,而是由测量对象的大量数据作为支持,是一种无模型预测方法。此种方法尝试识别具有与预测时刻系统相同的输入值或状态的一组过去案例,或者查找与当前输入X(t)类似的历史数据“集群”,根据这“簇”数据的输出值,决定预测值y(t+1)。此方法的关键是如何确定与预测时刻系统状态最为相似的一“簇”历史数据。通常,该最近邻域包括距输入状态点最近的K个点。由此可以看出,任何两次匹配的采样时间可能是不同的,它总是选出与当前状态模式最为匹配的历史数据,因此非参数回归方法实现了一定的动态预测。
本研究试图在一般K-邻域非参数回归算法基础上进行改进。采用的预测方法由主成分分析、模糊聚类、非参数回归、样本数据库和调节回路等部分组成,各组成部分之间不仅相互联系,而且每个组成部分又包括多个操作或算法,共同构成了预测的整体框架。算法框架如图 1所示。
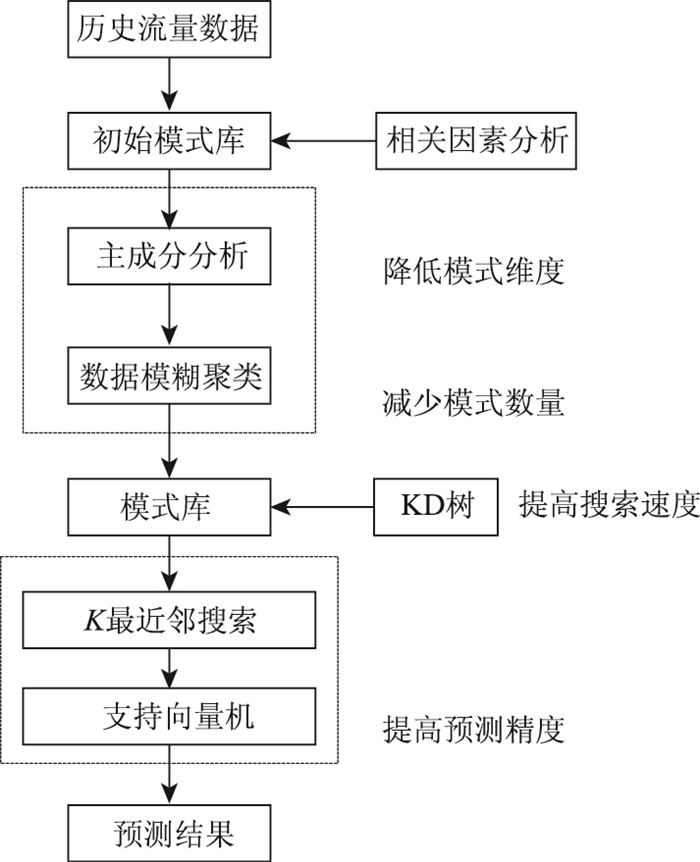
|
| 图 1 预测算法总体框架 Fig. 1 Overall framework of prediction algorithm |
| |
1.1 基于主成分分析的数据降维
对路段流量进行非参数回归预测的第1步是确定影响被测路段流量的因素。当路网结构复杂时,需要综合考虑上游位置、时间延迟等诸多因素,可能产生影响的因素将达到几十甚至上百个,模式库中的模式维度也非常高,存在的潜在问题如下:(1)增加了每条模式占用的存储空间;(2)在数据检索时,由于维度高容易造成检索不到合适的数据,并且降低了搜索速度;(3)因素是由先验经验得到的,因此可能有些因素实际上与待预测变量并不相关,在影响路段流量的大量因素中,有些因素的影响力非常小,有的甚至可有可无,较高影响力因素可能仅限于几个因素。如果不加区别地对待影响因素,就必然会消除重要因素的影响,降低预测的准确性;(4)由于许多指标变量间可能存在相关关系,问题的复杂性也随之增加。如果分别分析每个指标,分析又可能是独立进行的,而在实际中要求综合处理。因此,应该简化原始交通数据,同时确保不丢失重要信息和预测准确性。此时,主成分分析法(PCA)就非常适于此类问题。对主成分分析算法的具体原理介绍参见文献[15-16]。
1.2 基于模糊聚类的原始数据筛选采用模糊C均值聚类(FCM)算法[17]。通过对数据进行模糊划分来聚类,更适于在数据比较密集或分类边界不清晰的情况下使用。由模糊理论,用隶属度来确定每个数据实例属于某个类别的程度及其类矩阵U = (uij|i = 1, 2, …, n; j = 1, 2, …, k),其中元素uij为第i个数据实例属于第j类的隶属程度,并满足如下条件:
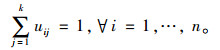
|
(1) |
定义价值函数为:
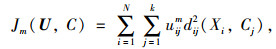
|
(2) |
式中,Jm为从每个数据实例到聚类中心距离的平方和;Xi为数据集I中的元素,Xi∈I;Cj为类中心,Cj∈I; uij为第i个数据实例属于第j类的隶属程度,其取值介于[0, 1]之间,U = {uij}是一个n×K矩阵;C = {c1, c2, …,ck}, ci为模糊组i的类中心;dij(Xi, Cj)为第i个数据实例与第j个类中心间的欧式距离;m为模糊系数(1≤m<∞);k为预先设定的分类组数。
分组数量k需要在聚类之前提前确定。本研究用聚类密集性和聚类临近性两个指标衡量聚为k类时聚类效果的优劣,对这两个指标分别介绍如下。
聚类密集度用于衡量同一类中数据的紧密程度,给定一个数据集X,首先计算其数据的方差:
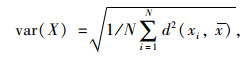
|
(3) |
式中,d(xi, x)为xi与x之间的距离;N为X的总个数;x为X的均值。若数据集X聚合到C个类,则其聚类密集度定义为:
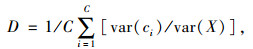
|
(4) |
式中,C为聚类个数;var(ci)为簇ci的方差。
聚类邻近性用于衡量不同类之间分开的程度,其定义为:
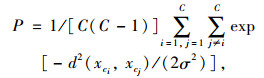
|
(5) |
式中,xci, xcj分别为类ci, cj的中心;d2(xci, xcj)为聚类ci中心与cj中心之间的距离;σ为常数,为简化计算,通常为简化计算取2σ2 = 1.0。
理想的聚类结果应当满足“类内密集而类间分开”的特点,因此将上面两个指标取加权平均,定义聚类的综合质量评价指标为:
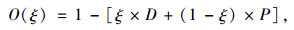
|
(6) |
式中ξ为权重, ξ∈[0, 1]。
1.3 基于多维搜索结构的模式库构建为进一步提升搜索效率,本研究提出的算法使用多维搜索结构代替常用的线性表作为模式库的存储结构,以实现模式的高速搜索。常用的多维搜索结构主要有KD树、R树等。本算法选用KD树作为模式库的存储结构,这一结构目前已有一些研究使用过[18],因此不作详细介绍。
1.4 基于支持向量机的预测值生成在传统的非参数回归预测中,对于搜索得到的K条最近邻模式P1~PK,一般是使用算数平均或加权平均的方式计算因变量的预测值,即:
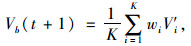
|
(7) |
式中,Vb(t+1)为待预测点位b下一时刻的预测流量;V′i为近邻模式Pi中对应的待预测因变量的值;wi为第i个近邻模式的权重。
这种做法隐含的思想是,假定状态向量和待预测变量之间存在一个连续的函数关系Vb = g(S)。因此,在状态向量接近的情况下,待预测变量应该也是相近的,所以使用平均或加权平均的方式,可以估计待预测变量的值,但这种方式实质上是一种线性的组合,当实际函数形式具有强的非线性时,估计的结果难以保证。针对这一缺点,使用支持向量机模型来拟合待预测点附近的函数关系,进而估计待预测变量的值。
支持向量机(SVM)最初用于处理两类数据分类问题,核心思想是找到一个超平面,使得训练集中属于不同类别的样本数据点位于超平面的两侧,同时这些点尽可能远离该超平面。与其他机器学习算法相比,具有理论基础完善、训练速度快、泛化能力强等优点。
预测点位b下一时刻的流量Vb(t+1)的具体步骤如下。
Step 1:在历史数据中提取影响Vb(t+1)的因素构成状态向量S。
Step 2:在模式库中搜索以获得S的K条最近邻模式P1~PK。
Step 3:以P1~PK作为训练集训练支持向量机模型至收敛,得到在S附近状态向量与待预测变量的非线性关系。
Step 4:输入S以获得预测值Vb(t+1)。
2 数据与试验设计 2.1 预测场景与数据来源试验选用的场景为深圳北站周边的主干道。选取接近深圳北站主要出口且流量较大的留仙大道为待预测位置,对其交通流量进行短时预测(图 2)。图 2中标出了待预测位置和作为状态分量的流量采集位置,其中交通流量来自干道上的微波和视频检测器。
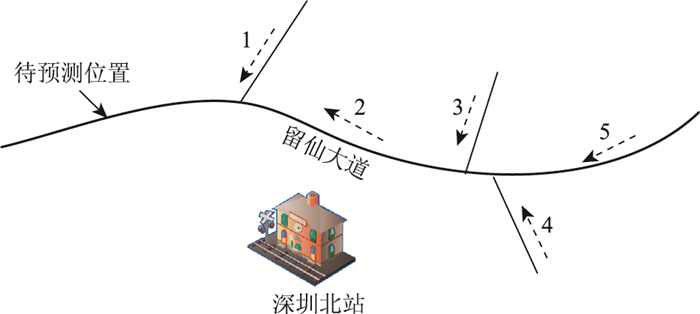
|
| 图 2 试验路网拓扑结构 Fig. 2 Experimental road network topology |
| |
选取的预测步长为5 min,即Vb(t+1)表示从当前时刻t开始5 min后的交通流量。因为交通系统存在一定的时变特性,因此过于久远的数据对预测并没有很大价值,所以试验采用的数据为2018年4月全月的数据,按5 min进行聚合,则每天有360条记录,全月共有10 800条记录。其中4月1日~4月25日为训练数据构建模式库,4月26日~4月30日的数据用于测试算法的效果。
2.2 基准算法基准算法采用文献[8]中提出的KNN-NPR算法和文献[13]中提出的KNN-NPR-LSPC算法,其中KNN-NPR算法是最经典的非参数回归算法,而KNN-NPR-LSPC算法在KNN-NPR算法的基础上改进了最近邻选择和结果生成两个环节。选取这两种方法进行对比,能够有效地说明文中算法的有效性。
通过对路网进行分析,认为图 2中编号为1~5的点位,其交通流与待预测点位的流量存在空间关联,于是选取点位1~5,以时间步t~t-4的流量构造状态向量用于预测Vb(t+1),初始状态向量共有25维。
2.3 性能指标本研究所提方案的目的不止是提升预测精度,还在于提升计算速度,因此需要从预测精度与计算速度两个角度来衡量算法的性能。
计算速度的衡量方式为:设定不同的近邻数量K值(需要搜索的最近邻数量K会影响到计算时间),对所有的待预测时间点进行预测,然后求出平均每次计算的耗时。
预测精度的衡量主要采用平均绝对百分比误差MAPE,其计算式为:
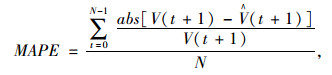
|
(8) |
式中,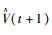
从主成分分析和聚类结果、性能指标几方面对试验结果进行分析与讨论。
3.1 主成分分析和聚类结果主成分分析结果如表 1所示。
| 主成分 | 主成分标准差 | 方差所占比例 | 累积贡献率 |
| Component 1 | 7.643 | 0.303 | 0.303 |
| Component 2 | 5.284 | 0.143 | 0.446 |
| Component 3 | 5.14 | 0.132 | 0.578 |
| Component 4 | 4.391 | 0.119 | 0.697 |
| Component 5 | 3.878 | 0.082 | 0.779 |
| Component 6 | 3.453 | 0.061 | 0.84 |
| Component 7 | 3.437 | 0.06 | 0.9 |
| Component 8 | 3.4 | 0.057 | 0.957 |
由表 1可知,前8个主成分的方差累积贡献率超过95%,这可以更好地概括原始数据。因此,选取分解后的Component 1~Component 8作为状态向量中的分量。
降维之后,对模式库实施减法模糊聚类操作。针对不同聚类数量计算由式(6)表达的聚类性能指标,得到当类中心的数量为3 100个时,效果最好。随后只保留每个类的聚类中心,生成最终的模式库。经过以上处理,极大地缩减了模式库的数量,并保留了与待预测变量关系最大的状态分量。
3.2 算法性能 3.2.1 计算速度需要搜索的最近邻数量K是影响算法平均耗时的重要因素,设定不同的K值,对1 000个测试点进行预测,然后求出平均耗时(表 2)。可以看到所提出的算法能够显著降低平均搜索时长。
| K值 | 本研究算法 | KNN-NPR | KNN-NPR-LSPC |
| K=2 | 8 | 20 | 25 |
| K=3 | 9 | 33 | 42 |
| K=4 | 9 | 45 | 54 |
| K=5 | 10 | 60 | 66 |
| K=6 | 12 | 78 | 87 |
| K=7 | 13 | 95 | 101 |
| K=8 | 16 | 113 | 116 |
| K=9 | 20 | 130 | 139 |
| K=10 | 20 | 156 | 176 |
从表 2可以看出,即使模式库中具备大量的历史模式,每个基本预测模块也仅需几十毫秒进行预测,系统结构确保了对于更大规模的预测需求,可将预测任务分解后在多个主机上完成。该系统能够处理真实情况下的多点预测。而作为对照的两种算法在预测时间方面比本研究所提算法落后较多,当数据量更大,情况更复杂时,进行实时预测可能会有问题。
3.2.2 预测精度设定不同的最近邻个数,对比3种方法的预测结果,如表 3所示。本研究所提算法的预测精度比KNN-NPR方法要小得多,比KNN-NPR-LSPC也有一定优势,在计算速度上具有优势,综合性能优于KNN-NPR-LSPC算法。
| K值 | 本研究算法 | KNN-NPR | KNN-NPR-LSPC |
| K=3 | 10.54 | 19.45 | 12.73 |
| K=6 | 8.81 | 14.26 | 10.02 |
| K=9 | 8.92 | 15.90 | 10.70 |
4 结论
非参数回归方法是一种以数据驱动、少参数的智能预测方法。与受到极端重视的深度学习方法相比,非参数回归具有数据需求不高、模型构建过程简单(无需训练过程)、可解释性强和不容易过拟合等优点,在一些实际的预测工作中具有优势。本研究在一般非参数回归的基础上进行了多方面的改进,使之更加满足较高的预测准确度、实时性和动态性的要求,进一步克服了标准非参数回归算法模式库体积大、计算过程效率低等缺点,并进一步提升了预测精度,具有一定的实用价值。
| [1] |
万玉龙, 李新春, 周红标. 基于WPD-PSO-ESN的短期交通流预测[J]. 公路交通科技, 2019, 36(8): 144-151. WAN Yu-long, LI Xin-chun, ZHOU Hong-biao. Prediction of Short-term Traffic Flow Based on WPD-PSO-ESN[J]. Journal of Highway and Transportation Research and Development, 2019, 36(8): 144-151. |
| [2] |
唐智慧, 郑伟皓, 董维, 等. 基于交互式BP-UKF模型的短时交通流预测方法[J]. 公路交通科技, 2019, 36(4): 117-124. TANG Zhi-hui, ZHENG Wei-hao, DONG Wei, et al. A Method for Predicting Short-term Traffic Flow Based on Interactive IMM-BP-UKF Model[J]. Journal of Highway and Transportation Research and Development, 2019, 36(4): 117-124. |
| [3] |
CHEN M, YU X H, LIU Y. PCNN:Deep Convolutional Networks for Short-term Traffic Congestion Prediction[J]. IEEE Transactions on Intelligent Transportation Systems, 2018, 19(11): 1-10. |
| [4] |
孙静怡, 牟若瑾, 刘拥华. 考虑大型车因素的支持向量机短时交通状态预测模型研究[J]. 公路交通科技, 2018, 35(10): 126-132. SUN Jing-yi, MOU Ruo-jin, LIU Yong-hua. Study on Short-term Traffic State Forecasting Model of SVM Considering Proportion of Large Vehicles[J]. Journal of Highway and Transportation Research and Development, 2018, 35(10): 126-132. |
| [5] |
HU R, CHIU Y C, HSIEH C W, et al. Mass Rapid Transit System Passenger Traffic Forecast Using a Re-sample Recurrent Neural Network[J]. Journal of Advanced Transportation, 2019, 2019: 8943291. |
| [6] |
ZHAO Z, CHEN W, WU X, et al. LSTM Network:A Deep Learning Approach for Short-term Traffic Forecast[J]. IET Intelligent Transport Systems, 2017, 11(2): 68-75. |
| [7] |
YU B, SONG X, GUAN F, et al. K-nearest Neighbor Model for Multiple-time-step Prediction of Short-term Traffic Condition[J]. Journal of Transportation Engineering, 2016, 142(6): 04016018. |
| [8] |
CLARK S. Traffic Prediction Using Multivariate Nonparametric Regression[J]. Journal of Transportation Engineering, 2003, 129(2): 161-168. |
| [9] |
KIM T, KIM H, LOVELL D J. Traffic Flow Forecasting: Overcoming Memoryless Property in Nearest Neighbor Non-parametric Regression[C]//Proceedings of 2005 Intelligent Transportation Systems. Vienna: IEEE, 2005.
|
| [10] |
ZHANG X L. The Forecasting Approach for Short-term Traffic Flow Based on Wavelet Analysis and Neural Network[J]. Information and Control, 2007, 36(4): 467-470,475. |
| [11] |
TUROCHY R E. Enhancing Short-term Traffic Forecasting with Traffic Condition Information[J]. Journal of Transportation Engineering, 2006, 132(6): 469-474. |
| [12] |
ZHANG X L, HE G G. The Forecasting Approach for Short-term Traffic Flow Based on Principal Component Analysis and Combined Neural Network[J]. Systems Engineering-Theory & Practice, 2007, 27(8): 167-171. |
| [13] |
ZHENG Z D, SU D C. Short-term Traffic Volume Forecasting:A K-nearest Neighbor Approach Enhanced by Constrained Linearly Sewing Principle Component Algorithm[J]. Transportation Research Part C:Emerging Technologies, 2014, 43: 143-157. |
| [14] |
ZHANG X L, HE G G, LU H P. Short-term Traffic Flow Forecasting Based on K-nearest Neighbors Non-parametric Regression[J]. Journal of Systems Engineering, 2009, 24(2): 178-183. |
| [15] |
WOLD S, ESBENSEN K, GELADI P. Principal Component Analysis[J]. Chemometrics & Intelligent Laboratory Systems, 1987, 2(1/2/3): 37-52. |
| [16] |
ABDI H, WILLIAMS L J. Principal Component Analysis[J]. Wiley Interdisciplinary Reviews Computational Statistics, 2010, 2(4): 433-459. |
| [17] |
BEZDEK J C. Pattern Recognition with Fuzzy Objective Function Algorithms[M]. New York: Plenum Press, 1981.
|
| [18] |
贾宁, 马寿峰, 钟石泉. 基于遗传算法优化和KD树的交通流非参数回归预测方法[J]. 控制与决策, 2012, 27(7): 991-996. JIA Ning, MA Shou-feng, ZHONG Shi-quan. Non-parameter-regression Traffic Flow Forecast Method Based on KD-tree and Genetic Optimization[J]. Control and Decision, 2012, 27(7): 991-996. |
 2020, Vol. 37
2020, Vol. 37
