扩展功能
文章信息
- 刘军, 翁贤杰, 张龙生, 张连震
- LIU Jun, WENG Xian-jie, ZHANG Long-sheng, ZHANG Lian-zhen
- 基于GA-BP神经网络的隧道围岩力学参数反演
- Inversion of Mechanical Parameters of Tunnel Surrounding Rock Based on GA-BP Neural Network
- 公路交通科技, 2020, 37(7): 90-96
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(7): 90-96
- 10.3969/j.issn.1002-0268.2020.07.012
-
文章历史
- 收稿日期: 2019-07-25
2. 江西省高速公路投资集团有限责任公司, 江西 南昌 330025;
3. 江西交通咨询有限公司, 江西 南昌 330008;
4. 中国石油大学(华东) 储运与建筑工程学院, 山东 青岛 266580
2. Jiangxi Provincial Expressway Investment Group Co., Ltd., Nanchang Jiangxi 330025, China;
3. Jiangxi Transport Consultation Co., Ltd., Nanchang Jiangxi 330008, China;
4. School of Pipeline and Civil Engineering, China University of Petroleum, Qingdao Shandong, 266580, China
随着计算机技术的发展,数值分析理论和计算在岩土工程中得到进一步的推广和应用。虽然数值模拟计算中有着较合理的计算模型,但是数值模拟中的岩体力学参数却由于岩体的尺度效应、取样有限等难以确定合理的取值。为了解决这一问题,岩体力学参数反分析成了确定数值模拟计算参数的有效方式之一。戴薇等[1]利用支持向量机方法反演得到了围岩的侧压力系数,并通过正演分析进行了验证;万智勇等[2]通过均匀设计建立了BP神经网络的样本,并反演得到了坝基的力学参数值;王军祥等[3]运用基于粒子群优化的BP神经网络算法对围岩力学参数进行了反演,并分析了台阶法开挖时隧道的变形情况;周冠南等[4]采用基于遗传算法与BP神经网络相耦合的计算方法,提高了反演分析的效率;杨茜[5]采用对比优选网络训练模式和传递函数,改进了BP神经网络方法,对隧道整体沉降进行了预测;赵杰[6]等运用有限元软件结合BP神经网络,对穿越粉质黏土层及砂卵石地层的地铁暗挖隧道进行了正演分析;吕志涛等[7]以隧道监控量测数据为依据,反演了隧道所在岩体的蠕变参数;饶云康等[8]根据收集的砾类数据样本,分别构建了基于GA-BP神经网络和标准BP神经网络的砾类土最大干密度预估模型,发现采用前者能较好地预估砾类土的最大干密度;张飞等[9]结合大岗山水电站洞室分层开挖的特点,利用GA-BP神经网络实现了施工期岩体参数的精细反演;盖宏健[10]结合单轮土槽试验,运用GA-BP神经网络预测了星壤的剪切和承压力学参数;李振涛等[11]利用正交设计、GA-BP神经网络,反演获得了较为精确的盾构扰动区砂土体力学参数;祝江林等[12]运用敏感性分析,获得了影响白水隧道围岩变形的主要力学参数,并通过GA-BP神经网络对围岩力学参数进行了反演;关永平等[13]利用GA-BP神经网络,结合均匀设计对绿春坝隧道围岩力学参数进行了反演。
本研究以江西省萍莲高速公路莲花隧道为依托工程,利用正交试验组合,结合有限差分法,构造了神经网络样本,并通过训练获得成熟的GA-BP神经网络模型。依据莲花隧道监控量测实测数据反演得到了隧道的围岩力学参数,并通过误差分析验证了参数反演结果的可靠性,这一方法可供隧道工程后续施工与设计使用。
1 工程概况莲花隧道起点位于萍乡市湘东区,终点位于莲花县六市乡,莲花隧道为分离式隧道,左线总长3 210 m,右线总长3 220 m。隧道围岩分级为Ⅳ,Ⅴ,Ⅲ级围岩,其中Ⅳ级围岩占隧道总长的47.6%,Ⅴ级围岩占隧道总长的33.7%,Ⅲ级围岩占隧道总长的18.7%。隧道最大埋深317 m。
隧道区穿越华夏板块华南造山系之东南造山带的武功山-会稽山前缘褶冲带之武功山隆起,基底褶皱强烈,区内断裂带发育。隧道区地表常年有水,主要地下水为基岩节理裂隙水,主要接受大气补给降水。据现场工程地质调绘及钻孔资料分析, 在钻孔揭露范围内隧址区地层结构自上面下依次为第四系粉质黏土及碎石土;青白口系库里组下段砂质板岩、泥盆系上统洋湖组砂岩、泥盆系上统麻山组钙质泥岩等。岩体较破碎至较完整,受地下水影响较大。
2 数值计算模型 2.1 数值模型为保证数值计算的准确性,隧道计算模型的几何尺寸按照施工设计图纸建模。选取莲花隧道右洞进洞口某段作为施工模拟对象。该段平均埋深26 m,围岩等级为Ⅴ级。为避免模型边界过大,致使计算缓慢,根据相关文献[14-15],隧道纵向长度取40 m,隧道的左右边界各取隧道洞径的3倍,隧道的下边界取3倍洞径;隧道的前边界、后边界、左边界、右边界以及模型的底部边界均施加法向约束,模型的上边界为自由边界。数值计算模型及网格划分情况如图 1所示。

|
| 图 1 计算模型及网格划分 Fig. 1 Calculation model and meshing |
| |
2.2 计算参数
数值模拟计算中,隧道围岩材料采用三维实体单元进行模拟。采用cable结构单元模拟超前小导管,长度取4 m,直径为42 mm,壁厚3.5 mm;利用shell结构单元来模拟初衬,厚为25 cm;二次衬砌采用实体单元来模拟,厚为55 cm。在材料本构属性方面,围岩材料采用莫尔—库伦模型,初衬以及二次衬砌则按弹性结构模型,隧道施工过程中的钢拱架、系统锚杆以及钢筋网片则利用适当提高喷射混凝土的弹性模量来模拟[16-17]。超前支护加固区域采用等效加固的效果模拟,其参数取值分别为:厚度取值1.0 m,按照弹性模量取值1.0 GPa,内摩擦角取值35°,黏聚力取值400 kPa。根据莲花隧道地质勘察报告、现行《公路隧道设计规范》,确定隧道围岩力学参数的取值范围,计算模型的力学参数如表 1所示。
| 材料 | 弹性模量/MPa | 泊松比 | 重度/(kN·m-3) | 黏聚力/kPa | 内摩擦角/(°) | 厚度/m |
| 初衬 | 24.0e6 | 0.2 | 22 | — | — | 0.25 |
| 二衬 | 32.5e6 | 0.2 | 25 | — | — | 0.55 |
| 围岩 | 200~350 | 0.32~0.40 | 18 | 60~180 | 20~28 | 26 |
2.3 计算过程
对拟开挖区域赋予null属性实现,通过一定的时步,模拟隧道实际开挖过程中各工序滞后产生的应力释放。隧道采用微台阶法开挖,仰拱快速闭合。隧道的开挖进尺取1 m,各台阶长度均匀3 m,开挖到第16步时,按照第13~15步的顺序循环开挖,直至隧道仰拱向前掘进了10 m,选取距离掌子面5 m处的断面为隧道监测断面。隧道从上台阶开挖到初期支护封闭成环,其具体开挖工序如表 2所示。
| 开挖顺序 | 开挖支护工序说明 |
| 1 | 隧道上台阶开挖1 m,施作初衬 |
| 2 | 隧道上台阶开挖1 m,施作初衬 |
| 3 | 隧道上台阶开挖1 m,施作初衬 |
| 4 | 隧道上台阶开挖1 m,施作初衬 |
| 5 | 隧道下台阶开挖1 m,施作初衬 |
| 6 | 隧道上台阶开挖1 m,施作初衬 |
| 7 | 隧道下台阶开挖1 m,施作初衬 |
| 8 | 隧道上台阶开挖1 m,施作初衬 |
| 9 | 隧道下台阶开挖1 m,施作初衬 |
| 10 | 隧道上台阶开挖1 m,施作初衬 |
| 11 | 隧道下台阶开挖1 m,施作初衬 |
| 12 | 隧道仰拱开挖1 m,施作初衬 |
| 13 | 隧道上台阶开挖1 m,施作初衬 |
| 14 | 隧道下台阶开挖1 m,施作初衬 |
| 15 | 隧道仰拱开挖1 m,施作初衬 |
| 16 | ...... |
3 GA-BP神经网络围岩力学参数反演 3.1 BP神经网络
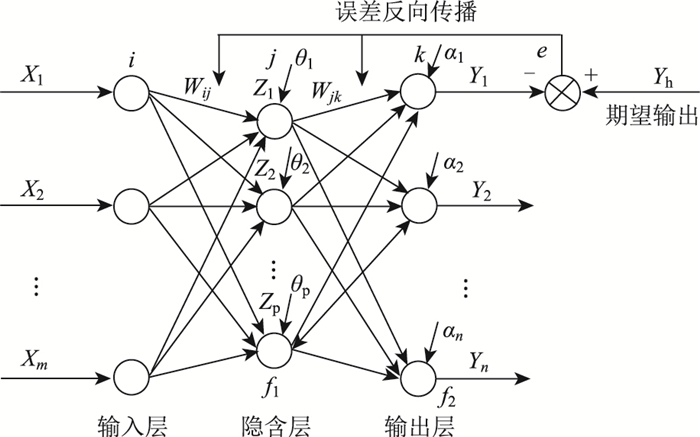
BP神经网络是采用误差反向传播计算的算法,有着良好的自组织学习能力,是目前应用最为广泛的神经网络模型之一。BP神经网络包括输入层、隐含层、输出层,它能够实现从输入到输出的任意非线性映射[18-19]。
如图 2所示,输入层神经元有m个,隐含层有p个,输出层有n个。输入层到隐含层的权值为Wij(i = 1, 2, …, m; j = 1, 2, …, p),隐含层到输出层的权值为Wjk(j = 1, 2, …, p; k = 1, 2, …, n),隐含层的阈值为θj(j = 1, 2, …, p),输出层的阈值为αk(k = 1, 2, …, n)。神经网络的输入向量为X1, X2, …,Xm,神经网络的输出向量为Y1, Y2, …,Ym, 期望输出为Yh,神经网络期望输出值与实际输出值的误差e。在BP神经网络训练时,权值为随机值,输入学习样本得到网络的输出值,然后通过输出值与期望值的误差值,再通过修改网络参数,达到使误差值不断减小的目的,如此反复,直至误差值不再下降,就能得到训练成熟的神经网络模型。
|
| 图 2 BP神经网络结构 Fig. 2 BP neural network structure |
| |
本研究先基于经验公式确定隐含层神经元节点数取值范围,再利用控制变量法,通过改变隐含层神经元个数,建立多个不同的神经网络模型,以误差为指标。经过多次试算,从而确定神经网络的拓扑结构为3-6-3。
3.2 GA-BP神经网络GA-BP神经网络通过优化BP神经网络中随机生成的初始权值与阈值,使得传统的BP神经网络具有更优的非线性映射能力,具有更好的预测能力。
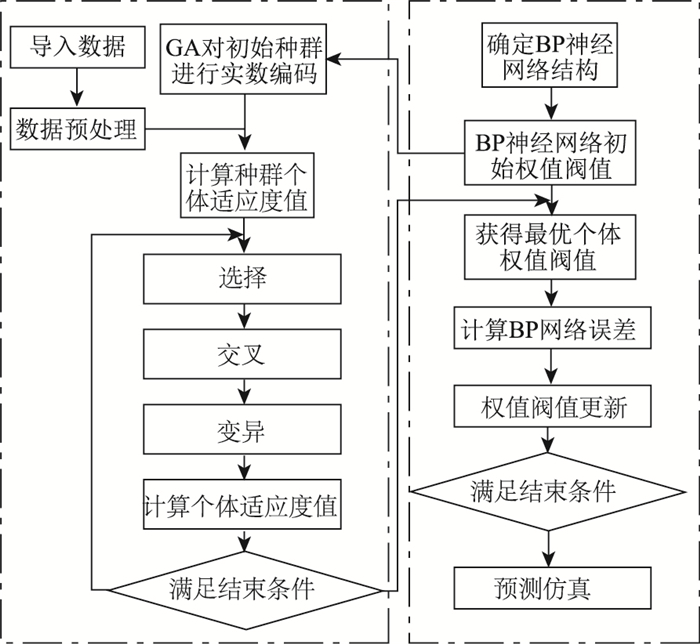
在GA-BP神经网络中,首先对种群个体进行编码;再利用神经网络训练误差并将此作为适应度函数;其次,通过选择、自适应交叉和变异算子,获得种群最佳适应度个体;最后将种群最佳适应度个体作为神经网络的最佳初始权值、阈值;继而代入到BP神经网络中进行训练、预测仿真,直到达到满足设定的预测误差要求或者达到设定的最大迭代次数结束,从而获得成熟的GA-BP神经网络。其算法流程如图 3所示。
|
| 图 3 GA-BP算法流程图 Fig. 3 Flowchart of GA-BP algorithm |
| |
3.3 神经网络样本
为了建立成熟的GA-BP神经网络,必须通过一定数量的神经网络样本对神经网络进行学习,并对训练好的神经网络模型进行检验。为此,设计了25组力学参数的正交试验,按照建立的数值模型和开挖支护工序分组计算,获得相应的拱顶沉降、周边位移以及地表沉降值。
以每组正交试验计算得到的拱顶沉降、周边位移以及地表沉降[U1, U2, U3]作为输入向量,对应的黏聚力、内摩擦角、弹性模量、泊松比[c, ψ, E, μ]作为输出向量。得到GA-BP神经网络样本如表 3所示。
| 试验号 | 输出向量 | 输入向量 | ||||||
| 黏聚力/kPa | 内摩擦角/(°) | 弹性模量/MPa | 泊松比 | 拱顶沉降/mm | 周边位移/mm | 地表沉降/mm | ||
| 1 | 60 | 20 | 200 | 0.32 | 19.09 | 17.82 | 8.44 | |
| 2 | 60 | 22 | 250 | 0.34 | 15.64 | 14.28 | 6.74 | |
| 3 | 60 | 24 | 300 | 0.36 | 13.18 | 11.78 | 5.58 | |
| 4 | 60 | 26 | 350 | 0.38 | 11.33 | 9.98 | 4.74 | |
| 5 | 60 | 28 | 400 | 0.40 | 15.66 | 12.23 | 6.84 | |
| 6 | 90 | 20 | 250 | 0.36 | 13.08 | 10.14 | 5.62 | |
| 7 | 90 | 22 | 300 | 0.38 | 11.20 | 8.61 | 4.63 | |
| 8 | 90 | 24 | 350 | 0.40 | 9.74 | 7.46 | 4.08 | |
| 9 | 90 | 26 | 400 | 0.32 | 14.18 | 10.18 | 6.78 | |
| 10 | 90 | 28 | 200 | 0.34 | 11.62 | 8.42 | 5.07 | |
| 11 | 120 | 20 | 300 | 0.40 | 10.07 | 7.19 | 4.33 | |
| 12 | 120 | 22 | 350 | 0.32 | 8.89 | 6.29 | 3.76 | |
| 13 | 120 | 24 | 400 | 0.34 | 13.80 | 8.38 | 6.30 | |
| 14 | 120 | 26 | 200 | 0.36 | 11.59 | 7.25 | 5.16 | |
| 15 | 120 | 28 | 250 | 0.38 | 9.37 | 6.37 | 4.06 | |
| 16 | 150 | 20 | 350 | 0.34 | 8.34 | 5.68 | 3.54 | |
| 17 | 150 | 22 | 400 | 0.36 | 12.93 | 7.58 | 5.99 | |
| 18 | 150 | 24 | 200 | 0.38 | 10.99 | 6.66 | 4.97 | |
| 19 | 150 | 26 | 250 | 0.40 | 9.62 | 5.98 | 4.26 | |
| 20 | 150 | 28 | 300 | 0.32 | 8.00 | 5.30 | 3.42 | |
| 21 | 180 | 20 | 400 | 0.38 | 12.44 | 7.11 | 5.81 | |
| 22 | 180 | 22 | 200 | 0.40 | 10.64 | 6.32 | 4.82 | |
| 23 | 180 | 24 | 250 | 0.32 | 9.38 | 5.72 | 4.18 | |
| 24 | 180 | 26 | 300 | 0.34 | 8.40 | 5.24 | 3.66 | |
| 25 | 180 | 28 | 350 | 0.36 | 19.09 | 17.82 | 8.44 | |
3.4 数据归一化及网络模型参数设置
由于神经网络样本数据的量级相差较大,如果不进行处理,可能会导致神经网络计算时间长。因此,为保证训练效果,需要先对输入向量和输出向量分别进行归一化处理。利用最大值最小值法,采用MATLAB内置的mapminmax函数对样本进行归一化处理。将样本中的输入向量、输出向量归化到[0, 1]区间,再利用MATLAB平台的BP神经网络对样本进行网络训练,并通过反归一化得到输出向量。
根据BP神经网络算法原理以及相关参数设置要求,隐含层的传递函数、输出层的传递函数选取为logsig函数,网络训练函数选取为改进的L-M算法,神经网络的学习速率η设定为0.05,网络的误差设定为0.01。在本次反分析中,根据控制变量法确定遗传算法控制参数,其中遗传算法种群规模取30;最大遗传代数取值25;交叉概率取值0.8,变异概率取值0.01。
利用表 3的神经网络样本对GA-BP神经网络训练,得到训练成熟的GA-BP神经网络。将部分样本代入到训练好的神经网络中进行检测,对比分析预测值与期望值之间的误差,以此检测训练好的GA-BP神经网络的仿真预测能力是否能够达到要求。如果未达到要求,通过调整参数,迭代计算直至满足误差要求。
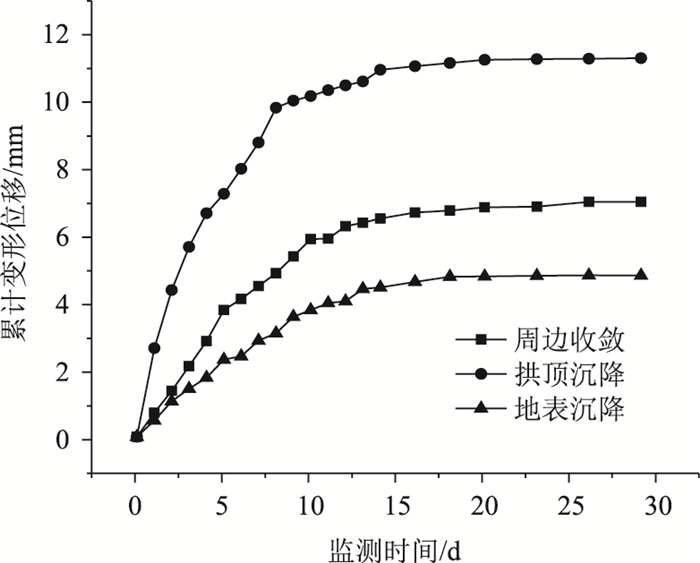
3.5 现场监控量测数据回归分析调取莲花隧道进口右洞YK35+115断面的监控量测数据进行分析探讨,围岩实测变形情况如图 4所示。利用最小二乘法对围岩的水平收敛、拱顶沉降及地表沉降位移监控量测数据进行回归分析:
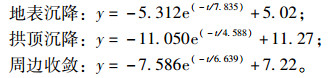
|
|
| 图 4 隧道变形位移随时间变化曲线 Fig. 4 Curves of tunnel displacement vs. time |
| |
3.6 位移反分析计算结果
调取莲花隧道断面YK35+115的监控量测数据,把实测变形位移值[11.21;6.95;4.73]作为输入向量,代入到成熟的GA-BP神经网络中,得到围岩力学参数输出向量[118.64;26.42;212.35;0.36]。
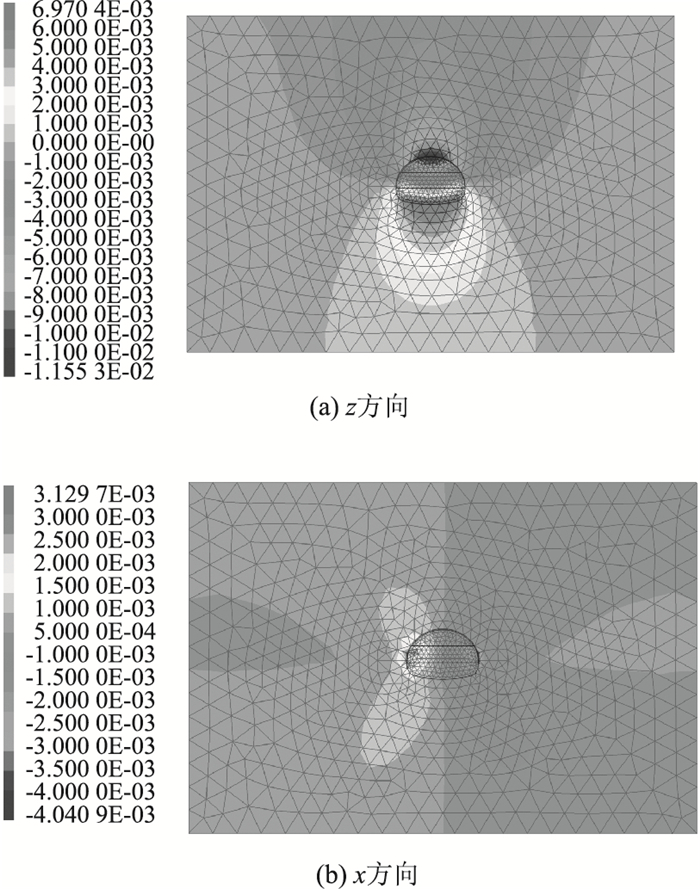
为了验证参数反演结果的可靠性和准确性,再将输出的围岩力学参数值代入到上述建立好的FLAC3D模型中进行正演计算,得到莲花隧道的拱顶沉降、周边位移、地表沉降数值(如图 5所示),并与实测位移进行误差分析。隧道围岩力学参数反演计算结果及误差情况如表 4所示。
|
| 图 5 正演计算位移云图(单位:m) Fig. 5 Nephograms of displacement by forward calculation(unit: m) |
| |
| 监测断面 | 监测项目 | 输入向量(实测值)/mm | 输出向量(反演的围岩力学参数) | 正演计算值/mm | 相对误差/% | |||
| c/kPa | φ/(°) | E/MPa | 泊松比 | |||||
| YK35+115 | 拱顶沉降 | 11.21 | 118.46 | 26.42 | 212.35 | 0.36 | 11.55 | 2.94 |
| 周边位移 | 6.95 | 7.17 | 3.16 | |||||
| 地表沉降 | 4.73 | 4.96 | 4.86 | |||||
分析表 4可知,基于隧道YK35+11断面拱顶沉降11.21 mm;周边位移6.95 mm;地表沉降4.73 mm的实测位移情况,通过GA-BP神经网络反演计算,得到隧道进洞口YK35+095~YK35+135段围岩的黏聚力118.46 kPa,内摩擦角26.42°,弹性模量212.35 MPa,泊松比0.36。根据反演得到的围岩力学参数,运用FLAC3D有限差分法计算,得到隧道拱顶沉降11.55 mm,与实测拱顶沉降相对误差2.94%;周边位移7.17 mm,与实测周边位移相对误差3.16%;地表沉降4.96 mm,与实测地表沉降相对误差4.86%;正演计算的各位移值与实测值相差很小。可见,采用GA-BP神经网络反演围岩力学参数方法准确度较高,对围岩变形预测较为接近。
4 结论(1) 应用GA-BP神经网络,对利用正交设计试验并结合有限差分法构造的样本集进行训练,得到了训练成熟的GA-BP神经网络,可以方便地反演计算围岩力学参数。
(2) 采用GA-BP神经网络反演分析方法,得到围岩力学参数的误差较小,具有较高的精度和可靠性。莲花隧道右洞进口段反演得到的力学参数应用到FLAC3D中正演计算,得到拱顶沉降,周边位移和地表沉降与现场实测值仅相差2.94%,3.16%和4.86%,反演结果较为准确。可见,基于GA-BP神经网络的隧道围岩力学参数反演方法,可为隧道设计提供所需的计算参数,对隧道信息化动态设计及施工有一定的应用价值。
| [1] |
戴薇, 石崇, 张金龙. 浅埋地下洞室围岩岩体力学参数反分析研究[J]. 河北工程大学学报:自然科学版, 2019, 36(1): 59-63. DAI Wei, SHI Chong, ZHANG Jin-long. Study on Inverse Analysis of Mechanical Parameters of Surrounding Rock Mass in Shallow Underground Cavern[J]. Journal of Hebei University of Engineering:Natural Science Edition, 2019, 36(1): 59-63. |
| [2] |
万智勇, 黄耀英, 朱赵辉, 等. 高寒地区碾压混凝土坝运行期力学参数反演分析[J]. 水利水电技术, 2017, 48(12): 50-55. WAN Zhi-yong, HUANG Yao-ying, ZHU Zhao-hui, et al. Back Analysis on Mechanical Parameters of RCC Dam during Operation Period in Alpine Region[J]. Water Resources and Hydropower Engineering, 2017, 48(12): 50-55. |
| [3] |
王军祥, 蔺雅娴, 孟津竹, 等. 沙湾特长隧道软弱破碎千枚岩围岩参数敏感性分析与反演研究[J]. 隧道建设, 2018, 38(增2): 87-97. WANG Jun-xiang, LIN Ya-xian, MENG Jin-zhu, et al. Sensitivity Analysis and Inversion Study of Parameters of Weak and Broken Phyllite of Shawan Extra-long Tunnel[J]. Tunnel Construction, 2018, 38(S2): 87-97. |
| [4] |
周冠南, 孙玉永, 贾蓬. 基于遗传算法的BP神经网络在隧道围岩参数反演和变形预测中的应用[J]. 现代隧道技术, 2018, 55(1): 107-113. ZHOU Guan-nan, SUN Yu-yong, JIA Peng. Application of Genetic Algorithm Based BP Neural Network to Parameter Inversion of Surrounding Rock and Deformation Prediction[J]. Modern Tunneling Technology, 2018, 55(1): 107-113. |
| [5] |
杨茜. BP神经网络预测方法的改进及其在隧道长期沉降预测中的应用[J]. 北京工业大学学报, 2011, 37(1): 92-97. YANG Qian. Improvement of the Improved BP Neural Network Forecast Method and Its Application in Long-term Settlement of the Tunnel[J]. Journal of Beijing University of Technology, 2011, 37(1): 92-97. |
| [6] |
赵杰, 刘历胜, 王桂萱, 等. 大连地铁暗挖隧道变形监测及参数智能反演[J]. 防灾减灾工程学报, 2016, 36(40): 640-645. ZHAO Jie, LIU Li-sheng, WANG Gui-xuan, et al. Deformation Monitoring and Inversion Analysis of Surrounding Rock Mechanics Parameters for Metro Construction with Mining Method in Dalian[J]. Journal of Disaster Prevention and Mitigation Engineering, 2016, 36(40): 640-645. |
| [7] |
吕志涛, 吴庚林, 靳晓光, 等. 隧道膨胀性围岩蠕变特性分析及参数反演[J]. 地下空间与工程学报, 2016, 12(6): 1504-1510. LÜ Zhi-tao, WU Geng-lin, JIN Xiao-guang, et al. Creep Characteristics Analysis and Parameter Inversion of Swelling Rock in Tunnel[J]. Chinese Journal of Underground Space and Engineering, 2016, 12(6): 1504-1510. |
| [8] |
饶云康, 丁瑜, 许文年, 等. 应用GA-BP神经网络预估砾类土的最大干密度[J]. 长江科学院院报, 2019, 36(4): 88-92. RAO Yun-kang, DING Yu, XU Wen-nian, et al. Estimating Maximum Dry Density of Gravel Soil by Back Propagation Neural Network Optimized by Genetic Algorithm[J]. Journal of Yangtze River Scientific Research Institute, 2019, 36(4): 88-92. |
| [9] |
张飞, 徐光黎, 魏志云, 等. 考虑松动圈的地下洞室群施工期岩体参数反演[J]. 长江科学院院报, 2013, 30(7): 75-80, 85. ZHANG Fei, XU Guang-li, WEI Zhi-yun, et al. Intelligent Back Analysis of Rockmass Parameters of Underground Caverns in Consideration of Loose Zone during Construction[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(7): 75-80, 85. |
| [10] |
盖宏健.基于轮壤相互作用模型的星壤力学参数反演研究[D].长春: 吉林大学, 2019. GAI Hong-jian. Estimation Research of Mechanical Parameters of Planet Soil Based on Wheel-soil Model[D]. Changchun: Jilin University, 2019. http://cdmd.cnki.com.cn/Article/CDMD-10183-1019160567.htm |
| [11] |
李振涛, 姜磊, 刘宇, 等. 砂土区间地铁盾构施工土体参数反演及其验证[J]. 地下空间与工程学报, 2014, 10(3): 630-634. LI Zhen-tao, JIANG Lei, LIU Yu, et al. Inverse Analysis and Verification of Soil Parameters for Metro Shield Construction in Sand Layer[J]. Chinese Journal of Underground Space and Engineering, 2014, 10(3): 630-634. |
| [12] |
祝江林, 陈秋南. 白水隧道围岩力学参数敏感性分析与智能反演[J]. 湖南文理学院学报:自然科学版, 2019, 31(2): 85-89. ZHU Jiang-lin, CHEN Qiu-nan. Analysis and Intelligent Inversion of Mechanical Parameters of Surrounding Rock in Baishui Tunnel[J]. Journal of Hunan University of Arts and Science:Science and Technology Edition, 2019, 31(2): 85-89. |
| [13] |
关永平, 宋建, 王述红, 等. 基于GA-BP算法的隧道围岩力学参数反分析[J]. 东北大学学报:自然科学版, 2012, 33(2): 276-278,283. GUAN Yong-ping, SONG Jian, WANG Shu-hong, et al. Back Analysis of Mechanical Parameters of Surrounding Rocks Based on GA-BP Algorithm[J]. Journal of Northeastern University:Natural Science Edition, 2012, 33(2): 276-278,283. |
| [14] |
赵旭峰, 王春苗, 孔祥利. 深部软岩隧道施工性态时空效应分析[J]. 岩石力学与工程学报, 2007, 26(2): 404-409. ZHAO Xu-feng, WANG Chun-miao, KONG Xiang-li. Analysis of Time-space Effects of Construction Behavior of Deep Soft Rock Tunnel[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(2): 404-409. |
| [15] |
施有志.双孔平行地铁隧道开挖的复变函数解析解与数值分析[D].厦门: 华侨大学, 2013. SHI You-zhi. Analytic Solution of Complex Function and Numerical Analysis of Double-hole Parallel Tunnel Excavation[D]. Xiamen: Huaqiao University, 2013. http://cdmd.cnki.com.cn/Article/CDMD-10385-1014006968.htm |
| [16] |
陈浩, 任伟中, 李丹, 等. 深埋隧道锚杆支护作用的数值模拟与模型试验研究[J]. 岩土力学, 2011, 32(增1): 719-724,786. CHEN Hao, REN Wei-zhong, LI Dan, et al. Numerical Simulation and Model Test Study of Mechanism of Bolt in Deep Tunnel[J]. Rock and Soil Mechanics, 2011, 32(S1): 719-724,786. |
| [17] |
杨超, 张永兴, 黄达, 等. 地形偏压隧道开挖变形特征及预加固措施[J]. 公路交通科技, 2012, 29(7): 97-103. YANG Chao, ZHANG Yong-xing, HUANG Da, et al. Deformation Behavior of Topographic Unsymmetrical Loaded Tunnel after Excavation and Its Pre-reinforcement[J]. Journal of Highway and Transportation Research and Development, 2012, 29(7): 97-103. |
| [18] |
肖大海, 谢全敏, 杨文东. 基于多变量的集成预测模型在隧道拱顶沉降变形预测中的应用[J]. 公路交通科技, 2017, 34(12): 90-96. XIAO Da-hai, XIE Quan-min, YANG Wen-dong. Application of Integrated Forecasting Model Based on Multivariable in Tunnel Vault Settlement Forecasting[J]. Journal of Highway and Transportation Research and Development, 2017, 34(12): 90-96. |
| [19] |
贠永峰, 范永慧, 孙扬. 基于BP神经网络的隧道围岩力学参数反分析方法[J]. 沈阳建筑大学学报:自然科学版, 2011, 27(2): 292-296,306. YUN Yong-feng, FAN Yong-hui, SUN Yang. Back-Analysis of Mechanical Parameters of Tunnel Surrounding Rock by BP Neural Network Method[J]. Journal of Shenyang Jianzhu University:Natural Science Edition, 2011, 27(2): 292-296,306. |
 2020, Vol. 37
2020, Vol. 37
