扩展功能
文章信息
- 王家林, 曹珂瑞
- WANG Jia-lin, CAO Ke-rui
- 一种基于指定应力的斜拉桥成桥索力调整方法
- A Method for Adjusting Cable Force of Cable-stayed Bridge in Finished State Based on Specified Stress
- 公路交通科技, 2020, 37(7): 72-78, 89
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(7): 72-78, 89
- 10.3969/j.issn.1002-0268.2020.07.010
-
文章历史
- 收稿日期: 2019-04-02
大部分斜拉桥的拉索张拉常采用一次张拉为主,成桥后再进行二次调索来保证结构在施工过程中的安全[1]。二次调索是在当前状态与设计成桥状态有偏差的情况下,通过调整索力使当前成桥状态的内力分布趋向于设计成桥状态的内力分布[2-5]。
斜拉桥作为高次超静定结构,内力情况较为复杂,如何通过二次调索使成桥索力达到目标索力一直是斜拉桥设计施工中的难点[6]。众多学者对斜拉桥的成桥索力调整问题进行了大量研究,提出了多种索力调整方法,分别是最小二乘法[7]、弯曲能量最小法[8]、弯矩最小法[9]、循环迭代法[10]、凝聚函数法[11]、影响矩阵法[12]、正装迭代法[13]。
最小二乘法是使误差平方和最小,经过多次迭代后得到最终值;弯曲能量最小法用斜拉桥桥塔和主梁的弯曲应变能为目标函数来进行优化求解;弯矩最小法用弯矩平方和最小作为优化目标;循环迭代法基于初应变或温度荷载,建立单根索力与其初应力或温度荷载之间的关系,通过改变各拉索的初应变或温度荷载来调整桥梁内力;凝聚函数法通过引入信息熵函数[14],将多目标多约束的非线性规划问题转化为光滑、可微的单目标、单约束优化问题进行求解;影响矩阵法是目前斜拉桥成桥索力调整中应用最为广泛的方法,将斜拉桥优化的多种目标函数统一用索力变量与广义影响矩阵表示,实现了一种方法对多种目标函数进行优化的目的,既可用于成桥阶段,也可用于施工阶段,具有便于电算的优点,缺点是计算复杂,计算量大,需要通过多次迭代才能得到各拉索近似非弹性变形影响,存在不够准确的问题;正装迭代法基于影响矩阵法,能方便地计入混凝土收缩徐变和几何非线性的影响,便于编程实现。
文献[15]提出了一种含非弹性收缩量的预应力筋桁架单元,在考虑预应力筋刚度的同时,可准确模拟预应力筋单元的有效预应力,实现了在分析结果中桁架单元的轴力(应力)等于指定的值。本研究将其用于模拟斜拉桥的拉索,提出了分析斜拉桥二次调索的一种新方法。以一座单塔双跨不对称布置的斜拉桥结构为模型,进行二次调索计算,并在Midas中建立相应的结构模型,对本方法的计算结果进行验证。
1 基于指定应力的全桥拉索调整以平面坐标系下为例,将斜拉桥的拉索用含非弹性收缩量的预应力筋单元[15]模拟时,单元平衡方程为:
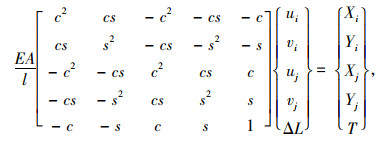
|
(1) |
式中,E,A,l分别为拉索单元的弹性模量、横截面面积、建模长度;c,s为拉索单元的方向余弦;ui,vi,uj,vj分别为节点i和j在直角坐标系下沿x,y方向的位移分量;Xi,Yi,Xj,Yj分别为与各位移分量对应的力分量;ΔL为拉索的非弹性收缩量;T为拉索的拉力。
对斜拉桥进行整体分析,建立的平衡方程为:
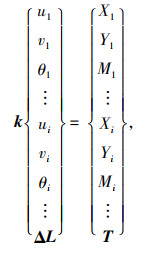
|
(2) |
或简写为:
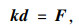
|
(3) |
式中,k为考虑斜拉索非弹性收缩量后的结构总刚度矩阵;ui, vi, θi分别为各节点的常规位移;Xi, Yi, Mi分别为常规的节点荷载;ΔL = {ΔL1 ΔL2 … ΔLj …}T,为各拉索的非弹性收缩量;T = { T1 T2 … Tj … }T,为各拉索的拉力;d = { u1 v1 θ1 … ui vi θi … ΔL }T,为含各拉索非弹性收缩量的结构广义位移向量;F = { X1 Y1 M1 … Xi Yi Mi … T }T,为含各拉索拉力的结构广义荷载向量。
基于指定应力有限元方法进行全部索力调整的算法步骤为:
1.1 确定当前索力对应的非弹性收缩量ΔLc将T设置为当前已知索力Tc,此时:
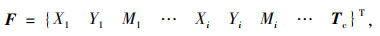
|
(4) |
解式(2),可得广义位移向量,记为d:
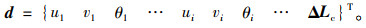
|
(5) |
式(4)中的非弹性收缩量ΔLc即为初始索力对应的斜拉索非弹性收缩量。
1.2 确定目标索力对应的非弹性收缩量ΔLm将T设置为目标索力Tm,重复步骤1.1的过程,可得到与目标索力对应的非弹性收缩量ΔLm。
1.3 确定调索长度ΔLt各拉索的无应力调索量(缩短为正) ΔLt的确定式为:
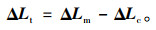
|
(6) |
根据指定应力法,对全桥斜拉索进行索力调整可以在理论上使得全部索力精确等于目标索力。但在实际工程中,斜拉桥索力调整的施工难度大,施工控制复杂,对全桥斜拉索进行索力调整很不经济。
从工程角度看,实际索力与目标值容许有较小的误差。这时需要解决的问题是如何调整部分斜拉索,使得全部拉索的索力满足工程要求精度。本研究基于指定应力法,提出一个以部分拉索的非弹性收缩量为优化变量、以全部拉索的索力差为目标函数的优化模型。
2.1 部分斜拉索索力调整方法将广义位移向量d和广义力向量F分为4类:
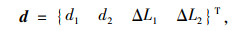
|
(7) |
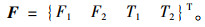
|
(8) |
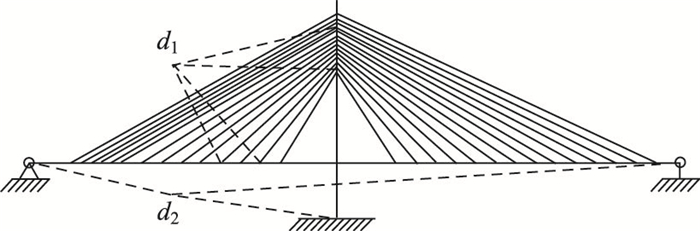
式(7)~ (8)中各项的含义与在结构有限元平衡方程中的状态见表 1,d1, d2示意图见图 1。
| 变量 | 含义 | 状态 |
| d1 | 非约束、非拉索自由度 | 未知 |
| d2 | 约束自由度 | 已知 |
| ΔL1 | 调索单元的非弹性收缩量 | 未知 |
| ΔL2 | 不调索拉索单元的非弹性收缩量 | 已知 |
| F1 | 非约束、非拉索自由度对应的荷载 | 已知 |
| F2 | 约束自由度对应的约束反力 | 未知 |
| T1 | 调索单元的优化后索力 | 未知 |
| T2 | 不调索的拉索单元的优化后索力 | 未知 |
|
| 图 1 d1, d2示意图 Fig. 1 Schematic diagram of d1 and d2 |
| |
根据式(7)~ (8),将式(2)中的k整理为分块矩阵形式,可得:
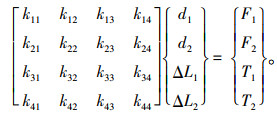
|
(9) |
根据上式可得:
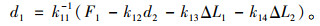
|
(10) |
由于F1,d2,ΔL2已知,式(10)可表达为:
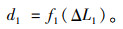
|
(11) |
进一步可得:
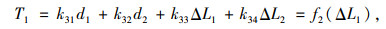
|
(12) |
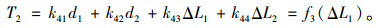
|
(13) |
式(12)~ (13)表明,全部索力是以调索单元的非弹性收缩量为自变量的函数。根据目标索力,可选择不同形式的索力误差作为目标函数进行索力优化。
例1 以目标索力与优化后索力的差值平方和为目标函数,按最小值进行优化:
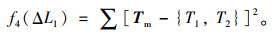
|
(14) |
例2 以目标索力与优化后索力的相对差值的绝对值最大值为目标函数,按最小值进行优化:
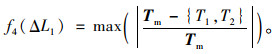
|
(15) |
对于调整部分拉索的优化问题,选择不同数量、不同位置的索会得到不同的优化结果。为选取尽可能少的斜拉索得到满足要求的优化结果,可按不同方法选择不同拉索组合进行索力优化,选择其中效果最好的拉索组合作为最终的调索方案。
2.2.1 穷举法对所有拉索组合进行分析,比较调索结果,找出最佳的索力调整方案。此方法的缺点是计算量很大,只适用于拉索数量较少的斜拉桥。
2.2.2 按索力误差一次排序,递增调索数量根据各索当前索力与目标索力的某种误差,从大到小排序,逐次增加调索数量,直到调索效果满足精度要求。此方法简便易用,计算速度快。缺点是难以获得最佳的拉索组合。
2.2.3 按索力误差逐次排序,递增调索数量在增加1根拉索进行调索时,在备选索中选择当前索力误差最大的索,与已选索组合成新的拉索组合进行调索优化,逐次递增调索数量,直到得到满足要求的调索方案。
2.2.4 穷举递增在上次组合基础上,穷举增加1根索的拉索组合,将效果最优的拉索组合作为新的拉索组合,比较优化效果,直到得到满足要求的调索方案。
3 算例分析利用前述方法,利用C++语言编制了1个有限元软件,单元类型包括常规桁架单元、梁单元及含非弹性收缩量的桁架单元。将每根拉索模拟为含非弹性收缩量的桁架单元,在指定索力时可计算其拉索非弹性收缩量;在指定非弹性收缩量时,可计算其索力。该软件可方便地解决全桥调索问题。
部分调索的计算思路为:
(1) 利用自编有限元软件输出总刚矩阵。
(2) 在Matlab软件中按式(9)分块,得到式(12)~ (13)。
(3) 利用fminimax函数选择式(15)的目标函数进行优化计算。
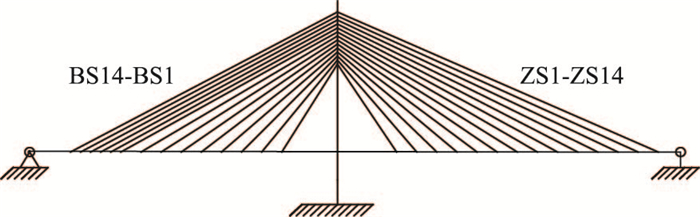
3.1 模型概况参考杨兴等[16]的结构数据,建立简化斜拉桥模型,布置情况见图 2。
|
| 图 2 斜拉桥总体布置 Fig. 2 General layout of cable-stayed bridge |
| |
斜拉桥采用独塔双跨不对称布置,主跨130 m,边跨145 m,桥面宽19 m。斜拉索采用扇形索面,主跨斜拉索ZS1-ZS14索距8.5 m, 边跨斜拉索BS9-BS1索距8.5 m,BS14-BS10索距4.25 m,用桁架单元模拟。主梁采用C50混凝土,采用换算实腹式长方形截面,梁高1.9 m,宽19 m,截面惯性矩10.86 m4。拉索弹性模量1.95×1011 Pa,线膨胀系数α=1.2×105/℃,换算面积0.017 08 m2,用梁单元模拟。全桥换算均布荷载307 kN/m, 作用在主梁上。
3.2 全桥索力调整根据资料,得到斜拉桥初始索力Tc和目标索力Tm,根据本研究的全桥拉索调整方法,分别计算初始索力的非弹性收缩量ΔLc和目标索力的非弹性收缩量ΔLm,其差值即为无应力调索量ΔLt。
在Midas中建立相同的结构模型,分别将本方法计算得到的非弹性收缩量ΔLc和ΔLm转换为温度荷载或初拉力施加Midas结构索单元上,此时相当于对Midas结构施加了1组荷载,观察其索力情况。若Midas计算得到的索力与对应的初始索力Tc和目标索力Tm相近,其误差在允许范围内,可认为本方法正确。
将非弹性收缩量ΔL转换为温度变化(降温为正) t的关系为:
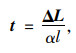
|
(16) |
式中,α为拉索线膨胀系数;l为拉索单元长度。
从表 2可以看出,全桥调索的计算结果与Midas验算结果很接近,误差主要来源于式(16)中数据输入、输出的有效位数截断,验证了前述方法和自编软件的正确性。
| 拉索编号 | 单元长度/m | 初始索力/kN | 初始索力非弹性收缩量/m | 初始索力换算温度/℃ | 初始索力温度荷载的Midas计算索力/kN | 差值[1]/% | 目标索力/kN | 目标索力非弹性收缩量/m | 目标索力换算温度/℃ | 目标索力温度荷载的Midas计算索力/kN | 差值[1]/% | 调索量[2]/m |
| BS1 | 45.962 | 4 107 | 0.215 | -388.917 | 4 099.405 | 0.185 | 5 307 | 0.336 | -609.277 | 5 292.390 | 0.275 | 0.122 |
| BS2 | 52.246 | 4 538 | 0.316 | -503.885 | 4 532.024 | 0.132 | 5 726 | 0.484 | -772.584 | 5 714.962 | 0.193 | 0.168 |
| BS3 | 59.143 | 4 627 | 0.405 | -570.115 | 4 622.517 | 0.097 | 6 115 | 0.619 | -871.642 | 6 107.053 | 0.130 | 0.214 |
| BS4 | 66.460 | 6 192 | 0.507 | -635.874 | 6 189.113 | 0.047 | 6 981 | 0.739 | -926.970 | 6 976.253 | 0.068 | 0.232 |
| BS5 | 74.075 | 5 672 | 0.550 | -618.750 | 5 669.985 | 0.036 | 6 724 | 0.810 | -910.711 | 6 720.955 | 0.045 | 0.260 |
| BS6 | 81.904 | 5 833 | 0.585 | -595.009 | 5 831.360 | 0.028 | 7 094 | 0.863 | -877.968 | 7 091.764 | 0.032 | 0.278 |
| BS7 | 89.891 | 6 991 | 0.624 | -578.337 | 6 989.290 | 0.024 | 7 590 | 0.890 | -825.142 | 7 588.010 | 0.026 | 0.266 |
| BS8 | 97.997 | 7 584 | 0.628 | -534.124 | 7 582.173 | 0.024 | 8 260 | 0.894 | -760.252 | 8 258.062 | 0.023 | 0.266 |
| BS9 | 106.195 | 6 765 | 0.567 | -444.836 | 6 762.988 | 0.030 | 7 898 | 0.839 | -658.396 | 7 895.910 | 0.026 | 0.272 |
| BS10 | 110.772 | 7 267 | 0.561 | -421.958 | 7 264.904 | 0.029 | 8 245 | 0.826 | -621.574 | 8 242.840 | 0.026 | 0.265 |
| BS11 | 115.353 | 7 647 | 0.546 | -394.145 | 7 644.885 | 0.028 | 8 629 | 0.808 | -583.637 | 8 626.872 | 0.025 | 0.262 |
| BS12 | 119.936 | 8 595 | 0.546 | -379.086 | 8 593.209 | 0.021 | 8 761 | 0.774 | -537.904 | 8 759.277 | 0.020 | 0.229 |
| BS13 | 124.521 | 9 517 | 0.542 | -362.429 | 9 515.844 | 0.012 | 8 903 | 0.735 | -491.580 | 8 902.031 | 0.011 | 0.193 |
| BS14 | 129.108 | 8 455 | 0.458 | -295.796 | 8 454.779 | 0.003 | 8 963 | 0.686 | -443.090 | 8 962.994 | 0.000 | 0.228 |
| ZS1 | 46.747 | 4 045 | 0.219 | -389.749 | 4 039.465 | 0.137 | 5 263 | 0.284 | -506.817 | 5 250.651 | 0.235 | 0.066 |
| ZS2 | 53.178 | 4 513 | 0.311 | -486.929 | 4 508.455 | 0.101 | 5 684 | 0.405 | -634.523 | 5 674.667 | 0.164% | 0.094 |
| ZS3 | 60.180 | 4725 | 0.394 | -545.002 | 4 721.452 | 0.075 | 6 042 | 0.514 | -712.125 | 6 035.380 | 0.110 | 0.121 |
| ZS4 | 67.574 | 5 906 | 0.485 | -598.650 | 5 903.517 | 0.042 | 6 334 | 0.605 | -745.870 | 6 329.899 | 0.065 | 0.119 |
| ZS5 | 75.245 | 5 690 | 0.537 | -594.691 | 5 688.478 | 0.027 | 6 643 | 0.675 | -747.289 | 6 640.573 | 0.037 | 0.138 |
| ZS6 | 83.117 | 5 794 | 0.580 | -581.862 | 5 792.939 | 0.018 | 7 094 | 0.726 | -728.106 | 7 092.382 | 0.023 | 0.146 |
| ZS7 | 91.138 | 6 813 | 0.634 | -579.696 | 6 811.882 | 0.016 | 8 003 | 0.769 | -703.146 | 8 001.538 | 0.018 | 0.135 |
| ZS8 | 99.271 | 7 219 | 0.659 | -553.532 | 7 217.845 | 0.016 | 8 229 | 0.774 | -649.331 | 8 227.711 | 0.016 | 0.114 |
| ZS9 | 107.490 | 6 970 | 0.652 | -505.231 | 6 968.933 | 0.015 | 7 969 | 0.743 | -576.042 | 7 967.923 | 0.014 | 0.091 |
| ZS10 | 115.779 | 7 234 | 0.648 | -466.436 | 7 232.621 | 0.019 | 8 105 | 0.707 | -508.978 | 8 103.641 | 0.017 | 0.059 |
| ZS11 | 124.122 | 7 658 | 0.641 | -430.285 | 7 656.329 | 0.022 | 8 252 | 0.658 | -441.448 | 8 250.404 | 0.019 | 0.017 |
| ZS12 | 132.509 | 8 128 | 0.629 | -395.543 | 8 126.103 | 0.023 | 8 281 | 0.592 | -372.600 | 8 279.174 | 0.022 | -0.036 |
| ZS13 | 140.933 | 8 695 | 0.617 | -364.884 | 8 692.848 | 0.025 | 8 323 | 0.520 | -307.677 | 8 320.879 | 0.025 | -0.097 |
| ZS14 | 149.388 | 9 300 | 0.606 | -338.116 | 9 297.639 | 0.025 | 8 335 | 0.443 | -247.252 | 8 332.610 | 0.029 | -0.163 |
| 注: 1.差值=(索力-索力换算温度荷载的Midas计算内力)/索力; 2.调索量=目标索力非弹性收缩量-初始索力非弹性收缩量。 | ||||||||||||
3.3 部分斜拉索索力优化调整
本研究使用穷举法,求解27, 26, 25根斜拉索进行优化调整时的最佳拉索组合的优化效果,目标函数取为式(15)。
调27根索时,不调整ZS11索的效果最优,目标索力与优化后索力相对差值绝对值的最大值为0.116%。
调26根索时,不调整ZS1,ZS5索的效果最优,目标索力与优化后索力相对差值绝对值的最大值为1.432%。
调25根索时,不调整ZS1,ZS5,ZS4索的效果最优,目标索力与优化后索力相对差值绝对值的最大值为1.497%。
| 拉索编号 | 目标索力/kN | 27根斜拉索的最优组合 | 26根斜拉索的最优组合 | 25根斜拉索的最优组合 | ||||||||||||||
| 优化拉索组合 | 优化后索力非弹性收缩量/m | 优化后索力/kN | 优化后索力与目标索力差值/% | Midas验算(代入非弹性收缩量后索力)/kN | 优化拉索组合 | 优化后索力非弹性收缩量/m | 优化后索力/kN | 优化后索力与目标索力差值/% | Midas验算(代入非弹性收缩量后索力)/kN | 优化拉索组合 | 优化后索力非弹性收缩量/m | 优化后索力/kN | 优化后索力与目标索力差值/% | Midas验算(代入非弹性收缩量后索力)/kN | ||||
| BS1 | 5 307 | BS1 | 0.341 | 5 313.147 | 0.116 | 5 298.852 | BS1 | 0.398 | 5 382.972 | 1.432 | 5 368.199 | BS1 | 0.399 | 5 386.443 | 1.497 | 5 371.635 | ||
| BS2 | 5 726 | BS2 | 0.491 | 5 732.633 | 0.116 | 5 721.664 | BS2 | 0.567 | 5 807.970 | 1.432 | 5 796.685 | BS2 | 0.569 | 5 811.716 | 1.497 | 5 800.400 | ||
| BS3 | 6 115 | BS3 | 0.627 | 6 122.083 | 0.116 | 6 114.084 | BS3 | 0.721 | 6 202.539 | 1.432 | 6 194.281 | BS3 | 0.723 | 6 206.539 | 1.497 | 6 198.270 | ||
| BS4 | 6 981 | BS4 | 0.749 | 6 989.087 | 0.116 | 6 984.268 | BS4 | 0.859 | 7 080.936 | 1.432 | 7 075.983 | BS4 | 0.861 | 7 085.502 | 1.497 | 7 080.533 | ||
| BS5 | 6 724 | BS5 | 0.820 | 6 731.789 | 0.116 | 6 728.629 | BS5 | 0.944 | 6 820.257 | 1.432 | 6 816.972 | BS5 | 0.947 | 6 824.655 | 1.497 | 6 821.391 | ||
| BS6 | 7 094 | BS6 | 0.875 | 7 102.217 | 0.116 | 7 099.894 | BS6 | 1.011 | 7 195.554 | 1.432 | 7 193.173 | BS6 | 1.014 | 7 200.194 | 1.497 | 7 197.810 | ||
| BS7 | 7 590 | BS7 | 0.903 | 7 598.792 | 0.116 | 7 596.805 | BS7 | 1.051 | 7 698.654 | 1.432 | 7 696.634 | BS7 | 1.054 | 7 703.619 | 1.497 | 7 701.585 | ||
| BS8 | 8 260 | BS8 | 0.908 | 8 269.568 | 0.116 | 8 267.728 | BS8 | 1.067 | 8 378.245 | 1.432 | 8 376.398 | BS8 | 1.070 | 8 383.648 | 1.497 | 8 381.778 | ||
| BS9 | 7 898 | BS9 | 0.854 | 7 907.149 | 0.116 | 7 905.297 | BS9 | 1.022 | 8 011.063 | 1.432 | 8 009.253 | BS9 | 1.025 | 8 016.229 | 1.497 | 8 014.395 | ||
| BS10 | 8 245 | BS10 | 0.842 | 8 254.551 | 0.116 | 8 252.720 | BS10 | 1.017 | 8 363.031 | 1.432 | 8 361.246 | BS10 | 1.021 | 8 368.424 | 1.497 | 8 366.646 | ||
| BS11 | 8 629 | BS11 | 0.824 | 8 638.996 | 0.116 | 8 637.271 | BS11 | 1.007 | 8 752.528 | 1.432 | 8 750.795 | BS11 | 1.011 | 8 758.172 | 1.497 | 8 756.463 | ||
| BS12 | 8 761 | BS12 | 0.791 | 8 771.148 | 0.116 | 8 769.933 | BS12 | 0.981 | 8 886.417 | 1.432 | 8 885.243 | BS12 | 0.985 | 8 892.148 | 1.497 | 8 890.961 | ||
| BS13 | 8 903 | BS13 | 0.752 | 8 913.313 | 0.116 | 8 912.921 | BS13 | 0.949 | 9 030.450 | 1.432 | 9 030.142 | BS13 | 0.953 | 9 036.274 | 1.497 | 9 035.978 | ||
| BS14 | 8 963 | BS14 | 0.704 | 8 973.382 | 0.116 | 8 974.056 | BS14 | 0.909 | 9 091.309 | 1.432 | 9 092.131 | BS14 | 0.913 | 9 097.172 | 1.497 | 9 097.997 | ||
| ZS1 | 5 263 | ZS1 | 0.279 | 5 256.903 | 0.116 | 5 244.921 | ZS1 | 0.219 | 5 194.632 | 1.299 | 5 183.126 | ZS1 | 0.219 | 5 187.701 | 1.431 | 5 176.144 | ||
| ZS2 | 5 684 | ZS2 | 0.398 | 5 677.416 | 0.116 | 5 668.218 | ZS2 | 0.318 | 5 602.631 | 1.432 | 5 593.715 | ZS2 | 0.319 | 5 598.913 | 1.497 | 5 589.970 | ||
| ZS3 | 6 042 | ZS3 | 0.506 | 6 035.001 | 0.116 | 6 028.425 | ZS3 | 0.409 | 5 955.506 | 1.432 | 5 949.141 | ZS3 | 0.409 | 5 951.554 | 1.497 | 5 945.151 | ||
| ZS4 | 6 334 | ZS4 | 0.595 | 6 326.663 | 0.116 | 6 322.505 | ZS4 | 0.482 | 6 243.326 | 1.432 | 6 239.303 | ZS4 | 0.485 | 6 374.544 | 0.640 | 6 370.461 | ||
| ZS5 | 6 643 | ZS5 | 0.664 | 6 635.305 | 0.116 | 6 632.811 | ZS5 | 0.537 | 6 547.903 | 1.432 | 6 545.480 | ZS5 | 0.537 | 6 543.557 | 1.497 | 6 541.117 | ||
| ZS6 | 7 094 | ZS6 | 0.714 | 7 085.783 | 0.116 | 7 084.110 | ZS6 | 0.574 | 6 992.446 | 1.432 | 6 990.802 | ZS6 | 0.574 | 6 987.806 | 1.497 | 6 986.147 | ||
| ZS7 | 8 003 | ZS7 | 0.756 | 7 993.730 | 0.116 | 7 992.249 | ZS7 | 0.604 | 7 888.434 | 1.432 | 7 887.036 | ZS7 | 0.603 | 7 883.199 | 1.497 | 7 881.790 | ||
| ZS8 | 8 229 | ZS8 | 0.759 | 8 219.468 | 0.116 | 8 218.217 | ZS8 | 0.597 | 8 111.198 | 1.432 | 8 109.999 | ZS8 | 0.596 | 8 105.816 | 1.497 | 8 104.623 | ||
| ZS9 | 7 969 | ZS9 | 0.728 | 7 959.769 | 0.116 | 7 958.805 | ZS9 | 0.556 | 7 854.920 | 1.432 | 7 853.926 | ZS9 | 0.555 | 7 849.708 | 1.497 | 7 848.727 | ||
| ZS10 | 8105 | ZS10 | 0.691 | 8 095.611 | 0.116 | 8 094.491 | ZS10 | 0.511 | 7 988.974 | 1.432 | 7 987.825 | ZS10 | 0.509 | 7 983.672 | 1.497 | 7 982.533 | ||
| ZS11 | 8 252 | 0.641 | 8 242.441 | 0.116 | 8 241.202 | ZS11 | 0.452 | 8 133.869 | 1.432 | 8 132.557 | ZS11 | 0.450 | 8 128.471 | 1.497 | 8 127.191 | |||
| ZS12 | 8 281 | ZS12 | 0.575 | 8 271.408 | 0.116 | 8 270.084 | ZS12 | 0.379 | 8 162.454 | 1.432 | 8 160.991 | ZS12 | 0.376 | 8 157.037 | 1.497 | 8 155.582 | ||
| ZS13 | 8 323 | ZS13 | 0.502 | 8 313.359 | 0.116 | 8 311.852 | ZS13 | 0.299 | 8 203.853 | 1.432 | 8 202.210 | ZS13 | 0.296 | 8 198.408 | 1.497 | 8 196.753 | ||
| ZS14 | 8 335 | ZS14 | 0.425 | 8 325.345 | 0.116 | 8 323.705 | ZS14 | 0.215 | 8 215.681 | 1.432 | 8 213.872 | ZS14 | 0.211 | 8 210.229 | 1.497 | 8 208.429 | ||
上述结果使用Midas进行验算,误差在允许范围内,计算正确且均满足规范要求。24根索拉索组合数多达20 475种,穷举较为困难,不再计算。除穷举法,还可采用2.2节中的其他方法等多种方法选择拉索组合进行部分索力调整,对每种方法的性能的研究等工作将在以后展开。
4 结论迄今为止,已经有多种方法可以实现斜拉桥的二次调索计算,但是都存在诸如计算量大、计算复杂、不够准确等缺点。本研究基于指定应力有限元法,提出了一种斜拉桥二次调索的新计算方法,可对斜拉桥全桥进行二次调索,也可对部分斜拉索进行二次调索。对于结构规模较小,非线性因素影响不大的斜拉桥二次调索计算具有计算简单、便于电算、力学意义明确等优点,在工程上具有广泛的应用价值。
对于斜拉桥的二次调索问题,得到调索量后,按照一定的调索顺序最终可以使全桥的索力达到目标索力。但在实际工程中,为保证结构的内力、应力、位移在施工过程中不超过限值,还需找到最优的调索顺序[17]。对于大型的斜拉桥结构,需要考虑索垂度、大变形、梁柱效应、混凝土收缩徐变等非线性因素才能得到较为准确的计算结果[18]。未来可以从选择更好的目标函数、更好的优化计算方法、考虑非线性因素、考虑施工控制等多方面进一步发展本方法,提高针对大型复杂斜拉桥结构的适用性。
| [1] |
任志刚, 刘为俊, 杜小勇, 等. 斜拉桥施工阶段二次调索计算方法[J]. 桥梁建设, 2011(3): 56-60. REN Zhi-gang, LIU Wei-jun, DU Xiao-yong, et al. Calculation Methods of Two-time Cable Force Adjustment for Cable-stayed Bridges at Construction Stage[J]. Bridge Construction, 2011(3): 56-60. |
| [2] |
项海帆. 高等桥梁结构理论[M]. 2版. 北京: 人民交通出版社, 2013. XIANG Hai-fan. Advanced Theory of Bridge Structures[M]. 2nd ed. China Communications Press, 2013. |
| [3] |
刘雄, 钟新谷, 熊先兰, 等. 基于无应力状态控制法的斜拉桥运营期调索计算方法研究[J]. 公路交通科技, 2015, 32(9): 80-86. LIU Xiong, ZHONG Xin-gu, XIONG Xian-lan, et al. Study of Cable Adjustment Calculation Method of Cable-stayed Bridge during Operation Period Based on Control Method of Unstressed State[J]. Journal of Highway and Transportation Research and Development, 2015, 32(9): 80-86. |
| [4] |
陈素君, 张国刚, 唐盛华, 等. 斜拉桥初始平衡构形的确定方法[J]. 公路交通科技, 2011, 28(2): 57-63. CHEN Su-jun, ZHANG Guo-gang, TANG Sheng-hua, et al. Study on Method of Determining Initial Equilibrium Configuration of Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2011, 28(2): 57-63. |
| [5] |
陈云海, 李宏江, 吕建鸣, 等. PC斜拉桥辅助墩摆索拉力支座恢复后的索力调整[J]. 公路交通科技, 2012, 29(6): 87-82. CHEN Yun-hai, LI Hong-jiang, LÜ Jian-ming, et al. Cable Force Adjustment after Rehabilitation of Tension Rocker Bearing of Subsidiary Piers in a PC Cable-stayed Bridge[J]. Journal of Highway and Transportation Research and Development, 2012, 29(6): 87-82. |
| [6] |
毛健.基于影响矩阵法的斜拉桥成桥索力优化与合理施工状态研究[D].长春: 吉林大学, 2017. MAO Jian. Research of Optimization of Bridge-completing Cable Force of Cable-stayed Bridge and Reasonable Construction State Based on Influence Matrix Method[D]. Changchun: Jilin University, 2017. http://cdmd.cnki.com.cn/Article/CDMD-10183-1017148395.htm |
| [7] |
钟继卫. 斜拉桥合龙后索力最优调整的实现[J]. 世界桥梁, 2002(4): 43-44. ZHONG Ji-wei. Realization of Optimal Adjustment of Cable Force after Closure of Cable-stayed Bridge[J]. World Bridge, 2002(4): 43-44. |
| [8] |
杨贤康.钢桁梁斜拉桥索力调整实用算法与施工控制[D].长沙: 中南大学, 2012. YANG Xian-kang. Practical Algorithm of Cable Force Adjustment and Construction Control of Steel Truss Girder Cable-stayed Bridge[D]. Changsha: Central South University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10533-1012476061.htm |
| [9] |
范立础, 杜国华, 马健中. 斜拉桥索力优化及非线性理想倒退分析[J]. 重庆交通大学学报:自然科学版, 1992, 11(1): 1-12. FAN Li-chu, DU Guo-hua, MA Jian-zhong. Cable-stayed Bridge Cable Force Optimization and Nonlinear Ideal Backward Analysis[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 1992, 11(1): 1-12. |
| [10] |
张杨永, 吴万忠, 周云岗. 斜拉桥索力精确模拟的矩阵分析法[J]. 重庆交通大学学报:自然科学版, 2009, 28(6): 979-981. ZHANG Yang-yong, WU Wan-zhong, ZHOU Yun-gang. Matrix Analysis Method for Precise Simulation of Cable Force of Cable-stayed Bridge[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2009, 28(6): 979-981. |
| [11] |
杜蓬娟, 张哲, 谭素杰. 斜拉桥合理成桥状态索力确定的优化方法[J]. 公路交通科技, 2005, 22(7): 82-89. DU Peng-juan, ZHANG Zhe, TAN Su-jie. Optimization of Cable Tension in Reasonably Finished State of Cable-stayed Bridges[J]. Journal of Highway and Transportation Research and Development, 2005, 22(7): 82-89. |
| [12] |
孙全胜, 孟安鑫. 基于影响矩阵法的非对称独塔斜拉桥索力优化[J]. 中外公路, 2016, 36(3): 85-88. SUN Quan-sheng, MENG An-xin. Cable Force Optimization of Asymmetric Single Pylon Cable-stayed Bridge Based on Influence Matrix Method[J]. Journal of China & Foreign Highway, 2016, 36(3): 85-88. |
| [13] |
覃耀柳, 覃耀东. 基于正装迭代法的斜拉桥二次调索计算方法研究[J]. 西部交通科技, 2013(7): 74-76, 96. TAN Yao-liu, TAN Yao-dong. Secondary Cable Adjustment Calculation Method Studies of Cable-stayed Bridge Based on Forward Iterative Method[J]. Western China Communication Science & Technology, 2013(7): 74-76, 96. |
| [14] |
杜蓬娟, 张哲, 孙建刚, 等. 凝聚函数法求解斜拉桥成桥后误差调整问题研究[J]. 大连理工大学学报, 2009, 49(4): 536-539. DU Peng-juan, ZHANG Zhe, SUN Jian-gang, et al. Analysis of Error Adjustment for Cable-stayed Bridges in Finished State via Aggregate Function Approach[J]. Journal of Dalian University of Technology, 2009, 49(4): 536-539. |
| [15] |
王家林, 何琳.一种含非弹性收缩量的预应力筋单元: 中国, 103870702A[P]. 2014-06-18. WANG Jia-lin, HE Lin. A Prestressing Tendon Element with Inelastic Shrinkage: China, 103870702A[P]. 2014-06-18. |
| [16] |
杨兴, 张敏, 周水兴. 影响矩阵法在斜拉桥二次调索中的应用[J]. 重庆交通大学学报:自然科学版, 2009, 28(3): 508-511. YANG Xing, ZHANG Min, ZHOU Shui-xing. Application of Influence Matrix Method to Secondary Cable Adjustment of Cable-stayed Bridges[J]. Journal of Chongqing Jiaotong University:Natural Science Edition, 2009, 28(3): 508-511. |
| [17] |
白先梅. 高速铁路斜拉桥二次调索计算分析[J]. 高速铁路技术, 2016, 7(4): 46-49. BAI Xian-mei. Calculation and Analysis of Secondary Adjustment of Cable Force of High-speed Railway Cable-stayed Bridge[J]. High Speed Railway Technology, 2016, 7(4): 46-49. |
| [18] |
陈务军, 关富玲, 袁行飞, 等. 斜拉桥施工控制分析中线性与非线性影响分析[J]. 中国公路学报, 1998, 11(2): 52-58. CHEN Wu-jun, GUAN Fu-ling, YUAN Xing-fei, et al. Analysis of Nonlinear and Linear Factor's Influences on Cable-stayed Bridge Construction Control Analysis[J]. China Journal of Highway and Transport, 1998, 11(2): 52-58. |
 2020, Vol. 37
2020, Vol. 37
