扩展功能
文章信息
- 黄侨, 关健, 梁程亮, 王涛, 王晓春
- HUANG Qiao, GUAN Jian, LIANG Cheng-liang, WANG Tao, WANG Xiao-chun
- 中美欧公路桥梁设计规范汽车荷载及作用效应对比研究
- Comparative Study on Vehicle Loads and Action Effects of Bridge Design Specifications of China, US and Europe
- 公路交通科技, 2020, 37(7): 62-71
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(7): 62-71
- 10.3969/j.issn.1002-0268.2020.07.009
-
文章历史
- 收稿日期: 2019-09-26
2. 中交公路规划设计院有限公司, 北京 100088;
3. 广东省交通规划设计研究院股份有限公司, 广东 广州 510507
2. CCCC Highway Consultants Co., Ltd., Beijing 100088, China;
3. Guangdong Communications Planning & Design Institute Co., Ltd., Guangzhou Guangdong 510507, China
随着全球经济一体化的进程,以及我国“一带一路”倡议,了解发达地区与国家的相关规范和技术标准,对引领我国桥梁走向国际市场具有重要意义。目前国际较为先进与成熟的桥梁设计规范主要有两部:美国荷载与抗力系数桥梁设计规范(AASHTO LRFD Bridge Design Specifications)[1](以下简称美国桥规)以及欧洲桥梁设计规范(Eurocode)[2-3](以下简称欧洲桥规)。在海外桥梁工程的建设过程中,需要确定选择哪部规范作为设计依据,因此需参考各国桥梁规范的对比结果。本研究对中美欧桥梁设计规范中的极限状态、设计状况、汽车荷载进行了对比研究,选取人民交通出版社2008出版的《公路桥梁通用图》中的样本桥梁进行了恒载与活载作用下的内力分析对比。
1 中美欧公路桥规极限状态与设计状况对比我国《公路桥涵设计通用规范》(JTG D60—2015)[4](以下简称中国桥规2015)及《公路桥涵设计通用规范》(JTG D60—2004)[5] (以下简称中国桥规2004)规定:公路桥涵结构设计应进行承载能力极限状态与正常使用极限状态设计,具体规定见表 1。
| 极限状态 | 定义 |
| 承载能力极限状态 | 结构或构件达到最大承载力或不适于继续承载的变形状态 |
| 正常使用极限状态 | 结构或结构构件达到正常使用或耐久性能的某项规定限值的状态 |
美国桥规定义了4类极限状态:正常使用极限状态、疲劳与断裂极限状态、强度极限状态、极端事件极限状态,具体规定见表 2[6-12]。
| 极限状态 | 定义 |
| 正常使用极限状态 | 结构在正常使用条件下的应力、挠度及裂缝宽度不应超过限值 |
| 疲劳与断裂极限状态 | 疲劳:结构在疲劳荷载作用既定循环次数后产生的应力幅不应超出限值断裂:对材料的韧性做出了规定 |
| 强度极限状态 | 在设计使用年限内,结构应满足强度及稳定性的要求 |
| 极端事件极限状态 | 保证桥梁在遭遇极端事件下不发生倒塌 |
欧洲桥规规定:桥梁结构设计时应进行承载能力极限状态与正常使用极限状态设计,具体规定见表 3。
| 极限状态 | 定义 |
| 承载能力极限状态 | 与行人、结构安全相关的状态 |
| 正常使用极限状态 | 与结构的正常使用、行人舒适、结构外观相关的状态 |
从极限状态的划分来看,中国桥规2004、中国桥规2015与欧洲桥规在极限状态方面的规定完全相同。美国桥规除了包含强度极限状态与正常使用极限状态外,还将疲劳与断裂极限状态和极端事件极限状态单独列为两类极限状态。
中国桥规规定在进行极限状态设计时,应考虑合适的设计状况。中国桥规2004分为持久状况、短暂状况、偶然状况。中国桥规2015将地震状况单独作为一类设计状况,4种设计状况均需要进行承载能力极限状态验算,其中持久状况还需进行正常使用极限状态验算。
由于美国所采用的荷载与抗力系数设计方法,不同极限状态对应着不同的荷载与抗力系数,进而对应着不同的作用组合,因此美国桥规不对设计状况进行规定,而直接采用不同类型荷载组合来针对不同的验算内容(施工阶段、使用阶段等)。
欧洲桥规在设计状况方面的规定与中国桥规2015完全相同。
中美欧桥规中的极限状态与设计状况的具体对应关系见表 4。
| 中国桥规2004 | 中国桥规2015 | 美国桥规 | 欧洲桥规 |
| 承载能力极限状态(持久状况、短暂状况) | 承载能力极限状态(持久状况、短暂状况) | 强度极限状态 | 承载能力极限状态(持久状况、短暂状况) |
| 正常使用极限状态(持久状况) | 正常使用极限状态(持久状况) | 使用极限状态 | 正常使用极限状态(持久状况) |
| — | — | 疲劳和断裂极限状态 | — |
| 承载能力极限状态(偶然状况) | 承载能力极限状态(偶然状况) | 极端事件极限状态 | 承载能力极限状态(偶然状况) |
| 承载能力极限状态(地震状况) | 承载能力极限状态(地震状况) |
2 中美欧汽车荷载对比 2.1 我国汽车荷载
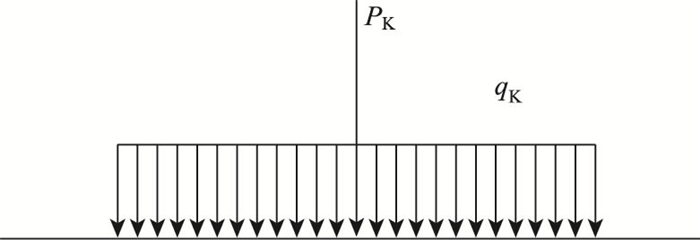
中国桥规规定汽车荷载分为公路- Ⅰ级和公路- Ⅱ级。汽车荷载又可分为车道荷载与车辆荷载。车道荷载由均布荷载和集中荷载组成,桥梁结构的整体计算采用车道荷载。局部加载时采用车辆荷载。车道荷载的图示见图 1。
|
| 图 1 中国车道荷载计算图示 Fig. 1 Diagram of Chinese lane loads |
| |
中国桥规2015及中国桥规2004规定公路- Ⅰ级车道荷载中的均布荷载标准值为qK=10.5 kN/m。中国桥规2015集中荷载标准值按式(1)计算,而中国桥规2004规定当跨径小于5 m时集中荷载标准值PK=180 kN,跨径大于50 m时PK=360 kN,中间段内插取值。
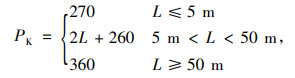
|
(1) |
式中,L为桥梁的计算跨径。当计算剪力效应时,上述集中荷载标准值PK应乘以1.2的系数。
中国桥规2015与中国桥规2004相比,车道荷载中的集中荷载对于中小跨径桥梁有所提高,对于计算跨径在50 m以上的桥梁保持不变。
中国桥规2015与中国桥规2004的车辆荷载均为1辆总重550 kN的标准车,由1根30 kN前轴、两根120 kN中轴及两根140 kN后轴组成。
中国桥规的冲击系数与桥梁结构的基频f有关。基频越大,冲击系数越大,冲击系数表达式为:
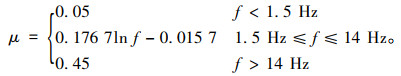
|
(2) |
美国桥规规定作用在桥梁或其附属结构上的汽车荷载取以下两项组合中的较大者[13-16]:
(1) 设计货车荷载+设计车道荷载;
(2) 设计双轴荷载+设计车道荷载。
上述3种荷载表述如下。
(1) 设计货车荷载
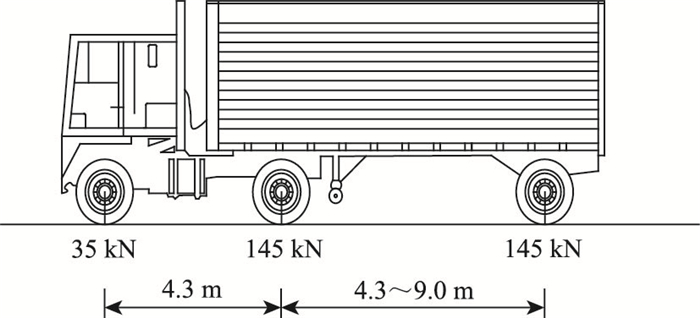
设计货车的轴重、轴距见图 2,3轴轴重分别为35, 145, 145 kN,总重325 kN。前轴与中轴轴距4.3 m,中轴与后轴轴距为一可变值,以此取得最不利效应,变化范围为4.3~9.0 m,采用该荷载模型时应考虑冲击系数。
|
| 图 2 设计货车荷载图示 Fig. 2 Diagram of designed truck load |
| |
(2) 设计双轴荷载
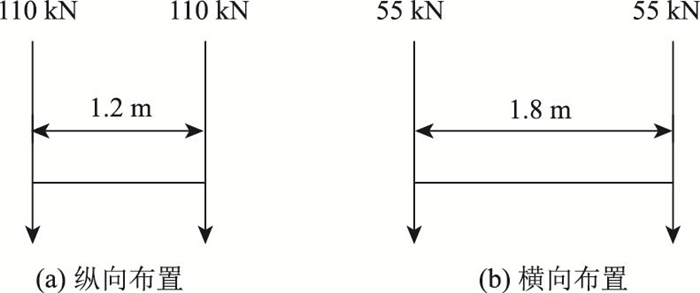
设计双轴包含两对110 kN的车轴,两轴轴距为1.2 m,轴长1.8 m,采用该荷载模型时应考虑冲击系数,设计双轴图示见图 3。
|
| 图 3 设计双轴图示 Fig. 3 Diagram of designed double axles |
| |
(3) 设计车道荷载
设计车道荷载为沿桥跨方向的均布荷载,集度为9.3 kN/m,车道荷载的横向分布宽度为3 m,无需考虑冲击系数。
冲击系数方面,设计货车与设计双轴荷载应计入冲击系数。在进行桥面板验算时,所有极限状态冲击系数均取0.75;在进行其他构件验算时,疲劳与断裂极限状态冲击系数取0.15,其他3种极限状态取0.33。
2.3 欧洲汽车荷载欧洲桥规(Eurocode)规定了4种荷载模型,即荷载模型1(LM1)~荷载模型4 (LM4)。所有设计状况均应考虑LM1~LM3,仅在某些短暂设计状况下使用LM4。上述4种荷载模型均已计入汽车荷载冲击系数,无需再单独考虑[17-20]。
(1) 荷载模型1
荷载模型1(LM1)由集中荷载与均布荷载组成,可用于整体验算和局部验算,由2个分项系统组成:
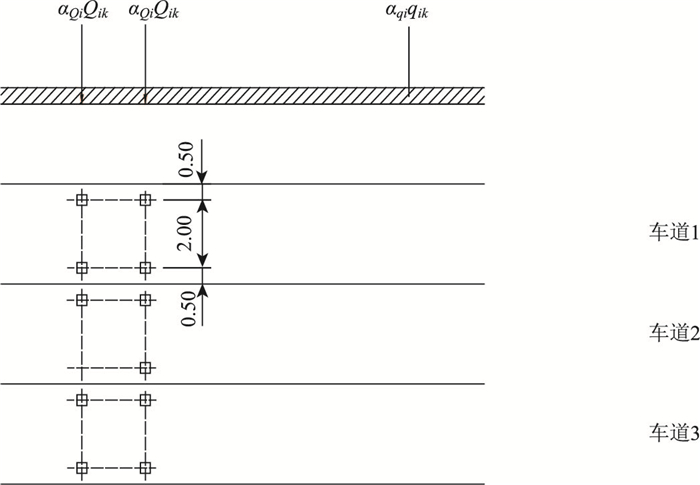
① 双轴集中荷载串联系统单轴重量为αQiQik,其中αQi为修正系数,下标i为车道编号。每条车道仅作用1个串联系统,串联系统的每轴都有2个相同的车轮,单个车轮荷载为0.5αQ iQik,对于第1~第3车道,集中荷载Qik分别取300, 200, 100 kN。
|
| 图 4 荷载模型1(单位:m) Fig. 4 Load model 1(unit: m) |
| |
② 车道每m2的荷载αqiqik,αqi为修正系数,对于第1~第3车道的均布荷载qik分别取9, 2.5, 2.5 kN/m2,在进行杆系结构分析时,需考虑车道宽度,将面均布荷载转化为线均布荷载。
(2) 荷载模型2
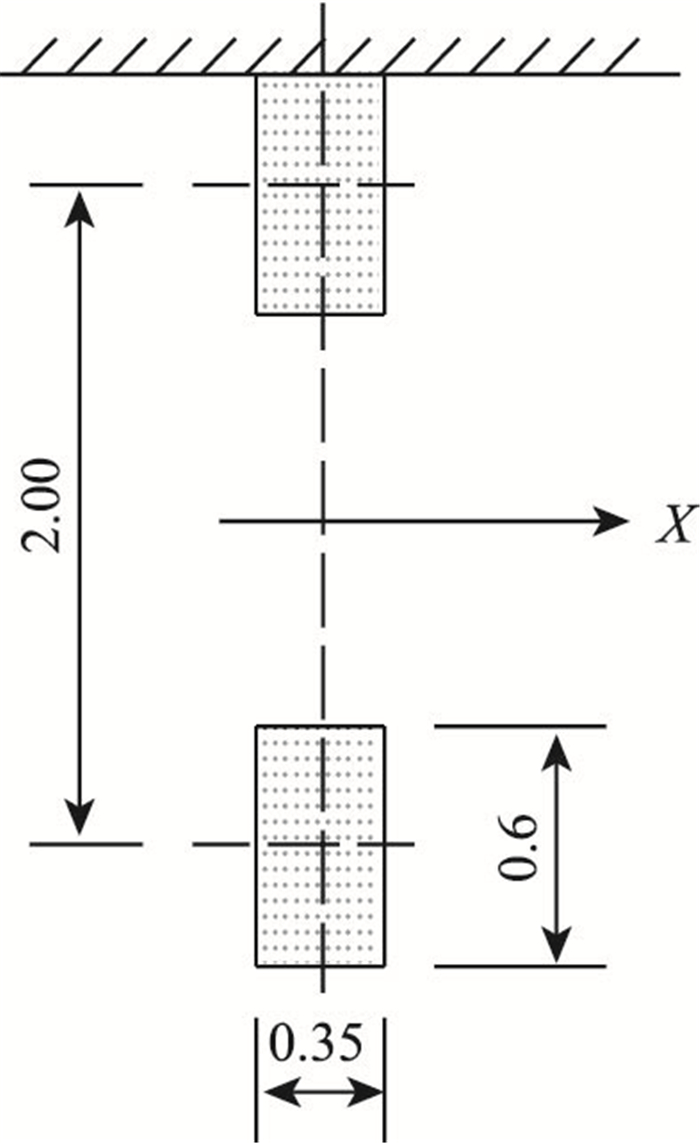
荷载模型2(LM2)为一个单轴荷载βQQak,其中集中荷载Qak为400 kN,已计入冲击系数,βQ为修正系数。荷载模型2荷载可作用在行车道的任何一个位置,每个车轮与地面的接触面是0.35 m×0.6 m的矩形区域(图 5)。
|
| 图 5 荷载模型2(单位:m) Fig. 5 Load model 2 (unit:m) |
| |
(3) 荷载模型3
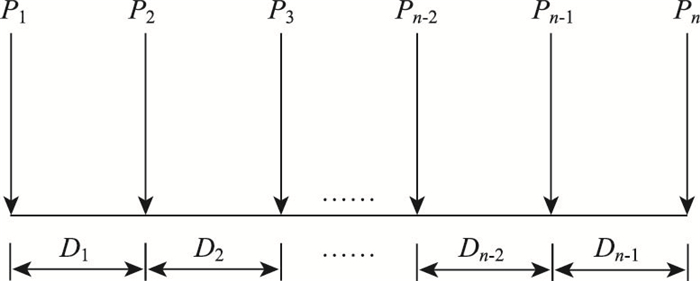
荷载模型3(LM3)是一系列集中荷载(图 6),P1~Pn为集中荷载,D1~Dn-1为荷载间距。这些荷载代表经有关部门授权在路上行驶的特种车辆,可用于整体验算与局部验算。欧洲桥规的附录给出了这些特殊车辆的荷载模型,车辆总重范围在600~3 600 kN间,而单轴轴载则分为150,200,240 kN这3种类型。
|
| 图 6 荷载模型3 Fig. 6 Load model 3 |
| |
中美欧公路桥规对汽车荷载的规定均有所差异,但是也不乏相似之处:3部规范中的汽车荷载都由均布荷载与集中荷载组成,只是在荷载大小及集中荷载数目上有所差异。
2.4 中美欧公路桥规横向车道布载系数对比中国桥规2015、中国桥规2004、美国桥规分别对横向分布系数进行了规定。欧洲桥规在定义汽车荷载模式中已经考虑了横向折减效应。具体的横向车道布载系数见表 5。
| 横向布置设计车道数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 中国桥规2015 | 1.20 | 1.00 | 0.78 | 0.67 | 0.60 | 0.55 | 0.52 | 0.50 |
| 中国桥规2004 | 1.00 | 1.00 | 0.78 | 0.67 | 0.60 | 0.55 | 0.52 | 0.50 |
| 美国桥规 | 1.20 | 1.00 | 0.85 | 0.65 | 0.65 | 0.65 | 0.65 | 0.65 |
3 中美欧公路桥规横向分布对比 3.1 中国公路桥规横向分布计算
中国桥规2015及中国桥规2004并未给出横向分布系数计算的明确方法,建议参考传统《桥梁工程》教材及文献[21]中的计算方法。根据桥梁各主梁之间的构造连接形式,采用不同的计算方法。荷载横向分布系数仅与结构本身形式有关,需将荷载布置在横向分布影响线上的最不利位置,以计算横向分布系数。
3.2 美国桥规公路桥规横向分布计算美国桥规根据截面形式、主梁连接方式,将上部结构划分为11类,并给出了每种截面形式对应的中梁及边梁的弯矩与剪力的横向分布系数计算方法[22-25]。可见美国桥规对横向分布系数的计算方法规定更细,但不考虑荷载横向分布系数沿桥跨方向的变化,而是直接给出了支点剪力与跨中弯矩的荷载横向分布系数。
3.3 欧洲公路桥规横向分布计算欧洲公路桥规未给出横向分布系数的计算方法,国内研究中均采用传统《桥梁工程》教材以及文献[21]中的方法进行计算。采用欧洲汽车荷载模型对单梁进行加载时,将荷载模型1中各车道的汽车荷载折算为第1车道的荷载,最终分别得到双轴荷载和均布荷载的横向分布系数。
3.4 横向分布系数对比本研究选取《公路桥梁通用图》中的预应力混凝土空心板及预应力混凝土T形梁进行计算。桥梁模型样本见表 6,对比等跨不等宽、等宽不等跨情况下的横向分布系数。采用中国桥规和欧洲桥规计算荷载横向分布系数时,对于支点截面,简支T梁与简支空心板梁均采用杠杆原理法。对于跨中截面,简支T梁采用刚接梁法,简支空心板梁采用铰接板梁法。美国桥规根据截面类型选择所对应的表达式进行计算。计算结果如下(由于边梁荷载横向分布系数较大,本研究仅列出边梁计算结果)。
| 结构类型 | 跨径/m | 桥面宽度/m | 主梁高度/m | 主梁间距/m | 主梁片数/片 |
| 预应力混凝土简支T梁(装配式后张法) | 20 | 12 | 1.5 | 2.40 | 5 |
| 25 | 1.7 | ||||
| 30 | 2.0 | ||||
| 35 | 2.3 | ||||
| 40 | 2.5 | ||||
| 30 | 11.25 | 2.0 | 2.25 | 5 | |
| 12.75 | 2.15 | 6 | |||
| 13.50 | 2.25 | 6 | |||
| 16.50 | 2.35 | 7 | |||
| 16.75 | 2.40 | 7 | |||
| 预应力混凝土简支空心板(装配式先张法) | 10 | 12 | 0.60 | 1.0 | 11 |
| 13 | 0.70 | ||||
| 16 | 0.80 | ||||
| 20 | 0.95 | ||||
| 20 | 11.25 | 0.95 | 1.0 | 10 | |
| 12.75 | 12 | ||||
| 13.50 | 13 | ||||
| 16.50 | 16 | ||||
| 16.75 | 16 |
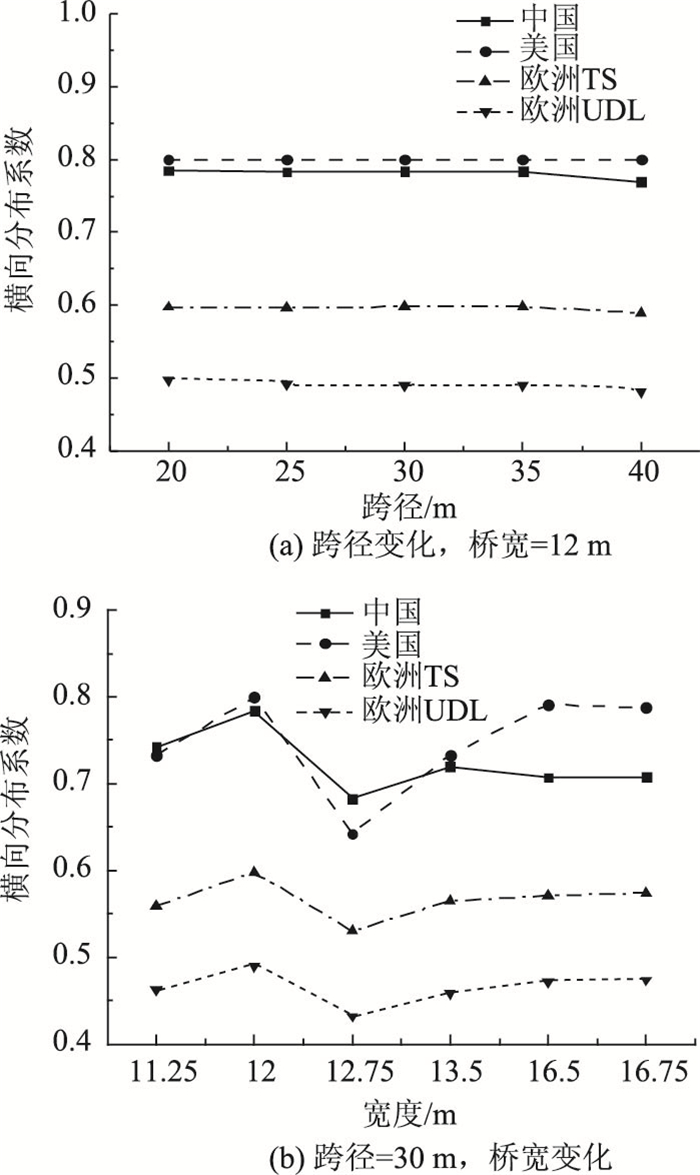
从图 7可以看出,对于简支T梁,中美桥规计算所得的边梁横向分布系数相差不大,而欧洲桥规采用串联系统与均布荷载计算所得的横向分布系数均小于按中美桥规计算的结果。由于欧洲桥规各车道的汽车荷载均有所差异,第1车道的汽车荷载最大,计算横向分布系数时,本研究将各车道的汽车荷载统一折算为第1车道的荷载,从而导致计算得到的横向分布系数较小。
|
| 图 7 简支T梁跨中横向分布系数 Fig. 7 Distribution factor of simply supported T-shaped beam |
| |
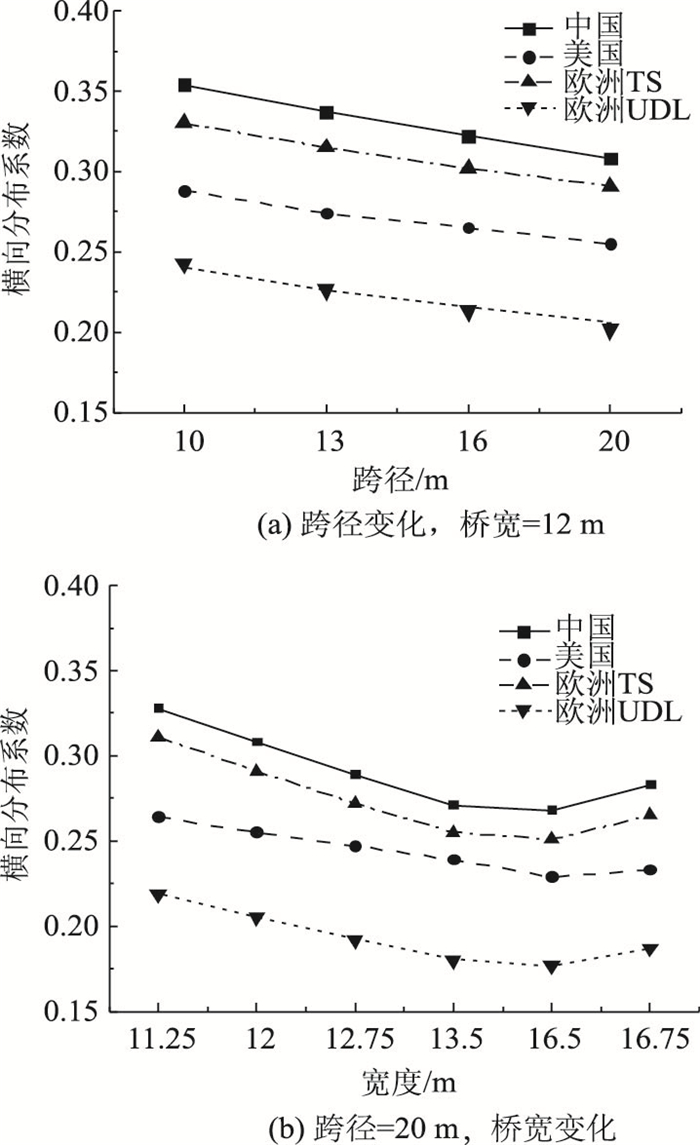
从图 8可以看出,对于简支空心板梁,中国桥规计算得到的横向分布系数最大,欧洲桥规计算得到的串联系统横向分布系数高于美国桥规的横向分布系数,欧洲桥规的均布荷载横向分布系数最小。可见横向分布系数主要取决于各国桥梁规范中的计算方法,还与汽车荷载的计模型有关。
|
| 图 8 简支空心板跨中横向分布系数 Fig. 8 Transverse distribution factor of simply supported hollow slab at mid-span |
| |
4 中美欧公路桥规主梁内力对比
本章采用MIDAS/Civil建立单梁模型,对比其在各国汽车荷载作用下的跨中弯矩与支点剪力效应(中欧桥规考虑荷载横向分布系数沿纵桥向变化),其次根据各国桥规进行作用组合,对相应组合进行对比研究。
4.1 活载内力对比研究由于边梁的荷载横向分布系数较大,因此在计算活载内力时,均以边梁作为研究对象,考虑荷载横向分布系数,建立边梁的单梁模型。中国桥规采用公路-Ⅰ级荷载,美国桥规采用2.2节所述荷载模型,欧洲桥规采用LM1,并按各国桥规计入冲击系数。依据中美欧公路桥规计算得到的汽车荷载作用下的跨中弯矩和支点剪力结果如下。
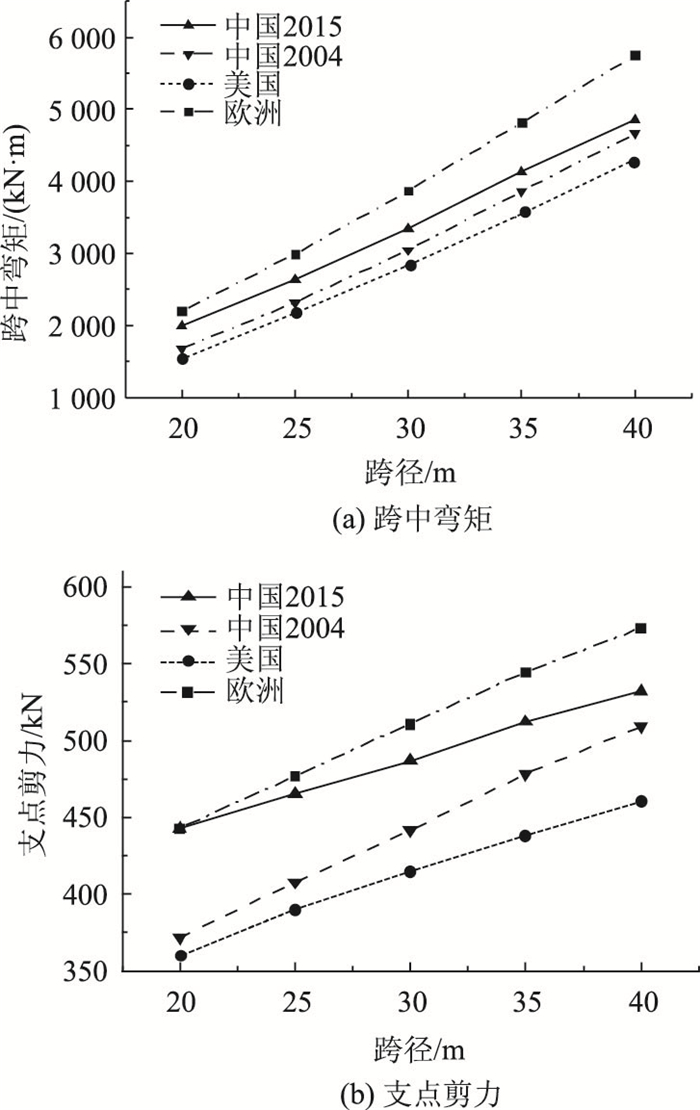
4.1.1 简支T梁作用效应对比从图 9可知,根据各国桥规计算所得汽车荷载在T梁上产生的内力效应均随跨径递增。其中根据欧洲桥规计算所得的活载效应最大,美国桥规计算所得效应最小,中国桥规介于两者之间。由于中国桥规2015所规定的车道荷载中的集中荷载大于中国桥规2004,故计算所得的弯矩及剪力也稍大,中国桥规2015与中国桥规2004的作用效应差异随着跨径增大而减小。
|
| 图 9 简支T梁活载作用下内力对比(跨径变化,桥宽=12 m) Fig. 9 Comparison of internal forces of simply supported T-shape beam under live loads (span variable, width=12 m) |
| |
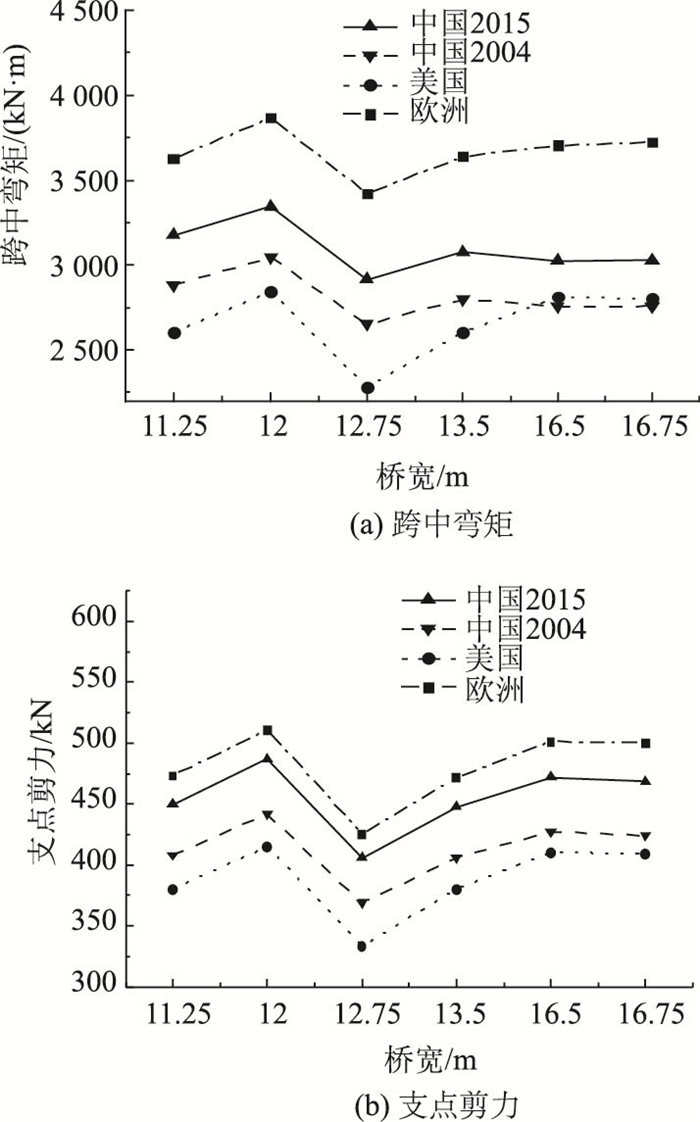
由图 10可知,根据各国桥规计算所得汽车荷载在T梁上产生的内力效应随桥宽增大变化不大。其整体特征为根据欧洲桥规计算所得弯矩、剪力效应最大,而根据美国桥规计算所得作用效应最小,根据中国桥规计算所得效应居中。随着桥宽增大,中美桥规计算所得的作用效应差异减小,中欧桥规计算所得的作用效应差异增大。
|
| 图 10 简支T梁活载作用下内力对比(跨径=30 m,桥宽变化) Fig. 10 Comparison of internal forces of simply supported T-shape beam under live loads (span=30 m, width variable) |
| |
4.1.2 简支空心板作用效应对比
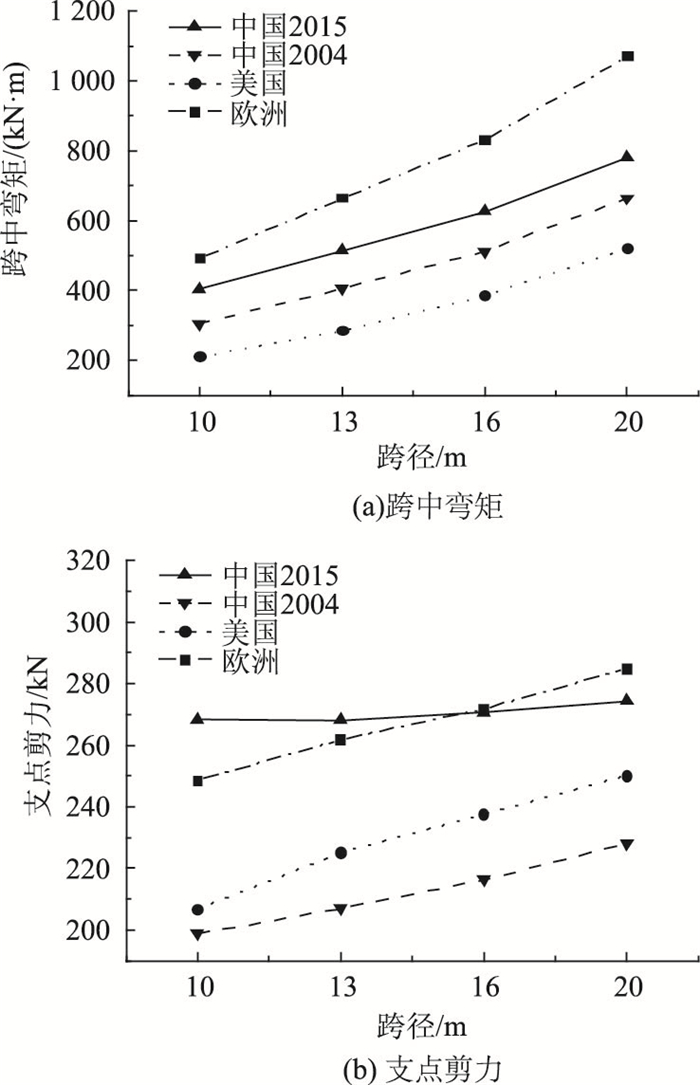
图 11表明,对简支空心板梁,根据欧洲桥规计算所得的弯矩最大,中国桥规居中,美国桥规最小,随着跨径的增加,根据欧洲桥规计算所得的弯矩与根据中美桥规计算所得弯矩差异增大。剪力效应方面,中国桥规2015整体增速不大,随跨径增大,欧洲桥规剪力效应将超过中国桥规2015,中国桥规2004计算结果最小。中国桥规2015剪力效应增速缓慢,主要原因是随着跨径增大,荷载横向分布系数减小,汽车荷载冲击系数减小,并且车道荷载中的集中荷载随跨径的增速为中国桥规2004增速的1/2。
|
| 图 11 简支空心板活载作用下内力对比(跨径变化,桥宽=12 m) Fig. 11 Comparison of internal forces of simply supported hollow slab under live loads (span variable, width=12 m) |
| |
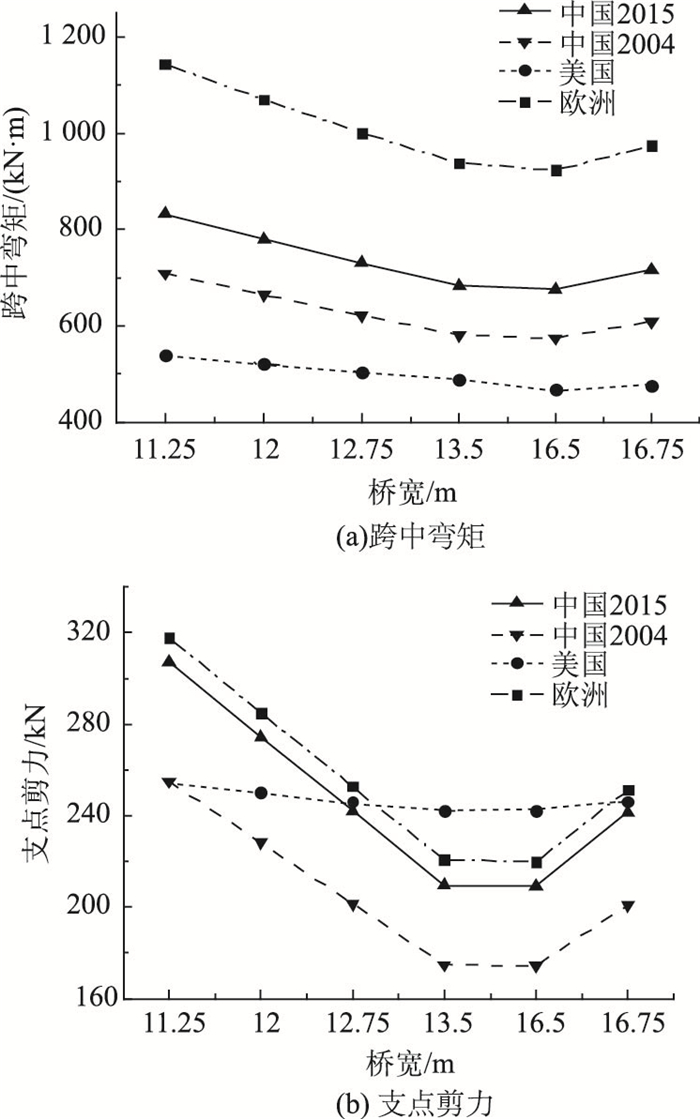
由图 12可知,根据各国规范计算所得汽车荷载在简支空心板上产生的内力效应随桥宽增大变化不大。跨中弯矩方面,欧洲桥规计算所得弯矩最大,美国桥规最小,中国桥规居中。对于支点剪力,中美欧桥规计算所得剪力效应呈现交替的趋势,中国桥规2015与美国桥规整体小于欧洲桥规计算所得的剪力效应,而中国桥规2004计算的剪力效应值整体偏小。根据美国桥规计算所得的剪力效应随桥宽增大而变化幅度较小,这是因为根据美国桥规计算所得的荷载横向分布系数随桥宽增大变化较小。
|
| 图 12 简支空心板活载作用下内力对比(跨径=20 m,桥宽变化) Fig. 12 Comparison of internal forces of simply supported hollow slab under live loads (span=20 m, width variable) |
| |
4.2 荷载组合对比研究
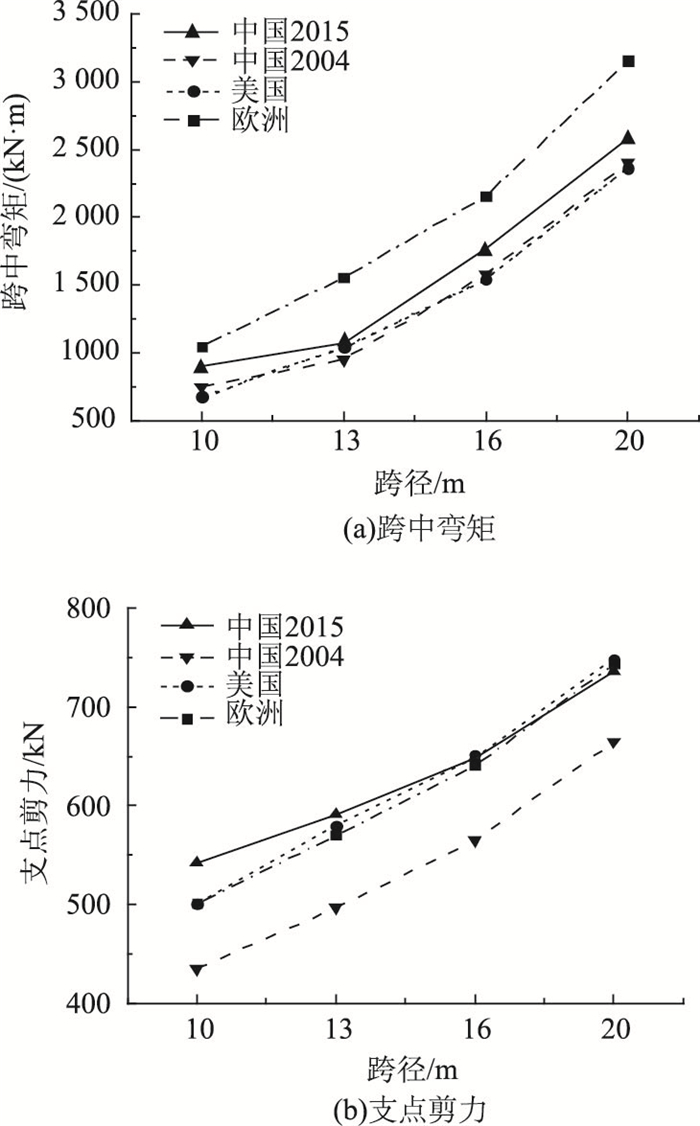
根据中美欧公路桥规,将恒载效应与活载效应进行组合,并计入结构重要性系数。中美欧桥规在计算承载能力极限状态(强度极限状态)所采用作用组合表达式如下,式中SG1和SG2分别为1期恒载效应及2期恒载效应;SQ1为汽车荷载效应。
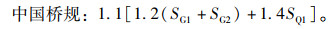
|
(3) |
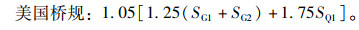
|
(4) |
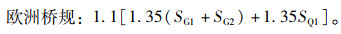
|
(5) |
依据上述组合对所选的简支T梁桥和简支空心板梁桥进行计算,计算结果如下。
4.2.1 简支T梁组合内力对比从图 13可以看出,对于桥宽为12 m的简支T梁,按中美欧桥规计算的恒载和汽车荷载在承载能力极限状态下的效应组合均随跨径增大而增大。跨中弯矩方面,欧洲桥规的计算结果最大,其次为美国桥规,中国桥规2015略大于中国桥规2004的计算结果。对于支点剪力,欧洲桥规计算结果仍为最大,其次为美国桥规,略大于中国桥规2015,中国桥规2004计算结果最小。随着跨径增大,欧洲桥规与中国桥规的效应组合差值有增大的趋势,而美国桥规与中国桥规的效应组合差值呈现出波动的趋势。
|
| 图 13 简支T组合内力对比(跨径变化,桥宽=12 m) Fig. 13 Comparison of combinative internal forces of simply supported T-shape beam(span variable, width=12 m) |
| |
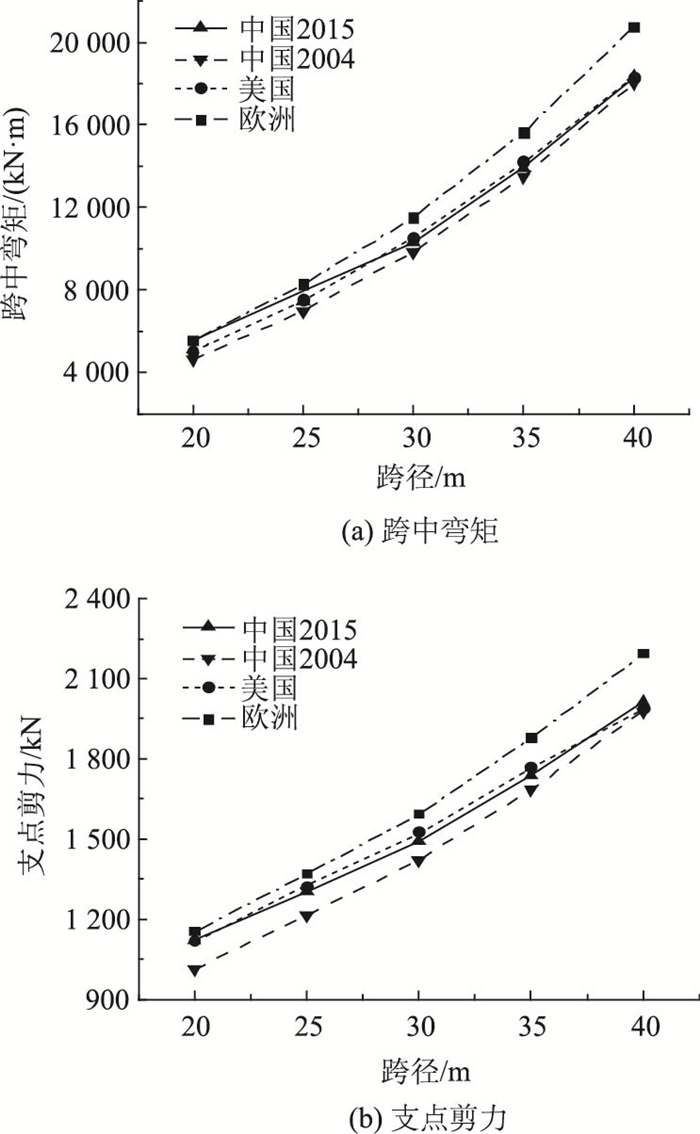
由图 14可知,对于跨径为30 m的简支T梁桥,随着桥宽的增加,各国荷载效应的基本组合值变化均不大。对于跨中弯矩与支点剪力效应而言,计算所得结果均为欧洲桥规作用效应组合最大,中国桥规2004计算结果最小,中国桥规2015与美国桥规计算结果差异较小。
|
| 图 14 简支T梁组合内力对比(跨径=30 m,桥宽变化) Fig. 14 Comparison of combinative internal forces of simply supported T-shape beam (span=30 m, width variable) |
| |
4.2.2 简支空心板组合内力对比
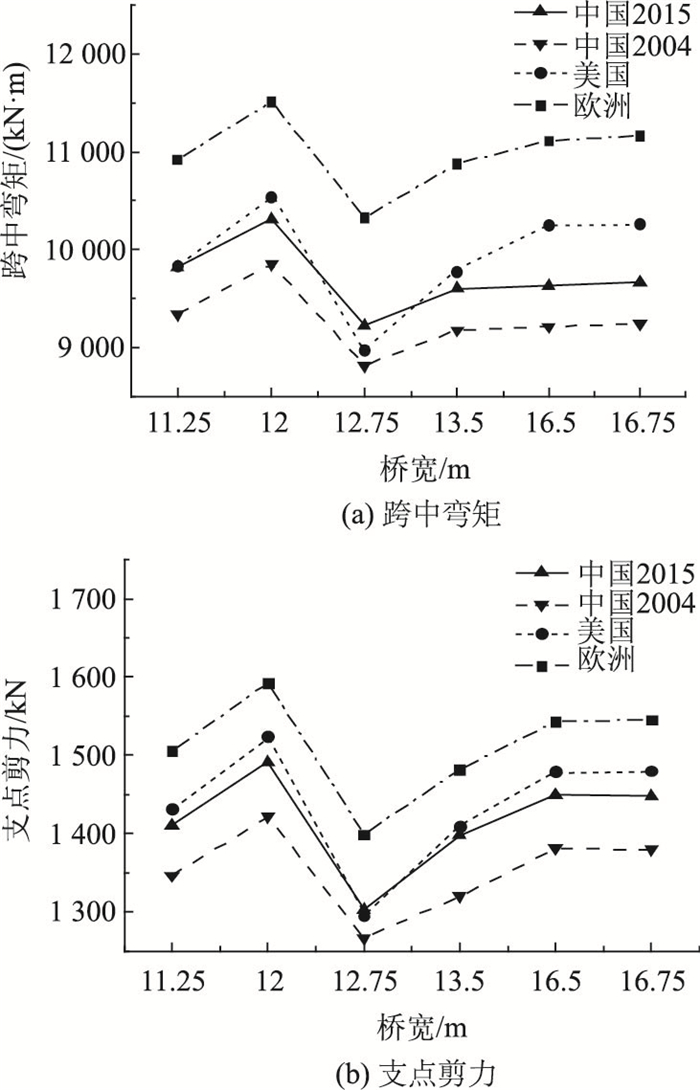
由图 15可知,对于桥宽为12 m的简支空心板梁桥跨中弯矩,根据欧洲桥规的组合结果最大,其次为中国桥规2015,其次为中国桥规2004,美国桥规的组合结果最小。对于支点剪力,在跨径较小时,中国桥规2015的效应组合最大,随着跨径变大,美国桥规的组合结果最大,其次为中国桥规2015,欧洲桥规次之,中国桥规2004的效应组合结果最小。
|
| 图 15 简支空心板组合内力对比(跨径变化,桥宽=12 m) Fig. 15 Comparison of combinative internal forces of simply supported hollow slab (span variable, width=12 m) |
| |
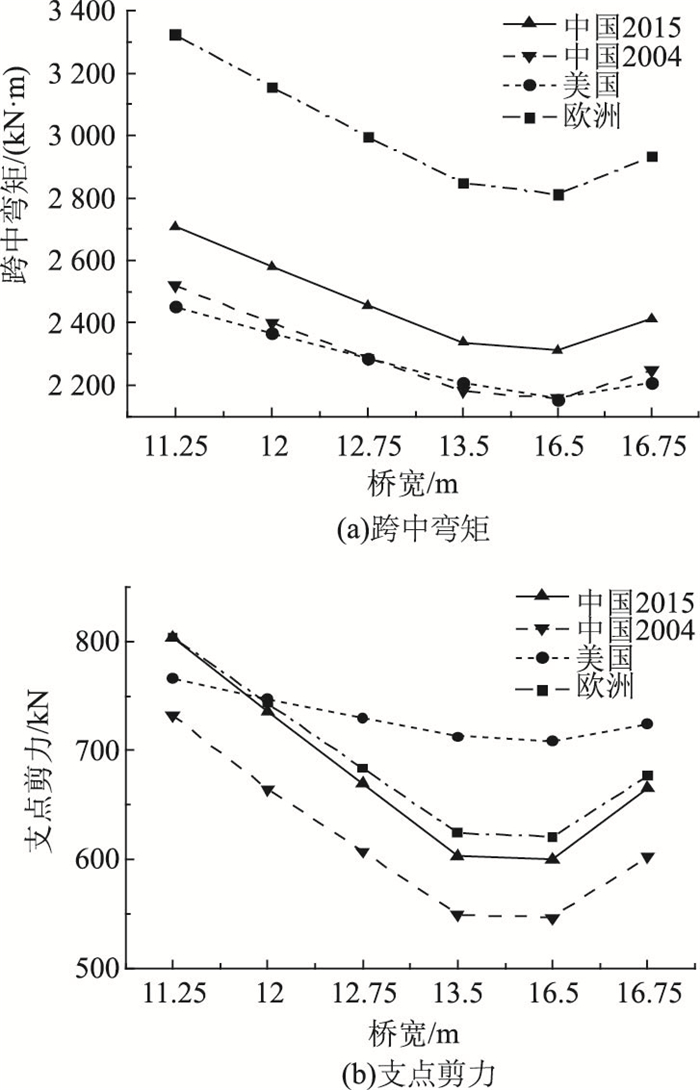
从图 16可以看出,对于跨径为20 m的简支空心板梁桥,随着桥宽的增大,弯矩和剪力的变化趋势均是先减后增。对于跨中弯矩,欧洲桥规效应组合结果最大,中国桥规2004和美国桥规的组合结果十分接近,但均小于中国桥规2015。支点剪力方面,美国桥规的效应组合结果最大,其次为欧洲桥规,中国桥规2015与中国桥规2004计算结果最小。美国桥规计算所得剪力效应变化较小是由于活载产生的剪力效应随桥宽增大变化较小,具体可见4.1.2节。
|
| 图 16 简支空心板梁桥组合内力对比(跨径=20 m,桥宽变化) Fig. 16 Comparison of combinative internal forces of simply supported hollow slab beam bridge (span=20 m, width variable) |
| |
5 结论
(1) 中国桥规2015与欧洲桥规对极限状态与设计状况的规定完全相同,均分为两类极限状态及4类设计状况;美国桥规划分了4类极限状态,不对设计状况作相关规定。
(2) 中国桥规中的车道荷载由均布荷载和集中荷载组成;美国桥规规定取用设计货车荷载+车道荷载与设计双轴荷载+车道荷载中的较大值;欧洲桥规规定了4个模型,所有设计状况均需考虑LM1~LM3,LM4仅需在某些短暂状况考虑。
(3) 中国桥规与欧洲未明确给出横向分布系数的计算方法,需根据具体情况采用不同的方法进行计算,且考虑横向分布系数沿桥跨方向的变化;美国桥规给出了11种截面类型的横向分布系数计算方法,无需考虑横向分布系数沿纵向的变化。
(4) 在活载单独作用及荷载组合情况下,根据欧洲桥规计算所得的弯矩及剪力效应多数偏高,中国桥规2015明显大于中国桥规2004,美国桥规计算的效应总体偏小。
| [1] |
AASHTO LRFD Bridge Design Specifications[S]. 4th ed. Washington, D.C.: AASHTO, 2007.
|
| [2] |
BS EN 1990: 2002, Eurocode - Basis of Structural Design[S].
|
| [3] |
BS EN 1991-02: 2003, Eurocode1: Actions on Structures-Part 2: Traffic Loads on Bridges[S].
|
| [4] |
JTG D60-2015, 公路桥涵设计通用规范[S]. JTG D60-2015, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [5] |
JTG D60-2004, 公路桥涵设计通用规范[S]. JTG D60-2004, General Specifications for Design of Highway Bridges and Culverts[S]. |
| [6] |
刘钊. 关于中美桥规设计准则的对比及思考[J]. 桥梁建设, 2007(6): 34-37. LIU Zhao. Comparison and Consideration of Design Philosophy in Chinese and American Bridge Design Specifications[J]. Bridge Construction, 2007(6): 34-37. |
| [7] |
王晓春.中美欧混凝土桥梁设计规范对比与评价体系研究[D].南京: 东南大学, 2016. WANG Xiao-chun. Comparison and Evaluation System Research on Concrete Bridge Design Norms of China, ASSHTO and Eurocodes[D]. Nanjing: Southeast University, 2016. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016324135.htm |
| [8] |
鲁玉忠, 于剑丽, 宋银平. 中美公路桥梁设计规范对比研究[J]. 铁道标准设计, 2013(5): 79-83. LU Yu-zhong, YU Jian-li, SONG Yin-ping. Comparative Study on Highway Bridge Design Standards between China and America[J]. Railway Standard Design, 2013(5): 79-83. |
| [9] |
曲春升. AASHTO规范在混凝土桥梁设计的应用指导[J]. 公路, 2018, 63(1): 86-89. QU Chun-sheng. Guidance of Applicating AASHTO Specification in Design of Concrete Bridges[J]. Highway, 2018, 63(1): 86-89. |
| [10] |
DU J S, AU F T K. Deterministic and Reliability Analysis of Prestressed Concrete Bridge Girders:Comparison of the Chinese, Hong Kong and AASHTO LRFD Codes[J]. Structural Safety, 2004, 10(4): 230-245. |
| [11] |
PUCKETT J, BARKER R M. Design of Highway Bridges:An LRFD Approach[M]. Hoboken: John Wiley & Sons, Inc., 2013.
|
| [12] |
NOWAK A S, PARK C H. Reliability Analysis of Prestressed Concrete Bridge Girders:Comparison of Eurocode, Spanish Norma IAP and AASHTO LRFD[J]. Structural Safety, 2001, 23(4): 331-344. |
| [13] |
梁程亮.中美混凝土桥梁设计规范对比与分析研究[D].南京: 东南大学, 2015. LIANG Cheng-liang. Reinforced Concrete and Prestressed Concrete Bridge Design: Comparison of the Chinese and AASHTO LRFD Codes[D]. Nanjing: Southeast University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016755075.htm |
| [14] |
阮怀圣, 马润平. 美国公路桥梁设计规范中关于设计汽车荷载的研究[J]. 世界桥梁, 2012, 40(1): 65-69. RUAN Huai-sheng, MA Run-ping. Study of Design Truck Load in AASHTO LRFD Bridge Design Specifications[J]. World Bridges, 2012, 40(1): 65-69. |
| [15] |
吴腾, 葛耀君, 熊洁. 现行国内外公路桥梁汽车荷载及其响应的比较[J]. 结构工程师, 2008, 24(5): 130-136. WU Teng, GE Yao-jun, XIONG Jie. Live Load and Its Response of Highway Bridges Based on International and Domestic Design Codes[J]. Structural Engineers, 2008, 24(5): 130-136. |
| [16] |
吴迅, 王刚, 范灏. 中、美、欧公路桥梁以及中国铁路桥梁可靠度对比[J]. 中国科技论文, 2013, 8(11): 1122-1125. WU Xun, WANG Gang, FAN Hao. Reliability Analysis:Comparison of Chinese, American, European Highway Bridges and Chinese Railway Bridges[J]. China Sciencepaper, 2013, 8(11): 1122-1125. |
| [17] |
王涛.中欧钢筋及预应力混凝土梁设计规范对比研究[D].南京: 东南大学, 2015. WANG Tao. Design Criteria Study of Reinforced Concrete and Prestressed Concrete Bridge Girders: Comparison of Chinese Norms and Eurocode[D]. Nanjing: Southeast University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10286-1016755076.htm |
| [18] |
黎述亮, 杨勇, 李俊, 等. 欧洲规范中公路桥梁设计活载分析[J]. 世界桥梁, 2011(5): 52-55, 60. LI Shu-liang, YANG Yong, LI Jun, et al. Analysis of Live Load of Highway Bridge Design in Eurocode[J]. World Bridges, 2011(5): 52-55, 60. |
| [19] |
苏武. BS5400与中国公路设计规范中的荷载及荷载组合[J]. 铁道工程学报, 2007(11): 42-47. SU Wu. Compare BS5400 with Chinese General Code for Design of Highway in Loads and Combination of Loads[J]. Journal of Railway Engineering Society, 2007(11): 42-47. |
| [20] |
CALGARO J A, TSCHUMI M, GULVANESSIAN H. Designers' Guide to Eurocode 1:Actions on Bridges EN 1991-2, EN 1991-1-1, -1-3 to -1-7 and EN 1990 Annex A2[M]. London: Thomas Telford Limited, 2010: 83-97.
|
| [21] |
李国豪. 公路桥梁荷载横向分布系数计算[M]. 2版. 北京: 人民交通出版社, 1984. LI Guo-hao. Calculation of Live Load Distribution Factor of Road Bridges[M]. 2nd ed. Beijing: China Communications Press, 1984. |
| [22] |
CAI C S. Discussion on AASHTO LRFD Load Distribution Factors for Slab-on-girder Bridges[J]. Practice Periodical on Structural Design and Construction, 2005, 10(3): 171-176. |
| [23] |
ZOKAIE T. AASHTO-LRFD Live Load Distribution Specifications[J]. Journal of Bridge Engineering, 2000(5): 131-138. |
| [24] |
YOUSIF Z, HINDI R. Live Load Distribution Factor for Highway Bridges Based on AASHTO-LRFD and Finite Element Analysis[C]//Structures Congress 2006. St. Louis: American Society of Civil Engineers, 2006.
|
| [25] |
KIM J B, KIM R H, EBERLE J. Simplified LRFD Bridge Design[M]. Boca Raton: Taylor & Francis Group, 2013.
|
 2020, Vol. 37
2020, Vol. 37
