扩展功能
文章信息
- 赵润民, 黄晓明
- ZHAO Run-min, HUANG Xiao-ming
- 基于沥青道路土基应力参数的轴载换算
- Vehicle Axle Load Conversion Based on Stress Parameters of Asphalt Road Soil Foundation
- 公路交通科技, 2020, 37(7): 9-16
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(7): 9-16
- 10.3969/j.issn.1002-0268.2020.07.002
-
文章历史
- 收稿日期: 2017-12-22
在设计公路沥青铺装层结构时,需进行轴载换算。国外最具代表性的为美国AASHTO设计法,其以服务性指数(Present Serviceability Index, PSI)为设计指标进行轴载换算[1-4]。AASHTO中轴载换算系数不是定值,而是随着服务性指数等参数在3.63~4.5之间变化。随着经济技术的发展和美国交通量、交通荷载的日益增大,传统经验法(AASHTO设计方法)的适用性在现代环境中日益低下,因此又产生了AASHTO2002力学-经验法[2-3, 5]。林绣贤[6]早在20世纪80年代即提出以轮压比公式进行轴载换算。长期以来,我国采用以设计弯沉值、沥青层层底拉应力为指标,或以半刚性材料层拉应力为指标的轴载换算方法。以设计弯沉值、沥青层层底拉应力为指标时,轴载换算系数为4.35,而以半刚性材料层拉应力为指标时,轴载换算系数为8[7]。同时对于轴重大于13 t的重载条件,往往需要增大轴载换算系数[8-10]。李雪涛[8]提出,对于轴重大于130 kN的重载交通,其研究结果中的轴载换算系数相比于规范值要大,且随着轴载重量的进一步提高,差距将越来越大。他提出轴载大于130 kN时,轴载换算系数应取为3.441+0.009 98Pi,其中Pi为被换算轴的轴载重量。类似地,王辉等[11]也提出了重载交通下的变化换算指数,其以路面弯沉为指标,建议当轴重大于130 kN时换算指数取值为5.92/Ac+0.011(Pi-130),其中Ac为公路等级系数,高速公路、1级公路取为1.0,二级公路取为1.1,3级、4级公路取为1.2。然而蒋建明等[12]通过对柔性基层沥青路面进行研究后发现,当轴重在80~200 kN范围内变化时,以弯沉为指标的轴载换算系数b值变化幅度仅有2%,说明对于柔性路面对于轴重不敏感。
由于我国以往设计方法中以设计弯沉为指标,通过调整容许弯沉来控制路面结构的做法缺乏严谨性及理论依据[13],我国现行规范[14]中已摒弃原有以设计弯沉、沥青层层底拉应力及半刚性材料层层底拉应力为指标的轴载换算方法,转而寻求基于土基应力应变、结构层应变等指标的轴载换算方法。
在利用土基顶面参数为换算指标研究方面,孙志林等[15]利用BISAR程序, 提出了轴载换算系数建议值为4.93。类似地,宋鑫等[16]利用了APBI程序,认为同一结构与轴载作用下,路基顶面压应变随着胎压的增大而增大;同一结构与胎压作用下,路基顶面压应变随轴载的增大而大幅度增大,并给出了轴载换算系数为4.64。
目前国内关于以路基参数为指标的研究方面有着明显的局限性:现有研究都是基于理论程序分析总结出轴载换算的规律,而对于实际情况下的综合情况考虑有所不足。此外,目前的研究均未考虑基于路基应力的轴载换算方法,且对于轴载大于130 kN的重载条件下的考虑不足。故本研究通过RIOHTRACK实际试验获得的数据,分析归纳基于路基应力参数的轴载换算方法,并将其结论与现有研究结论综合比较,得出更为完善的换算方法。
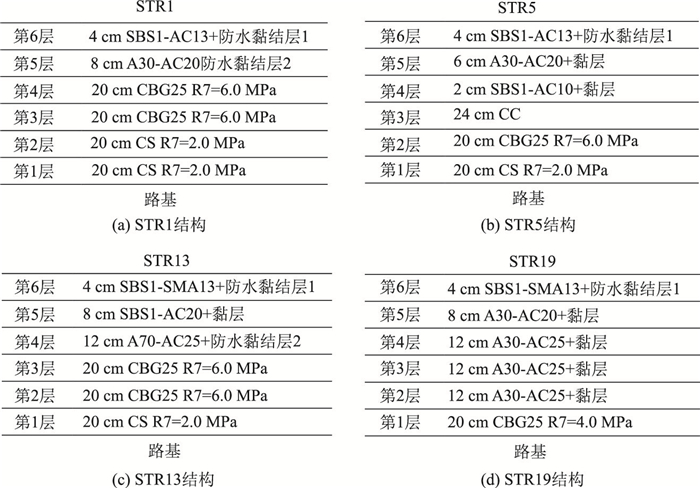
1 试验断面结构的选择及试验方法 1.1 试验断面的选取本试验研究采用的RIOHTRACK试验道路拥有沥青混凝土与水泥混凝土路面共38种结构。每种结构中均拥有1处包含各结构层的层应力应变传感器、温度传感器等传感器的断面。同时,由于环道沥青路面部分中STR1,STR5,STR13,STR19这4种结构处于直线与缓直段的交界处,4种结构各有2个传感器断面,因此在试验过程中该4种结构均可以得到2套传感器数据,以作相互之间的参照对比。故本研究选用该4种结构作为轴载换算系数的研究目标。其中STR1结构属于强基薄面沥青混凝土道路结构,STR5结构属于复合式结构,STR13结构属于典型半刚性基层沥青混凝土路面结构,STR19结构则属于全厚式结构。4种结构断面图如图 1所示。
|
| 图 1 试验路面结构 Fig. 1 Structures of experimental road |
| |
1.2 试验过程
本研究进行时,RIOHTRACK试验路已经完成3期加载试验,其中1期加载进行于2016年12月,3期加载进行于2017年4月。加载试验使用4台双轴双轮组车型。每次加载前对加载车进行加载/卸载,使其后轴轴重达到规定轴重。加载时,4台加载车均布于环道上,以规定速度40 km/h沿环道行驶,其对路面各层结构的荷载响应通过各结构中的传感器断面进行感知,并由电信号方式进行传出与存储。3期加载试验中,每期试验加载累计里程为60 000 km。其中1期加载与3期加载分别由累计20 000 km的10 t轴重作用、累计20 000 km的13 t轴重作用和累计20 000 km的16 t轴重作用组成。而2期加载以改变路面结构使用状态为主要目的,故全部累计60 000 km的加载里程均由16 t轴重的作用完成。由于3期加载试验的目的不同,同时考虑到1期加载试验及3期加载试验中的轴重多样性、路面结构使用状态的差异性及季节气温的不同,本研究中使用1期加载与3期加载得出的数据为分析对象。
2 以路基竖向应力参数为指标确定轴载换算系数的基本方法轴载换算时按以下两项基本原则进行:(1)换算以达到相同临界状态为标准;(2)对某种交通组成,不论以哪种轴载标准进行换算,换算所得轴载作用次数所计算的路面厚度应相同[17-18]。以弹性层状体系理论为分析基础,可以得出路基顶面竖向应变与不同轴重存在以下关系[15]:
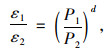
|
(1) |
式中,P1与P2为两种类型相同、轴重不同的轴载;ε1与ε2为P1与P2两种轴载作用下路基顶面的竖向压应变;d为表征路基顶面竖向压应变比值与相应的轴重比值关系的指数,可由试验得出。式(1)说明了对于同一种路面结构和同一种轴型下,在弹性层状体系理论假设中,路基顶面竖向压应变比值与相应的轴重比值的指数相同。
《公路沥青路面设计规范》(JTG D50—2017)[14]给出了分析路基永久变形时,路基顶面容许压应变与设计期内车道上累计当量作用系数之间的关系,即:
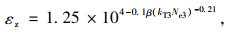
|
(2) |
式中,εz为路基顶面容许压应变(微应变10-6);Ne3为设计期内车道上累计当量作用次数;β为可靠度指标,由公路等级而定;kT3为温度调整系数。
则由式(2)可以得出分别对应于P1与P2轴型的累计当量作用次数N1与N2,其路基顶面容许压应变εz1与εz2有如下关系:
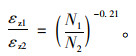
|
(3) |
根据轴载换算原则,相同的路面结构达到相同的临界状态,则若P1与P2轴型分别作用N1与N2次后,路面达到相同的临界状态。这时对于相同的路面结构,用P1与P2轴型测得的土基应变值,即相当于两者的容许应变值,即有εz1=ε1;εz2=ε2。
因此通过上述关系,将式(1)与式(3)联立可得:
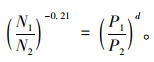
|
(4) |
令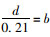
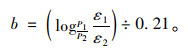
|
(5) |
利用APBI程序,分别按照表 1~表 4中所示参数,建立4种试验路断面结构模型。同时以双圆均布荷载为基本形式,参照实际试验中加载车10,13,16 t轴重时标定的胎压及胎径数据,按照表 5中得荷载布局数据,在APBI中进行数值模拟,确定双圆中心下位于路基顶面及顶面以下一定深度处的竖向应力与竖向应变关系。
| 结构层 | 材料 | 模量/MPa | 泊松比 | 层厚/cm | 层间连续条件 |
| 1 | SBS1-AC13+防水黏结层1 | 2 400 | 0.25 | 4 | 完全连续 |
| 2 | A30-AC20+防水黏结层2 | 2 200 | 0.25 | 8 | 完全连续 |
| 3 | CBG25 R7=6.0 MPa | 2 500 | 0.20 | 20 | 完全连续 |
| 4 | CBG25 R7=6.0 MPa | 2 500 | 0.20 | 20 | 完全连续 |
| 5 | CS R7=2.0 MPa | 1 000 | 0.25 | 20 | 完全连续 |
| 6 | CS R7=2.0 MPa | 1 000 | 0.25 | 20 | 完全连续 |
| 7 | 土基 | 60 | 0.35 | — | — |
| 结构层 | 材料 | 模量/MPa | 泊松比 | 层厚/cm | 层间连续条件 |
| 1 | SBS1-AC13+防水黏结层1 | 2 400 | 0.25 | 4 | 完全连续 |
| 2 | A30-AC20+黏层 | 2 200 | 0.25 | 6 | 完全连续 |
| 3 | SBS1-AC10+黏层 | 2 200 | 0.25 | 2 | 完全连续 |
| 4 | CC | 30 000 | 0.20 | 24 | 完全连续 |
| 5 | CBG25 R7=6.0 MPa | 2 500 | 0.20 | 20 | 完全连续 |
| 6 | CS R7=2.0 MPa | 1 000 | 0.25 | 20 | 完全连续 |
| 7 | 土基 | 60 | 0.35 | — | — |
| 结构层 | 材料 | 模量/MPa | 泊松比 | 层厚/cm | 层间连续条件 |
| 1 | SBS1-SMA13+防水黏结层1 | 2 400 | 0.25 | 4 | 完全连续 |
| 2 | SBS1-AC20+黏层 | 2 200 | 0.25 | 8 | 完全连续 |
| 3 | A70-AC25+防水黏结层2 | 2 200 | 0.25 | 12 | 完全连续 |
| 4 | CBG25 R7=6.0 MPa | 2 500 | 0.20 | 20 | 完全连续 |
| 5 | CBG25 R7=6.0 MPa | 2 500 | 0.20 | 20 | 完全连续 |
| 6 | CS R7=2.0 MPa | 1 000 | 0.25 | 20 | 完全连续 |
| 7 | 土基 | 60 | 0.35 | — | — |
| 结构层 | 材料 | 模量/MPa | 泊松比 | 层厚/cm | 层间连续条件 |
| 1 | SBS1-SMA13+防水黏结层1 | 2 400 | 0.25 | 4 | 完全连续 |
| 2 | A30-AC20+黏层 | 2 200 | 0.25 | 8 | 完全连续 |
| 3 | A30-AC25+黏层 | 2 200 | 0.25 | 12 | 完全连续 |
| 4 | A30-AC25+黏层 | 2 200 | 0.25 | 12 | 完全连续 |
| 5 | A30-AC25+黏层 | 2 200 | 0.25 | 12 | 完全连续 |
| 6 | CBG25 R7=4.0 MPa | 2 500 | 0.20 | 20 | 完全连续 |
| 7 | 土基 | 60 | 0.35 | — | — |
| 胎压/MPa | 荷载圆半径/cm | X/cm | Y/cm |
| 0.707/0.910/1.070 | 10.65/10.66/10.95 | 15.975 | 0 |
| 0.707/0.910/1.070 | 10.65/10.66/10.95 | -15.975 | 0 |
令参数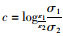
| 轴重比 | 路基顶面 | 顶面下108 cm |
| 13/10 | 0.995 758 012 | 0.988 425 142 |
| 16/13 | 0.997 858 095 | 1.069 024 618 |
| 16/10 | 0.996 718 700 | 1.025 412 870 |
| 轴重比 | 路基顶面 | 顶面下20 cm |
| 13/10 | 1.017 939 184 | 0.963 794 497 |
| 16/13 | 0.953 174 535 | 0.995 214 835 |
| 16/10 | 0.988 228 514 | 0.978 204 106 |
| 轴重比 | 路基顶面 | 顶面下20 cm |
| 13/10 | 0.973 978 861 | 1.017 727 847 |
| 16/13 | 1.024 463 293 | 1.018 762 751 |
| 16/10 | 0.997 129 146 | 1.018 202 611 |
| 轴重比 | 路基顶面 | 顶面下32 cm |
| 13/10 | 0.980 879 5 | 0.969 205 205 |
| 16/13 | 1.010 859 189 | 1.038 250 182 |
| 16/10 | 0.994 584 851 | 1.000 803 378 |
表 6~表 9中全部c值,计算得其均值为1.000 6,变异系数为2.5%。故认为c值随路面结构及轴重比的变化没有明显变化,均在1附近。为简化,取c值为1,故可得以路基竖向应力参数为指标确定轴载换算系数的表达式:
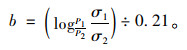
|
(6) |
由于RIOHTRACK试验路传感器断面中的传感器数据采集方式为随时间不间断采集,且采集频率极高,故原始电信号数据量极大,且大多数数据为没有荷载作用时的无用数据点。同时,由于试验进行时的电磁干扰等外部干扰,传感器原始数据波形较为杂乱。故本研究中对于原始电信号数据的处理分为4步进行:首先对原始电信号进行截取,去除大部分没有荷载进行时的无用电信号;之后进行滤波处理,对由于电磁干扰等造成的杂波进行过滤,使传感器的电信号呈现更易识别的良好波形;第3步进行波峰数值的分析截取,认为传感器波形数据中波峰点即为荷载作用时的应力响应值;最后将传感器电信号根据换算公式转换为实际的竖向压力值。RIOHTRACK试验路中使用的压力传感器电信号与实际压力值之间得换算关系式为:
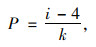
|
(7) |
式中,P为实际土压力;i为经过数据截取、数据滤波及峰值分析后的传感器电信号数值;k为传感器系数,在0.032附近,具体值随不同传感器有略微差异。
3.2 试验结果与讨论经过上述数据处理过程,得出1期与3期加载试验中不同轴重下最终传感器数据,如表 10~表 11所示。根据表 10~表 11中的数值,由式(1)得出各结构轴载换算系数b值,如表 12~表 13所示。
| 传感器位置 | 轴重/t | 传感器位置 | 轴重/t | ||||
| 10 | 13 | 16 | 10 | 13 | 16 | ||
| HZSTR1路基顶面 | 1.01 | 1.32 | 2.41 | STR13路基顶面 | 2.47 | 3.39 | 4.68 |
| HZSTR1路基顶面下108 cm | 3.64 | 4.76 | 5.93 | STR13路基顶面下20 cm | 1.58 | 2.05 | 2.57 |
| STR5路基顶面 | 0.61 | 0.86 | 1.43 | STR19路基顶面 | 3.08 | 3.93 | 5.04 |
| STR5路基顶面下20 cm | 1.43 | 1.87 | 2.63 | STR19路基顶面下32 cm | 3.61 | 4.73 | 5.45 |
| HZSTR5路基顶面 | 0.42 | 0.54 | 1.03 | HZSTR19路基顶面 | 1.54 | 1.79 | 2.79 |
| HZSTR5路基顶面下74 cm | 0.73 | 0.93 | 1.08 | HZSTR19路基顶面下82 cm | 2.85 | 3.76 | 4.7 |
| 传感器位置 | 轴重/t | 传感器位置 | 轴重/t | ||||
| 10 | 13 | 16 | 10 | 13 | 16 | ||
| STR1路基顶面 | 7.07 | 10.03 | 11.76 | STR13路基顶面 | 4.97 | 6.84 | 9.36 |
| STR1路基顶面下108 cm | 1.36 | 1.95 | 2.49 | STR13路基顶面下20 cm | 2.14 | 3.07 | 3.76 |
| STR5路基顶面 | 1.06 | 2.14 | 2.4 | STR19路基顶面 | 3.77 | 4.85 | 5.63 |
| STR5路基顶面下20 cm | 1.62 | 2.84 | 3.54 | STR19路基顶面下32 cm | 4.89 | 6.46 | 7.75 |
| HZSTR5路基顶面 | 0.55 | 0.78 | 0.89 | HZSTR19路基顶面 | 4.97 | 5.76 | 5.71 |
| HZSTR5路基顶面下74 cm | 0.7 | 0.92 | 1.22 | HZSTR19路基顶面下82 cm | 4.18 | 5.31 | 6.03 |
| 传感器位置 | 轴重/t | 传感器位置 | 轴重/t | ||
| 13 | 16 | 13 | 16 | ||
| HZSTR1路基顶面 | 4.97 | 8.83 | STR13路基顶面 | 5.7 | 6.46 |
| HZSTR1路基顶面下108 cm | 4.9 | 4.95 | STR13路基顶面下20 cm | 4.71 | 4.94 |
| STR5路基顶面 | 6.3 | 8.67 | STR19路基顶面 | 4.41 | 4.99 |
| STR5路基顶面下20 cm | 4.91 | 6.2 | STR19路基顶面下32 cm | 4.9 | 4.17 |
| HZSTR5路基顶面 | 4.36 | 8.96 | HZSTR19路基顶面 | 2.75 | 6.03 |
| HZSTR5路基顶面下74 cm | 4.37 | 3.98 | HZSTR19路基顶面下82 cm | 5.05 | 5.07 |
| 传感器位置 | 轴重/t | 传感器位置 | 轴重/t | ||
| 13 | 16 | 13 | 16 | ||
| STR1路基顶面 | 6.34 | 5.15 | STR13路基顶面 | 5.79 | 6.41 |
| STR1路基顶面下108 cm | 6.46 | 6.11 | STR13路基顶面下20 cm | 6.55 | 5.71 |
| STR5路基顶面 | 12.7 | 8.27 | STR19路基顶面 | 4.59 | 4.08 |
| STR5路基顶面下20 cm | 10.2 | 7.91 | STR19路基顶面下32 cm | 5.04 | 4.66 |
| HZSTR5路基顶面 | 6.51 | 4.91 | HZSTR19路基顶面 | 2.67 | 1.4 |
| HZSTR5路基顶面下74 cm | 5.06 | 5.74 | HZSTR19路基顶面下82 cm | 4.35 | 3.73 |
(1) 对于强基薄面结构两个断面STR1及HZSTR1,其轴载换算系数实测值多数在5~6.5之间,平均为5.96。16 t轴重的换算指数相比于13 t轴重,除了HZSTR1路基顶面,两个断面呈现相同的规律。认为对于强基薄面结构,16 t轴重时换算指数相较于13 t轴重的换算指数没有明显增大。另外,两个断面数据结果均显示,以路基顶面以下一定深度处的荷载响应计算出的换算指数与以路基顶面荷载响应计算出的换算指数相比,其大小差异也不大。
(2) 对于复合式结构STR5及HZSTR5两个断面,其中STR5断面13 t的换算指数明显较其余数值大。两个断面结果均显示,春季3期加载相比于冬季1期加载b值有明显增大,说明轴载换算系数与路面结构使用状态及季节因素有明显的关系。同时,两个断面的数据结果均未体现出16 t轴重的换算指数一定大于13 t轴重的换算指数。对于该结构的换算指数b值,除STR5断面两个传感器春季13 t的换算指数明显高于其他值外,其余b值均值为6.15。
(3) 对于典型半刚性基层路面结构STR13,计算结果表明, 半刚性基层路面结构换算指数集中于4.5~6.5之间,平均值为5.78。这也与前述各结构的多数结论相吻合。同时,该结构中16 t的换算指数相比于13 t的换算指数有小幅度提高,春季3期加载比冬季1期加载也有小幅度提高, 但两者提高幅度均不大,可以看做基本稳定。
(4) 对于全厚式结构STR19及HZSTR19两个断面,其换算指数明显小于前面3种结构。STR19结构计算出的b值集中于4~5之间,均值为4.61, 且3期春季加载后的换算指数b值相比于冬季1期加载有一定幅度的增大。这说明该结构的轴载换算系数亦受季节与路面结构使用状态影响,但其增大幅度不大。16 t的换算指数也不一定大于13 t的换算指数,且总体而言两者差异不大。HZSTR19断面中,土基顶面传感器的结果较为特别,而土基下82 cm处的传感器数值计算结果则与STR19结果较为相符。其换算指数平均值为4.55。该结构结果也表明,全厚式路面结构的换算指数与两期加载中的路面使用状态及季节影响关系不大。其原因可能是全厚式沥青路面使用寿命较长,相较于其使用寿命,两个加载周期间隔仍较短,仍属于同一时间节点。
由于实际试验中加载车荷载作用时不能保证后轮轮隙中心正好经过传感器正上方。为考察上述试验结果的可靠性,利用APBI程序,仍使用表 1~表 5中的参数设置,但是将应力计算点按照双轮间隙中心平移不同距离,分别偏移20,40 cm,考察偏移距离对结果的影响,得出不同偏移情况下轴载换算系数b值,如表 14~表 17所示。
| 轴重/t | 路基顶面 | 顶面下108 cm | |||||||
| 偏移距离/cm | 平均 | 偏移距离/cm | 平均 | ||||||
| 0 | 20 | 40 | 0 | 20 | 40 | ||||
| 13 | 4.60 | 4.48 | 4.70 | 4.59 | 4.56 | 4.56 | 4.76 | 4.63 | |
| 16 | 4.74 | 4.76 | 4.85 | 4.78 | 4.88 | 4.58 | 4.76 | 4.74 | |
| 轴重/t | 路基顶面 | 顶面下108 cm | |||||||
| 偏移距离/cm | 平均 | 偏移距离/cm | 平均 | ||||||
| 0 | 20 | 40 | 0 | 20 | 40 | ||||
| 13 | 4.70 | 4.89 | 4.61 | 4.74 | 4.45 | 4.56 | 4.94 | 4.65 | |
| 16 | 4.70 | 4.88 | 4.80 | 4.79 | 4.66 | 4.58 | 4.92 | 4.72 | |
| 轴重/t | 路基顶面 | 顶面下108 cm | |||||||
| 偏移距离/cm | 平均 | 偏移距离/cm | 平均 | ||||||
| 0 | 20 | 40 | 0 | 20 | 40 | ||||
| 13 | 4.49 | 4.71 | 4.73 | 4.64 | 4.70 | 4.47 | 4.87 | 4.68 | |
| 16 | 4.74 | 4.83 | 4.87 | 4.81 | 4.85 | 4.79 | 4.86 | 4.83 | |
| 轴重/t | 路基顶面 | 顶面下108 cm | |||||||
| 偏移距离/cm | 平均 | 偏移距离/cm | 平均 | ||||||
| 0 | 20 | 40 | 0 | 20 | 40 | ||||
| 13 | 4.53 | 4.62 | 4.67 | 4.61 | 4.48 | 4.65 | 4.70 | 4.61 | |
| 16 | 4.73 | 4.82 | 4.78 | 4.78 | 4.76 | 4.79 | 4.70 | 4.75 | |
由表 14~表 17中可看出,偏移距离与最终计算出的轴载换算系数b值大小没有必然关系。且无论偏移量为多少,换算指数大部分均集中在4.5~5之间。且观察最终平均值可知,考虑了不同偏移量后得出的轴载换算系数,其数值受不同种类结构影响不大。故可推知,在实际RIOHTRACK试验路试验时,在加载车辆运行时即使出现较大偏移(>20 cm, < 40 cm),其对最终计算推演出的轴载换算系数b值影响也不大。故认为RIOHTRACK加速加载试验的结论准确性不会因轮迹偏移受到明显影响。
4 结论(1) 对于强基薄面结构、典型半刚性基层路面结构及复合式结构,以路基应力参数计算出的轴载换算系数b值均在6左右,均值为5.96。其与结构种类及路基中荷载响应位置无关,但是与季节和路面结构使用状态有关。故对于这3种结构,在目前的路面结构使用状态下轴载换算系数可取5.96,即换算式为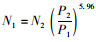
(2) 对于全厚式路面结构,其轴载换算系数相比于前述3种结构明显减小,均值为4.61,且在目前加速加载试验进行完成的两种路面结构使用状态及冬季、春季两种季节条件下,其换算指数变化不大,较为稳定。故可取其换算式为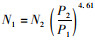
(3) 4种结构中,冬季1期加载时,16 t轴重的换算指数普遍大于13 t轴重的换算指数,而春季3期加载时的大部分数据结果却呈现相反规律。故无论哪种结构,从试验结果中都不能得出16 t重轴载条件下转换为标准轴时,其轴载换算系数一定大于以13 t轴重换算为标准轴时的换算指数的结论,其应与季节和温度等外界因素有关。
(4) 本研究进行的RIOHTRACK试验加载车为双后轴车型,并未考虑双后轴之间的相互影响,而将其视为两根单独的轴进行了分析。因而造成了一定的误差。
| [1] |
AASHTO. AASHTO Guide for Design of Pavement Structure[S]. Washington, D. C.: AASHTO, 1986.
|
| [2] |
林绣贤. 评AASHO的车辆换算[J]. 同济大学学报, 1980, 8(3): 75-86. LIN Xiu-xian. A Comment on the Traffic Conversion of AASHO[J]. Journal of Tongji University, 1980, 8(3): 75-86. |
| [3] |
孙立军. 沥青路面结构行为理论[M]. 北京: 人民交通出版社, 2003. SUN Li-jun. Structural Behavior Study for Asphalt Pavements[M]. Beijing: China Communications Press, 2003. |
| [4] |
邓学钧, 黄晓明. 路面设计原理与方法[M]. 2版. 北京: 人民交通出版社, 2008. DENG Xue-jun, HUANG Xiao-ming. Principles and Design Methods of Pavement[M]. 2nd ed. Beijing: China Communications Press, 2008. |
| [5] |
黄卫, 何平. 柔性路面弯沉和路基压应变指标分析[J]. 岩土工程学报, 1998, 20(3): 66-69. HUANG Wei, HE Ping. Analysis of Deflection and Compressive Strain on the Surface and the Subgrade of Flexible Pavement[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(3): 66-69. |
| [6] |
林绣贤. 柔性路面设计中车辆换算的研究[J]. 同济大学学报, 1980, 8(1): 113-123. LIN Xiu-xian. A Study of Traffic Conversion for Flexible Pavement Design[J]. Journal of Tongji University, 1980, 8(1): 113-123. |
| [7] |
JTG D50-2006, 公路沥青路面设计规范[S]. JTG D50-2006, Specifications for Design of Highway Asphalt Pavement[S]. |
| [8] |
李雪涛. 重载作用下按实测弯沉等效的沥青路面轴载换算[J]. 交通世界, 2016(15): 42-43. LI Xue-tao. Heavy Axle Load Conversion of Asphalt Pavement Based on the Measured Deflection Equivalent Principle[J]. TranspoWorld, 2016(15): 42-43. |
| [9] |
李海军, 黄晓明. 重载条件下沥青路面按弯沉等效的轴载换算[J]. 公路交通科技, 2004, 21(7): 5-8. LI Hai-jun, HUANG Xiao-ming. Axle Load Conversion Formula Based on Deflection Equivalent for Semi-rigid Base Asphalt Pavement under Heavy-load[J]. Journal of Highway and Transportation Research and Development, 2004, 21(7): 5-8. |
| [10] |
田力琼.重轴载条件下沥青路面轴载换算研究[D].武汉: 武汉理工大学, 2010. TIAN Li-qiong. Study on Asphalt Pavement Axle Load Conversion under Condition of Heavy Axle Load[D]. Wuhan: Wuhan University of Technology, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10497-1011058921.htm |
| [11] |
王辉, 武和平. 沥青路面按弯沉等效轴载换算的研究[J]. 中国公路学报, 2003, 16(1): 19-21. WANG Hui, WU He-ping. Research on Axle Exchange Based on Deflection Equivalent for Asphalt Pavement[J]. China Journal of Highway and Transport, 2003, 16(1): 19-21. |
| [12] |
蒋建明, 张立文, 罗雪坤. 基于弯沉等效的柔性基层沥青路面轴载换算原则[J]. 山西建筑, 2013, 39(1): 120-121. JIANG Jian-ming, ZHANG Li-wen, LUO Xue-kun. Axle Load Conversion Principle of Asphalt Pavement with Flexible Base Based on Deflection Equivalent[J]. Shanxi Architecture, 2013, 39(1): 120-121. |
| [13] |
黄卫, 何平. 柔性路面弯沉和路基压应变指标分析[J]. 岩土工程学报, 1998, 20(3): 66-69. HUANG Wei, HE Ping. Analyis of Deflection and Compressive Strain on the Surface and the Subgrade of Flexible Pavement[J]. Chinese Journal of Geotechnical Engineering, 1998, 20(3): 66-69. |
| [14] |
JTG D50-2017, 公路沥青路面设计规范[S]. JTG D50-2017, Specifications for Design of Highway Asphalt Pavement[S]. |
| [15] |
孙志林, 黄晓明. 基于路基顶面压应变的沥青路面轴载换算方法[J]. 公路交通科技, 2007, 24(7): 28-30. SUN Zhi-lin, HUANG Xiao-ming. Conversion Method of Axle Load for Asphalt Pavement Based on Compression Strain on Top of Subgrade[J]. Journal of Highway and Transportation Research and Development, 2007, 24(7): 28-30. |
| [16] |
宋鑫, 曾靖. 基于应变等效的柔性基层沥青路面轴载换算方法研究[J]. 石油沥青, 2012, 26(6): 19-24. SONG Xin, ZENG Jing. Equivalent for Asphalt Pavement with Flexible Base[J]. Petroleum Asphalt, 2012, 26(6): 19-24. |
| [17] |
黄晓明. 路基路面工程[M]. 4版. 北京: 人民交通出版社, 2014. HUANG Xiao-ming. Road Subgrade and Pavement Engineering[M]. 4th ed. Beijing: China Communications Press, 2014. |
| [18] |
张碧琴, 马亚坤, 张强, 等. 重载作用下沥青路面结构验算方法[J]. 长安大学学报:自然科学版, 2014, 34(1): 1-6. ZHANG Bi-qin, MA Ya-kun, ZHANG Qiang, et al. Checking Measures of Asphalt Pavement Structure under Overloading[J]. Journal of Chang'an University:Nature Science Edition, 2014, 34(1): 1-6. |
 2020, Vol. 37
2020, Vol. 37
