扩展功能
文章信息
- 马荣影, 韩锐, 艾曦锋, 李宏刚, 储江伟
- MA Rong-ying, HAN Rui, AI Xi-feng, LI Hong-gang, CHU Jiang-wei
- 基于Python的汽车油耗多参数回归模型构建方法
- A Method for Constructing Multi-parameter Regression Model of Vehicle Fuel Consumption Based on Python
- 公路交通科技, 2020, 37(6): 145-150
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 145-150
- 10.3969/j.issn.1002-0268.2020.06.018
-
文章历史
- 收稿日期: 2019-07-17
汽车保有量的持续不断增加,以至于石化能源消耗呈加速增长的趋势。能源短缺和环境污染等一系列问题接踵而至。汽车燃油消耗的问题得到广泛关注,国内外的学者也不断地致力于研究燃油消耗模型。文献[1-2]使用主成分分析方法对影响汽车燃油消耗的变量进行压缩,建立了BP神经网络的油耗组合预测模型。文献[3]从影响油耗的道路和交通特性方面,并利用大量出租车油耗数据构建了BP神经网络的油耗模型。文献[4]利用GPS位置、速度、高度等参数数据,提出了一种基于BP神经网络并利用智能手机测量车辆的瞬时油耗。文献[5]采用皮尔逊系数相关分析方法对与高油耗相关的驾驶行为指标进行滤波,由高度相关的驾驶行为指标生成了12个以上的聚合模型。文献[6]建立了城市道路工况下的平峰期和高峰期的油耗模型、不同道路类型的速度油耗模型以及不同速度、不同加速度下的瞬时油耗模型。文献[7]使用质量和速度因素对油耗影响独立计算的方法,建立了客车燃油消耗量的计算模型。文献[8]在稳态油耗模型的基础上引入瞬态修正模块,建立了一种新的瞬态油耗模型BIT-TFCM。文献[9]使用车辆速度与加速度并凭借最小二乘法构建了一种瞬态燃油消耗模型。文献[10]采用支持向量机(SVM)、人工神经网络和多元线性回归3种统计模型来预测总油耗和瞬时油耗。文献[11]利用决策树数据挖掘方法构建了燃油消耗模型。文献[12]利用快速路、主干路、次干路和支路道路油耗实测的数据建立了道路燃油经济性评价模型。文献[13]使用汽车油耗的主要影响因素建立计算油耗的理论模型。文献[14]建立了汽车燃油消耗和排放随瞬时速度和行驶方式变化的数学模型。文献[15]在不同速度下采集相应油耗数据, 并借助统计软件建立油耗回归模型, 搭建了油耗测量系统。文献[16]使用主成分分析和神经网络相结合的方法并基于行驶工况特征参数,创建了燃油消耗预测模型。
因Python语言通俗易懂且其中含有丰富和功能强大的类库,非常适于深入的数据处理和机器学习等领域。本研究运用Python语言,以采集到的7万余条车辆运行状态实时数据为基础,提取对油耗有影响的车辆运行状态特征参数;基于特征参数分别建立多元线性回归模型、多层感知器(MLP)神经网络回归模型和集成回归模型;通过对3种回归模型进行十折交叉验证,对比分析模型的误差和平均得分,为进一步阐明汽车运行油耗与车辆运行状态参数之间的关系提供理论依据。
1 数据获取与预处理 1.1 实时运行状态数据采集本研究所用数据样本是通过OBD检测仪获取的车辆多次短时运行的数据集,其实时记录车辆运行状态的相关参数有怠速时间IT、加速度a、负荷率L、冷却液温度CT、发动机转速n、车速v、节气门位置TP、进气管绝对压力P与平均油耗FC等,各参数相关含义见文献[17]。采样平均间隔为1.1 s,数据格式如表 1所示。
| 采样序号 | IT/s | a/(m·s-2) | L/% | CT/℃ | n/(r·min-1) | v/(km·h-1) | TP/% | P/kPa | FC/(L·100 km-1) |
| 1 | 0.00 | 0.00 | 0.00 | 14.00 | 0.00 | 0.00 | 7.06 | 99.00 | 50.00 |
| 2 | 0.00 | 0.00 | 0.00 | 14.00 | 227.00 | 0.00 | 7.06 | 99.00 | 50.00 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 70 162 | 103 | -3.02 | 26.67 | 83 | 1 792 | 23 | 4.31 | 63 | 9.08 |
1.2 数据预处理
在数据预处理阶段,对各项参数数据基本统计量进行统计,对不符合实际情况的数据进行调整或剔除,提高数据质量为后续建模做好准备。导入Python中的数据分析包(pandas)进行数据预处理,使用read_csv函数读取数据集。使用describe( )函数可以对各个参数的基本统计量进行描述,包括数量Q、平均值M、标准差Std、最小值Min、上四分位数Uq、中位数Median、下四分位数Lq、最大值Max。基于采集的实时运行状态数据的基本统计量,如表 2所示。
| 参数 | IT/s | a/(m·s-2) | L/% | CT/℃ | n/(r·min-1) | v/(km·h-1) | TP/% | P/kPa | FC/(L·100 km-1) |
| Q | 70 162 | 70 162 | 70 162 | 70 162 | 70 162 | 70 162 | 70 162 | 70 162 | 70 162 |
| M | 322.00 | 0.00 | 38.51 | 77.40 | 1 373.00 | 34.40 | 4.30 | 46.05 | 12.50 |
| Std | 357.50 | 0.49 | 18.09 | 16.30 | 563.52 | 28.70 | 4.90 | 17.83 | 8.70 |
| Min | 0.00 | -4.00 | 0.00 | -17.00 | 0.00 | 0.00 | 0.00 | 14.00 | 3.80 |
| Uq | 65.00 | -0.22 | 24.31 | 81.00 | 751.00 | 3.00 | 0.00 | 32.00 | 8.20 |
| Median | 212.00 | 0.00 | 32.16 | 83.00 | 1 408.00 | 34.00 | 2.00 | 41.00 | 9.30 |
| Lq | 413.00 | 0.26 | 50.20 | 84.00 | 1 762.00 | 56.00 | 8.20 | 59.00 | 13.10 |
| Max | 1 733.00 | 2.22 | 100.00 | 97.00 | 3 178.00 | 118.00 | 27.00 | 101.00 | 50.00 |
从表 2的数据统计描述中可看出,样本中各项参数计数均为70 162条,无空缺值且无异常值。但是存在着数据的量值范围差距大、位数不统一、有正负值等情况,需要对数据进行预处理。以使原始数据转化为无量纲化、同量级的参数以进行综合分析。
2 车辆燃油消耗特征参数提取及建模 2.1 特征参数提取影响车辆油耗的参数众多,且每个影响参数都有各自的量纲和数量级,单纯依靠方差判断影响程度的效果可能不理想。因此,为减少建立模型的计算量和使模型泛化能力更强,需要进行特征参数选择。调用Python中的特征选择库,使用其中的SelectKBest函数,通过设定阈值n,选出n个最佳特征参数进行建模。从试验中可获取的怠速时间、冷却液温度、速度、加速度、负荷率、转速、节气门位置和进气管绝对压力等对油耗有影响的实时运行参数数据,进行特征提取选出特征参数。分别设置n=1,2, …, 8, 则可将参数按与因变量的相关性强弱顺序排出:冷却液温度(1)、车速(2)、节气门位置(3)、发动机转速(4)、怠速时间(5)、负荷率(6)、加速度(7)、进气管绝对压力(8)。
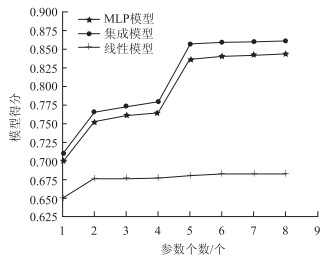
选取参数个数n所对应的模型得分(模型得分由score函数计算所得),如图 1所示。
|
| 图 1 参数个数所对应的模型得分 Fig. 1 Model score corresponding to number of parameters |
| |
从图 1中可看出,对于多元线性回归模型,当选取前2个参数时线性回归模型平均得分为0.68,且再增加建模参数个数n时模型得分也无明显变化。对于MLP回归模型和集成回归模型,当选取前5个参数时模型平均得分分别为0.84和0.86,且再增加建模参数个数n时模型得分也无明显变化, 即建立MLP回归模型和集成回归模型时可选取前5个参数。
2.2 车辆燃油消耗模型建立 2.2.1 模型构建简介回归与预测方法是在分析自变量与因变量相关性的基础上,建立变量之间的回归模型,并以回归模型为预测方法。本研究将基于机器学习库分别建立多元回归线性模型和非线性回归模型两种,在分析回归误差的基础上评价其精度。
在构建模型时,将数据集划分成训练集和测试集,其中训练集用来构造模型,测试集则用来检验最终选择最优模型的性能。建立的3种回归模型中的共同设置条件为,机器学习函数库对数据集进行划分,调用train_test_split函数对数据集进行样本划分,并使用随机数种子33进行随机分割,训练集与测试集样本的比例是9:1。
2.2.2 线性模型的构建使用机器学习函数库中的Linear Regression来建立线性多元回归预测模型,针对非线性问题,提出了一种线性化方法,使用fit( )分析模型参数,predict( )是通过fit( )算出的模型参数构出的模型,对自变量进行预测来获得其值并使用predict函数预测出油耗值,再对预测值进行综合分析,确定最后的预测值。使用lr.intercept函数计算出截距,使用lr.coef函数计算出油耗FC、冷却液温度CT、车速v各个参数的系数,求出的油耗多元线性回归的方程为:
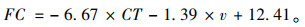
|
(1) |
多层感知器神经网络模型的构建,调用Python机器学习库中的MLP Regressor( )对油耗进行MLP回归建模。MLP回归模型是感知器的推广,当输出层有输出的时候,可以将其与已知值进行比较,并相应地调整权重; 重复此过程,直至达到允许迭代的最大数量或可接受的错误率,解决了单层感知器非线性不可分的缺点。输入层神经元数为输入变量的数量n为8,输出层神经元数为输出变量的数量m为1。有关研究表明,一个隐含层的神经网络,只要隐层的神经元数量足够多,就可以任意精度逼近一个非线性函数,调用hidden_layer_sizes函数设置神经网络参数;在MLP回归模型中,隐层的神经元数量的设定与实际问题的复杂程度、输入和输出层的神经元数量以及对期望误差有直接的联系,其可以使用经验公式来确定[18]:

|
(2) |
式中,L为隐层的神经元数量; n为输入层的神经元数量; m为输出层的神经元数量; a为[1, 10]之间的常数。本研究中选取a为6,即L=10。解决器设置为adam,学习率设置为adaptive,激活函数选择relu,其他参数使用机器学习库中的默认参数。
集成回归模型的构建,一些简单模型对于数据量大或很难训练的数据集只能学习到一部分,而集成学习方法可以有策略地将数据集划分成一些小数据集,并分别进行训练,之后再根据一些策略进行组合,集成学习就是组合很多子模型以得到一个预测效果较好的强模型。子模型的数量设置对模型的预测能力有着直接的影响,数量少容易欠拟合,数量多计算量大并导致过拟合的问题,所以一般选择一个适中的数值,默认是100。在数据少或者特征少的时候可忽略树的深度值,则决策树在建立子树的时候不限制子树的深度。反之则推荐限制最大深度,一般取值为10~100之间。叶节点最小样本值默认是1,其值的设定限制了叶节点最少的样本数。如果样本量不大,则可忽略这个值,反之则应增大这个值。
本研究使用的集成模型的子模型数量为100,树的最大深度为10,叶节点最小样本数为14,学习率为0.001,其他参数使用机器学习库中的默认参数。
3 模型的验证构建的回归预测模型是否可应用于实际,需要对回归预测模型进行检验和对预测误差计算。只有通过各种检验且预测误差较小,才能将回归方程作为预测模型应用。因此有必要使用cross_val_score函数对数据集进行指定次数的交叉验证,从样本中随机按比例选取训练集和测试集,对模型得分进行10次交叉验证。用metrics.mean_squared_error函数计算的结果开方即得均方根误差(RMSE),是观测值与真值偏差的平方和与观测次数m比值的平方根,其是用来衡量观测值同真值之间的偏差。用metrics.mean_absolute_error函数计算平均绝对误差(MAE)。上述验证模型的结果如表 3所示。
| 参数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Mean | RMSE | MAE |
| 线性 | 0.68 | 0.66 | 0.70 | 0.68 | 0.67 | 0.68 | 0.68 | 0.66 | 0.67 | 0.67 | 0.68 | 4.80 | 3.01 |
| MLP | 0.82 | 0.84 | 0.84 | 0.84 | 0.84 | 0.84 | 0.85 | 0.84 | 0.85 | 0.83 | 0.84 | 0.48 | 0.30 |
| 集成 | 0.85 | 0.85 | 0.85 | 0.87 | 0.87 | 0.85 | 0.87 | 0.86 | 0.87 | 0.85 | 0.86 | 0.38 | 0.23 |
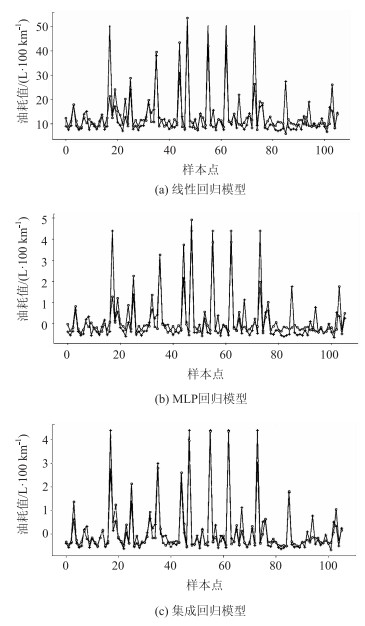
截取使用Python绘图库matplotlib绘出的部分油耗预测值与实际值二者之间的关系图,如图 2所示。
|
| 图 2 预测值与真实值 Fig. 2 Predicted values and real values |
| |
4 结论
本研究利用OBD实时检测车辆运行状态参数和瞬时油耗数据,并调用Python机器学习库中的相关算法,对构建汽车运行油耗多参数回归模型的方法进行了相关研究。但是,作为研究油耗影响因素的一种方法,在实际应用中还与车型种类、主要总成配置、装载情况、驾驶行为等有关。依据本研究采样数据处理分析得出的主要结论为:
(1) 调用Python的特征选择库,得到的影响车辆运行油耗的运行状态参数的排序结果为:冷却液温度、车速、节气门位置、发动机转速、怠速时间、负荷率、加速度、进气管绝对压力。
(2) 基于Python的机器学习库,建立的多元线性回归模型的平均绝对误差为3.01,均方根误差为4.80,模型平均得分为0.68,这表明车辆运行油耗与运行状态参数之间的线性关系不明显。
(3) 基于Python的机器学习库,对非线性的多层感知器(MLP)神经网络回归模型和集成回归模型进行十折交叉验证的结果表明,MLP神经网络回归模型平均绝对误差为0.30,均方根误差为0.48,模型平均得分为0.84;集成回归模型平均绝对误差为0.23, 均方根误差为0.38,模型平均得分为0.86,这表明车辆运行油耗与运行状态参数之间的非线性关系明显,适宜建立非线性回归模型。
| [1] |
赵晓华, 姚莹, 伍毅平, 等. 基于主成分分析与BP神经元网络的驾驶能耗组合预测模型研究[J]. 交通运输系统工程与信息, 2016, 16(5): 185-191, 204. ZHAO Xiao-hua, YAO Ying, WU Yi-ping, et al. Prediction Model of Driving Energy Consumption Based on PCA and BP Network[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(5): 185-191, 204. |
| [2] |
张登, 祖春胜, 赵超超. 主成分分析与神经网络结合的燃油消耗预测[J]. 农业装备与车辆工程, 2015, 53(6): 47-52. ZHANG Deng, ZU Chun-sheng, ZHAO Chao-chao. Principal Component and Neural Network Combined Fuel Consumption Forecast[J]. Agricultural Equipment and Vehicle Engineering, 2015, 53(6): 47-52. |
| [3] |
侯亚美, 陈艳艳, 吴克寒, 等. 基于BP神经网络的北京市出租车油耗模型研究[J]. 道路交通与安全, 2015, 15(5): 43-49. HOU Ya-mei, CHEN Yan-yan, WU Ke-han, et al. Study on Taxi Fuel Consumption Model in Beijing Based on BP Neural Network[J]. Road Traffic and Safety, 2015, 15(5): 43-49. |
| [4] |
KANARACHOS S, MATHEW J E, FITZPATRICK M. Instantaneous Vehicle Fuel Consumption Estimation Using Smartphones and Recurrent Neural Networks[J]. Expert Systems with Applications, 2019, 120: 436-447. |
| [5] |
YAMASHITA R J, YAO H H, HUNG S W, et al. Accessing and Constructing Driving Data to Develop Fuel Consumption Forecast Model[J]. IOP Conference Series Earth and Environmental Science, 2018, 113(1): 012217. |
| [6] |
隗海林, 王劲松, 王云鹏, 等. 基于城市道路工况的汽车燃油消耗模型[J]. 吉林大学学报:工学版, 2009, 39(5): 1146-1150. KUI Hai-lin, WANG Jin-song, WANG Yun-peng, et al. Vehicle Fuel Consumption Model Based on Urban Road Operations[J]. Journal of Jilin University:Engineering and Technology Edition, 2009, 39(5): 1146-1150. |
| [7] |
蔡团结, 王旭斌, 陈春梅. 客车燃油消耗计算模型的构建及验证[J]. 公路交通科技, 2009, 26(9): 150-153. CAI Tuan-jie, WANG Xu-bin, CHEN Chun-mei. Modeling and Verification of Fuel Consumption Calculating Model for Passenger Vehicles[J]. Journal of Highway and Transportation Research and Development, 2009, 26(9): 150-153. |
| [8] |
金辉, 周敏, 李世杰. 基于瞬态修正的车辆燃油消耗模型建模[J]. 北京理工大学学报, 2017, 37(5): 473-477, 484. JIN Hui, ZHOU Min, LI Shi-jie. Transient Fuel Consumption Modelling Based on Transient Correction[J]. Transactions of Beijing Institute of Technology, 2017, 37(5): 473-477, 484. |
| [9] |
张金辉, 李克强, 徐彪, 等. 基于最小二乘法的车辆瞬态燃油消耗估计[J]. 汽车工程, 2008, 40(10): 1151-1157. ZHANG Jin-hui, LI Ke-qiang, XU Biao, et al. Estimation of Vehicle Instantaneous Fuel Consumption Based on Least Square Method[J]. Automotive Engineering, 2008, 40(10): 1151-1157. |
| [10] |
ÇAPRAZ A G, ÖZEL P, ŞEVKLI M, et al. Fuel Consumption Models Applied to Automobiles Using Real-time Data:A Comparison of Statistical Models[J]. Procedia Computer Science, 2016, 83: 774-781. |
| [11] |
朱广宇, 赵蕾, 黄达, 等. 基于决策树方法的车辆油耗估计模型[J]. 交通运输系统工程与信息, 2016, 16(3): 200-206. ZHU Guang-yu, ZHAO Lei, HUANG Da, et al. A Method of Vehicle Fuel Consumption Estimation Based on Decision Tree[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(3): 200-206. |
| [12] |
冯雨芹, 冷军强, 张亚平, 等. 城市道路路段燃油经济性评价模型[J]. 华南理工大学学报:自然科学版, 2011, 39(8): 104-108. FENG Yu-qin, LENG Jun-qiang, ZHANG Ya-ping, et al. Evaluation Model of Fuel Economy of Urban Road Section[J]. Journal of South China University of Technology:Natural Science Edition, 2011, 39(8): 104-108. |
| [13] |
付百学, 胡胜海. 汽车油耗检测系统数学模型的建立与应用研究[J]. 测试技术学报, 2008, 23(1): 38-43. FU Bai-xue, HU Sheng-hai. The Mathematical Model of Oil-consumption Detecting Systems and Its Application Research[J]. Journal of Test and Measurement Technology, 2008, 23(1): 38-43. |
| [14] |
HUNG W T, TONG H Y, CHEUNG C S. A Modal Approach to Vehicular Emissions and Fuel Consumption Model Development[J]. Journal of the Air & Waste Management Association, 2005, 55(10): 1431-1440. |
| [15] |
马健军, 黄玉华, 龙志军, 等. 市郊道路工况车辆油耗模型研究[J]. 南方农机, 2017, 48(8): 12-13. MA Jian-jun, HUANG Yu-hua, LONG Zhi-jun, et al. Study on Fuel Consumption Model of Vehicles under Suburban Road Condition[J]. China Southern Agricultural Machinery, 2017, 48(8): 12-13. |
| [16] |
姜平, 石琴. 基于行驶工况特征的汽车燃油消耗的预测[J]. 汽车工程, 2014, 36(6): 643-647. JIANG Ping, SHI Qin. Vehicle Fuel Consumption Prediction Based on Driving Cycle Characteristics[J]. Automotive Engineering, 2014, 36(6): 643-647. |
| [17] |
周晓飞. 别克世纪轿车发动机电控系统数据流及诊断分析[J]. 汽车维修, 2009, 15(5): 47-48. ZHOU Xiao-fei. Data Flow and Diagnostic Analysis of Engine Electronic Control System of Buick Century Sedan[J]. Automobile Maintenance, 2009, 15(5): 47-48. |
| [18] |
龙马高新教育. Python3数据分析与机器学习实战[M]. 北京: 北京大学出版社, 2018. Longma High and New Education. Python3 Data Analysis and Machine Learning Practice[M]. Beijing: Peking University Press, 2018. |
 2020, Vol. 37
2020, Vol. 37
