扩展功能
文章信息
- 赵靖, 葛庆红, 韩印
- ZHAO Jing, GE Qing-hong, HAN Yin
- 考虑需求起讫点及需求等级的响应型社区公交行车调度优化
- Optimization of Responsive Community Transit Scheduling Considering Demand OD and Level
- 公路交通科技, 2020, 37(6): 128-137
- Journal of Highway and Transportation Research and Denelopment, 2020, 37(6): 128-137
- 10.3969/j.issn.1002-0268.2020.06.016
-
文章历史
- 收稿日期: 2019-07-03
社区规模逐渐扩大,大型社区居民出行“最后一公里”问题愈加凸显,社区公交的出现有助于解决这一问题,极大地方便居民出行。为进一步满足居民出行的个性化需求,有必要在目前的需求响应型公交的基础上进行优化改进,提出一种响应型社区公交,对响应型社区公交行车调度进行优化,有助于减少公交公司的运营成本、居民的步行路程、等待时间,从而提高社区公交服务质量。
社区公交在现实生活中的主要功能是服务社区内部交通和接驳其他交通,优化社区公交的行车调度不仅能提高乘客出行满意度,而且可以节约公交运营成本[1]。以往的社区公交调度大多沿用了常规公交调度方法,主要集中在固定线路公交的车辆调度上,通过公交时刻表来优化车辆发车间隔来为乘客提供高水平服务[2-5]。近年来,有不少学者开始以社区公交为研究对象对其行车调度进行优化,Verma[6]分析了区域内轨道交通线网的布设和现有的接驳公交运营状况,基于此建立社区公交行车路径优化模型,减少需求等待时间。Schittekat[7]针对校车这一特殊社区公交, 考虑学生可以选择的潜在站点,以公交行驶路程最小为目标建立了公交运营路径规划模型。Xiong等[8]采用启发式算法求解了社区公交行车线路优化模型。张思林等[9]以接驳轨道交通的社区公交为研究对象,分析乘客选择站点的影响因素,考虑公交运营成本和乘客在车时间、步行时间与候车时间的成本建立多目标优化模型研究了社区公交站点的布设。
学者在社区公交行车调度研究领域取得了不错的成果,但现有的社区公交运营模式对需求波动的适用性不是非常好。为提高公共交通对乘客出行需求空间和时间分布波动性的适应能力,需求响应型公交被提出,提供了更为个性化的服务,更加方便了市民出行[10]。
需求响应型公交,在学界也被称为定制公交、灵活型公交、可变线路公交[11-13]。关于需求响应型公交的行车调度[14-30],ANK等[16]研究了需求不确定情况下的灵活型服务公交的线网规划问题,提出了一种两阶段随机规划的解决方案。Nourbakhsh等[18]基于低需求水平区域研究了一种灵活型公交服务系统,以成本为评价指标建立优化模型求解灵活型公交的行车路径选择问题。Qiu F等[19]针对站点偏移式的灵活公交服务提出了一种动态站点策略,通过最优化途径站点来确定车辆的最优行车路径。Wei T等[20]考虑响应型公交计划行程时间与实际行程时间存在差值,为减少车辆到站延误,提出了一种协同调度模型,使模型具有一定的鲁棒性。邱丰等[21]考虑动静态需求对可变线路公交分两阶段建立了行车调度模型。潘述亮等[22]针对确定的车辆规模和需求,综合考虑乘客和公交公司利益,并以此为目标建立了响应型公交协同调度优化模型。郑汉等[25]分析了需求响应型公交服务效率和服务质量之间的矛盾,研究了多车型的响应型公交行车调度问题,以最小化使用车辆数目和步行距离建立数学模型,并通过案例分析对模型进行验证。柳伍生等[26]从绿色交通的角度出发研究了多需求下的定制公交线网优化问题建立线网优化模型。王健等[27]以静态需求对研究对象,考虑需求起讫点研究了多线路定制公交的调度问题。
学者对响应型公交行车调度做了丰富研究,但以往研究中对于出行需求均假设所有需求都预先给定,较少考虑运行过程中的动态需求,对需求起讫点一般只考虑出行起点需求的响应,出行终点是固定站点,对出行起终点均响应的研究较少,也未检索到同时考虑动态需求和需求起讫点的响应型公交调度模型。对于需求等级,由于以往研究需求均预先给定,未对不同时刻提出的需求进行等级划分。针对上述研究的不足,本研究提出一种新的响应型社区公交,统筹考虑需求起讫点、需求等级、动态需求,研究该社区公交的行车调度优化,用来解决社区公交运营中存在的乘客等待时间长、步行距离长、服务时段不合理等问题。
1 优化方法的基本思想 1.1 基于需求起讫点的响应型社区公交常规的社区公交发车时间固定,运营线路固定,停靠站点固定。其特征主要有:(1)主要功能是服务社区内部交通与接驳其他交通;(2)单次运营线路里程较小;(3)站点密度要求高。
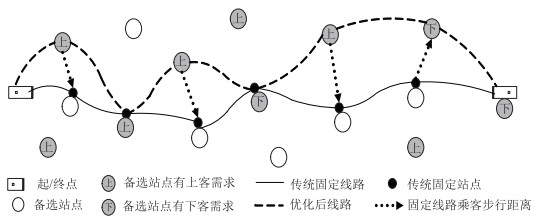
需求响应型公交运营线路由需求决定。本研究在站点偏移式公交的基础上考虑需求的起讫站点对其运营模式进行优化,将传统的公交站点分割成上车站点和下车站点,车辆根据需求信息行驶至有需求的站点接客,途中仅经过需求信息中的下车站点,具体如图 1所示。
|
| 图 1 基于需求起讫点的响应型社区公交运营 Fig. 1 Responsive community transit operation based on demand OD |
| |
针对社区公交特征,本研究将通过终点站、备选站点和设置运营里程约束进行应对。对于社区公交的接驳功能,通过将其他交通换乘站点设置为需求响应型社区公交的起终点站,实现接驳功能,并且布设高密度备选站点,这些备选站点可根据社区内潜在交通产生吸引点设置,包含居民住宅、超市、医院、学校等社区居民出行密度较大的区域。在下述模型中,乘客可以根据实际需求在高密度的备选站点中进行选择。此外,接下来的模型中将考虑车辆单次运营的最长、最短里程,以适应社区公交的特征。
乘客通过手机客户端或短信发送上车站点、下车站点和接受服务的时间窗等需求信息进行预约出行,公交公司收到请求后将考虑需求等级及相关规则后来判断是否响应,并将最终结果反馈给乘客,若不响应,公交公司会建议乘客等待下一班次车辆,乘客根据反馈结果决定是否接受建议,并将最终决定反馈至公交公司。
1.2 基于需求等级的响应规则在车辆行车调度前,对第k班车需要考虑的需求进行分析,如表 1所示。
| 情形 | 需求 |
| Ⅰ | k-1次班车发车前已申请但未响应的需求 |
| Ⅱ | k-1次班车发车后至k次班车发车前申请的且k-1次班车未响应的需求 |
| Ⅲ | k+1班车发车前,k班车发车后产生的新需求 |
为避免产生二次等待影响乘客出行,情形Ⅰ的需求,车辆必须响应,优先级最高。情形Ⅱ的需求在情形Ⅰ需求的基础上根据评价指标的变化进行选择性响应,优先级仅次于情形Ⅰ的需求。情形Ⅲ的需求发生在情形Ⅰ和Ⅱ需求的后面,在前两种需求的基础上,考虑接受此需求后能否进一步优化评价指标,从而来判断是否接受该点的需求,若可以,则将该需求点考虑到本班次公交的行驶路线中;若不可以,则将该需求点考虑到下一班次公交的行驶路线中。若本次班车已行驶过了该需求预约点,该预约需求点将直接放到下一班车中考虑,故情形Ⅲ的需求优先级最低。
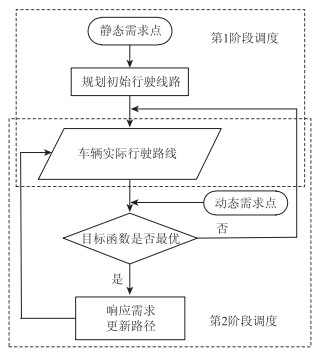
2 行车调度优化模型 2.1 行车调度流程如上所述,将发车前的预约需求定义为静态需求(即情形Ⅰ需求、情形Ⅱ需求),发车后产生的预约需求定义为动态需求(即情形Ⅲ需求),基于此可以分别建立两阶段行车调度模型(静态和动态)。两阶段行车调度流程如图 2所示。
|
| 图 2 需求响应型社区公交行车调度流程图 Fig. 2 Flowchart of demand responsive community transit scheduling |
| |
2.2 评价指标
选取空载率最小,乘客不满意度最小,单次运营里程(归一化)最小作为目标建立模型。
2.2.1 空载率空载率是指公交的剩余载客容量与公交的额定载客容量比值,如式(1)所示。
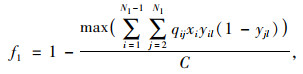
|
(1) |
式中,N1为需求点数量;qij为i需求站点上车至j需求站点下车人数;C为公交车辆的额定载客容量;xi, yij为0-1变量,分别如下所示。

|
居民的预约需求被响应后,车辆不能保证在所有乘客期望的时间区间内到达。为尽可能保证公交的准点率和提升乘客乘坐满意度,本研究从乘客角度出发采取软时间窗对车辆的到达时间进行约束。
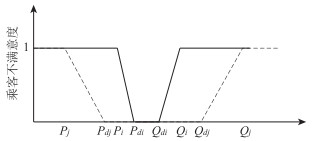
软时间窗是指车辆能在乘客的期待服务时间窗[Pdi, Qdi]内到达i需求站点时,乘客的满意度为1;若车辆的到达时间ti早于Pdi或晚于Qdi时,乘客的满意度将逐渐减小。在可接受的时间窗[Pi, Pdi]和[Qdi, Qi]内,乘客的满意度将由1逐渐减小到0;在不能接受的时间窗[0, Pi]和[Qi, +∞]内,乘客的满意度将一直为0。假设乘客不满意度的波动是按线性变化的[31-32],对应的乘客不满意度如式(2)所示。
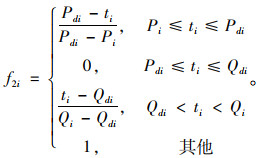
|
(2) |
考虑不同乘客出行目的不同,将[Pi, Pdi]和[Qdi, Qi]的取值完全交给乘客自主选择,乘客在提交预约需求信息时可以根据自己的出行目的确定上述时间窗,从而满足乘客对时间的个性化要求。如图 3所示,虚线线条表示j乘客的不满意度曲线,实线线条表示i乘客的不满意度曲线,可以看出,i乘客对时间的要求比j乘客对时间的要求更高。
|
| 图 3 乘客不满意度函数图 Fig. 3 Curve of passenger dissatisfaction function |
| |
2.2.3 单次运营里程归一化
单次运营里程归一化后如式(3)所示。
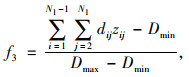
|
(3) |
式中,dij为路网中i需求站点到j需求站点的最短路径距离;Dmin为社区公交单次运营的最短里程;Dmax为社区公交单次运营的最长里程;zij为0-1变量,如下所示:
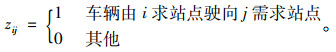
|
所有车辆每次必须从起始站出发,终点站停车。k班车需要考虑的需求即上述情形Ⅰ、情形Ⅱ、情形Ⅲ中的需求,这3种预约需求分别用集合M1,M2和M3表示。
第1阶段静态调度的目标函数如式(4)所示。
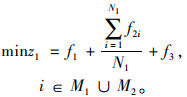
|
(4) |
式(4)由3部分组成,分别是空乘率、乘客不满意度、单次运营里程。式中,NⅠ为静态阶段的需求点数量;f2i为i号需求站点上乘客的不满意度。
约束有需求响应约束,要求k-1班次没响应的需求站点在本班次中必须被响应;且对于任一需求,其对应的上、下车需求站点均应响应,分别如式(5)、式(6)所示:
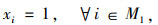
|
(5) |
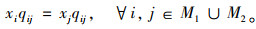
|
(6) |
公交车辆载客容量约束,要求第k班次车辆到达需求i时的车内人数不超过车辆的额定载客数,如式(7)所示。
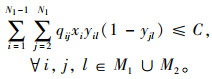
|
(7) |
公交车辆到达时刻约束,车辆到达需求j的时刻的计算方法如式(8)所示。
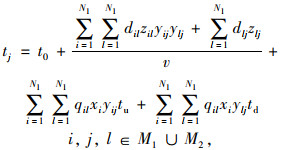
|
(8) |
式中,v为公交车辆的平均行驶速度;tu为乘客的平均上车时长;td为乘客的平均下车时长。
2.4 响应型社区公交第2阶段动态调度模型第1阶段行车调度(静态)中必须经过的预约需求用集合M4表示(M4⊆M1∪M2),在发车前规划出一条最优线路将M4中的预约需求点连接起来。第2阶段调度(动态)要以第1阶段调度(静态)的行驶线路为初始线路,公交发出时遵循初始线路运营,若有动态需求发出申请,考虑动态需求申请时刻与车辆此刻的位置,借助相关算法来决定是否将该预约需求点放到初始线路中,同时将车辆的运营线路进行实时更新。
第2阶段动态调度的目标函数如式(9)所示。
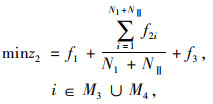
|
(9) |
式中,NⅡ为动态需求点的数量;M3为动态需求集合。
约束有需求响应约束,要求第1阶段行车调度中已决定响应的需求站点在第2阶段动态调度中必须被响应,且对于任一需求,其对应的上、下车需求站点均应响应,分别如式(10)、式(11)所示。
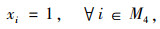
|
(10) |
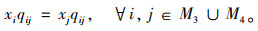
|
(11) |
公交车辆载客容量约束,要求第k班次车辆到达需求i时的车内人数不超过车辆的额定载客数,如式(12)所示。
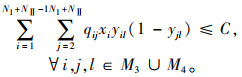
|
(12) |
公交车辆到达时刻约束,车辆到达需求j的时刻的计算方法如式(13)所示。
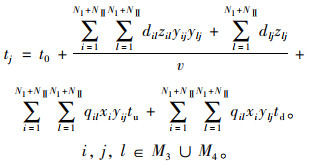
|
(13) |
动态需求发出时刻约束,要求动态需求i发出需求申请的时间要早于车辆到达i需求站点前方j站点的到达时间,从而保证车辆驾驶人员在行驶至下一站点前有时间做出是否调整线路的决定,如式(14)所示。
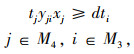
|
(14) |
式中dti为动态需求i发出需求申请的时间。
若响应某动态需求后目标函数值得到优化,则重新规划线路行驶,否则按照初次规划的线路行驶,即第2阶段行车调度模型的目标函数值不能大于第1阶段行车调度的目标函数值,如式(15)所示:
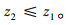
|
(15) |
遗传算法借鉴生物领域上的优胜劣汰,适者生存遗传机制,模拟染色体的选择、交叉、变异,生成有用的解决方案进行优化、搜索问题。量子计算的计算速度较快,量子状态较多,求解时陷入局部最优解的概率较小。量子遗传算法综合了上述优点,所以选取量子遗传算法进行模型求解。下述案例中,量子遗传算法的相关参数参数选择如下:最大代数为500;交叉概率0.9;变异概率0.3;群体规模30;染色体量子位数为2;染色体串长按需求数量取;量子旋转角度为0.01pi。
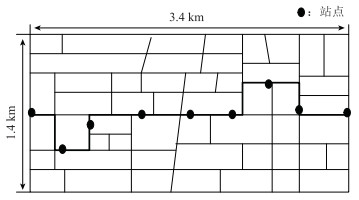
3.2 案例分析 3.2.1 相关数据收集本研究以上海市宝山区温泰线社区公交为研究对象,其现有的运营模式为定时发车定点停车的固定式公交运营,研究区域简化为一个矩形,其长为横向边界距离3.4 km, 宽为纵向边界距离1.4 km,如图 4所示。
|
| 图 4 社区公交线路 Fig. 4 Community transit route |
| |
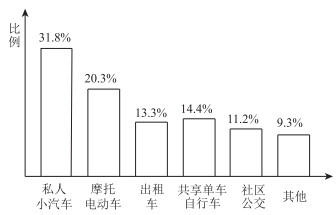
现有的社区公交车辆有两种车队规模:1辆18座、4辆20座。公交发车间隔为15 min,平均行驶速度为35 km/h,线路总长4.3 km,周边为住宅区集聚地,主要服务的小区为泰和新城、共富小区、顾村家园、成亿宝盛家苑等。该线路自运营起,方便了居民出行,但运营中存在的公交公司运营亏损、乘客等待时间长、线路覆盖范围不完善等问题需要继续解决。首先,对周边居民的出行方式进行调查,调查结果如图 5所示。
|
| 图 5 周边居民出行方式分布 Fig. 5 Distribution of peripheral residents' trip ways |
| |
从图中可以看出目前社区公交占出行方式的11.2 %,高峰时段(06:30—08:30、16:30—18:30)周边小区的平均出行密度为860人/h。乘客可接受步行距离设定为0.4 km,乘客的平均上车时长tu为5 s,平均下车时长td为3 s。
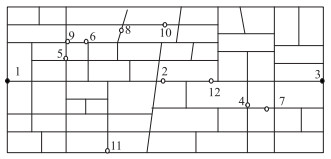
3.2.2 第1阶段模型输入以早第1班(06:30)社区公交为例,基于相关数据的收集,在上述矩形路网上利用MATLAB软件随机生成一系列有预约需求的站点和人数,需求人数取高峰期发车间隔内乘坐社区公交居民数量的均值,需求分布如图 6所示。
|
| 图 6 第1阶段预约需求点分布图 Fig. 6 Distribution of reservation demand points in stage 1 |
| |
1号点为社区公交起始站,3号点为社区公交终点站。各预约需求的预约时间信息如表 2所示。第1阶段需求起讫站点信息如表 3所示,采用Floyd算法求得路网中第1阶段各需求站点间的最短路径距离如表 4所示。
| 需求编号 | 类型 | 期望的时间区间 | 可接受的时间区间 |
| 1 | 起点 | — | — |
| 2 | 下车 | 6:33—6:42 | 6:33—6:42 |
| 3 | 下车、终点 | 6:36—6:42 | 6:36—6:42 |
| 4 | 上车 | 6:35—6:40 | 6:33—6:42 |
| 5 | 上车 | 6:30—6:35 | 6:28—6:37 |
| 6 | 上车 | 6:30—6:35 | 6:28—6:37 |
| 7 | 上车 | 6:35—6:40 | 6:33—6:42 |
| 8 | 上车 | 6:31—6:36 | 6:29—6:38 |
| 9 | 上车 | 6:30—6:35 | 6:28—6:37 |
| 10 | 上车 | 6:33—6:38 | 6:31—6:40 |
| 11 | 上车 | 6:30—6:35 | 6:28—6:37 |
| 12 | 上车 | 6:34—6:39 | 6:32—6:41 |
| 起点i | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 终点j | 3 | 2 | 3 | 3 | 2 | 2 | 3 | 3 | 3 |
| 人数 | 2 | 2 | 1 | 3 | 2 | 3 | 1 | 2 | 3 |
| 点i | 点j | |||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| 1 | 0 | 2.05 | 3.4 | 2.51 | 0.99 | 1.27 | 2.95 | 1.72 | 1.04 | 1.97 | 1.27 | 2.28 |
| 2 | 2.05 | 0 | 1.36 | 0.47 | 1.14 | 0.9 | 0.9 | 0.71 | 1.15 | 0.78 | 1.11 | 0.23 |
| 3 | 3.4 | 1.36 | 0 | 0.89 | 2.45 | 2.18 | 0.52 | 1.81 | 2.43 | 1.67 | 2.41 | 1.15 |
| 4 | 2.51 | 0.47 | 0.89 | 0 | 1.57 | 1.3 | 0.49 | 0.98 | 1.56 | 0.92 | 1.57 | 0.31 |
| 5 | 0.99 | 1.14 | 2.45 | 1.57 | 0 | 0.28 | 2.04 | 0.73 | 0.1 | 0.99 | 0.9 | 1.38 |
| 6 | 1.27 | 0.9 | 2.18 | 1.3 | 0.28 | 0 | 1.77 | 0.46 | 0.26 | 0.72 | 0.94 | 1.13 |
| 7 | 2.95 | 0.9 | 0.52 | 0.49 | 2.04 | 1.77 | 0 | 1.47 | 2.03 | 1.39 | 1.91 | 0.67 |
| 8 | 1.72 | 0.71 | 1.81 | 0.98 | 0.73 | 0.46 | 1.47 | 0 | 0.67 | 0.27 | 1.27 | 0.91 |
| 9 | 1.04 | 1.15 | 2.43 | 1.56 | 0.1 | 0.26 | 2.03 | 0.67 | 0 | 0.92 | 0.99 | 1.39 |
| 10 | 1.97 | 0.78 | 1.67 | 0.92 | 0.99 | 0.72 | 1.39 | 0.27 | 0.92 | 0 | 1.52 | 0.93 |
| 11 | 1.27 | 1.11 | 2.41 | 1.57 | 0.9 | 0.94 | 1.91 | 1.27 | 0.99 | 1.52 | 0 | 1.28 |
| 12 | 2.28 | 0.23 | 1.15 | 0.31 | 1.38 | 1.13 | 0.67 | 0.91 | 1.39 | 0.93 | 1.28 | 0 |
3.2.3 第一阶段模型求解
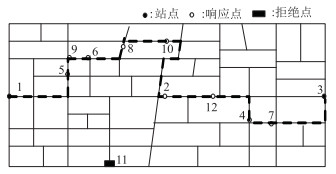
借助数学软件MATLAB2018a求解得到的结果:发车车型为18座型公交车辆,第1阶段静态调度的最优路径为:1-5-9-6-8-10-2-12-4-7-3,社区公交行驶路径如图 7所示。最优解的目标函数值为:1.070 6。
|
| 图 7 第1阶段静态调度路径图 Fig. 7 Static scheduling route (stage 1) |
| |
3.2.4 第2阶段模型输入
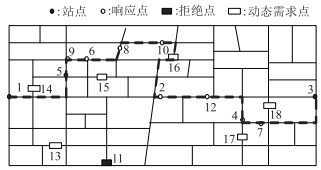
第2阶段的动态调度是在第1阶段的静态调度基础上进行的,在路网上随机生成动态预约需求如图 8所示。
|
| 图 8 第2阶段动态需求分布图 Fig. 8 Dynamic scheduling route(stage 2) |
| |
第2阶段新增的动态需求点信息如表 5所示。各动态需求起讫站点信息如表 6所示。采用Floyd算法求得路网中第2阶段各需求站点间的最短路径距离如表 7所示。
| 需求编号 | 类型 | 收到动态需求时间 | 期望的时间区间 | 可接受的时间区间 |
| 13 | 上车 | 6:30 | 6:30—6:33 | 6:30—6:35 |
| 14 | 上车 | 6:30 | 6:30—6:32 | 6:30—6:35 |
| 15 | 上车 | 6:31 | 6:31—6:35 | 6:30—6:38 |
| 16 | 上车 | 6:31 | 6:32—6:37 | 6:30—6:39 |
| 17 | 上车 | 6:31 | 6:31—6:36 | 6:20—6:38 |
| 18 | 上车 | 6:34 | 6:34—6:40 | 6:32—6:42 |
| 起点i | 13 | 14 | 15 | 16 | 17 | 18 |
| 终点j | 3 | 3 | 2 | 3 | 3 | 3 |
| 人数 | 1 | 2 | 1 | 1 | 2 | 1 |
| 点i | 点j | |||||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
| 1 | 0 | 2.05 | 3.4 | 2.51 | 0.99 | 1.27 | 2.95 | 1.72 | 1.04 | 1.97 | 1.27 | 2.28 | 0.69 | 0.61 | 1.42 | 2.14 | 2.72 | 2.86 |
| 2 | 2.05 | 0 | 1.36 | 0.47 | 1.14 | 0.9 | 0.9 | 0.71 | 1.15 | 0.78 | 1.11 | 0.23 | 1.73 | 1.44 | 0.67 | 0.48 | 0.75 | 0.83 |
| 3 | 3.4 | 1.36 | 0 | 0.89 | 2.45 | 2.18 | 0.52 | 1.81 | 2.43 | 1.67 | 2.41 | 1.15 | 3.08 | 2.8 | 1.98 | 1.34 | 0.92 | 0.55 |
| 4 | 2.51 | 0.47 | 0.89 | 0 | 1.57 | 1.3 | 0.49 | 0.98 | 1.56 | 0.92 | 1.57 | 0.31 | 2.2 | 1.9 | 1.1 | 0.54 | 0.56 | 0.36 |
| 5 | 0.99 | 1.14 | 2.45 | 1.57 | 0 | 0.28 | 2.04 | 0.73 | 0.1 | 0.99 | 0.9 | 1.38 | 1 | 0.42 | 0.48 | 1.16 | 1.87 | 1.91 |
| 6 | 1.27 | 0.9 | 2.18 | 1.3 | 0.28 | 0 | 1.77 | 0.46 | 0.26 | 0.72 | 0.94 | 1.13 | 1.21 | 0.69 | 0.25 | 0.87 | 1.64 | 1.63 |
| 7 | 2.95 | 0.9 | 0.52 | 0.49 | 2.04 | 1.77 | 0 | 1.47 | 2.03 | 1.39 | 1.91 | 0.67 | 2.58 | 2.34 | 1.56 | 1.02 | 0.42 | 0.33 |
| 8 | 1.72 | 0.71 | 1.81 | 0.98 | 0.73 | 0.46 | 1.47 | 0 | 0.67 | 0.27 | 1.27 | 0.91 | 1.65 | 1.15 | 0.44 | 0.47 | 1.44 | 1.27 |
| 9 | 1.04 | 1.15 | 2.43 | 1.56 | 0.1 | 0.26 | 2.03 | 0.67 | 0 | 0.92 | 0.99 | 1.39 | 1.1 | 0.51 | 0.49 | 1.12 | 1.89 | 1.89 |
| 10 | 1.97 | 0.78 | 1.67 | 0.92 | 0.99 | 0.72 | 1.39 | 0.27 | 0.92 | 0 | 1.52 | 0.93 | 1.92 | 1.41 | 0.7 | 0.38 | 1.43 | 1.15 |
| 11 | 1.27 | 1.11 | 2.41 | 1.57 | 0.9 | 0.94 | 1.91 | 1.27 | 0.99 | 1.52 | 0 | 1.28 | 0.7 | 0.8 | 0.83 | 1.45 | 1.58 | 1.93 |
| 12 | 2.28 | 0.23 | 1.15 | 0.31 | 1.38 | 1.13 | 0.67 | 0.91 | 1.39 | 0.93 | 1.28 | 0 | 1.93 | 1.67 | 0.9 | 0.58 | 0.52 | 0.65 |
| 13 | 0.69 | 1.73 | 3.08 | 2.2 | 1 | 1.21 | 2.58 | 1.65 | 1.1 | 1.92 | 0.7 | 1.93 | 0 | 0.61 | 1.24 | 1.97 | 2.28 | 2.57 |
| 14 | 0.61 | 1.44 | 2.8 | 1.9 | 0.42 | 0.69 | 2.34 | 1.15 | 0.51 | 1.41 | 0.8 | 1.67 | 0.61 | 0 | 0.82 | 1.55 | 2.12 | 2.25 |
| 15 | 1.42 | 0.67 | 1.98 | 1.1 | 0.48 | 0.25 | 1.56 | 0.44 | 0.49 | 0.7 | 0.83 | 0.9 | 1.24 | 0.82 | 0 | 0.74 | 1.4 | 1.44 |
| 16 | 2.14 | 0.48 | 1.34 | 0.54 | 1.16 | 0.87 | 1.02 | 0.47 | 1.12 | 0.38 | 1.45 | 0.58 | 1.97 | 1.55 | 0.74 | 0 | 1.06 | 0.8 |
| 17 | 2.72 | 0.75 | 0.92 | 0.56 | 1.87 | 1.64 | 0.42 | 1.44 | 1.89 | 1.43 | 1.58 | 0.52 | 2.28 | 2.12 | 1.4 | 1.06 | 0 | 0.66 |
| 18 | 2.86 | 0.83 | 0.55 | 0.36 | 1.91 | 1.63 | 0.33 | 1.27 | 1.89 | 1.15 | 1.93 | 0.65 | 2.57 | 2.25 | 1.44 | 0.8 | 0.66 | 0 |
3.2.5 第2阶段模型求解
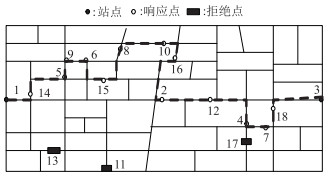
相关算法参数取值与第1阶段静态调度类似,求得最优解的目标函数值为:0.981 8。第2阶段行车调度的最优路径为:1-14-5-9-6-15-8-10-16-2-12-4-18-7-3,社区公交行驶路径如图 9所示。
|
| 图 9 第二阶段动态调度路径图 Fig. 9 Dynamic scheduling route (stage 2) |
| |
3.2.6 结果分析
将上述静态与动态需求信息放入当前固定线路式路社区公交运营中。考虑对象为同一班次车辆(6:30),不考虑下一班车的运营,即没赶上这一班车的乘客数会影响空载率。居民期望乘车时间区间的均值作为居民到达公交车站的时间,本班次的车辆在这个时间或这个时间之后到达该站点,乘客均可以上车;居民的平均步行速度取4.5 km/h, 步行到站时间视为乘客耗费的等待时间(即乘客到站时间减去步行时间为模型中的Pi,乘客到站时间加上步行时间为模型中的Qi);社区公交的单次运营里程为常数4.3 km,其他参数和评价指标的计算方法与模型中相同。求解得到的结果为1.575 4,而本研究中模型得到的结果为0.981 8,评价指标相对优化了37.68%,优化效果显著。
以往响应型公交行车调度模型的评价指标大多选取价格来衡量公交公司和乘客的成本,对乘客时间成本的差异性与不稳定性考虑不全,且未判断公交公司成本价格与乘客成本价格两者之间是否独立;本研究的模型在评价指标上也统筹考虑了乘客和公交公司利益,选取的是空载率、乘客不满意度和单次运营里程作为评价指标,并对评价指标归一化后整合成了单指标优化模型。在约束上,本研究的模型基于需求起讫站点的分析可使车辆不必每次经过所有固定站点,并通过划分需求等级来避免乘客产生二次等待;以往模型通常采用硬时间窗约束车辆到达需求点时间,而本研究中的模型采用软时间窗来约束车辆到达时间,并刻画乘客满意度,相对符合实际生活中乘客等车场景。
4 结论(1) 针对社区公交运营中乘客等待时间长、步行时间长、服务时段不合理等问题,提出了一种响应型社区公交及其行车调度方法,并基于路网建立了响应型社区公交行车调度优化模型,当设置的起讫站点密度足够大时,能相对实现居民“零步行”乘车。建立的两阶段调度优化模型是在给定发车时间的情况下,对需求响应和行驶路径进行优化,适用于乘客需求信息完备的情况,包括乘客起讫站点和可接受时间窗。
(2) 针对需求的波动,在常规社区公交上增加需求响应这一特点,在需求响应型公交的基础上考虑乘客出行的起讫站点,使得车辆不必每次都经过所有固定站点, 并划分需求等级避免乘客产生二次等待。综合考虑乘客和公交公司利益,以单次运营里程、乘客不满意度、空载率作为评价目标,分两阶段建立了静态、动态调度模型,对需求的考虑全面,在静态调度模型的基础上实现动态调度。将此响应型社区公交及其行车调度模型应用于文中案例,评价指标的优化效果达到了37.68%。模型中的站点构成包括了公交起始站、终点站和中间备选站点,这些站点可以根据需要灵活设置,对于循环式公交,需要将起始站、终点站设成同一个站点,因此本模型也适用于循环式公交行车调度。
(3) 行车调度模型中采用最大/最小单次运营里程对车辆到达终点站的时间进行约束,当决策者设置的最大运营里程值过大时,将减小车辆的空载率,但对先上车且目的地在终点站的乘客不利;当最大运营里程值设置的过小时,单次运营里程会得到减小,但不利于公交公司和未上车乘客。所以在实际应用中,决策者设置最大运营里程时要综合考虑上述影响。
(4) 本研究建立的模型中忽略了社区其他交通和道路设计参数对响应型社区公交车辆行驶的影响,未来的研究可针对此不足进行。
| [1] |
熊杰, 关伟, 黄爱玲. 社区公交接驳地铁路径优化研究[J]. 交通运输系统工程与信息, 2014, 14(1): 166-173. XIONG Jie, GUAN Wei, HUANG Ai-ling. Research on Optimal Routing of Community Shuttle Connect Rail Transit Line[J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(1): 166-173. |
| [2] |
杨信丰, 李引珍, 何瑞春. 基于服务水平的区域公交协调调度优化研究[J]. 系统工程, 2017, 35(6): 89-96. YANG Xin-feng, LI Yin-zhen, HE Rui-chun. Research on Regional Public Transit Coordinated Scheduling Optimization Based on Service Level[J]. Systems Engineering, 2017, 35(6): 89-96. |
| [3] |
杨信丰, 李引珍, 何瑞春. 多目标公交同步换乘协同调度优化及决策[J]. 系统工程, 2016, 34(3): 111-116. YANG Xin-feng, LI Yin-zhen, HE Rui-chun. A Multi-objective Transfer Synchronization Optimization and Decision of Public Transit[J]. Systems Engineering, 2016, 34(3): 111-116. |
| [4] |
CHANG S K, SCHONFELD P M. Multiple Period Optimization of Bus Transit Systems[J]. Transportation Research, Part B:Methodological, 1991, 25(6): 453-78. |
| [5] |
CEDER A. Stepwise Multi-criteria and Multi-strategy Design of Public Transit Shuttles[J]. Journal of Multi-Criteria Decision Analysis, 2009, 16(1/2): 21-38. |
| [6] |
VERMA A, DHINGRA S L. Feeder Bus Routes Generation within Integrated Mass Transit Planning Framework[J]. Journal of Transportation Engineering, 2005, 131(11): 822-834. |
| [7] |
SCHITTEKAT P, SEVAUX M, SORENSEN K. A Mathematical Formulation for a School Bus Routing Problem[C]//International Conference on Service Systems and Service Management. Troyes: IEEE, 2007: 1552-1557.
|
| [8] |
XIONG J, WEI G, SONG L, et al. Optimal Routing Design of a Community Shuttle Joint for Metro Sations[J]. Journal of Transportation Enbineering, 2013, 139(12): 1211-1223. |
| [9] |
张思林, 袁振洲, 曹志超. 基于出行成本和运营成本的接驳城市轨道交通社区公交站点布设研究[J]. 北京交通大学学报, 2016, 40(6): 57-63. ZHANG Si-lin, YUAN Zhen-zhou, CAO Zhi-chao. Study on Locating Sitting of Community Shuttle Feeder URT Based on the User and Operator Costs[J]. Journal of Beijing Jiaotong University, 2016, 40(6): 57-63. |
| [10] |
YU Y, MACHEMEHL R B, XIE C. Demand-responsive Transit Circulator Service Network Design[J]. Transportation Research Part E:Logistics and Transportation Review, 2015, 76: 160-175. |
| [11] |
孙杨, 宋瑞, 何世伟. 弹性需求下的接运公交网络设计[J]. 吉林大学学报:工学版, 2011, 41(2): 349-354. SUN Yang, SONG Rui, HE Shi-wei. Feeder Bus Network Design under Elastic Demand[J]. Journal of Jilin University; Engineering and Technology Edition, 2011, 41(2): 349-354. |
| [12] |
蒋蕊, 卓健. 定制公交竞争力分析与规划应对[J]. 规划师, 2018, 34(8): 113-119. JIANG Rui, ZHUO Jian. Competitiveness of Customized Bus System and Its Planning Strategy[J]. Planners, 2018, 34(8): 113-119. |
| [13] |
林叶倩, 李文权, 邱丰, 等. 可变线路式公交车辆调度优化模型[J]. 交通信息与安全, 2012, 30(5): 14-18, 33. LIN Ye-qian, LI Wen-quan, QIU Feng, et al. An Optimal Model for Flex-route Transit Scheduling Problem[J]. Journal of Transport Information and Safety, 2012, 30(5): 14-18, 33. |
| [14] |
孙博, 杨春风, 魏明, 等. 考虑乘客个性化出行的需求响应型接驳公交调度模型[J]. 昆明理工大学学报:自然科学版, 2019, 44(1): 122-126, 137. SUN Bo, YANG Chun-feng, WEI Ming, et al. A Demand-responsive Feeder Bus Scheduling Model for Personalized Travel[J]. Journal of Kunming University of Science and Technology:Natural Science Edition, 2019, 44(1): 122-126, 137. |
| [15] |
邵孜科, 张泉, 王树盛, 等. 可变线路公交车辆调度算法优化研究[J]. 交通信息与安全, 2018, 36(5): 83-89. SHAO Zi-ke, ZHANG Quan, WANG Shu-sheng, et al. Optimization Algorithms for Scheduling of Flex-route Buses[J]. Journal of Transport Information and Safety, 2018, 36(5): 83-89. |
| [16] |
AN K, LO H K. Two-phase Stochastic Program for Transit Network Design under Demand Uncertainty[J]. Transportation Research Part B, 2016, 84: 157-181. |
| [17] |
ALSHALALFAH B, SHALABY A. Feasibility of Flex-route as a Feeder Transit Service to Rail Stations in the Suburbs:Case Study in Toronto[J]. Journal of Urban Planning and Development, 2012, 138(1): 90-100. |
| [18] |
NOURBAKHSH S M, OUYANG Y. A Structured Flexible Transit System for Low Demand Areas[J]. Transportation Research Part B, 2012, 46(1): 204-216. |
| [19] |
QIU F, LI W, ZHANG J. A Dynamic Station Strategy to Improve the Performance of Flex-route Transit Services[J]. Transportation Research Part C, 2014, 48: 229-240. |
| [20] |
WEI T W, LIU B R, JINA W. Designing Robust Schedule Coordination Scheme for Transit Networks with Safety Control Margins[J]. Transportation Research Part B, 2016, 93: 495-519. |
| [21] |
邱丰, 李文权, 沈金星. 可变线路式公交的两阶段车辆调度模型[J]. 东南大学学报:自然科学版, 2014, 44(5): 1078-1084. QIU Feng, LI Wen-quan, SHEN Jin-xing. Two-stage Model for Flex-route Transit Scheduling[J]. Journal of Southeast University:Natural Science Edition, 2014, 44(5): 1078-1084. |
| [22] |
潘述亮, 卢小林, 邹难. 灵活型接驳公交路径优化及协同调度模型[J]. 吉林大学学报:工学版, 2016, 46(6): 1827-1835. PAN Shu-liang, LU Xiao-lin, ZOU Nan. Route Planning and Coordinated Scheduling Model for Flexible Feeder Transit Service[J]. Journal of Jilin University:Engineering and Technology Edition, 2016, 46(6): 1827-1835. |
| [23] |
雷永巍, 林培群, 姚凯斌. 互联网定制公交的网络调度模型及其求解算法[J]. 交通运输系统工程与信息, 2017, 17(1): 157-163. LEI Yong-wei, LIN Pei-qun, YAO Kai-bin. The Network Scheduling Model and Its Solution Algorithm of Internet Customized Shuttle Bus[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(1): 157-163. |
| [24] |
PERUGIA A, MOCCIA L, CORDEAU J F, et al. Designing a Home-to-work Bus Service in a Metropolitan Area[J]. Transportation Research Part B:Methodological, 2011, 45(10): 1710-1726. |
| [25] |
郑汉, 张星臣, 王志美. 混合车型需求响应公交服务定制问题研究[J]. 交通运输系统工程与信息, 2018, 18(2): 157-163. ZHENG Han, ZHANG Xing-chen, WANG Zhi-mei. Design of Demand-responsive Service by Mixed-type Vehicles[J]. Journal of Transportation Systems Engineering and Information Technology, 2018, 18(2): 157-163. |
| [26] |
柳伍生, 周向栋, 贺剑, 等. 基于多需求响应的定制公交绿色线网优化[J]. 公路交通科技, 2018, 35(3): 132-142. LIU Wu-sheng, ZHOU Xiang-dong, HE Jian, et al. Optimization of Green Customized Public Transport Network Based on Multiple Demand Response[J]. Journal of Highway and Transportation Research and Development, 2018, 35(3): 132-142. |
| [27] |
王健, 曹阳, 王运豪. 考虑出行时间窗的定制公交线路车辆调度方法[J]. 中国公路学报, 2018, 31(5): 143-150. WANG Jian, CAO Yang, WANG Yun-hao. Customized Bus Route Vehicle Schedule Method Considering Travel Time Windows[J]. China Journal of Highway and Transport, 2018, 31(5): 143-150. |
| [28] |
何民, 李沐轩, 税文兵, 等. 可靠性和舒适性对响应式定制公交线路设计的影响[J]. 公路交通科技, 2019, 36(5): 145-151. HE Min, LI Mu-xuan, SHUI Wen-bing, et al. Influence of Reliability and Comfort on Responsive Custom Bus Route Design[J]. Journal of Highway and Transportation Research and Development, 2019, 36(5): 145-151. |
| [29] |
PARK J, KIM B I. The School Bus Routing Problem:A Review[J]. European Journal of Operational Research, 2010, 202(2): 311-319. |
| [30] |
TSUBOUCHI K, YAMATO H, HIEKATA K. Innovative On-demand Bus System in Japan[J]. IET Intelligent Transport Systems, 2010, 4(4): 270-279. |
| [31] |
XU J P, YAN F, LI S. Vehicle Routing Optimization with Soft Time Windows in a Fuzzy Random Environment[J]. Transportation Research Part E:Logistics and Transportation Review, 2011, 47(6): 1075-1091. |
| [32] |
GUERRIERO F, SURACE R, LOSCRI V, et al. A Multi-objective Approach for Unmanned Aerial Vehicle Routing Problem with Soft Time Windows Constraints[J]. Applied Mathematical Modelling, 2014, 38(3): 839-852. |
 2020, Vol. 37
2020, Vol. 37
